Five principles for high-quality mathematics teaching: Combining normative, epistemological, empirical, and pragmatic perspectives for specifying the content of professional development
- 1German Center for Mathematics Teacher Education (DZLM Network), Network of 14 Universities, Berlin, Germany
- 2IPN–Leibniz Institute for Science and Mathematics Education, Berlin, Germany
- 3Mathematics Education, TU Dortmund University, Dortmund, Germany
- 4Mathematics Education, University of Education, Freiburg, Germany
- 5Primary Mathematics Education, Humboldt University of Berlin, Berlin, Germany
The academic search for principles of high-quality subject-matter teaching has been informed by different perspectives, in particular normative, epistemological, empirical, and pragmatic perspectives. While these perspectives have sometimes been treated as competing, we emphasize the need of their integration to identify sets of principles that can inform professional development programs for quality development. This paper starts from characterizing the four perspectives, and then shows how they are iteratively intertwined in providing a research base for specifying high-quality principles for teaching, in our case exemplified for the school subject mathematics. For this goal, we present the set of five principles that we have deemed as core principles for a new nationwide, ten-year professional development program in Germany: Conceptual Focus, Cognitive Demand, Student Focus and Adaptivity, Longitudinal Coherence, and Enhanced Communication. We will discuss these five principles against their backgrounds stemming from combing normative, epistemological, empirical, and pragmatic perspectives. This set of principles serves as an exemplary case to substantiate our general argumentation that contemporary educational research and professional development activities should not choose between perspectives but strive for combining them.
Introduction
How to specify principles for good teaching?
Is good teaching a myth? In this article, a team of subject-matter education researchers with a special focus on teachers’ professional development treats the provocative title question of this Frontiers series by means of three hypotheses, exemplified for the case of the school subject mathematics:
(1) There is no unique simple way to determine what good teaching is, as instructional quality must be characterized from different perspectives, in particular normative, epistemological, empirical, and pragmatic perspectives.
(2) A large body of generic education research and subject-specific mathematics education research converges on a set of principles that can intertwine these perspectives. The subject-specific substantiation of these principles is crucial to really make a difference in subject-matter classrooms and to reflect established normative perspectives on (in our case mathematical) literacy.
(3) Although various proofs of existence of “good” teaching according to these principles have already been provided, many teachers need further and ongoing support in implementing them in the classroom. Thus, professional development programs should not focus on single principles, but take the responsibility to also treat their complex interplay and to offer a coherent vision of quality.
But how to come to such a coherent vision on instructional quality? This paper is not a classical empirical research report nor a classical literature review paper. Instead, it intends to contribute to this meta-theoretical, practical and methodological question by (a) distinguishing and connecting four perspectives on instruction quality (presented in the next four subsections of the introduction section), (b) suggesting an approach for this research-based academic specification work to inform professional development programs (methods section), and (c) presenting a possible outcome of such specification work, namely five core principles for high-quality mathematics teaching and their justifications by combining the four perspectives in different ways (result section).
Normative perspectives on instructional quality—Contributing to Bildung for all
In the European Didaktik tradition (summarized by Westbury et al., 2000; Blum et al., 2019), the discourse on “good” teaching started from normative perspectives (Klafki, 1958): Good teaching has been conceptualized by its contribution to the overall normative educational aims, in particular to students’ Bildung, a major German theoretical construct that can only badly be translated to “education” or “literacy” (scientific literacy, mathematical literacy, cf. OECD, 2007). Comenius (1657) Didactica Magna started its considerations about good teaching by a long philosophical treatment on the nature of humans, from which the need of Bildung was derived.
In the tradition of Klafki (1958) and Heimann et al. (1979), lesson planning starts from the core question of what the content in view can contribute to students’ Bildung, and good teaching is thus evaluated by its realized contribution. Various conceptualizations of Bildung have been discussed in general education (see overview in Westbury et al., 2000) and in particular in mathematics education (summarized in Jablonka, 2003). For example, the OECD states operated PISA based on the following consensual characterization of mathematical literacy as “[…] an individual’s capacity to identify and understand the role that mathematics plays in the world, to make well-founded judgments and to use and engage with mathematics in ways that meet the needs of that individual’s life as a constructive, concerned and reflective citizen” (OECD, 2007, p. 304).
While such kind of educational aims normatively specify what students should learn, normative perspectives on instructional quality also prescribe who should learn and how the teaching should be realized.
Whom to address is a highly normative question, as exemplified by Comenius (1657) call for Bildung for all children, notwithstanding their gender or social status that has been technically realized by compulsory education for all students for 200 years. Since then, our normative standards about equal access have substantially been extended, not only by including also students with disabilities (who were explicitly excluded by Comenius), but in particular from the formal school enrollment to the factual access to the subject-matter learning it entails. Today, equity is one of the most important normative standards that school systems strive for Clements et al. (2013).
Also, how-questions have been discussed from various normative perspectives, e.g., Berliner (1987) distinguished good teaching (in a normative perspective) from effective teaching (in an empirical perspective) and described good teaching as endorsing a culture-specific set of norms about acceptable (e.g., ethical) teaching practices such as treating students with respect.
Empirical perspectives on instructional quality—Reaching measurable learning goals and process qualities
Whereas the sketched normative perspectives mainly stem from human science approaches to (general or subject-specific) education, empirical quantitative perspectives on instructional approaches were first developed in psychology and educational sciences. They characterize effective teaching as those approaches contributing best to predefined, measurable learning goals (Brophy, 2000; Klieme et al., 2009). Two major quantitative research designs contributed to effectiveness research, (a) interventionist research in controlled trials with pretest, posttest, control groups, in which particular instructional principles are systematically compared in a very focused way (e.g., by experimentally varying only one design principle), or (b) by non-interventionist classroom studies with pretests and posttests, capturing the instructional qualities by videos or questionnaires. In both research designs, the instructional quality (of particular design principles or more holistic quality dimensions hypothesized as being relevant) is measured by their effectiveness for revealing higher student learning gains than in the comparison groups (Brophy, 2000; Praetorius and Charalambous, 2018). For example, the German framework of three Basic Dimensions characterizes effective instruction by cognitive activation, learner support, and classroom management (Klieme et al., 2009; Praetorius et al., 2018), and the CLASS framework (Pianta and Hamre, 2009) by instructional support, emotional support, and classroom management. Many subject-specific studies (classroom video studies and controlled trials) have subsequently disentangled what these dimensions of cognitive demand and instructional support entail in detail (Seidel and Shavelson, 2007).
The hypotheses on potentially effective design principles or quality dimensions validated in quantitative research designs are often generated in other kinds of empirical perspectives, stemming mostly from qualitative research designs, (c) in interventionist design research studies investigating the teaching-learning processes initiated by specific instructional design principles (Artigue, 1992; Gravemeijer and Cobb, 2006), or (d) in non-interventionist classroom video studies of regular classroom interaction which serve to identify quality aspects such as the relevance of particular forms of communication (Walshaw and Anthony, 2008).
Although normative and empirical perspectives adopt different approaches, Berliner (1987) emphasized their interplay as each empirical quality study aiming at identifying effective teaching is based on normative decisions. Thus, the quantitative studies in the mentioned designs are based on a particular selection of learning goals, bringing in a content-specific normative perspective. For example, teaching practices toward fostering students’ procedural skills were deemed to be efficient to increase students’ respective proficiency. However, from a normative perspective, conceptual understanding is considered a more relevant learning goal, so this relativizes these empirical findings (Hiebert and Grouws, 2007). In order to substantiate such prioritizations depending on choices between specific learning goals, the normative perspective on Bildung is required to argue why the selected learning goals are relevant, and constitutes a need for additional empirical research directions.
Additionally, qualitative studies often refer to normative decisions on process qualities to be reached rather than only effectiveness, so good teaching in the sense of Berliner, 1987 involves, e.g., engaging all students in a deep and substantial classroom discussion promoting their agency (Schoenfeld, 2014).
Epistemological perspectives on instructional quality—Disentangling the core and the intertwinement of subject-matter contents
Within subject-matter education research disciplines such as mathematics education research, the search for principles of high-quality teaching was also informed by epistemological perspectives.
Epistemological perspectives are adopted for the subject-specific and topic-specific substantiation of normative overarching educational aims (Bildungsziel), in terms of creating opportunities for authentic experiences with the core of the subject matter (Bruner, 1966; Freudenthal, 1983; Winter, 1996). An epistemological analysis [e.g., by methods of didactical phenomenology (Freudenthal, 1983), or by conceptual fields (Vergnaud, 1996)] is needed to specify the educationally relevant core of subject-matter contents with respect to (a) the typical subject-specific, e.g., mathematical practices, (b) the big ideas across mathematical topics to reach an overarching long-term coherence in a spiral curriculum, (c) the meanings of mathematical concepts and operations, and (d) typical modeling examples as substantiated contributions of a particular mathematical topic to “well-founded judgments and to use […] mathematics […] as a constructive, concerned and reflective citizen” (OECD, 2007, p. 304).
A (slightly different) epistemological perspective is also required to disentangle learning trajectories within a teaching unit and long-term learning progressions across several teaching units, i.e., what content learning goal must be achieved before others can be successfully learned, also considering the connections between different knowledge elements. Although the structuring of learning trajectories and long-term learning progressions stems from epistemological analysis, it can then be empirically investigated and refined by design research studies (Gravemeijer and Cobb, 2006). That is, when conceptualizing and operationalizing instructional quality within empirical perspectives, the relevance of an epistemological perspective should not be neglected. This need is emphasized by Spreitzer et al. (2022) in their review with examples of quality captured by empirical instruments that are blind to subject-matter richness (does it target the core of the subject matter?) or subject-related accuracy. For instance, while the richness of the content (e.g., a conceptual focus of the lesson, cf. Kilpatrick et al., 2001) is sometimes included in the operationalization of the construct cognitive demand, various subject-specific quality instruments have been developed based on epistemological perspectives, accounting systematically also for subject-specific teaching quality (cf. Hill et al., 2008; Spreitzer et al., 2022).
Pragmatic perspectives on realizing instructional quality—A complex challenge in professional development
By combining normative, empirical, and epistemological perspectives, many principles for high-quality instruction can be identified, iteratively refined, and connected. The examples in the result section exemplarily show how the repeated and iterative intertwinement of these perspectives has supported the academic discipline of mathematics education research to develop a deep and comprehensive vision of high-quality mathematics instruction (Brophy, 2000; Kilpatrick et al., 2001).
However, as this vision of high-quality mathematics instruction is far from being realized in most classrooms, a major task of the academic discipline is also to enable mathematics teachers to realize this vision with increasing expertise (Schoenfeld, 2014). This requires program coherence, identified as critical feature for effective professional development (PD) programs: “the extent to which professional development activities are perceived by teachers to be a part of a coherent program, [whereas so far, PDs are] frequently criticized … that the activities are disconnected from one another” (Garet et al., 2001, p. 927).
For creating this PD program coherence on high-quality teaching, selecting a reasonable number of principles is only a first step; more essentially, they must be restructured according to the challenges they bear and sequenced from easy to complex for making them accessible for teachers (Ball et al., 2009; Schoenfeld, 2014). In this pragmatic perspective, it is crucial to clarify which part of the larger vision can be reached within teacher education, particularly professional development programs with limited time, by the majority of teachers and which are mainly reachable for specific (for instance expert) teachers. So, professional development programs for practicing teachers should seek for a coherent set of principles that can successfully guide so-called high-leverage practices, i.e., those practices that can be reached by (novice) teachers and are promising to make a difference in teaching for student achievement (Ball et al., 2009). An important part of this pragmatic work is to keep the number of principles small to avoid teacher overload.
Summary and question for the paper
Summing up, there are multiple approaches to determine what instructional quality entails, connected to different research traditions and providing overlapping yet not necessarily coherent results. Given the immense complexity of the current state of research on good (subject-specific) teaching, it is a challenge not to overload professional development programs with isolated aspects of instructional quality, but to specify a small set of principles which are coherently used and systematically intertwined to achieve instructional program coherence (Newmann et al., 2001; Schoenfeld, 2014). For this, we ask two main questions in this paper:
• How can PD program designers specify relevant core principles for a coherent PD program in research-based ways?
• What can we suggest as core principles for a PD program in K-12 mathematics education?
In the next methods section, we present our approach for research-based academic specification work to inform professional development programs. The results section will then show how the intertwinement of perspectives can help to do the specification work, yielding five core principles for high-quality mathematics teaching, and their justifications disentangled by combining the four perspectives in different ways.
Method for specifying core principles: Intertwining four perspectives on instructional quality
For our nationwide, ten-year professional development program QuaMath1 in Germany in the DZLM network, we took an eight-year process to successively specify core principles that can inform professional development programs for quality development. In this section we unfold our approach to specifying these core principles in research-based way. This process iteratively intertwined four different work packages:
Work Package 1—Systematizing findings from literature: We have based our work on existing research findings on instructional quality documented in the research literature. For this, we summarized many generic and subject-specific research papers and their multiple findings. We systematized the different approaches found in the literature into a meta-framework of four perspectives on instructional quality as presented in Sections “Normative perspectives on instructional quality—contributing to Bildung for all,” “Empirical perspectives on instructional quality—reaching measurable learning goals and process qualities,” “Epistemological perspectives on instructional quality—disentangling the core and the intertwinement of subject-matter contents,” “Pragmatic perspectives on realizing instructional quality—a complex challenge in professional development.” The structured summaries allowed us to specify large sets principles from normative, epistemological, and empirical perspectives, before restructuring them in Work Package 2 and 3 from the pragmatic perspective.
Work Package 2—Discussions with stakeholders for PD: In order to substantiate and reduce them to core principles that can guide high-leverage practices (Ball et al., 2009), we conducted iterative discussions with different stakeholders (PD facilitators, PD program heads in the districts and states, regional authorities and education ministries) in several cycles to find a minimal set of principles that can cover all relevant aspects (Knipping et al., 2017).
Work Package 3—Experimenting with teachers and facilitators: To find out whether the specified subsets of principles can fruitfully guide the decision-making of teachers and facilitators (Schoenfeld, 2014), we conducted several action research cycles in which we discussed complex classroom situations or PD situations with tentatively chosen set of principles: Does the set of tentatively chosen principles sufficiently support the teachers and facilitators to justify their decisions? What obstacles do they hinder to enact the principles, and how can the intertwinement with other principles help to overcome this obstacle? In several cycles, the final sets were successively composed (e.g., Prediger et al., 2022).
Work Package 4—Consulting with research experts: In several cycles, the tentative sets of principles were also discussed with groups of mathematics education researchers who helped us to create coherence with the research literature. The final set of five high-quality principles was discussed with 25 mathematics education and PD researchers from the DZLM research network, so that their structure, wording and definition was made compatible for all PD modules K-12 (from Kindergarten to Grade 12). Finally, the individual chapters were discussed several times by the author team and appropriate revisions were made in order to establish a shared understanding of the principles and their subject-specific background.
The Work Packages were iteratively intertwined in several cycles. Whereas Work Packages 1 and 4 assured the research-based nature of the process, Work-Packages 2 and 3 assured the practice-based nature and provide a suggestion for an approach also in other contexts to strengthen the pragmatic perspective in the specification work. In the following section we present the result of this iteratively intervening process.
Results: Five principles and their backgrounds—Intertwining different perspectives on quality
In this section, we will discuss five principles and their backgrounds stemming from combing normative, empirical, epistemological, and pragmatic perspectives in different ways. This set of principles serves as an exemplary case to substantiate our general argument that contemporary educational research and professional development activities should not choose between the perspectives but strive for combining them.
Principle of Conceptual Focus
The Principle of Conceptual Focus entails that high-quality instruction should aim at developing conceptual understanding and connect all mathematical procedures to the underlying mathematical concepts (Hiebert and Carpenter, 1992). This widely agreed principle prescribes a normative goal-setting practice. It is justified in normative perspectives as being derived from overarching conceptualizations of Bildung and treated also in other subjects, e.g., by Wagenschein’s (2000) claim that understanding is a human right, needed to educate citizens with a stable identity toward mathematics rather than mathematics anxiety. The Conceptual Focus contributes to the educational aim of intellectual autonomy of students as being able “to only accept new mathematical knowledge of which they can judge the validity themselves” (Gravemeijer, 2004, p. 109). Furthermore, the Principle of Conceptual Focus contributes to the aim of authentic encounters with mathematics (Freudenthal, 1983; Vergnaud, 1996; Winter, 1996), when in an epistemological perspective, the authentic core of mathematics refers to its semantics, not to the syntactical core of procedures and formalisms, alone (Vergnaud, 1996; Kilpatrick et al., 2001).
Of course, the Conceptual Focus is only one small part of the very rich and encompassing ideals of normative conceptualizations of Bildung. However, curriculum designers and mathematics teachers have difficulties substantiating and realizing general and holistic conceptualizations of Bildung as they encompass too many different aspects and risk staying as abstract as the definition of mathematical literacy cited above. Instead, curriculum designers and mathematics teachers often tend to reduce their educational ambitions to easier goals such as procedural skills and hope for later applications (as evidenced by Neubrand et al., 2013, in an analysis of tasks used by teachers).
So, from a pragmatic perspective, the all-encompassing conceptualizations of Bildung must be elementarized to those educational goals on which teachers can productively work. As a Conceptual Focus is seen as a key step to improve learning opportunities substantially, conceptual goal-setting is considered one of the high-leverage practices (Ball et al., 2009; Cobb and Jackson, 2021) on which teacher professional development should concentrate.
For a while, Conceptual Focus and Procedural Focus were discussed as dichotomic in practical discourses. However, increasing empirical evidence exists that also higher procedural learning goals can only be reached when students acquire conceptual understanding of basic concepts (Rittle-Johnson and Schneider, 2015; Prediger et al., 2022), so nowadays, reaching conceptual learning goals and procedural learning goals must be considered as interdepending learning goals (see Figure 1 from Kilpatrick et al., 2001). In this way, the empirical perspective revealed an additional argument: the Conceptual Focus is not only a normative decision, but proved to be a prerequisite for acquiring other goals in long-term learning progressions.
Many empirical design research studies and controlled trials provided evidence of existence that conceptual learning goals can be reached and provide guidance for its realization with the following sub-principles:
• Using and connecting everyday contexts and multiple representations to study mathematical structures first in meaningful situations and then support the meaning construction for new mathematical concepts and operations (Freudenthal, 1983; Hiebert and Carpenter, 1992; Wagenschein, 2000).
• Sequencing learning goals in learning trajectories always by starting with meaning construction before deriving procedures (Freudenthal, 1983; Van den Heuvel-Panhuizen, 2003).
• Connecting the procedures back to the underlying meanings (Hiebert and Carpenter, 1992; Kilpatrick et al., 2001).
From a pragmatic perspective focusing teachers’ challenges and support needs for realizing the principle, adopting a Conceptual Focus has turned out to be more challenging for many teachers than initially assumed (Neubrand et al., 2013; Schoenfeld, 2014; Cobb and Jackson, 2021). Although conceptual understanding is a key goal among the higher educational aims of Bildung, it is still not in the core of many teachers’ goal-setting practices (Cobb and Jackson, 2021; Prediger et al., 2022). Typical obstacles for teachers are the following:
• Many teachers lack instructional approaches and pedagogical tools to prepare and conduct teaching in ways that students can really develop conceptual understanding (these can be supported by the Principles of Cognitive Demand and Enhanced Communications, see Section “Principle of cognitive demand” and “Principle of enhanced communication” as well as Student Focus in the sense of starting from students’ initial ideas, see Section “Principle of student focus and adaptivity”).
• A current misunderstanding of Adaptivity suggests a simple differentiation of learning goals (Boaler, 2002; Cobb and Jackson, 2021): conceptual understanding for higher-achieving students and merely procedural skills for lower-achieving students (this misunderstanding must be overcome by alternative conceptualizations of Adaptivity, see Section “Principle of student focus and adaptivity”).
• In short-term instructional strategies, many teachers evaluate their teaching success not by sustainable learning gains, but simply by the number of tasks students have completed (Watson and Geest, 2005; Prediger et al., 2022). Hence, a Conceptual Focus must be connected to Longitudinal Coherence and sustainable learning (see Section “Principle of enhanced communication”).
The analysis of typical obstacles reveals why the first principle must be connected to the other four principles.
Principle of Cognitive Demand
The Principle of Cognitive Demand (Henningsen and Stein, 1997) entails that all students should be deeply engaged in higher-order thinking processes (Anderson et al., 2001) focusing the relevant knowledge elements in view (Renkl, 2015).
In Germany, the principle is often termed cognitive activation (Klieme et al., 2009; Praetorius et al., 2018) or focused cognitive activation (Renkl, 2015), and described to require subject-specific substantiation (Praetorius and Charalambous, 2018; Spreitzer et al., 2022). In mathematics education, Cognitive Demand can be realized by meaningful learning environments that allow all students to participate in rich mathematical practices and develop own mathematical ideas (Henningsen and Stein, 1997; Leuders and Holzäpfel, 2011). One often described way includes engaging students in productive struggle (Doyle and Carter, 1984; Hiebert and Grouws, 2007).
Different sources of justification interact also for this principle: From an empirical perspective, cognitive psychology provided empirical evidence that higher-order thinking processes are required for sustainable learning, in particular for developing conceptual understanding (Seidel and Shavelson, 2007), this might explain why Cognitive Demand and Conceptual Focus are often merged into one dimension in generic quality studies (as in Klieme et al., 2009; Praetorius et al., 2018), even if considered separately in mathematics education research (Hiebert and Grouws, 2007). From an epistemological perspective, lower-order thinking processes do not sufficiently reflect the epistemological core of mathematics as authentic mathematics is typically characterized by higher-order mathematical practices such as modeling, arguing, problem solving, generalizing, systematizing, etc.).
In spite of these epistemological and empirical justifications for the Principle of Cognitive Demand, many classrooms have been shown to be shaped by low expectation teaching in which students are only engaged in superficial lower-order processes such as rote learning of facts, reproducing procedural routines, guessing (Henningsen and Stein, 1997; Neubrand et al., 2013). Hence, from a pragmatic perspective, improving Cognitive Demand seems to be a critical starting point for changing the quality of teaching (Schoenfeld, 2014) as it is the prerequisite for realizing a Conceptual Focus (Seidel and Shavelson, 2007).
Many generic quantitative video studies provided empirical evidence that Cognitive Demand forms indeed a quality dimension with measurable impacts on students’ learning gains (Pianta and Hamre, 2009; Kunter et al., 2013; Praetorius et al., 2018), but they adopted a wide definition of the principle and subsumed also aspects that mathematics education researchers would disentangle into neighbor principles (Hiebert and Grouws, 2007; Hill et al., 2008):
• Posing mathematical tasks that elicit higher-order thinking processes by design elements of cognitive dissonance, productive irritation or questions to the learners (in the core of the principle).
• Providing learning opportunities for rich mathematical practices such as arguing, generalizing, systematizing (in the core of the principle).
• Engaging all students in rich mathematical discussions (separated here from Cognitive Demand into the own principle of Enhanced Communication).
• Focusing also conceptual learning goals and connecting procedures to conceptual underpinnings (separated here from the first as Conceptual Focus).
As the effectiveness of posing cognitive demand in this comprehensive sense has empirically been shown (Pianta and Hamre, 2009; Kunter et al., 2013; Praetorius et al., 2018), various studies in cognitive psychology (Renkl, 2015) and mathematics education research have unpacked the principle of Cognitive Demands in more detail (Leuders and Holzäpfel, 2011).
With respect to the pragmatic perspective, empirical studies provided insights into typical challenges teachers meet when trying to realize Cognitive Demand so that students really engage in demanding cognitive processes:
• According to several studies, cognitively demanding tasks are only rarely used by German teachers (Neubrand et al., 2013), and rarely occur in German textbooks (Lenz et al., 2019). With narrow routine tasks, it is almost impossible to conduct cognitively demanding mathematics teaching unless you have high teaching skills that make it possible to spontaneously work with students’ errors or alternative ideas and develop them further in such a way that challenging demands can be triggered.
• Cognitive Demand can be misunderstood as engaging students in arbitrary (hands-on) activities which are not necessarily cognitive activations, or cognitively demanding, and not focused to the key knowledge elements (Renkl, 2015), so it should be combined with a Conceptual Focus (see Section “Principle of conceptual focus”).
• In spite of the limited availability, many teachers have started to work with cognitively demanding tasks to engage all students in higher-order thinking processes, but once the task is launched and first struggles occur, the cognitive demand is narrowed down in teachers’ attempts to support students’ task completion, so that the students’ cognitive processes are much less rich than the task intended (Henningsen and Stein, 1997). Besides launching cognitively demanding tasks, teachers thereby also need practices to maintain the Cognitive Demand throughout the discussions (i.e., by Enhanced Communication, see Section “Principle of enhanced communication”).
• Maintaining cognitive demand also requires to provide sufficient student support to meet all students’ demands (so Student Focus is needed on all levels to engage all students in cognitively demanding activities, see Section “Principle of student focus and adaptivity”).
• A current misunderstanding of Adaptivity suggests to pose cognitive demand only for higher-achieving students (Boaler, 2002; Wilhelm et al., 2017; Cobb and Jackson, 2021), this misunderstanding must be overcome by alternative conceptualizations of Adaptivity, see Section “Principle of student focus and adaptivity”).
This analysis of the principle from different perspectives reveals that the subject-specific substantiation of the generic principle is needed in order to focus on a targeted quality dimension without subsuming very different aspects. The analysis of typical teacher challenges reveals a direction on what to focus in professional development: Selecting or adapting tasks with high cognitive demands to engage students in rich mathematical practices, support strategies to maintain the cognitive demands in the further rollout. The second aspect indicates why the principle must be connected to other principles.
Principle of Student Focus and Adaptivity
Quantitative empirical perspectives on generic instructional quality have identified three quality dimensions, classroom management, cognitive activation (which comprises Cognitive Demand and Conceptual Focus), and student support (Kunter et al., 2013; Praetorius et al., 2018). Similarly, the CLASS framework identified the three dimensions instructional support (including Cognitive Demand and Conceptual Focus), classroom management and emotional support (Pianta and Hamre, 2009). Whereas emotional support focuses exclusively on generic social-emotional aspects aside the subject-matter learning (e.g., an appreciative student-teacher relationship and a positive classroom climate), the basic dimension of student support refers also to the ways teachers support students’ subject-matter learning, e.g., in the practices for delaying for errors. It is this second area that in the core of the subject-specific principle of Student Focus and Adaptivity.
The principle of Student Focus must be understood much more deeply from an epistemological perspective: Freudenthal conceptualized “mathematical concepts, structures, and ideas [as serving…] to organize phenomena from the concrete world as well as from mathematics” (1983, pp. 28). In his influential instructional approach of Realistic Mathematics Education (RME), Freudenthal (1983) thereby normatively claimed that students should gain authentic experiences with mathematics by re-inventing mathematical concepts through mathematizing from realistic imaginable contexts, that means through “organizing and structuring activity during which acquired knowledge and abilities are called upon in order to discover still unknown regularities, connections, structures” (Treffers, 1987, p. 247). In order to support students’ mathematizing pathways, teachers need a Student Focus, which means teachers should carefully monitor students’ ways of thinking and use them for planning, conducting, and evaluating the teaching/learning processes so that collectively, they can successively leverage students’ thinking into formal mathematical knowledge (Treffers, 1993, p. 105). While building upon students’ knowledge in processes of progressive mathematizing, students should be engaged as actively as possible, with the teachers’ task to mediate between students and mathematics by connecting students’ ideas with the formal mathematics (Dewey, 1904; Selter, 1998).
Whereas the first component of the principle, Student Focus, conceptualizes students as epistemic subjects (with prototypical learning pathways), its second component Adaptivity emphasizes the individual subjects.
Adaptivity is defined as “teachers’ adjustments to students’ individual developmental states … and … to students’ individual differences and learning needs” (Hardy et al., 2019, p. 169/171; Corno, 2008). From a normative perspective, Adaptivity is required to meet the normative standard of achieving equity in the school systems by doing justice to the diversity of students’ abilities, backgrounds, needs, and learning stages (Clements et al., 2013). Adapting teaching to students’ differences can be realized in teachers’ lesson planning by differentiating tasks, activity structures, and support means so that they adjust to the learners’ learning stages and individual needs (macro-adaptivity) and within lessons in the teacher-student interaction by teachers’ micro-adaptive questions and prompts (micro-adaptivity) (Corno, 2008; Bardy et al., 2021).
Both components are intertwined, because the epistemological ambitions of Student Focus can only be realized for all students when the learning opportunities are adaptive to students’ individual learning stages. Vice versa, Adaptivity falls short in terms of cognitive demand if only realized by instructional adaptations of surroundings (e.g., adapting the language level of the worksheet) without curricular adaptations (adapting to the students’ state of content learning, see Janney and Snell, 2006).
Both components, Student Focus and Adaptivity, require teachers’ continuous noticing (Jacobs et al., 2010; Mason, 2021) and formative assessments (Wiliam, 2010), i.e., by dealing intensively with students’ written or oral productions to continuously monitor students’ learning stages, their assets and backgrounds for their possible difficulties, and grounding instructional decisions on this basis: assessment for learning instead of assessment of learning (Carpenter et al., 1999). This requires teachers’ diagnostic competence (Hoth et al., 2016), i.e., their abilities to notice students’ mathematical thinking with respect to strategies and understandings, based on which adaptive instructional decisions can be made (Jacobs et al., 2010, p. 172f.). Formative assessments for Student Focus and Adaptivity do not aim at judgment accuracy (aiming mainly at ranking students, e.g., Hosoya et al., 2021), but on diagnostic depth, with an asset-oriented rather than deficit-oriented attitude (Carpenter et al., 1999) in which errors are considered integral components of a constructive learning process (Manalo and Kapur, 2018).
Empirical evidence for the functioning of Student Focus and Adaptivity have been provided in different empirical perspectives: Design research studies revealed that student-focused teaching units can indeed leverage students’ understanding (Selter, 1998; Gravemeijer, 2004), and quantitative evidence for their effectiveness was provided in controlled trials (e.g., Carpenter et al., 1999; Prediger et al., 2022). Numerous studies on formative assessment also revealed the relevance of focusing student thinking (Hattie, 2009; Wiliam, 2010), so formative assessment is considered one of the most effective frameworks for promoting school-based learning (Schütze et al., 2018). Beyond formative assessment, making constructive use of students’ contributions has been identified as quality dimension with measurable effect on students’ learning gains (Hattie, 2009).
Also from a pragmatic perspective, engaging teachers in working with students’ thinking and monitoring students’ progress has been identified as high-leverage practices that can make a difference in instructional quality (Carpenter et al., 1999; Jacobs et al., 2010), so this is a promising starting point. However, studies also unpacked typical challenges teachers have in realizing Student Focus and Adaptivity:
• Adaptivity is misinterpreted by many teachers as call for completely individualized pedagogies, i.e., students’ isolated independent work on work packages without communicating with their classmates or the teacher about the learning content themselves. This results in isolation of learning processes (Dumont, 2019) and contradicts the principle of Enhanced Communication (see Section “Principle of enhanced communication”). Completely individualized pedagogies have been shown to coincide with procedural goal-setting practices, hence to contradict a Conceptual Focus (Krähenmann et al., 2019).
• Student Focus and Adaptivity for low-achieving or socially disadvantaged students is often also misinterpreted as reducing the Conceptual Focus and Cognitive Demands: These students are then offered poor learning opportunities with low cognitive demands and procedural focus (Wilhelm et al., 2017; Prediger et al., 2022).
• Many teachers tend to enact formative assessments without an in-depth focus (more and more often also technology-based), with only a priority on superficial or generic aspects such as attention and motivation instead of monitoring the progress in the mathematical content (Hoth et al., 2016). Other studies showed that the quality of teachers’ informal diagnostic judgments depends on their (pedagogical) content knowledge (Philipp, 2018) and their (missing) Conceptual Focus (Prediger et al., 2022). So, the Conceptual Focus is crucial to be intertwined with the Student Focus.
• (Prospective and practicing) teachers tend to perform better in perceiving and interpreting student thinking than in responding and supporting learners (Jacobs et al., 2010; Brandt, 2022). In particular, formative assessment and the developed support are often not appropriately aligned (Schulz, 2014). Instead, Adaptivity is realized by instructional adaptations to increase the access to the task by adapting text complexity or number domains, but not by curricular adaptations of the tasks that adapt the curricular content to the stage of students’ progress (Janney and Snell, 2006). Again, Student Focus and Adaptivity needs to be connected to the Conceptual Focus and mathematically deep formative assessments.
• One identified background for the missing alignment of many teachers’ formative assessments and adaptation decisions is their short-term orientation: The success of an instructional decision is often evaluated solely by its contribution to make students complete a task, but not by its contribution to progress on a long-term learning trajectory (Watson and Geest, 2005; Prediger et al., 2022). It is our hypothesis that teachers need to develop a long-term orientation by connecting the Student Focus and Adaptivity to Longitudinal Coherence (see Section “Principle of longitudinal coherence”).
Principle of Longitudinal Coherence
The Principle of Longitudinal Coherence entails that subject-matter content should be organized in long-term learning trajectories along a coherent spiral curriculum. This involves systematically connecting new content to prior knowledge, thus teaching in a way that fosters students’ longitudinal learning progress (Bruner, 1966). Bruner justified this principle by the normative assumption that “any subject can be taught effectively in some intellectually honest form to any child at any stage of development” (1966, p. 33), and called for introducing ideas in intuitive ways, which are later revisited and taken up in more formal and elaborated ways.
Many countries have organized their STEM syllabus and curricula according to Bruner’s spiral ideas. However, spiraling of content in curricula can be realized quite differently as Schmidt et al. (2005) could show: Whereas many U.S. state curricula list the same mathematical topics in every year from K-8, the six highest-achieving TIMSS countries organize their curricula in mathematics and science by introducing new topics gradually, and then reorganize them in later years into more abstract contents. This comparison of curricula reveals that the principle of Longitudinal Coherence needs substantial underpinning and specific decisions regarding what topic is when introduced and revisited and how connected to earlier/later stages.
Bruner (1966) developed his spiral curriculum ideas with respect to well-structured subjects such as mathematics, physics, and history and the way how concepts and knowledge in these domains are organized, in an epistemological perspective on how concepts are structured along so-called big ideas, so that learning goals on different levels can be connected to each other. Since then, mathematics educators tried to make big ideas explicit in their epistemological analysis, emphasizing not only the longitudinal potential of big ideas, but also their potential to connect mathematical contents across domains, times and with everyday thinking (Schweiger, 1984). For example, Wittmann (1999) identified seven big ideas in the epistemological analysis by which a longitudinal coherence of the geometry curriculum can be created, e.g., geometrical figures and their construction, operating with figures, coordinates.
Besides the spiral approach to connect contents by big ideas, a second kind of longitudinal connections gained increasing importance in epistemological perspectives, namely long-term learning trajectories for subject-matter concepts (Fortus and Krajcik, 2012). For example, Kirsch (1976) elaborated a long-term learning trajectory across several years for exponential growth and Van den Heuvel-Panhuizen (2003) for part-whole-relationships in percentages. Even stronger than the big ideas, well-specified learning trajectories can inform the design of teaching materials by locating to connect new content to prior knowledge (Fortus and Krajcik, 2012; Siemon et al., 2017) and by promoting graphical representations (such as the number line, dot array or fraction bars) that can strengthen the longitudinal coherence between various topics and concepts (Wittmann, 1998).
In empirical perspectives, Longitudinal Coherence does rarely appear in classical video studies on instructional quality since the longitudinal connections drawn can hardly be observed in the moment (except for teachers’ in-the-moment connections to students’ prior knowledge, cf. Pianta and Hamre, 2009). However, rich empirical studies have been conducted to specify and validate long-term learning trajectories, showing that some knowledge elements must be acquired before the next ones so that they should be focused in formative assessments and connecting activities (Siemon et al., 2017). Additionally, empirical evidence was provided that instruction that regularly revises and connects prior knowledge can result in more sustainable learning (Dhunny and Angateeah, 2019).
Furthermore, empirical perspectives on teachers’ decision making repeatedly identified a long-term orientation as crucial for good teaching: In her seminal work, Ma (1999) identified longitudinal coherence as one of four relevant properties of the (elementary) mathematics classroom, the others being connectedness, multiple perspectives, and basic ideas. With respect to teachers’ knowledge, Ma characterized longitudinal coherence as “the awareness of the span of topics across grades” (1999, p. xxiv). In contrast, the analysis of teachers’ decision-making in other studies repeatedly revealed that many teachers take decisions in short-term orientations optimizing the teaching so that all students can complete the task, yet not long-term learning progress (“short-termism,” Watson and Geest, 2005, p. 228; Prediger et al., 2022). These studies revealed that with respect to pragmatic perspectives searching for reachable high-leverage practices, teachers’ shift from short-term to long-term orientations thereby seems to be essential.
Although the principle is widely esteemed of high value, it is not easy to be realized in the classroom, and has potential overlap with the other four principles. Typical teacher challenges when realizing the principle and supports by other principles are the following ones:
• In a false understanding of Student Focus and Adaptivity, many teachers tend to adopt a short-term orientation in that they evaluate the success of their teaching according to the number of students who were able to complete the tasks. But the individual evaluation category of task completion often contradicts decisions that contribute to sustainable learning progress (Watson and Geest, 2005, p. 228). For example, instructional adaptation practices are often short-term oriented in that they compensate students’ difficulties by massive support (increasing students’ task completion rates), but cannot enhance students long-term learning progress unless also curricular adaptations guarantee that essential knowledge elements are remediated. Orienting to Longitudinal Coherence might thereby support the teachers’ development also with respect to Adaptivity (Prediger et al., 2022).
• Given the strong intertwinement of learning trajectories for procedures and concepts (see Figure 1; Kilpatrick et al., 2001), a Conceptual Focus for all students can only be achieved with Longitudinal Coherence.
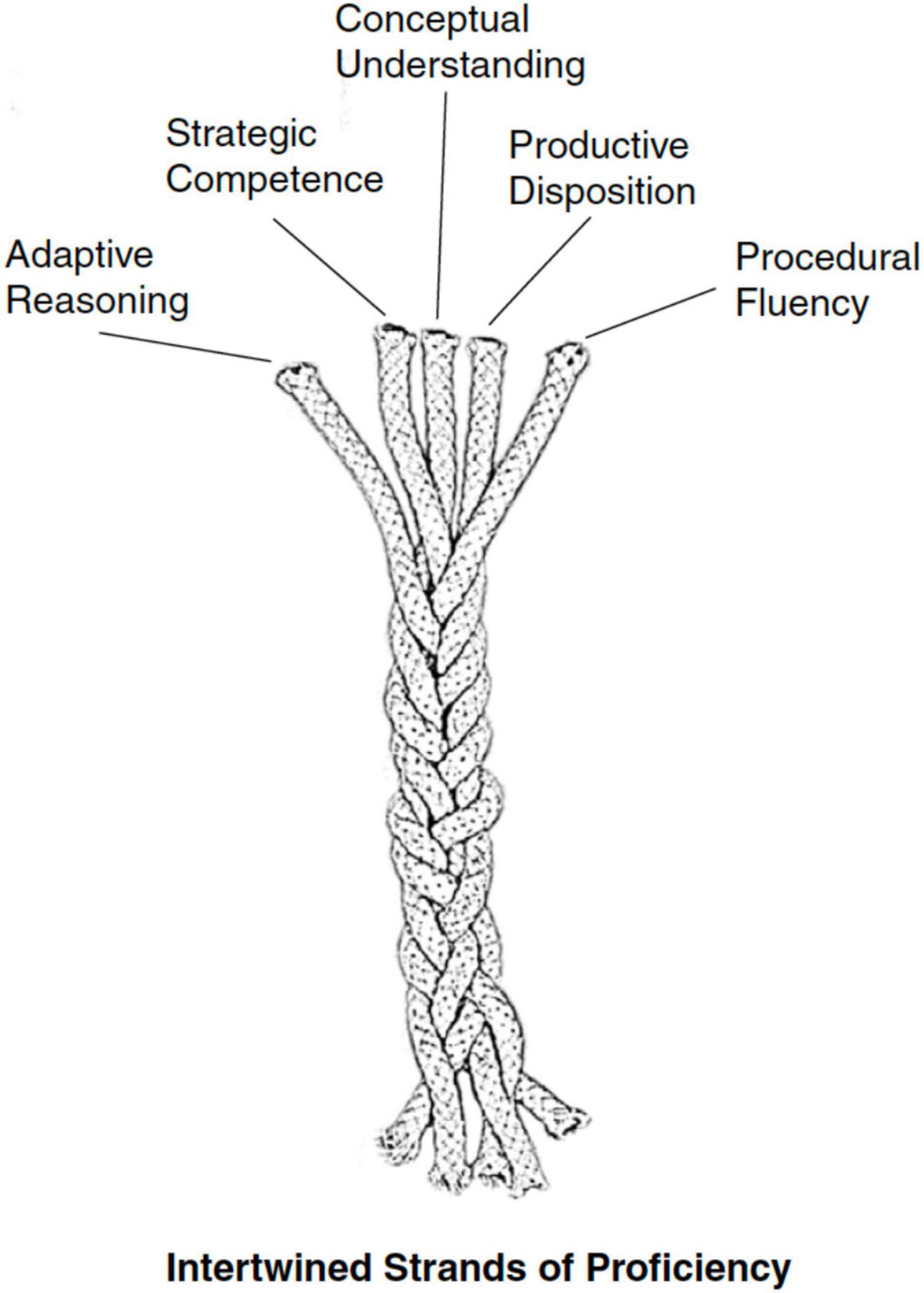
Figure 1. Intertwinement of different learning goals and the particular role of conceptual understanding (Kilpatrick et al., 2001, p. 5).
• Longitudinal Coherence requires teachers’ profound and holistic understanding of mathematics, and being sensitive to how learning goals depend on prior knowledge, and what changes are involved on the conceptual level when concepts are revisited. Such a deep understanding of the content is essential for being able to deal with basic ideas as being fundamental for students’ later and longitudinal learning (Ma, 1999). This includes the identification of those basic concepts which are essential for students’ long-term learning progress (Confrey et al., 2017; Prediger et al., 2022).
Principle of Enhanced Communication
In various empirical perspectives, multiple qualitative studies (Walshaw and Anthony, 2008; Webb et al., 2019) and (more rare) quantitative studies (e.g., Brophy, 2000; Ing et al., 2015; Howe et al., 2019) have repeatedly shown that engaging students in mathematical communication in small group or whole-class discussions is crucial for their mathematical learning progress. Whereas facts and procedural skills can be learnt without communication, acquiring conceptual understanding and higher-order mathematical practices (such as reasoning, modeling, problem-problem) requires rich mathematical discourses. These discourses reveal an important learning medium in mathematics classrooms (Lampert and Cobb, 2003) as the participation in articulating ideas, explanations and concepts allow students to revise their own thinking and to recognize misconceptions (Götze, 2007; Ing et al., 2015) and to follow “reflective shifts in discourse” (Sfard et al., 1998, p. 47). In this way, communication is crucial for maintaining Cognitive Demands and realizing a Conceptual Focus.
In many qualitative studies, this connection between mathematics learning and communication is not an empirical finding, but the adopted epistemological perspective, i.e., their theoretical starting point: Interactionist or participationist theoretical approaches epistemologically conceptualize learning as an increasing participation in mathematical discourses (Krummheuer, 2011), some combine cognition and communication inseparably into commognition (Sfard, 2008). These empirical studies do not aim at further evidence that communication is necessary for learning, but to provide deeper insides into how the mathematical practices and mathematical concepts emerge in the interaction and how teachers can promote these discourses, e.g., by interactively establishing socio-mathematical norms and practices (see research overviews by Lampert and Cobb, 2003; Walshaw and Anthony, 2008).
However, further empirical investigations revealed that communicative processes in mathematics classrooms do not automatically contribute to the development of conceptual understanding, but students have to learn how to communicate (for an overview see Rojas-Drummond and Mercer, 2003). In particular, classes are no homogenous collectives, and some students can participate in rich mathematical discourses more easily than others due to diverse competences to enact rich discourse practices such as explaining meanings and arguing (Ing et al., 2015), which raises normative perspectives on equity in communication (DIME, 2007). Therefore, instead of only initiating any communication, good teaching involves Enhanced Communication.
The principle of Enhanced Communication takes into account both aspects, (a) communicate to learn and (b) learn to communicate (Lampert and Cobb, 2003; Rojas-Drummond and Mercer, 2003): (a) Rich mathematical discourses need to be initiated in which students can develop their mathematical concepts and mathematical practices, and (b) students should be systematically enabled to participate in these discourses by promoting their agency, discourse practices and language (DIME, 2007; Moschkovich, 2015; Erath et al., 2021).
For enhancing students’ agency and discourse practices, “[t]eachers are expected to work to enable students to justify their conclusions, communicate conclusions to others, listen to arguments of others, decide whether those arguments make sense, and ask useful questions to clarify or improve the arguments” (Ing et al., 2015, p. 342). This can be realized by establishing rich socio-mathematical norms and making the expectations of discourse practices explicit (Moschkovich, 2015). For small group communication, this also involves scaffolding the activity structures with scripted communication (Rojas-Drummond and Mercer, 2003; Götze, 2007), and settings of well-designed communicative dependency (Webb et al., 2014).
For enhancing students’ ability to engage in the most challenging discourse practices of arguing, describing general pattern and explaining meanings (Moschkovich, 2015), language-responsive instructional approaches have been developed that provide targeted learning opportunities for the academic language needed for the articulation of these discourse practices (summarized in Erath et al., 2021). These approaches combine micro-scaffolding (i.e., teacher moves supporting students’ contributions in the interaction), with the subprinciple of macro-scaffolding in which the conceptual learning trajectories throughout teaching units are enhanced by systematic language learning opportunities on each stage (ibid.). Empirical evidence exists that micro- and macro-scaffolding can contribute to learn to communicate, but also to enhance students’ conceptual understanding, hence to communicate to learn (ibid.).
In spite of this rich state of research, the realization of Enhanced Communication in mathematics classrooms is not as widespread as desired. In many classrooms, teachers continue to have the major space to talk while students’ contributions are often constrained to small contributions (Howe et al., 2019). From a pragmatic perspective, it is thereby important to consider steps that can convince and enable teachers to develop their instructional practices with respect to communication:
• Teachers should be convinced that completely individualized pedagogies without any communication (Dumont, 2019) or whole-class sessions with only marginal student contributions can hardly contribute to realizing a Conceptual Focus.
• Many teachers are ready to launch tasks with high Cognitive Demands and have a comparison of solution strategies afterward. However, maintaining the Cognitive Demands in the discussion requires an Enhanced Communication with good facilitation practices. Stein et al. (2008) provided evidence that teachers can acquire such kind of these practices.
• A misunderstood Student Focus and Adaptivity leads to differential learning milieus: Rich communication is facilitated more often in classes with many students from privileged social backgrounds, whereas students from socially underprivileged backgrounds are kept in classes without rich discourses (Boaler, 2002; DIME, 2007) and simplified language demands. Rather than reducing the demands for students with limited language, Enhanced Communication with the subprinciples of language-responsive instruction aim at amplifying students’ language (Moschkovich, 2015; Erath et al., 2021) so that all students can gain equitable access to rich mathematical discourses (DIME, 2007). This requires teachers’ long-term orientation on language learning trajectories, and thereby a Longitudinal Coherence in language and communication as a learning content for which classrooms provide learning opportunities.
Discussion
Looking back
By combining different perspectives, we specified a set of five core principles for instructional quality. We used this example of a specification process for a mathematics professional development program in order to strengthen three arguments:
(1) Good teaching cannot be determined by only normative or only epistemological or only empirical perspectives. In each of the five principles, these three perspectives have implicitly or explicitly influenced each other (in slightly different ways for each principle) and should thereby not be discussed as controversial, but as mutually supportive in a successively emerging state of research.
(2) Although our set of five principles can successfully be related to the state of empirical research in generic disciplines (mainly general education sciences and instructional psychology), it is always the epistemological perspective and the subject-specific normative perspective that contributes substantially to deepening the subject-specific substantiation of the principles.
(3) It is the fourth perspective, the pragmatic perspective on what teacher can do and struggle to do, that enforces to strive not for separating the principles for analytical clarity (in the extreme case, for quantitative factorial independence), but to investigate and emphasize the multiple connections between the principles that lead us to hypothesize that for professional development, the principles must be treated together and in their multiple intertwinements to achieve a comprehensive and connected vision of good teaching.
Even if the particular set of five principles might appear reductionist (Couldn’t there have been much more?), contingent (Wouldn’t there have been also other candidates?) and subject-specific (Don’t they apply only for mathematics?), we hope that these three arguments are of interest also for many other subjects and can enhance the general discussion. In our view, good teaching is not a myth, but much more complex to determine than some researchers with a very particular focus might suggest.
However, although the research discourses seem to converge toward a certain consensus of what good teaching might entail, good teaching is still a non-realized myth because many teachers have not yet found sufficient learning opportunities and targeted support to develop their teaching into the intended directions. So, professional development is crucial (Ball et al., 2009). Our method to achieve professional development program coherence (Newmann et al., 2001) was presented in this paper.
Outlook
In the current preparation phase of our ten-year large-scale professional development program QuaMath, we share with the stakeholders (of our Federal States professional development systems) the vision that the specified five core principles and their mutual interplays can guide teachers and facilitators in their reflections and developments of their teaching practices. From 2023 on, we qualify several hundreds of facilitators who will then work with several thousand schools in developing their mathematics teaching.
In the following ten years, we will have the research opportunities to support this vision empirically and investigate in how far the five principles can coherently guide teachers’ professional development program toward instructional quality in the mathematics classroom.
Data availability statement
The original contributions presented in this study are included in the article, further inquiries can be directed to the corresponding author.
Author contributions
All authors contributed collectively to the conceptualization of the principles and the writing of the article. SP, CS, and LH were responsible for the fundraising of the project.
Funding
The DZLM network (DZLM—Deutsches Zentrum für Lehrkräftebildung Mathematik—German Center for Mathematics Teacher Education) was attached to the IPN Leibniz Institute for Science and Mathematics Education and funded by the Leibniz Association. The project QuaMath (QuaMath—Unterrichts- und Fortbildungs-Qualität in Mathematik entwickeln—Developing quality for mathematics classrooms and mathematics professional development) was funded by the Kultusministerkonferenz (Standing Conference of the Ministers of Education and Cultural Affairs of the Länder in the Federal Republic of Germany).
Acknowledgments
The authors cordially thank Jürg Kramer who led the DZLM until 2021 and the fundraising for QuaMath. The authors also thank all partners of the DZLM network for the inspiring discussions and collaboration in the project.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
- ^ The project QuaMath (QuaMath—Unterrichts- und Fortbildungs-Qualität in Mathematik entwickeln—Developing quality for mathematics classrooms and mathematics professional development) is a nationwide, 10-year PD design research project that the Ministries of Education of the Federal States (KMK Kultusministerkonferenz der Länder) have launched together with the DZLM (Deutsches Zentrum für Lehrkräftebildung Mathematik—German Centre for Mathematics Teacher Education) network. The preparations for the years 2023–2033 started in 2021.
References
Anderson, L. W., Krathwohl, D. R., Airasian, P. W., Cruikshank, K. A., Mayer, R. E., Pintrich, P. R., et al. (eds) (2001). A taxonomy for learning, teaching, and assessing: A revision of bloom’s taxonomy of educational objectives. Harlow: Longman.
Artigue, M. (1992). “Didactical engineering,” in Recherches en didactique des mathématiques, eds R. Douady and A. Mercier (Paris: La Pensèe Sauvage) 41–70.
Ball, D., Sleep, L., Boerst, T. A., and Bass, H. (2009). Combining the development of practice and the practice of development in teacher education. Elem. Sch. J. 109, 458–474. doi: 10.1086/596996
Bardy, T., Holzäpfel, L., and Leuders, T. (2021). Adaptive tasks as a differentiation strategy in the mathematics classroom: Features from research and teachers’ views. Math. Teach. Educ. Dev. 23, 26–53.
Berliner, D. C. (1987). “Simple views of effective teaching and a simple theory of classroom instruction,” in Talks to teachers, eds D. C. Berliner and B. Rosenshine (New York, NY: Random House) 93–110.
Blum, W., Artigue, M., Mariotti, M. A., Sträßer, R., and van den Heuvel-Panhuizen, M. (eds) (2019). European traditions in didactics of mathematics. Berlin: Springer. doi: 10.1007/978-3-030-11069-7
Boaler, J. (2002). Experiencing school mathematics. Traditional and reform approaches to teaching and their impact on student learning. Mahwah, NJ: Lawrence Erlbaum. doi: 10.4324/9781410606365
Brandt, J. (2022). Diagnose und Förderung erlernen – Untersuchung zu Akzeptanz und Kompetenzen in einer universitären Großveranstaltung. Berlin: Springer Spektrum. doi: 10.1007/978-3-658-36839-5
Brophy, J. (2000). Teaching educational practices series vol. 1. Michigan: International Academy of Education.
Carpenter, T., Fennema, E., Franke, M., Levi, L., and Empson, B. (1999). Children’s mathematics: Cognitively guided instruction. Portsmouth, NH: Heinemann.
Clements, M. A. K., Keitel, C., Bishop, A. J., Kilpatrick, J., and Leung, F. K. S. (2013). “From the few to the many: Historical perspectives on who should learn mathematics,” in Third international handbook of mathematics education, eds M. A. K. Clements, A. J. Bishop, C. Keitel, J. Kilpatrick, and F. K. S. Leung (Berlin: Springer), 7–40. doi: 10.1007/978-1-4614-4684-2_1
Cobb, P., and Jackson, K. (2021). An empirically grounded system of supports for improving the quality of mathematics teaching on a large scale. Implement. Replication Stud. Math. Educ. 1, 77–110. doi: 10.1163/26670127-01010004
Comenius, J. A. (1657). Didactica magna: The great didactic. The whole art of teaching all things to all. Published in English 1907. London: Adam and Charles Black.
Confrey, J., Gianopulos, G., McGowan, W., Shah, M., and Blecher, M. (2017). Scaffolding learner-centered curricular coherence using learning maps and diagnostic assessments designed around mathematics learning trajectories. ZDM-Math. Educ. 49, 717–734. doi: 10.1007/s11858-017-0869-1
Corno, L. (2008). On teaching adaptively. Educ. Psychol. 43, 161–173. doi: 10.1080/00461520802178466
Dewey, J. (1904). “The relation of theory to practice in education,” in The third yearbook of the national society for the scientific study of education, ed. C. A. McMurry (Chicago: The University of Chicago Press), 9–30.
Dhunny, R. H., and Angateeah, K. (2019). “Impact of spiral teaching on quadratics: Action research with grade 11 students in Mauritius,” in Proceedings of the 42nd annual conference of the mathematics education research group of Australasia, eds G. Hine, S. Blackley, and A. Cooke (Perth: MERGA), 220–227.
DIME (2007). “Culture, race, power in mathematics education,” in Second handbook of research on mathematics teaching and learning, ed. F. Lester (Charlotte, NC: Information Age), 405–433.
Doyle, W., and Carter, K. (1984). Academic tasks in classrooms. Curric. Inq. 14, 129–149. doi: 10.1080/03626784.1984.11075917
Dumont, H. (2019). Neuer Schlauch für alten Wein? Eine konzeptuelle Betrachtung von individueller Förderung im Unterricht. Z. Erziehwiss. 22, 249–277. doi: 10.1007/s11618-018-0840-0
Erath, K., Ingram, J., Moschkovich, J., and Prediger, S. (2021). Designing and enacting instruction that enhances language for mathematics learning – A review of the state of development and research. ZDM-Math. Educ. 53, 245–262. doi: 10.1007/s11858-020-01213-2
Fortus, D., and Krajcik, J. (2012). “Curriculum coherence and learning progressions,” in Second international handbook of science education, eds B. J. Fraser, K. Tobin, and C. J. McRobbie (Netherlands: Springer), 783–798. doi: 10.1007/978-1-4020-9041-7_52
Garet, M., Porter, A., Desimone, L., Birman, B., and Yoon, K. S. (2001). What makes professional development effective? Results from a national sample of teachers. Am. Educ. Res. J. 38, 915–945. doi: 10.3102/00028312038004915
Gravemeijer, K. (2004). Local instruction theories as means of support for teachers in reform mathematics education. Math. Think. Learn. 6, 105–128. doi: 10.1207/s15327833mtl0602_3
Gravemeijer, K., and Cobb, P. (2006). “Design research from a learning design perspective,” in Educational design research: The design, development and evaluation of programs, processes and products, eds J. V. D. Akker, K. Gravemeijer, S. McKenney, and N. Nieveen (London: Routledge), 17–51.
Hardy, I., Decristan, J., and Klieme, E. (2019). Adaptive teaching in research on learning and instruction. J. Educ. Res. Online 11, 169–191.
Hattie, J. (2009). Visible learning. A synthesis of over 800 meta-analyses relating to achievement. London: Routledge.
Heimann, P., Otto, G., and Schulz, W. (1979). Unterricht: Analyse und Planung. Santa Cruz, CA: Schroedel.
Henningsen, M., and Stein, M. K. (1997). Mathematical tasks and student cognition: Classroom-based factors that support and inhibit high-level mathematical thinking and reasoning. J. Res. Math. Educ. 28, 524–549. doi: 10.2307/749690
Hiebert, J., and Carpenter, T. P. (1992). “Learning and teaching with understanding,” in Handbook of research on mathematics teaching and learning, ed. D. A. Grouws (London: Macmillan), 65–97.
Hiebert, J., and Grouws, D. A. (2007). “The effects of classroom mathematics teaching on students’ learning,” in Second handbook of research on mathematics teaching and learning: A project of the national council of teachers of mathematics, ed. F. K. Lester (Charlotte, NC: Information Age Publishing), 371–404.
Hill, H. C., Blunk, M. L., Charalambous, C. Y., Lewis, J. M., Phelps, G. C., Sleep, L., et al. (2008). Mathematical knowledge for teaching and the mathematical quality of instruction. Cogn. Instr. 26, 430–511. doi: 10.1080/07370000802177235
Hosoya, G., Blömeke, S., Eilerts, K., Jenßen, L., and Eid, M. (2021). Absolute and relative judgment accuracy: Early childhood teachers’ competence to evaluate children’s mathematical skills. Front. Psychol. 12:701730. doi: 10.3389/fpsyg.2021.701730
Hoth, J., Döhrmann, M., Kaiser, G., Busse, A., König, J., and Blömeke, S. (2016). Diagnostic competence of primary school mathematics teachers during classroom situations. ZDM-Math. Educ. 48, 41–53. doi: 10.1007/s11858-016-0759-y
Howe, C., Hennessy, S., Mercer, N., Vrikki, M., and Wheatley, L. (2019). Teacher–student dialogue during classroom teaching: Does it really impact on student outcomes? J. Learn. Sci. 28, 462–512. doi: 10.1080/10508406.2019.1573730
Ing, M., Webb, N. M., Franke, M. L., Turrou, A. C., Wong, J., Shin, N., et al. (2015). Student participation in elementary mathematics classrooms: The missing link between teacher practices and student achievement? Educ. Stud. Math. 90, 341–356. doi: 10.1007/s10649-015-9625-z
Jablonka, E. (2003). “Mathematical literacy,” in Second international handbook of mathematics education, eds A. Bishop, M. A. Clements, C. Keitel, J. Kilpatrick, and F. K. S. Leung (Alphen aan den Rijn, NL: Kluwer), 77–104.
Jacobs, V. R., Lamb, L. L. C., and Philipp, R. A. (2010). Professional noticing of children’s mathematical thinking. J. Res. Math. Educ. 41, 169–202. doi: 10.5951/jresematheduc.41.2.0169
Janney, R. E., and Snell, M. E. (2006). Modifying schoolwork in inclusive classrooms. Theory Pract. 45, 215–223. doi: 10.1207/s15430421tip4503_3
Kilpatrick, J., Swafford, J., and Findel, B. (2001). Adding it up. Helping children learn mathematics. Washington, DC: National Academy Press.
Kirsch, A. (1976). Vorschläge zur Behandlung von Wachstumsprozessen und Exponentialfunktionen im Mittelstufenunterricht. Didaktik Math. 4, 257–284.
Klafki, W. (1958). Didactic analysis as the core of preparation of instruction. J. Curric. Stud. 27, 13–30. doi: 10.1080/0022027950270103
Klieme, E., Pauli, C., and Reusser, K. (2009). “The pythagoras study. Investigating effects of teaching and learning in Swiss and German mathematics classrooms,” in The power of video studies in investigating teaching and learning in the classroom, eds T. Janik and T. Seidel (Münster: Waxmann), 137–160.
Knipping, C., Korff, N., and Prediger, S. (2017). “Mathematikdidaktische Kernbestände für den Umgang mit Heterogenität – Versuch einer curricularen Bestimmung,” in Diagnose und förderung Heterogener Lerngruppen – Theorien, Konzepte und Beispiele aus der MINT-Lehrerbildung, eds C. Selter, S. Hußmann, C. Hößle, C. Knipping, and K. Lengnink (Münster: Waxmann), 39–60.
Krähenmann, H., Moser Opitz, E., Schnepel, S., and Stöckli, M. (2019). “Inclusive mathematics instruction: A conceptual framework and selected research results of a video study,” in Inclusive mathematics education. State-of-the-art research from Brazil and Germany, eds D. Kollosche, R. Marcone, M. Knigge, M. Godoy Penteado, and O. Skovsmose (Berlin: Springer), 179–196. doi: 10.1007/978-3-030-11518-0_13
Krummheuer, G. (2011). Representation of the notion ‘learning-as-participation’ in everyday situations of mathematics classes. ZDM-Math. Educ. 43, 81–90. doi: 10.1007/s11858-010-0294-1
Kunter, M., Baumert, J., Blum, W., Klusmann, U., Krauss, S., and Neubrand, M. (eds) (2013). “Mathematics teacher education,” in Cognitive activation in the mathematics classroom and professional competence of teachers: Results from the COACTIV project, Vol. 8, (Berlin: Springer). doi: 10.1007/978-1-4614-5149-5
Lampert, M., and Cobb, P. (2003). “Communication and language,” in A research companion to principles and standards for school mathematics, eds J. Kilpatrick and D. Shifter (Reston, VA: National Council of Teachers of Mathematics), 237–249.
Lenz, K., Holzäpfel, L., and Wittmann, G. (2019). Aufgaben als Lerngelegenheiten für konzeptuelles und prozedurales Wissen zu Brüchen: Eine vergleichende Schulbuchanalyse. Math. Didact. 42, 105–121.
Leuders, T., and Holzäpfel, L. (2011). Kognitive Aktivierung im Mathematikunterricht. Unterrichtswissenschaft 39, 213–230.
Ma, L. (1999). Knowing and teaching elementary mathematics: Teachers’ understanding of fundamental mathematics in China and the United States. Mahwah, NJ: Lawrence Erlbaum. doi: 10.4324/9781410602589
Manalo, E., and Kapur, M. (2018). The role of failure in promoting thinking skills and creativity: New findings and insights about how failure can be beneficial for learning. Think. Skills Creat. 30, 1–6. doi: 10.1016/j.tsc.2018.06.001
Mason, J. (2021). Learning about noticing, by, and through, noticing. ZDM-Math. Educ. 53, 231–243. doi: 10.1007/s11858-020-01192-4
Moschkovich, J. (2015). Academic literacy in mathematics for english learners. J. Math. Behav. 40, 43–62. doi: 10.1016/j.jmathb.2015.01.005
National Council of Teachers of Mathematics [NCTM] (2014). Principles to actions: Ensuring mathematical success for all. Reston, VA: NCTM.
Neubrand, M., Jordan, A., Krauss, S., Blum, W., and Löwen, K. (2013). “Task analysis in COACTIV: Examining the potential for cognitive activation in German mathematics classrooms,” in Cognitive activation in the mathematics classroom and professional competence of teachers, eds M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krausss, and M. Neubrand (Berlin: Springer), 125–144. doi: 10.1007/978-1-4614-5149-5_7
Newmann, F. M., Smith, B., Allensworth, E., and Bryk, A. S. (2001). Instructional program coherence: What it is and why it should guide school improvement policy. Educ. Eval. Policy Anal. 23, 297–321. doi: 10.3102/01623737023004297
OECD (2007). PISA 2006. Science competencies for tomorrow’s world. Paris: OECD. doi: 10.1787/9789264040014-en
Philipp, K. (2018). “Diagnostic competences of mathematics teachers with a view to processes and knowledge resources,” in Diagnostic competence of mathematics teachers. Unpacking a complex construct in teacher education and teacher practice, eds T. Leuders, K. Philipp, and J. Leuders (Berlin: Springer), 109–127. doi: 10.1007/978-3-319-66327-2_6
Pianta, R. C., and Hamre, B. K. (2009). Conceptualization, measurement, and improvement of classroom processes: Standardized observation can leverage capacity. Educ. Res. 38, 109–119. doi: 10.3102/0013189X09332374
Praetorius, A.-K., and Charalambous, C. Y. (2018). Classroom observation frameworks for studying instructional quality: Looking back and looking forward. ZDM-Math. Educ. 50, 535–553. doi: 10.1007/s11858-018-0946-0
Praetorius, A.-K., Klieme, E., Herbert, B., and Pinger, P. (2018). Generic dimensions of teaching quality: The german framework of three basic dimensions. ZDM-Math. Educ. 50, 407–426. doi: 10.1007/s11858-018-0918-4
Prediger, S., Dröse, J., Stahnke, R., and Ademmer, C. (2022). Teacher expertise for fostering at-risk students’ understanding of basic concepts: Conceptual model and evidence for growth. J. Math. Teach. Educ. doi: 10.1007/s10857-022-09538-3 [Epub ahead of print].
Renkl, A. (2015). Different roads lead to Rome: The case of principle-based cognitive skills. Learn. Res. Pract. 1, 79–90. doi: 10.1080/23735082.2015.994255
Rittle-Johnson, B., and Schneider, M. (2015). “Developing conceptual and procedural knowledge of mathematics,” in Oxford handbook of numerical cognition, eds R. C. Kadosh and A. Dowker (Oxford: Oxford University Press), 1102–1118. doi: 10.1093/oxfordhb/9780199642342.013.014
Rojas-Drummond, S., and Mercer, N. (2003). Scaffolding the development of effective collaboration and learning. Int. J. Educ. Res. 39, 99–111. doi: 10.1016/S0883-0355(03)00075-2
Schmidt, W. H., Hsing Chi, W., and McKnight, C. C. (2005). Curriculum coherence: An examination of US mathematics and science content standards from an international perspective. J. Curric. Stud. 37, 525–559. doi: 10.1080/0022027042000294682
Schoenfeld, A. H. (2014). What makes for powerful classrooms, and how can we support teachers in creating them? A story of research and practice, productively intertwined. Educ. Res. 43, 404–412. doi: 10.3102/0013189X14554450
Schulz, A. (2014). Fachdidaktisches Wissen von Grundschullehrkräften: Diagnose und Förderung bei besonderen Problemen beim Rechnenlernen. Berlin: Springer, doi: 10.1007/978-3-658-08693-0_2
Schütze, B., Souvignier, E., and Hasselhorn, M. (2018). Stichwort - formatives assessment. Z. Erziehwiss. 21, 697–715. doi: 10.1007/s11618-018-0838-7
Schweiger, F. (1984). “Fundamental ideas in mathematics — can they help to develop positive mathematical attitudes?,” in A collection of papers on pre-service teacher education from ICME-5, eds W. Dörfler, C. Gaulin, G. Jones, and H. Shuard (Stanford, CA: ICME), 111–116.
Seidel, T., and Shavelson, R. J. (2007). Teaching effectiveness research in the past decade: The role of theory and research design in disentangling meta-analysis results. Rev. Educ. Res. 77, 454–499. doi: 10.3102/0034654307310317
Selter, C. (1998). Building on children’s mathematics. A teaching experiment in Grade 3. Educ. Stud. Math. 36, 1–27. doi: 10.1023/A:1003111425076
Sfard, A. (2008). Thinking as communicating: Human development, the growth of discourses, and mathematizing. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511499944
Sfard, A., Nesher, P., Streefland, L., Cobb, P., and Mason, J. (1998). Learning mathematics through conversation: Is it as good as they say? Learn. Math. 18, 41–51.
Siemon, D., Horne, M., Clements, D., Confrey, J., Maloney, A., Samara, J., et al. (2017). “Researching and using learning progressions (trajectories) in mathematics education,” in Proceedings of the 41st conference of the international group for the psychology of mathematics education, Vol. 1, eds B. Kaur, W. K. Ho, T. L. Toh, and B. H. Choy (Singapore: PME), 109–136.
Spreitzer, C., Hafner, S., Krainer, K., and Vohns, A. (2022). Effects of generic and subject-didactic teaching characteristics on student performance in mathematics in secondary school: A scoping review. Eur. J. Educ. Res. 11, 711–737. doi: 10.12973/eu-jer.11.2.711
Stein, M. K., Engle, R. A., Smith, M. S., and Hughes, E. K. (2008). Orchestrating productive mathematical discussions: Five practices for helping teachers move beyond show and ell. Math. Think. Learn. 10, 313–340. doi: 10.1080/10986060802229675
Treffers, A. (1987). Three dimensions. A model of goal and theory description in mathematics instruction - The wiskobas project. Kufstein: Reidel. doi: 10.1007/978-94-009-3707-9
Treffers, A. (1993). Wiskobas and Freudenthal: Realistic mathematics education. Educ. Stud. Math. 25, 89–108. doi: 10.1007/BF01274104
Van den Heuvel-Panhuizen, M. (2003). The didactical use of models in realistic mathematics education: An example from a longitudinal trajectory on percentage. Educ. Stud. Math. 54, 9–35. doi: 10.1023/B:EDUC.0000005212.03219.dc
Vergnaud, G. (1996). “The Theory of Conceptual Fields,” in Theories of mathematical learning, eds L. P. Steffe and P. Nesher (Mahwah, NJ: Lawrence Erlbaum), 219–239.
Wagenschein, M. (2000). “Teaching to understand: On the concept of the exemplary in teaching,” in Teaching as a reflective practice. The german didaktik tradition, eds I. Westbury, S. Hopmann, and K. Riquarts (Mahwah, NJ: Lawrence Erlbaum), 161–175.
Walshaw, M., and Anthony, G. (2008). The teacher’s role in classroom discourse: A review of recent research into mathematics classrooms. Rev. Educ. Res. 78, 516–551. doi: 10.3102/0034654308320292
Watson, A., and Geest, E. D. (2005). Principled teaching for deep progress: Improving mathematical learning beyond methods and materials. Educ. Stud. Math. 58, 209–234. doi: 10.1007/s10649-005-2756-x
Webb, N. M., Franke, M. L., Ing, M., Turrou, A. C., Johnson, N. C., and Zimmerman, J. (2019). Teacher practices that promote productive dialogue and learning in mathematics classrooms. Int. J. Educ. Res. 97, 176–186. doi: 10.1016/j.ijer.2017.07.009
Webb, N. M., Franke, M. L., Ing, M., Wong, J., Hernandez, C. H., Shin, N., et al. (2014). Engaging with others’ mathematical ideas: Interrelationships among student participation, teachers’ instructional practices and learning. Int. J. Educ. Res. 63, 79–93. doi: 10.1016/j.ijer.2013.02.001
Westbury, I., Hopmann, S., and Riquarts, K. (eds) (2000). Teaching as a reflective practice. The german didaktik tradition. Mahwah, NJ: Lawrence Erlbaum.
Wilhelm, A. G., Munter, C., and Jackson, K. (2017). Examining relations between teachers’ explanations of sources of students’ difficulty in mathematics and students’ opportunities to learn. Elem. Sch. J. 117, 345–370. doi: 10.1086/690113
Wiliam, D. (2010). “The role of formative assessment in effective learning environments,” in The nature of learning. Using research to inspire practice, eds H. Dumont, D. Istance, and F. Benavides (Paris: OECD), 135–159. doi: 10.1787/9789264086487-8-en
Wittmann, E. C. (1998). Standard number representations in the teaching of arithmetic. J. Math. Didaktik 19, 149–178. doi: 10.1007/BF03338866
Keywords: good teaching, effective teaching, mathematics education, instructional quality, teacher professional development
Citation: Prediger S, Götze D, Holzäpfel L, Rösken-Winter B and Selter C (2022) Five principles for high-quality mathematics teaching: Combining normative, epistemological, empirical, and pragmatic perspectives for specifying the content of professional development. Front. Educ. 7:969212. doi: 10.3389/feduc.2022.969212
Received: 14 June 2022; Accepted: 29 September 2022;
Published: 25 October 2022.
Edited by:
Klaus Zierer, University of Augsburg, GermanyReviewed by:
Alik Palatnik, Hebrew University of Jerusalem, IsraelSung-Jae Moon, Gyeongin National University of Education, South Korea
Copyright © 2022 Prediger, Götze, Holzäpfel, Rösken-Winter and Selter. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Susanne Prediger, susanne.prediger@dzlm.de
 Susanne Prediger
Susanne Prediger Daniela Götze1,3
Daniela Götze1,3  Lars Holzäpfel
Lars Holzäpfel