1 INTRODUCTION

Due to increased requirements for the plan of a high-speed highway (HSH), the need to arrange intersections with other roads only at different levels, the share of bridges on the highway increases significantly [1–3] and reaches 94% of the total length of the line. Since the installation is simple and low cost, the simply supported beam has become the preferred design for the construction of high-speed railway bridges. However, as train speed continually increases, problems associated with the vibration response of the bridge become more important. Therefore, the dynamic analysis of bridges under the load of high-speed trains attracts the attention of many researchers from different countries. Over the past few decades, a number of theoretical studies on the vibration response and control of a simply supported girder bridge in a high-speed railway have been carried out [4–6]. However, due to the increase in beam travel speed, this area of research remains relevant and challenging.

The introduction of high-speed train traffic at speeds of up to 111 m/s (400 km/h) makes it possible to generate resonant oscillations in the most common bridge structures, namely, beam bridges [7]. In this case, the dynamic coefficient reaches 4 [7]. Resonance is also dangerous due to the deterioration of the interaction between the wheel and the rail and leads to the wheel derailment [8].

Elastic beam models are used to describe mechanical systems in a wide class of applications. Bridges, rails, manipulators, and resonators are some examples of structures that have been modeled as beams to study their behavior. Certain materials, as well as geometric and external parameters, can significantly affect their performance. Among the parameters that have a significant impact on the behavior of structures is the applied load. The type of load varies from simple static load at a point to load dependent on space and time.

The behavior of a flexible beam with a moving load or mass-spring system has attracted the attention of researchers for decades. One can note the studies [9, 10]. It has become a popular topic in the literature due to its widespread use in many engineering applications, such suspension bridges, overhead cranes, and tethered satellite systems [11]. Several models have been proposed to describe the system performance and the effect of moving load or mass on the dynamic response of the beam. Monograph [12] is one of the first comprehensive studies in this regard. Analytical solutions of beam response have been presented for various types of loads such as moving constant load, moving harmonic load and moving masses. Because the structure is subjected to a load that varies in space and time, the resulting stresses and strains are significantly higher than those observed under stationary loads. The most common are beams using the Euler-Bernoulli model with a constant moving load. More accurate models use a dynamic moving mass-spring-damper system on a beam; these models take into account the inertia and rebound effect of a moving object [12, 15]. Various analytical and numerical approaches have been used to solve the equations of motion of the system, such as the finite element method [16], the penalty method [17], and the Lagrange multiplier [18]. A brief overview of articles on moving loads with their applications is provided in [19].

In [20] and [21], the suppression of vibrations of beams by a train, which excites these vibrations, is considered. In [22], the phenomenon of antiresonance or suppression of vibrations of beams by load is considered in relation to real design solutions on high-speed railways (HSR). The term “anti-resonance” is apparently introduced by Panovko and Gubanova in their book (see, for example, [23]). Classical anti-resonance is shown in Fig. 1. Anti-resonance manifests itself in the form of a monotonic decrease in the amplitude of forced vibrations in the middle of the beam during the passage of a train [22]. After the train passes (t > 4.5 s), free vibration occur. The problem of applying the conditions for suppressing beam vibrations by rolling stock proposed in the monograph [20] is solved by strictly fulfilling the ratio of the length of the span and the car. Thus, for a common car length of 25 m (ICE3, CRH380B, CRH3C, AVE-103, Siemens Velaro Rus, etc.) the length of the span must be equal to 12.5, or 37.5, or 62.5 m to exhibit the vibration suppression effect. However, when moving trains with a different car length, for example, TGV (18.7 m), resonance of these spans becomes possible at a speed of 78 m/s (281 km/h). On the other hand, with an established length of the span of 33 m, the length of the car should be equal to 13.2, 22 or 66 m. With other cars, resonance in such beams is realized at speeds less than the designed ones.

Fig. 1
figure 1

. The phenomenon of anti-resonance.

Full size image

All these conditions significantly complicate the practical implementation of vibration suppression by a train as an inertial damper. In reality, crossing various obstacles requires a wide variety of beam spans. For example, on the HSR in China [21] mainly use standard beams with a length of 20, 24, 32, 40 m. At the same time, the length of the average cars of various types of trains varies from 24.77 to 26.6 m.

Determination of critical motion speeds that cause resonance or, conversely, suppression of oscillations with traffic safety assessment based on the derailment coefficient is carried out using complex methods of optimal control theory and mathematical analysis, as well as proper software [20, 22]. When designing, relatively simple practical methods are required that allow the engineer not only to determine the mode of dynamic behavior of beam span structures before the detailed development of design documentation, but also to assign successful dynamic parameters of beams at the stage of pre-design constructure development.

Thus, the development of other conditions that make it possible to determine the behavior of beam spans during high-speed movement, or to preset satisfactory dynamic parameters of beams, is a relevant problem.

2 METHOD FOR DETERMINING THE CONDITIONS OF RESONANCE AND SUPPRESSION OF BEAM VIBRATIONS

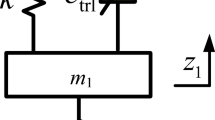
We study the following problem. We consider the elastic rectilinear beam shown in Fig. 2.

Fig. 2
figure 2

. Elastic beam under the action of a moving force \(P(t)\).

Full size image

A beam with flexural stiffness \(EJ\) and linear density \({{\rho }}\) has length \(L\). It is believed that the beam is subjected to action of a constant vertical force \(P(t) = {\text{const}}\) moving along the horizontal axis with a speed \(V = {\text{const}}\). At the initial moment of time, the beam is at rest, i.e., \(y(0,x) = y{\kern 1pt} '(0,x) = 0\) the force P is applied to the left end of the beam x = 0. At the moment of time \(t = L{\text{/}}V\) when the force is applied to the right end, a new force P arises at the left end. This force moves along the beam with a speed \(V = {\text{const}}\). Thus, the beam is subjected to a periodic load with a period \(T = L{\text{/}}V\). The boundary conditions do not depend on time and are determined by the fixing conditions: \(y(0,0) = y{\kern 1pt} '{\kern 1pt} '(0,0) = y(0,L) = y{\kern 1pt} '{\kern 1pt} '(0,L) = 0\).

The motion of the beam is described by an ordinary differential equation with constant coefficients

$$EJ\frac{{{{\partial }^{4}}y(t,x)}}{{\partial {{x}^{4}}}} + {{\rho }}\frac{{{{\partial }^{2}}y(t,x)}}{{\partial {{y}^{2}}}} = {{\delta }}(x - Vt)P.$$
(1.1)

In this case, damping is not taken into account. Here \({{\delta }}(x)\) is the delta function.

We seek a solution in the form

$$y(t,x) = \sum\limits_{m = 1}^\infty {{{q}_{m}}} (t)\sin \frac{{m{{\pi }}x}}{L},$$
(1.2)

where m is an element of the natural sequence. By successively multiplying Eq. (1.1) by \(\sin \frac{{i{{\pi }}x}}{L}\) and integrating it over the length of the beam from 0 to L, Eq. (1.1) is reduced to a countable number of independent equations for finding the functions \({{q}_{m}}(x),i = 1,...,\infty \)

$$\frac{{{{\partial }^{2}}{{q}_{m}}(t)}}{{\partial {{t}^{2}}}} + \frac{{{{{{\pi }}}^{4}}{{m}^{4}}}}{{{{L}^{4}}}}\frac{{EJ}}{{{\rho }}}{{q}_{m}}(t) - \frac{{2P\sin }}{{{{\rho }}L}}\left( {\frac{{{{\pi }}mVt}}{L}} \right) = 0,\quad m = 1,...,\infty .$$
(1.3)

The solution of the equations (1.3) has the form

$$\begin{gathered} {{q}_{m}}(t) = {{C}_{1}}\cos \left( {\frac{{{{{{\pi }}}^{2}}{{m}^{2}}\sqrt {EJ} }}{{{{L}^{2}}\sqrt {{\rho }} }}t} \right) + {{C}_{2}}\sin \left( {\frac{{{{{{\pi }}}^{2}}{{m}^{2}}\sqrt {EJ} }}{{{{L}^{2}}\sqrt {{\rho }} }}t} \right) \\ \, + \frac{{2P\sin \left( {\frac{{{{\pi }}mVt}}{L}} \right){{L}^{3}}}}{{{{{{\pi }}}^{2}}{{m}^{2}}(EJ{{{{\pi }}}^{2}}{{m}^{2}} - {{L}^{2}}{{V}^{2}}{{\rho }})}}. \\ \end{gathered} $$
(1.4)

For the first interval of motion (\(0 < t < L{\text{/}}V\)), taking into account the initial conditions \({{q}_{m}}(0) = \frac{{\partial {{q}_{m}}(0)}}{{\partial t}} = 0\), the solution has the form

$${{q}_{m}}(t) = \frac{{2P{{L}^{3}}}}{{\sqrt {EJ} {{m}^{3}}{{{{\pi }}}^{3}}}}\frac{{\left[ {VL\sqrt \rho \sin \left( {\frac{{{{{{\pi }}}^{2}}{{m}^{2}}\sqrt {EJ} }}{{{{L}^{2}}\sqrt {{\rho }} }}t} \right) - {{\pi }}m\sqrt {EJ} \sin \left( {\frac{{{{\pi }}Vmt}}{L}} \right)} \right]}}{{(EJ{{{{\pi }}}^{2}}{{m}^{2}} - {{L}^{2}}{{V}^{2}}{{\rho }})}}.$$
(1.5)

In order to construct a solution for the second interval (\(L{\text{/}}V < t < 2L{\text{/}}V\)), it is necessary to consider that the terminal conditions of the first motion are the initial ones for the second motion

$$\begin{gathered} {{q}_{m}}\left( {\frac{L}{V}} \right) = - \frac{{2P{{L}^{4}}V\sqrt {{\rho }} \sin \left( {\frac{{{{{{\pi }}}^{2}}{{m}^{2}}\sqrt {EJ} }}{{VL\sqrt {{\rho }} }}} \right)}}{{\sqrt {EJ} {{m}^{3}}{{{{\pi }}}^{3}}(EJ{{{{\pi }}}^{2}}{{m}^{2}} - {{L}^{2}}{{V}^{2}}{{\rho }})}} \\ {{\left. {\frac{{\partial {{q}_{m}}}}{{\partial t}}} \right|}_{{t = \frac{L}{V}}}} = - \frac{{2P{{L}^{2}}V\left( {\cos \left( {\frac{{{{{{\pi }}}^{2}}{{m}^{2}}\sqrt {EJ} }}{{VL\sqrt \rho }}} \right) - {{{( - 1)}}^{m}}} \right)}}{{m{{\pi }}(EJ{{{{\pi }}}^{2}}{{m}^{2}} - {{L}^{2}}{{V}^{2}}{{\rho }})}} \\ \end{gathered} $$
(1.6)

We introduce the parameter

$${{{{\beta }}}_{0}} = \frac{{{{\pi }}\sqrt {EJ} }}{{VL\sqrt {{\rho }} }}.$$
(1.7)

Then relations (1.6) are rewritten in the form

$$\begin{gathered} {{q}_{m}}\left( {\frac{L}{V}} \right) = \frac{{2P{{L}^{2}}\sin ({{\pi }}{{m}^{2}}{{{{\beta }}}_{0}})}}{{\sqrt {{{\rho }}EJ} {{m}^{3}}{{{{\pi }}}^{3}}V({{\beta }}_{0}^{2}{{m}^{2}} - 1)}}, \\ {{\left. {\frac{{\partial {{q}_{m}}}}{{\partial t}}} \right|}_{{t = \frac{L}{V}}}} = \frac{{2P(\cos ({{\pi }}{{m}^{2}}{{{{\beta }}}_{0}}) - {{{( - 1)}}^{m}})}}{{m{{\pi \rho }}({{\beta }}_{0}^{2}{{m}^{2}} - 1)}}. \\ \end{gathered} $$
(1.8)

An interesting case is when the parameter β0 is an integer

$${{{{\beta }}}_{0}} = 1,2,....$$
(1.9)

In this case, the first relation from (1.8) is identically equal to zero

$${{q}_{m}}\left( {\frac{L}{V}} \right) = 0$$

and the second one has the form

$${{\left. {\frac{{\partial {{q}_{m}}}}{{\partial t}}} \right|}_{{t = \frac{L}{V}}}} = \frac{{2P}}{{m{{\pi \rho }}({{\beta }}_{0}^{2}{{m}^{2}} - 1)}}({{( - 1)}^{{{{m}^{2}}{{{{\beta }}}_{0}}}}} - {{( - 1)}^{m}}).$$
(1.10)

Obviously, the value of expression (1.10) is determined by the value of the bracket, which, without loss of generality, can be rewritten as

$$({{( - 1)}^{{m{{{{\beta }}}_{0}}}}} - {{( - 1)}^{m}}) = \left\{ \begin{gathered} 0,\quad {{{{\beta }}}_{0}} = 2i + 1 \hfill \\ 2{{( - 1)}^{m}},\quad {{{{\beta }}}_{0}} = 2i \hfill \\ \end{gathered} \right.,\quad i = 1,2, \ldots .$$
(1.11)

Thus, if the parameter value β0 is an odd number \({{{{\beta }}}_{0}} = 2i - 1\), \(i = 1,2,...\) then the anti-resonance conditions are realized and the terminal conditions for this motion have the form

$${{q}_{m}}\left( {\frac{L}{V}} \right) = 0,\quad {{\left. {\frac{{\partial {{q}_{m}}}}{{\partial t}}} \right|}_{{t = \frac{L}{V}}}} = 0.$$
(1.12)

Using this property, it can be argued that for any system of sequentially acting concentrated forces along the beam, the amplitudes of the resulting vibrations are always limited. And provided that dissipative forces are present, such oscillations attenuate.

If the parameter value \({{{{\beta }}}_{0}}\) is an even number \({{\beta }}_{0}^{*} = 2i\), \(i = 1,2,...\) then despite the fact that at the end of the motion, zero displacements are realized along the entire length of the beam, the velocity distribution may not be zero

$${{\left. {\frac{{\partial {{q}_{m}}}}{{\partial t}}} \right|}_{{t = \frac{L}{V}}}} = \frac{{2P[{{{( - 1)}}^{{m{{{{\beta }}}_{0}}}}} - {{{( - 1)}}^{m}}]}}{{m{{\pi \rho }}({{\beta }}_{0}^{2}{{m}^{2}} - 1)}} = \left\{ \begin{gathered} \frac{{ - 4P}}{{m{{\pi \rho }}({{\beta }}_{0}^{2}{{m}^{2}} - 1)}},\quad m = 2i - 1 \hfill \\ 0,\quad m = 2i \hfill \\ \end{gathered} \right.,\quad i = 1,2, \ldots .$$
(1.13)

Thus, for even values of the parameter m (even modes), just as in the previous case, the phenomenon of anti-resonance is observed. It can be assumed that for odd modes with periodic loading of a beam with running forces, the phenomenon of resonance can be observed.

We consider the following process of loading a beam with transverse forces running along it with intensity \(P\). At the initial moment of time t = 0, a force is applied to the left end of the beam \(P\) and moves towards the right end with a speed V. At the moment of time when the force reaches the right end, a force appears at the left end of the beam \(P\) and moves towards the right end with the same speed \(V\). Then the process is repeated.

We assume that at some point in time \({{t}_{j}} = j\frac{L}{V}\) there is a change of forces and a force \({{P}_{j}}\) arises at the left end. By induction we can prove that the initial condition for this problem (1.13) has the form

$${{\left. {\frac{{\partial {{q}_{m}}}}{{\partial t}}} \right|}_{{t = j\frac{L}{V}}}} = \frac{{ - 4P(2j - 1)}}{{m{{\pi \rho }}({{\beta }}_{0}^{2}{{m}^{2}} - 1)}}.$$
(1.14)

To complete the picture, it remains to consider one special case. From relation (1.8) it follows that if \(m = {{{{\beta }}}_{0}} = 1\), then the denominator becomes zero. Therefore, we consider this case separately. Then equation (1.3) takes the form

$$\frac{{{{\partial }^{2}}{{q}_{1}}(t)}}{{\partial {{t}^{2}}}} + \frac{{{{\pi }^{2}}{{V}^{2}}}}{{{{L}^{2}}}}{{q}_{1}}(t) - \frac{{2P\sin (\pi Vt)}}{{\rho L}} = 0.$$
(1.15)

Solution (1.15) has the form

$${{q}_{1}}(t) = \sin \left( {\frac{{{{\pi }}Vt}}{L}} \right){{c}_{2}} + \cos \left( {\frac{{{{\pi }}Vt}}{L}} \right){{c}_{1}} - \frac{{Pt}}{{{{\pi \rho }}V}}\cos \left( {\frac{{{{\pi }}Vt}}{L}} \right) + \frac{{PL}}{{{{{{\pi }}}^{2}}\rho {{V}^{2}}}}\sin \left( {\frac{{{{\pi }}Vt}}{L}} \right).$$
(1.16)

From (1.16) it is clear that the initial conditions \({{q}_{m}}(0) = \frac{{\partial {{q}_{m}}(0)}}{{\partial t}} = 0\) are satisfied at \({{c}_{1}} = {{c}_{2}} = 0\). In this case, the terminal conditions are

$$q_{1}^{1}\left( {\frac{L}{V}} \right) = \frac{{PL}}{{{{\pi \rho }}{{V}^{2}}}} \ne 0,\quad {{\left. {\frac{{\partial q_{1}^{1}}}{{\partial t}}} \right|}_{{t = \frac{L}{V}}}} = 0.$$
(1.17)

Using conditions (1.17) as initial ones for the second movement, we obtain

$$q_{1}^{{(2)}}(t) = \frac{P}{{{{{{\pi }}}^{2}}{{\rho }}{{V}^{2}}}}\left( {{{\pi }}(L - Vt)\cos \left( {\frac{{{{\pi }}Vt}}{L}} \right) + L\sin \left( {\frac{{{{\pi }}Vt}}{L}} \right)} \right).$$
(1.18)

The terminal conditions for this motion have zero motion

$$q_{1}^{1}\left( {\frac{L}{V}} \right) = 0,\quad {{\left. {\frac{{\partial q_{1}^{1}}}{{\partial t}}} \right|}_{{t = \frac{L}{V}}}} = 0.$$
(1.19)

Thus, in contrast to the general case (β0 are odd numbers), periodic movements are realized in two cycles of movement.

3 VERIFICATION OF THE METHOD USING NUMERICAL SIMULATION

It is obvious that the conditions formulated in Section 2 do not fully correspond to real conditions, since the rolling stock for the span represents a set of moving variable forces, and not a single constant force. Therefore, due to the superposition of contact forces, suppression of oscillations in the form of anti-resonance may not occur. However, in our opinion, suppression of oscillations can manifest itself in the form of limited oscillation amplitude.

The verification of the formulated conditions for the manifestation of resonance and suppression or limitation of oscillations has been carried out using a complex of numerical integration of ordinary differential equations of oscillations of a rolling stock of 10 cars with 10 degrees of freedom each, partial differential equations for the upper structure of the track and beams of spans [24]. The car model with 10 degrees of freedom takes into account the bouncing and galloping vibrations of the car body and bogies that are excited by the passage through the bridge. Such oscillations of the car as wobbling, lateral drift, and sideways rolling are not considered, since such oscillations are not excited by bridges.

Consider the movement of a train at a speed of 82.5 m/s (297 km/h) along a 50 m beam for various values of \({{{{\beta }}}_{0}}\). This speed (causing resonance) is critical for the original beam of a real design.

As predicted,resonant vibrations of the beam occur for β0 = 4 and the corresponding ratio \(EJ{\text{/}}m\) occur (Fig. 3). It is obvious that the amplitude of resonant vibration increases with increasing length of the train (on the St. Petersburg-Moscow line, the length of the Sapsan train reaches 20 cars).

Fig. 3.
figure 3

Diagram of vibration y (t) in the middle of the beam of 50 m from 10-car train at resonance and \({{{{\beta }}}_{0}}\, = \,4\), \(V\, = \,82.5\) m/s.

Full size image

At \({{{{\beta }}}_{0}} = 3\) in accordance with Section 2, the phenomenon of anti-resonance has been expected. Due to the superposition of vibrations from the passage of at least 4 wheels that fit on this beam at the same time, a monotonous decrease in the amplitude of forced vibrations is not observed. At the same time (Fig. 4) it is clear that the amplitude of forced oscillations remains limited. According to the norms [25], the maximum deflection for such a beam is 2.2 cm. However, it seems important that there are practically no free vibrations after the train leaves, which confirms the fulfillment of condition (2.12). Thus, we can state the confirmation by numerical simulation for a more detailed model [24] of the theoretical results of the transformations and calculations given in Section 2.

Fig. 4.
figure 4

Diagram of oscillations y (t) in the middle of the beam of 50 m at \({{{{\beta }}}_{0}} = 3\), \(V = 82.5\) m/s.

Full size image

4 CONCLUSIONS

A new method for predicting the dynamic behavior of beam superstructures of bridges on high-speed lines has been developed. This engineering method allows, without the use of complex software, at the stage of pre-design work to assign the dynamic parameters of a beam with a prescribed dynamic behavior. In this way, beam resonance, which can occur during high-speed motion, can be avoided.