Skip to main content
SpringerLink
Log in

On stability of relative equilibria of a double pendulum with vibrating suspension point

  • Published:
Mechanics of Solids Aims and scope Submit manuscript

Abstract

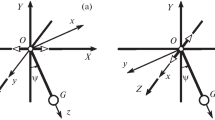
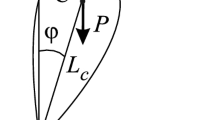
We consider the motions of a double pendulum consisting of two hinged identical rods. The pendulum suspension point is assumed to perform harmonic vibrations of arbitrary frequency and arbitrary amplitude in the vertical direction. We carry out a complete nonlinear analysis of the stability of the four pendulum relative equilibria on the vertical.

The problem on the stability of the relative equilibria of the mathematical pendulum in the case where the suspension point performs vertical harmonic vibrations of arbitrary frequency and arbitrary amplitude was considered in a linear setting [1–3] and a nonlinear setting [4, 5]. In the case of small-amplitude rapid vertical vibrations of the suspension point, linear and (mathematically not fully rigorous) nonlinear stability analysis of the relative equilibria was carried out for an ordinary pendulum [6–9] and a double pendulum [10, 11]. In [12], for the same case of rapid vibrations, stability conditions in the linear approximation were obtained for the four relative equilibria of a system consisting of two physical pendulums. In the special case of a system consisting of two identical rods, the problem was solved in the nonlinear setting.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M. J. O. Strutt, Lame’sche-Mathieusche-und verwandte Funktionen in Physik und Technik (Springer, Berlin, 1932; Gostekhizdat, Kharkov-Kiev, 1935).

    Book  Google Scholar 

  2. N.W. Mac-Lachlan, Theory and Applications of Mathieu Functions (Clarendon Press, Oxford, 1947; Izdvo Inostr. Lit., Moscow, 1953).

    Google Scholar 

  3. J. J. Stoker, Nonlinear Vibrations in Mechanical and Electrical Systems (Wiley, New York-London, 1950; Izd-vo Inostr. Lit.,Moscow, 1953).

    MATH  Google Scholar 

  4. A. P. Markeyev, “The Behaviour of a Non-Linear Hamiltonian System with one Degree of Freedom at the Boundary of a Parametric Resonance Domain,” Prikl. Mat. Mekh. 59(4), 569–580 (1995) [J. Appl. Math. Mech. (Engl. Transl.) 59 (4), 541–551 (1995)].

    MathSciNet  Google Scholar 

  5. B. S. Bardin and A. P. Markeyev, “The Stability of the Equilibrium of a Pendulum for Vertical Oscillations of the Point of Suspension,” Prikl. Mat. Mekh. 59(6), 922–929 (1995) [J. Appl. Math. Mech. (Engl. Transl.) 59 (6), 879–886 (1995)].

    MathSciNet  Google Scholar 

  6. A. Stephenson, “On a New Type of Dynamical Stability,” Mem. Proc.Manch. Lit. Phil. Soc. 52(2, 8), 1–10 (1908).

    Google Scholar 

  7. A. Erdélyi, “Über die Kleinen Schwingungen eines Pendels mit Oszillierendem Aufhängepunkt,” ZAMM 14(4), 235–247 (1934).

    Article  MATH  Google Scholar 

  8. P. L. Kapitsa, “Pendulum with Vibrating Suspension,” Uspekhi Fiz. Nauk 44(1), 7–20 (1951).

    Google Scholar 

  9. P. L. Kapitsa, “Dynamical Stability of a Pendulum with Vibrating Suspension Point,” Zh. &Eksp. Teor. Fiz. 21(5), 588II–597 (1951) [Soviet Phys. JETP (Engl. Transl.)].

    Google Scholar 

  10. A. Stephenson, “On Induced Stability,” Phil. Mag. Ser. 7 17, 765–766 (1909).

    Article  Google Scholar 

  11. T. G. Strizhak, Methods for Studying C PendulumT-Type Dynamical Systems (Nauka, Alma-Ata, 1981) [in Russian].

    Google Scholar 

  12. O. V. Kholostova, “On the Motions of a Double Pendulum with Vibrating Suspension Point,” Izv. Akad. Nauk.Mekh. Tverd. Tela, No. 2, 25–40 (2009) [Mech. Solids (Engl. Transl.) 44 (2), 184–197 (2009)].

  13. A. P. Markeyev, “A Constructive Algorithm for the Normalization of a Periodic Hamiltonian,” Prikl. Mat. Mekh. 69(3), 355–371 (2005) [J. Appl.Math. Mech. (Engl. Transl.) 69 (3), 323–337 (2005)].

    MathSciNet  Google Scholar 

  14. V.A. Yakubovich and V.M. Starzhinskii, Parametric Resonance in Linear Systems (Nauka, Moscow, 1987) [in Russian].

    MATH  Google Scholar 

  15. A. P. Markeev, Libration Points in Celestial Mechanics and Space Dynamics (Nauka, Moscow, 1978) [in Russian].

    Google Scholar 

  16. A. M. Lyapunov, “On Stability of Motion in a Special Case of the Three-Body Problem,” in Collection of Works, Vol. 1 (Izd-vo AN SSSR, Moscow-Leningrad, 1954), pp. 327–401 [in Russian].

    Google Scholar 

  17. V. I. Arnold, V. V. Kozlov, and A. I. Neishtadt, Mathematical Aspects of Classical and Celestial Mechanics (Springer-Verlag, New York, 1988; Editorial URSS,Moscow, 2002).

    Google Scholar 

  18. J. Moser, “New Aspects of the Theory of Stability of Namiltonian Systems,” Comm. Pure Appl. Math. 11(1), 81–114 (1958).

    Article  MathSciNet  MATH  Google Scholar 

  19. J. Glimm, “Formal Stability of Namiltonian Systems,” Comm. Pure Appl.Math. 17(4), 509–526 (1964).

    Article  MathSciNet  MATH  Google Scholar 

  20. A. P. Markeev, “Stability of Planar Rotations of a Satellite in a Circular Orbit,” Izv. Akad. Nauk. Mekh. Tverd. Tela, No. 4, 63–85 (2006) [Mech. Solids. (Engl. Transl.) 41 (4), 46–63 (2006)].

Download references

Author information

Authors and Affiliations

  1. Moscow Aviation Institute (State University of Aerospace Technologies), Volokolamskoe sh. 4, GSP-3, A-80, Moscow, 125993, Russia

    O. V. Kholostova

Authors
  1. O. V. Kholostova
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to O. V. Kholostova.

Additional information

Original Russian Text © O.V. Kholostova, 2011, published in Izvestiya Akademii Nauk. Mekhanika Tverdogo Tela, 2011, No. 4, pp. 18–30.

About this article

Cite this article

Kholostova, O.V. On stability of relative equilibria of a double pendulum with vibrating suspension point. Mech. Solids 46, 508–518 (2011). https://doi.org/10.3103/S0025654411040029

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S0025654411040029

Keywords

Search

Navigation