1 Introduction

In the design of engineering structures, uncertain factors always exist in their material properties, load conditions, geometrical dimensions, and so on, and these uncertain factors must be taken into consideration in the design process since they will result in fluctuation of the mechanical properties of structures (Ben-Haim, 2004; Verhaeghe et al., 2013; Wu et al., 2015b; Xia et al., 2015). Reliability-based design optimization is frequently conducted to enhance the reliability of engineering structures and reduce the chance of function failure under potentially critical conditions.

The probabilistic methods (Allen and Maute, 2004; Luo et al., 2006; Missoum et al., 2007; Cheng et al., 2008; 2014; Ge et al., 2008; Deb et al., 2009; Kundu et al., 2014) require a large amount of sample data to obtain the accurate probabilistic distribution information of uncertain factors, and gathering the data is usually a difficult task. Moreover, the probabilistic reliability may be sensitive to the distribution information of random parameters. Small errors in the parameters of a probabilistic model may lead to large errors in the calculation of a structure’s reliability (Elishakoff, 1995b).

To overcome the limitations of probabilistic methods in the process of reliability-based design optimization, scholars have gradually turned to non-probabilistic methods for handling uncertainties since non-probabilistic models have advantages such as low requirements for sample data and simplicity of calculation (Ben-Haim, 1994; 1995; Elishakoff et al., 1994; Qiu et al., 1995; 2004; Elishakoff and Elettro, 2014). Ben-Haim (1994) first proposed the concept of non-probabilistic reliability based on convex set theory, where non-probabilistic convex models of uncertainty were utilized to formulate reliability in terms of acceptable system performance given an uncertain operating environment or uncertain geometrical imperfections. Elishakoff (1995a) later put forward a possible definition in the discussion of this concept, which indicated that non-probabilistic reliability index should be an interval rather than a specific value. Nowadays, interval reliability-based design optimization has become a research hotspot of structural optimization (Wang et al., 2008; Du, 2012; Elishakoff et al., 2013; Jiang et al., 2013). For example, Jiang et al. (2011) developed a new reliability analysis technique for uncertain structures based on random distributions with interval parameters. Guo et al. (2001; 2005) presented a non-probabilistic model of structural reliability based on interval analysis and described the procedures for computing the interval reliability index. Jiang T. et al. (2007) proposed a semi-analytic method for calculating the interval reliability index, which proved to be simple and have several advantages over the existing unconstrained multivariate nonlinear optimization approach. Cheng and Zhang (2011) investigated the robust reliability-based design optimization of a steering mechanism for trucks based on an interval model. Jiang C. et al. (2007) proposed an improved “six formulas model” for calculating interval reliability. Wang and Qiu (2009) proposed an intuitive graphical method for calculating interval reliability by transforming the comparison of two intervals into the comparison of 2D graphical areas. However, the positional relationship of the left and right bounds of two intervals needs to be determined in the application of the graphical method, which is a somewhat tedious and difficult task and limits the application of these methods in engineering. To overcome these shortcomings, a unified formula for the efficient calculation of interval reliability is proposed in this paper, avoiding the determination of the positional relationship of two intervals in computing the interval reliability.

Interval optimization algorithms are very significant in realizing the reliability-based design optimization of structures based on interval models. Scholars have conducted a great deal of research work on interval linear programming over the past decades. For instance, Inuiguchi and Sakawa (1995; 1997) proposed the minimax regret solution to linear programming problems with an interval objective function. However, the objective and constraints corresponding to the mechanical performance indices of the structures are often nonlinear for most of the reliability-based design optimization problems of engineering structures. Therefore, nonlinear interval programming algorithms are more promising for the optimization of uncertain structures. Elishakoff and Ohaski (2010) formulated the problem of identifying the worst responses of a structure with respect to the interval parameters as an anti-optimization problem, which resulted in a two-level optimization problem. Jiang C. et al. (2007; 2008a; 2008b; 2008c) and Jiang (2008) put forward several algorithms for nonlinear interval optimization. The interval objective and constraint functions were transformed into deterministic ones by prescribing their acceptable possibility levels, and the resulting deterministic model was further transformed into an unconstrained single-objective one by weighting and penalty function methods, which was then solved by deterministic algorithms. Wu et al. (2013; 2014; 2015a) proposed the high-order Taylor inclusion function to compress overestimation in interval arithmetic and utilized the Chebyshev surrogate model to approximate the high-order coefficients of the Taylor inclusion function. They further integrated the Chebyshev inclusion function and an interval bisection algorithm to avoid the inner layer optimization.

Most of the present methods for solving nonlinear interval optimization models are indirect ones based on model conversion. However, the model conversion process deviates from the original intention of interval modeling for factually reflecting the uncertainty of engineering structures. At the same time, a variety of parameters need to be introduced in the model conversion process, which makes the interval optimization process complicated and often results in different solutions when prescribing different values for these parameters. To overcome these shortcomings, we proposed a novel optimization algorithm for directly solving the nonlinear constrained interval optimization models in our previous work (Cheng et al., 2016). However, the algorithm cannot solve the interval reliability-based design optimization model investigated here. Therefore, a new concept of the degree of interval reliability violation (DIRV) and the DIRV-based preferential guidelines are proposed in this paper, which enable the direct ranking of various design vectors according to their corresponding interval objective and constraint values. Considering that the genetic algorithm (GA) provides robust, efficient, and effective search capabilities in complex spaces based on natural genetics and that it needs no information about the search space besides a fitness function for each solution (Costa et al., 2005; Fernandez-Prieto et al., 2011), GA is chosen as the algorithm for calculating the interval bounds of the objective and constraint functions in inner layer optimization and realizing the direct rank of various design vectors in the outer layer optimization. An efficient optimization algorithm integrating the Kriging model and nested GA is proposed to realize the direct interval ranking and directly solve the interval reliability-based design optimization model. The adaptive resampling technology proposed in our previous study (Cheng et al., 2015) is utilized to ensure the prediction accuracy of the Kriging models. Other than indirect algorithms, the proposed algorithm can yield interval solutions to the interval reliability-based design models of engineering structures and provide more insights into the interval optimization problems.

In this study, the interval reliability-based design optimization model of an uncertain structure is constructed first. Then, the unified formula for calculating the interval reliability is proposed, the definition of DIRV and the DIRV-based preferential guidelines for direct interval ranking are proposed, the direct interval optimization algorithm is put forward, and a numeric example is provided to verify the effectiveness of the proposed direct interval reliability-based design optimization method, the superiority of which to the indirect one is discussed in detail. Finally, the proposed interval reliability-based design optimization method is applied to the upper beam of a high-speed press with uncertain material properties.

2 Interval reliability-based design optimization model of an uncertain structure

The uncertain factors influencing the mechanical properties of the structure are described as interval variables. The interested mechanical properties of the structure are described as the objective and constraint functions, which are nonlinear functions of both the design variables and interval variables. The interval reliability R, defined as the order relation between the structure’s interval mechanical properties and the given interval constants, is introduced to make the structural properties in constraint functions meet their corresponding reliability requirements. Then, the interval reliability-based design optimization model of the structure is described as follows:

$$\begin{array}{*{20}c} {\underset {x}{{\min}}f\left({x,U} \right),\;\;\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ {{\rm{s}}{.}{\rm{t}}{{.}}\;{R_i}\left[ {{g_i}\left({x,U} \right) \leq {B_i} = \left[ {b_i^{\rm{L}},b_i^{\rm{R}}} \right]} \right] \geq {\eta _i},\quad }\\ {i = 1,\;2, \cdots, p, \quad \quad \quad \quad \quad \quad }\\ {x = \left({{x_1},{x_2}, \cdots, {x_n}} \right) \in {{\mathbb{R}}^n},\quad \quad \quad \quad }\\ {U = \left({{U_1},{U_2}, \cdots, {U_m}} \right),\quad \quad \quad \quad \quad \;} \end{array}$$
(1)

where x is the n-dimensional design vector of the structure while U is the m-dimensional interval uncertain vector with all its components described as interval numbers; the superscripts “L” and “R” denote the left and right bounds of an interval, respectively; f(x, U) and g i (x, U) (i=1, 2, …, p) are the objective and constraint functions indicating the structure’s mechanical performance indices, the values of which depend on the design vector x and interval vector U; B i is the given interval constant of the ith constraint, which can also be a deterministic value; R i is the interval reliability of the ith constraint while η i is the prescribed reliability requirement of the ith constraint; p and m are the numbers of constraints and uncertain parameters, respectively.

3 Unified formula for the efficient calculation of interval reliability

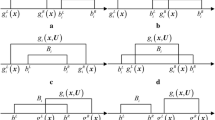
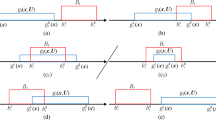
The graphical method proposed by Wang and Qiu (2009) for calculating the interval reliability converts the comparison of two intervals A and B into the comparison of 2D graphical areas. As shown in Fig. 1, the line A=B indicates the limit state equation of two intervals, and the interval reliability of A≤B is the area ratio of the shaded part and the whole rectangle. The graphical method is very intuitive and easy understanding. However, there are six kinds of positional relationships between the line A=B and the rectangle. In the application of graphical method, one should first draw the graph, and then determine the six kinds of positional relationships between A and B, calculate the areas of the shaded part and rectangle, and finally calculate the interval reliability P(A≤B). The determination process of the interval reliability P(A≤B) is somewhat complicated, which limits the application of the graphical method in engineering. To overcome the limitation, Qi and Qiu (2013) described the interval reliability of six different positional relationships as a “two formulas model”. However, it is still not simple and convenient enough since it still requires the determination of the positional relationship of the left bounds of the two intervals.

Fig. 1
figure 1

Sketch map of the graphical method

Full size image

To overcome the limitations of graphical methods, the unified formula in Eq. (2) is proposed for efficiently calculating the interval reliability P(A≤B). The intervals A and B may be in six different relative positions.

$$\begin{array}{*{20}c} {P(A \leq B) = \max \left\{ {\min ({A^{\rm{R}}} - {A^{\rm{L}}},\;{B^{\rm{R}}} - {A^{\rm{L}}})\quad \quad \quad \quad \quad \quad \quad \quad \quad } \right.}\\ { \times \left[ {\max (0,\;{B^{\rm{R}}} - {A^{\rm{L}}}) + \max (0,\;{B^{\rm{R}}} - {A^{\rm{R}}})} \right]\;}\\ {/\left[ {2{\mathop{\rm sign}\nolimits} \left({0{.}5 + {\mathop{\rm sign}\nolimits} ({A^{\rm{L}}} - {B^{\rm{L}}})} \right)\quad \quad \quad \quad } \right.}\\ {\left. { \times ({A^{\rm{R}}} - {A^{\rm{L}}}) \times ({B^{\rm{R}}} - {B^{\rm{L}}})} \right],\,\;\;\quad \quad \quad \quad \quad }\\ {1 - \left[ {\min ({A^{\rm{R}}} - {B^{\rm{L}}},\;{B^{\rm{R}}} - {B^{\rm{L}}})\quad \quad \quad \quad \quad } \right.}\\ {\left. { \times \left({\max (0,\;{A^{\rm{R}}} - {B^{\rm{L}}}) + \max (0,\;{A^{\rm{R}}} - {B^{\rm{R}}})} \right)} \right]}\\ {\left. {/\left[ {2({A^{\rm{R}}} - {A^{\rm{L}}}) \times ({B^{\rm{R}}} - {B^{\rm{L}}})} \right]} \right\}{.}\quad \quad \quad \quad \quad } \end{array}$$
(2)

If interval B degenerates into a real number b, the interval reliability can be calculated by

$$P(A \leq b) = \min \left({{{\max ({A^{\rm{L}}},\;b) - {A^{\rm{L}}}} \over {{A^{\rm{R}}} - {A^{\rm{L}}}}},\;1} \right){.}$$
(3)

Similarly, if interval A degenerates into a real number a, the interval reliability can be calculated by

$$P(a \leq B) = \max \left({{{{B^{\rm{R}}} - \max ({B^{\rm{L}}},\;a)} \over {{B^{\rm{R}}} - {B^{\rm{L}}}}},\;0} \right){.}$$
(4)

It is obvious that there is no need to draw a graph and determine the positional relationship of the left bounds of the two intervals when applying the unified formula to the calculation of interval reliability P(A≤B). Hence, the calculation of the interval reliability based on the unified formula in Eq. (2) is simple and easy to program.

4 DIRV and DIRV-based preferential guidelines

Definition 1 Degree of interval reliability violation (DIRV): As far as the ith interval constraint g i (x, U)≤B i =[b L i , b R i ] in the reliability-based design optimization model in Eq. (1) is concerned, the DIRV V i (x) corresponding to a design vector x is defined as

$${V_i}(x) = \max \left\{ {0,\;\;{\eta _i} - {R_i}\left[ {{g_i}(x,\;U) \leq {B_i} = \left[ {b_i^{\rm{L}},\;b_i^{\rm{R}}} \right]} \right]} \right\},$$
(5)

where R i is calculated by the unified formula for computing interval reliability in Eq. (2). Specifically, there is V i (x)=0 when R i ≥η i and V i (x)=η i −R i when R i <η i .

After the DIRVs of all the constraint functions in the reliability-based design model in Eq. (1) are calculated according to Definition 1, the total DIRV (denoted as TDIRV for concision) corresponding to a design vector x can be obtained by

$${V_{\rm{T}}}(x) = \sum\limits_{i = 1}^p {{V_i}} (x){.}$$
(6)

Then, a design vector x is feasible when VT(x)= 0, and it is infeasible when VT(x)>0.

Once the TDIRV values of all the design vectors have been calculated based on Eq. (6) and Definition 1, the merit ranking of different design vectors can be determined by the following DIRV-based preferential guidelines:

  1. (1)

    A feasible vector x i is superior to an infeasible vector x j . That is, vector x i is superior to vector x j when VT(x i )=0 and VT(x j )>0.

  2. (2)

    For two infeasible design vectors x i and x j , x i is superior to x j if VT(x i )≤VT(x j ).

  3. (3)

    For two feasible design vectors x i and x j , x i is superior to x j when fC(x i )<fC(x j ) or fC(x i )=fC(x j ) and fW(x i )<fW(x j ). The superscripts “C” and “W” denote the center and halfwidth of an interval, respectively.

5 Algorithm for direct interval reliability-based design optimization

An integrated algorithm for directly solving the interval reliability-based design optimization model of an uncertain structure is proposed based on nested GA and Kriging technique. The inner layer GAs calculate the interval bounds of the structural performance indices based on Kriging models while the outer layer GA locates the optimal design vector according to the DIRV-based preferential guidelines. As shown in Fig. 2, the implementation of the proposed algorithm proceeds as follows.

  • Step 1 Establish the interval reliability-based design optimization model according to the design requirements and determine the varying ranges of design variables and uncertain factors.

  • Step 2 Construct the parameterized finite element model of the structure and collect enough sample points based on Latin hypercube sampling (LHS) and finite element analysis (FEA). Establish the Kriging models for computing the mechanical performance indices of the structure based on the collected sample data.

  • Step 3 Initialize the GA parameters involved in the nested optimization, including the population sizes Popi and Popo of the inner and outer layer GAs, the maximum iteration numbers Iteri max and Itero max of the inner and outer layer GAs, the crossover and mutation probabilities, and the convergence threshold for outer layer GA. Set the iteration number of the outer layer GA Itero=1 and generate the initial population of the outer layer GA.

  • Step 4 If Itero<Itero max, go to Step 5. Otherwise, go to Step 8.

  • Step 5 For every individual in the current population of outer layer GA, inner layer GAs are called for computing fR(x), fL(x), g R i (x), and g L i (x), during which the Kriging models constructed in Step 2 are invoked repeatedly for computing the structure’s mechanical performance indices corresponding to different interval parameters. After the interval reliability of every constraint function R i [g i (x, U)≤B i ] is calculated by the unified formula in Eq. (2) and the DIRV of every constraint function V i (x) is computed by Eq. (5), the TDIRV VT(x) can be obtained by Eq. (6).

  • Step 6 All the design vectors are ranked according to the DIRV-based preferential guidelines proposed in Section 4, and then the design vector x i (i=1, 2, …, Popo) is assigned a rank number Rank i (i=1, 2, …, Popo), to the effect that the better design vector has the lower rank number while the worse design vector has the higher rank number. Then, the fitness value of every design vector x i (i=1, 2, …, Popo) can be calculated by Eq. (7), as a result of which the better design vector is assigned a larger fitness value.

    $$\begin{array}{*{20}c} {{\rm{Fit}}\left({{x_i}} \right) = 1/{\rm{Ran}}{{\rm{k}}_i},} & {i = 1, 2, \cdots, {\rm{Po}}{{\rm{p}}_{\rm{o}}}{.}} \end{array}$$
    (7)

  • Step 7 If the convergence threshold is reached, go to Step 8, otherwise, let Itero=Itero+1, and implement the GA operations of crossover and mutation to generate Popo number of new individuals as the next population of the out layer GA, go to Step 4.

  • Step 8 The design vector with the largest fitness value is output as the optimal solution to the interval reliability-based design optimization model.

Fig. 2
figure 2

Flowchart of algorithm for solving the interval reliability-based design model

Full size image

6 Numeric example

The numeric example in Eq. (8) is utilized to verify the effectiveness of the proposed algorithm for directly solving the interval reliability-based design model, where f(x, U) is the interval objective function, R1 and R2 are the interval reliabilities of constraint functions g1(x, U) and g2(x, U), η1 and η2 are the required reliabilities of constraint functions g1(x, U) and g2(x, U), respectively.

$$\begin{array}{*{20}c} {\min \limits_x f\left({x,\;U} \right) = 130{.}0 - U_1^2({x_1} + 2) - {U_2}x_2^2 - U_3^2x_3^2,\quad \quad \quad \quad }\\ {{\rm{s}}{.}{\rm{t}}.\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ {{R_1}\left[ {{g_1}(x,\;U) = {U_1}x_1^2 - U_2^2{x_2} + {U_3}{x_3} \leq [8{.}0,\;10{.}0]} \right]\quad \quad \quad \quad \quad }\\ { \geq {\eta _1} = 0{.}80,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ {{R_2}\left[ {{g_2}(x,\;U) = {U_1}{x_1} + {U_2}{x_2} + U_3^2x_3^2 + 1{.}0 \geq [75{.}0,\;90{.}0]} \right]\quad \quad \,}\\ { \geq {\eta _2} = 0{.}85,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ {{x_1} \in [ - 1{.}0,\;5{.}0],\;\;{x_2} \in [ - 3{.}0,\;6{.}0],\;\;{x_3} \in [ - 2{.}0,\;7{.}0],\quad \quad \quad \quad }\\ {{U_1} = \left[ {1{.}0,\;1{.}3} \right],\;\;{U_2} = \left[ {0{.}9,\;1{.}1} \right],\;\;{U_3} = \left[ {1{.}2,\;1{.}4} \right]{.}\quad \quad \quad \quad \quad } \end{array}$$
(8)

The interval reliability-based design model in Eq. (8) is firstly solved by the proposed direct optimization algorithm. The outer layer GA terminates when the absolute difference between the objective mid-point value of the optimal solution and the average value of the current population is less than 10−3 for 10 consecutive generations. GA involves a number of parameters, different levels of which greatly affect its performance (Kucukkoc et al., 2013). The parameter combination of the nested GA for solving the numeric example is determined based on many trials of different parameter combinations, and the one producing the best results is selected for the program (Table 1). Fig. 3 shows the GA evolution curves of the objective function, which converges at the 63rd generation with the optimal solution obtained as xP=(1.97, 5.99, 7.00).

Fig. 3
figure 3

GA evolution of the objective value obtained by proposed algorithm

Full size image
Table 1 Parameters of nested GA for solving the numeric example
Full size table

To solve the interval reliability-based design model of the numeric example by Jiang (2008)’s indirect algorithm, the interval model in Eq. (8) is transformed into a deterministic one. The relevant parameters are set as follows: the weight coefficients of the mid-point and halfwidth of the objective function equal 1.0 and 0.0, respectively, the parameter to ensure a non-negative mid-point and halfwidth of the objective function equals 0, the penalty factor is 100 000 while the regularization factors for fC(x) and fW(x) are 1.33 and 0.34, respectively. The nested GA parameters as well as the convergent condition of the outer layer GA are set the same as those utilized in the proposed direct algorithm. Fig. 4 shows the GA evolution curves of the objective function, which converges at the 92nd generation with the optimal solution obtained as xJ=(1.89, 5.93, 7.00).

Fig. 4
figure 4

GA evolution of the objective value obtained by Jiang ( 2008 )’s algorithm

Full size image

Table 2 provides a comparison of the optimization results of the numeric example obtained by the proposed algorithm and Jiang (2008)’s indirect algorithm. As can be seen from Table 2, the optimal solutions located by both algorithms satisfy the reliability requirements of two interval constraints, namely, VT(xP)=VT(xJ)=0. However, the optimal solution obtained by the proposed algorithm is better than that of Jiang (2008)’s since its corresponding objective mid-point value is much smaller than that of Jiang (2008)’s although there is a slight increase in the objective halfwidth. Moreover, the proposed algorithm is much simpler than Jiang (2008)’s since it avoids the model transformation process involving the determination of various parameters such as weighting coefficients, penalty, and regularization factors. The convergent curves of the optimal solution in Figs. 3 and 4 also demonstrate that the proposed algorithm is more efficient than Jiang (2008)’s indirect algorithm.

Table 2 Comparison of the optimization results of numeric example obtained by different algorithms
Full size table

7 Application in engineering

7.1 Construction of the interval reliability-based design optimization model

The upper beam of a high-speed press shown in Fig. 5 is utilized to verify the feasibility of the proposed interval reliability-based design optimization method in engineering. The dimensions h1, h2, l1, l2, and l3 in the cross section (Fig. 6) of the upper beam are chosen as design variables while its material density ρ and elastic modulus E are regarded as uncertain factors, the varying ranges of which are listed in Table 3.

Fig. 5
figure 5

The 3D model of the upper beam

Full size image
Fig. 6
figure 6

Cross section of the upper beam

Full size image
Table 3 Varying ranges of design variables and uncertain factors
Full size table

According to the performance requirements of the upper beam, the maximum deformation indicating stiffness is described as the objective function while its weight and maximum equivalent stress are described as constraint functions, the reliability requirements of which are 0.95 and 0.98, respectively. Then the interval reliability-based design optimization model of the upper beam is established as

$$\begin{array}{*{20}c} {\min \limits_x d(x,\;U) = \min \limits_x d({h_1},\;{h_2},\;{l_1},\;{l_2},\;{l_3},\;\rho, \;E)\,\,\,\;\;\;\quad \quad \quad \quad }\\ {{\rm{s}}{.}{\rm{t}}.\,\,\;\;\;\;\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ {{R_1}\left[ {w(x,\;{U_1}) = w(x,\;\rho) \leq [4990,\;5010]\;{\rm{kg}}} \right]\quad \;\;\;\,\,\,}\\ { \geq {\eta _1} = 0{.}95,\,\,\,\;\;\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ {{R_2}\left[ {\delta (x,\;U) \leq [44,\;45]\;{\rm{MPa}}} \right] \geq {\eta _2} = 0{.}98,\quad \,\quad \quad }\\ {x = ({h_1},\;{h_2},\;{l_1},\;{l_2},\;{l_3}),\;\;\;U = ({U_1},\;{U_2});\;\;\quad \quad \quad \quad \quad \quad \quad }\\ {210\;{\rm{mm}} \leq {h_1} \leq 250\;{\rm{mm}},\;\;\;250\;{\rm{mm}} \leq {h_2} \leq 300\;{\rm{mm}},\quad \quad }\\ {80\;{\rm{mm}} \leq {l_1} \leq 120\;{\rm{mm}},\;\;\;25\;{\rm{mm}} \leq {l_2} \leq 55\;{\rm{mm}},\quad \quad \quad \quad \;}\\ {330\;{\rm{mm}} \leq {l_3} \leq 390\;{\rm{mm}};\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\,\,}\\ {{U_1} = \rho = [7280,\;7320]\;{\rm{kg}}/{{\rm{m}}^3},\,\,\,\quad \quad \quad \quad \quad \quad \quad \quad \quad \,\,\,\,\,}\\ {{U_2} = E = [126,\;154]\;{\rm{GPa}},\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad } \end{array}$$
(9)

where x=(h1, h2, l1, l2, l3) is the design vector, U=(ρ, E) is the uncertain vector, d(x, U) indicating stress is the objective function, w(x, U1) indicating weight and δ(x, U) indicating strength are the constraint functions, R1 and R2 are the interval reliabilities of two constraint functions w(x, U1) and δ(x, U) while η1 and η2 are their corresponding desired reliabilities, respectively.

Fig. 7 illustrates the 1/4 FEA model of the upper beam that acts as a high-fidelity simulation model for computing mechanical performance indices of the upper beam. The upper beam is limited at the bottom by the adjusting nuts on four columns, and thus a fixed support is exerted at its bottom (arrow A). Two frictionless supports are applied on two symmetric planes of the 1/4 FEA model of the upper beam (arrows B and C). The upper beam is connected with four driving oil cylinders and there is a pressure of 800 kN at every connected position (arrow D). A bearing load of 250 kN is applied on the end bearing hole in the 1/4 FEA model of the upper beam (arrow E) while a bearing load of 500 kN is applied on the mid bearing hole (arrow F) during the stamping process.

Fig. 7
figure 7

FEA model of 1/4 upper beam: loads and constraints

Full size image

The performance indices of the initial design scheme of the upper beam are shown in Table 4. It is obvious that neither constraint in Eq. (9) is satisfied for the initial design scheme.

Table 4 Performance indices of the initial design scheme of the upper beam
Full size table

7.2 Optimization results obtained by the proposed algorithm

The Kriging models for computing the performance indices of the upper beam in the objective and constraint functions are constructed based on adaptive resampling technology (Cheng et al., 2015). Readers can refer to the previous study (Cheng et al., 2015) for a detailed description of the technology, which is not given here to save space. The construction of every Kriging model is an iterative process, which is terminated when the multiple correlation coefficient R2>0.95 and the relative maximum absolute error RMAE<0.05 for ensuring its prediction accuracy. The R2 and RMAE values of the Kriging models for computing the performance indices of the upper beam in the iterative process are listed in Table 5.

Table 5 R 2 and RMAE values of Kriging models in the iteration process
Full size table

The interval reliability-based design optimization model of the upper beam in Eq. (9) is firstly solved by the proposed direct interval optimization algorithm. The outer layer GA terminates when the absolute difference between the objective mid-point value of the optimal solution and the average value of the current population is less than 10−4 for 10 consecutive generations. The parameter combination of the nested GA for solving the reliability-based design optimization model of the upper beam is listed in Table 6. Fig. 8 shows the GA evolution curves of the performance indices in the objective and constraint functions, where the objective function converges at the 134th generation with the optimal solution obtained as xP=(249.89, 262.32, 80.36, 36.88, 388.40). The interval reliabilities of the weight and maximum stress of the upper beam corresponding to xP are 0.95 and 1.00, respectively, while the maximum deformation is <0.2017, 0.0196>, meaning that the interval reliabilities of the upper beam’s weight and maximum stress have been greatly improved after optimization although there is a slight increase in the mid-point of the maximum deformation in the objective function.

Fig. 8
figure 8

GA evolution curves of the performance indices of the upper beam obtained by the proposed algorithm

(a) GA evolution of weight; (b) GA evolution of maximum equivalent stress; (c) GA evolution of maximum deformation

Full size image
Table 6 Parameters of nested GA for solving the upper beam’s reliability-based design model
Full size table

7.3 Comparison with the indirect algorithm

To solve the interval reliability-based design optimization model of the upper beam by Jiang (2008)’s indirect algorithm, the interval model in Eq. (9) is first transformed into a deterministic one. The relevant parameters are set as follows: the weighting coefficients of the mid-point and halfwidth of the objective function equal 1.0 and 0.0, respectively, the parameter for ensuring non-negative mid-point and halfwidth of the objective function is 0, the penalty factor is 10 000 while the regularization factors for fC(x) and fW(x) are 0.25 and 0.03, respectively. The nested GA parameters as well as the convergent condition of the outer layer GA are set the same as those utilized in the proposed algorithm. Fig. 9 illustrates the GA evolution curves of the objective and constraint functions obtained by the indirect algorithm, where the objective function converges at the 197th generation with the optimal solution obtained as xJ=(243.34, 251.46, 80.15, 32.24, 389.39). The interval reliabilities of the upper beam’s weight and maximum stress corresponding to xJ are 0.95 and 0.99, respectively, while the maximum deformation is <0.2162, 0.0196>, meaning that the interval reliabilities of the weight and maximum stress have been improved after optimization while there is a slight increase in the mid-point of the maximum deformation in the objective function.

Fig. 9
figure 9

GA evolution curves of the performance indices of the upper beam obtained by the indirect algorithm

(a) GA evolution of weight; (b) GA evolution of maximum equivalent stress; (c) GA evolution of maximum deformation

Full size image

Table 7 provides a comparison of the optimization results of the upper beam obtained by the proposed algorithm and Jiang (2008)’s algorithm. As can be seen from Table 7, the optimal solutions located by both algorithms satisfy the reliability requirements of two interval constraints, namely, there is VT(xP)=VT(xJ)=0. However, the optimal solution obtained by the proposed algorithm is better than that obtained by Jiang (2008)’s since the mid-point of its corresponding objective value is much smaller than that obtained by Jiang (2008)’s. Moreover, the proposed algorithm is much simpler than Jiang (2008)’s since it avoids the model transformation process. The convergent curves of the optimal solutions in Figs. 8 and 9 also demonstrate that the proposed algorithm is more efficient than Jiang (2008)’s algorithm. Hence, the proposed direct interval reliability-based design optimization method is feasible and effective in engineering, and it is superior to the indirect one.

Table 7 Comparison of the optimization results of the upper beam obtained by the proposed algorithm and Jiang ( 2008 )’s algorithm
Full size table

8 Conclusions

An interval reliability-based design model was constructed for the optimization of an uncertain structure with interval parameters. A unified formula for the efficient computation of interval reliability and a new concept of DIRV as well as the DIRV-based preferential guidelines were put forward for the direct ranking of various design vectors. A direct interval optimization algorithm integrating nested GA and Kriging technique was proposed for solving the interval reliability-based design model. A numeric example was utilized to verify the validity of the proposed algorithm as well as its superiority to conventional indirect optimization algorithms. Finally, the proposed direct interval reliability-based design optimization method was applied to the optimization of a press upper beam, the results of which demonstrated the feasibility and effectiveness of the proposed method in engineering.