1 Introduction

With increasingly stringent emission regulations, selective catalytic reduction (SCR) seems to be one of the most promising methods for the abatement of NOx emissions from diesel engines. In typical SCR systems, urea-water-solution (UWS, containing 32.5% (in weight) urea, adblue) is sprayed into the hot exhaust gas. Normally, water evaporates first from the UWS and the remaining urea undergoes thermolysis and hydrolysis to produce ammonia (NH3) as a reducing agent. Considering the continuous variation in load and engine speed combined with spatial limitations, it is difficult for the UWS to decompose completely when it reaches the catalyst. Incomplete decomposition of the UWS leads to spray wall interaction and the formation of a wall film. Side reactions may take place in the wall film producing undesired deposit by-products such as biuret, cyanuric acid (CYA), ammelide, ammeline, melamine, and more complex polymerization products (Stradella and Argentero, 1993; Chen and Isa, 1998; Zhong et al., 2013). These undesired by-products are the main components of solid deposits which may block the exhaust pipe and catalyst leading to higher exhaust pressure and lower conversion efficiency of urea decomposition. Recently, the impact of UWS soaking and deposits on the performance of SCR catalysts were also investigated by Yao et al. (2016).

The UWS process is very complex. From the injection point to the entrance of the SCR catalyst, relevant processes include: (1) momentum interaction between the droplets and gas phase; (2) evaporation and thermolysis of UWS droplets; (3) heat transfer among the wall, droplets, and gas phase; (4) spray-wall interaction; (5) wall film formation and chemical reactions in the film.

The evaporation and thermolysis processes of UWS droplets have been studied by many researchers. For a basic understanding of UWS spray evaporation, it is necessary to investigate the evaporation characteristics of a single UWS droplet. Wang et al. (2009) experimented using a suspended droplet. The droplet evaporation rates were extracted for a variety of initial droplet diameters and ambient temperatures. Musa et al. (2006) investigated the evaporation characteristics of a single UWS droplet on a heated surface and the evaporation of a suspended UWS droplet in an electric furnace. The lifetimes of droplets were measured and the data were compared with results from distilled water. Three stages, including primary evaporation, transition, and crystallization were found during the UWS droplet heating process. Although the above two investigations were both conducted in a stagnant environment, the droplet evaporation rate in a forced convection environment can be calculated with a stagnant rate by using empirical correlations (Chiu, 2000). Urea thermolysis begins when the water content evaporates completely. Stradella and Argentero (1993) and Chen et al. (1998) found that ammonia and iso-cyanic were produced during the urea thermolysis process. High molecular compounds such as biuret, CYA, ammelide, and ammeline also appeared in their investigation. Schaber et al. (1999; 2004) studied urea thermal decomposition in an open vessel condition. Details of the reaction mechanism for urea thermolysis were proposed, and the process was divided into four reaction regions based on different ambient temperatures. Lundström et al. (2009) studied ammonia and iso-cyanic production during thermal decomposition of urea under flow reactor conditions. Different heating rates and types of reactors including monolith and cup were compared to investigate their influence on the ammonia and iso-cyanic production process.

The fuel spray wall interaction has been investigated for many years (Senda et al., 1994; Bai and Gosman, 1995; Stanton and Rutland, 1996). The regimes that an impinging droplet may undergo differently were identified as stick, spread, rebound, rebound with break-up, boiling-induced break-up, break-up, and splash (Bai and Gosman, 1995). A UWS spray wall interaction also cannot be avoided in most SCR applications due to insufficient entrainment, slow evaporation and thermolysis, and the inertia of the droplets. It causes local cooling of the wall and a wall film will form if the wall temperature decreases below a critical temperature (Birkhold et al., 2006; Varna et al., 2014; Spiteri et al., 2015). Kuhnke et al. (2004) and Abu-Ramadan et al. (2012) divided the UWS spray impingement into four regimes based on the properties and energy of the droplet, and the wall surface condition. Birkhold (2007) extended the spray wall interaction regimes by adding two partial regimes (partial rebound, partial break-up), which provided a better prediction of urea deposition at the wall.

Numerical simulation is an effective approach for scientific research because of its low cost and high efficiency. Various models have been proposed to simulate UWS evaporation, thermolysis, and spray wall interaction. Birkhold et al. (2007) investigated the influence of urea on the evaporation of water from a UWS droplet using different evaporation models. The thermolysis process was described by an extended Arrhenius expression and urea was assumed to decompose into NH3 and HNCO directly. Birkhold et al. (2006) developed a model of two-phase flow and spray wall interaction. The wall film distribution can be simulated. However, these studies did not take account of the formation of solid by-products, such as biuret and CYA.

Several investigators have attempted to derive a kinetic scheme for urea thermolysis. In Ebrahimian et al. (2012)’s study, urea thermolysis reactions were supposed to take place in solid phase. The solid by-products were supposed to be biuret, CYA, and ammelide since they were the main components during urea thermolysis in experiments. The kinetic scheme consisted of 12 steps, the first nine of which occurred in dry media and the last three in UWS. Ebrahimian (2011) implemented the kinetic scheme into a computational fluid dynamics (CFD) code to simulate deposit formation in a typical automotive SCR system. However, only the results at time 0.01 s were presented. Brack et al. (2014) developed a more complicated kinetic scheme of urea thermolysis which contained 15 steps. Besides biuret, CYA, and ammelide as the main components, other intermediate products like biuret-matrix and triuret were taken into consideration.

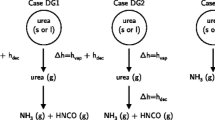
Previous studies showed that the conditions under which urea thermolysis is performed strongly influence urea decomposition behavior. Lundström et al. (2009) showed that urea on a monolith (impregnated with a 32.5% UWS) can totally decompose into NH3 and HNCO, while urea on a cup will form by-products (i.e., CYA) during the heating process. In thermogravimetric analysis (TGA) experiments, Eichelbaum et al. (2010) and Brack et al. (2014) found that the geometric structure of the crucible has a significant impact on urea decomposition. All these findings indicate that a quick removal of HNCO can effectively reduce or even prevent the formation of by-products. In SCR applications, the atomization of UWS can significantly enlarge the surface that is exposed to the bulk gas, and gaseous products can be easily removed, thus avoiding high local concentrations of HNCO. Therefore, it seems reasonable that urea in the droplet phase can decompose into NH3 and HNCO completely, just as Birkhold et al. (2007) supposed. However, if the UWS spray hits the wall and forms a wall film, side reactions will take place and form by-products, since the mass transfer rate of gaseous product from the film to the bulk gas is low because of the small area of the contact surface. The discussion above indicates that the mechanisms of urea thermolysis differ between the droplet phase and the wall film in SCR applications. A combination of Birkhold et al. (2007)’s direct decomposition model (in the droplet phase) and Ebrahimian et al. (2010)’s kinetic model (in the wall film) seems to be a good approach for simulation.

Analyzing the literature, a reliable mathematical model which can predict not only the generation of reducing agent but also the formation of deposits still remains an important topic of research. Considering that the formation of deposits requires a long time (minutes to hours) in actual SCR applications, a transient 3D simulation also requires a large amount of computation. 1D simulation costs much less computational resource than 3D simulation and can provide guidance when designing an SCR system at a system level. Therefore, a quasi 1D model of two-phase flow and deposit formation was developed in this study. The gas phase flow is solved by the Euler method and the semi-implicit method for pressure-linked equation (SIMPLE) algorithm is employed to decouple the pressure and velocity. The liquid phase is treated using Lagrangian particle tracking, which solves the equations of motion, evaporation, thermolysis, and spray wall interaction. The interaction between two phases was considered by adding source terms to the gas phase equation. Furthermore, a new 1D wall film model is presented that considers the motion, mass, and heat transfer of the wall film. A combination of the Birkhold and Ebrahimian models is implemented to describe the different decomposition behaviors of urea in droplet phase and wall film.

2 Modeling

The primary scope of this study was the modeling of evaporation, thermolysis, spray wall interaction, and wall film formation inside a 1D exhaust pipe. Considering that HNCO is very stable in the gas phase (Koebel et al., 2000), the hydrolysis of HNCO is neglected for simplicity. The presented model is quasi 1D as the radial velocity of a droplet and the diameter of the pipe are considered.

2.1 Gas phase model (Wurzenberger et al., 2008)

Compared with exhaust mass flow, the mass flow of UWS spray is extremely small, hence the mass source term of the continuity equation is neglected. The continuity equation of the 1D gas phase with a constant cross section is:

$${{\partial {\rho _{\rm{g}}}} \over {\partial t}} + {{\partial {\rho _{\rm{g}}}{u_{\rm{g}}}} \over {\partial x}} = 0,$$
(1)

where ρg is the gas density, ug is the gas velocity, t is the time, and x is the axial position of the pipe.

It can be considered that the pressure drop in the pipe is mainly caused by the friction loss, therefore, the momentum equation can be simplified as Darcy’s law:

$${{{\rm{d}}{P_{\rm{g}}}} \over {{\rm{d}}x}} = - {K_{\rm{d}}}{u_{\rm{g}}},$$
(2)

where Pg is the gas pressure, and Kd is a friction coefficient, calculated as

$${K_{\rm{d}}} = \varphi {{{u_{\rm{g}}}} \over 2}{{{\rho _{\rm{g}}}} \over {{d_{{\rm{hyd}}}}}}\zeta,$$
(3)

where φ is the pipe channel shape factor, dhyd is the pipe diameter, and ζ is a generic friction coefficient:

$$\zeta = \left\{ {\begin{array}{*{20}c} {{\zeta _{\rm{L}}},\quad \quad \quad \quad \quad \quad Re < R{e_{\rm{L}}},\quad \quad }\\ {{\zeta _{\rm{T}}},\quad \quad \quad \quad \quad \quad Re \geq R{e_{\rm{T}}},\quad \quad }\\ {{\zeta _{\rm{L}}}\left({1 - {{Re - R{e_{\rm{L}}}} \over {R{e_{\rm{T}}} - R{e_{\rm{L}}}}}} \right) + {\zeta _{\rm{T}}}\left({{{Re - R{e_{\rm{L}}}} \over {R{e_{\rm{T}}} - R{e_{\rm{L}}}}}} \right),}\\ {\quad \quad \quad \quad \quad \quad \quad R{e_{\rm{L}}} < Re < R{e_{\rm{T}}},} \end{array}} \right.$$
(4)

where ReL is the laminar Reynolds number (ReL = 2300), and ReT is the turbulent Reynolds number (ReT=5000).

The energy equation of the gas phase is:

$${{\partial {\rho _{\rm{g}}}{H_{\rm{g}}}} \over {\partial t}} + {{\partial {\rho _{\rm{g}}}{u_{\rm{g}}}{H_{\rm{g}}}} \over {\partial x}} = {\alpha _{{\rm{gw}}}}({T_{\rm{w}}} - {T_{\rm{g}}}){a_{{\rm{geo}}}} + {S_{{\rm{qgs}}}},$$
(5)

where Hg is the gas enthalpy, αgw is the heat transfer coefficient, Tg and Tw are the gas and wall temperatures, respectively, ageo is the geometrical surface area of the pipe wall inner side, and Sqgs is the source term of spray and wall film.

The species conservation equation is:

$${{\partial {\rho _{\rm{g}}}{w_{i,{\rm{g}}}}} \over {\partial t}} + {{\partial {\rho _{\rm{g}}}{u_{\rm{g}}}{w_{i,{\rm{g}}}}} \over {\partial x}} = {S_{{\rm{species}}}},$$
(6)

where wi,g is mass fraction of gas species (i), and Sspecies is the source term of gas species (i).

2.2 Liquid phase model

The liquid phase model describes the evaporation, thermolysis, motion, and spray wall interaction processes of UWS droplets based on a statistical method referred to as the discrete droplet method (DDM). To simplify the calculation, the concept of a “parcel” is employed. Each parcel represents a group of identical non-interacting droplets with the same properties. One member of the droplet group represents the behavior of the complete parcel. Parcels are introduced in the flow domain with initial conditions of position, size, velocity, temperature, and number of droplets in the parcel, and each time step introduces one parcel.

Some other investigations indicated that the physical state of UWS (mainly temperature) can affect the behavior of the spray and the evolution of the spray structure when injected into a hot environment (Vuuren et al., 2015). However, this is beyond the scope of this paper and the temperature effect on the spray characteristics was neglected in this study.

The evaporation of spray is based on a modified Abramzon-Sirignano model. The differential equations for droplet mass and temperature are:

$${{{\rm{d}}{m_{\rm{d}}}} \over {{\rm{d}}t}} = - \pi {D_{\rm{d}}}{\rho _{{\rm{g}},{\rm{mix}}}}\Gamma Sh\ln [(1 + {B_{\rm{M}}}) \times ({T_\infty }/673)],$$
(7)
$${{{\rm{d}}{T_{\rm{d}}}} \over {{\rm{d}}t}} = {{(- {\rm{d}}{m_{\rm{d}}}/{\rm{d}}t){c_{{\rm{p}},{\rm{vap}}}}({T_{\rm{g}}} - {T_{\rm{d}}})/{B_{\rm{T}}} - {L_{{\rm{vap}}}}} \over {{m_{\rm{d}}}{c_{{\rm{p}},{\rm{d}}}}}},$$
(8)

where md is the mass of droplet, Dd is the droplet diameter, ρg,mix is the density of exhaust gas and water vapor mixture, Γ is the mass diffusion coefficient, Sh is the Sherwood number, T∞ is the ambient temperature, Td is the droplet temperature, cp,vap is the specific heat of vapor, Lvap is the latent heat of vapor, cp,d is the specific heat of droplet, B is the Spalding number, and subscripts M and T represent mass and temperature, respectively.

Urea thermolysis begins when water content evaporates completely. In the droplet, urea is supposed to decompose into NH3 and HNCO directly. The thermolysis process of a droplet is described by an extended Arrhenius expression:

$${{{\rm{d}}{m_{\rm{d}}}} \over {{\rm{d}}t}} = - {m_{\rm{d}}}{D_{\rm{d}}}A{{\rm{e}}^{ - {\rm{Ea}}/\left({R{T_{\rm{d}}}} \right)}},$$
(9)

where A is the pre-exponential factor (A=40 s−1), and Ea is the activation energy (Ea=5000 kJ/mol).

The momentum equation of the droplet can be written as follows if the buoyancy and gravity forces are neglected:

$${{{\rm{d}}{u_{\rm{d}}}} \over {{\rm{d}}t}} = {3 \over 4}{{{\rho _{\rm{g}}}} \over {{\rho _{\rm{d}}}}}{{{C_{\rm{d}}}} \over {{D_{\rm{d}}}}}\left\vert {{u_{\rm{g}}}} \right. - \left. {{u_{\rm{d}}}} \right\vert ({u_{\rm{g}}} - {u_{\rm{d}}}),$$
(10)

where ud is the droplet velocity, and Cd is the drag coefficient which is a function of the droplet Reynolds number. Schiller and Naumann’s formula is used (Tian et al., 2014):

$${C_{\rm{d}}} = \left\{ {\begin{array}{*{20}c} {{{24} \over {R{e_{\rm{d}}}}}(1 + 0{.}15Re_{\rm{d}}^{0{.}687}),} & {R{e_{\rm{d}}} < {{10}^3},}\\ {0{.}44,\quad \quad \quad \quad \quad \quad } & {R{e_{\rm{d}}} \geq {{10}^3}{.}} \end{array}} \right.$$
(11)

The spray wall interaction and wall film formation are discussed in Sections 2.4 and 2.5, respectively.

2.3 Heat transfer of pipe wall

The thermal behavior of the pipe wall is important for an accurate simulation of the spray wall interaction and wall film formation. Therefore, a transient 2D energy balance equation covering heat transfer in axial and radial directions was modeled in this study. Details of the model are presented by Wurzenberger et al. (2008). Note that the heat transfer of spray wall interaction and wall film depletion should be added to the source term of the energy equation.

2.4 Spray wall interaction

To describe the droplet impingement process in the 1D exhaust pipe, the radial velocity of the droplet is considered. The momentum equation in the radial direction is the same as Eq. (10). The impingement occurs when the radial displacement of the droplet is larger than the critical length.

$${s_{\rm{d}}} = \left\vert {\int {{u_{\rm{r}}}{\rm{d}}t} } \right\vert \geq {D_{\rm{c}}},$$
(12)

where sd is the droplet radial displacement, ur is radial velocity, and Dc is the critical length. If the UWS injector is mounted in the center of the pipe, Dc equals half of Dhyd, and if it is mounted on the wall of the pipe, Dc equals Dhyd.

The spray wall interaction model is based on Birkhold (2007). Some modifications are made to fit the present model. Six impingement regimes (Fig. 1) are classified based on two dimensionless parameters, dimensionless number (K) and dimensionless temperature (T*):

$$K = {{(\rho D)_{\rm{d}}^{0{.}75}u_{\rm{d}}^{1{.}25}} \over {\sigma _{\rm{d}}^{0{.}5}\mu _{\rm{d}}^{0{.}25}}} = W{e^{0{.}5}} \cdot R{e^{0{.}25}},$$
(13)

where σd is the surface tension of droplet, We is the Weber number, and Tsat is the saturation temperature of water.

Fig. 1
figure 1

Regime map for spray wall interaction

Full size image

The six regimes are calculated as follows:

  1. (1)

    Deposition: if T*<1.1 and K<150, the impacting droplets are completely deposited on the wall and create a wall film.

  2. (2)

    Splash: if T*<1.1 and K≥150, the droplets are atomized and smaller secondary droplets are formed after the impact. A fraction of the droplet mass is transferred to the wall film. The diameters of secondary droplets are calculated as

    $$\left\{ {\begin{array}{*{20}c} {{d_1} = {d_0},\quad \quad \quad \quad \quad \quad \quad \quad } & {We \leq 50,\quad \quad }\\ {{d_1} = {d_0}[1 - (We - 50)/500],} & {50 < We \leq 300,}\\ {{d_1} = 0{.}5{d_0},\quad \quad \quad \quad \quad \quad \quad } & {We > 300,\quad \quad } \end{array}} \right.$$
    (14)

    where d1 and d0 are the diameters of the initial and secondary droplets, respectively.

    The fraction of the droplet mass transferred to the wall film is calculated as

    $${{{m_1}} \over {{m_0}}} = \left\{ {\begin{array}{*{20}c} {0{.}2 + 0{.}6\chi,} & {{\rm{dry}}\,{\rm{wall}},\quad \;}\\ {0{.}2 + 0{.}9\chi,} & {{\rm{wetted}}\,{\rm{wall}},} \end{array}} \right.$$
    (15)

    where m1 and m0 are the masses of the initial and secondary droplets, respectively, and χ is the random number in [0, 1].

    After the impingement, the direction of radial velocity reverses and the magnitude of velocity can be calculated by the Weber number:

    $$W{e_1} = \left({0{.}678W{e_0}} \right){{\rm{e}}^{ - 0{.}04415W{e_0}}} = {{\rho u_1^2D} \over \sigma }{.}$$
    (16)
  3. (3)

    Partial rebound: if 1.1T*<1.4 and K<40, some droplets transfer to the wall film and the others rebound. The diameters of the rebounded droplets remain the same. The fraction and the velocity are calculated from Eqs. (15) and (16).

  4. (4)

    Partial break-up: if 1.1T*<1.4 and K≥40, the features of this regime are similar to those of the splash regime, and Eqs. (14)–(16) are applied.

  5. (5)

    Rebound: if T*≥1.4 and K<40, all the impact droplets rebound and the diameters are unchanged. The velocities are calculated from Eq. (16). No wall film forms in this regime.

  6. (6)

    Break-up: if T*≥1.4 and K≥40, all the impact droplets disintegrate into secondary droplets. Their diameters and the velocities are calculated from Eqs. (14) and (16). No wall film is formed.

The heat transfer during spray impingement is taken into consideration. The heat transferred by the droplets in a parcel (Qw-d) is given as

$${Q_{{\rm{w}} - {\rm{d}}}} = {A_{{\rm{cont}}}}{{2\sqrt {{t_{{\rm{cont}}}}} } \over {\sqrt {{\pi }} }}{{{b_{\rm{w}}}{b_{\rm{d}}}} \over {{b_{\rm{w}}} + {b_{\rm{d}}}}}({T_{\rm{w}}} - {T_{\rm{d}}}),$$
(17)

where Acont is the contact area, and b n is the heat penetration coefficient:

$${b_n} = \sqrt {{{(\lambda \rho {c_{\rm{p}}})}_n}},$$
(18)

where λ is the heat conductivity, n represents the subscript b or w, cp is the specific heat, and tcont is the contact time, calculated using the K number dependence:

$${t_{{\rm{cont}}}} = \left\{ {\begin{array}{*{20}c} {{\pi \over 4}\sqrt {{{{\rho _{\rm{d}}}D_{\rm{d}}^3} \over {{\sigma _{\rm{d}}}}}},} & {K < 40,}\\ {\sqrt {{\pi \over 2}} \left({{{\rho {D^5}} \over {\sigma {u^2}}}} \right)_{\rm{d}}^{0{.}25},} & {K \geq 40{.}} \end{array}} \right.$$
(19)

2.5 Wall film model

A new 1D wall film model simplified from a 3D model is proposed. The model assumes that the wall film distributes evenly on the inner surface of the pipe mesh. Because of this assumption, the film thickness in this model is very different from its literal meaning. It represents the average film thickness along a unit mesh area of the pipe and is calculated as

$${\delta _i} = {{{V_i}} \over {{a_i}}},$$
(20)

where δ is the wall film thickness, V is the wall film volume, a is the wall film surface area, and the subscript i represents unit mesh.

The continuity equation of the wall film is described as

$${{\partial {m_{\rm{f}}}} \over {\partial t}} + {{\partial {m_{\rm{f}}}{u_{\rm{f}}}} \over {\partial x}} = {S_{\rm{m}}} + {S_{{\rm{th}}}} + {S_{{\rm{eva}}}},$$
(21)

where mf is the mass of wall film, Sm is the source term from spray wall interaction, Sth is the source term from urea thermolysis, Seva is the source term from film evaporation, and uf is the mean velocity of the wall film and is estimated under a laminar flow condition (neglecting gravity and pressure gradients):

$${u_{\rm{f}}} = {\bar u_{\rm{L}}} = {{\delta {\tau _i}} \over {2\mu }},$$
(22)

where μ is the dynamic viscosity, uL is the wall film velocity under laminar flow condition, and τ is the shear force, calculated as

$${\tau _i} = {{{F_i}} \over {{a_i}}},$$
(23)

where F is the drag force which is assumed to be proportional to relative velocity and film thickness:

$$F = ({u_{\rm{g}}} - {u_{\rm{f}}})\delta {f_i},$$
(24)

where f i is the drag coefficient. It is somehow related to film surface roughness and liquid properties. Here, it equals 20 by empirical analysis.

The equation for the evaporation rate of the wall film is modified from the AVL List GmbH (2010a):

$${\dot m_{{\rm{eva}}}} = - {a_{\rm{f}}}{Y_{\rm{w}}}{\rho _{\rm{g}}}{h_{\rm{m}}}\ln (1 + {B_{\rm{M}}})\beta {\left({{{{T_{\rm{w}}}} \over {{T_{{\rm{sat}}}}}}} \right)^2},$$
(25)

where Yw is the mass fraction of water, β is the empirical factor, and hm is the mass transfer coefficient, calculated as (Yang and Tao, 2006)

$${{{h_{\rm{m}}}D} \over \Gamma } = Sh = 0{.}023R{e^{0{.}83}}S{c^{0{.}44}},$$
(26)

Analyzing the previous studies (Strots et al., 2009; Zheng et al., 2010), wall film formation is a key cause of deposits. To predict deposit formation, a semi-detailed kinetic model of urea thermolysis is implemented into the wall film. The thermolysis of urea inside the wall film occurs when the mass fraction of water is less than 5% (AVL List GmbH, 2010b). The kinetic scheme is shown in Table 1. The kinetic parameters are re-optimized to best match the published experimental data (Schaber et al., 2004).

Table 1 Kinetic scheme for urea thermolysis
Full size table

The reactions are supposed to take place in the solid phase, and the species are assumed to be randomly distributed on a uniform surface. An active surface (As) is defined to calculate the mass change during the reactions:

$${A_{\rm{s}}} = {m \over {M\varepsilon }},$$
(27)

where M is molecular weight, and ε is urea site density (ε=5.3×10−10 mol/cm2).

Detailed information about the kinetic model is presented by Ebrahimian et al. (2012). The active surface is assumed to be conserved throughout the reactions, therefore, the mass of each species can be calculated using Eq. (27). To implement the kinetic model and calculate the mass of each species in the wall film, a continuity equation of the active surface is introduced.

$${{\partial {A_{\rm{s}}}} \over {\partial t}} + {{\partial {A_{\rm{s}}}u} \over {\partial x}} = {{{S_{\rm{m}}}{Y_{\rm{u}}}} \over {W\varepsilon }},$$
(28)

where Yu is the mass fraction of urea.

Because the semi-detailed kinetic model is implemented, species of ions (NH4+, NCO—, H+) and by-products are inside the wall film. The species conservation equation in the wall film is described as

$${{\partial {m_i}} \over {\partial t}} + {{\partial {m_i}u} \over {\partial x}} = {S_i}{.}$$
(29)

The energy equation of the wall film is not considered in this model since the heat transfer from the pipe wall and gas phase to the wall film is closely related to film thickness, but the film thickness in this model is an average value. To simulate the evaporation and thermolysis process inside the wall film, the temperature of the film has to be defined since the physical properties and reactions are all temperature dependent. In this study, the temperature of film is treated as the saturation temperature of water when calculating evaporation of the film, and treated as the inner wall temperature of the pipe when calculating urea thermolysis of the film. Neglecting the heat transfer process may slightly overestimate the thermolysis rate and gas and wall temperatures.

2.6 Two-phase coupling

The interaction of the two phases was considered by adding source terms to the gas phase equation. Since the mass flow of the UWS spray is much smaller than that of the exhaust gas, the source terms of the continuity and the momentum equations of the gas phase are neglected. The source terms caused by the liquid phase are added only in energy and species equations.

The energy source term during droplet evaporation is the heat transferred from ambient to the droplet which is consumed by heating of the droplet and vaporization of the water.

$${S_{{\rm{qgs}}}} = - {{({c_{{\rm{p}},{\rm{d}}}}{m_{\rm{d}}}{T_{\rm{d}}} - c_{{\rm{p}},{\rm{d}}}^0m_{\rm{d}}^{{0}}T_{\rm{d}}^{{0}}) + (m_{\rm{d}}^{{0}} - {m_{\rm{d}}}){L_{{\rm{vap}}}}} \over {{\rm{d}}V \cdot {\rm{d}}t}}{.}$$
(30)

The energy source term during droplet thermolysis is calculated as

$${S_{{\rm{qgs}}}} = - {{\pi }}{D_{\rm{d}}}Nu\lambda ({T_{\rm{g}}} - {T_{\rm{d}}}){.}$$
(31)

The species source term of water is caused by evaporation of the droplet and the wall film:

$${S_{{\rm{species}} - {{\rm{H}}_{{2}}}{\rm{O}}}} = - {\textstyle{{{\rm{d}}{m_{\rm{d}}}} \over {{\rm{d}}t \cdot {\rm{d}}V}}}{.}$$
(32)

The species source term of NH3 and HNCO caused by droplet thermolysis is calculated according to relative molecular weight.

$${S_{{\rm{species}} - {\rm{HNCO}}}} = - {{{\rm{d}}{m_{\rm{d}}}} \over {{\rm{d}}t\cdot{\rm{d}}V}}{.}{{{M_{{\rm{HNCO}}}}} \over {{M_{{\rm{HNCO}}}} + {M_{{\rm{N}}{{\rm{H}}_3}}}}},$$
(33)
$${S_{{\rm{species}} - {{\rm{NH}}_{{3}}}}} = - {{{\rm{d}}{m_{\rm{d}}}} \over {{\rm{d}}t\cdot{\rm{d}}V}}{.}{{{M_{{\rm{N}}{{\rm{H}}_3}}}} \over {{M_{{\rm{HNCO}}}} + {M_{{\rm{N}}{{\rm{H}}_3}}}}},$$
(34)

where V is the volume of unit mesh, MHNCO is the molecular weight of HNCO, and \({M_{{\rm{HNCO}}}}\) is the molecular weight of NH3.

The species source terms of NH3 and HNCO and other by-products caused by wall film thermolysis are calculated through the reaction rate.

2.7 Numerical solution procedure

The unsteady term is discretized by the first-order Euler explicit scheme, and the convection term is discretized by the first-order upwind difference scheme. For the gas phase, the variables are stored on staggered grids and the SIMPLE algorithm is applied to decouple the pressure and velocity. The algebraic equations created by the discretization process are solved by the tridiagonal matrix algorithm (TDMA) method. Fig. 2 shows the numerical solution procedure. The mathematical models described above are all calculated using a Fortran code developed in house.

Fig. 2
figure 2

Numerical solution procedures for simulation

Full size image

3 Results and discussion

3.1 Model validation

The model developed in this study can predict not only the generation of reducing agent but also the formation of deposits in the exhaust pipe. To validate the accuracy of the proposed model, the simulation results were compared with experimental data. In this study, the injector is mounted in the center of the pipe, and has four orifices, each injecting in a radial direction. Therefore, the initial axial velocity of the droplet was zero and the radial velocity was set to 28 m/s according to the calibration between simulation and experimental results. The initial droplet diameter was 68 µm.

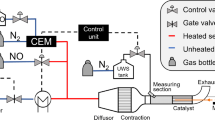
The experiment was conducted on a hot gas generator (Fig. 3) designed to provide the same conditions of gas flow rate and temperature as in diesel engines. The gaseous products were analyzed using a Fourier transform infrared spectrometer (SESAM-FTIR). The distance from the injector to the sampling point was 1.85 m and the pipe diameter was 0.1 m. To measure the weight of deposits, the exhaust pipe was divided into six parts, each 30 cm in length. For each operating condition, UWS injection stopped after 15 min, and we waited for the system cool down. The deposits were then weighed using electronic scales. The catalyst was removed in the deposit experiment considering that deposits may damage it.

Fig. 3
figure 3

Schematic diagram of the hot gas generator

Full size image

Since HNCO hydrolysis was not considered, to eliminate the impact of this factor, the sum of NH3 and HNCO were compared between simulation and experimental results. Urea decomposition efficiency is defined as

$$\eta = {{{X_1} + {X_2}} \over {{X_0}}},$$
(35)

where X1 is the NH3 concentration, X2 is the HNCO concentration, and X0 is the NH3 concentration when urea decomposes completely.

Fig. 4 shows a comparison of simulation and experimental data under different exhaust temperatures. The results show that a higher exhaust temperature can promote the efficiency of urea decomposition. This can be explained by the acceleration of evaporation and thermolysis rate at high temperatures. The figure also shows that temperature does not have a significant influence on urea decomposition in this test condition (from 45% at 568 K to 55% at 715 K in simulation results). This can be explained by the large exhaust mass flow and long distance from the injector to the sampling point compared with the study by Tang et al. (2014). This indicates that urea decomposition in the SCR system is very complex and can be affected by many factors.

Fig. 4
figure 4

Comparison of simulation and experimental data of NH 3 and HNCO under different exhaust temperature conditions (exhaust mass flow: 428 kg/h, UWS injection rate: 1200 ml/h)

Full size image

Fig. 5 shows that the exhaust mass flow has a significant effect on urea decomposition. An increase in exhaust mass flow can bring a lot of positive effects. Firstly, it increases dimensionless numbers, like Re, Sh, and Nu, which are good for heat and mass transfer for the droplet. Secondly, it improves heat transfer from the gas phase to the wall and leads to higher and more stable gas and wall temperatures because of higher flow velocity. However, the negative impact of the exhaust mass flow increment is the decrease in residence time of the droplet. From 293 kg/h to 683 kg/h, the residence time of the droplets declines by more than half in the exhaust pipe. The simulation and experimental results show that an increase in exhaust mass flow leads to a decrease in urea decomposition efficiency, which means a decrease in residence time predominates. Overall, the results in Figs. 4 and 5 show reasonable agreement both in magnitude and tendency, therefore, the proposed model can predict the generation of gaseous products under various operating conditions.

Fig. 5
figure 5

Comparison of simulation and experimental data of NH 3 and HNCO under different exhaust mass flow conditions (UWS injection rate: 900 ml/h, exhaust temperature: around 610 K)

Full size image

Urea deposits on the exhaust pipe can also be simulated since a 1D wall film model is proposed. Fig. 6 shows the simulated weight of deposits compared with experimental data. The weight of deposits here represents the weight of the total deposits formed on the exhaust pipe. The simulation results agree with the experimental data quite well. An increase in exhaust temperature can significantly reduce the weight of deposits in the exhaust pipe. When the temperature is 588 K, no deposits form on the exhaust pipe.

Fig. 6
figure 6

Comparison of simulation and experimental data of the weight of deposits at different exhaust temperatures (exhaust mass flow: 394 kg/h, UWS injection rate: 180 ml/h)

Full size image

Fig. 7 shows the distribution of the weight of deposits along the exhaust pipe. The horizontal coordinate represents each part of the pipe mentioned above. It is easy for urea spray to hit the pipe wall since each orifice injects in a radial direction. As a result, deposits are found at four temperatures (464 K, 495 K, 507 K, and 539 K) in the first pipe. When the temperature is 464 K, deposits can be found in every part of the pipe. As the temperature rises gradually, the area of deposits becomes smaller and it is found closer to the injector. Since a 1D assumption is made, the specific flow field of the exhaust pipe cannot be simulated accurately. Therefore, the distribution of the weights of deposits is difficult to predict using a 1D model. However, the simulation results can indicate a tendency.

Fig. 7
figure 7

Experimental (a) and simulation (b) results of the distribution of deposit weights (exhaust mass flow: 394 kg/h, UWS injection rate: 180 ml/h)

Full size image

3.2 Deposit by-products analysis

Since a semi-detailed kinetic model of urea thermolysis is implemented into the wall film calculation, the deposit by-products can be analyzed in this simulation. Fig. 8 shows the mass distribution of deposit by-products along the exhaust pipe at different gas inlet temperatures. The UWS injection rate was 180 ml/h. The injector was mounted 15 cm from the inlet of the pipe. From these figures, we conclude that: (1) The lower the exhaust temperature, the larger will be the wall film region and weight of deposits; (2) The main component of the deposit close to the injector is urea; as the distance from the injector increases, deposit by-products begin to form; (3) Deposit components are highly dependent on temperature: when the temperature is low, most deposits are urea; as the temperature increases, deposit by-products such as biuret and CYA begin to form and accumulate.

Fig. 8
figure 8

Distribution of deposit by-products along the exhaust pipe at different gas inlet temperatures (exhaust mass flow: 394 kg/h, UWS injection rate: 180 ml/h, duration of UWS injection: 900 s): (a) 464 K; (b) 495 K; (c) 507 K; (d) 539 K

Full size image

For the 1D assumption, only a straight pipe is considered, therefore, the position of the spray wall interaction is very near the injector because of radial injection. A wall film forms because of spray wall interaction and it is spread by shear force of the bulk flow. Fig. 9 shows the growth of film length over time. Here, film length represents the length along the axial direction of the pipe. The length of the film expands with time until it reaches the maximum. At the start of injection, film length growth is almost the same under different temperatures. This is because the impingement regimes of the four cases are all in ‘partial break-up’, and the fraction of the droplet mass transferred to the film is calculated according to Eq. (15). This indicates that differences in the region of film under different temperatures are caused mainly by the film evaporation rate, rather than the droplet mass transferred to the film in this spray-wall interaction model. Although not proven yet, the simulation results are reasonable compared with experimental data.

Fig. 9
figure 9

Growth of film length over time under different exhaust temperatures (exhaust mass flow: 394 kg/h, UWS injection rate: 180 ml/h)

Full size image

The components of the film are affected by the spray wall interaction source term, species transport, and chemical reactions occurring in the wall film. New UWS droplets are added to the film because of spray wall interaction, and no chemical reactions occur since the mass fraction of water inside the film is high near the interaction position. Therefore, the main component of deposits close to the injector is urea. As distance from the injector increases, water content evaporates gradually and urea thermolysis begins when the mass fraction of water is less than 5%. As a result, deposit by-products appear in specific positions. Among the four deposit by-products assumed in this study, very little ammelide is produced throughout the temperature range, and urea and biuret are easily decomposed. Consequently, CYA seems to be the most harmful deposit component, since it will not decompose completely unless the temperature is higher than 653 K (Schaber et al., 2004) and is difficult to remove. In our simulation, CYA begins to form from 495 K and becomes the dominant component of deposits at 539 K. This indicates that deposits formed at higher temperatures are more difficult to deal with.

3.3 Effect of UWS injection rate on urea deposits

The UWS injection rate has a significant influence on deposit formation in the SCR system. Fig. 10 shows the weight of deposits under different exhaust temperatures and UWS injection rates. The duration of UWS injection was 900 s. The exhaust mass flow was 394 kg/h. An increase in UWS injection rate had a positive correlation with deposits weight. However, deposits weight became zero when the temperature was 588 K at each UWS injection rate. This is because the wall film forms when the wall temperature is lower than the critical temperature (T*<1.4), and no deposits form when the temperature is as high as in these three cases.

Fig. 10
figure 10

Weight of deposits under different exhaust temperatures and UWS injection rates (exhaust mass flow: 394 kg/h, duration of UWS injection: 900 s)

Full size image

Fig. 11 shows the growth of film length over time under different UWS injection rates. For the ‘360 ml/h’ case, as in Fig. 9, the higher temperature resulted in a smaller film region. Since the film evaporation rate plays an important role in the film growth process, and is affected by the film region, the film growth rate diverges when the film grows to a certain extent. An increase in UWS injection rate can certainly increase the droplet mass transferred to the film. Therefore, the film length grew to the maximum at all four temperatures of the ‘540 ml/h’ case. Moreover, the film length growth rate also increased, as it took 270 s to reach the maximum in the ‘360 ml/h-464 K’ case, but only 200 s in the ‘540 ml/h-464 K’ case.

Fig. 11
figure 11

Comparison of film length growth under different UWS injection rates (exhaust mass flow: 394 kg/h): (a) 360 ml/h; (b) 540 ml/h

Full size image

Fig. 12 shows the distribution of deposit by-products along the exhaust pipe under different UWS injection rates. An increase in UWS injection rate not only expands the film region but also increases the film thickness. However, it seems that the components of deposits cannot be affected by UWS injection rate since the proportions of deposit by-products are similar at the same exhaust temperature. Temperature is believed to be the dominant factor for urea thermolysis, hence the components of deposit by-products are mostly affected by temperature. An increase in UWS injection rate can affect the temperature but the influence is very weak, since the mass flow of the UWS injection rate is very small compared with the exhaust mass flow. Fig. 13 shows the temperature distribution along the exhaust pipe under different UWS injection rates. Only a reduction of 1 K is observed in both the gas and wall temperatures from ‘180 ml/h’ to ‘540 ml/h’ case. The inner wall temperature drop occurring in the position of’ 15 cm’ is caused by spray-wall impingement. As for the inner wall temperature, note that it is an average value in the computational grid because of the 1D assumption. Therefore, the simulated temperature reduction of the wall is different from those of other studies (Birkhold et al., 2006; Zheng et al., 2010). This may lead to a slight overestimation of the film temperature.

Fig. 12
figure 12

Distribution of deposit by-products along the exhaust pipe under different UWS injection rates (exhaust mass flow: 394 kg/h, exhaust temperature: 539 K, duration of UWS injection: 900 s): (a) 360 ml/h; (b) 540 ml/h

Full size image
Fig. 13
figure 13

Temperature distribution along the exhaust pipe under different UWS injection rates (exhaust mass flow: 394 kg/h, duration of UWS injection: 900 s, exhaust temperature: 539 K): (a) gas temperature; (b) inner wall temperature

Full size image

3.4 Effect of exhaust mass flow on urea deposits

The exhaust mass flow can affect the trajectory and residual time of droplets, and can also affect the Reynold and Nusselt numbers, thus changing the heat and mass transfer process. Fig. 14 shows the weight of deposits under different exhaust temperatures and mass flows. The UWS injection rate was 540 ml/h and the duration was 900 s. An increase in exhaust mass flow can decrease the total weight of deposits on the pipe wall. The comparison of film length growth in Fig. 15 indicates that an increase in exhaust mass flow can decrease the film region under the same exhaust temperature condition. The film length growth rate is very similar between the ‘500 kg/h’ case and the ‘600 kg/h’ case. This is because the mean velocity of the wall film is affected by both the relative velocity and film thickness (Eqs. (22)–(24)). Although an increase in exhaust mass flow can accelerate the gas velocity, it also decreases the film thickness. Fig. 16 shows that an increase in exhaust mass flow not only decreases the film region but also leads to a thinner film. The components of deposit by-products were not affected by exhaust mass flow, and CYA became the dominant component of deposits in the 539 K condition. A higher exhaust mass flow caused mainly the following changes which are beneficial for reducing deposits: firstly, it increases the Sherwood number (Eq. (26)) which accelerates the film evaporation rate; secondly, the heat transfer from the gas to the wall is improved, leading to higher and more stable gas and wall temperatures. The gas temperature fell 7 K and the wall temperature fell 15 K at the outlet of the pipe from ‘600 kg/h’ to ‘394 kg/h’ (Fig. 17).

Fig. 14
figure 14

Weight of deposits under different exhaust temperatures and mass flow conditions (UWS injection rate: 540 ml/h, duration of UWS injection: 900 s)

Full size image
Fig. 15
figure 15

Comparison of film length growth under different exhaust mass flow conditions (UWS injection rate: 540 ml/h): (a) 500 kg/h; (b) 600 kg/h

Full size image
Fig. 16
figure 16

Distribution of deposit by-products along the exhaust pipe at different exhaust mass flow conditions (UWS injection rate: 540 ml/h, duration of UWS injection: 900 s, exhaust temperature: 539 K): (a) 500 kg/h; (b) 600 kg/h

Full size image
Fig. 17
figure 17

Temperature distribution along the exhaust pipe under different exhaust mass flow conditions (UWS injection rate: 540 ml/h, duration of UWS injection: 900 s, exhaust temperature: 539 K): (a) gas temperature; (b) inner wall temperature

Full size image

4 Conclusions

A simplified 1D model of gas-liquid two-phase flow is presented. The gas phase flow is solved using the Euler method and the liquid phase is treated with Lagrangian particle tracking, which solves the equations of droplet motion, mass and heat transfer, and spray wall interaction. The developed model can calculate not only the generation of the reducing agent but also the formation of deposits in the exhaust pipe. The simulation results were verified with experimental data both in gas phase production and deposit formation.

A combination of Birkhold’s direct decomposition model and Ebrahimian’s kinetic model was implemented to describe the different decomposition behaviors of urea in the droplet phase and wall film, respectively. A new 1D wall film model was developed. The wall film distribution and average film thickness can be calculated through the simplified droplet motion and spray wall interaction model. The position, weight and components of deposits can be simulated after implementing the semi-detailed kinetic model.

Based on the developed model, we can draw the following conclusions: the exhaust temperature and mass flow are important factors for ammonia production and deposit formation in an SCR system. A decrease in exhaust temperature will increase the wall film region and weight of deposits. Deposit components are highly dependent on temperature: when the temperature is low, most deposits are urea, but when the temperature rises, by-products such as biuret and CYA begin to form and accumulate. CYA becomes the dominant component of deposits at 539 K, which indicates that deposits formed at higher temperatures are more difficult to deal with. The UWS injection rate can affect the total mass of wall film and expand the film region, but it has little influence on deposit components. The effect of the UWS injection rate on gas and wall temperatures is very weak since the mass flow of the UWS injection rate is very small compared with the exhaust mass flow. An increase in exhaust mass flow can decrease the total weight of deposit and the film region on the pipe wall because of the promotion of the mass and heat transfer process both in the droplets and wall film.

However, the proposed model needs further improvement. Currently, only the diameter and length of the pipe are considered (a cylindrical pipe). In the next step of the work, complex geometric structures can be taken into consideration such as mixers and bent pipes. Under the 1D assumption, the effects of a mixer on spray include mainly spray impingement, which helps the droplets disintegrate into smaller droplets, and the production of strong turbulence, which promotes the mass and heat transfer process. The effects of a bent pipe include mainly spray impingement in the elbow position and increased pressure loss from the flow. All of these effects can be simulated through mathematical methods but, of course, further experimental investigation is required.