1 Introduction

The expansion of cities and increased population lead to heavy traffic, which, especially in towns, causes air pollution and traffic jams. These are among the most serious urbanization problems. Subways are considered to be an efficient medium of public transportation and are widely used to alleviate traffic problems and environmental pollution. Although there have been many successful metro projects all over the world, tunneling for new metro lines still poses high risks. Instability of the tunnel working face can cause many fatal accidents during tunneling because face collapse induces uncontrollably large soil deformation that jeopardizes adjacent construction. Thus, the sustainment of working face stability is of the highest importance in tunneling. In shield tunneling, the working face is sustained by applying support pressure at the face. The so-called earth pressure balance shields (EPB) turn the excavated material into a soil paste that is used as a pliable, plastic support medium (Maidl et al., 1996; Yang et al., 2015). However, the slurry in the chamber acts as the support medium in the slurry shield. Regardless of the shield tunneling method, assessment of the face stability, and evaluation of the support pressure are difficult, especially if regions of permeable soil with groundwater seepage are involved.

To assess the appropriate support pressure, analytical approaches including limit equilibrium analysis and limit analysis are commonly applied in the design process. Anagnostou and Kovári (1996) introduced the seepage effect into silo theory (Horn, 1961; Jancsecz and Steiner, 1994) and proposed the silo and wedge model, which considers groundwater seepage. As a result, an estimation of the support pressure is obtained via limit equilibrium analysis. Seepage in the silo and wedge model was later investigated by Perazzelli et al. (2014) via approximate analytical solutions. However, in the analysis of groundwater seepage in shield tunneling, the excavated material in the working chamber was not mentioned in the simulation. Moreover, the silo and wedge model was improved by Broere (1998; 2001) to investigate the problem of face stability in heterogeneous soils. Based on the model, the excess pore pressure at the tunnel face affected by the infiltration of slurry was also investigated by Broere and van Tol (2000) and Broere (2001). By limit analysis, Atkinson and Potts (1977) and Davis et al. (1980) obtained lower bound solutions for the face stability. Atkinson and Potts (1977) investigated the face stability in a cohesionless soil by 2D analysis. Davis et al. (1980) also performed a 2D study on the face stability, but they investigated cohesive soils and studied the stability in both longitudinal and transverse planes. Later, Leca and Dormieux (1990) proposed a 3D kinematically admissible mechanism for the upper bound analysis and obtained the upper bound solution for face stability in low-cohesion soil. The multi-block mechanism modeling for the slip surface in the collapses was introduced into upper bound analysis (Soubra 2000; Mollon et al., 2010). To study this problem in layered soils, Tang et al. (2014) modified the kinematically admissible mechanism of Leca and Dormiuex (1990) for layered soils and investigated the influence of different soil layers on tunnel face stability. Senent and Jimenez (2015) improved the mechanism of Mollon et al. (2010) to investigate the possibility of partial collapse in layered soils. The rational mechanism for the problem of face collapse in frictional layered soils was also discussed well in Ibrahim et al. (2015)’s research. Based on the work of Leca and Dormieux (1990), Lee and Nam (2001) and Lee et al. (2003) included the seepage effect into the upper bound analysis of face stability in the New Austrian Tunneling Method (NATM) and studied its influence on tunnel face stability. In NATM tunneling, Lee and Nam (2001) and Lee et al. (2003) considered seepage forces on the tunnel face to be the dominant factor for the face stability under groundwater seepage. However, the seepage forces are not only applied to the tunnel face but also work on the soil particles in the failed soil. Thus, the influence of seepage is underestimated by Lee and Nam (2001) and Lee et al. (2003). Regardless of the tunneling method, de Buhan et al. (1999) introduced seepage forces on soil particles into Leca and Dormieux (1990)’s upper bound analysis and studied face stability via numerical calculation. Lv et al. (2014) investigated face stability under groundwater seepage using finite element simulation. Subsequently, according to the plastic strain distribution in the collapse state obtained by simulation, 2D upper bound analysis was conducted to study the limit support pressure.

In this paper, a face collapse accident in layered soil under seepage conditions is presented. To investigate this case, the 3D conical mechanism model for the layered soils (Tang et al., 2014) is applied to upper bound analysis; furthermore, both the seepage forces on the tunnel face and those within the unstable soil are considered. The influence of seepage on face stability is studied, and the applicability of the improved solution is compared with that of other solutions.

2 Case overview

Guangzhou metro line 3, from Guangzhou east station to Fanyu south station, has a length of 36.1 km with 18 stations and is divided into 15 sections. A terrible ground surface collapse caused by tunnel face instability took place in the section between Datang station and Lijiao station. A double-tube parallel tunnel was to be built in this section, and two Herrenknecht EPB shields were used in the construction. The diameter of each tunnel is 6 m, and the thickness of the lining is 0.3 m. Two ground surface settlement monitoring sections were installed at mileages ZDK9+85 and ZDK9+105 (Fig. 1). In the construction of the left line, as the tunneling approached ZDK9+100 (ring No. 181), groundwater along with sand, silty mud, and gravel suddenly spewed from the conveyor. As a result of this extraordinary event, the road was closed off in case of danger. Finally, a notable collapse of approximately 25 m2 with a length of 5 m and a width of 5 m appeared on the ground surface in front of the tunnel face (Fig. 1). During the collapse, the soil extruding from the chamber mainly consisted of sand and completely weathered rock. Remarkable ground surface settlement was observed simultaneously (Zhu et al., 2002; Huang et al., 2006). The amount of output indicated an increase in groundwater seepage, and the settlement showed that large deformation took place in the soil induced by the tunnel excavation. In the tunneling, five earth pressure sensors were installed at the tunnel face. As shown in Fig. 2, the sensors were distributed around the cutter wheel, and the angle between consecutive sensors was 72°. The minimum support pressures detected in the construction of tunnel ring No. 181 are listed in Table 1. The minimum pressure at the upper part of the tunnel face detected by sensor 1 was 38 kPa. The minimum pressure in the middle of the tunnel face was detected by both sensors 2 and 3, and the average value of the minimum pressure was 65 kPa. The minimum pressure at the bottom of the tunnel face was detected by both sensors 4 and 5, and its average value was 97 kPa. However, at that time, the low measurement of the support pressure did not raise an alarm for the operator. Soon after that, the advance rate of the shield decreased to 2–8 mm/min, but the volume of excavated soil increased extraordinarily. The expelled soil became very wet, and the sediment concentration grew by more than 50%. It is assumed that the so-called ‘excessive excavation’ occurred. Additionally, during that time, extremely wet soil spewed twice from the conveyor into the shield. Eventually, failure of the tunnel face was detected by the observation of a huge collapse on the ground surface. According to supplemental geological exploration after the collapse, the depth from the ground surface to the tunnel crown was 12 m. The cover layer consisted of miscellaneous fill, silt soil, and sand diluvium, whereas the crossed layer was sand diluvium and completely weathered rock. The latter was found to be stable, but the sand layers and layers above collapsed during the accident (Fig. 3). It was also found that most of the area of the tunnel face was in sand diluvium; thus, in this work, it is assumed that the shield drilled entirely through the sand diluvium, and the bottom layer is assumed to be weathered rock. The geological conditions are sketched in Fig. 4, and the properties of the soils are listed in Table 2. The accident shows that it is very important to estimate the appropriate support pressure under complicated conditions. In the next section, we will discuss the support pressure needed for face stability in layered soil under seepage via upper bound analysis.

Fig. 1
figure 1

Plan of the ground surface collapse

Full size image
Fig. 2
figure 2

Locations of the sensors

Full size image
Fig. 3
figure 3

Sketch of the face collapse accident

Full size image
Fig. 4
figure 4

Sketch of the simplified model

Full size image
Table 1 Results of support pressure
Full size table
Table 2 Soil properties
Full size table

3 Upper bound analysis for face stability

3.1 Model

EPB shield tunneling was used for the construction of the Guangzhou metro line 3 tunnel. The EPB shield sustains working face stability by balancing pressures applied to the face. Under undrained conditions, the support pressure, primarily provided by the excavated soil in the chamber, resists the earth pressure at the tunnel face. However, the situation becomes more complicated once the shield passes through drained soils. The necessary support pressure then consists of both the effective earth pressure and the pore pressure. As shown in Fig. 5a, in the working chamber, the effective earth pressure is \(\sigma _{\rm{T}}^\prime\) and the piezometric head is hF. In the case of common sized tunnels (6 m or smaller), although the support pressure at the upper part of the face is larger than that at the lower part of the face, the difference is not so notable. Furthermore, the injection of foam and bentonite into the chamber can decrease the difference. In light of the small difference in support pressure, regardless of the support pressure fluctuation, uniform support pressure was commonly assumed in previous research (Leca and Dormieux, 1990; Anagnostou and Kovári, 1996; Soubra, 2000; Lee and Nam, 2001; Lee et al., 2003; Lv et al., 2014; Tang et al., 2014; Ibrahim et al., 2015; Senent and Jimenez, 2015). The assumption is also used here, considering common sized tunnel engineering described in Section 2. The groundwater head is H. Once H is larger than the piezometric head hF, the head difference Δh generates groundwater seepage inflow into the tunnel, and seepage profoundly deteriorates face stability. Because, in this example, tunneling is conducted under drained conditions, and the earth pressure, groundwater seepage, and support pressure act together on the tunnel face. Specifically, both seepage forces and gravity apply to the soil grains within the failed soil (Fig. 5a). Moreover, when the seepage outflows from the failed soil, the seepage forces σsf apply to the working face (Lee and Nam, 2001; Lee et al., 2003). As a result, the support pressure on the face is partly offset by σsf (Fig. 5b). Thus, the residual support pressure on the tunnel face is \((\sigma _{\rm{T}}^\prime - {\sigma _{{\rm{sf}}}})\). To maintain the stability of the tunnel face, in the region under the groundwater level, the residual support pressure \((\sigma _{\rm{T}}^\prime - {\sigma _{{\rm{sf}}}})\) at the working face should be large enough to resist the soil in front of the chamber.

Fig. 5
figure 5

Diagram of the EPB shield tunnel face: (a) seepage within the failed soil; (b) seepage at the tunnel face

Full size image

3.2 Upper bound solution

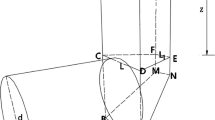
In upper bound theory, the stability of the kinematically admissible failure mechanism is designed by the condition that the work of the external loads Pe is equal to the work Pv dissipated by the movement of the mechanism (Chen and Liu, 1990; Powrie, 2002). Assuming that the soil is modeled as Mohr-Coulomb material and follows the yield criterion obeying the associated flow rule, Leca and Dormieux (1990) proposed a 3D mechanism that consists of conical blocks for a homogeneous frictional soil, and they found the upper bound solution for face stability. These results have been verified by Chambon and Corté (1994) using centrifuge experiments. For multilayered soils, an improved 3D kinematically admissible mechanism was proposed by Tang et al. (2014). This upper bound solution additionally considers influences of covering and crossed layers. Additionally, Senent and Jimenez (2015) improved the rotational mechanism model, whose velocity field is more complicated than the conical mechanism models, to investigate working face stability in composite soils. To study the case of Guangzhou metro line 3 presented above, upper bound analysis is applied with consideration of groundwater seepage in layered soil. Therefore, for the sake of convenient computation, Tang et al. (2014)’s 3D conical mechanism model is applied in this paper. As shown in Fig. 6, the kinematically admissible mechanism in the crossed stratum consists of a conical block \(\mathscr{B}_1\) and a block \(\mathscr{B}_2\), whereas in the cover soil, it is composed of conical blocks \(\mathscr{C}_1\) and \(\mathscr{C}_2\). The weathered rock underneath is assumed to be impermeable and rigid; in the crossed soil, the effective weight is \(\gamma _0^\prime\), the cohesion is \(c_0^\prime\), the friction angle is \(\varphi_0^\prime\), and the permeability is k0; in the layered cover soil, the parameters of sublayer (1) are the weight \(\gamma _1^\prime\), the thickness d1, the cohesion \(c_1^\prime\), the friction angle \(\varphi_1^\prime\), and the permeability k1; correspondingly, in sublayer (2), we have the effective weight \(\gamma _2^\prime\), the thickness d2, the cohesion \(c_2^\prime\), the friction angle \(\varphi_2^\prime\), and the permeability k2.

Fig. 6
figure 6

Kinematically admissible mechanism for layered soil

Full size image

According to Tang et al. (2014)’s solution, the volume \({v_{{\mathscr{B}_1}}}\) and lateral surface \({\varepsilon_{{\mathscr{B}_1}}}\) of block \(\mathscr{B}_1\) are

$${v_{{\mathscr{B}_{{1}}}}} = {{{{\pi }}{D^3}} \over {12}}\left({{R_A}{R_B} - {{\cos \varphi \prime} \over {2\sin \varphi \prime}}R_C^3} \right),$$
(1)
$${\varepsilon _{{\mathscr{B}_1}}} = {{{{\pi }}{D^2}} \over 4}\left[ {{{\cos \alpha } \over {\sin \varphi \prime}}{R_A} - \cos (\alpha +\varphi \prime){R_C}{R_D}} \right],$$
(2)

and the volume \({v_{{\mathscr{B}_2}}}\) and lateral surface \({\varepsilon_{{\mathscr{B}_2}}}\) of block \(\mathscr{B}_2\) are

$${v_{{\mathscr{B}_{{2}}}}} = {{{{\pi }}{D^3}} \over {24}}\left[ {{{\cos \varphi \prime} \over {\sin \varphi \prime}}R_C^3 - R_E^3{{\tan }^2}\varphi \prime} \right],$$
(3)
$${\varepsilon _{{\mathscr{B}_{{2}}}}} = {{{{\pi }}{D^2}} \over 4}\left[ {\cos (\alpha +\varphi \prime){R_C}{R_D} - {{{{\tan }^2}\varphi \prime} \over {\sin \varphi \prime}}R_E^2} \right],$$
(4)

where the coefficients are presented as follows:

$$\left\{ {\begin{array}{*{20}c} {{R_A} = {{\sqrt {\left[ {\cos (\alpha - \varphi \prime)\cos (\alpha {{ + }}\varphi \prime)} \right]} } \over {\cos \varphi \prime}},}\\{{R_B} = {{\cos (\alpha - \varphi \prime)\cos (\alpha {{ + }}\varphi \prime)} \over {\sin \varphi \prime}},\quad } \end{array}} \right.$$
(5)
$$\left\{ {\begin{array}{*{20}c} {{R_C} = {{\cos (\alpha + \varphi \prime)} \over {\cos \varphi \prime}}\left[ {{{\sin (\beta - \varphi \prime)} \over {\sin (\beta + \varphi \prime)}}} \right]^{1/2},}\\{{R_D} = {{\sin \beta } \over {\sin \varphi \prime\sin (\beta {{ + }}\varphi \prime)}},\quad \quad \quad \quad \;\;\;} \end{array}} \right.$$
(6)
$$\left\{ {\begin{array}{*{20}c} {{R_E} = {{\sin \beta \cos \alpha } \over {\sin \varphi \prime\sin (\beta {{ + }}\varphi \prime)}} - 1,}\\{\beta = {{{\pi }} \over {{4}}}{{ + }}{\alpha \over {{2}}}{.}\quad \;\;\; \;\;\; \;\;\; \;\;\; \;\;\;} \end{array}} \right.$$
(7)

The intersection ∑1 of block \(\mathscr{B}_1\) with the tunnel face is elliptic. The area A1 of ∑1 is

$${A_1} = {{\pi {D^{{2}}}} \over {{4}}}{R_A}{.}$$
(8)

The intersection ∑12 of block \(\mathscr{B}_1\) with block \(\mathscr{B}_2\) is also elliptic. The area A12 of ∑12 is

$${A_{12}} = {{{{\pi }}{D^2}} \over 4}{{\cos (\alpha + \varphi \prime)} \over {\sin (\beta + \varphi \prime)}}{R_C}{.}$$
(9)

The velocities of block \(\mathscr{B}_1\) block \(\mathscr{B}_2\) and intersection ∑12 are related by

$${V_1} = {{\sin (\beta {{ + }}\varphi \prime)} \over {\sin (\beta - \varphi \prime)}}{V_2},\;\;\;{V_{12}} = {{\cos \alpha } \over {\sin (\beta - \varphi \prime)}}{V_2}{.}$$
(10)

Owing to continuity of the rigid mechanism, blocks \(\mathscr{C}_1\) and \(\mathscr{C}_2\) in the cover layer have the same velocity V2 as block \(\mathscr{B}_2\). The angle between the discontinuity surface and the velocity V2 is \(\varphi_1^\prime\), and that of block \(\mathscr{C}_2\) is \(\varphi_2^\prime\).

The radius r1 of the intersection of block \(\mathscr{B}_2\) and block \(\mathscr{C}_1\) equals

$${r_1} = {D \over 2}{R_E}\tan \varphi \prime{.}$$
(11)

The volume \({v_{{\mathscr{C}_1}}}\) and the lateral surface \({\varepsilon_{{\mathscr{C}_1}}}\) of block \(\mathscr{C}_1\) can be obtained by removing the cone with radius r2 from the cone with radius r1:

$$\left\{ {\begin{array}{*{20}c} {{v_{{\mathscr{C}_1}}} = {{{\pi }} \over 3}\cot {{\varphi \prime}_1}\left({r_1^3 - r_2^3} \right),}\\{{\varepsilon _{{\mathscr{C}_1}}} = {{{\pi }} \over {\sin {{\varphi \prime}_1}}}\left({r_1^2 - r_2^2} \right),\quad }\\{{r_2} = {r_1} - {d_1}\tan {{\varphi \prime}_1}{.}\quad \quad \quad } \end{array}} \right.$$
(12)

Analogously, the volume and lateral surface of block \(\mathscr{C}_2\) are

$$\left\{ {\begin{array}{*{20}c} {{v_{{\mathscr{C}_2}}} = {{{\pi }} \over 3}\cot {{\varphi \prime}_2}\left({r_2^3 - r_3^3} \right),}\\{{\varepsilon _{{\mathscr{C}_2}}} = {{{\pi }} \over {\sin {{\varphi \prime}_2}}}\left({r_2^2 - r_3^2} \right),\;\;\; }\\{{r_3} = {r_2} - {d_2}\tan {{\varphi \prime}_2}{.}\;\;\; \;\;\; \;\;\; } \end{array}} \right.$$
(13)

The work of the external load Pe includes the work of the residual support pressure at the tunnel face \({P_{\sigma _{\rm{T}}^\prime }}\), the seepage forces on the failed soil \({P_{{\gamma _{\rm{w}}}}}\) and the work of the soil weight P γ

$${P_{{\rm e}}} = {P_{{{\sigma \prime}_{\rm T}}}} + {P_{{\gamma _{\rm w}}}} + {P_\gamma }{.}$$
(14)

In Eq. (14), the work of the residual support pressure on the tunnel face is

$${P_{{{\sigma \prime}_{\rm T}}}} = - \left({{{\sigma \prime}_{\rm T}} - {\sigma _{{\rm sf}}}} \right){A_1}{V_1}\cos \alpha {.}$$
(15)

The work of the water pressure \({P_{{\gamma _{\rm{w}}}}}\) is the sum of the work of the pore pressure on the skeleton expansion and the work of the water pressure on the boundary. Based on 2D analysis, Michalowski (1995) and Viratjandr and Michalowski (2006) derived the work of the water pressure \({P_{{\gamma _{\rm{w}}}}}\) as

$${P_{{\gamma _{\rm w}}}} = {\gamma _{\rm w}}\int\nolimits_v {\left({ - {{\partial h} \over {\partial {x_i}}}} \right){V_i}{\rm{d}}v + } {\gamma _{\rm w}}\int\nolimits_v {\left({ - {{\partial Z} \over {\partial {x_i}}}} \right)} \;{V_i}{\rm{d}}v,$$
(16)

where γw is the unit weight of water, Z is the elevation head, v is the volume of the submerged soil mass, and \( - {{\partial h} \over {\partial {x_i}}}\) is the hydraulic gradient ix in the x-direction. The first item of Eq. (16) is the work of seepage forces on the soil skeleton Psf, and the latter is the work of the buoyancy forces on the soil skeleton Pbf. Eq. (16) can be rewritten as

$${P_{{\gamma _{\rm w}}}} = {P_{{\rm{sf}}}} + {P_{\rm{bf}}}{.}$$
(17)

The work of the seepage forces Psf within the failed soil is the sum of the seepage forces in the crossed stratum and in the cover layer. The work of the seepage forces Psf can be obtained by

$$\begin{array}{*{20}c} {{P_{{\rm{sf}}}} = {\gamma _{\rm{w}}}\iint \!\!\!\int\nolimits_v {\left\{ {{i_i}} \right\}{V_i}{\rm{d}}v\quad \quad \quad \quad \quad \quad \quad \quad \quad \;} }\\ { = {\gamma _{\rm{w}}}\iint \!\!\!\int\nolimits_{{v_{{\rm{cro}}}}} {\left\{ {{i_i}} \right\}{V_i}{\rm{d}}v} + {\gamma _{\rm{w}}}\iint \!\!\!\int\nolimits_{{v_{{\rm{cov}}}}} {\left\{ {{i_i}} \right\}{V_i}{\rm{d}}v},}\end{array}$$
(18)

where {i i }={i x ,i y ,i z } is the seepage gradient in the layers.

Similarly, the work of the buoyancy force in the failed soil is

$$\begin{array}{*{20}c} {{P_{{\rm{bf}}}} = {\gamma _{\rm{w}}}\iint \int\nolimits_v {\left({ - {{\partial Z} \over {\partial z}}} \right){V_i}{\rm{d}}v\quad \quad \quad \quad \quad \quad \quad \quad \;} }\\ { = - {\gamma _{\rm{w}}}\iint \int\nolimits_{{v_{{\rm{cro}}}}} {{{\partial Z} \over {\partial z}}{V_i}{\rm{d}}v} - {\gamma _{\rm{w}}}\iint \int\nolimits_{{v_{{\rm{cov}}}}} {{{\partial Z} \over {\partial z}}{V_i}{\rm{d}}v} {.}} \end{array}$$
(19)

The work of the soil weight P γ is

$$\begin{array}{*{20}c} {{P_\gamma } = \iint \int\nolimits_{{v_{{\rm{cro}}}}} {\gamma {V_1}\sin \alpha {\rm{d}}v} + \iint \int\nolimits_{{v_{{\rm{cro}}}}} {\gamma {V_2}{\rm{d}}v\quad \quad \quad \quad \quad \quad } }\\ { = \iint \int\nolimits_{{v_{{\mathscr B}1}}} {\gamma {V_1}\sin \alpha {\rm{d}}v} + \iint \int\nolimits_{{v_{{\mathscr B}2}}} {\gamma {V_2}{\rm{d}}v} + \sum\limits_{i = 1}^n \gamma {V_2}{v_{{\mathscr C}i}}{.}} \end{array}$$
(20)

The sum of the work of water pressure and soil weight in the failed soil is

$$\begin{array}{*{20}c} {{P_{{\gamma _{\rm w}}}} + {P_\gamma }\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;}\\{ = {P_\gamma } + {P_{\rm{sf}}} + {P_{\rm{bf}}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;}\\{ = \iint \!\!\!\int\nolimits_{{v_{\mathscr{B}1}}} {\gamma \prime{V_1}\sin \alpha {\rm{d}}v} + \iint \!\!\!\int\nolimits_{{v_{\mathscr{B}2}}} {\gamma \prime{V_2}{\rm{d}}v} + \sum\limits_{i = 1}^n {\gamma \prime} {V_2}{v_{\mathscr{C}i}} + {P_{\rm{sf}}}}\\{ = {{{{\pi }}{D^3}} \over {12}}\gamma \prime{V_1}\sin \alpha \left({{R_A}{R_B} - {{\cos \varphi \prime} \over {2\sin \varphi \prime}}R_C^3} \right)\quad \quad \quad \quad \quad \;\;\;}\\{ + {{{{\pi }}{D^3}} \over {24}}\gamma \prime{V_2}\left[ {{{\cos \varphi \prime} \over {\sin \varphi \prime}}R_C^3 - R_E^3ta{n^2}\varphi \prime} \right]\quad \quad \quad \quad \quad \quad }\\{ + {{{\pi }} \over 3}\gamma \prime{V_2}\sum\limits_{i = 1}^2 {\cot {{\varphi \prime}_i}\left({r_i^3 - r_{i + 1}^3} \right) } + {P_{\rm{sf}}}{.}\;\quad \quad \quad \quad \quad \quad \;\;} \end{array}$$
(21)

By substituting Eqs. (21) and (15) into Eq. (14), the external load Pe is

$$\begin{array}{*{20}c} {{P_{\rm e}} = {{{{\pi }}{D^3}} \over {12}}\gamma \prime{V_1}\sin \alpha \left({{R_A}{R_B} - {{\cos \varphi \prime} \over {2\sin \varphi \prime}}R_C^3} \right)}\\{ + {{{{\pi }}{D^3}} \over {24}}\gamma \prime{V_2}\left[ {{{\cos \varphi \prime} \over {\sin \varphi \prime}}R_C^3 - R_E^3ta{n^2}\varphi \prime} \right]}\\{ + {{{\pi }} \over 3}\gamma \prime{V_2}\sum\limits_{i = 1}^2 {\cot {{\varphi \prime}_i}\left({r_i^3 - r_{i + 1}^3} \right)\quad \quad \quad } }\\{ + {P_{\rm{sf}}} - \left({{{\sigma \prime}_{\rm T}} - {\sigma _{{\rm sf}}}} \right){A_1}{V_1}\cos \alpha {.}\quad \quad \quad } \end{array}$$
(22)

The energy dissipated in the system is the sum of the dissipation energy along the failure surface of block \(\mathscr{B}_1\), P1V, the dissipation energy along the failure surface of block \(\mathscr{B}_2\), P2V, the dissipation energy along the intersection surface ∑12 of blocks \(\mathscr{B}_1\) and \(\mathscr{B}_2\), P12V, and the dissipation energy along the failure surface of the blocks in the cover layer, \({P_{{c_i}V}}\),

$${P_V} = {P_{1V}}{{ + }}{P_{2V}}{{ + }}{P_{12V}}{{ + }}{P_{{c_i}V}}{.}$$
(23)

Because of the associated flow rule, the dissipation energies per unit area in the crossed layer and in layer i of the cover layer are, respectively,

$${{{\rm{d}}{P_V}} \over {{\rm{d}}\sum }} = c \prime V\cos \varphi \prime,\;\;\;\;{{{\rm{d}}{P_V}} \over {{\rm{d}}\sum }} = {c\prime_i}{V_2}\cos {\varphi \prime_i}{.}$$
(24)

Thus, the dissipation energies in Eq. (23) can be calculated by

$$\begin{array}{*{20}c} {{P_{1V}} = \iint \nolimits_{{\mathscr{B}_1}} {{{{\rm{d}}{P_V}} \over {{\rm{d}}\sum }}}{\rm{d}}\sum \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\{ = {{{{\pi }}{D^2}} \over 4}c\prime{V_1}\cos \varphi \prime\left[ {{{\cos \alpha } \over {\sin \varphi \prime}}{R_A} - \cos \left({\alpha + \varphi \prime} \right){R_C}{R_D}} \right],\;\;} \end{array}$$
(25)
$$\begin{array}{*{20}c} {{P_{2V}} = \iint \nolimits_{{{\mathscr B}_2}} {{{{\rm{d}}{P_V}} \over {{\rm{d}}\sum }}} {\rm{d}}\sum \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ { = {{\pi {D^2}} \over 4}c\prime {V_2}\cos \varphi \prime \left[ {\cos \left({\alpha + \varphi \prime } \right){R_A}{R_D} - {{{{\tan }^2}\varphi \prime } \over {\sin \varphi \prime }}R_E^2} \right],\;\;\;} \end{array}$$
(26)
$$\begin{array}{*{20}c} {{P_{12V}} = \iint \nolimits_{{\Sigma _{12}}} {{{{\rm{d}}{P_V}} \over {{\rm{d}}\Sigma }}} {\rm{d}}\Sigma \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ { = {{\pi {D^2}} \over 4}c\prime {V_{12}}{R_C}{R_D}{{\sin \varphi \prime \cos \varphi \prime \cos (\alpha + \varphi \prime)} \over {\sin \beta }},} \end{array}$$
(27)
$${P_{{c_i}V}} = \iint \nolimits_{\mathscr C} {{{{\rm{d}}{P_V}} \over {{\rm{d}}\sum }}} {\rm{d}}\sum = \pi {V_2}\sum\limits_{i = 1}^2 {c{\prime _i}\cot \varphi {\prime _i}\left({r_i^2 - r_{i + 1}^2} \right)} {.}$$
(28)

When the limit state is reached, the work of the external load is equal to the energy dissipated by the movement of the kinematically admissible mechanism (Pe=Pv). Consequently, the limit support pressure can be derived and written as

$${\sigma \prime_{\rm T}} = \gamma \prime{D}{N_{\gamma \mathscr{B}}}{{ - }}c\prime{N_{c\mathscr{B}}}{{ + }}{1 \over {{D^2}}}\sum\limits_{i = 1}^2 {{N_{{\gamma _i}\mathscr{C}}}} + {\gamma _{\rm w}}{N_{\rm{sf}}}{{ + }}{\sigma _{\rm{sf}}},$$
(29)
$$\begin{array}{*{20}c} {{N_{\gamma\mathscr{ B}}} = {{\tan \alpha } \over {3{R_A}}}\left({{R_A}{R_B} - {{\cos \varphi \prime} \over {2\sin \varphi \prime}}R_C^3} \right)\quad \quad \;}\\{ + {{{R_F}} \over 6}\left({{{\cos \varphi \prime} \over {\sin \varphi \prime}}R_C^3 - R_E^3{ta}{{n}^2}\varphi \prime} \right),} \end{array}$$
(30)
$$\begin{array}{*{20}c} {{N_{c\mathscr{B}}} = \cot \varphi \prime - R_E^2{R_F}\tan \varphi \prime\quad \quad \quad \;\;\quad \quad \quad \quad \quad }\\{ + {{\cos \left({\alpha + \varphi \prime} \right)\cos \varphi \prime{R_C}{R_D}} \over {{R_A}}}\quad \quad \;\quad \quad \;\;\;}\\{ \times \left({{{R_A^2{R_F}} \over {{R_C}}} + {{\sin \varphi \prime} \over {\sin \beta \sin \left({\beta + \varphi \prime} \right)}} - {1 \over {\cos \alpha }}} \right),} \end{array}$$
(31)
$${N_{{\gamma _i}{\mathscr{C}_i}}} = {{4{R_F}{\gamma _i}\cot {{\varphi \prime}_i}} \over 3}\left({r_i^3 - r_{i + 1}^3} \right) - 4{R_F}{c\prime_i}\left({r_i^2 - r_{i + 1}^2} \right)\cot {\varphi \prime_i},$$
(32)
$${N_{{\rm{sf}}}} = {{\iint \!\!\!\int\nolimits_{{v_{{\rm{cro}}}}} {\left\{ {{i_i}} \right\}{V_1}{\rm{d}}v} + \iint \!\!\!\int\nolimits_{{v_{{\rm{cro}}}}} {\left\{ {{i_i}} \right\}{V_2}{\rm{d}}v} } \over {{A_1}{V_1}\cos \alpha }}{.}$$
(33)

The coefficients \({N_{\gamma \mathscr{B}}},\;{N_{c\mathscr{B}}}\), and \({N_{{\gamma _i}{\mathscr{C}_i}}}\) are mainly controlled by the mechanical soil properties. Eq. (29) can be written as

$${\sigma \prime_{\rm{T}}} = {\sigma _{{\rm{soil}}}} + {\sigma _{{\rm{seepage}}}},$$
(34)

where

$$\left\{ {\begin{array}{*{20}c} {{\sigma _{{\rm{soil}}}} = \gamma \prime D{N_{\gamma \mathscr{B}}} - c\prime{N_{c\mathscr{B}}}{{ + }}{1 \over {{D^2}}}\sum\limits_{i = 1}^n {{N_{{\gamma _i}\mathscr{C}}}},}\\{{\sigma _{{\rm{seepage}}}} = {\gamma _{\rm{w}}}{N_{{\rm{sf}}}} + {\sigma _{{\rm{sf}}}}{.}\quad \quad \quad \quad \quad \quad } \end{array}} \right.$$
(35)

For σsoil, the influence of the different layers on support pressure has already been discussed (Tang et al., 2014). Therefore, only the seepage part, σseepage, will be analyzed.

3.3 Seepage analysis

3.3.1 Seepage forces acting on the tunnel face

Subsequently, to study the seepage forces acting on the tunnel face, the commercial finite difference code FLAC3D is used. Steady-state seepage analysis is based on Darcy’s law. Furthermore, in spite of ground settlement during drainage, soil deformation is neglected; this is because settlement takes place during a much longer time than sudden collapse, which occurs within a very short time.

Based on the case study in Section 2, the symmetric model for the computation is shown in Fig. 7. The tunnel diameter is D=6 m, and the corresponding width and length of the model are chosen to be 4D and 6D, respectively. The seepage in the case of the face collapse mentioned in Section 2 is studied by numerical simulation. The crossed sand is 6 m thick. The cover layer is composed of a sand layer of 3 m thickness and a silt layer of 9 m thickness. The bottom layer is impermeable and consists of completely weathered rock. The soil properties have been summarized in Table 2. Considering the shield tunneling in Section 2, the working chamber has been modeled in this work to study the influence of the excavated material in the chamber on the seepage. As shown in Fig. 7, the darker gray zones represent the working chamber of 1 m thickness in the tunnel shield. The seepage forces acting on the tunnel face σsf can be obtained by calculating the average pore pressure at each node at the tunnel face. In tunneling, soil conditioning is one of the best means to adjust the permeability and reduce operational difficulties. Usually, a mixture of foam and bentonite is used in conditioning to reduce the permeability of the excavated material in the chamber. The effect of conditioning has been discussed in previous studies (Maidl and Cordes, 2003; Babendererde et al., 2004; Borghi and Mair, 2006; Gugliemetti et al., 2008; Liu and Yuan, 2014; Yin et al., 2016). In this work, two types of excavated soils in the chamber are considered. The first is excavated sand without any conditioning; the other is a well-conditioned mixture of sand, bentonite, and foam. Without conditioning, the permeability of the excavated soil equals that of the sand in the crossed layer. While well-conditioned, the permeability of the material in the chamber is much lower than that of the excavated sand. The relevant parameters are listed in Table 3. The parameters of different layers have already been listed in Table 2. The groundwater level H remains constant during seepage because the potential is recharged by adjacent groundwater or rainfall. The piezometric head in the chamber is hF. The tunnel is waterproof, so seepage into the tunnel face takes place only once the water head difference Δh (Δh=H−hF) is greater than zero. The excavated soil in the chamber is regarded as an integral part. Thus, we assume that the pore pressures in this part are the same everywhere. Considering the spewing mentioned in the demonstration of the case study in Section 2, the pore pressure in the chamber remains at an extremely low value and is assumed to be zero in this analysis. To avoid the influence of pore pressure on the seepage forces on the tunnel face, the piezometric head hF at the backside of the chamber is assumed to be constantly zero in the simulation. Consequently, Δh is essentially determined by the groundwater level H. The ratio H/C, which describes the variation of the groundwater level, is used to analyze the influence of Δh on seepage. We consider only the cases in which H/C≥1. For instance, H/C=1 means that the groundwater level is located at the ground surface, whereas H/C>1 indicates that the ground surface is submerged, which represents underwater cases.

Fig. 7
figure 7

Numerical model

Full size image
Table 3 Permeability of the excavated material in the chamber
Full size table

In the analysis of seepage forces acting on the working face, the concept of seepage pressure ratio (SPR), i.e., the ratio of the average seepage pressure on the tunnel face σsf to the hydrostatic pressure at the central face, presented by Lee and Nam (2001) and Lee et al. (2003) is used. For the sake of real time in each excavation step, in each simulation, the calculation time is 3600 s. With unconditioned material in the chamber, the dependence of σsf and the SPR on time is illustrated in Fig. 8. It is clear that in the first 100 s, σsf and SPR steeply decrease; in the subsequent 1200 s, the downtrend of σsf and SPR slows down; and afterwards, both σsf and SPR become constant. The decrease of σsf is from 150 kPa to 38 kPa, which corresponds to an SPR decrease from 100% to 23%. For the case of conditioned material in the chamber, the dependence of σsf and the SPR on time is illustrated in Fig. 9. A slight decrease of σsf and SPR is visible. During the 3600 s, σsf decreases from 150 kPa to 145 kPa, which corresponds to an SPR decrease from 100% to 96.5%. The steady σsf is close to the hydrostatic pressure, and the slight decrease indicates that seepage scarcely occurs in this situation. This is also verified by studying the maximum flow velocity around the tunnel face, as shown in Fig. 10. The decrease in the flow velocity for unconditioned material shows that in the first 1200 s, the flow velocity decreases by approximately 75% from more than 2×10−2 m/s to 5.5×10−3 m/s and becomes constant afterward, which is similar to the variation of σsf and SPR found in Fig. 8. The decrease in the flow velocity shows the developing process of groundwater seepage: the high flow velocity indicates that there is unsteady-state seepage at first; the final constant flow means that steady-state seepage is achieved. However, at the same time, the flow velocity for the conditioned material scarcely changes and remains at approximately 1.9×10−4 m/s. The low flow velocity also confirms that there is very little seepage in the vicinity of the tunnel face, so the influence of the seepage on the face stability is overestimated. For the ‘unconditioned’ case, the flow vectors in the steady seepage are shown in Fig. 11. The water head around the tunnel face remains at a very low level, and the maximum flow vector measured is 5.5×10−3 m/s. Both the vertical and horizontal flow vectors vary significantly in the chamber. The vertical flow vectors enlarge with increasing closing distance from the bulkhead. Outside the chamber, the vertical flow vectors are not as large as those in the chamber, and the vectors diminish with increasing distance from the working face. The horizontal flow vectors are clearly seen in the crossed layer. For the ‘conditioned’ case, the flow vectors in steady seepage are shown in Fig. 12. The water head around the outside of the chamber remains at a high level, but that in the chamber varies quickly. The maximum flow vector measured is 1.9×10−4 m/s. Compared with the ‘unconditioned’ case, the maximum flow vector measured is much too small. This means that the conditioned soil in the chamber could effectively reduce the groundwater flow toward the chamber. Both the vertical and horizontal flow vectors are obvious in the chamber. Outside the chamber, the horizontal flow vectors are dominant in the crossed layer. In the following, the case of unconditioned material in the chamber will be considered to investigate face stability with groundwater seepage. For steady-state seepage, the influence of the groundwater level (H/C) on σsf and SPR is shown in Fig. 13. SPR is at a constant 23% and is not influenced by the variation of H/C. Moreover, Lee and Nam (2001) and Lee et al. (2003) proved that the SPR is independent of the groundwater level. σsf increases linearly from 35 kPa to 65 kPa as H/C increases from 1 to 2. Because of seepage, the increase in the rate of σsf is not as steep as that of the hydrostatic pressure.

Fig. 8
figure 8

Variation of σ sf and SPR dependent on seepage time (unconditioned)

Full size image
Fig. 9
figure 9

Variation of σ sf and SPR dependent on seepage time (conditioned)

Full size image
Fig. 10
figure 10

Variation of the flow velocity on the tunnel face dependent on seepage time

Full size image
Fig. 11
figure 11

Flow vectors in seepage around the tunnel face (unconditioned)

Full size image
Fig. 12
figure 12

Flow vectors in seepage around the tunnel face (conditioned)

Full size image
Fig. 13
figure 13

Influence of the groundwater level on σ sf and SPR

Full size image

3.3.2 Seepage gradients in layered soil

The seepage gradient in the plane of symmetry is plotted in Fig. 14. From the contours of the horizontal seepage gradient, it becomes clear that horizontal seepage mainly occurs in the crossed layer. As the distance to the face decreases, the horizontal gradient increases gradually. However, in the cover layers, no horizontal seepage appears. The gradient vector also shows that in the crossed layer, only the horizontal seepage is noteworthy, and the vertical seepage is negligible. In the cover layers, the vertical gradient gradually grows with increasing depth. The elementary theory for semi-confined aquifers (Verruijt, 1970) can be applied to calculate the seepage forces in the crossed layer. The respective element is shown in Fig. 15. Considering the bottom layer as impermeable, seepage occurs in the crossed and cover layers. The piezometric heads in the cover layer and in the crossed layer are denoted by φ1 and φ, respectively. The permeabilities in the crossed layer and cover layer are k0 and \(\tilde k\), and the thicknesses of the crossed layer and the cover layer are D and \(\bar d = {d_1} + {d_2}\), respectively.

Fig. 14
figure 14

Contour of the z -direction seepage gradient in the plane of symmetry

Full size image
Fig. 15
figure 15

Seepage in symmetrical plane

Full size image

Continuity causes the net outward flux in the mid layer to be equal to the amount of water percolating through the cover layer. Hence, the relationship can be presented as

$${k_0}D\left({{{{\partial ^2}\varphi } \over {\partial {x^2}}} + {{{\partial ^2}\varphi } \over {\partial {z^2}}}} \right) - \tilde k{{\varphi - {\varphi _1}} \over {\bar d}} = 0{.}$$
(36)

Because of symmetry, the resultant seepage forces in the x-direction are equal to zero, so Eq. (36) can be simplified to

$${k_0}D{{{\partial ^2}\varphi } \over {\partial {z^2}}} - \tilde k{{\varphi - {\varphi _1}} \over {\bar d}} = 0{.}$$
(37)

The boundary conditions are

$$\left\{ {\begin{array}{*{20}c} {z = 0,\quad } & {\varphi = {h_{\rm {F}}},}\\{z = + \infty,} & {\varphi = {h_0}{.}} \end{array}} \right.$$
(38)

Considering the boundary conditions, the solution is obtained as

$$\varphi = {h_0} - \Delta h{{\rm {e}}^{ - z/\lambda }},\;\;\lambda = \sqrt {{{kD\bar d} \over {\tilde k}}} {.}$$
(39)

Consequently, the seepage forces in the crossed layer can be expressed as

$${i_{{\rm{cro}}}} = - {{\partial \varphi } \over {\partial z}} = {{\Delta h{{\rm {e}}^{ - z/\lambda }}} \over \lambda }{.}$$
(40)

The work of the seepage forces applied on the mechanism in the crossed layer is

$$\begin{array}{*{20}c} {\iint \!\!\!\int\nolimits_{{v_{{\rm{cro}}}}} {{\gamma _{\rm{w}}}\left\{ {{i_i}} \right\}{V_1}{\rm{d}}v} = {\gamma _{\rm{w}}}\iint \!\!\!\int\nolimits_{{v_{{\rm{cro}}}}} {{i_{{\rm{cro}}}}{V_1}\cos \alpha {\rm{d}}v} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\{ = {\gamma _{\rm{w}}}{V_1}\cos \alpha {{\left. {{{\Delta h{{\rm {e}}^{ - z/\lambda }}} \over \lambda }} \right\vert }_{z = 1}}\iint \!\!\!\int\nolimits_{{v_{{\rm{cro}}}}} {{\rm{d}}v} {.}} \end{array}$$
(41)

In the layered cover soil, the average permeability \(\tilde k\) of the cover layer has been derived as (Holtz and Kovacs, 1981; Whitlow, 1991)

$$\tilde k = {{{d_1} + {d_2}} \over {{d_1}/{k_1} + {d_2}/{k_2}}}{.}$$
(42)

According to the results of the simulation, the seepage gradient in the layered cover soil is vertically downward. The seepage gradient icov in the cover soil is calculated by \({i_{{{\rm cov}} }} = {{{h_0} - {h_{\rm{F}}}} \over {{d_1} + {d_2}}}\) and this clearly obeys Darcy’s law. Thus, the power of the seepage forces applied to the failed soil in the cover soil is

$$\iint \!\!\!\int\nolimits_{{v_{{\rm{cro}}}}} {{\gamma _{\rm{w}}}\left\{ {{i_i}} \right\}{V_2}{\rm{d}}v} = {\gamma _{\rm{w}}}\iint \!\!\!\int\nolimits_{{v_{{\rm{cro}}}}} {{i_{{\rm{cov}}}}{V_2}{\rm{d}}v} = {\gamma _{\rm{w}}}{{\Delta h} \over {{d_1} + {d_2}}}{V_2}\iint \!\!\!\int\nolimits_{{v_{{\rm{cro}}}}} {{\rm{d}}v} {.}$$
(43)

Therefore, the work of the seepage forces within the entire mechanism is

$${P_{{\rm{sf}}}} = {\gamma _{\rm{w}}}{{\Delta h} \over {{d_1} + {d_2}}}{V_2}\iint \!\!\!\int\nolimits_{{v_{{\rm{cro}}}}} {{\rm{d}}v} + {\gamma _{\rm{w}}}{V_1}\cos a{\left. {{{\Delta h{{\rm {e}}^{ - z/\lambda }}} \over \lambda }} \right\vert _{z = 1}}\iint \!\!\!\int\nolimits_{{v_{{\rm{cro}}}}} {{\rm{d}}v} {.}$$
(44)

According to Eq. (44), the coefficient Nsf can be refined as

$$\begin{array}{*{20}c} {{N_{{\rm{sf}}}} = {{4{\gamma _{\rm{w}}}} \over {{{\pi }}{D^2}{R_A}}}\left[ {{{\Delta h\sin (\beta - \varphi \prime)} \over {({d_1} + {d_2})\sin (\beta + \varphi \prime)}}\iint \!\!\!\int\nolimits_{{v_{{\rm{cro}}}}} {{\rm{d}}v} } \right.}\\ {\left. {{{\left. { + {{\Delta h{{\rm {e}}^{ - z/\lambda }}} \over \lambda }} \right\vert }_{z = 1}}\iint \!\!\!\int\nolimits_{{v_{{\rm{cro}}}}} {{\rm{d}}v} } \right]{.}\quad \quad \quad \;\;} \end{array}$$
(45)

According to the case study mentioned in Section 2, seepage in the vicinity of the tunnel face is studied via the analytical solution. Fig. 16 shows the variation of the water head along the tunnel axis. Without conditioning in the chamber, the relevant numerical result shows that as the distance from the tunnel face increases from 0 m to 5 m, the water head gradually rises from approximately 2 m to 7 m. The analytical result shows a similar variation of the water head. The water head equals 1.7 m and gradually rises to 7 m as the distance increases from 0 m to 5 m. However, with conditioning, the variation of the water head is quite different from the previous two results. The water head is very close to the hydrostatic head h0 and is independent of the distance, which is attributed to the extremely low seepage in the vicinity of the tunnel face discovered in Section 3.3.1.

Fig. 16
figure 16

Variation of water head along the tunnel axis (C/D=2, H/C=1)

Full size image

Furthermore, the variation of the horizontal seepage gradient along the tunnel axis is shown in Fig. 17. Without conditioning in the chamber, both the numerical and analytical results show a similar variation of horizontal seepage gradients. Both of the seepage gradients drop nonlinearly with increasing distance from the tunnel face. When the distance is smaller than 2 m, the seepage gradients are very close. However, the difference changes as the distance increases. The extremely low seepage gradient, which is independent of the distance, also indicates that the influence of seepage can be neglected with conditioning in the chamber. Without conditioning in the chamber, the seepage in the vicinity of the tunnel face predicted by the analytical method is close to that predicted by the numerical solution. Therefore, the analytical model for seepage is introduced into the upper bound analysis for the estimation of the support pressure.

Fig. 17
figure 17

Variation of horizontal seepage gradient along the tunnel axis (C/D=2, H/C=1)

Full size image

3.3.3 Influence of groundwater seepage

In Eq. (34), the pressure σseepage is introduced as the sum of the seepage forces in the unstable soil γwNsf and the seepage forces acting on the tunnel face σsf. In Fig. 18, for different depth ratios C/D ≥ 1, the behavior of the seepage pressure and its components is illustrated. From Fig. 18a, it becomes evident that for each C/D, the seepage forces in the unstable soil increase linearly with increasing H/C. The seepage forces acting on the tunnel face σsf are shown in Fig. 18b; for 1≤C/D≤2, σsf also increases linearly with increasing H/C. Thus, as shown in Fig. 18c, σseepage shows the same behavior. Lee and Nam (2001) and Lee et al. (2003) regarded σsf as the only factor that determines the support pressure for the face stability. By illustrating the ratio σsf/σseepage, Fig. 18d shows that the other part of Eq. (40) is also important. The dashed line represents the influence of the depth ratio C/D, and it increases nonlinearly from 76% to 83% with increasing C/D. In contrast, the straight lines represent the influence of H/C on σsf/σseepage. It can be easily seen that σsf/σseepage, in contrast to the ratio C/D, is unaffected by H/C.

Fig. 18
figure 18

Seepage pressure and its components dependent on H/C

(a) γwNsf vs. H/C; (b) σsf vs. H/C; (c) σseepage vs. H/C; (d) σsf/σseepage vs. H/C and C/D

Full size image

4 Support pressure analysis

In this section, the solution of a support pressure is analyzed under the geological conditions presented in the case study overview (Section 2). Fig. 19 shows the relationship between the support pressure and the tunnel diameter. It becomes clear that regardless of depth, the support pressures increase linearly with increasing diameter, which is consistent with results of other studies (Leca and Dormieux, 1990; Anagnostou and Kovári, 1996; Broere, 2001). The coincidence of the dashed lines also indicates that the support pressure of Tang et al. (2014)’s solution is not influenced by depth ratio. For shallow tunnels (C/D=0.5), the support pressure predicted by the present study increases from 32.4 kPa to 67.4 kPa, and for deep tunnels, it linearly increases from 54.1 kPa to 110.8 kPa. The rate of increase is larger for deep tunnels than that for shallow ones. In addition, the support pressure of this study is affected by depth ratio. For any diameter, the support pressure grows as the depth increases.

Fig. 19
figure 19

Variation of the support pressure \({\sigma _{\bf{T}}}^\prime\) dependent on the diameter D (H/C=1, d 1 /d 2 =1.5, cover layer: silt sand; crossed layer: sand diluvium)

Full size image

The influence of the groundwater level on the support pressure is shown in Fig. 20. It is obvious that both the limit equilibrium solution (Anagnostou and Kovári, 1996) and the upper bound solutions (this study; Lee and Nam (2001)) increase linearly with increasing groundwater level. However, the limit equilibrium solution predicts larger values, and the rate of increase is higher than that of the upper bound solutions. A comparison of the two upper bound solutions shows that for the same groundwater level, the present work predicts a higher support pressure than that of Lee and Nam (2001). This is because in Lee and Nam (2001)’s work, the effects of the seepage forces within the unstable soil and the effective soil weight are neglected. For the case of C/D=2, H/C=1, the support pressure resulting from this work is 46 kPa, which is 16 kPa greater than Lee and Nam (2001)’s result. However, in Anagnostou and Kovári (1996)’s approach, the height of the model is assumed to be equal to the cover depth, so the stability is significantly influenced by cover soil and surcharge; this leads to an overestimation of the support pressure, especially for deep tunnels. It should be noted that the possibility of face collapse increases once the support pressure is between Anagnostou and Kovári (1996)’s solution and the solution of this study.

Fig. 20
figure 20

Influence of groundwater level H/C on the support pressure \({\sigma _{\bf{T}}}^\prime\) (C/D=1.5, d 1 /d 2 =1.5, cover layer: silt sand, crossed layer: sand diluvium)

Full size image

The limit support pressures of the case study in Section 2 predicted by different upper bound solutions are presented in Table 4. Without considering seepage, Tang et al. (2014)’s solution predicts that the lowest support pressure is 21 kPa. The higher support pressure of 28 kPa is predicted by Senent and Jimenez (2015)’s solution, in which the seepage is also not considered. The larger support pressure predicted by the rotational mechanism model than that predicted by the conical mechanism model has been verified in Senent and Jimenez (2015)’s research. Considering the seepage forces on the tunnel face, Lee and Nam (2001) and Lee et al. (2003)’s solution gives a support pressure of 30 kPa, which is 50% greater than that predicted by Tang et al. (2014)’s solution. From the 2D analysis, Lv et al. (2014)’s solution predicts a support pressure of 32 kPa. Although the seepage forces applied on the mechanism are considered in Lv et al. (2014)’s upper bound analysis, a 2D mechanism model causes underestimation of the support pressure. Returning to the case study, it can be found that the support pressures predicted by the previous solutions are even lower than the smallest pressure measured in practice. This study results in the highest support pressure of 46 kPa among all upper bound solutions. The pressure of 38 kPa measured at the upper part of the tunnel face is lower than 46 kPa. It can be inferred that the failure starts from the upper part of the face because of the low support pressure and eventually moves to most of the area of the face. This study predicts a higher, and thus relatively safe, support pressure, which is needed for face stability under groundwater seepage.

Table 4 Results of support pressure predicted by upper bound solutions
Full size table

5 Conclusions

In this paper, we study the face collapse accident in layered soil under groundwater seepage in the construction of Guangzhou metro line 3. This type of face collapse is investigated via upper bound analysis. Both the effects of the seepage forces acting on the tunnel face and seepage forces in the failed soil are considered in the analysis. The numerical simulation indicates that the groundwater seepage in the well-conditioned cases is not as significant as that in the unconditioned cases. For the unconditioned cases, the numerical analysis for groundwater seepage in layered soil shows that the seepage forces acting on the tunnel face and the seepage pressure ratio become steady after a steep decrease within 1200 s. During steady-state seepage in the crossed layer, the groundwater moves horizontally towards the tunnel, while in the cover layer, the groundwater vertically percolates into the crossed layer. The seepage forces acting on the tunnel face and those in the unstable soil increase linearly with increasing groundwater level, and both play an important role in the upper bound analysis of the face stability. Consequently, this upper bound solution of support pressure considers both the seepage forces acting on the tunnel face and the seepage within the soil and predicts a higher, and thus relatively safe, support pressure, which is needed for face stability under groundwater seepage.