1 Introduction

Wide-span buildings require the adoption of light-weight roof structures, with few vertical supports, due to the architectural requirement of large column-free interior spaces, which can be obtained by either shaping efficient structural forms and/or optimizing the spatial arrangement of the resisting material.

When the shape of the roof is predetermined, as in the case of flat roof structures, the only strategy toward lightness is the rational distribution of the structural material, namely the best allocation of the material for resisting the global bending action and the insertion of voids in useless zones. Historically, this approach has driven the development of new structural concepts, forms, and aesthetics, with precious contributions provided by innovative engineers and smart researchers: from the prototype tetrahedron kites and the pioneering space frames conceived by Bell (Chilton, 2000); through the huge theoretical and practical contributions by Fuller (1982) on geodesic domes and tensegrity structure, then further developed by his student, Snelson (Snelson, 2012); to the thought of Le Ricolais, who pushed the ancient builders’ ethic of doing the most with the least to its extreme consequence “infinite span zero weight” (Emmerich, 1994). The challenge of long-span structures has been the search for lightness and structural efficiency, mainly focused on the articulation of form, i.e., on how material is locally distributed within a fixed structural shape (Sandaker, 2008).

What is most important in this approach is the material philosophy behind it: “matter is no longer solid; it is made of air, a structured void, it is a reversal from the stone, monolithic view of matter, into a metallic, composite one. It looks not at the materiality of space but at the spatiality of matter” (Spuybroek, 2008).

The line traced by this new philosophy can also be found in the forms and structures of nature, “which reflect the unquestionable laws of economy and efficiency: seashells, radiolariae and crystals are examples of veils, networks and skeleton structures that can be transposed into actual projects”. In the words of Le Ricolais (McClearly, 1998) “... structures composed of holes, all different in dimension and distribution, but with an unmistakable purpose in their occurrence. So we arrive at an apparently paradoxical conclusion that the art of structure is how and where to put holes: to build with holes, to use things which are hollow, things which have no weight.”

This lesson has been absorbed by the engineering design disciplines, but in different ways, at the micro-scale and the macro-scale (Hashin and Shtrikman, 1963; Nemat-Nasser and Hori, 1999): while composite materials, foam structures, and sandwich panels are typical applications at the micro-scale level, a more superficial and incomplete awareness of the material philosophy taught by nature is found at the macro-scale in the field of civil engineering.

In fact, in materials engineering, micromechanics and physical properties of heterogeneous media have been intensely studied in recent decades (Gibson and Ashby, 1988; Evans, 2001; Evans et al., 2001). The starting point is the observation of the countless examples of natural heterogeneous media, made of different elements, cells, or fibres, differently arranged to form intricate interior structural networks, self-organized in hierarchies to produce modularity, redundancy, and differentiation, which guarantee the optimal mechanical performance; with this background, synthetic materials, composites, foams, and lattices, all belonging to the category of cellular materials, are nowadays developed for different engineering applications, with special attention to design strategies and optimization techniques for creating high-performance man-made products.

According to Weinstock (2006), cellular materials display open and ductile structural systems which are stiff, strong, and permeable, making them an attractive proposition for developments not only in materials science, but also for new structural systems in architecture and engineering.

In this sense, the material distribution method (Bendsøe and Sigmund, 2003), which is largely adopted in structural applications, seeks the optimum lay-out of a structure, and aims to solve the structural design problem in terms of sizing, shape, and topology optimization with the goal of minimizing (or maximizing) a physical quantity, such as the strain energy, the local stress, and deflection.

However, while the idea of optimal material organization has been worked out in the search for lightness and exploited in the conception of large-scale space frames throughout the last century, civil engineers and architects are not familiar with cellular materials, and preserve the obsolete ways of thinking about material as something independent of form and structure. The fundamental unawareness and conservatism lead to limited and constrained design visions and produce architectural applications dominated by a substantial lack of novelty.

However, some very recent examples contradict this general trend.

The idea of porous media conceived on a very large scale, with void inclusions thought of as part of continuity and not as interruptions, is at the core of the Taichung Metropolitan Opera House in Taiwan, China (Fig. 1a), designed by Toyo ITO, where the orthogonal external form is punctured with countless holes, cave-like holes that penetrate the form, giving rise to an interior space made up of continuous convex surfaces (Ito, 2012).

Fig. 1
figure 1

Structure of the Taichung Metropolitan Opera House in Taiwan, China (a) and the bubble-like structure of the Water Cube, National Aquatics Center, China (b)

Full size image

The concept of foam structure and the relevant physical model has also been tested for applications involving different scale dimensions, giving rise to the bubble-like structure of the Water Cube, China (Fig. 1b), an example of foam structures at extremely large scale.

The Water Cube exemplifies how science cross-fertilization and knowledge transfer among different fields of science and engineering can produce innovative forms and structure. The design starts from the Weaire-Phelan physical-mathematical model, which provides the most efficient subdivision of space into equal volume cells, by assembling bubble clusters made of eight polyhedrons, with either 14 or 12 faces; filling the notional building volume according to the bubble packing rules, then by cutting the bubbles at the exterior and interior surface intersection, the steel structural wire frame is obtained.

The Water Cube can be taken as a benchmark for innovative space frame structures, and provides data, knowledge, and inspiration for future projects. However, the variety of tetrahedral nets that could be inspired by nature, from the diamond nets to the closed-cell foams, is almost infinite, and all exhibit interesting structural properties to be transposed in large scale applications.

While some examples of structures with apparently random organization of steel elements have been recently proposed or realized (e.g., the Federation Square complex in Melbourne, Australia, designed by Lab Architecture Studio with the structural engineering consultancy of Atelier One, UK), major questions arise for the structural engineers: how to deal with, how to model, analyze, and design these complex structures, where the load paths, the local resisting mechanisms, and deformation modes cannot be intuitively derived?

Tristram CARFRAE, Arup’s structural designer of the Water Cube, reported that the structure was tested using algorithmic optimization allied to informed personal judgement, using purpose-built tools, as well as rapid prototyping and building information modelling (Hill, 2008). However, as Hyde (2010) observed, “… given that … Carfrae’s tetrahedral space frames in Beijing are structures long known to certain scientists …”, many steps of the design process could have been carried out by means of a simpler, more straightforward and aware procedure, “... rather than relying on computational black-boxes.”

In this paper the authors propose an alternative, more general, methodology for dealing with these complex, foam-like macrostructures, made of thousands interconnected beam elements: the idea is to idealize them as continuous depleted media, characterized by penalized mechanical properties, namely by using the classical micromechanical approach based on homogenization methods; the starting point is the mechanical study of the representative volume element (RVE), the unit, repetitive structure of the specific depleted medium (Nemat-Nasser and Hori, 1999). This deterministic method is based on a continuum theory where the micro-structural properties are incorporated in prescribed architectural variables, whose choice is generally suggested by analytical results. The connectivity as well as the distribution of the media within the representative volume are described by topological measures, such as the apparent density (volume fraction) or stereological surveys (Turner and Cowin, 1987).

In Toreno et al. (2011), this approach has been successfully applied to the Water Cube structure. In fact, behind the highly random appearance of the Water Cube, it is simply a recursive structure like other space frame structures, with the repetitive module obtained on the basis of the Weaire-Phelan bubble cluster. The application has confirmed the potential of classical micromechanical-based strategies for the design and assessment of mega-scale civil structures, generated by complex, non-conventional patterns. Furthermore, since the main parameters governing the model are the RVE density, connection degree, and orientation, topological optimization procedures are relatively effortless and retain conceptual consistency and control capacity.

In this paper, an additional step towards generalization of the approach is made; in particular, an analytical procedure is proposed for defining a design tool for long-span structures made by recursive patterns of a base unit (RVE). Two different RVE topologies are studied through the finite element method (FEM), and related penalty coefficients of the homogenization law are found.

2 Object, aim, and method

This paper establishes the analytical framework for dealing with a three-layered (sandwich) thin plate made of depleted materials, to define simplified tools for the preliminary design of large-span, weight efficient structures.

Depleted media are materials whose overall stiffness and strength are reduced due to presence of cavities in the solid matrix, but are characterized by potentially high stiffness/weight ratios, thanks to optimal void distribution.

Of particular interest are the low volume fraction (LVF) ones, where a structurally ordered or randomly-arranged network of thin elements (beams and/or plates) can be generally observed at the micro-scale level, as in trabecular bone tissues, honeycomb materials, or truss structures. In particular, spatially organized truss structures can be interpreted as overall macroscopically arranged depleted media, and the micromechanical approaches can be employed for analyzing and designing civil engineering structures.

In this framework, a key point is how macroscopic effective physical properties of heterogeneous materials can be derived from their microstructures. From a mechanical standpoint, a continuum-theory-based approach may be adopted for analyzing complex microstructures, once the RVE, i.e., the smallest homogeneous material volume which macroscopic constitutive relationships must be referred to, is chosen (Chilton, 2000). Overall mechanical properties of depleted media depend on the elasticity and strength of the solid matrix and upon RVE micro-structural features, namely topology, density, and orientation. Therefore, following a classical homogenization approach, it is possible to deduce the response of the whole structure from the mechanical properties of the single unit element.

In particular, with reference to the sandwich plate, given a specific depletion strategy for plate layers, and given the performance requirements (namely, the maximum vertical deflection of the plate), the procedure provides the level/degree of depletion, i.e., the volume solid fraction, to be adopted in each layer for ensuring the required performance; since the volume fraction is related to the geometrical parameters which define the layer microstructure, the procedure finally results in the size of the structural elements in the plate layers.

For this purpose, the following steps are developed.

First, the flexural behaviour of a sandwich plate structure, with three solid layers, is examined, and the governing mechanical parameters are identified.

Then, two different microstructures are considered and the relevant RVEs are analyzed to define the flexural stiffness as a function of the volume fraction and to investigate the sensitivity of the RVE response to additional parameters, related to the specific microstructure.

Finally, adopting the RVE flexural stiffness for characterizing the plate layers, and following a homogenization approach, a design formula is suggested that provides the volume fraction in each layer as a function of the global geometry, of the prescribed displacement and of the layer microstructure.

3 Flexural stiffness of a thin three-layer plate

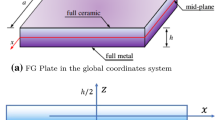
A thin plate made of three layers, as it is schematically illustrated in Fig. 2, is considered. The sandwich structure, composed of stiff external layers and a low-density core arrangement, is adopted as a weight efficient structure (Evans, 2001).

Fig. 2
figure 2

A thin plate made of three layers

Full size image

The plate is square, with dimension a, total thickness H=h1+h2+h3, external layer thickness h1 and h3, and core thickness h2; it is simply supported at the edges and subject to a uniform vertical pressure, q, applied statically to the top surface of the plate; the pressure q is given by q=qw+qa, i.e., made up of the weight of the plate per unit area (qw) and for possible additional load (qa).

Each layer is assumed as transversely isotropic and homogeneous, in a way that the plate structure is characterized, at the macroscopic level, by transversal isotropic mechanical behaviour, with the plane of isotropy coincident with the plane of the plate.

We here consider a section of the plate of length b=1, supported at the edges. Thus, invoking the Kirchhoff-Love theory for a thin elastic plate, the maximum vertical displacement δmax=u y {G}, in the case of small deformations, is directly related to the vertical load q:

$${\delta _{\max }} = {q \over K},$$
(1)

with

$$K = {K_\chi }/({a^4} \cdot {C_{\rm{f}}}),$$
(2)

where K χ =M/χ is the ratio between the flexural moment per unit length and the relative curvature, and Cf relates to the geometry and the boundary conditions of the problem. In the case of an infinite plate the term Cf can be determined analytically, for example for a simply supported plate of infinite length it results in Cf=5/384, while in the case of a plate of finite dimension it can be deduced by the Fourier series of the displacement field equations (e.g., for a squared plate clamped at the edges, Cf ≈ 0.004 06) (Timoshenko, 1936).

The overall flexural stiffness exhibited by a generic multilayered plate made of N layers can be computed as the summation of the single layer contributions, k χi =E i I i :

$${K_\chi } = \sum\limits_{i = 1}^N {{{{k_{\chi i}}} \over {1 - \nu _i^2}}},$$
(3)

where E i and ν i are Young’s modulus and Poisson’s ratio, respectively, of the material in the ith layer; I i is the inertia per unit length of the cross sectional area.

The problem presented in this framework deals with the optimal design of a model of the three layered structure subject to uniform distribute vertical load, whose parts (layers) are characterized by distinct mechanical response, in a way that the flexural stiffness can be mainly addressed to the external layers, in such specific case Eq. (3) becomes

$${K_\chi } = {{{E_1}{I_1}} \over {1 - \nu _1^2}} + {{{E_2}{I_2}} \over {1 - \nu _2^2}} + {{{E_3}{I_3}} \over {1 - \nu _3^2}}{.}$$
(4)

4 Design and optimization procedure of multilayered plate with depleted materials

The analytical model developed in Section 3 for the thin sandwich plate composed by three homogeneous and transversely isotropic layers, is adopted for describing the overall behaviour of a thin sandwich plate with depleted materials, i.e., a plate constituted by three layers realized through a recursive arrangement of a specific microstructure of an isotropic material which is defined by two elastic constants, Young’s modulus E0i and Poisson’s ratio ν0i, and by the specific density s 0 i .

In this framework, the volume fraction ρ i is adopted as the basic measure of the arrangement of the solid material that composes the microstructure of each layer, defined as

$${\rho _i} = {{{V_i}} \over {{h_i}{a^2}}},$$
(5)

where h i is the thickness of the ith layer, and V i is the volume of the total amount of material employed in the structure.

The idea is to deal with the design flexural problem of the inhomogeneous sandwich plate through Eqs. (1)–(3) previously defined for the homogeneous sandwich plate, provided that a homogenization process of the single layers is first carried out. Thus, the procedure able to design the inner microstructure of a heterogeneous plate subject to a vertical distributed load is presented and verified. Therefore, an analytical design procedure for the inner microstructure of a heterogeneous plate under uniform vertical pressure is proposed and verified against numerical results.

The depleted material in the single layers is assumed to be given by a repetitive spatial pattern of a microstructure unit, the RVE, which is able to account for the mechanical response associated to the specific structure connectivity. Therefore, the starting point for the definition of the homogenized model of each layer is the assessment of the mechanical performance of the RVE; then, the layer flexural stiffness k χi can be defined as a function of the layer volume fraction and of the parameters related both to the RVE connectivity and to the plate global geometry. The next paragraph deals with this issue.

Now, let us assume that the flexural stiffness k χi of the ith layer of the heterogeneous plate has been determined following the same approach commonly used in the homogenization procedure of the mechanical response of depleted media, and that it is expressed according to the general power function:

$${k_{\chi i}} = {f_{ki}}({\rho _i},\;{k_{0i}}) \approx {k_{0i}}{c_i}\rho _i^{{m_i}},$$
(6)

where k0i is the corresponding value for the solid layer (i.e., in the case of ρ i →1), and c i and m i are constants related to the specific topology of the microstructure. Note that the value of Poisson’s ratio of the depleted media ν i is assumed to be equal to the respective value of the solid material constituting the microstructure ν0i, i.e.,

$${\nu _i} \approx {\nu _{{{0}}i}}{.}\,$$
(7)

Moreover, it is assumed that, from the macroscopic point of view, the material is homogeneously disposed in the layer in such a way that the global value of the inertia can be calculated through the inertia of the section diminished by the value of the volume fraction:

$${I_i} = {I_{0i}}\,{\rho _i},$$
(8)

where I0i is the inertia per unit length of the cross sectional area A i respect to the neutral axis, defined as

$${I_{0i}} = b{{{h_i}^3} \over {12}} + b\,{h_i}y_i^2,$$
(9)

with y i the distance between the neutral axis and the centre of the area A i .

Eq. (6) calculated for each layer allows the calculation of the global flexural stiffness as prescribed in Eq. (3).

To highlight the dependence of the maximum vertical displacement on the volume fraction of the layers, it is also necessary to express the weight per unit area of the plate qw as a function of the layer volume fractions and of the density of the material constituting the layer microstructure, s 0 i , i.e.,

$${q_{\rm{w}}} = g\sum\limits_{i = 1}^3 {s_i^0{h_i}{\rho _i}},$$
(10)

where g is the acceleration due to gravity. From the definitions of the vertical load and the flexural stiffness, Eqs. (3)–(10), Eq. (1) can be rewritten taking into account Eqs. (2)–(10), in a form that highlights the dependence of the maximum vertical displacement on the volume fraction of the layers in the form of

$${\delta _{\max }} = {a^4} \cdot {C_{\rm{f}}}{{{q_{\rm{a}}} + g\sum\limits_{i = 1}^N {s_i^0{h_i}{\rho _i}} } \over {\sum\limits_{i = 1}^N {{{{k_{0i}}} \over {1 - \nu _{0i}^2}}{c_i}\rho _i^{{m_i}}} }},$$
(11)

where N is the number of the layers presented in the sandwich structure, and Cf depends on the plate dimensions and boundary conditions. As already stated, the coefficients c i and m i of the homogenization power function have to be specified depending on the microstructure connectivity, as will be done in the next paragraph.

Eq. (11) represents a useful tool for the design, and eventually for the optimization, of multilayered plates of depleted material in pure bending. In fact, once a limit value for δmax is fixed, it allows the derivation in a numerical way of the volume fractions ρ i , as a function of the coefficients c i and m i and of the global plate parameters (geometry, boundary conditions, layer thickness, etc.), and then, through Eq. (10), the weight of the structure.

Moreover, given the flexural stiffness calculated in the general form of Eq. (3), Eq. (11) can be easily applied, in most common applications, to many cases of a thin composite structure, starting from the multilayer film characterized by nano-scale dimension (Ariga et al., 2014) up to the macro-scale level of wide span roof structures (Sandaker, 2008). A further step towards a more direct and handy design tool can be made by adopting some simplified, though reasonable, assumptions, as reported in the following.

It is assumed that the microstructure of each layer is constituted by the same material, characterized by Young’s modulus E0, Poisson’s ratio ν0, and density s0.

The inner and external layers are characterized by a diverse density of the same isotropic recursive arrangement; in other words, the structural connectivity of each layer is provided through the same heterogeneous material, but is characterized by a different amount of material per unit of volume (i.e., different ρ i ).

Furthermore, considering the optimal design of three layered structures in pure bending (i.e., the lightest weight solution), it is possible to assume that the greater part of the material is concentrated in the external layers and symmetrically distributed, in such a way that I01=I03>>I02 and consequently k χ 1= kχ3>>k χ 2, and the volume fractions follow the relations of

$${\rho _1} = {\rho _3} = n{\rho _2},$$
(12)

with the ratio between the volume fraction of the outer layers and the middle layer n≥1.

Finally, it is assumed that no additional load is applied on the structure, i.e., qa = 0.

Given the last hypothesis, it is possible to invert Eq. (11) and deduce the volume fraction of the layers in the algebraic form:

$${\rho _1} = {\rho _3} \approx {\left[ {{{{a^4}{C_{\rm{f}}}} \over {{\delta _{\max }}}}{{g{s_0}({h_2} + 2n{h_1})} \over {2{{{k_{01}}} \over {1 - \nu _0^2}}n{c_1}}}} \right]^{{1 \over {{m_1} - 1}}}},$$
(13)
$${\rho _2} \approx {1 \over n}{\left[ {{{{a^4}{C_{\rm{f}}}} \over {{\delta _{\max }}}}{{g{s_0}({h_2} + 2n{h_1})} \over {2{{{k_{01}}} \over {1 - \nu _0^2}}n{c_1}}}} \right]^{{1 \over {{m_1} - 1}}}}{.}$$
(14)

However, it is possible, in a general form to compute any additional value of the vertical load qa, and obtain from Eq. (11) the volume fraction of the layers in a numerical way.

Therefore, setting a maximum displacement allowable for the plate structure, Eqs. (13) and (14) furnish the volume fractions ρ i of the inner and outer layers able to satisfy the performance requirement expressed in terms of vertical displacement limitation.

Eqs. (13) and (14) of ρ1 and ρ2 can be substituted into Eq. (10), thus providing the weight of the structure per unit area as

$${q_{\rm{w}}} \approx {1 \over n}{\left[ {g{s_0}({h_2} + 2n{h_1})} \right]^{{{{m_1}} \over {{m_1} - 1}}}}{\left[ {{{{a^4}{C_{\rm{f}}}} \over {2{\delta _{\max }}{{{k_{01}}\;} \over {1 - \nu _0^2}}n{c_1}}}} \right]^{{1 \over {{m_1} - 1}}}}{.}$$
(15)

Finally, the flexural stiffness of the plate given by Eq. (4), and considering Eq. (6), can be estimated through the approximate expression:

$${K_\chi } \approx 2\,{c_1}\,\rho _1^{{m_1}}{{{k_{\chi 01}}\;} \over {1 - \nu _0^2}}{.}$$
(16)

The strength of the method lies in the definition of the optimum topological distribution of the material employed along the section of the plate following the objective of maximizing the flexural stiffness. To evaluate the effective flexural stiffness K χ of a plate made of three heterogeneous layers, we consider a reference, a section of dimensions b×H of a depleted medium made of a material with Young’s modulus E0 and characterized by a volume fraction of

$$\bar \rho = {{2{\rho _1}b{h_1} + {\rho _2}b{h_2}} \over {b(2{h_1} + {h_2})}},$$
(17)

and the value of the flexural stiffness of the section follows the relation:

$${\bar K_\chi } \approx \; c{\bar \rho ^m}{{{E_0}} \over {1 - \nu _0^2}}{{b{H^3}} \over {12}}{.}$$
(18)

In such a way, the ratio

$${\eta _\chi } = {{{K_\chi }} \over {{{\bar K}_\chi }}}$$
(19)

accounts for the gain of the overall stiffness of the layered plate for that amount of material.

For such a microstructure it is possible now to investigate the dependence of the ratio η χ on the design parameters. Fig. 3 highlights the meaning of η χ , based on Eqs. (16) and (18), in relation to the parameters h1/H and n=ρ1/ρ2; note that in the calculation it is assumed c=c1 and m=m1 to pass over the dependence on \(\bar \rho\).

Fig. 3
figure 3

Gain of the overall stiffness of the layered plate in relation to the thickness of the layers. The maximum value for each value of the ratio n is highlighted (gray line)

Full size image

On the other hand, starting from a prescribed value of the flexural stiffness, the proposed approach can also be adopted to find the optimum topological distribution of the material employed along the section of the plate with the objective of minimizing the amount of material required.

Let \({\bar K_\chi } \) be the flexural stiffness of a homogeneous section as presented in Eq. (18) and

$$\bar \Omega = \bar \rho b(2{h_1} + {h_2})$$
(20)

be the amount of material used per unit length of the plate. Then it is possible to design an heterogeneous section made of three layers with volume fraction ρ1=nρ2=ρ3 and a total amount of material

$$\Omega = {\rho _1}b(2{h_1} + {h_2}{{/}}n),$$
(21)

characterized by a flexural stiffness K χ , see Eq. (16), that respects the position:

$${K_\chi } = {\bar K_\chi }{.}$$
(22)

Finally, the ratio

$${\eta _\Omega } = {\Omega \over {\bar \Omega }}$$
(23)

expresses the reduction of the amount of material required.

Fig. 4 highlights the meaning of ηΩ, based on Eqs. (20) and (21), in relation of the parameters h1/H and n=ρ1/ρ2; note that in the calculation it is assumed c=c1 and m=m1 in order to pass over the dependence on \(\bar \rho\).

Fig. 4
figure 4

Total amount of material required in the layered plate in relation to the thickness of the layers. The minimum value for each value of the ratio n is highlighted (gray line)

Full size image

5 Microstructure of depleted layers

In the present framework the elastic properties of each layer are associated to the flexural stiffness; through the homogenization procedure already introduced, it is thus possible to correlate ρ i to the mechanical response of that kind of microstructure. In fact the volume fraction can be adopted as a scalar measure of the elastic behaviour of the media. Moreover, the periodic spatial pattern of the microstructure, as well as the stress distribution in each of the layers, allows the definition of a specific material unit that is able to report the mechanical response associated to the type of connectivity of that kind of structure: the RVE. The RVE approach has been widely used to account for several mechanical behaviours of a recursive medium, such as static strength, fatigue, and non-linear behaviour (Hill, 1963; Hild et al., 1996; Nemat-Nasser and Hori, 1999). In this study it is adopted to deduce the linear elastic response of the structure. Compared with traditional design methods, the homogenization method based on the definition of the RVE of a recursive structure furnishes the analytical solution to the problem of the mechanical response of complex and wide structures giving the optimal configuration with respect to any specific application. Thus, we first investigate the specific RVE model for variable volume fraction in such a way as to provide insights on the global response of each single layer to use in the optimal design of multilayered plate structures.

From a homogenization approach it is actually possible to deduce the stiffness K of the plate section, Eq. (3), through the mechanical properties of the single unit elements. Furthermore, the flexural stiffness k χi of each layer can be easily determined through the flexural stiffness of the relative RVE, which is identified by a measure of its volume fraction ρ i in the form of the penalization power law, i.e., Eq. (6).

To understand the effect of different orders of connectivity on the mechanical response of depleted media, two different types of recursive microstructure are here considered:

  1. 1.

    A porous solid structure with cubic depleting voids, with the recursive unit reported in Fig. 5.

  2. 2.

    A truss structure, with the recursive unit reported in Fig. 6.

Fig. 5
figure 5

Porous solid structure with cubic depleting voids, setting of the boundary conditions, and finite element (FE) model

Full size image
Fig. 6
figure 6

Truss structure, setting of the boundary conditions, and FE model

Full size image

In the following, the two microstructures are analyzed through the FEM and the specific form of the penalization law Eq. (6) is derived, i.e., the coefficients c i and m i are evaluated.

5.1 Porous solid structure

A specific morphology of a solid porous RVE is here considered and analyzed through the FEM, to evaluate how the presence of a recursive arrangement of voids and the geometrical parameters characterizing the voids affect the overall mechanical response.

The specific morphology of a solid porous RVE is depicted in Fig. 5: it has a cubic shape of dimension ℓ (spatial period of the recursive microstructure) and is occupied by a solid isotropic matrix (with Young’s modulus E0 and Poisson’s ratio ν0) depleted by a cubic cavity of dimension d. The depleting void is positioned at the RVE centre.

Several solid porous RVEs of this type have been realized with different volume fraction values, with the aim of finding the correlation between the flexural stiffness penalization of the medium and its level of geometrical depletion.

For this purpose, bending tests on the RVEs have been performed using the FEM, and varying the volume fraction. As the point of the bending tests is to investigate the flexural response of the structure, represented by the RVE, within the bended plate, the distance of the mass centre of the RVE from the neutral axis will change in such a way to account for the different positions that the depleted layers take along the plate cross section. The setting of the boundary conditions is shown in Fig. 5: with reference to the o-xyz coordinate system, the RVE has been forced to assume the deformed configuration related to a pure bending with the neutral axis parallel to the x direction, the mass centre of the RVE being at distance yI from the neutral axis, through a prescribed displacement w applied on all nodes of the model that lie at z = ± ℓ/2assigned in the following form:

$$w = 2({y_{{\rm{node}}}} - {y_{\rm{I}}}) \times {10^{ - 3}},$$
(24)

where ynode is the y coordinate of the node in the reference system. The curvature associated with the configuration can be thus deduced through a first-order approximation as

$$\chi \approx {{2 \times {{10}^{ - 3}}} \over {\ell/2}}{.}$$
(25)

Finally, the finite element (FE) procedure allows the calculation of the reaction solution Rnode in each node, hence the value M of the related moment as

$$M = \sum\limits_{{\rm{node}}} {\left\vert {{R_{{\rm{node}}}}} \right\vert } ({y_{{\rm{node}}}} - {y_{\rm{I}}}),$$
(26)

and the flexural stiffness consequently being given by

$${k_\chi } = M/\chi {.}$$
(27)

The normalized flexural stiffness, kχ/k0χ, has been computed as the response parameter, with k0χ the flexural stiffness of the RVE with ρ i →1, equal to:

$${k_{0\chi }} = {E_0}{I_0} = {E_0}\left({{{{\ell ^4}} \over {12}} + {\ell ^2}y_{\rm{I}}^2} \right){.}$$
(28)

Note that the normalized flexural stiffness is a function of the volume fraction and of the distance of the neutral axis from the mass centre of the RVE, i.e., \({k_\chi }/{k_{{0\chi }}} = {f_\chi }(\rho, \;{y_{\rm{I}}})\); for this reason, the bending tests have been performed for different values of yI, with \(0 \leq {y_{\rm{I}}}/\ell \leq 10\)

Fig. 7 shows the results of the parametric numerical analysis, reporting the value of the ratio \({k_\chi }/{k_{0\chi }}\) obtained for each value of ρ. The grey dashed curves represent the third polynomial regression functions of ρ that best fit the numerical values.

Fig. 7
figure 7

Normalized flexural stiffness as a function of the volume fraction ρ and of the distance of the neutral axis from the centre of mass of the RVE

Full size image

The curves show that starting from a value yI/ℓ > 1 the term that takes into account the distance of the neutral axis from the mass centre becomes the most relevant part of the inertia calculation, and the gradient of stress in the media drops sufficiently to allow the consideration of the RVE as subject to a simple axial load to a good approximation.

For the specific mechanical problem examined in this study (multilayered plate with recursive structure), the above observation suggests analysis of the results referring to two main conditions, i.e., yI/ℓ = 0 and yI/ℓ > 1

The first case (yI/ℓ = 0) represents the middle layer of the plate, since the stiffness can be entirely related to the inertia of the section. Conversely in the second case (yI/ℓ1) the inertia of the section is negligible compared to the term \({\ell ^2}y_{\rm{I}}^2 \), thus, it represents the external layers of the plate.

For the two cases, the power functions of ρ that best fit the numerical values can be written as: case yI/ℓ = 0,

$${{{k_\chi }} \over {{k_{0\chi }}}} = {f_\chi }\left({\rho, \;\;{{{y_{\rm{I}}}} \over \ell } = 0} \right) \approx {c_0}{\rho ^{{m_0}}},\;\;\;\;{c_0} = 1,\;\;{m_0} = 0{.}71289;$$
(29)

case yI/ℓ = 1,

$${{{k_\chi }} \over {{k_{0\chi }}}} = {f_\chi }\left({\rho, \;\;{{{y_{\rm{I}}}} \over \ell } > 1} \right) \approx c{\rho ^m},\;\;\;\;c = 1,\;\;m = 1{.}42928{.}$$
(30)

The above functions are defined for the specific microstructure herein considered, i.e., a solid isotropic matrix depleted by a cubic cavity. Varying the void shape produces a unique influence on the distribution of stress in the matrix and on the overall stiffness. As an example, in the case of spherical voids, the stiffness penalization laws are: case yI/ℓ = 0,

$${{{k_\chi }} \over {{k_{0\chi }}}} = {f_\chi }\left({\rho, \;{{{y_{\rm{I}}}} \over \ell } = 0} \right) \approx {c_0}{\rho ^{{m_0}}},\;\;\;\;{c_0} = 1,\;\;{m_0} = 1{.}0846;$$
(31)

case yI/ℓ = 1,

$${{{k_\chi }} \over {{k_{0\chi }}}} = {f_\chi }\left({\rho, \;{{{y_{\rm{I}}}} \over \ell } > 1} \right) \approx c{\rho ^m},\;\;\;\;c = 1,\;\;m = 1{.}63226{.}$$
(32)

5.2 Truss structure

The connectivity related to a spatial arrangement of beams is analyzed by the FEM to evaluate how the geometrical properties of the beam section affect the overall mechanical response in terms of flexural stiffness.

The representative volume has a cubic shape of dimension ℓ. In particular, the RVE is occupied by 24 beams connected at their ends, with connections arranged to lie on a spherical surface of radius \(\ell/\sqrt 2 \) as shown in Fig. 6. The linear length of all 24 beams that form the RVE is defined as λ. The beam material is isotropic with Young’s modulus E0 and Poisson’s ratio ν0, and the beam cross section is a hollow circle, with inner radius ri and outer radius ro.

Since the RVE volume fraction ρ depends on the beam cross sectional area, in the following we refer to the equivalent area radius rae, defined as

$${r_{{\rm{ae}}}} = \sqrt {r_{\rm{o}}^2 - r_{\rm{i}}^2},$$
(33)

and to the equivalent inertia radius rie, defined as

$${r_{{\rm{ie}}}} = \sqrt[4]{r_{\rm{o}}^4 - r_{\rm{i}}^4} {.}$$
(34)

To compute the dependence of the mechanical properties penalization on the geometrical properties of the beam section, several RVEs are realized with different values of the volume fraction ρ, i.e., different values of rae and different values of rie. For the specific purpose of the following analyses, a sensitivity parameter is introduced: the ratio between rae and rie, rr=rae/rie. Note that rr=1 in the case of a solid circular section, while rr<1 in the case of a hollow circular section.

Bending tests have been performed using the FEM (refer to Eq. (24) and Fig. 6 for the specific boundary conditions), assuming the relative normalized flexural stiffness \({k_\chi }/{k_{0\chi }} \) as the response parameter (refer to Eqs. (25)–(28)). The results show that the normalized flexural stiffness is not only a function of the volume fraction and the ratio rr, but also depends on the distance of the neutral axis from the RVE mass centre, i.e., \({k_\chi }/{k_{0\chi }} = {f_x}(\rho, \;{\rm{rr}},\;{y_{\rm{I}}}) \). The bending tests are performed for different values of yI, with 0 ≤ yI/ℓ ≤ 10.

The FE results are highlighted in Figs. 8 and 9, which show the relation between the normalized flexural stiffness \({k_\chi }/{k_{0\chi }} \) and the volume fraction ρ. This, in turn, is directly related to rae. In particular, from Fig. 8 it is possible to evaluate the sensitivity of the results for yI, in the case rr=0.5, while Fig. 9 shows (in the case of yI/ℓ = 0) the sensitivity of the results for the ratio rr, which, once defined ρ, is directly related to rie.

Fig. 8
figure 8

Normalized flexural stiffness as a function of the volume fraction and of the distance of the neutral axis from the centre of mass of the RVE

Full size image
Fig. 9
figure 9

Normalized flexural stiffness as a function of the volume fraction and of the equivalent area radius and the equivalent inertia radius

Full size image

The grey dashed curves (Figs. 8 and 9) show the third polynomial regression functions of ρ that best fit the numerical values. Similar to the previous case, it is worth noting that, starting from the values of yI/ℓ > 1 the term that takes into account the distance of the neutral axis from the mass centre becomes the most relevant part of the inertia calculation, and the gradient of stress in the media drops sufficiently to make it possible, to a good approximation, to consider the RVE as subject to a simple axial load.

Then the power functions of ρ that best fit the numerical values can be written as:

$$\begin{array}{*{20}c} {{{{k_\chi }} \over {{k_{0\chi }}}} = {f_\chi }\left({\rho, {\rm{rr}}, {{{y_{\rm{I}}}} \over \ell } = 0} \right) \approx c{\rho ^m},\quad \quad \quad \quad \quad \quad \quad \quad }\\ {c = {{2}}{.}{{40765}} - {{1}}{.}91875{\rm{rr}},\;m = 1{.}33006 + 0{.}507134{\rm{rr}},} \end{array}$$
(35)
$$\begin{array}{*{20}c} {{{{k_\chi }} \over {{k_{0\chi }}}} = {f_\chi }\left({\rho, \;{\rm{rr}},\;{{{y_{\rm{I}}}} \over \ell } > 1} \right) \approx c{\rho ^m},\quad \quad \quad \quad \quad \quad \quad \quad }\\ {c = 2{.}01178 - 1{.}91875{\rm{rr}},\;\;m = 1{.}33388 + 0{.}507134{\rm{rr}}{.}} \end{array}$$
(36)

The above functions are defined for the specific microstructure considered, i.e., the spatial arrangement of beams shown in Fig. 6, which reacts to the load through a unique distribution of stress, and corresponds, in general, to a specific overall stiffness.

6 Design applications

In the following, the design procedure provided in Section 4 is applied to a three-layer plate of depleted material, characterized by the different cases of connectivity already presented; two design examples are developed, namely a plate realized through a porous solid structure, and a plate with a truss structure. Then, the design procedure is tested by assessing the linear mechanical response of detailed FE models of the plates. Then, to present a practical application, an example of a long-span structure subject to self-weight is proposed. A structure subject to its self-weight and an additional vertical load can be designed via the same procedure. The steps followed in the design procedure are: (i) setting the global plate geometric parameters, i.e., the plate dimension a, the layer thickness h i , and the ratio n between the inner and the outer layer volume fractions, as well as the matrix material properties, i.e., E0 and v0; (ii) setting the vertical load condition, q=qw, and the relevant structural performance requirement, defined in terms of maximum vertical displacement δmax under the applied load q; (iii) defining the local connectivity of the single layer of depleted material, through the parameters c i and m i ; (iv) computing the layer volume fractions ρ i able to satisfy the vertical displacement condition (from Eqs. (13) and (14), or, more generally, by inverting Eq. (11) and through the relation Eq. (12)).

In other words, the procedure defines the level of depletion that furnishes the global flexural stiffness able to support the vertical distributed load qw, Eq. (10), without exceeding a maximum vertical deflection δmax. It is worth noting that, because of the linearity of the method, the vertical displacement δmax is directly related to the inverse of the ratio E0/s0, as the analytical expression Eq. (11), by means of the relation Eq. (4), highlights.

In the former case (plate with a porous solid structure), 3D, eight-node, and brick elements are used in the FE model, while in the latter case (plate with a truss structure) 1D beam elements are used. Fig. 10 shows the porous solid structure and Fig. 11 shows the truss structure.

Fig. 10
figure 10

Three-layer plate of depleted material (plate with porous solid structure)

Full size image
Fig. 11
figure 11

Three-layer plate of depleted material (plate with truss structure)

Full size image

Each multilayered plate has a basic unit that is repetitive in the long direction (perpendicular to the cross-section in Fig. 2). The vertical load is assumed to be independent of the coordinate in the long direction, and therefore, it is possible to consider just one 3D unit of the structure that repeats periodically along its length. The recursive unit is simply supported at the edge, and symmetry boundary conditions are applied at the sides.

6.1 Sandwich plate with solid structure

The design example refers to a square plate, with dimension 90 m×90 m and the total thickness H=2.5 m; upper and lower thicknesses are h1=h3=0.5 m, and the middle layer thickness is h2=1.5 m. The solid matrix is made of a material with ratio between Young’s modulus and density of E0/s0=2.6×106 (m/s) and Poisson’s ratio v0=0.3. The ratio between the volume fractions of the inner and the outer layer is n=10; no vertical load is applied in addition to the plate self-weight, and the allowed vertical displacement is δmax=(90/500) m=0.18 m.

Combining Eq. (30) with Eqs. (13) and (14), it is possible to determine the optimal values of ρ i which gives the design value of the vertical displacement (δmax); the following values of the volume fraction were obtained: ρ1=ρ3=0.1874980 and ρ2=0.018 7498; the dimension of the cubic voids in the three layers, i.e., the main design parameters, corresponding to such values of ρ i are obtained from the expression of

$${d_i} = {h_i}\sqrt[3]{1 - {\rho _i}},$$
(37)

which provides that d1=d3=0.466564 m and d2 = 1.490 570 m.

The FE results of the model of the porous plate are reported in Fig. 12, with a sketch of the inner microstructure shown in detail at the upper right corner. It is clearly shown that the prescribed displacement δmax is in good agreement with the maximum vertical displacement \(\delta _{\max }^{{\rm{FE}}} = 0{.}1901\;{\rm{m}}\) such that:

$${{{\delta _{\max }} - \delta _{\max }^{{\rm{FE}}}} \over {\delta _{\max }^{{\rm{FE}}}}} \times 100\% = - 5{.}31285\% {.}$$
(38)
Fig. 12
figure 12

FE results of the model of the plate with porous solid structure, contour of the vertical displacement (unit: m). It is a sketch of the inner microstructure in the upper right corner

Full size image

6.2 Sandwich plate with truss structure

As in the previous design example, the square plate has dimension 90 m×90 m and the total thickness H=2.5 m, with thickness values for the external layers h1=h3=0.5 m, and for the middle layer h2=1.5 m. The ratio of Young’s modulus to density of the solid matrix material is still E0/s0=2.6×106 (m/s)2, and Poisson’s ratio v0=0.3; the ratio between the volume fractions is equal to the previous design example, i.e., n=10; the allowed vertical displacement under vertical load deriving from the self-weight is δmax=(90/500) m=0.18 m. The total length of the beams in each recursive element is set as λ1=λ3=5.226 m and λ2=15.679 m; the ratio rr between the equivalent area and inertia radii has been assumed the same in the three layers, i.e., rr1=rr2=rr3=0.8.

Combining Eq. (36) with Eqs. (13) and (14), it is possible to determine the optimal values of ρ i which give the design value of the vertical displacement (δmax); the following values of the volume fraction were obtained: ρ1=ρ3=0.1439290 and ρ2=0.0143929; the equivalent area radii raei of the beam circular hollow sections in the three layers, corresponding to such values of ρ i , are obtained from the expression of

$${r_{{\rm{ae}}i}} = \sqrt {{{{h_i}{\rho _i}} \over {{{\pi }}{\lambda _i}}}} {.}$$
(39)

Then, having fixed the ratio rr=rae/rie, the equivalent inertia radii rie can be calculated from the values of rae and rr; finally through the inverse of Eqs. (33) and (34) it is possible to determine, for each single layer, the inner and outer radii of the hollow sections, i.e., the main design parameters, with the result: ri1=ri3=0.028102 m, ro1=ro3=0.043 422 m, ri2=0.026 660 m, and ro2=0.041 194 m.

The FE results of the model of the plate truss structure are shown in Fig. 13, where a sketch of the inner microstructure is shown in detail. Meanwhile, in this case, the prescribed displacement δmax is in good agreement with the maximum vertical displacement obtained through the FE analysis, \(\delta _{\max }^{{\rm{FE}}} = 0{.}8889\;{\rm{m}}\), resulting in

$${{{\delta _{\max }} - \delta _{\max }^{{\rm{FE}}}} \over {\delta _{\max }^{{\rm{FE}}}}} \times 100\% = 1{.}25033\% {.}$$
(40)
Fig. 13
figure 13

FE results of the model of the plate with truss structure, contour of the vertical displacement (unit: m). It is a sketch of the inner microstructure in the upper right corner

Full size image

7 Conclusions

In this paper a general design procedure has been developed for thin plates made of three layers of depleted material subject to vertical distributed load. The approach allows the locally definition of the optimal amount of material for a specific microstructure with the objective of maximizing the overall flexural stiffness/weight ratio of the structure.

To assess the influence of connectivity both a porous solid structure and a truss arrangement were investigated using the FEM.

For each kind of microstructure the flexural stiffness has been successfully correlated to the level of depletion by means of a power law function by setting very few parameters. Starting from the local response of the media, it has been possible to describe, to a good approximation, the global flexural response of the structure.

To test the accuracy of the method, each type of microstructure has been employed in a case study of a squared thin plate made of three layers subject to a vertical distributed load: with the aid of the FEM, the structure has been modelled in detail by reproducing the geometries at the micro scale. The accurate mechanical response has been calculated and compared with the results furnished by the homogenization approach proposed in this paper. The good agreement between the analytical and numerical results for both types of the microstructure, proves that the procedure is able to provide, with good reliability, the most favorable design of light-weight roof structures.

In more general terms, the method prescribes, for a thin plate made of a depleted material, the definition of a penalization law able to predict the flexural stiffness of the specific microstructure, and then it is able to provide a very straightforward procedure for the structural optimization. Moreover, the method based on homogenization theory is suitable for every kind of architecture of the microstructure.