1 Introduction

In recent years, many large span structures with membrane roofs have been built. The membrane is usually flexible, with a low mass and is lightly damped, which may result in aero-elastic instability in some wind conditions, with a possible catastrophic outcome or unacceptable vibration amplitudes and deformations (Cermak, 2003; Zhang and Tamura, 2007). It is believed that wind-structure interaction is one of the reasons for the failure of some membrane structures (Yang and Liu, 2005). The wind-induced aero-elastic response of membrane structures is useful for studying the wind-structure interaction of membrane structures.

Some researchers have studied the aero-elastic response of one-way tensioned flexible roofs, which have similar flexible properties to membrane structures, and suggested aero-elastic instability categories. For example, Minami et al. (1993) studied the vibration behavior of a one-way tensioned membrane and defined the state of membrane vibration with progressive waves as flutter. Sygulski (2007) investigated the stability of a two edge supported latex rubber membrane and found that the membrane vibrated like a standing wave and exhibited a three half-wave mode shape. He suggested the vibration was a divergent flutter. Kawamura and Kimoto (1979) used modified thin airfoil theory to deduce the aerodynamic stability criteria for one-way tensioned membranes and defined the first two critical velocities as the wind velocity where the total damping was equal to zero and the wind velocity where one mode disappears and another mode appears. They also tested the response of a full-scale one-way tensioned membrane under the action of the wind (Kimoto and Kawamura, 1983) and found that above a certain wind velocity the vibration amplitude of the roof increased rapidly; that wind velocity was called the critical velocity. A similar phenomenon was found by Matsumoto (1990) in his study of tensioned cable roofs in smooth flow; a self-excited oscillation in the first anti-symmetric mode was found at the critical velocity and it was shown to be caused by vortices forming above the roof and shedding downwind at a certain velocity. Miyake et al. (1992) found that the vortices generated on stationary suspended roofs played an important role in the excitation of the roofs. Wu et al. (2008) studied the wind-structure interaction mechanism of a closed-type 2D membrane using a computational fluid dynamics (CFD) simulation method and found that the vibration of the roof was induced by vortex shedding from the membrane's leading edge. Similar phenomena were found by Rojratsirikul et al. (2010) in their study of 2D air foils using a particle image velocimetry (PIV) system and smoke visualization in aero-elastic model wind tunnel tests. Uematsu and Uchiyama (1982) studied the wind-induced dynamic behavior of closed type suspended roofs. They defined three items. First, the wind velocity at which the mean roof tension became zero, was defined as the static critical velocity; second, the wind velocity at which the fluctuating pressure on a roof could be reduced to the static forces in estimating the dynamic response of the roof, as the boundary velocity; and then, the wind velocity at which the non-dimensional root mean square (RMS) nodal displacement of the roof reached a pronounced peak, as the ratio-peak velocity.

However, little information on the aero-elastic response and aero-elastic instability mechanism of 3D membrane structures can be found in the literature. This is probably due to the difficulties resulting from the noncontact measurement methods and the complexity of the fluid-structure interaction problem (Jenkins and Korde, 2006). Yang and Liu (2005) and Haruo (1975) deduced the flutter critical wind velocity of 3D membrane structures by an analytical method; they defined the critical wind velocity as the wind velocity at which the eigenvalue of the ordinary differential equations of vibration took a real value, which was also the wind velocity when positive damping vanished. Uematsu and Uchiyama (1986) investigated the response of a hyperbolic-parabolic shaped membrane roof in a wind tunnel; they found that a self-excited oscillation occurred in a flow velocity range for a certain wind direction and its amplitude was strongly affected by the structural damping of the roof. Yang et al. (2010) studied the response of a saddle-shaped cable membrane with different covered areas in still air, and found that the structural natural frequency of the model was significantly influenced by the added mass. They also tested the response of a saddle-like membrane in wind and found that the aerodynamic damping was influenced by the wind speed and considered the relevance of structural vibration to wind loading. Similar phenomena were found by Kim et al. (2011) in their long-term monitoring of the wind-induced response of a large-span membrane roof. Michalski et al. (2011) suggested that particular transient wind loads could lead to dynamic amplification of the structural response; they developed a CFD method to simulate the wind induced response of a real-scale flexible 29 m umbrella in a natural wind flow. Uematsu and Uchiyama (1985) and Uematsu et al. (2001) investigated the wind load on a thin circular cylindrical shell and found that the occurrence of vibration altered the characteristics of the pressure fluctuations on the structure to a great extent, even when the amplitude was quite small.

It can be concluded, from these studies, that wind-structure interaction effects should not be neglected; however, the interaction mechanisms, especially the aero-elastic instability mechanism for membrane structures, are still unclear. Some investigators suggested that the instability of the membrane is flutter and assumed that it will occur when positive damping vanishes; however, no negative damping has been reported in the aero-elastic experiments or in full scale tests. Assuming that flutter will occur in membrane structures, it is believed that the flutter of membrane structure will be quite different to the classical flutter of airfoils and bridge decks because of the special properties of membrane structures. Some other researchers believe that the aero-elastic instability of membrane structures is related to the vortex formed around the roof. However, it is still unclear how the vortex affects the vibration properties of the membrane.

The main object of this study is to investigate the aero-elastic instability mechanism of 3D membrane structures and to ensure unacceptable amplitudes of vibration do not occur. Wind tunnel tests on two aero-elastic models of closed-type saddle-shaped tensioned membrane structures, with the same shape but different pre-tensions, are described. Here two different pre-tensions are used to decide the influence of the pre-tension on the aero-elastic instability critical velocity. The response of the membrane and the flow field around the roofs with different on-coming flow velocities are measured simultaneously. The damping ratios of each vibration mode are studied. The critical wind velocity is defined and calculated. Finally, some conclusions are derived.

2 Aero-elastic model

The experiments were carried out in a 25 m long closed circuit wind tunnel with a working section 4 m wide by 3 m high. For tests, a smooth flow with a turbulence intensity of 0.5% at the level of the roof was used.

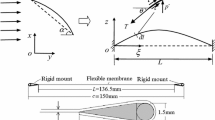
Usually, it is difficult to fabricate scale models which fully fulfill the similitude scales. Here, two physical models which were not able to reproduce any roof structure at prototype were used to study the aero-elastic instability mechanism of the membrane structures. The two models, with pre-tensions of 10 and 40 N/m, were labeled models I and II. The two models were fabricated with the shape shown in Fig. 1, with the ratio of sag (f) to span (L), f/L, being 1/12. The rigid frame was made from acrylic glass and the elastic roof was made from a 0.4-mm thick latex sheet. The mass per unit area ? and the elastic force per unit length E of the latex were 0.413 kg/m2 and 655.2 N/m2, respectively.

Fig. 1
figure 1

Schematic diagram of the test model (a) Top view; (b) Side view; W1 is the side length of the plane projection of the model; H1 and H2 are the heights of the high and low points of the model, respectively

Full size image

Five laser displacement meters were used to measure the displacements of the roof and three hotwires were used to measure the wind velocities above the roof (actually, only the hotwire above the central line of the roof was valid when the wind didirections changed; as a result, only the wind velocity measuring points for this hotwire were used here). The location of the measuring points is shown in Fig. 1, where points 1-5 are the displacement measuring points and points 6-8 are the wind velocity measuring points. The heights h1, h2, and h3 of points 6-8 are 10, 40, and 70 mm, respectively. The laser displacement meters were installed under the wind tunnel floor in the internal cavity of the model as shown in Fig. 2a. The hotwire was fixed at the tip of horizontal rods as shown in Fig. 2b. The horizontal rods could be moved in the vertical direction so that the wind velocities at all of the measuring positions could be recorded. Five on-coming flow velocity directions were considered (Fig. 1), and the wind velocity for each direction was changed from 4 to 16 m/s in steps of 1 m/s. Note that the tension stiffness of the membrane would change greatly under the action of the wind. However, the instantaneous load of the membrane was not measured in the test because it is difficult to find an appropriate non-contact stress measurement sensor.

Fig. 2
figure 2

Photos of laser displacement sensors (a) and hot wire and model (b)

Full size image

The pre-tension of the membrane was applied as follows. First, a latex sheet was stretched in two directions on a horizontal plane by four steel rulers so that the strain in each direction reached a prescribed value. Next, the sheet was fixed on to the model wall using adhesive tape on its four sides. Then, the steel rulers were taken off and the surplus membrane was cut off. The pre-tension applied to the roof was checked by comparing the mode frequencies of the roof obtained from a free vibration experiment with results from a finite element analysis. The free vibration experiment was carried out by applying an initial deformation, either symmetrical or anti-symmetrical according to the mode shape, and then releasing it. Power spectra density (PSD) of displacement was used to determine the vibration frequencies.

Table 1 shows the first five mode frequencies of the models from the finite element model and the free vibration experiment. The results show that the pre-tensions applied on the roof were sufficiently accurate.

figure Tab1

No actual full-scale prototype relates to the elastic model; however, the pre-tension and frequency of such a prototype, calculated according to the similarity law, should be in a reasonable range. The membrane material for the prototype is assumed to be PVDF 1002T, made by the Ferrari Company, France, with a mass per unit area ?P of 1.05 kg/m2, a thickness of 1.05 mm, and a longitude elastic force per unit length of 1039 kN/m. The aero-elastic model scale parameters can be calculated according to the similarity law introduced by Tryggvason (1979). The scaling parameters of the aero-elastic model are shown in Table 2.

figure Tab2

In Table 2, the length scale ratio ?L is determined by selecting a reasonable size for the prototype, the mass scale ratio ?m is equal to ?L, and the wind velocity scale ratio ?U is chosen to be 1:2. The internal cavity of the model was open to ensure that the aero-dynamic stiffness caused by the vibrations could be ignored. The 1st mode frequencies of the models for the pre-tensions of 10 and 40 N/m in still air are 11.2 and 18.1 Hz, respectively, and the corresponding frequencies of the full-scale prototype, obtained by finite element analysis, are 4.8 and 6.2 Hz, which are within a reasonable range.

From Table 2 it can be seen that the mass of the material for the model is greater than the ideal mass required and the elastic forces per unit length of the model are much smaller than the required elastic forces per unit length. This will result in the response from the experiment being larger than the actual response of the prototype. However, the aim of this study is to clarify the aero-elastic instability of membrane structures and not to predict the response of the prototype. The amplification of the model response will make it easier to observe the aero-elastic instability phenomena in the limited on-coming flow velocity in the wind tunnel. As a result, the mass and elastic forces per unit length scales are relaxed in this study.

3 Test results analysis

3.1 Time-average deformation and RMS deformation of the roof

We take model II as an example to illustrate the aero-elastic instability mechanism of the saddle-shaped membrane structure and define the upward direction as the positive direction for displacement.

Fig. 3 shows the displacement time history of point 2 for 30° wind direction at an on-coming flow velocity of 8 m/s, where di is the displacement of point i, and and ?i are the mean and RMS values of di, respectively. Here, and ?i are used to evaluate the time average deformation and RMS deformation. The former is caused by the average component of the wind load and corresponds to the equilibrium position of the membrane; the latter is caused by the fluctuating component of the wind load and corresponds to the vibration amplitude of the membrane.

Fig. 3
figure 3

Displacement time history of point 2 for 30° wind direction at an on-coming flow velocity of 8 m/s

Full size image

Fig. 4 shows the time-average deformations of the membrane at different on-coming flow velocities, where ? is the wind direction. From Fig. 4a, it can be seen that the time-average deformations of points 1-5, at the 30° wind direction, increase with the on-coming flow velocity, nearly linearly, and the maximum deformation occurs at point 2. Fig. 4b shows that the time-average deformations of point 2, at different wind directions, increase nearly linearly with the on-coming flow velocity. The time-average deformations of point 2, for the 0° wind direction, are much smaller than the values in other wind directions at the same velocity. The maximum average deformation at high on-coming flow velocity occurs at the 30° and 45° wind directions.

Fig. 4
figure 4

Time-average deformations of the roof for points 1-5 at 30° direction (a) and point 2 at 0-90° directions (b)

Full size image

Fig. 5 shows the amplitudes of the roof for different on-coming flow velocities. It can be seen from Fig. 5a that the amplitudes of points 1-3 increase slowly with increasing flow velocity, up to 9 m/s, and then begin to increase rapidly for velocities between 9-12 m/s, reaching a peak at 12 m/s, and then decreasing slowly until 15 m/s. Such a phenomenon is usually considered to be related to vortex-induced resonance. Fig. 5b shows the change of the amplitude for point 2 with different wind directions. It can be seen that the aero-elastic instabilities occur for 30° and 45° wind directions and the amplitudes of the roof at these two wind directions are 2-4 times those at other directions.

Fig. 5
figure 5

Amplitudes of the roof for different on-coming flow velocities for points 1-5 at 30° direction (a) and points 2 at 0-90° directions (b)

Full size image

3.2 Vibration modes identification

In many previous studies it has been mentioned that the actual vibration frequencies of the membrane are lower than those in still air (Li et al., 2009; 2011; 2012; Kim et al., 2011; Zhou et al., 2014). As a result, the vibration modes of the roof in moving air cannot be identified by the ordinary mode analyzing method. However, the displacement of points 1–5 (Fig. 1) were recorded synchronously in this study, so that the PSD of the displacements and the phase relationship between the displacement measurement points can be used to identify the vibration modes. Fig. 6 shows the first six modal shapes and frequencies of the membrane with a pre-tension of 40 N/m, analyzed by the finite element method, where fn represents the nth mode vibration frequency of the membrane. It can be seen in Fig. 6a that, for the 1st mode, all the nodes on the membrane vibrate synchronously; for the 2nd mode, points 4 and 5 vibrate anti-phase; for the 3rd mode, points 1 and 3 vibrate anti-phase (the positions of points 1–5 are shown in Fig. 1). Similar phase relationships between the measuring points can be obtained for the other vibration modes.

Fig. 6
figure 6

First six mode shapes of the roof with a pre-tension of 40 N/m in still air (a) The 1st mode (f1=18.1 Hz); (b) The 2nd mode (f2=26.7 Hz); (c) The 3rd mode (f3=26.7 Hz); (d) The 4th mode (f4=33.5 Hz); (e) The 5th mode (f5=37.0 Hz); (f) The 6th mode (f6=37.1 Hz)

Full size image

Fig. 7 shows an example of the mode identification for the displacements with an on-coming flow velocity of 8 m/s at a 30° direction. Fig. 7a shows the normalized PSDs of the displacements d1-d5, where S(f) and ? represent the PSD and RMS value of the displacement. It can be seen that there are two peaks at 16.5 Hz and 24.3 Hz in the PSD curves for d1-d3. In the PSDs for d4 and d5, the peak at 16.5 Hz disappears and another is seen at 17.8 Hz. This is because the deformation-induced tension at points 4 and 5 is not the same as that at points 1–3. Figs. 7b and 7c are the displacements of the five points at the two frequencies obtained by band-pass filtering. The cut-off frequencies for the first two peak frequencies are 13.1–20.0 Hz and 20.0–27.4 Hz. Fig. 7b shows that the five displacement measurement points vibrate synchronously at a frequency of 16.5 Hz; hence this vibration is the 1st mode vibration. Fig. 7c shows that, at a frequency of 24.3 Hz, points 1 and 3 vibrate anti-phase; points 4 and 5 vibrate anti-phase. As a result, both the 2nd and 3rd modes occur at a frequency of 24.3 Hz. The other vibration modes can be identified using this method.

Fig. 7
figure 7

7 Mode identification for the displacements (a) Normalized PSDs of the displacements; (b) Displacements at 16.5 Hz for d1-d3 and displacements at 17.8 Hz for d4 and d5; (c) Displacements at 24.3 Hz for d1-d5

Full size image

3.3 Correlation between the wind and structural displacement

Both the time history of displacements di (i=1, 2, 3, 4, 5) and wind velocities uj (j=6, 7, 8) above the roof are random processes. The correlation coefficients of di and uj are used to study the relationship between the wind and the structural displacements. The sampling frequencies for displacement and wind velocity are the same, then the correlation coefficients can be calculated by

((1))

where rdu represents the correlation coefficient of displacement and wind velocity, di(tm) and uj(tm) represent the mth sampling values of di and uj at time tm, and and represent the mean values of di and uj, respectively. Considering that di and uj in this study are not sampled synchronized and the sign of rdu has no meaning in this study, the absolute value of rdu is used to evaluate the relationship between the wind and the structure.

Fig. 8 shows the correlation coefficients of d2 and uj for model II at the 30° wind direction for different on-coming flow velocities. The results show that the displacements of d2 correlate significantly with the wind velocities of u6, u7, and u8 for on-coming flow velocities of 10–14 m/s. This type of strong correlation phenomenon is usually caused by vortex-induced vibration.

Fig. 8
figure 8

Correlation coefficient for displacement and wind velocity

Full size image

The normalized PSD of displacement d2 and wind velocity u6 for different on-coming flow velocities are shown in Figs. 9–11.

Fig. 9 shows the PSD of displacements and wind velocities for the 0° wind direction. It can be seen that several vibration modes are excited simultaneously. The vibration of the roof, in this wind direction, is of stochastic nature. Similar behavior was found for the 60° and 90° wind directions.

Fig. 9
figure 9

PSD of displacements and wind velocities for 0° wind direction with on-coming flow velocities of 5–10 m/s (a) and on-coming flow velocities of 11–16 m/s (b)

Full size image

Fig. 10 shows that, for the 30° wind direction, even at low on-coming flow velocities (around 5–8 m/s), only one mode (the 1st mode) vibration is excited. At 9 m/s, a vortex with a frequency of 15.3 Hz, which is close to the frequency of the 1st mode of vibration, occurs above the roof, which indicates that a vortex-induced resonance occurs. It can be seen that, once vortex-induced resonance occurs, the amplitude of the roof vibration increases sharply for flow velocities around 9–12 m/s (Fig. 5a); the frequency of the vortex is nearly equal to the frequency of the vibration mode for the flow velocity range around 9–16 m/s, which is usually called a lock-in phenomenon.

Fig. 10
figure 10

PSD of displacements and wind velocities for 30° wind direction with on-coming flow velocities of 5–10 m/s (a) and on-coming flow velocities of 11–16 m/s (b)

Full size image

Similarly vortex-induced resonance phenomena can be seen in Fig. 11 for the vibration in the 45° wind direction. It can be seen that the vortex-induced resonance in the 1st mode occurs at 8 m/s and disappears at 13 m/s. Another vortex-induced resonance at 24.0 Hz, which is equal to the frequency of the 2nd and 3rd modes, occurs at 12 m/s.

Fig. 11
figure 11

PSD of displacements and wind velocities for 45° wind direction with on-coming flow velocities of 5–10 m/s (a) and on-coming flow velocities of 11–16 m/s (b)

Full size image

3.4 Damping ratio for the structure

Usually, it is believed that when the damping of the structure decreases to zero, flutter will occur (Haruo, 1975; Kawamura and Kimoto, 1979; Yang and Liu, 2005). As a result, the damping of the structure is usually used to judge whether flutter occurs. The damping ratio is used to evaluate the variations of damping in this study. A band-pass filter method is used to obtain the signals for each vibration mode; the random decrement technique (RDT) (Kareem and Gurley, 1996; Marukawa et al., 1996; Takeuchi et al., 2010) is applied to get the random decrement signal of each vibration mode, and the improved Hilbert-Huang transform (HHT) methods (Peng et al., 2005) are used to evaluate the damping ratio of the membrane from the random decrement signals.

Fig. 12a shows the variation of the damping ratios of the first four modes for model II in the 0° direction at different wind velocities. This shows that the higher mode damping ratios are generally smaller than those of the lower mode and the damping ratio of each mode increases with the wind velocity. It is known, from Section 3.1, that no vortex-induced resonance occurs for this wind direction. As a result, this shows the variation law of a vibration without vortex-induced resonance.

Fig. 12
figure 12

12 Damping ratios of the roof at 0° wind direction (a), 30° wind direction (b), and 45° wind direction (c)

ξ i represents the damping ratio of the membrane for the ith mode vibration; ξ2,3 represents the damping ratio of the membrane for the 2nd and 3rd modes vibration which occur at the same time with equal frequency values; VIV represents the vortex-induced vibration

Full size image

Figs. 12b and 12c show the variation of the damping ratios for the 30° and 45° wind directions, where vortex-induced vibration occurs. The result shows that, with increasing wind velocity, the damping ratio increases, reaches a peak value and then decreases suddenly, nearly reaching zero. The wind velocities at which the damping ratios begin to decrease are those where the vortex occurs. As a result, the decrease of the damping ratio is thought to be caused by the vortex-induced vibration. The variation laws of the damping ratios, which increase firstly and then decrease suddenly, are quite similar to the change laws of the damping ratios for the torsional branch flutter of thin plates defined by Matsumoto (2013). The difference is that, for thin plates, the damping ratio can decrease and reach a negative value; while for the membrane structure, no negative damping ratio is found. This is because that the stiffness of the membrane structure is much smaller than that of the plate, so no torsional force exists on the roof.

No zero or negative damping is found in this study; as a result, the vibration caused by vortex-induced resonance is not a flutter.

Based on the research mentioned above, the aero-elastic instability for membrane structures can be defined as follows:

  1. 1.

    When exceeding a certain on-coming flow velocity, the amplitude of vibration of the membrane begins to increase suddenly, or the vibration mode of the roof changes suddenly from one mode to another. This vibration is an aero-elastic instability, which indicates that the structure cannot maintain its equilibrium state and jumps from one state to another.

  2. 2.

    The aero-elastic instability is caused by vortex-induced resonance. When the dominant frequency of the vortex is close to that of the membrane, a resonance and lock-in phenomenon will occur. The damping ratio of the membrane will begin to decrease sharply once aero-elastic instability occurs. In this case, the membrane will absorb energy from the wind, vibrate more severely, and may jump to another vibration mode.

4 Critical wind velocity for aero-elastic instability

Considering that the resonance is caused by a vortex, whose frequency is close to a natural frequency of the roof, the critical wind velocity for the nth mode vibration instability Ucr,n is defined as the wind speed that a vortex forms, whose shedding frequency is close to the nth order natural frequency of the structure.

The nth mode reduced critical wind velocity can be defined as

((2))

where fs,n is the nth order mode frequency of the membrane considering the added mass effect.

Table 3 shows the reduced critical wind velocities of the roof for different wind directions. The results show that the reduced critical wind speeds for the first two modes and are around 0.8–1.0.

figure Tab3

5 Conclusions

The aero-elastic instability mechanisms of two closed-type saddle-shaped tensioned membrane structures with different pre-tension levels were studied. The response and wind velocities above the roofs were measured in uniform flow and analyzed. Some preliminary conclusions can be drawn as follows:

  1. 1.

    Membrane structures deform to an equilibrium position and vibrate around it with certain amplitudes under the action of the wind.

  2. 2.

    For most wind directions, several vibration modes are excited; the amplitude and damping ratio of the roof increase uniformly with the on-coming flow velocity.

  3. 3.

    For some particular wind directions, only one vibration mode is excited; the amplitude and damping ratio of the vibration mode increase slowly with the on-coming flow velocity at first. Then, on exceeding a certain on-coming flow velocity, an aero-elastic instability caused by vortex-induced resonance occurs. The amplitude of the roof vibration begins to increase sharply and the damping ratio of the vibration mode begins to decrease quickly, to near zero, with the increasing on-coming flow velocity; the frequency of the vortex above the roof is locked in by the vibration within a certain wind velocity range. The amplitudes of the roof vibration at these wind directions reach 2–4 times the amplitudes for other wind directions. With an increase in on-coming flow velocity, the membrane can experience several aero-elastic instabilities.

  4. 4.

    The reduced critical wind speeds for the first two modes are around 0.8–1.0.