Predicting the dislocation nucleation rate as a function of temperature and stress

Abstract

Predicting the dislocation nucleation rate as a function of temperature and stress is crucial for understanding the plastic deformation of nanoscale crystalline materials. However, the limited time scale of molecular dynamics simulations makes it very difficult to predict the dislocation nucleation rate at experimentally relevant conditions. We recently develop an approach to predict the dislocation nucleation rate based on the Becker–Döring theory of nucleation and umbrella sampling simulations. The results reveal very large activation entropies, which originated from the anharmonic effects, that can alter the nucleation rate by many orders of magnitude. Here we discuss the thermodynamics and algorithms underlying these calculations in greater detail. In particular, we prove that the activation Helmholtz free energy equals the activation Gibbs free energy in the thermodynamic limit and explain the large difference in the activation entropies in the constant stress and constant strain ensembles. We also discuss the origin of the large activation entropies for dislocation nucleation, along with previous theoretical estimates of the activation entropy.

Appendices

Appendix A: Equality of Critical Sizes $n_c^{{\sigma }}$ and $n_c^{{\gamma }}$

Suppose that the Gibbs free energy G(n,σ,T)is maximized at $n_c^{{\sigma }}$, then

$${\left. {\frac{{\partial G\left( {n,{{\sigma }},T} \right)}}{{\partial n}}} \right|_{{{\sigma }},n = n_c^{{\sigma }}}} = 0\quad.$$

((A1))

Note that T is held constant throughout this section. Through the Legendre transform, Eq. (5), we have the following property forthe Helmholtz free energy F(n,γ,T):

$$ {{{\left. {\frac{{\partial F\left( {n,{{\gamma }},T} \right)}}{{\partial n}}} \right|}_{{{\gamma }},n = n_{\text{c}}^{{\sigma }}}}} \;\; = \;\; {{{\left. {\frac{\partial }{{\partial n}}} \right|}_{\gamma,n = n_{\text{c}}^{{\sigma }}}}\left[ {G\left( {n,{{\sigma }},T} \right) + {{\sigma \gamma }}V} \right]} \\ {} \;\; = \;\; {{{\left. {\frac{{\partial G\left( {n,{{\sigma }},T} \right)}}{{\partial n}}} \right|}_{{{\sigma }},n = n_c^{{\sigma }}}}} \\ {} \;\; {} \;\; { + {{\left. {\frac{{\partial G\left( {n,{{\sigma }},T} \right)}}{{\partial {{\sigma }}}}} \right|}_{{{\sigma }},n = n_c^{{\sigma }}}}\frac{{\partial {{\sigma }}}}{{\partial n}} + \frac{{\partial {{\sigma }}}}{{\partial n}}{{\gamma }}V} \\ {} \;\; = \;\; {0 - V{{\gamma }}\frac{{\partial {{\sigma }}}}{{\partial n}} + V{{\gamma }}\frac{{\partial {{\sigma }}}}{{\partial n}} = 0\quad.} \\ $$

((A2))

By definition, F(n,γ,T) reaches maximum at $n = n_c^{{\gamma }}$ at constant γ and T,

$${\left. {\frac{{\partial F\left( {n,{{\gamma }},T} \right)}}{{\partial n}}} \right|_{{{\gamma }},n = n_{\text{c}}^{{\gamma }}}} = 0\quad.$$

((A3))

Therefore, we establish that $n_c^{{\gamma }} = n_c^{{\sigma }},$ that is, the maxi-mizer $n_c^{{\sigma }}$ of G(n,σ,T) is also the maximizer $n_c^{{\gamma }}$ of F(n,γ,T).

Appendix B: Equality of Activation Gibbs and Helmholtz Free Energies

The activation Gibbs free energy is the free energy difference between state 0, a perfect crystal, and state 1, a crystal containing a critical dislocation loop under a same shear stress σ. Because of the plastic shear deformation caused by the dislocation loop, state 1 has a higher strain (γ) than state 0 (γ₀). It has been shown that the maximizer $n_c^{{\sigma }}$ of G(n,σ,T) equals the maximizer of $n_c^{{\gamma }}$ of F(n,γ,T) when σ equals σ(n_c,γ,T), as defined in Eq. (6). Note that we keep σ to be the stress at n_cγ, and T. Then at the same σ, but for n = 0, the strain becomes γ₀. Hence, the activation Gibbs free energy barrier can be written as

$$ {{G_c}} \;\; = \;\; {G\left( {{n_{\text{c}}},{{\sigma }},T} \right) - G\left( {0,{{\sigma }},T} \right)} \\ {} \;\; = \;\; {F\left( {{n_{\text{c}}},{{\gamma }},T} \right) - {{\sigma \gamma }}V - F\left( {0,{{{\gamma }}_0},T} \right) + {{\sigma }}{{{\gamma }}_0}V\,\,\,.} \\ $$

((B1))

Note that F(n_c,γ,T) and F(0,γ₀,T) do not correspond to the same strain state, so that their difference is not the activation Helmholtz free energy. To construct the activation Helmholtz free energy, we subtract and add the F(0,γ,T) term in the right hand side,

$$ {{G_c}} \;\; = \;\; {F\left( {{n_{\text{c}}},{{\gamma }},T} \right) - F\left( {0,{{\gamma }},T} \right) + F\left( {0,{{\gamma }},T} \right) - F\left( {0,{{{\gamma }}_0},T} \right)} \\ {} \;\; {} \;\; { - V{{\sigma }}\left( {{{\gamma }} - {{{\gamma }}_0}} \right) \approx {F_c} + {{\left. {\frac{{\partial F}}{{\partial {{\gamma }}}}} \right|}_{{{{\gamma }}_0},V}}\left( {{{\gamma }} - {{{\gamma }}_0}} \right)} \\ {} \;\; {} \;\; { + \frac{1}{2}{{\left. {\frac{{{\partial ^2}F}}{{\partial {{{\gamma }}^2}}}} \right|}_{{{{\gamma }}_0},V}}{{\left( {{{\gamma }} - {{{\gamma }}_0}} \right)}^2}} \\ {} \;\; = \;\; {{F_c} + \frac{1}{2}{{\left. {\frac{{{\partial ^2}F}}{{\partial {{{\gamma }}^2}}}} \right|}_{{{{\gamma }}_0},V}}{{\left( {{{\gamma }} - {{{\gamma }}_0}} \right)}^2}} \\ {} \;\; = \;\; {{F_c} + \frac{1}{2}V{{\left. {\frac{{{\partial ^2}F}}{{\partial {{{\gamma }}^2}}}} \right|}_{{{{\gamma }}_0},V}}{{\left( {{{\gamma }} - {{{\gamma }}_0}} \right)}^2}\quad.} \\ $$

((B2))

Note that ${{\gamma }}V\,\, = \,\,\, - \partial G\left( {{n_{\text{c}}},{{\sigma,}}T} \right)/\partial {{\sigma }}$ and ${{{\gamma }}_0}V\,\, = \,\,\, - \partial G\left( {{n_{\text{c}}},{{\sigma,}}T} \right)/\partial {{\sigma }}$. Then $\left( {{{\gamma }}V\,\, - \,\,{{{\gamma }}_0}V} \right)$ is equivalent to $- \left( {{\partial \mathord{\left/ {\vphantom {\partial {\partial {{\sigma }}}}} \right. } {\partial {{\sigma }}}}} \right)\left( {G\left( {{n_{\text{c}}},{{\sigma,}}T} \right) - G\left( {0,{{\sigma,}}T} \right)} \right) = - \left( {\partial {G_{\text{c}}}/\partial {{\sigma }}} \right) \equiv {\Omega _c}$,that is, the activation volume. By plugging $\left( {{{\gamma }} - {{{\gamma }}_0}} \right){\Omega _c}/V$ into the equation, we have

$$ {{G_c}} \;\; = \;\; {{F_c} + \frac{1}{2}\frac{1}{V}{{\left. {\frac{{\partial {{\sigma }}}}{{\partial {{\gamma }}}}} \right|}_{{{{\gamma }}_0},V}}{{\left( {{\Omega ^*}} \right)}^2} + O\left( {{V^{ - 2}}} \right)} \\ {} \;\; = \;\; {{F_c} + O\left( {{V^{ - 1}}} \right)\quad.} \\ $$

((B3))

In the thermodynamics limit $\left( {V \to \infty } \right)$, we have G_c = F_c. Hence, the nucleation rate does not depend on whether the crystal is subjected to constant stress or constant strain loading. The equality allows us to compute the activation Gibbs free energy${G_c}\left( {{{\sigma,}}T} \right)$ by combining the activation Helmholtz free energy F_c(γ,T) and the stress–strain relations of the perfect crystal shown in Fig. 2(b) and (d).

Appendix C: Physical Interpretation of Activation Entropy Difference ΔS_c

It is well known that entropy is a thermodynamic state variable that is independent of the ensemble of choice, that is, $S\left( {n,{{\gamma }},T} \right) \equiv \partial F{\left. {{{\left( {n,{{\gamma }},T} \right)} \mathord{\left/ {\vphantom {{\left( {n,{{\gamma }},T} \right)} {\partial T}}} \right. } {\partial T}}} \right|_{n{\text{,}\gamma }}}$ and $S\left( {n,{{\sigma }},T} \right) \equiv \partial G{\left. {{{\left( {n,{{\sigma }},T} \right)} \mathord{\left/ {\vphantom {{\left( {n,{{\sigma }},T} \right)} {\partial T}}} \right. } {\partial T}}} \right|_{n{\text{,}\sigma }}}$ equal to each other as long as ${{\sigma }} = {V^{ - 1}}{\left. {{{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial {{\gamma }}}}} \right. } {\partial {{\gamma }}}}} \right|_{n,T}}$. At the same time, the activation entropy is just the entropy difference between the activated state and the metastable state, that is, ${S_c}\left( {{{\gamma,}}T} \right) = S\left( {{n_c},{{\gamma,}}T} \right) - S\left( {0,{{\gamma }},T} \right)$ and ${S_c}\left( {{{\sigma,}}T} \right) = S\left( {{n_c},{{\sigma,}}T} \right) - S\left( {0,{{\sigma }},T} \right)$. If the entropies in two ensembles can equal each other, it may seem puzzling how the activation entropies can be different.

The resolution of this apparent paradox is that under the constant applied stress, the nucleation of a dislocation loop causes a strain increase. Let γ be the strain at the state defined by n = n_c, σ, and T, and γ₀ be the strain at the state defined by n = 0, σ, and T, then γ > γ₀. Hence, we have $S\left( {{n_c},{{\sigma,}}T} \right) = S\left( {{n_c},{{\gamma,}}T} \right)$ and $S\left( {{n_c},{{\sigma,}}T} \right) = S\left( {{n_c},{{\gamma,}}T} \right)$, but $S\left( {0,{{\gamma,}}T} \right) \ne S\left( {0,{{{\gamma }}_0}{\text{,}}T} \right)$.

$$ {{S_c}\left( {{{\sigma }},T} \right)} \;\; = \;\; {S\left( {{n_c}{{,\sigma }},T} \right) - S\left( {0{{,\sigma }},T} \right)} \\ {} \;\; = \;\; {S\left( {{n_c}{{,\gamma }},T} \right) - S\left( {0{\text{,}}{{{\gamma }}_0},T} \right)} \\ {} \;\; = \;\; {S\left( {{n_c}{{,\gamma }},T} \right) - S\left( {0{{,\gamma }},T} \right)} \\ {} \;\; {} \;\; { + S\left( {0{{,\gamma }},T} \right) - S\left( {0{\text{,}}{{{\gamma }}_0},T} \right)} \\ {} \;\; = \;\; {{S_c}\left( {{{\gamma }},T} \right) + S\left( {0{{,\gamma }},T} \right) - S\left( {0{\text{,}}{{{\gamma }}_0},T} \right)\quad.} \\ $$

((C1))

This shows that the activation entropy difference $\Delta {S_c} \equiv {S_c}\left( {{\sigma }} \right) - {S_c}\left( {{\gamma }} \right)$ equals to $S\left( {0,{{\gamma,}}T} \right) - S\left( {0,{{{\gamma }}_0}{\text{,}}T} \right)$, which is the entropy difference of the perfect crystal at two slightly different strains.

In the limit of $V \to \infty$, because we expect $\left( {{{\gamma }} - {{{\gamma }}_0}} \right) \to 0$, we might reach a false conclusion that $\Delta {S_c} = \left( {S\left( {{\text{0,}\gamma },T} \right) - S\left( {{\text{0,}}{{{\gamma }}_0},T} \right)} \right) \to 0$. Instead, the correct behavior in the thermodynamic limit can be obtained by expanding ΔS_c in a Taylor series,

$$ {s\left( {{\gamma }} \right) - S\left( {{{{\gamma }}_0}} \right)} \;\; = \;\; {\frac{{\partial S}}{{\partial {{\gamma }}}}\left( {{{\gamma }} - {{{\gamma }}_0}} \right) + \cdots } \\ {} \;\; = \;\; {{{\left. { - \frac{{\partial {{\sigma }}}}{{\partial T}}} \right|}_{{{\gamma,}}V}}V\left( {{{\gamma }} - {{{\gamma }}_0}} \right) + \cdots \quad.} \\ $$

((C2))

where the Maxwell relationship ${\left. {{{\partial S} \mathord{\left/ {\vphantom {{\partial S} {\partial {{\gamma }}}}} \right. } {\partial {{\gamma }}}}} \right|_T} = - V{\left. {{{\partial {{\sigma }}} \mathord{\left/ {\vphantom {{\partial {{\sigma }}} {\partial T}}} \right. } {\partial T}}} \right|_{{{\gamma }},V}}$ is used. The term (γV–γ₀V) equals the activation volume Ω_c and can be interpreted as plastic strain γ^pl due to the formation of a dislocation loop times the volume of the crystal, that is,

$$\left( {{{\gamma }}V - {{{\gamma }}_0}V} \right) = {\Omega _c} = {{{\gamma }}^<PublisherLocation></PublisherLocation>}V = b{A_{\text{c}}}\quad,$$

((C3))

where b is the magnitude of the Burgers vector and A_c is the area of the critical dislocation loop. Using the relation $\left( {{{\gamma }} - {{{\gamma }}_0}} \right) = {{{\Omega _c}} \mathord{\left/ {\vphantom {{{\Omega _c}} V}} \right. } V}$, we have

$$\Delta {S_c} = S\left( {{\gamma }} \right) - S\left( {{{{\gamma }}_0}} \right) = - {\left. {\frac{{\partial {{\sigma }}}}{{\partial T}}} \right|_{{{\gamma,}}V}}{\Omega _c} + O\left( {{V^{ - 1}}} \right)\quad,$$

((C4))

which is exactly the same as Eq. (24).

A similar expression has been obtained for the difference between point defect formation entropies under constant pressure (S_p) and under constant volume (S_v),39 with

$${S_{\text{p}}} - {S_{\text{v}}} = {{\beta }}B{V_{{\text{rel}}}}\quad,$$

((C5))

where ${{\beta }} \equiv {V^{ - 1}}{\left. {\left( {{{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial T}}} \right. } {\partial T}}} \right)} \right|_{p = 0}}$ is the thermal expansion factor at zero hydrostatic pressure p, B is the isothermal bulk modulus, and V_rel is the relaxation volume of the defect. In Cu, the value of S_p–S_v is estimated to be–1.7 k_B for a vacancy and 13.7 k_B for an interstitial.36 Comparing Eq. (C5) with Eq. (C4), we note that relaxation volume V_rel for point defects corresponds to the activation volume X for dislocation nucleation and that ßß corresponds to the ${\left( {{{\partial {{\sigma }}} \mathord{\left/ {\vphantom {{\partial {{\sigma }}} {\partial T}}} \right. } {\partial T}}} \right)}$ term. The similarity between these two equations is because they both express the entropy difference between two states, and the choice of the two states depends on whether the stress or the strain is kept constant when the defect is introduced. In contrast, there are also some differences between the physics expressed by these two equations. First, thermal expansion plays a prominent role in Eq. (C5) because it focuses on hydrostatic stress and strain effects. In comparison, thermal expansion does not play a role in Eq. (C4) because it focuses on shear stress and strain effects. Second, the formation entropy of a point defect is the entropy difference between two metastable states and governs equilibrium properties, for example, the density of vacancies at thermal equilibrium. In comparison, the activation entropy is the entropy difference between a saddle (i.e., unstable) state and a metastable state and governs kinetics, such as the dislocation nucleation rate. In addition, the saddle state (i.e., the size of the critical nucleus) depends on stress and temperature, whereas such complexity does not arise in the formation entropy of point defects.

Appendix D: Approximation of ${S_c}\left( {{\sigma }} \right)$

We now introduce a series of simplifying approximations to estimate the magnitude of ${S_c}\left( {{\sigma }} \right)$ in the low temperature, low stress limit. In the temperature range of 0–300 K, the activation entropy is found to be insensitive to temperature. Starting from Eqs. (24) and (38), we have

$${S_c}\left( {{\sigma }} \right) = {S_c}\left( {{\gamma }} \right) + \Delta {S_c} \approx - \frac{{{E_c}\left( {{\gamma }} \right)}}{{{{\mu }}\left( 0 \right)}}\frac{{\partial {{\mu }}}}{{\partial T}} - {\Omega _c}{\left. {\frac{{\partial {{\sigma }}}}{{\partial T}}} \right|_{{\gamma }}}\quad.$$

((D1))

If we assume the crystal is linear elastic, that is, σ = μγ, then

$${S_c}\left( {{\sigma }} \right) \approx - \frac{{{H_c}\left( {{\sigma }} \right) + {\Omega _c}\left( {{\sigma }} \right)\cdot{{\sigma }}}}{{{{\mu }}\left( 0 \right)}}\frac{{\partial {{\mu }}}}{{\partial T}}\quad.$$

((D2))

Similar expressions can be obtained for normal (com-pressive) loading by replacing γ with e and replacing μ by the Young’s modulus.

To gain more intuition, we note that in the limit of σ →0, the line tension model estimates that ${H_c}\left( {{\sigma }} \right) \propto {{{\sigma }}^{ - 1}}$. In addition, in the limit of $T \to 0,{\Omega _c}\left( {{\sigma }} \right) \approx {{\partial {H_c}} \mathord{\left/ {\vphantom {{\partial {H_c}} {\partial {{\sigma }}}}} \right. } {\partial {{\sigma }}}}$. Under these conditions, ${\Omega _c}\left( {{\sigma }} \right) \times {{\sigma }} \approx {H_c}\left( {{\sigma }} \right)$, so that

$${S_c}\left( {{\sigma }} \right) \approx - \frac{{2{H_c}\left( {{\sigma }} \right)}}{{{{\mu }}\left( 0 \right)}}\frac{{\partial {{\mu }}}}{{\partial T}}\quad.$$

((D3))

Comparing Eq. (D3) with Eq. (38), we have

$$\frac{{{S_c}\left( {{\sigma }} \right)}}{{{H_c}\left( {{\sigma }} \right)}} \approx 2\frac{{{S_c}\left( {{\gamma }} \right)}}{{{{\text{E}}_c}\left( {{\gamma }} \right)}}\quad.$$

((D4))

This trend is qualitatively observed in heterogeneous nucleation, when comparing Fig. 8(b) and (d), and is less clear in homogeneous nucleation, when comparing Fig. 8(a) and (c). This is probably because the stress-strain relationship is more nonlinearin the case ofhomogeneous nucleation.

Appendix E: Activation Free Energy Data

Table E.I and Table E.II provide the activation free energy data at all temperature and strain conditions in this study so that interested readers can use them as a benchmark. For homogeneous nucleation, the strain γ_xy is defined as ${{\Delta x} \mathord{\left/ {\vphantom {{\Delta x} {h_y^0}}} \right. } {h_y^0}}$, where Δx is the displacement of the repeat vector initially in the y direction along the x axis at each pure shear stress condition and ${h_y^0}$ is the height of the cell along the y axis at zero temperature without external loading. Shear stress σ_xy is determined from the x–y component of the average Virial stress. For heterogeneous nucleation, we take only the elastic strain into account. The elastic strain ϵ_zz at T is defined as ${{\left[ {{L_z}\left( {{{\sigma }},T} \right) - {L_z}\left( {{{\sigma = 0,}}T} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {{L_z}\left( {{{\sigma }},T} \right) - {L_z}\left( {{{\sigma = 0,}}T} \right)} \right]} {L_z^0}}} \right. } {L_z^0}}$, where ${{L_z}\left( {{{\sigma }},T} \right)}$ is the length of the repeat vector along the z axis;${{L_z}\left( {{{\sigma = 0,}}T} \right)}$ is the equilibrium length at temperature T under zero stress; and $L_z^0 = 20{a_0} = 72.3{\text{{\AA}}}$ is the reference length (before relaxation), where a₀ is the lattice constant of copper. The compressional stress σ_zz is defined by ${{{\sigma }}_{zz}} = < {\text{F}} >/{d^2}$, where F> is the axial force computed from the z–z component of the average Virial stress and d = 15a₀ = 54.225 Å is the reference side length of the nanorod.

TABLE E.I.

Data for homogeneous nucleation: σ_xy, (Gpa); E_c ${\tilde E_c}$, and F_c (eV); and $f_c^ + \left( {{{10}^{14}}{{\text{s}}^{ - 1}}} \right)$.

TABLE. E.II.

Data for heterogeneous nucleation: σ_zz (Gpa), E_c and F_c (eV), and $f_c^ + \left( {{{10}^{14}}{{\text{s}}^{ - 1}}} \right)$.

Appendix F: Activation Volume and Critical Loop Size

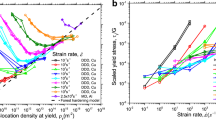
The activation volume Ω_c is defined as the derivative of activation free energy with stress, that is, ${\Omega _c}\left( {{{\sigma }},T} \right) = - {\left. {{{\partial {G_c}} \mathord{\left/ {\vphantom {{\partial {G_c}} {\partial {{\sigma }}}}} \right. } {\partial {{\sigma }}}}} \right|_T}$, and measures the sensitivity of the nucleation rate to the stress. Physically, it is interpreted as plastic strain associated with the dislocation loop times the volume of the crystal, that is, Ω_c = bA_c,where A_c is theareaof the critical dislocation loop (see Appendix C). Here, we use our numerical data to test the validity of the latter interpretation.

Because the activation volume measures the sensitivity of G_c(σ,T) to applied stress [see Eq. (10)], it must be proportional to the Schmid factor S in uniaxial loading. Hence, the hypothesis we wish to test is

$${\Omega _c} = {n_c}b{A_{\text{a}}}S\quad,$$

((F1))

where b is the magnitude of the Burgers vector and A_a is the average area each atom occupies on the {111} slip plane. Given that the lattice constant of Cu is a₀ = 3.615 Å, we have b = a₀/√6 = 1.48 Å and ${A_{\text{a}}} = \sqrt 6 {{a_0^2} \mathord{\left/ {\vphantom {{a_0^2} 4}} \right. } 4} = 5.66{{\text{{\AA}}}^2}$, so that bA_a = 8.35 ų. For the pure shear loading in our homogeneous nucleation case, the Schmid factor S = 1. For the uniaxial loading in our heterogeneous nucleation case, S = 0.471.

Figure E1 plots n_c versus Ω_c for both homogeneous and heterogeneous dislocation nucleations. In both cases, Ω_c appears to be roughly linear with n_c as expected from Eq. (F1). For homogeneous nucleations under pure shear [Fig. E.I(a)], the slope of the curves is roughly ${\Omega _c}/{n_{\text{c}}} \approx 10{{\text{{\AA}}}^3}$, close to the expected value of 8.35 ų. For heterogeneous nucleation under compression, [Fig. E1(a)], the slopes of the curves after correction for the Schmid factor is roug hly ${\Omega _c}/\left( {{n_{\text{c}}}S} \right) \approx 8{{\text{{\AA}}}^3}$, which is similar to the case of homogeneous nucleation. Therefore, our data confirm that the activation volume is proportional to the size of the critical dislocation loop. That ${\Omega _c}/\left( {{n_{\text{c}}}S} \right)$ is somewhat smaller than bA_a supports the notion that the Burgers vector of a critical dislocation nucleus is smaller than that of a fully formed dislocation.9,11

FIG. E1.

The relation between critical dislocation size n_c and the activation volume Ω ≡ −(∂G_c/∂σ). (a) Homogeneous nucleation and (b) heterogeneous nucleation. Circles represent the activation volume obtained from the derivative of G_c with respect to σ. Squares represent the activation volume data multiplied by 1/S, where S is the Schmid factor. Dashed lines are linear fits to the data.