Abstract
We present an experimental technique to better control the phase of an electron charge qubit, formed by a GaAs double quantum dot. A standard non-adiabatic gate pulse is used to generate the qubit rotation around the x-axis of the Bloch sphere. To gain good control of the z-rotation (the phase) on a short time scale, a fast 130 ps tipping pulse is superimposed on the non-adiabatic pulse. The two-axis gate operation is exhibited in the composite pulse excited qubit evolution spectrum. We demonstrate that the dynamic phase can be varied continuously from 0 to 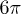 by varying the amplitude of the tipping pulse. The understanding of the spectrum is validated through simulation of the von Neumann equation.
by varying the amplitude of the tipping pulse. The understanding of the spectrum is validated through simulation of the von Neumann equation.
Export citation and abstract BibTeX RIS
Introduction
Solid-state quantum computing based on semiconductor quantum dots is appealing because of the potential for large-scale integration. A variety of quantum dots have been used to construct qubits based on spin [1–5]. Recently, charge qubits have regained much interest [6–11]. In comparison with its spin counterpart, the operation time can be very fast, even though the dephasing time is relatively short. The attractive short operation time, however, presents an experimental challenge to manipulate both the superposition and phase of the charge qubit state vector on a time scale shorter than the coherence time.
Double hat pulses have been designed to control the evolution of spin qubit [12,13]. For a single electron charge qubit, rotations around the x-axis, corresponding to the Larmor precession, have recently been demonstrated in gate defined GaAs [6,7] and SiGe [10] double quantum dot. Researchers have also performed Ramsey fringe experiments [8–10] to show the z-rotations. In this letter we firstly prepare a superposition with a non-adiabatic square pulse. Differently from the Ramsey fringe method, where the phase accumulation around the z-axis is determined by the interval of two 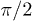 pulses, we, alternatively, superimpose a narrow tipping pulse on the non-adiabatic square pulse and demonstrate the possibility of arbitrary phase-shift gate operation of the charge qubit.
pulses, we, alternatively, superimpose a narrow tipping pulse on the non-adiabatic square pulse and demonstrate the possibility of arbitrary phase-shift gate operation of the charge qubit.
Results
Our sample is fabricated on the  heterostructure using electron beam lithography (EBL). The two-dimensional electron gas (2DEG) is about 100 nm below the sample surface. The density of the 2DEG is
heterostructure using electron beam lithography (EBL). The two-dimensional electron gas (2DEG) is about 100 nm below the sample surface. The density of the 2DEG is 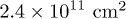 and mobility is
and mobility is 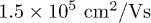 , which are determined by quantum Hall measurement. The sample is mounted in a dilution refrigerator with the base temperature of 30 mK. Figure 1(a) shows the scanning electron microscopy (SEM) image of a device which is similar to the one measured in this experiment. The metal gates are arranged in a quadruple quantum dot structure. The double quantum dot is formed by applying negative voltages to the five upper and two horizontal gates, denoted by U1–U5 and H1–H2. The lower three gates D1–D3 confine the quantum point contact (QPC) to be the detector. To enhance the sensitivity of the QPC detector, there is a small gap between H1 and H2. Electrons cannot pass through the gap directly when the sample is working. The number of electrons in the dots can be controlled by tuning the voltage on the gates. An Agilent fast pulse generator (Agilent 81134A) with a time resolution of 1 ps is used to generate fast pulse sequences. The pulse sequences pass through a semi-rigid coaxial transmission line to the device. A sinusoidal voltage is superimposed on the negative dc voltage of U1. A dc bias voltage applies on the QPC channel, and a lock-in detector measures the differential current of the QPC for the sinusoidal modulation.
, which are determined by quantum Hall measurement. The sample is mounted in a dilution refrigerator with the base temperature of 30 mK. Figure 1(a) shows the scanning electron microscopy (SEM) image of a device which is similar to the one measured in this experiment. The metal gates are arranged in a quadruple quantum dot structure. The double quantum dot is formed by applying negative voltages to the five upper and two horizontal gates, denoted by U1–U5 and H1–H2. The lower three gates D1–D3 confine the quantum point contact (QPC) to be the detector. To enhance the sensitivity of the QPC detector, there is a small gap between H1 and H2. Electrons cannot pass through the gap directly when the sample is working. The number of electrons in the dots can be controlled by tuning the voltage on the gates. An Agilent fast pulse generator (Agilent 81134A) with a time resolution of 1 ps is used to generate fast pulse sequences. The pulse sequences pass through a semi-rigid coaxial transmission line to the device. A sinusoidal voltage is superimposed on the negative dc voltage of U1. A dc bias voltage applies on the QPC channel, and a lock-in detector measures the differential current of the QPC for the sinusoidal modulation.
Fig. 1: (Colour online) (a) Scanning electron microscope image of the sample structure. The upper metal gates U1–U5 and two horizontal gates H1–H2 define the double quantum dot. We use the lower channel formed by D1–D3 to be the QPC channel. (b) The charge diagram of the double quantum dot at  . (c) The honeycomb pattern corresponds to the red-circle area in (b) with four different charge states at
. (c) The honeycomb pattern corresponds to the red-circle area in (b) with four different charge states at 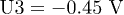 , which noted as (0, 0), (0, 1), (1, 0), (1, 1). (d) The same region as in (c) is shown but a 130 ps width pulse on gate U1 is applied.
, which noted as (0, 0), (0, 1), (1, 0), (1, 1). (d) The same region as in (c) is shown but a 130 ps width pulse on gate U1 is applied.
Download figure:
Standard imageFigure 1(b) shows a charge stability diagram [14–16] of the double quantum dot. To avoid electrons tunneling out from the barriers when applying pulses, we tune the two barriers tunneling to be very slow so that the random telegraphy signals appear [17,18]. Figure 1(c), corresponding to the red-circle region of fig. 1(b) with a different gate voltage U3, shows the state we encode and manipulate the charge qubit. Though the system is not working in the last electron region, we only consider the valence electron and describe the system as having four relevant charge states: (0, 0), (1, 0), (0, 1) and (1, 1), where 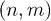 is the relative valence electron number in the left and right dot. Figure 1(d) is the same as fig. 1(c) but with an application of a 120 ps width pulse at a repetition rate of 40 MHz on gate U1. The multiple lines (indicated as yellow arrows), which are parallel to the anti-cross line, are the Landau-Zener- Stückelberg interference fringes [9,19–26].
is the relative valence electron number in the left and right dot. Figure 1(d) is the same as fig. 1(c) but with an application of a 120 ps width pulse at a repetition rate of 40 MHz on gate U1. The multiple lines (indicated as yellow arrows), which are parallel to the anti-cross line, are the Landau-Zener- Stückelberg interference fringes [9,19–26].
The Hamiltonian of a charge qubit in a double quantum dot is approximated by a two-level system as

where  represents the energy level detuning, ER and EL are the energy levels for an electron in the right and left dot, respectively, which can be adjusted continuously by sweeping the gate voltages U1 and U5. Δ is the tunnel coupling between the two dots, which can be tuned using the middle gate U3, and it remains by fixing the voltage on U3 in the experiment.
represents the energy level detuning, ER and EL are the energy levels for an electron in the right and left dot, respectively, which can be adjusted continuously by sweeping the gate voltages U1 and U5. Δ is the tunnel coupling between the two dots, which can be tuned using the middle gate U3, and it remains by fixing the voltage on U3 in the experiment.  and
and  are the Pauli matrices. The energy levels of the system are shown in fig. 2(a). For
are the Pauli matrices. The energy levels of the system are shown in fig. 2(a). For  , the electron occupies the right (left) dot which is denoted as
, the electron occupies the right (left) dot which is denoted as 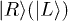 .
.
Fig. 2: (Colour online) (a) The energy level of the system. The initial qubit is in (0, 1) (denoted by  ). The pulse non-adiabatically drives the qubit to the anti-crossing point
). The pulse non-adiabatically drives the qubit to the anti-crossing point  . The qubit rotates between
. The qubit rotates between  and
and  until the pulse non-adiabatically takes the qubit far away from the degeneracy point at its falling edge. The QPC detector reads out the final charge state. (b) The Bloch sphere evaluation of the qubit when the non-adiabatic pulse is applied. (c) Experimental results of the Larmor oscillations after subtracting the background signal of the QPC. From the period of the oscillations, the couple tunneling between the two dots is determined to be 5.5 GHz. (d) The simulation results of the Larmor oscillations using the von Neumann equation with
until the pulse non-adiabatically takes the qubit far away from the degeneracy point at its falling edge. The QPC detector reads out the final charge state. (b) The Bloch sphere evaluation of the qubit when the non-adiabatic pulse is applied. (c) Experimental results of the Larmor oscillations after subtracting the background signal of the QPC. From the period of the oscillations, the couple tunneling between the two dots is determined to be 5.5 GHz. (d) The simulation results of the Larmor oscillations using the von Neumann equation with 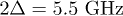 .
.
Download figure:
Standard imageFirst, we control the single charge qubit rotation around the x-axis using Larmor oscillations. When the qubit is non-adiabatically taken to the anti-crossing point, where 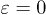 , the Hamiltonian of eq. (1) can be written as
, the Hamiltonian of eq. (1) can be written as 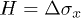 . The qubit undergoes a rotation only around the x-axis in the Bloch sphere. The rotation frequency is determined by the tunnel coupling strength, Δ, between
. The qubit undergoes a rotation only around the x-axis in the Bloch sphere. The rotation frequency is determined by the tunnel coupling strength, Δ, between 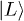 and
and  . This process is equivalent to a NOT gate of the single qubit since it completely inverts the single qubit between state
. This process is equivalent to a NOT gate of the single qubit since it completely inverts the single qubit between state 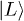 and
and  .
.
The pulse shape is illustrated in fig. 2(a). Experimentally, we first initialize the qubit at 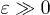 in state
in state 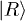 , then apply a non-adiabatic square pulse that drive the qubit to
, then apply a non-adiabatic square pulse that drive the qubit to 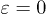 non-adiabatically. The initially prepared state
non-adiabatically. The initially prepared state 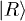 evolves between
evolves between 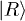 and
and  around the x-axis on the Bloch sphere as shown in fig. 2(b). Following the pulse, the qubit returns non-adiabatically to the initial position. Figure 2(c) shows the experimental result after the background signal of QPC is subtracted [4–10]. Figure 2(c) clearly shows coherent oscillations with a 5.5 GHz frequency corresponding to the tunnel coupling
around the x-axis on the Bloch sphere as shown in fig. 2(b). Following the pulse, the qubit returns non-adiabatically to the initial position. Figure 2(c) shows the experimental result after the background signal of QPC is subtracted [4–10]. Figure 2(c) clearly shows coherent oscillations with a 5.5 GHz frequency corresponding to the tunnel coupling 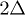 , between the double quantum dots. This evolution can be described using the von Neumann equation [27,28]:
, between the double quantum dots. This evolution can be described using the von Neumann equation [27,28]:

where 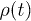 is the density matrix of the system and
is the density matrix of the system and 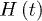 is the Hamiltonian in eq. (1) with the energy level detuning parameter
is the Hamiltonian in eq. (1) with the energy level detuning parameter 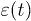 while applying the non-adiabatic square pulse. The pulse has a rise time of about 100 ps. We simulate the evolution of the qubit using the pulse profiles which were acquired at the end of the coaxial line in the dilution refrigerator. Substituting the initial state
while applying the non-adiabatic square pulse. The pulse has a rise time of about 100 ps. We simulate the evolution of the qubit using the pulse profiles which were acquired at the end of the coaxial line in the dilution refrigerator. Substituting the initial state  , the results of the numerical simulation of the Larmor oscillations are displayed in fig. 2(d). In the simulation, to account the charge noise, we convolve each vertical sweep with a Gaussian function which has width
, the results of the numerical simulation of the Larmor oscillations are displayed in fig. 2(d). In the simulation, to account the charge noise, we convolve each vertical sweep with a Gaussian function which has width 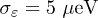 [7]. These results are in good agreement with fig. 2(c).
[7]. These results are in good agreement with fig. 2(c).
Furthermore, we use an alternative gate operation scheme. Based on coherent control around the x-axis, we superimpose a narrow tipping pulse on the non-adiabatic square pulse that monitors the coherent evolution around the z-axis. (The non-adiabatic square pulse and tipping pulse are both generated by an Agilent 81134A and combined using a Pasternack PE2064 at room temperature.) The basic idea is that we first initialize the system in the state  . While the qubit is rotating around the x-axis driven by the non-adiabatic square pulse, the tipping pulse takes the qubit away from the anti-crossing point, which accumulates a phase around the z-axis for the non-zero ε in eq. (1). At the end of the tipping pulse, the qubit returns to the anti-crossing point and keeps rotating around the x-axis until the non-adiabatic square pulse is terminated. Following the pulse manipulation, the charge state is finally detected by the QPC. This scheme allows us to give the qubit a phase ∅ around the z-axis on the Bloch sphere, and the probability of finding the system in
. While the qubit is rotating around the x-axis driven by the non-adiabatic square pulse, the tipping pulse takes the qubit away from the anti-crossing point, which accumulates a phase around the z-axis for the non-zero ε in eq. (1). At the end of the tipping pulse, the qubit returns to the anti-crossing point and keeps rotating around the x-axis until the non-adiabatic square pulse is terminated. Following the pulse manipulation, the charge state is finally detected by the QPC. This scheme allows us to give the qubit a phase ∅ around the z-axis on the Bloch sphere, and the probability of finding the system in 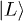 state will oscillate with phase ∅.
state will oscillate with phase ∅.
The phase shift evolution can be considered as a Landau-Zener-Stückelberg process. When the qubit cross the anti-crossing point, there will be a probability for the non-adiabatic transition to the ground state 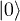 and the excited state
and the excited state  . The accumulated phase between the two different paths can be calculated using [9]
. The accumulated phase between the two different paths can be calculated using [9]

where 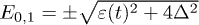 represents the eigenvalues of the Hamiltonian as shown in fig. 2(a).
represents the eigenvalues of the Hamiltonian as shown in fig. 2(a).
An arbitrary phase can be achieved by continuously changing the tipping pulse width Tt or amplitude 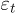 . In the experiment, the pulse can be treated as a Gaussian or triangular wave if the pulse width
. In the experiment, the pulse can be treated as a Gaussian or triangular wave if the pulse width 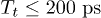 for the attenuation of the coaxial transmission line, otherwise the pulse can be treated as a trapezoidal pulse or a square pulse. In addition, the coherence time will decrease rapidly when the qubit is far away from the anti-crossing point. Here we only change the amplitude of the tipping pulse for simplicity. The tipping pulse follows the square pulse after 900 ps. Figure 3(a) shows the timing chart of the manipulation sequence pulses. There are three different situations with increasing square pulse width Tp: i) When
for the attenuation of the coaxial transmission line, otherwise the pulse can be treated as a trapezoidal pulse or a square pulse. In addition, the coherence time will decrease rapidly when the qubit is far away from the anti-crossing point. Here we only change the amplitude of the tipping pulse for simplicity. The tipping pulse follows the square pulse after 900 ps. Figure 3(a) shows the timing chart of the manipulation sequence pulses. There are three different situations with increasing square pulse width Tp: i) When 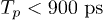 , the two pulses are separated from each other. The qubit will rotate around the x-axis driven by the square pulse. The tipping pulse makes no allowance for the qubit since the amplitude is too small to take the qubit to the anti-crossing point. ii) When
, the two pulses are separated from each other. The qubit will rotate around the x-axis driven by the square pulse. The tipping pulse makes no allowance for the qubit since the amplitude is too small to take the qubit to the anti-crossing point. ii) When 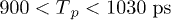 , the two pulses are combined. Driven by the tipping pulse, the qubit will rotate around the z-axis after the x-axis rotation. iii) When
, the two pulses are combined. Driven by the tipping pulse, the qubit will rotate around the z-axis after the x-axis rotation. iii) When 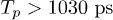 , the qubit will go through three stages: rotation around the x-axis, rotation around the z-axis and then the x-axis again. The z-axis rotation will accumulate an additional phase, thus realizing a phase shift gate. It should be noted that although the x component is non-zero in eq. (1), we can treat the tipping pulse process as the z-axis rotation and attribute the x-rotation to the square pulse simply because we can continuously change the square pulse width. This continuous control makes it possible to cancel out the effect of the x-rotation during the tipping pulse. The qubit evolutions in the Bloch sphere under three different processes are represented in fig. 3(b). Figure 3(c) shows the data from measurements by sweeping the tipping pulse amplitude while keeping
, the qubit will go through three stages: rotation around the x-axis, rotation around the z-axis and then the x-axis again. The z-axis rotation will accumulate an additional phase, thus realizing a phase shift gate. It should be noted that although the x component is non-zero in eq. (1), we can treat the tipping pulse process as the z-axis rotation and attribute the x-rotation to the square pulse simply because we can continuously change the square pulse width. This continuous control makes it possible to cancel out the effect of the x-rotation during the tipping pulse. The qubit evolutions in the Bloch sphere under three different processes are represented in fig. 3(b). Figure 3(c) shows the data from measurements by sweeping the tipping pulse amplitude while keeping 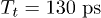 . As mentioned above, when the tipping pulse amplitude changes, the oscillations appear only when the pulse width
. As mentioned above, when the tipping pulse amplitude changes, the oscillations appear only when the pulse width 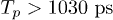 . These oscillations suggest a significant change of the z-rotation phase with a period of
. These oscillations suggest a significant change of the z-rotation phase with a period of 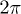 . As shown in fig. 3(c), more than
. As shown in fig. 3(c), more than 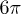 rotations around the z-axis have been continuously realized. Figure 3(d) shows the simulation result using eq. (2). The results of the simulation are in good agreement with the experimental data. However, the mismatch indicated as green rectangles in fig. 3(c) cannot be understood. This mismatch is a common problem, which limits the improvement of fidelity for the charge qubit. It may be caused by the pulse reflection between the pulse generator and sample [7–10].
rotations around the z-axis have been continuously realized. Figure 3(d) shows the simulation result using eq. (2). The results of the simulation are in good agreement with the experimental data. However, the mismatch indicated as green rectangles in fig. 3(c) cannot be understood. This mismatch is a common problem, which limits the improvement of fidelity for the charge qubit. It may be caused by the pulse reflection between the pulse generator and sample [7–10].
Fig. 3: (Colour online) (a) Three different situations when the width of square pulse is changed are shown. (b) The qubit evaluation in the Bloch sphere at different stages of the pulse sequences: rotation around the x-axis, z-axis and x-axis. (c) Experimental results of the phase shift manipulation. The superposition of the two pulses is 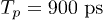 which is in agreement with the delay time between the two pulses set by the pulse generator. (d) The simulation of the manipulation. (e) The simulation results with two reflection pulses locating at
which is in agreement with the delay time between the two pulses set by the pulse generator. (d) The simulation of the manipulation. (e) The simulation results with two reflection pulses locating at  and
and  with fixed amplitude
with fixed amplitude 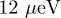 and
and 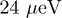 , respectively.
, respectively.
Download figure:
Standard imageTo further understand the reflection pulses effect, here we simulate the reflection pulses as two tailing pulses. The two reflection tailing pulses are defined using a 100 ps pulse profile which was acquired at the end of coaxial line in the dilution refrigerator. The two reflection pulses are located at 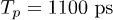 and
and 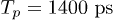 with fixed amplitude
with fixed amplitude 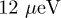 and
and  , respectively. The simulation result is shown in fig. 3(e). Compared with fig. 3(d), fig. 3(e) describes the experimental results even better. Especially it shows the horizontal enhancement of the QPC current in green rectangles when
, respectively. The simulation result is shown in fig. 3(e). Compared with fig. 3(d), fig. 3(e) describes the experimental results even better. Especially it shows the horizontal enhancement of the QPC current in green rectangles when  . These enhanced signals can be understood as Landau-Zener-Stückelberg processes caused by the reflection pulses.
. These enhanced signals can be understood as Landau-Zener-Stückelberg processes caused by the reflection pulses.
Conclusions
In summary, universal quantum gates are key elements in a quantum computer, as they provide the fundamental building blocks for encoding complex algorithms and operations. We demonstrate the ability to perform universal single-qubit operations at a sub-nanosecond time scale in double quantum dot. Rotations on the Bloch sphere around the x-axis are performed with a non-adiabatic square pulse. More than 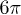 rotations around the z-axis are continuously realized under 130 ps by changing the narrow tipping pulse which is superimposed on the non-adiabatic pulse. These results demonstrate phase shift control at a short time scale. Together with our tunable phase shift the electrically controllable Larmor rotations can be applied to any desired angle in the Bloch sphere. These two axes rotations can be used to implement universal quantum control.
rotations around the z-axis are continuously realized under 130 ps by changing the narrow tipping pulse which is superimposed on the non-adiabatic pulse. These results demonstrate phase shift control at a short time scale. Together with our tunable phase shift the electrically controllable Larmor rotations can be applied to any desired angle in the Bloch sphere. These two axes rotations can be used to implement universal quantum control.
Acknowledgments
This work was supported by the National Basic Research Program of China (Grant No. 2011CBA00200), "Strategic Priority Research Program (B)" of the Chinese Academy of Sciences (Grant No. XDB01030100), and National Natural Science Foundation (Grant Nos. 11304301, 11222438, 11174267 and 61306150).








