Abstract
Based on the non-extensive Tsallis entropy, a distribution function of rockfall sizes is suggested. Our result demonstrates the applicability of fundamental principles of non-extensivity of fragmentation into the cumulative distribution of rockfall volumes. Historical data discussed along with an analysis of recent rockfalls data where the observed volumes estimated using the high-accuracy and precision technique of terrestial laser scanner (TLS). The analysis leads to the non-extensive index q = 1.4 in agreement with that presented in other fracture effects in geodynamic or laboratory scale. The work suggests that the non-extensive physics approach can lead to a groundbreaking statistical physics of rockfalls, one of the worldwide natural hazard.
Export citation and abstract BibTeX RIS
Rockfalls, rockslides and rock avalanches are defined as rapid movements of rocks driven by gravity forces, having their origin on steep rock slopes, including subvertical cliffs [1]. Rockfalls as a geomorphic process play a major role in the sediment budget of high-mountain regions and are an important influencing factor for other geomorphic processes (e.g., debris flows) within sediment cascades in high-mountain catchments. Their occurrence and magnitude depend on many influencing factors including chemical weathering, frost bursting, rainfall and water pressure, melting or mechanical influences due to earthquake activity [2]. It is obvious that their statistical characterization is critical for understanding the processes of slope failure and their contributions to erosion and landscape evolution.
The statistical characterization of rockfalls is even more complicated due to the difficulty of obtaining accurate data, particularly volumetric data, from steep slopes that have often difficult access. Most of the up to date approaches are based on the analysis of historical inventories, of aerial photographs to measure remotely the areas of past slope failures and digital photogrammetry for measuring these in three dimensions and computing volumes of slope failures and relevant erosion rates [3]. In the last decade, terrestrial laser scanner (TLS) applications have grown in importance for measuring and analysing geomorphic processes such as rockfalls. Explicit information on the performance of TLS can be found in [4]. Its increasing use is due to its capability to provide quickly and easily, digital data of high accuracy and precision. TLS may capture information for unaccessible outcrops, and acquire large data sets which can be used to determine the size and spatial distribution of potentially unstable rock mass volumes [5] obtaining the spatial distribution and size of rockfall events (see [6] and references therein).
The statistical physics of rockfalls involves the evaluation of their volume-frequency distribution. This is an important parameter for the calculation of the rockfall hazard [7], along with other potential applications in detecting climatic and environmental change and modeling sediment transfer [8]. Many empirical distribution functions were already proposed in the past decade, mainly based on empirical and not physically justified approaches [9–11]. Among them power law distributions have been suggested to statistical characterize rockfall distributions [9–12], based on the argument that rockfalls are examples of self-organized criticality (SOC) in nature [13]. In the context of SOC, the frequency size distribution of rockfalls can be well described by the power law relation  and as a consequence by the power law cumulative distribution function
and as a consequence by the power law cumulative distribution function  . The power law frequency size distribution is the only distribution that does not have a characteristic scale and can be explained in terms of scale invariance, i.e. fractal statistics [13].
. The power law frequency size distribution is the only distribution that does not have a characteristic scale and can be explained in terms of scale invariance, i.e. fractal statistics [13].
Recently non-extensive statistics [14] has been becoming a challenging framework for geophysical complex phenomena, specially when fragmentation effects are involved [15]. The fundamental idea is the concept of fragmentation, in which the sum of the entropies of the parts that constitute a fractioning object after the division is larger than the entropy of the whole object [16]. Since disorder and fractality are two of the key components of any physical process based on fragmentation [15], we can use a current generalization of Boltzmann-Gibbs (BG) statistical physics due to Tsallis, referred as non-extensive statistical physics (NESP) [17], to explore the statistical distribution of size in a fragmentation process as rockfalls are. The advantage of considering the Tsallis distribution is that, based on the principle of entropy, it can be related to statistical mechanics and reduces to the traditional BG statistical physics as a special case. Fracture-related phenomena, present fractality, long-range interaction and memory effects [15, 16]. It is precisely such phenomena that constitute the scope of non-extensive statistical mechanics [17]. We note that recent applications to fracture [15, 16] and solid-earth physics (in regional or planetary scale) summarized into [17], mainly focused on seismology [18–24], fault lengths distribution [25] and very recently to natural hazards [26], plate tectonics [27] and geomagnetic reversals [28]; they support the applicability of non-extensive statistical physics in fracture and in complex geosystems as well.
According to the non-extensive formalism ([17] and references therein), the entropy Sq is given by  , kB is Boltzman's constant, pi is a set of probabilities and W is the total number of microscopic configurations. The non-extensive entropy Sq is, in some sense, a generalization of the classical entropic functional, since in the limit q → 1 for the Tsallis entropy, we obtain the well-known Boltzmann-Gibbs (BG) entropy,
, kB is Boltzman's constant, pi is a set of probabilities and W is the total number of microscopic configurations. The non-extensive entropy Sq is, in some sense, a generalization of the classical entropic functional, since in the limit q → 1 for the Tsallis entropy, we obtain the well-known Boltzmann-Gibbs (BG) entropy,  . In most, if not all, of the studied applications, q appears to reflect some (multi) fractality in the system [17]. The Tsallis entropy is known to share many common properties with the Boltzmann-Gibbs entropy [17]. For a system composed of two statistically independent systems, A and B, the Tsallis entropy satisfies
. In most, if not all, of the studied applications, q appears to reflect some (multi) fractality in the system [17]. The Tsallis entropy is known to share many common properties with the Boltzmann-Gibbs entropy [17]. For a system composed of two statistically independent systems, A and B, the Tsallis entropy satisfies
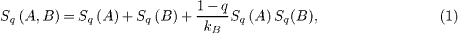
which is referred to as pseudoadditivity. The last term on the right-hand side of this equation brings the origin of non-additivity. Therefore the value 1 − q or q indicates the degree of non-additivity in the complex system under consideration. Since additivity is violated, q < 1, q = 1 and q > 1, respectively, correspond to superadditivity, additivity and subadditivity. This is the fundamental principle for non-extensive statistical physics. All other quantities which are concerned with thermodynamics may be derived from it [14, 17].
The main motivation of our work is starting from a fragmentation procedure to establish a magnitude (i.e., volume)-frequency distributions of rockfalls using concepts of non-extensive statistical mechanics and to relate our results with that previously published using empirical power law fitting to historical records, extracted from different geological settings and different volume ranges, in order to overcome the length restriction, uncertainties and errors that are associated with the latter. We note that rockfalls in situ fragmentation is a very complex process and the detailed description of the parameters affecting the temporal occurrence of them are described in [5–12] and references therein. Furthermore, we will test our results using rockfalls data collected and presented in the geotechnical literature [29] based on new innovative observation techniques such as the TSL is.
Rockfalls are in principle in situ fragmentation of rock volumes and thus the question whether they are described by non-extensive statistical physics, even at the phenomenological level (i.e., without specifying any underlying model), represents a challenge. This is the problem we address here. Our aim is not to develop a precise model, but rather to present a simple argument of physical plausibility. Recently, a model for fragmentation was proposed to explain the earthquake generation mechanism [30, 31], based on the interaction of two rough profiles where fragments are produced by the local breakage of the geomaterial filling the gaps between them. By using the non-extensive formalism, the aforementioned authors, showed the influence of the size distribution of fragments on the energy distribution of earthquakes and introduced an energy-distribution function, including the Gutenberg-Richter law as a particular case. We apply it to approach the fragment's volume distribution in the case of rockfalls.
Tsallis entropy [14] in an integral form is defined as  , where
, where  (S) is the probability of finding a fragment of surface S, q is the entropic index and kB is the Boltzmann constant. Under the normalization of
(S) is the probability of finding a fragment of surface S, q is the entropic index and kB is the Boltzmann constant. Under the normalization of  (S),
(S),  and the condition about the q-expectation value
and the condition about the q-expectation value  , where the escort distribution function is given by
, where the escort distribution function is given by  , so we are led to the expression for the fragment size distribution function [30, 31] given as
, so we are led to the expression for the fragment size distribution function [30, 31] given as
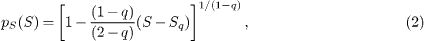
which corresponds to the area distribution for the fragments of the rockfall planes. Since the proportionality between the rockfall volume V and fragments' surface is  [31], where A is a geometric factor, we are led to the rockfalls distribution function
[31], where A is a geometric factor, we are led to the rockfalls distribution function
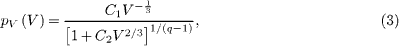
with  and
and  . Equation (3) is an analytic expression for the volume distribution of rockfalls based on the first principles, as introduced by the definition of non-extensive Tsallis entropy. Integrating eq. (3) we are led to the cumulative distribution function
. Equation (3) is an analytic expression for the volume distribution of rockfalls based on the first principles, as introduced by the definition of non-extensive Tsallis entropy. Integrating eq. (3) we are led to the cumulative distribution function
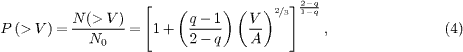
where N(>V) is the number of rockfalls with volume larger than V, N0 the total number of them and q and A are the non-extensive parameters and the geometrical factor, respectively.
An inspection of eqs. (3) and (4) indicate that for rockfall volumes bigger than a given one (see fig. 1) we are led to a power law description of the distribution function and in such a case  , where
, where  and the exponent of the power law is
and the exponent of the power law is  , with a cumulative distribution
, with a cumulative distribution  with an exponent
with an exponent  and
and  in agreement with the power law empirically used to describe the rockfalls distribution [13]. To have an estimation of Vc we select the volume where the power law approximation of P(>V) takes the value P(>V) = 1 (see fig. 1), leading to
in agreement with the power law empirically used to describe the rockfalls distribution [13]. To have an estimation of Vc we select the volume where the power law approximation of P(>V) takes the value P(>V) = 1 (see fig. 1), leading to  . Using historical archives [32, 33] which describe a variety of geological settings and volume ranges, we observe that 1 < β1 < 2 leading to
. Using historical archives [32, 33] which describe a variety of geological settings and volume ranges, we observe that 1 < β1 < 2 leading to  , in agreement with previous published results on fragmentation in a broad range of scales from laboratory up to the geodynamic one. We note that most of the reported β1-values ([32, 33] and references therein) are between 1.4 and 1.6 and thus q lies in the range 1.52–1.62.
, in agreement with previous published results on fragmentation in a broad range of scales from laboratory up to the geodynamic one. We note that most of the reported β1-values ([32, 33] and references therein) are between 1.4 and 1.6 and thus q lies in the range 1.52–1.62.
Fig. 1: (Colour on-line) Non-extensive fit (red line) with q = 1.4 of the normalized cumulative distribution function of volumes V (in m3) of rockfall scars (blue points) observed using TLS techniques in Solà d'Andorra, in the Principality of Andorra, Eastern Pyrenees, as reported in [29].
Download figure:
Standard imageWe analyse rockfall scar data from one of the most recent surveys analysed in [29], where laser scanning data are used to enable a better quantification of geomorphic processes in a pilot zone at Forat Negre and Borrassica, in the Principality of Andorra, Eastern Pyrenees [29]. The study area is a steep slope originated by the excavation of the Pleistocene glaciers. The outcrop is made of granodiorites, which are intensely fractured as the result of the Alpine and Hercynian orogeneses [10].
Figure 1 presents the cumulative distribution function P(>V) of rockfalls data. Fitting it with eq. (4) we obtain q = 1.4 and for the geometrical factor A ≈ 0.44, which result in Vc ≈ 0.7 m3 in agreement with the result in [29], where it is stated that a rollover effect is observed for volumes below 0.75 m3. As pointed in [29] the TLS-based procedure prevents from under-sampling small (less than 0.75 m3) scar volumes and therefore no censoring effect is expected. The resolution of the technique allows the detection of areas and spacings as small as 0.1 m2 and 0.2 m, respectively, which corresponds to volumes as small as 0.02 m3. Taking into account the accuracy of the TLS technique in [29], it was stated that "the rollover observed must have another explanation and is probably ought to the existent fracture patterns rather than to censoring effects related to low-precision".
The latter speculation is fully justified in the frame of non-extensive statistical physics description as eq. (4) suggests a rollover in the cumulative distribution function for V < Vc, a property which is generic in the frame of the Tsallis approach. Furthermore the fit in the volume cumulative distribution function shows that non-extensivity describes well the source of self-similarity associated with the process' increments ``infinite'' variance [34], even if an additional source of self-similarity may come from the process' memory in analogy with the long-range temporal correlations between earthquake magnitudes, as reported in the frame of natural time analysis (see [34] and references therein). The generic expression for the frequency-magnitude distribution given in eq. (3) is a straightforward generalization of the power law up to now used for rockfalls hazard calculations. The latter expression could explain the behavior of the distribution in a broad range of volumes possibly leading to new estimations of hazard and risk [26].
We here demonstrate the feasibility of the non-extensive statistics applied to the volume distribution of the rockfall scars. The distribution shows exactly the same power law features as other distributions of rockfall regions mentioned in [13] with q-values in the range 7/5 < q < 2. Equation (4) can fit the TLS dataset well with  . The q-value is a quantitative measure of the scale of the spatial interactions. A q-value close to 1 indicates short-ranged spatial correlations. As q increases the physical state (in the sense of statistical physics) becomes much more unstable (see [35]). Note that eq. (4) is not an empirical guess for the rockfalls volume distribution but derived from the first principle of non-extensive Tsallis entropy formalism, which is completely universal and has a long range of application [17, 35]. The physical meaning underlying the non-extensive entropy formalism is that the final physical state can be considered as a collection of fragmented parts which, after division, have the sum of individual entropies larger than the entropy of the initial state in a similar way as pointed out for landslides [36, 37]. The latter is straightforward from the concept of not additivity since
. The q-value is a quantitative measure of the scale of the spatial interactions. A q-value close to 1 indicates short-ranged spatial correlations. As q increases the physical state (in the sense of statistical physics) becomes much more unstable (see [35]). Note that eq. (4) is not an empirical guess for the rockfalls volume distribution but derived from the first principle of non-extensive Tsallis entropy formalism, which is completely universal and has a long range of application [17, 35]. The physical meaning underlying the non-extensive entropy formalism is that the final physical state can be considered as a collection of fragmented parts which, after division, have the sum of individual entropies larger than the entropy of the initial state in a similar way as pointed out for landslides [36, 37]. The latter is straightforward from the concept of not additivity since  [36]. Furthermore, we note that the entropic index q introduces a bias in the probabilities. Given the fact that generically 0 < pi < 1, we have that
[36]. Furthermore, we note that the entropic index q introduces a bias in the probabilities. Given the fact that generically 0 < pi < 1, we have that  if q < 1 and
if q < 1 and  if q > 1. Therefore, q < 1 enhances the rare events, those which have probabilities close to zero, whereas q > 1 enhances the frequent events, i.e., those whose probabilities are close to unity. In addition, since we can assume that rockfalls consist of many non-independent subvolumes, the non-additivity index q could be interpreted as an approximate measure of the long-range interacting subsystems.
if q > 1. Therefore, q < 1 enhances the rare events, those which have probabilities close to zero, whereas q > 1 enhances the frequent events, i.e., those whose probabilities are close to unity. In addition, since we can assume that rockfalls consist of many non-independent subvolumes, the non-additivity index q could be interpreted as an approximate measure of the long-range interacting subsystems.
Summarizing we can state that the use of non-extensive statistics is a suited tool to describe the distribution function of the rockfall scars frequency-volume distribution. The obtained distribution function incorporates the characteristics of non-extensivity of in situ fragmentation into the cumulative distribution of rockfall volumes and explains the observed power law behavior for great volumes, along with a rollover observed for very small fragment's volume, which fits the real data very well, thus indicating that the rollover is a generic property in the frequency distribution at small volumes and can be regarded as the manifestation of the physical foundation of the non-extensive Tsallis entropy.
Acknowledgment
This research has been co-funded by the European Union (European Social Fund) and Greek national resources under the framework of the "THALES Program: SEISMO FEAR HELLARC" project of the "Education & Life long Learning" Operational Programme. We express our gratitude to the Department of Geotecnical Engineering and Geosciences, Technical University of Catalonia, Spain (Prof. J. Corominas) providing us with the rockfall data of ref. [29].






