Skip to main content
SpringerLink
Log in

Autologistic models with interpretable parameters

  • Published:
Journal of Agricultural, Biological, and Environmental Statistics Aims and scope Submit manuscript

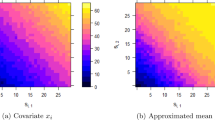
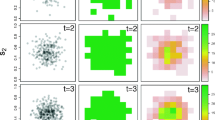
Abstract

Ecologists are interested in characterizing succession processes, in particular monitoring the spread of invasive species and their effect on resident species. In situations for which binary response variables representing presence or absence of plants are observed over a spatial lattice, it may be desirable to use a model that accounts for the statistical dependence in the data, as well as the effect of potential covariates. One such model is the autologistic regression model. We show that the typical parameterization of the autologistic model presents difficulties in interpreting model parameters across varying levels of statistical dependence, and propose an alternative (centered) parameterization that overcomes this difficulty.We use the centered autologistic model to study the dynamics over time of two species, Rumex acetosella and Lonicera japonica, in an abandoned agricultural field in New Jersey, and compare the results to those obtained from using the traditional autologistic parameterization.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Barden, L. S., and Matthews, J. F. (1980), “Change in Abundance of Honeysuckle (Lonicera japonica) and Other Ground Flora After Prescribed Burning of a Piedmont Pine Forest,” Castanea, 45, 257–260.

    Google Scholar 

  • Besag, J. (1974), “Spatial Interaction and the Statistical Analysis of Lattice Systems” (with discussion), Journal of the Royal Statistical Society, Ser. B, 36, 192–236.

    MATH  MathSciNet  Google Scholar 

  • — (1975), “Statistical Analysis of Non-Lattice Data,” The Statistician, 24, 179–195.

    Article  Google Scholar 

  • Buell, M. F., Buell, H. F., Small, J. A., and Siccama, T. G. (1971), “Invasion of Trees in Secondary Succession on the New Jersey Piedmont,” Bulletin of the Torrey Botanical Club, 98, 67–74.

    Article  Google Scholar 

  • Cressie, N. (1993), Statistics for Spatial Data (2nd ed.), New York: Wiley.

    Google Scholar 

  • Dormann, F. C., McPherson, J. M., Araújo, M. B., Bivand, R., Bolliger, J., Carl, G., Davies, R. G., Hirzel, A., Jetz, W., Kissling, W. D., Kühn, I., Ohlemüller, R., Peres-Neto, P. R., Reineking, B., Schröder, B., Schurr, F. M., and Wilson, R. (2007), “Methods to Account for Spatial Autocorrelation in the Analysis of Species Distributional Data: A Review,” Ecography, 30 (5), 609–628.

    Article  Google Scholar 

  • Gelman, A., and Meng, X. L. (1998), “Simulating Normalizing Constants: From Importance Sampling to Bridge Sampling and Path Sampling,” Statistical Science, 13, 163–185.

    Article  MATH  MathSciNet  Google Scholar 

  • Geyer, C. J., and Thompson, E. A. (1992), “Constrained Monte-Carlo Maximum Likelihood for Dependent Data” (with discussion), Journal of the Royal Statistical Society, Ser. B, 54, 657–699.

    MathSciNet  Google Scholar 

  • Gumpertz,M. L., Graham,M. J., and Ristaino, J. B. (1997), “Autologistic Model of Spatial Pattern of Phytophtora Epidemic in Bell Pepper: Effects of Soil Variables on Disease Presence,” Journal of Agricultural, Biological, and Environmental Statistics, 2, 131–156.

    Article  MathSciNet  Google Scholar 

  • Guyon, X. (1995), Random Fields on a Network: Modeling, Statistics, and Applications, New York: Springer.

    MATH  Google Scholar 

  • Hoeting, J. A., Leecaster, M., and Bowden, D. (2000), “An Improved Model for Spatially Correlated Binary Responses,” Journal of Agricultural, Biological, and Environmental Statistics, 5, 102–114.

    Article  MathSciNet  Google Scholar 

  • Kaiser, M. S., Daniels, M. J., Furukawa, K., and Dixon, P. (2002), “Analysis of Particulate Matter Air Pollution Using Markov Random Field Models of Spatial Dependence,” Environmetrics, 13, 615–628.

    Article  Google Scholar 

  • Myster, R.W., and Pickett, S. T. A. (1994), “A Comparison of Rate of Succession Over 18 Years in 10 Contrasting Old Fields,” Ecology, 75 (2), 387–392.

    Article  Google Scholar 

  • Pickett, S. T. A. (1982), “Population Patterns Through Twenty Years of Oldfield Succession,” Vegetatio, 49, 45–59.

    Article  Google Scholar 

  • Wu, H., and Huffer, F. W. (1997), “Modeling the Distribution of Plant Species Using the Autologistic Regression Model,” Environmental and Ecological Statistics, 4, 49–64.

    Article  Google Scholar 

  • Yurkonis, K. A., Meiners, S. J., and Wachholder, B. E. (2005), “Invasion Impacts Diversity Through Altered Community Dynamics,” Journal of Ecology, 93, 1053–1061.

    Article  Google Scholar 

  • Zhu, J., Huang, H.-C., and Wu, J. (2005), “Modeling Spatial-Temporal Binary Data Using Markov Random Fields,” Journal of Agricultural, Biological, and Enviromental Statistics, 10, 212–225.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Statistics, Iowa State University, 50011-1210, Ames, IA

    Petruţa C. Caragea (Assistant Professor) & Mark S. Kaiser (Professor)

Authors
  1. Petruţa C. Caragea
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mark S. Kaiser
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Petruţa C. Caragea.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Caragea, P.C., Kaiser, M.S. Autologistic models with interpretable parameters. JABES 14, 281–300 (2009). https://doi.org/10.1198/jabes.2009.07032

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1198/jabes.2009.07032

Key Words

Search

Navigation