Abstract
We present and analyze a model for polycrystalline electrode surfaces based on an improved continuum model that takes finite ion size and solvation into account. The numerical simulation of finite size facet patterns allows to study two limiting cases: While for facet size diameter  we get the typical capacitance of a spatially homogeneous but possible amorphous or liquid surface, in the limit
we get the typical capacitance of a spatially homogeneous but possible amorphous or liquid surface, in the limit ![$1[\mathrm{nm}]\ll {d}^{\mathrm{facet}}$](https://content.cld.iop.org/journals/1945-7111/167/10/106512/revision2/jesab9ccaieqn2.gif) , an ensemble of non-interacting single crystal surfaces is approached. Already for moderate size of the facet diameters, the capacitance is remarkably well approximated by the classical approach of adding the single crystal capacities of the contributing facets weighted by their respective surface fraction. As a consequence, the potential of zero charge is not necessarily attained at a local minimum of capacitance, but might be located at a local capacitance maximum instead. Moreover, the results show that surface roughness can be accurately taken into account by multiplication of the ideally flat polycrystalline surface capacitance with a single factor. In particular, we find that the influence of the actual geometry of the facet pattern in negligible and our theory opens the way to a stochastic description of complex real polycrystal surfaces.
, an ensemble of non-interacting single crystal surfaces is approached. Already for moderate size of the facet diameters, the capacitance is remarkably well approximated by the classical approach of adding the single crystal capacities of the contributing facets weighted by their respective surface fraction. As a consequence, the potential of zero charge is not necessarily attained at a local minimum of capacitance, but might be located at a local capacitance maximum instead. Moreover, the results show that surface roughness can be accurately taken into account by multiplication of the ideally flat polycrystalline surface capacitance with a single factor. In particular, we find that the influence of the actual geometry of the facet pattern in negligible and our theory opens the way to a stochastic description of complex real polycrystal surfaces.
Export citation and abstract BibTeX RIS

This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 License (CC BY, http://creativecommons.org/licenses/by/4.0/), which permits unrestricted reuse of the work in any medium, provided the original work is properly cited.
The theoretical and experimental investigation of polycrystalline electrode surfaces provides valuable information for the understanding of the performance for many types of real electrochemical devices. Fundamental concepts like the structure of the electrochemical double layer, double layer capacitance, Faradaic reaction rate equations and others have been derived and verified experimentally for single crystal or liquid metal electrodes, see e.g.1–3 In either case, the physicochemical properties of these electrodes surfaces can be idealized as entirely homogeneous. In contrast, real solid metal electrodes are most often polycrystalline. Surfaces of polycrystalline electrodes in general exhibit a complex unstructured and random pattern of facets with different crystallographic orientation as sketched in Fig. 2 left. It is well known that the electron work function depends on the crystallographic orientation of a surface.4,5 As a consequence, the differential capacity and the corresponding potential of zero charge (PZC) of the surface in contact to an electrolyte depend on the crystallographic orientation as well, cf.6–8
In this paper we propose a mathematically sound approach which allows to derive characteristics of polycrystalline electrodes from a thermodynamically well founded model. We focus on double layer capacitance and potential of zero charge as equilibrium properties. In particular, we aim at the characterization of an ideal polycrystalline surface where typical facet size, characterized by the diameter  , is large compared to a suitable reference length of the electrolyte. Here we always set the reference length for an aqueous electrolyte to
, is large compared to a suitable reference length of the electrolyte. Here we always set the reference length for an aqueous electrolyte to ![$1[\mathrm{nm}]$](https://content.cld.iop.org/journals/1945-7111/167/10/106512/revision2/jesab9ccaieqn4.gif) . For the ideal polycrystalline surface, the influence of edge effects related to facet boundaries can be neglected such that compact asymptotic equations defining potential of zero charge and potential dependent double layer capacitance can be derived. Numerical simulations of the spatial charge distribution in the boundary layers confirm that contributions from facet boundary effects indeed are marginal. Ultimately, we replace discrete facet configurations by probability distributions of facets with identical physical properties. This allows a very compact reformulation of the polycrystalline electrode properties in terms of convolution integrals.
. For the ideal polycrystalline surface, the influence of edge effects related to facet boundaries can be neglected such that compact asymptotic equations defining potential of zero charge and potential dependent double layer capacitance can be derived. Numerical simulations of the spatial charge distribution in the boundary layers confirm that contributions from facet boundary effects indeed are marginal. Ultimately, we replace discrete facet configurations by probability distributions of facets with identical physical properties. This allows a very compact reformulation of the polycrystalline electrode properties in terms of convolution integrals.
The development of the classical Gouy-Chapman-Stern-Grahame theory of the electrochemical double layer9,10 strongly relied on experimental measurements at mercury electrodes. Since these electrodes consist of a liquid metal, their clean surface in contact with an electrolyte typically can be considered as ideally smooth and physical homogeneous. Thus, when trying to transfer the theory from liquid to solid metal electrodes, first an awareness about the relevance of surface roughness and individual properties of surfaces facets of different crystallographic orientation needed to be established, cf.11 Valette and Harmelin12 first related careful capacity measurements of silver single crystal surfaces with the corresponding experimental results for polycrystalline silver electrodes. Although not explicitly written in Ref. 12, a relation for the capacity of the polycristalline surface was assumed that is the same as the limiting Eq. 3 below. In Ref. 13 different equivalent circuits for the representation of polycrystalline surfaces are proposed and analyzed by comparison with experimental data. The comparison supported a model related to Eq. 3. In Ref. 14 the range of applicability of 3 is discussed based on a spatially resolved analysis according to the Gouy-Chapman-Stern-Grahame model in Ref. 15. Moreover, it was shown that in the limit of vanishing size of the facets, the alternative equivalent circuit model of Ref. 13 is approached.
To describe a polycrystalline electrode-electrolyte interface, we apply in this work a model on the basis of continuum non-equilibrium thermo-electrodynamics that was derived and analyzed in Refs. 16–19. For a review of the prior development of generalized Nernst-Planck models, we refer to Ref. 20. The model applied here incorporates the pressure in the electrolyte as a variable and the momentum balance, which ensures thermodynamic consistency. Further, it allows to account for volume exclusion effects of all species, and especially of the solvation effect. In Ref. 17 it has been shown that this model is capable to predict qualitatively and in the correct quantitative range the differential capacity of single crystal electrodes with respect to the applied voltage and with respect to the salt concentration. For further discussion of the underlying model, we refer to the supplementary material (available online at stacks.iop.org/JES/167/106512/mmedia). For a single crystal electrode in contact with a non-adsorbing electrolyte, the capacity is exclusively due to the charging of the double layer. As long as the bulk electrolyte concentration is not too large, it shows the typical symmetric camel shape capacitance curve. Figure 1 (left) demonstrates the good agreement between the model predictions and the experimental measurements. The potential of zero charge (PZC) is located at the local capacity minimum and does not change with salt concentration. The absolute value of the PZC depends on the crystallographic orientation of the metal surface. Between differently oriented surfaces, the difference of their respective PZC values are known to correspond well to the differences of the electron work function.5,17 In addition, we can observe in Fig. 1 (left) the expected behavior such that for increasing bulk salt concentration the local minimum at the PZC becomes less deep and eventually vanishes, leading to a single maximum capacity curve.
Figure 1. Left: Computed boundary layer capacity of a single crystal surface for different concentrations of a non-adsorbing electrolyte. Right: Measured capacitance at a (110) surface of Ag (Fig. 3a of Ref. 6, reprinted the permission of Elsevier).
Download figure:
Standard image High-resolution imageFor a polycrystalline electrode surface, we derive expressions of the double layer charge, the potential of zero charge, and the differential capacitance and compare these to the (theoretically) more simple and well understood case of single crystal surfaces. Within some reasonable scaling it is a remarkable and non-obvious feature of the resulting model that double layer charge, and subsequently the potential of zero charge, as well as the differential capacity can be determined from solutions of an algebraic equation system, rather than solving space dependent differential equations. This even holds true for a stochastic description of a polycrystalline electrode surface, which we show within this work.
The inhomogeneity of the surface capacitance is commonly believed to cause so called "frequency dispersion" in electrochemical impedance spectroscopy, cf.,21 and the effects of surface inhomogeneity can be expected to have even more serious impact in the presence of Faradayic reactions. We plan to investigate these non-equilibrium aspects in follow-up research.
Outline. In the next section, we give a brief overview over our general approach and the main results. Next, we summarize the general equilibrium conditions of the applied continuum model and appropriate material models from Refs. 17, 19. In the following , we apply the model to solid electrode surfaces. The differential capacity of a single crystal surface is introduced and a model for polycrystalline surfaces is developed. Then, there is a section devoted to an assessment of the results obtained by numerical solution of the boundary value problem in 2D and in 3D for periodically patterned surfaces of finite size facets. In particular, the limiting behavior for extreme facet size parameters and the influence of surface roughness on the length scale of the facets are analyzed. We proceed with a discussion of the polycrystal model in the case of large facet size, including the effects of adsorption and the stochastic description of polycrystalline surfaces. We close with some concluding remarks .
General Approach and Main Results
We model the polycrystalline electrode surface by a regular surface pattern with N > 1 different types of facets. Each facet corresponds to certain crystallographic orientation. To each facet Σi, 1 ≤ i ≤ N, we assign a value of the electron work function and its surface fraction  with
with  , where
, where  denotes the surface area. We show, based on our thermodynamic model of Section 3, that the electric potential
denotes the surface area. We show, based on our thermodynamic model of Section 3, that the electric potential  on each facet Σi is related to the work function, or in our notation, to the chemical potential
on each facet Σi is related to the work function, or in our notation, to the chemical potential  of surface electrons of the respective surface orientation. The polycrystalline electrode surface
of surface electrons of the respective surface orientation. The polycrystalline electrode surface  is then considered to be in contact to some electrolytic solution in the volume domain
is then considered to be in contact to some electrolytic solution in the volume domain  . The electrolyte in thermodynamic equilibrium is described by an improved Poisson-Boltzmann systema
, i.e. the system
. The electrolyte in thermodynamic equilibrium is described by an improved Poisson-Boltzmann systema
, i.e. the system
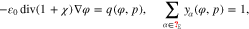
where yα refers to the species mole fractions and p is the pressure. On the electrode surface, facet-wise constant boundary values for the electric potential are prescribed. Then, the adjacent space charge layer in the electrolyte can be computed numerically. Figure 2 (right, bottom) shows a typical 3D numerical computation of the electric potential iso-surfaces in the electrolyte  for a periodical checkerboard electrode surface. Based on such numerical solution we can compute, (i) the overall double layer charge
for a periodical checkerboard electrode surface. Based on such numerical solution we can compute, (i) the overall double layer charge  as function of the applied voltage E, (ii) the potential of zero charge
as function of the applied voltage E, (ii) the potential of zero charge  of a polycrystalline electrode-electrode interface, and (iii) the corresponding double layer capacity
of a polycrystalline electrode-electrode interface, and (iii) the corresponding double layer capacity  (see Fig. 2 (right, top) ). This approach is valid for arbitrary geometries and facet sizes. The only assumption here is that the intersecting lines between two facets do not have independent thermodynamic quantities.
(see Fig. 2 (right, top) ). This approach is valid for arbitrary geometries and facet sizes. The only assumption here is that the intersecting lines between two facets do not have independent thermodynamic quantities.
Figure 2. Sketch of the facet structure of a polycrystalline surface (left) and isosurfaces of the electric potential in the electrolyte from 3D-FEM computation (right). The surface consists of a periodic checkerboard pattern of equally sized facets. The corresponding double layer charge  and capacity
and capacity  as function of the applied voltage E.
as function of the applied voltage E.
Download figure:
Standard image High-resolution imageFor a non-adsorbing electrolyteb we have in general
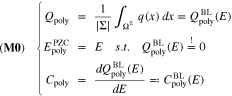
subject to the coupled equation system 1.
A scale analysis of the boundary value problem yields two characteristic length scales of the model: the typical diameter  of the facets Σi and a reference length
of the facets Σi and a reference length  related to the non-dimensionalization of the Poisson equation in 1. This reference length is in the order of the Debye length
related to the non-dimensionalization of the Poisson equation in 1. This reference length is in the order of the Debye length  of the electrolyte, however, independent of the bulk electrolyte concentration. We found that
of the electrolyte, however, independent of the bulk electrolyte concentration. We found that ![${L}^{{ref}}=1[\mathrm{nm}]$](https://content.cld.iop.org/journals/1945-7111/167/10/106512/revision2/jesab9ccaieqn21.gif) is a proper scaling for for aqueous solutions, which is used throughout the manuscript.
is a proper scaling for for aqueous solutions, which is used throughout the manuscript.
If the facet or facet diameter  is large compared to
is large compared to ![$1[\mathrm{nm}]$](https://content.cld.iop.org/journals/1945-7111/167/10/106512/revision2/jesab9ccaieqn23.gif) , the double layer charge
, the double layer charge  can be obtained as a sum of the single facet boundary layer charges
can be obtained as a sum of the single facet boundary layer charges  , weighted by their respective surface fraction
, weighted by their respective surface fraction  . Subsequently, the potential of zero charge
. Subsequently, the potential of zero charge  can be determined from an algebraic equation system, and the differential capacity
can be determined from an algebraic equation system, and the differential capacity  obeys also an algebraic representation, i.e.
obeys also an algebraic representation, i.e.
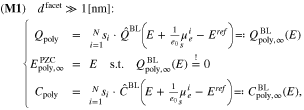
where  and
and  are nonlinear functions specified in Section 3. The construction of the capacity
are nonlinear functions specified in Section 3. The construction of the capacity  of a polycristalline electrode in the case of facets with two equal surface fractions is illustrated in Fig. 3 (right). Remarkably, the potential of zero charge
of a polycristalline electrode in the case of facets with two equal surface fractions is illustrated in Fig. 3 (right). Remarkably, the potential of zero charge  of this polycrystalline surface in this case is located at the capacity maximum and not at a local minimum of the curve!
of this polycrystalline surface in this case is located at the capacity maximum and not at a local minimum of the curve!
Figure 3. Double layer charge and differential capacitance of a polycrystalline electrode determined from 3 with  .
.
Download figure:
Standard image High-resolution imageFor realistic polycrystalline electrodes, the consecutive labeling of all facets might be impractical. We propose thus a stochastic description of the surface in terms of a probability density f, modeling the surface fraction as function of the surface chemical potential of electrons. We derive in the limit ![$1[\mathrm{nm}]\ll {d}^{\mathrm{facet}}$](https://content.cld.iop.org/journals/1945-7111/167/10/106512/revision2/jesab9ccaieqn34.gif) the model
the model

Figure 4 (left) shows two different distributions functions of the surface fraction and Fig. 4 (right) the corresponding differential capacitance. We observe, that a sharp peak of the distribution function leads to a capacitance close to that of a single crystal surface. More general, in Section 6.4, we see that a discrete distribution of PZC values can be well approximated by a distribution function consisting of a finite number of clearly separated peaks. Increasing the standard deviation of the normal-distribution, results in stronger smearing of the capacitance over the potential range such that the capacity minima actually disappear, while the overall shape broadens. We discuss this aspect more in detail within this work.
Figure 4. Left: densities of the surface chemical potential  given by normal distributions with different standard deviation. Right: Capacity curves for the respective densities (solid —) and for the planar single crystal case (dotted line ⋯). For large σ, the the capacity has a single maximum unlike the camel shape for perturbations of the single crystal surface by small σ.
given by normal distributions with different standard deviation. Right: Capacity curves for the respective densities (solid —) and for the planar single crystal case (dotted line ⋯). For large σ, the the capacity has a single maximum unlike the camel shape for perturbations of the single crystal surface by small σ.
Download figure:
Standard image High-resolution imageIn the opposite limiting case of vanishing facet diameter  , the potential of zero charge is given as the surface fraction weighted average of the corresponding single crystal quantities, while the charge
, the potential of zero charge is given as the surface fraction weighted average of the corresponding single crystal quantities, while the charge  and the capacity
and the capacity  remain non-linear expressions identical to the ones of a typical single crystal surface, i.e.
remain non-linear expressions identical to the ones of a typical single crystal surface, i.e.
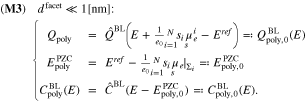
Continuum Model
We use a continuum model that is based on a coupled volume-surface description of charged and possibly reacting mixtures coupled with the electromagnetic field. Detailed description of the modeling can be found in Refs. 16, 17, 19. Following the standard approach in non-equilibrium thermodynamics, the modeling consists of two steps. The fist step is universal, i.e. material independent, leading to the general model equations in Section 3.1. In the second step, which is material dependent, non-negative entropy production is guaranteed by application of an entropy principle, cf.19 After this, specific behavior of a certain considered material is described in terms of free energy densities in each volume domain and on the surface. We summarize the free energy densities derived in Refs. 16, 17 in Section 3.2. In general these free energy densities have to be derived from models of different character on an underlying finer scale.
In this model, as a convention, each quantity defined in the volume has a corresponding quantity confined to the electrode surface Σ. We use the same letters for bulk and surface quantities and indicate the surface quantities by an underset "s". For a surface Σ, we choose the orientation of the a normal vector that we denote by  . Then, we denote the adjacent bulk volumes by
. Then, we denote the adjacent bulk volumes by  and
and  , such that
, such that  is the outer normal of
is the outer normal of  . For a generic function u in the volume, we can define the tracec
and jump at Σ by
. For a generic function u in the volume, we can define the tracec
and jump at Σ by
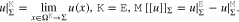
Bulk positions far away from the surface Σ are denoted by  and the evaluation of some function u(x) the bulk points is denoted by
and the evaluation of some function u(x) the bulk points is denoted by  .
.
Description of mixtures. To refer to the constituents of a mixture on the surface Σ or the adjacent volume domains  , we use according index sets
, we use according index sets  , resp.
, resp.  of species. For each constituent, we denote the molecular mass by mα, the partial molar volume by
of species. For each constituent, we denote the molecular mass by mα, the partial molar volume by  , the charge number by zα, and the number density of particles per
, the charge number by zα, and the number density of particles per  by nα, where
by nα, where  or
or  , respectively. Then, we introduce the partial mass density ρα = mα nα. The free charge density is (
, respectively. Then, we introduce the partial mass density ρα = mα nα. The free charge density is ( )
)
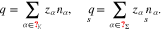
General assumptions. We restrict our considerations to the isothermal case, where the temperature T enters the equations only as a constant parameter and on the surface there holds  . Moreover, we only consider the electrostatic case where the electric field is given as
. Moreover, we only consider the electrostatic case where the electric field is given as  . Excluding surface dipoles, the electric potential φ is continuous at the surface, i.e. we can set
. Excluding surface dipoles, the electric potential φ is continuous at the surface, i.e. we can set  . Within this work, we assume a simple material model with a constant dielectric susceptibility χ. In the following, we neglect gravitation and restrict the presentation to planar interfaces with no tangential transport on the surface.
. Within this work, we assume a simple material model with a constant dielectric susceptibility χ. In the following, we neglect gravitation and restrict the presentation to planar interfaces with no tangential transport on the surface.
Model equations
The general continuum model relies on universal, i.e. material independent balance equations in the volume domains and on the surface. However, the model equations contain several material dependent constitutive quantities which need appropriate modeling. We summarize here the equilibrium equations that result from the much more complex modeling framework.19 The key ingredients for the material modeling are the free energy densitiesd
ρψ,  in the bulk and on the volume, respectively. Due to the assumed constant dielectric susceptibility, the free energy densities are of the rather general structure
in the bulk and on the volume, respectively. Due to the assumed constant dielectric susceptibility, the free energy densities are of the rather general structure
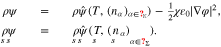
The chemical potentials are defined as
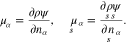
By means of Gibbs-Duhem relations, we introduce the material pressure p and surface tension  as
as
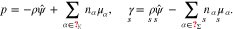
Equilibrium bulk equations. The equilibrium of an incompressible mixture in a bulk domain Ω is characterized by
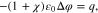
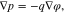
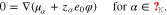
The Poisson Eq. 11a determines the electric potential, 11b is the momentum equation, 11c states that the electrochemical potentials of all species are constant in equilibrium. We remark that these equations are not independent, but 11a and 11c together with 10(left) already imply 11b.
Equilibrium surface equations. On the surface Σ between the bulk domains  , for
, for  , the equilibrium is given by
, the equilibrium is given by
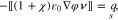
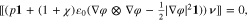
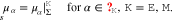
Specific material models
Suitable free energy densities for the volume domains  of the electrolyte,
of the electrolyte,  of the metal and for the metal-electrolyte surface Σ have been derived in Refs. 16–18 and are summarized here. The free energy densities account for the entropy of mixing and elastic effects due to the finite size of the molecules. For simplicity, we consider only the incompressible limit case. The rather simplistic assumption of constant surface chemical potential of electrons turns out to be just the appropriate way to capture a central feature of metals. It results in the necessary constraint that excess charge is stored on the metal surface.
of the metal and for the metal-electrolyte surface Σ have been derived in Refs. 16–18 and are summarized here. The free energy densities account for the entropy of mixing and elastic effects due to the finite size of the molecules. For simplicity, we consider only the incompressible limit case. The rather simplistic assumption of constant surface chemical potential of electrons turns out to be just the appropriate way to capture a central feature of metals. It results in the necessary constraint that excess charge is stored on the metal surface.
Not included into the free energy density of the electrolyte are Debye-type electrostatic interactions between ions. As a consequence, the model cannot be expected to reproduce typical square-root behavior in the limit of strong dilution. For the determination of interface capacitance however, the most relevant regime is the opposite limit of concentrated solutions.
Bulk electrolyte material model in  . The electrolyte in the domain
. The electrolyte in the domain  is a mixture of several species, one of them being the solvent that we refer to by the index α = 0. The index set of the electrolytic species is denoted by
is a mixture of several species, one of them being the solvent that we refer to by the index α = 0. The index set of the electrolytic species is denoted by  . The mole fractions yα of the constituents are defined as
. The mole fractions yα of the constituents are defined as
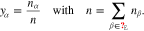
In many solvents, ions are solvated, meaning that a number κα of solvent molecules are bound into a solvation shell around a center ion. Thus, the partial volume  of a solvated ion in the electrolyte is typically much larger than the partial volume of the solvent
of a solvated ion in the electrolyte is typically much larger than the partial volume of the solvent  . Consequently, we consider the electrolyte as an incompressible liquid mixture of free solvent molecules, undissociated species and solvated ions.e
The incompressibility of the mixture is characterized by the constraint
. Consequently, we consider the electrolyte as an incompressible liquid mixture of free solvent molecules, undissociated species and solvated ions.e
The incompressibility of the mixture is characterized by the constraint

The chemical potentials for an ideal mixture of solvated ions according to Ref. 17 are in the incompressible limitf
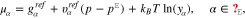
with reference Gibbs free energy  , with a constant reference energy
, with a constant reference energy  .
.
Let  ,
,  and
and  denote the values of the mole fractions, the electric potential and the pressure at some bulk point
denote the values of the mole fractions, the electric potential and the pressure at some bulk point  in
in  . In equilibrium, the constant electrochemical potentials according to 11c and the material model 15 then imply for the bulk mole fractions
. In equilibrium, the constant electrochemical potentials according to 11c and the material model 15 then imply for the bulk mole fractions
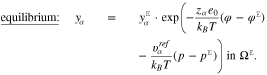
Note that the pressure p in the electrolytic boundary layer can be expressed as a function of the potential difference φ −  by solving the condition 13 with the representations 16, i.e. the non-linear implicit relation
by solving the condition 13 with the representations 16, i.e. the non-linear implicit relation
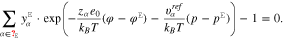
yields  .
.
Bulk metal material model in  . We consider a metal in the domain
. We consider a metal in the domain  as a binary mixture of positive metal ions M and free electrons e with ze = −1, i.e.
as a binary mixture of positive metal ions M and free electrons e with ze = −1, i.e.  . For the metal bulk free energy density, we adopt the Sommerfeld model22 and assume incompressibility, cf.17 We do not specify the model here, because as a consequence of the following surface material model, it turns out that the metal bulk does not influence any of the results in this paper and therefore can be ignored.
. For the metal bulk free energy density, we adopt the Sommerfeld model22 and assume incompressibility, cf.17 We do not specify the model here, because as a consequence of the following surface material model, it turns out that the metal bulk does not influence any of the results in this paper and therefore can be ignored.
Surface material model on Σ. The surface Σ between the domains  and
and  is considered as mixture of the surface metal ions, surface electrons, electrolytic adsorbates and possibly reaction products of the aforementioned species. The index set of surface constituents is denoted by
is considered as mixture of the surface metal ions, surface electrons, electrolytic adsorbates and possibly reaction products of the aforementioned species. The index set of surface constituents is denoted by  with
with  . Note that we consider on the surface also a solvation effect, whereby each adsorbed ion binds
. Note that we consider on the surface also a solvation effect, whereby each adsorbed ion binds  solvent molecules which propagates into the partial molar area
solvent molecules which propagates into the partial molar area  .
.
We adopt the surface free energy model proposed in Ref. 17. In particular, the surface chemical potential of the electrons is assumed to be a constant value depending only on the material and the crystallographic surface orientation. We propose to choose this value related to the electron work function WΣ of the surface Σ. Analogously to the metal volume, we have an incompressibility constraint on the surface stating  , where
, where  is the partial area of surface metal ions. On the electrolyte side, we have to account for adsorption from the volume. Since the surface is not necessarily completely covered with adsorbates, we introduce a number density of surface vacancies via
is the partial area of surface metal ions. On the electrolyte side, we have to account for adsorption from the volume. Since the surface is not necessarily completely covered with adsorbates, we introduce a number density of surface vacancies via
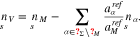
Then, we define the surface fractions of vacancies and adsorbates by
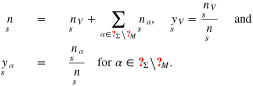
The chemical potentials of the surface species are
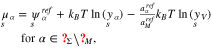
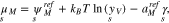
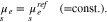
With respect to the same bulk point in the electrolyte as above, i.e. the values  ,
,  and
and  , the surface mole fraction of the vacancies, the electrolytic adsorbates, and the surface reaction products, have the representations in terms of the potential difference
, the surface mole fraction of the vacancies, the electrolytic adsorbates, and the surface reaction products, have the representations in terms of the potential difference  ,
,
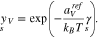
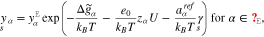
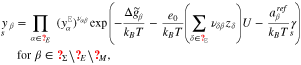
where the amount of adsorbates and reaction products on the surface is controlled by the corresponding Gibbs energies defined by
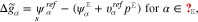
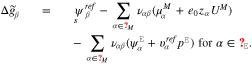
The above representations and the definition 19 of the surface mole fractions yield an algebraic equation which determines the surface tension  as a function of U.
as a function of U.
Model Application for Solid Electrode Surfaces
It is well known that at the surface Σ between a metal and an electrolyte a charged double layer exists, which decays into the electrolyte bulk electrolyte. For Poisson–Boltzmann and Gouy-Chapman type models the space charge layer width is in the order of the Debye length

where c is the bulk salt concentration. However, for the incompressible mixture model of Section 3.2, which incorporates solvation effect of the ionic species, we find that the space charge layer width is in the order of ![${L}^{{ref}}=1[\mathrm{nm}]$](https://content.cld.iop.org/journals/1945-7111/167/10/106512/revision2/jesab9ccaieqn100.gif) , almost independent of the bulk concentration c, however, dependent on the applied voltage. Figure 5 displays the computed space charge layer, i.e. the cation and anion densities nα as function of the electrode distance z for an applied voltage of
, almost independent of the bulk concentration c, however, dependent on the applied voltage. Figure 5 displays the computed space charge layer, i.e. the cation and anion densities nα as function of the electrode distance z for an applied voltage of  V.
V.
Figure 5. Numerical computation of the space charge layer in front of a single crystal metal surface at an applied voltage of  for various bulk concentrations c.
for various bulk concentrations c.
Download figure:
Standard image High-resolution imageIf the dimension of the considered experimental setup is considerably larger than ![$1[\mathrm{nm}]$](https://content.cld.iop.org/journals/1945-7111/167/10/106512/revision2/jesab9ccaieqn103.gif) , say in the range of several
, say in the range of several  , it often is reasonable to consider the surface Σ as an infinite planar surface and the electrolyte domain
, it often is reasonable to consider the surface Σ as an infinite planar surface and the electrolyte domain  as a half space. We chose the coordinates (x, y, z) such that Σ corresponds to the plane z = 0. Since we are only interested in the boundary layer, we can choose a sufficiently large zE and approximate the electrolyte domain as
as a half space. We chose the coordinates (x, y, z) such that Σ corresponds to the plane z = 0. Since we are only interested in the boundary layer, we can choose a sufficiently large zE and approximate the electrolyte domain as ![${{\rm{\Omega }}}^{{\mathtt{E}}}={\rm{\Sigma }}\times [0,{z}^{{\mathtt{E}}}]$](https://content.cld.iop.org/journals/1945-7111/167/10/106512/revision2/jesab9ccaieqn106.gif) .
.
Planar single crystal surface
Given the simple geometric setting and assuming the surface to be homogeneous in space, all quantities in the electrolyte can only depend on the spatial coordinate normal to Σ. Then, we define the boundary layer- and the surface charge density by
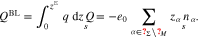
In equilibrium, both quantities are completely determined by the potential difference  It is a remarkable feature of the applied material model in Section 3.2 that it is possible to determine the boundary layer charge density
It is a remarkable feature of the applied material model in Section 3.2 that it is possible to determine the boundary layer charge density  as function of Ug
without needing to spatially resolve the bulk Eqs. 11–12, i.e.
as function of Ug
without needing to spatially resolve the bulk Eqs. 11–12, i.e.
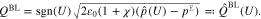
where  is the material pressure determined from 17. Moreover, all surface mole fractions are determined according to 21 and we get for the surface charge density
is the material pressure determined from 17. Moreover, all surface mole fractions are determined according to 21 and we get for the surface charge density
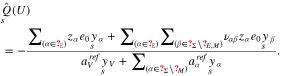
Thus, we can introduce the differential capacity as
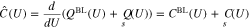
Under the standard assumption that the potential difference between an ideally non-polarizable reference electrode and the bulk electrolyte remains constant under potential variations, it is possible to show17 that
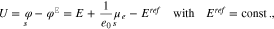
where E is the applied voltage in a three electrode setup,  the surface chemical potential of electrons, and
the surface chemical potential of electrons, and  a constant which depends on the actual reference electrode. For a specific surface Σ, the differential capacity in the absolute scale E is given by an appropriate shift of 27, i.e.
a constant which depends on the actual reference electrode. For a specific surface Σ, the differential capacity in the absolute scale E is given by an appropriate shift of 27, i.e.
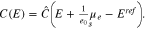
Modeling of planar polycrystal surfaces
We consider now a planar surface Σ which is composed of N facets Σi, i.e.  as sketched in Fig. 2. We assume finite size surfaces patterns that can be periodically extended to the whole plane. We denote by
as sketched in Fig. 2. We assume finite size surfaces patterns that can be periodically extended to the whole plane. We denote by  the area of the facet Σi whereby the total area of Σ is
the area of the facet Σi whereby the total area of Σ is  and surface fraction
and surface fraction  . We make the assumption
. We make the assumption
- The facet boundaries
 for
for  constitute no independent thermodynamic entities.
constitute no independent thermodynamic entities.
Thus, each facet Σi can be treated as a finite size planar single crystal surface, and we can apply the material model of Section 3.2 on each facet Σi separately. Since the surface density of metal ions depends on the cystallographic orientation of the surface, the material parameter aM is different for each individual facet Σi. As a consequence, in the absence of adsorption to the surface, the surface tension  differs between the facets Σi.h
In addition, we have to assign to each facet Σi a constant value of
differs between the facets Σi.h
In addition, we have to assign to each facet Σi a constant value of  , which has to be related to the electron work function on a surface of the respective cystallographic orientation. Because all facets are connected by electric conductors, the electrochemical potential of the electrons is constant over all grains in the metal
, which has to be related to the electron work function on a surface of the respective cystallographic orientation. Because all facets are connected by electric conductors, the electrochemical potential of the electrons is constant over all grains in the metal  , i.e.
, i.e.
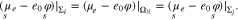
Between each two surfaces, we thus have the pairwise potential difference
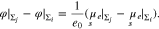
Patterned planar surface. As in the single crystal case before, we can expect boundary layers that decay exponentially from the surface Σ into the electrolyte bulk. The length scale of the boundary layer is given by the Debye length according to 23 and the electrolyte bulk can be characterized by certain constant far field values  ,
,  and
and  in a distance from the surface that is large compared to
in a distance from the surface that is large compared to  . We assume that the electrolyte in
. We assume that the electrolyte in  is not influenced by any other boundary layer than the one at Σ. Given the applied potential E −
is not influenced by any other boundary layer than the one at Σ. Given the applied potential E −  we set
we set  , which corresponds to an ideally polarizable reference electrode. Then, the state in the electrolyte in
, which corresponds to an ideally polarizable reference electrode. Then, the state in the electrolyte in  is given by the the generalized Poisson-Boltzmann boundary value problem similar to Refs. 16, 17, 19
is given by the the generalized Poisson-Boltzmann boundary value problem similar to Refs. 16, 17, 19
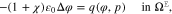
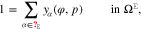
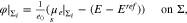
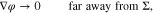
where yα(φ, p) is given by 16 for  .
.
Given a solution of 32 in  , the boundary layer charge q is determined by yα according to 7 and 14. The surface charge density can be calculated by 26 on each facet Σi separately and we get
, the boundary layer charge q is determined by yα according to 7 and 14. The surface charge density can be calculated by 26 on each facet Σi separately and we get
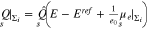
Thus for the surface Σ, we conclude
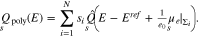
Upon solution of the boundary value problem, the boundary layer charge density is computed from
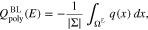
Finally, the total surface charge is  and the differential capacity of the patterned surface is computed by taking the derivative with respect to the applied potential E.
and the differential capacity of the patterned surface is computed by taking the derivative with respect to the applied potential E.
Ensemble of planar single crystal surfaces. The total boundary layer charge density can be decomposed into the contributions adjacent to the different facets Σi, viz.
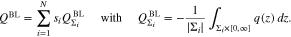
Since boundary effects propagate into the interior with a length scale in the order of the chosen reference length of the electrolyte, boundary effects due to the finite size of Σi can be neglected once the characteristic facet diameter is sufficiently large, i.e. ![$1[\mathrm{nm}]\ll {d}^{\mathrm{facet}}$](https://content.cld.iop.org/journals/1945-7111/167/10/106512/revision2/jesab9ccaieqn134.gif) . Then, the charge density in front of Σi is well approximated by the boundary layer charge 25 at a planar single crystal with the same material parameters as Σi, i.e.
. Then, the charge density in front of Σi is well approximated by the boundary layer charge 25 at a planar single crystal with the same material parameters as Σi, i.e.
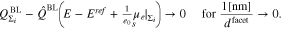
Thus, in the limit of large facets, the boundary layer charge density  of the polycrystal is given by the according density of an ensemble of non-interacting (infinitely large) planar single crystal surfaces, all in contact with the same electrolyte, viz.
of the polycrystal is given by the according density of an ensemble of non-interacting (infinitely large) planar single crystal surfaces, all in contact with the same electrolyte, viz.
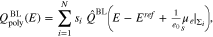
The boundary layer capacity related to 38 is given by 3. As 33 can be applied independent of the size of  , we conclude
, we conclude
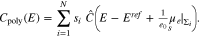
The potential of zero charge EPZC is determined from Eq. 37, i.e.  . Intuitively one would expect that the potential of zero charge EPZC is determined as
. Intuitively one would expect that the potential of zero charge EPZC is determined as  . But since the functions
. But since the functions  are non-linear with respect to their argument, this does not hold, i.e. in general
are non-linear with respect to their argument, this does not hold, i.e. in general
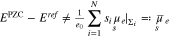
but

In Section 6 we provide some exemplary calculations showing the difference between  and
and  for several parameter variations.
for several parameter variations.
Surfaces of Finite Size Pattern and Approached Limit Relations
Given a polycrystalline surface with a finite size pattern of facets and their individual surface potentials, one has to expect that the capacitance can only be determined numerically from a spatially resolved FEM solution in  and that this solution depends on the specific geometry of the facets. In this section, we study numerically the capacitance for certain examples of surface patterns. We assume that the electrolyte consists of the solvent, denoted by S, and the anions A and cations C of a completely dissociated salt, i.e.
and that this solution depends on the specific geometry of the facets. In this section, we study numerically the capacitance for certain examples of surface patterns. We assume that the electrolyte consists of the solvent, denoted by S, and the anions A and cations C of a completely dissociated salt, i.e.  . For the numerical simulations we solve 35 with physical constants and material parameters as given in Table I. We chose the reference number density according to pure water. Since we apply the simplified model of a constant dielectric susceptibility, we chose a value for χ that refers to a strongly concentrated solution and thus is considerably lower than
. For the numerical simulations we solve 35 with physical constants and material parameters as given in Table I. We chose the reference number density according to pure water. Since we apply the simplified model of a constant dielectric susceptibility, we chose a value for χ that refers to a strongly concentrated solution and thus is considerably lower than  , cf. e.g.23
, cf. e.g.23
Table I. Physical constants and parameters used in the numerical simulations.
| dielectric constant |

|
| Boltzmann constant |

|
| elementary charge |

|
| Avogadro number |

|
| temperature |

|
| reference pressure |

|
| dielectric susceptibility | χ = 15 |
| charge number | −zA = zC = 1, zS = 0 |
| solvation number | κα = 10 |
| reference number density |

|
| bulk salt concentration |
![${c}^{{\mathtt{E}}}[\mathrm{mol}\,{{\rm{l}}}^{-1}]$](https://content.cld.iop.org/journals/1945-7111/167/10/106512/revision2/jesab9ccaieqn152.gif)
|
| specific volumes |

|
In order to keep the focus of this section sharp, we assume here that the electrolyte is non-adsorbing. If in addition also adsorption has to be take in to account, surface charge and surface capacity can be computed in purely algebraic manner by a post-processing step applying 34 and its derivative with respect to the applied potential, respectively.
Pattern of two equally sized facets
We consider first the most simple configuration of a symmetric bi-crystalline surface, where N = 2,  . We choose an average potential
. We choose an average potential  such that
such that  . On the surface, we thus have the boundary values
. On the surface, we thus have the boundary values  for i = 1, 2 with
for i = 1, 2 with  . The simplest realization of this configuration consists of a pattern of parallel stripes with alternating prescribed potential. Here, we let
. The simplest realization of this configuration consists of a pattern of parallel stripes with alternating prescribed potential. Here, we let  denote the width of the stripes. With an appropriate choice of the coordinate system, the boundary values can be described by a 1D-function such that
denote the width of the stripes. With an appropriate choice of the coordinate system, the boundary values can be described by a 1D-function such that

and periodic continuation. Accordingly, the potential and the charge density in the electrolyte domain z > 0 can be determined from a 2D-FEM computation by integration of the free charge q in space according to 35. The choice of the boundary values implies that in the far field the potential approaches  . Plots of the electric potential for
. Plots of the electric potential for  and an electrolyte with a bulk concentration of
and an electrolyte with a bulk concentration of  and the remaining parameters according to Table I are given in Fig. 6 (left). In the upper plot, where the facet size was chosen as
and the remaining parameters according to Table I are given in Fig. 6 (left). In the upper plot, where the facet size was chosen as  , one can observe that the piece-wise constant boundary data to a large extend propagates into the electrolyte and decays with increasing distance to the boundary. To the contrary, in the lower plot, where
, one can observe that the piece-wise constant boundary data to a large extend propagates into the electrolyte and decays with increasing distance to the boundary. To the contrary, in the lower plot, where  , the profile of the potential is dominated by facet boundary effects such that the regions of parallel iso-lines almost disappear.
, the profile of the potential is dominated by facet boundary effects such that the regions of parallel iso-lines almost disappear.
Figure 6. Left: profile of the electric potential for different diameters of the surface stripes. Right: capacity curves for different electrolyte concentrations, where solid lines (—) refer to the algebraic solution according to 3, FEM solution for facet size  is indicated by markers (+), and for
is indicated by markers (+), and for  by dashed lines (- - ).
by dashed lines (- - ).
Download figure:
Standard image High-resolution imageNext, the applied potential is varied in positive and in negative direction and the boundary value problem 32 is solved. From this solution, the free charge density q and  are computed. Figure 6 (right) shows the resulting capacity for different electrolyte concentrations in dependence of the facet size
are computed. Figure 6 (right) shows the resulting capacity for different electrolyte concentrations in dependence of the facet size  . We observe for increasing facet size
. We observe for increasing facet size  a convergence of the computed capacity curves to the algebraic solution 3. In particular, in the potential range outside of the lowest and the largest position of the maxima, the algebraic expression 3 is always a good characterization of the polycrystalline surface, independent of the facet size. Figure 6 also shows that the convergence depends on the electrolyte bulk concentration. We thus repeat the numerical experiment over a larger range of parameter variation, such that the bulk concentration is varied between
a convergence of the computed capacity curves to the algebraic solution 3. In particular, in the potential range outside of the lowest and the largest position of the maxima, the algebraic expression 3 is always a good characterization of the polycrystalline surface, independent of the facet size. Figure 6 also shows that the convergence depends on the electrolyte bulk concentration. We thus repeat the numerical experiment over a larger range of parameter variation, such that the bulk concentration is varied between  and
and  and the facet diameter is changed between
and the facet diameter is changed between  and
and  . We observe in Fig. 7 that while the behavior with respect to the bulk concentration is not monotonous, in any case the approximation error of 3 in the maximum norm can be bounded by some term proportional to the inverse of
. We observe in Fig. 7 that while the behavior with respect to the bulk concentration is not monotonous, in any case the approximation error of 3 in the maximum norm can be bounded by some term proportional to the inverse of  .
.
Figure 7. Approximation error of 3 over the characteristic diameter  of the facets for the symmetric bi-crystal and various electrolyte concentrations.
of the facets for the symmetric bi-crystal and various electrolyte concentrations.
Download figure:
Standard image High-resolution imageIn addition, 3D-FEM simulations with a checkerboard pattern of the surface were performed where the boundary values are given by periodic continuation of
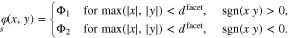
The observations from the 3D computations are analogous as for the 2D case. Since for given  , the length of the contact lines in the checkerboard pattern is double compared to the striped pattern represented by the 2D case, convergence for increasing facet size is a bit slower here. Together, the 2D and the 3D results indicate that the shape of the facets is not relevant as long as the facet diameter
, the length of the contact lines in the checkerboard pattern is double compared to the striped pattern represented by the 2D case, convergence for increasing facet size is a bit slower here. Together, the 2D and the 3D results indicate that the shape of the facets is not relevant as long as the facet diameter  is sufficiently large compared to a reference length in the order of
is sufficiently large compared to a reference length in the order of ![$1[\mathrm{nm}]$](https://content.cld.iop.org/journals/1945-7111/167/10/106512/revision2/jesab9ccaieqn178.gif) . We conclude that already the covered surface fraction of the facets and the corresponding single crystal capacities fully determine the capacity of a polycrystalline surface of sufficiently large facet size.
. We conclude that already the covered surface fraction of the facets and the corresponding single crystal capacities fully determine the capacity of a polycrystalline surface of sufficiently large facet size.
As FEM simulations in 3D are computationally expensive, we used anisotropic grids with a mesh grading with respect to the a-priori known structure of the potential, see Fig. 8. To check that the grid is sufficiently fine, we compared the resulting capacity curves from numerical solutions of the boundary value problem 32 on different refinement levels of the initial mesh. Refined meshes on the refinement levels 3, 4 and 5 consisted of 2 601, 18 513 and 139 425 nodes, respectively. Figure 8 shows the convergence of the computed capacity curves when refining the mesh.
Figure 8. Left: numerical grid on refinement level 3, as used for computation in Fig. 2. Right: computed capacity curves for different levels of grid refinement.
Download figure:
Standard image High-resolution imageCharacterization of PZC and limiting behavior
In the previous section, we did not discuss the PZC for the patterned polycrystalline surface. The reason is that due to the symmetry, i.e.  , it always coincides with the chosen reference potential. In order to introduce some asymmetry, we slightly modify the configuration to N = 2,
, it always coincides with the chosen reference potential. In order to introduce some asymmetry, we slightly modify the configuration to N = 2,  ,
,  , and again set
, and again set  . For a 2D-FEM simulation of this configuration, we choose
. For a 2D-FEM simulation of this configuration, we choose
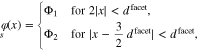
with periodic continuation of the boundary data. As in the previous example, we again observe that the capacity of the patterned surface approaches 3 for large facet sizes  , see Fig. 9 (left). From the computed boundary charge as a function of the applied potential according to 35, we can now determine the potential of zero charge of the patterned surface with finite
, see Fig. 9 (left). From the computed boundary charge as a function of the applied potential according to 35, we can now determine the potential of zero charge of the patterned surface with finite  . We observe that for a fixed facet size
. We observe that for a fixed facet size  , the PZC is not constant but increases with the bulk electrolyte solution, cf. Fig. 9 (right). Moreover, the potential range, in which the PZC varies with respect to the bulk concentration, gets wider for increasing
, the PZC is not constant but increases with the bulk electrolyte solution, cf. Fig. 9 (right). Moreover, the potential range, in which the PZC varies with respect to the bulk concentration, gets wider for increasing  . As a limit for
. As a limit for  , the PZC reaches the values we get from the surface fraction weighted averaging of single crystals according to 3. Since the capacity of a planar single crystal is approximately quadratic at its PZC, the boundary layer charge behaves almost cubic. Thus, one should not expect, that the linear combination of single crystal capacities would attain its PZC at the respective linear combination of the individual PZCs.
, the PZC reaches the values we get from the surface fraction weighted averaging of single crystals according to 3. Since the capacity of a planar single crystal is approximately quadratic at its PZC, the boundary layer charge behaves almost cubic. Thus, one should not expect, that the linear combination of single crystal capacities would attain its PZC at the respective linear combination of the individual PZCs.
Figure 9. Left: capacity curves for  electrolyte and different facet size parameters (dashed lines - - ). Limits for large facet diameter (blue, solid —) and vanishing facet diameter (red, solid —). Right: lines show the position of the PZC of the patterned surface in dependence of the facet size
electrolyte and different facet size parameters (dashed lines - - ). Limits for large facet diameter (blue, solid —) and vanishing facet diameter (red, solid —). Right: lines show the position of the PZC of the patterned surface in dependence of the facet size  for different bulk concentrations. The circles on the to indicate the values of
for different bulk concentrations. The circles on the to indicate the values of  according to 3 that are approached for
according to 3 that are approached for  and the dashed line refers to
and the dashed line refers to  according to 5.
according to 5.
Download figure:
Standard image High-resolution imageIn addition, another limit is of interest, however more from a theoretical point of view. Let us consider  , although a pattern at the atomic length scale or even blow that scale cannot be realized in practice. We observe, that for
, although a pattern at the atomic length scale or even blow that scale cannot be realized in practice. We observe, that for  , the capacity curve changes from the three-maxima shape according to 3 into the typical two-maxima or camel shape that is well known from the planar single crystal. In fact, for
, the capacity curve changes from the three-maxima shape according to 3 into the typical two-maxima or camel shape that is well known from the planar single crystal. In fact, for  , the capacity converges to the capacity of a planar single crystal surface where the PZC is determined as the sum of the PZCs on the contributing facets weighted by their respective surface fraction
, the capacity converges to the capacity of a planar single crystal surface where the PZC is determined as the sum of the PZCs on the contributing facets weighted by their respective surface fraction  according to 5. Moreover, this limit of the PZC is independent of the bulk electrolyte concentration.
according to 5. Moreover, this limit of the PZC is independent of the bulk electrolyte concentration.
Surface roughness
Because of surface roughness, the actual surface area of real surfaces is larger compared to their ideally plain counterparts which are characterized by their so called visible surface area. As a measure of this effect, the surface roughness factor W is introduced as the quotient of the real surface area over the visible. Surface roughness appears on a large range of different length scales, from "physical inhomogeneity" on the atomic length scale to "geometric roughness" on a macroscopic scale of several  . A lot of attention was devoted to the analysis of "geometric" surface roughness which in experiments may be caused e.g. by electrode pre-treatment like polishing. In the context of electrochemical impedance analysis, roughness is then often analyzed in the framework of fractal geometry, where on the larger scales, an interaction of the boundary layer with bulk transport properties of electrolyte has to be expected.
. A lot of attention was devoted to the analysis of "geometric" surface roughness which in experiments may be caused e.g. by electrode pre-treatment like polishing. In the context of electrochemical impedance analysis, roughness is then often analyzed in the framework of fractal geometry, where on the larger scales, an interaction of the boundary layer with bulk transport properties of electrolyte has to be expected.
We want to concentrate on the effect of surface roughness on the boundary layer capacitance and therefore consider only deformations of an ideally plain surface that are on a length scale of the facet size  . We return to the setting of the symmetric bi-crystal of Section 5.1 and let the surface be given by
. We return to the setting of the symmetric bi-crystal of Section 5.1 and let the surface be given by
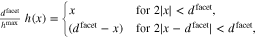
where the parameter  is the maximal elevation of the surface over the supporting pane, see Fig. 10. This results in a surface roughness factor of
is the maximal elevation of the surface over the supporting pane, see Fig. 10. This results in a surface roughness factor of
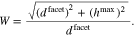
Figure 10. Electric potential for an electrolyte of  salt concentration in contact with a symmetric bi-crystal surface at the applied potential
salt concentration in contact with a symmetric bi-crystal surface at the applied potential  . Top: flat surface, i.e.
. Top: flat surface, i.e.  , bottom: differently oriented facets with
, bottom: differently oriented facets with  .
.
Download figure:
Standard image High-resolution imageWe performed 2d FEM simulations of the boundary layer in dependence of the applied potential and the electrolyte concentration varying the surface roughness parameter relative to the Debye length as  ,
,  ,
,  . The respective surface roughness factors according to 46 are
. The respective surface roughness factors according to 46 are  , 1.0078, 1.031. We observe that with increasing
, 1.0078, 1.031. We observe that with increasing  , the capacity curves deviate stronger from the calculated capacity of the perfectly smooth surface, see Fig. 11 left. Moreover, Fig. 11 right indicates that surface roughness can be very accurately taken into account by multiplying the surface roughness factor W to the capacity of the perfectly plain surface, i.e.
, the capacity curves deviate stronger from the calculated capacity of the perfectly smooth surface, see Fig. 11 left. Moreover, Fig. 11 right indicates that surface roughness can be very accurately taken into account by multiplying the surface roughness factor W to the capacity of the perfectly plain surface, i.e.
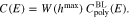
Figure 11. Left: detail of the boundary layer capacity for different electrolyte concentrations and surface roughness with  (markers +),
(markers +),  (⋯) and
(⋯) and  (- - ). Right: correction by surface roughness factor according to 46.
(- - ). Right: correction by surface roughness factor according to 46.
Download figure:
Standard image High-resolution imageDiscussion of the Idealized Polycrystal
Within this discussion, we always apply the limit of large facet size ![$1[\mathrm{nm}]\ll {d}^{\mathrm{facet}}$](https://content.cld.iop.org/journals/1945-7111/167/10/106512/revision2/jesab9ccaieqn212.gif) related to 3, keeping in mind, that this limit is already well approached for
related to 3, keeping in mind, that this limit is already well approached for  .
.
Difference of PZC
In the previous section, we kept the potential difference between the two considered facets constant (viz.  ), However, this difference is a material dependent characteristic quantity that varies between different materials or different crystallographic orientations. While differences of the PZC, respective
), However, this difference is a material dependent characteristic quantity that varies between different materials or different crystallographic orientations. While differences of the PZC, respective  , between differently oriented surfaces are considered minor for some metals, e.g. "low melting metals" like
, between differently oriented surfaces are considered minor for some metals, e.g. "low melting metals" like  , Sn, Pb, Zn and Bi, cf.,5,10 considerable differences between the low index facets are reported for e.g. Ag, Au, Cu, Pt and W, cf.24 Thus, we examine the situation of an bi-crystal with equal surface fractions
, Sn, Pb, Zn and Bi, cf.,5,10 considerable differences between the low index facets are reported for e.g. Ag, Au, Cu, Pt and W, cf.24 Thus, we examine the situation of an bi-crystal with equal surface fractions  and vary the difference of the surface chemical potential of the electrons
and vary the difference of the surface chemical potential of the electrons  between
between  and
and  . This corresponds to varying the boundary values such that
. This corresponds to varying the boundary values such that  . We observe, that for
. We observe, that for  the capacity retains the typical camel shape. For
the capacity retains the typical camel shape. For  there is a three maximum shape, whereas for larger potential differences between the facets, we have a four-maximum configuration that again allows to identify the two local extrema of the individual facets, see Fig. 12. Once more, we stress that in experiments one should be aware of the fact that for a polycrystalline surface the PZC in general is not found at a local capacity minimum! For a sufficiently large potential difference Φ1 − Φ2, the PZC is in general found between the inner two local maxima of the capacity, and only for specific configurations of the surface fractions
there is a three maximum shape, whereas for larger potential differences between the facets, we have a four-maximum configuration that again allows to identify the two local extrema of the individual facets, see Fig. 12. Once more, we stress that in experiments one should be aware of the fact that for a polycrystalline surface the PZC in general is not found at a local capacity minimum! For a sufficiently large potential difference Φ1 − Φ2, the PZC is in general found between the inner two local maxima of the capacity, and only for specific configurations of the surface fractions  the PZC is located at a local capacity minimum. Even more, for moderate
the PZC is located at a local capacity minimum. Even more, for moderate  , the PZC is located near a local capacity maximum!
, the PZC is located near a local capacity maximum!
Figure 12. Capacity curves for varying difference  for a bi-crystal with equal surface fractions
for a bi-crystal with equal surface fractions  .
.
Download figure:
Standard image High-resolution imageAs stated in Section 4.2, the potential of zero charge
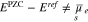
but, it has to be determined from a solution of the non-linear equation  . This solution is dependent on the salt concentration c, the the surface fractions si, and the
. This solution is dependent on the salt concentration c, the the surface fractions si, and the  . For a bi-crystal, Fig. 13 displays the difference
. For a bi-crystal, Fig. 13 displays the difference  .
.
Figure 13. Numerical computation of the difference between the potential of zero charge  and the average surface chemical potential of electrons
and the average surface chemical potential of electrons  for a bi-crystal as function of
for a bi-crystal as function of  for various surface fractions s1 (s2 = 1−s1 and electrolyte concentrations c.
for various surface fractions s1 (s2 = 1−s1 and electrolyte concentrations c.
Download figure:
Standard image High-resolution imageFigure 14. Left: Capacity curves for an adsorbing electrolyte and different bulk electrolyte concentrations where the higher peak at potentials more positive than the PZC is due to adsorption of anions. Right: Construction of the capacity of a polycrystal surface as the sum of the single crystal capacities of the contributing facets weighted by their surface fraction.
Download figure:
Standard image High-resolution imageAdsorption to the surface
To study the effect of adsorption, we return to the simple configuration of a symmetric bi-crystal in Section 5.1, i.e. we choose N = 2,  . We assume that the adsorption energies Δ gα do not differ between the different facets. In particular, by the choice of
. We assume that the adsorption energies Δ gα do not differ between the different facets. In particular, by the choice of
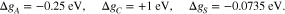
we assume, that cations effectively do not adsorb while anions and the solvent are allowed to adsorb to the surface. For simplicity and clarity of presentation, we do not consider surface reactions like solvation shell stripping or electron transfer reactions. An extension is straightforward by applying 21c for the reaction products and 26 for the surface charge. In the numerical computation, we use for the radius and the partial area of the adsorbed species
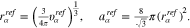
According to 34, the surface capacity of a patterned surface only depends on the material parameters of the contributing facets and their surface fractions  , but not on the facet geometry or the facet size parameter
, but not on the facet geometry or the facet size parameter  . Thus, we can combine 3 and 34 to conclude that for large facet size, the capacity of a perfectly plain polycrystal surface is
. Thus, we can combine 3 and 34 to conclude that for large facet size, the capacity of a perfectly plain polycrystal surface is
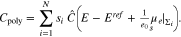
Figure 14 shows the capacity curves of a single crystal surface and illustrates the construction for a bi-crystal according to 51. As already known for single crystal surfaces, if there is adsorption from the electrolyte, the PZC depends on the electrolyte and its bulk concentration, cf. e.g.17 The same also holds true for the polycrystal and we conclude from 3 and 34 thati
for ![$1[\mathrm{nm}]\lt {d}^{\mathrm{facet}}\to \infty $](https://content.cld.iop.org/journals/1945-7111/167/10/106512/revision2/jesab9ccaieqn238.gif) , the determination of
, the determination of  requires the solution of the non-linear algebraic equation
requires the solution of the non-linear algebraic equation
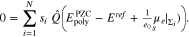
Multiple different facets
The above results can easily be extended to more complex polycrystalline surfaces with many facets of different type. We consider the case of N = 4 different types of facets Σ1, Σ2, Σ3, Σ4 with the respective surface fractions  ,
,  ,
,  . Also, we want to have junction points where more than two different facets meet. One possible simple realization on a 2D surface is the periodic symmetric continuation of the pattern sketched in Fig. 15. The boundary data is given as
. Also, we want to have junction points where more than two different facets meet. One possible simple realization on a 2D surface is the periodic symmetric continuation of the pattern sketched in Fig. 15. The boundary data is given as  on Σi, for i = 1, 2, 3, 4. We choose
on Σi, for i = 1, 2, 3, 4. We choose  . First, we let
. First, we let  and Φ3 = Φ2 and get slightly non-symmetric capacity curvesj
, see Fig. 15. Next, we change Σ3 such that
and Φ3 = Φ2 and get slightly non-symmetric capacity curvesj
, see Fig. 15. Next, we change Σ3 such that  while still Φ4 = Φ1. Finally, set
while still Φ4 = Φ1. Finally, set  and keep the remaining boundary values as before, see Fig. 15 bottom line.
and keep the remaining boundary values as before, see Fig. 15 bottom line.
Figure 15. Top left: surface pattern as used in the 3D-FEM simulations of Section 6.3. Top right and bottom row: capacity curves, when assigning the indicated different boundary values on the facets.
Download figure:
Standard image High-resolution imageAs in Section 5.1, we checked convergence of the capacity calculated from 3D-FEM simulation for finite facet size  to the limit Eq. 3 for
to the limit Eq. 3 for  and grid convergence of the numerical solutions.
and grid convergence of the numerical solutions.
Stochastic distribution of surface patterns
A precise measurement of all surface facets and their corresponding work functions is extremely expensive, if possible, and even measurements on very similar facets may contain some scatter. Hence, the input values for the mathematical model of the foregoing section can only be determined to a certain precision, which has to be taken into account when realistic polycrystalline surfaces are to be described. We sketch therefore a stochastic description of the polycrystalline surface based on the derived deterministic model and provide some numerical examples of the double layer capacity.
Consider a surface Σ of N > 1 facets Σi. We define the set  of all different values of
of all different values of  on Σ. Moreover we introduce the sets
on Σ. Moreover we introduce the sets  . Then we denote with Σμ all facets which have the value μ for
. Then we denote with Σμ all facets which have the value μ for  and the according surface fraction with
and the according surface fraction with  , i.e.
, i.e.
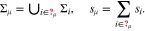
Doing so, we switch the facet labeling from a consecutive numbering of all facets to values of  . Since
. Since  , we can introduce the discrete probability density
, we can introduce the discrete probability density
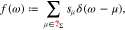
where δ is the Dirac-distribution. The charge  stored in the polycrystalline boundary layer thus rewrites as
stored in the polycrystalline boundary layer thus rewrites as
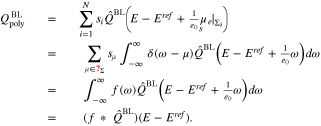
With the convolution operator  we obtain thus a very compact expression for
we obtain thus a very compact expression for  in terms of the distribution function f(ω), which describes the facet density parametrized over the surface potential
in terms of the distribution function f(ω), which describes the facet density parametrized over the surface potential  . The potential of zero charge
. The potential of zero charge  is thus (implicitly) defined via
is thus (implicitly) defined via  and the double layer capacity is
and the double layer capacity is
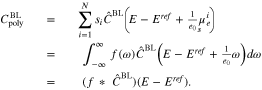
Note that  and
and  remain the non-linear functions described in Section 4.
remain the non-linear functions described in Section 4.
For realistic polycrystalline electrodes, the Dirac-distribution might smear, whereby f becomes a continuous function. In order to show the consequences of the smearing of the convolution operator * on the non-linear functions of  we consider the following example. Let the density f be given by a normal distribution of facets with respect to its mean value
we consider the following example. Let the density f be given by a normal distribution of facets with respect to its mean value  and with the standard deviation σ, see Fig. 4. For small standard deviation like σ = 0.025, the resulting capacity according to 4 is close to the single crystal capacity, see Fig. 4. However, for σ = 0.2, the local capacity minimum has disappeared and there is only a single capacity maximum. Due to the symmetry of the chosen density f(ω), the PZC is in either case located at the maximum of the density f. We want to stress, that this particular configuration of facets with a broad scatter of the individual facet properties is very different from the limit related to 5 where on each finite size part of the surface a large number of accordingly small facets are considered.
and with the standard deviation σ, see Fig. 4. For small standard deviation like σ = 0.025, the resulting capacity according to 4 is close to the single crystal capacity, see Fig. 4. However, for σ = 0.2, the local capacity minimum has disappeared and there is only a single capacity maximum. Due to the symmetry of the chosen density f(ω), the PZC is in either case located at the maximum of the density f. We want to stress, that this particular configuration of facets with a broad scatter of the individual facet properties is very different from the limit related to 5 where on each finite size part of the surface a large number of accordingly small facets are considered.
Next, we want to investigate the effect of a polycrystal surface that is mainly covered by facets near to low index surfaces like (100), (110) and (111). For the low index facets of Ag we chose values of  related to the (negative) work function as given in Table II. To describe a non-ideal Ag polycrystal, we consider a probability density that consists of a superposition of scaled normal distributions around the potentials of the low index facets and a standard deviation small enough, such that the peaks do not overlap, see Fig. 16 where σ = 0.025 is chosen. The resulting capacity curve remains close to the capacity of an ideal polycrystal with equal surface fractions
related to the (negative) work function as given in Table II. To describe a non-ideal Ag polycrystal, we consider a probability density that consists of a superposition of scaled normal distributions around the potentials of the low index facets and a standard deviation small enough, such that the peaks do not overlap, see Fig. 16 where σ = 0.025 is chosen. The resulting capacity curve remains close to the capacity of an ideal polycrystal with equal surface fractions  for i = 1, 2, 3. Moreover, we perturb the configuration such that an equi-distribution in a
for i = 1, 2, 3. Moreover, we perturb the configuration such that an equi-distribution in a  potential range is superimposed in the probability density. As a result, we obtain a much more smooth capacity curve. The pure equi-distribution for ω(u) results in a capacity similar to the normal distribution with large standard deviation.
potential range is superimposed in the probability density. As a result, we obtain a much more smooth capacity curve. The pure equi-distribution for ω(u) results in a capacity similar to the normal distribution with large standard deviation.
Figure 16. Left: different probability densities describing the surface chemical potential of electrons on a Ag-polycrstal where the surface is covered by facets close to the three low index facets (100), (110) and (111) (blue), the low index facets and additionally an equi-distribution other facets (red), an a pure equi-distribution of facets (yellow). Right: Capacity curves for the respective densities (solid —) and capacity of the ideal polycrystal of only the three low index facets with equal surface fraction (dotted line ⋯).
Download figure:
Standard image High-resolution imageTable II. Recommended values for the electron work function on Ag surfaces according to Ref. 24.
| surface | (110) | (100) | (111) |
| work function |

|

|

|

|

|

|

|
Conclusions
The double layer model16,17,19 is build on a thermodynamically consistent generalized Nernst-Planck model and serves as the theoretical basis of this work. In Ref. 17 it was successfully validated against the most reliable experimental data of single crystal capacitance.6–8 This validation now allows to turn the attention from the single crystal to the less well defined conditions of polycrystalline surfaces. By the approach of numerically solving improved Poisson-Boltzmann problems for patterned surfaces, simple representations for the differential capacitance of polycystalline solid metal electrode surfaces in terms of single crystal capacitance have been obtained. While for a not too small facet size parameter  , the result for the capacity of a polycrystalline surface is the expected surface fraction weighted average, some caution is required when considering PZC. Due to the non-linearity in the relation between applied potential and boundary layer charge, the PZC is not given by a weighted average and moreover, it also varies with the electrolyte concentration. The result for
, the result for the capacity of a polycrystalline surface is the expected surface fraction weighted average, some caution is required when considering PZC. Due to the non-linearity in the relation between applied potential and boundary layer charge, the PZC is not given by a weighted average and moreover, it also varies with the electrolyte concentration. The result for  can be interpreted in the way that for an amorphous solid material or a liquid material the surface is inhomogeneous on an infinitesimal scale such that the surface properties for each point are independent. Both limits, for large and for small facet size, allow a to get rather clear picture of the electrochemical double layer at pattered surfaces like polycrystal surfaces. Moreover, the results justify the simple correction for rough surfaces by a multiplication with a single geometry dependent factor. In the intermediate cases, where the facets diameters are in the order of
can be interpreted in the way that for an amorphous solid material or a liquid material the surface is inhomogeneous on an infinitesimal scale such that the surface properties for each point are independent. Both limits, for large and for small facet size, allow a to get rather clear picture of the electrochemical double layer at pattered surfaces like polycrystal surfaces. Moreover, the results justify the simple correction for rough surfaces by a multiplication with a single geometry dependent factor. In the intermediate cases, where the facets diameters are in the order of ![$1[\mathrm{nm}]$](https://content.cld.iop.org/journals/1945-7111/167/10/106512/revision2/jesab9ccaieqn281.gif) , the capacitance of a polycrystalline surface has to be determined from spatially resolved numerical simulation in 2D or 3D and the results depend on the actual geometric surface pattern.
, the capacitance of a polycrystalline surface has to be determined from spatially resolved numerical simulation in 2D or 3D and the results depend on the actual geometric surface pattern.
The results obtained here are in rather close resemblance to previous results of Refs. 13, 14 where similar to 3, the capacitance of the polycrystal is given as a surface fraction weighted sum of single crystal capacitances. However, criteria about the applicability of such representations are not directly comparable, since they depend on quantities related to a different model which are not applicable in the context of this work. Spatially resolved and linearized Gouy-Chapman-Stern models were analyzed in Ref. 15 to derive that in the case of sufficiently large differences between the  -values, the facet size has to be small compared to a length which is related to an inner-layer or Helmholtz capacitance of the individual facets, i.e.
-values, the facet size has to be small compared to a length which is related to an inner-layer or Helmholtz capacitance of the individual facets, i.e.  . Here, the lower bound is assumed to be independent of the bulk concentration and in any case to be less than
. Here, the lower bound is assumed to be independent of the bulk concentration and in any case to be less than  in aqueous solution. For small differences in the surface chemical potential of the electrons,15 derives
in aqueous solution. For small differences in the surface chemical potential of the electrons,15 derives  as the sufficient and necessary condition for the applicability of 3. We do not derive a similar criterion here, because one can easily see that the difference between the two opposite limit Eqs. 3 for
as the sufficient and necessary condition for the applicability of 3. We do not derive a similar criterion here, because one can easily see that the difference between the two opposite limit Eqs. 3 for  and 5 for
and 5 for  vanishes quadratically for small difference of the
vanishes quadratically for small difference of the  values, leaving no space for the intermediate cases.
values, leaving no space for the intermediate cases.
Another interesting aspect of the approach followed here is the possibility to develop a stochastic description of complex polycrystalline surfaces. The results indicate that assembly of an electrode from a huge number of particles with different properties can be represented by a distribution function with a large standard deviation. As a consequence, the capacity of such a surface does not show the typical single crystal camel shape or multiple clearly separated maxima but a rather constant capacity over a broader potential range. In light of this result, the function of supercapacitors can be explained by the inhomogeneity of the fine faceted granular electrode surface.
Outlook. In the modeling of the patterned surfaces with finite facet size parameter  , we neglected distinguished contributions from the facet boundary lines. While the according effects on the capacity might be neglected for large enough facets, accurate description of the finite size facet structure might require an extension of the underlying thermodynamic continuum model to line thermodynamics.
, we neglected distinguished contributions from the facet boundary lines. While the according effects on the capacity might be neglected for large enough facets, accurate description of the finite size facet structure might require an extension of the underlying thermodynamic continuum model to line thermodynamics.
The modeling framework applied within this work strictly distinguishes between a universal and a material dependent part. The constitutive functions for the material modeling were chosen here with the emphasis on simplicity. Various extensions of the material model are possible, as for example different concepts of incompressibility, different relations between solvation number and partial volume of solvated ions, concentration dependent dielectric susceptibility. Moreover, the surface model only contains entropic interaction of the ions. Considering also e.g. enthalpic interactions is in principle possible, however it would lead relations between  and the surface chemical potential
and the surface chemical potential  that are implicit. Partial charge transfer is possible within the model framework. It entails adsorbed species on the surface with fractional charge number. However, systematic investigations how the (surface) solvation number, the partial molar volume (or area), and the charge number of the ions are related to each other are yet outstanding.
that are implicit. Partial charge transfer is possible within the model framework. It entails adsorbed species on the surface with fractional charge number. However, systematic investigations how the (surface) solvation number, the partial molar volume (or area), and the charge number of the ions are related to each other are yet outstanding.
Surface reactions like solvation shell striping of adsorbed ions can be included into the presented models for polycrystalline surfaces in a straightforward manner. The same also holds true for electron transfer reactions, as long as the reaction products do not leave the surface. In the presence of Faradayic currents additional length scales for the non-equilibrium transport of ions have to be taken into account. In non-equilibrium, surface roughness on larger length scales might lead to interactions of bulk transport and layer charging causing deviations from ideal behavior of perfectly plain surfaces.
Footnotes
- a
Compared to the standard Poisson-Boltzmann equation, the charge density q in 1 does not only depend on the electric potential φ, but also on the pressure p and the Poisson equation is additionally coupled to an algebraic equation.
- b
Note that specific adsorption is also discussed within this work.
- c
The notation indicates that the definition can be made for both domains
 and
and  in analogous manner. If u is not defined in either
in analogous manner. If u is not defined in either  or
or  , the respective trace value is set to 0.
, the respective trace value is set to 0. - d
Where not necessary, we omit the labels
 or
or  for the volume domains.
for the volume domains. - e
This is in contrast to the model of a mixture of undissociated species, the bare center ions and solvent molecules, regardless whether they are free or bound into a solvation shell.
- f
In the classical Poisson-Boltzmann setting, the pressure dependent term
 is missing. This elastic contribution leads to a limitation of the possible ion concentration. Moreover, the mole fraction yα also includes ion-solvent interaction.
is missing. This elastic contribution leads to a limitation of the possible ion concentration. Moreover, the mole fraction yα also includes ion-solvent interaction. - g
The typeface
 indicates that this is a function
indicates that this is a function  and not the applied voltage E.
and not the applied voltage E. - h
One has to be careful with an interpretation of this fact. Surface tension of planar solid surfaces is difficult to measure and one has to distinguish between the "thermodynamic" surface tension and the "interfacial tension", cf.18
- i
- j
This situation is equivalent to the slightly non-symmetric case N = 2 and
 ,
,  .
.































