1 Introduction

Oscillatory excitation is often encountered in fluid dynamics. This kind of excitation for liquids is of interest in engineering applications [1], biology [2, 3], microfluidics and controlled motion [4,5,6]. Oscillatory fluid behavior can occur not only due to external perturbation but also to self-induced flow [7, 8].

Over the last decades, scientists have been fascinated by liquid surface waves [9,10,11,12,13,14,15] and Faraday instabilities [16, 17], phenomena induced by oscillatory excitation, too. For the surface wave problem in the above-mentioned papers, wave propagation, dispersion, sloshing, and resonance have been mainly investigated.

The natural frequency of sloshing can be calculated starting from the phase speed formula \(v=\sqrt{gh_0}\), where \(h_0\) represents the undisturbed water depth and g is the gravity acceleration. This formula is valid for h much smaller than the wavelength (shallow water) and small wave amplitudes [17]. Otherwise, we need higher approximations, for example those given in [12] and [13] and in references therein. For sloshing resonances, there are papers which interpret the resonance frequencies using mass-spring models (Duffing equation) [15]. We will interpret the resonances in harmonic excited water channels using ping-pong models [18, 19].

The present paper analyzes the resonance related to sloshing phenomena in a circular channel. Our channel has a high ratio L/D, where L is the channel length and D is the width, and also a relatively low ratio \(h_0/L\). In Sect. 2, we present the experimental device and methods, in Sect. 3, the theoretical model used for performing the numerical simulations. We discuss and compare the results in Sect. 4. We gather the conclusions in Sect. 5.

2 Experimental setup

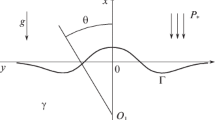
For our investigation, we use a circular horizontal channel placed on a rotating table (Fig. 1). The rotation and the channel symmetry axes coincide. This is a part of an experimental device initially designed for studying baroclinic waves in a wide gap. In contrast, the narrow gap marked with a red arrow in Fig. 1a and usually used to heat the fluid in the wide gap, is the working area for the present experiment. For the sloshing experiments, we use a fluid depth of \(h_0=4\) cm. The channel is approximately 476 cm long (75.75 cm radius in the middle of the gap) and 8.5 cm wide. Eight ultrasonic distance sensors are placed above the liquid surface. The sensors are unevenly distributed, as can be seen in Fig. 1b, to avoid that they are preferentially located above the wave nodes or bellies. The sensors positions are given in table 1.

Table 1 Sensors (S) and barrier (B) positions in the experimental setup
Full size table
Fig. 1
figure 1

The experimental setup. General view of the tank placed on a rotating table. For the actual setup, the outer channel marked with a red arrow is used to study surface waves (a). View of the rotating tank equipped with ultrasonic distance sensors (blue/chrome housing and red display) (b)

Full size image

In [13], the authors plotted the resonance curve as function of the frequency using constant amplitude A. However, to construct a resonance curve, there are several reasons to choose not A but the velocity (or angular velocity) to be constant. One of the reasons is that the kinetic energy pumped per unit time will be almost the same for all frequencies. The second one is of more technical nature: if one maintains the oscillation amplitude constant, the mechanical parts of the rotating table and of the tank will be heavily loaded at high frequencies and the experiment would work either at very small amplitudes or stop for safety reasons before the higher resonance peaks can be reached.

3 Numerical solutions

For the numerical calculations, we consider the system in simplified two-dimensional form with the same length as the circumference of the circular channel from the experiment. We compute the evolution of the incompressible Navier–Stokes equations (NSE) using the method presented in [6], according to which the time-dependent, arbitrarily shaped surface \(h=h(x,t)\) is mapped onto a constant rectangular domain (Fig. 2). The nonlinear coordinate transformation \(z=h{\tilde{z}}\) obviates the need for tracking the surface and reduces the necessary interpolations. Applying this to the scaled NSE and to the continuity equation yields

$$\begin{aligned}{} & {} \frac{\partial \vec{v}}{\partial t} = z{\dot{\xi }}\frac{\partial \vec{v}}{\partial z} - u\left( \frac{\partial \vec{v}}{\partial x} - z\xi ' \frac{\partial \vec{v}}{\partial z} \right) - \frac{w}{h}\frac{\partial \vec{v}}{\partial z} \nonumber \\ {}{} & {} \quad + \left( \vec{e}_x zh' - \vec{e}_z\right) \frac{1}{h}\frac{\partial P}{\partial z} - \vec{e}_x \frac{\partial P}{\partial x} + {\tilde{\Delta }}\vec{v} + \vec{f}(t) \end{aligned}$$
(1)

and

$$\begin{aligned} \frac{\partial u}{\partial x} -z\xi ' \frac{\partial u}{\partial z} + \frac{1}{h} \frac{\partial w}{\partial z} = 0 , \end{aligned}$$
(2)

respectively, where \(\vec{f}(t)\) comprises all gravitational forces including the time-periodic excitation, \(\vec{v} = (u, w)\) denotes the velocity field and

$$\begin{aligned} {\tilde{\Delta }} = \frac{\partial ^2}{\partial x^2} + \frac{(zh')^2 + 1}{h^2} \frac{\partial ^2}{\partial z^2} + \frac{z}{h}\left( \frac{2h^{\prime 2}}{h} -h'' \right) \frac{\partial }{\partial z} - 2z\xi ' \frac{\partial ^2}{\partial x \partial z} \end{aligned}$$

is the transformed Laplacian with \(\xi (x,t)=\ln {h(x,t)}\). In the above equations, the common abbreviation \(q'\) is used to denote the derivative of an arbitrary quantity q (h or \(\xi\)) with respect to x. Its time derivative is abbreviated as \({\dot{q}}\). Pressure is computed by deriving a sparse linear system for P from the discretized form of Eq. (1) and (2) whose solution satisfies the conservation of mass and momentum. To prevent odd–even oscillations during the computations, the discretization is performed on a staggered grid.

Fig. 2
figure 2

A nonlinear transformation eliminates the time dependence of the surface \(z=h(x,t)\) by mapping region (A) to rectangular domain (B)

Full size image

Due to the reduction to two spatial dimensions, we find that the loss of kinetic energy through viscous dissipation in the fluid bulk is lower in the simulation than in the experiment. Also, in two dimensions, there are no lateral sidewalls producing additional friction. These effects can be approximately taken into account by tuning the (kinematic) viscosity \(\nu\). For this purpose, the maximum amplitude at the first resonance is measured and \(\nu\) is adjusted to match the amplitude observed in the experiment.

Fig. 3
figure 3

Resonance curves for \(h_0=4\) cm water height and 0.35 RPM amplitude. \(\langle h^2\rangle\) of each sensor—symbols joined by a thin line—and the envelope of \(\langle h^2\rangle\) for all simulation points—thick line. The first resonance frequency can be calculated as \(f_0=\frac{v}{2L}=\frac{\sqrt{gh_0}}{2L}=0.067\) Hz. The following resonances take place at around \(3f_0\), \(5f_0\), \(7f_0\), namely at 0.2, 0.34 and 0.47 Hz

Full size image
Fig. 4
figure 4

Wave strengthening or weakening explained using an intuitive “ping-pong” model: for a frequency close to the first resonance the wave front arrives simultaneously with the returning of the whole tank, including the barrier (a); in the left side of the sketch, the ping-pong ball is synchronized with the paddle and therefore the ball is returned and accelerated; for the right side, the paddle moves back when the ball arrives and the ball is decelerated (b)

Full size image
Fig. 5
figure 5

Space-time plots of the water surface height for different excitation frequencies

Full size image
Fig. 6
figure 6

2D time-space Fourier transform of the signal plotted in Fig. 5. We plot only modes for lower frequencies and wave numbers because only those have significant values. The labels are normalized to the excitation frequency \(\omega _0\) and the channel characteristic wave number \(k_0=\frac{1}{L}\). Note that the excitation frequency is different for each subfigure. In dimensional units, the oblique line plotted in some cases corresponds with the front wave velocity \(\sqrt{gh}\)

Full size image

The centrifugal force has been neglected, because the ratio between the maximal value of the centrifugal acceleration and the gravity acceleration is very small (see also [14]).

The simplest model which can explain the resonance appearing in the sloshing channel is the “ping-pong ball” model, as one can further see in Sect. 4.

Fig. 7
figure 7

Transient phase of the bore formation at \(f=0.07\) Hz near the first resonance—numerical simulations

Full size image

4 Discussion

We perform experiments and numerical simulations for different excitation frequencies. The angular velocity amplitude is 0.35 rotations per minute (maximum velocity 2.8 cm/s). This means amplitudes in the order of 8 mm for the highest frequencies to 88 mm for the lowest ones. If we compare with [13], in our experiment, the channel length is larger and the excitation frequencies are smaller. Each time, we wait until the signal becomes periodic. For a given excitation frequency we compare for each sensor the mean value of \((h-h_0)^2\),

$$\begin{aligned} \langle (h-h_0)^2\rangle (x)=\frac{1}{T}\int _0^T{(h-h_0)^2(x,t)\textrm{d}t}, \end{aligned}$$
(3)

where h is the liquid height measured by the sensor at position x. For our experimental setup, we can measure only at eight sensor points. For the simulations, we can consider values at all grid points. Due to discretization in both experiment and numerical simulations, the integral is replaced by the corresponding sum. In Fig. 3, we plot the measured quantities for each sensor and only the envelope of all curves from the numerical data. We find a very good agreement between the simulations and the experiment. Because the space resolution is much higher for the numerical simulation, we will discuss in the following our findings mainly based on the numerical results. We prefer to use \(\langle (h-h_0)^2\rangle\) in place of the maximal height of the surface elevation as was considered in [13]. Our choice has two reasons: this quantity \(\langle (h-h_0)^2\rangle\) can be put into relation with the system energy and also it is less susceptible to errors.

To explain why only odd multiples of the first mode \(f_0\) appear in the resonance curves (Fig. 3), one can use the similarity within the wave front propagation and a ping-pong ball movement. The wave front is reflected at the two barriers like in Fig. 4a, the ball is reflected by the paddles like in Fig. 4b. If the paddle and the ball are synchronized and move in opposite direction when the ball arrives at the paddle, it is returned and receives enough energy to compensate friction. In the right side of Fig. 4b, the ball and paddle are anti-synchronized and they move in the same direction in the moment of collision. The ball will not receive enough energy for a back-and-forth “travel” between the paddles.

From the shallow water equations, one can calculate the velocity of the wave front: \(v=\sqrt{gh}\) [17]. For very small surface deflections, one can consider \(h \approx\) constant, i.e. the wave front moves with constant velocity. Assuming (as we did in the numerical model) that the channel is straight, let us suppose that the wave starts its propagation to the right at the left barrier. The first resonance frequency \(f_1\) corresponds to the case when the left barrier moves to the left when the front arrives. This will happen first after a half of period \(t=T_0/2=\frac{1}{2f_0}\). During the time t, the wave travels the length L of the tank:

$$\begin{aligned} L=vt=\frac{\sqrt{gh}_0}{2f_0}, \end{aligned}$$
(4)

and thus the first resonance is \(f_0=\frac{\sqrt{gh_0}}{2L}\). For our experiment this is 0.066 Hz. Due to the periodicity of the excitation, a synchronization of the wave and barrier will occur again after another period \(T_0\) or multiples of \(T_0\). Generally, for obtaining the resonance, the time necessary for the wave to travel along the channel length is \(t=nT_0+\frac{T_0}{2}=(2n+1)\frac{T_0}{2}\), with \(n=0,1,2,\dots\). It follows that the corresponding frequencies are \(f_n=(2n+1)\frac{\sqrt{gh_0}}{2L}=(2n+1)f_0\). For the frequencies \(2nf_0\), a wave front generated at one of the barriers will arrive at the other barrier when this is moving in the same direction. This corresponds to the situation represented in the left side of the Fig. 4b.

If we imagine an experiment where the two barriers are moving in opposite direction, following the same logic, the even multiple of \(f_0=\frac{\sqrt{gh_0}}{2L}\) will correspond to the maxima of the wave–wave interaction response.

In Fig. 5, we plot for several frequencies the time-space diagram of the numerically calculated water surface corresponding to a whole excitation period. One can distinguish between two different main patterns. For cases close to the maxima in the resonance curve, propagation of the wave fronts can be observed. The inclination is always the same, given by the front wave velocity \(v=\sqrt{gh_0}\), although in the plots, it looks to be different due to time scaling related to the excitation period (increasing from subfigure (a) to (i)). Far away from resonance (for anti-resonance cases), harmonic patterns are present (standing waves with nodes and anti-nodes). Note that also the amplitude in these cases is much smaller. We observe that near the first resonance only one wave can be seen in the system. For the other resonances 3, 5, and so on, waves coexist. For the second resonance, two collision regions can be observed at about one third and two thirds of the tank length. For the third resonance, four such points where waves collide exist. If we interpret the wave reflection as a collision with itself then the number of evenly distributed points where collisions take place is \(f/f_0\): only reflection for the first resonance, reflection plus two collision points for the second one and so on. As can be seen in Fig. 5, the wave travels with the same velocity after the collision. The phase shift is rather small, indicating small nonlinear effects.

For a better understanding, we plot in Fig. 6 also the 2D time-space Fourier spectra corresponding to each subplot of Fig. 5. Also, here one can observe that the pattern is dominated by the fundamental mode (\(k_0,\omega _0\)) for frequencies close to \(2nf_0\) and the modes along the line \((2n+1)/2\) are present near the resonance peaks. In addition, modes corresponding to the excitation frequency and low wave numbers are also discerned. This can be put into relation with the peaks width. The first two resonance peaks are narrow so that the focus of the energy happens only for frequency near \(f_0\) or \(2f_0\). The localization of the energy near the wave front happens only for a narrow frequency interval. In the regions between peaks, the energy is distributed so only steady waves are dominant. For higher resonance frequencies, the intervals where the energy is confined by a wave front are brighter so that propagation patterns are visible in the time-space plots and consequently in the corresponding Fourier 2D spectra.

Also of interest is to investigate numerically the transient phase from the start of the excitation until the fully development of the periodic water wave. The most interesting cases are near the resonances when periodic traveling bores are formed. The simplest example is the formation of the bore for a frequency \(f=0.07\) Hz near the first resonance as shown in Fig. 7. In the early stage (see Fig. 7a), a steady wave with the wavelength equal to the tank length L is formed. The wave elevation is increasing leading to the formation of a traveling front (Fig. 7b). Due to non-linearity, the front is starting to form ripples, which corresponds to higher wave numbers (Fig. 7c). In the fully developed state, these ripples have higher amplitudes and the wave looks very similar to a bore (Fig. 7d) [17].

5 Conclusion

In conclusion, wave development, collision, and resonance have been investigated in a circular tank following an oscillating movement around its symmetry axis with an harmonic angular velocity of constant amplitude and different frequencies. Surprisingly, at the resonance frequencies, we do not find steady waves as main pattern as we will expect if we compare with the resonance of a string, but strongly localized waves. Also, the lack of the even modes is an important difference in comparison with string resonance. This can be explained to the anti-symmetrical way of the excitation. If one can imagine the experiment with pumping barriers which moves always in the opposite directions, only even modes (at frequencies \(f=2nf_0\)) can be expected. This task will be investigated in the future with barriers where the wave will be partially reflected and partially transmitted. In this case, the advantage of having a circular channel allowing for periodic boundary conditions will be obvious.