1 Introduction

At present, the explanation of universe evolution is based on gravity theories associated with the use of various types of exotic matter and different gravity theories, including general relativity (GR) and its modifications [1,2,3,4,5,6]. These gravity theories require the analysis of cosmological perturbations which lead to the formation of a large-scale structure and relic gravitational waves [7,8,9,10,11] in the framework of the inflationary paradigm.

Considering GR scalar field cosmology in the early universe, we accept that observational constraints on the parameters of cosmological perturbation values due to anisotropy and polarization of the cosmic microwave background (CMB) [12, 13] are directly connected with the shape of the scalar field potential [14, 15]. It is possible to select a certain class of the scalar field potentials corresponding to inflationary models and satisfying observational constraints in GR scalar field cosmology. This procedure can be considered as an effective method of inflationary model verification [16,17,18,19].

On the other hand, inflationary models based on modified gravity theories allow us to consider arbitrary physically motivated potentials as relevant ones, since the spectra of cosmological perturbations depend not only on the form of the scalar field potential, but also on the chosen version of modified gravity [20, 21]. The different methods for constructing and analyzing the inflationary models based on the scalar–tensor gravity theories were described earlier in [22,23,24,25,26,27].

Nevertheless, we suggest the consideration of a new approach for constructing the phenomenologically correct models of cosmological inflation in modified gravity theories. This approach is based on the correspondence to observational constraints not due to the choice of the model parameters, but through certain relationships between these parameters.

Such an approach was proposed in [28] for Einstein–Gauss–Bonnet gravity, and in [29,30,31,32] for the scalar–tensor gravity theories. In [29,30,31,32], the connection \(H=\lambda \sqrt{F}\) between the Hubble parameter H(t) and the coupling function \(F(\phi )\), which defined the class of the scalar–tensor gravity theory, was used to construct the exact solutions for verified inflationary models with different types of cosmological dynamics. It is clear that the cosmological dynamic equations should be defined by the scale factor a(t) or the Hubble parameter H(t), the scalar field evolution \(\phi (t)\), and the coupling function \(F(\phi )\) if the potential \(V(\phi )\) is given.

The motivation for using the proposed ansatz \(H=\lambda \sqrt{F}\) was discussed in [29,30,31,32]. Initially given relations between various parameters are often used to build physically correct cosmological models both in the framework of general relativity and for modified theories of gravity (see, for example, [33,34,35,36,37]). In the case of the proposed quadratic relation between the Hubble parameter and the coupling function, the non-minimal coupling of the scalar field and curvature induces deviations from the purely exponential (de Sitter) expansion of the early universe, which corresponds to Einstein gravity. This approach makes it possible to construct quasi-de Sitter models of the early universe that satisfy observational constraints for various types of inflationary dynamics [29,30,31,32]. In [29], the inflationary solutions for the power-law Hubble parameter were considered. In [30, 31], such models were analyzed in the context of the exponential power-law inflation, and the exact solutions for cosmological models with linear deviation from de Sitter expansion were obtained in [32]. We also note that all these inflationary models satisfy the observational constraints on the values of the parameters of cosmological perturbations [29,30,31,32].

In this work, we follow on the described approach and determine a certain type of cosmological dynamics from the correspondence to well-known scalar–tensor theories of gravity for these models. A direct correspondence between the physical potentials of a scalar field and the well-known types of the scalar–tensor theory of gravity for the generalized scalar–tensor models is obtained. We also demonstrate that the cosmological models with quadratic connection between the Hubble parameter and the coupling function \(H=\lambda \sqrt{F}\) correspond to observational constraints on the parameters of cosmological perturbations for an arbitrary inflationary scenario with a certain dynamic of accelerated expansion of the early universe.

We also determine the spectrum of relic gravitational waves predicted in the proposed models. In this case, we take into account the specifics of the post-inflationary evolution of the early universe, which implies the presence of an additional stage of the stiff energy domination. The presence of this stage between the end of inflation and the beginning of the radiation-dominated era affects the spectrum of relic gravitational waves and distinguishes the proposed models from standard inflationary scenarios.

Finally, taking into account the spectrum of relic gravitational waves obtained, we evaluate the possibility of direct verification of the proposed cosmological models based on the possibility of the observation of the gravitational waves with high and low frequencies by existing and promising detectors [38,39,40,41,42,43,44] as well.

This paper is organized as follows. In Sect. 2, we consider the cosmological dynamic equations for the proposed models and consider satisfying the slow-roll conditions for arbitrary background parameters. In Sect. 3, we reconstruct and analyze a specific type of cosmological dynamics based on the correspondence of the type of scalar–tensor gravity to the Brans–Dicke theory. Section 4 investigates the correspondence between physically motivated potentials of the scalar field for the Brans–Dicke gravity and other well-known scalar–tensor gravity theories for the given dynamics of the accelerated expansion of the early universe. Section 5 shows the correspondence of the proposed cosmological models to any observational constraints (current and future) on the parameters of cosmological perturbations for arbitrary background parameters. We note that further measurement of the values of the parameters of cosmological perturbations leads to a refinement of the energy scale of inflation and the rate of accelerated expansion of the early universe only, and such refinement does not eliminate the possibility for verification of such models. Section 6 demonstrates that the models under consideration differ from standard inflationary models by the additional stiff energy-dominant stage, which leads to a significant discrepancy between these models in the spectrum of relic gravitational waves at high frequencies. In Sect. 7, we calculate the spectrum of relic gravitational waves in accordance with known observational constraints. The parameters of relic gravitational waves predicted by the proposed cosmological models are estimated. A summary of our investigations is presented in Sect. 8.

2 The inflationary dynamic equations

We start from a consideration of inflationary models based on the generalized scalar–tensor (GST) gravity theory described by the action [29,30,31,32]

$$\begin{aligned} S_{\mathrm{GST}}= & {} \frac{1}{\kappa }\int \mathrm{d}^4x\sqrt{-g}\left[ \frac{1}{2}F(\phi ) R - \frac{\omega (\phi )}{2}g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu } \phi - V(\phi )\right] \nonumber \\&+S_{\mathrm{m}} S_{\mathrm{m}}=\int \mathrm{d}^4x\sqrt{-g} L_{\mathrm{m}}, \end{aligned}$$
(1)

where \(\kappa \) is the Einstein gravitational constant, g is a determinant of the spacetime metric \(g_{\mu \nu }\), \(\phi \) is a scalar field with the potential \(V=V(\phi )\), \(\omega (\phi )\) and \(F(\phi )\) are differentiable functions of \(\phi \), R is the Ricci scalar, and \(L_{\mathrm{m}}\) is the matter Lagrangian. The case of vacuum spacetime corresponds to the absence of matter; therefore, the matter part of the action \(S_{\mathrm{m}}\) should be equal to zero: \(S_{\mathrm{m}}=0\). Further, we use a natural system of units where \(\kappa =8\pi G=c=1\).

The background dynamic equations in spatially flat four-dimensional Friedmann–Robertson–Walker (FRW) spacetime

$$\begin{aligned} \mathrm{d}s^2=-\mathrm{d}t^2+a^{2}(t)\left( \mathrm{d}x^{2}+\mathrm{d}y^{2}+\mathrm{d}z^{2}\right) , \end{aligned}$$
(2)

corresponding to the action (1) under condition \(S_{\mathrm{m}}=0\) in the chosen system of units are [29,30,31,32]

$$\begin{aligned}&3FH^{2}+3H{\dot{F}}-\frac{\omega }{2}{\dot{\phi }}^{2}-V(\phi )=0, \end{aligned}$$
(3)
$$\begin{aligned}&3FH^{2}+2H{\dot{F}}+2F{\dot{H}}+{\ddot{F}}+\frac{\omega }{2}{\dot{\phi }}^{2}-V(\phi )=0,\end{aligned}$$
(4)
$$\begin{aligned}&\omega \ddot{\phi } + 3\omega H{\dot{\phi }} + \frac{1}{2}{\dot{\phi }}^{2}\omega '+V'-6H^{2}F'-3{\dot{H}}F'=0. \end{aligned}$$
(5)

Here, an overdot represents a derivative with respect to the cosmic time t, \(H \equiv {\dot{a}}/a\) denotes the Hubble parameter, and \(F'\equiv \partial F/\partial \phi \).

In addition, we note that the scalar field equation (5) can be derived from Eqs. (3)–(4). For this reason, Eqs. (3)–(4) completely describe the cosmological dynamics, and can be represented in terms of the field \(\phi \) as follows

$$\begin{aligned}&V(\phi )=3FH^{2}+\frac{5}{2}H{\dot{F}}+F{\dot{H}}+\frac{1}{2}{\ddot{F}}, \end{aligned}$$
(6)
$$\begin{aligned}&\omega (\phi ){\dot{\phi }}^{2}=H{\dot{F}}-2F{\dot{H}}-{\ddot{F}}. \end{aligned}$$
(7)

A number of cosmological models were considered earlier on the basis of dynamic equations (3)–(5) with certain scalar field potentials \(V(\phi )\) and the coupling functions \(F(\phi )\) (see, for example, [22, 23, 25,26,27]).

However, we are interested in inflationary models corresponding to observational constraints on the parameters of cosmological perturbations without restrictions on the shape of the potential \(V(\phi )\) or on the parameters of GST gravity theory \(F(\phi )\) and \(\omega (\phi )\). This is the cornerstone of the given investigation which distinguishes our new approach from methods applied earlier.

To this end, we consider models with quadratic connection between the Hubble parameter and coupling function [29,30,31,32]

$$\begin{aligned}&H=\lambda \sqrt{F}, \end{aligned}$$
(8)

where \(\lambda \) is a constant.

The main equations of the quadratic connection models (QCMs) using the ansatz (8) in Eqs. (6)–(7) can be represented as

$$\begin{aligned}&{\tilde{F}}(\phi )\equiv \lambda ^{2}F(\phi )=H^{2},\end{aligned}$$
(9)
$$\begin{aligned}&{\tilde{V}}(\phi )\equiv \lambda ^{2}V(\phi )=3H^{4}+6H^{2}{\dot{H}}+{\dot{H}}^{2}+H{\ddot{H}},\end{aligned}$$
(10)
$$\begin{aligned}&{\tilde{X}}(\phi ,{\dot{\phi }})\equiv \lambda ^{2}X(\phi ,{\dot{\phi }})={\dot{H}}^{2}+H{\ddot{H}}, \end{aligned}$$
(11)

where the kinetic term is

$$\begin{aligned} {\tilde{X}}(\phi ,{\dot{\phi }})\equiv -\frac{1}{2}{\tilde{\omega }}(\phi ){\dot{\phi }}^{2}, \quad {\tilde{\omega }}(\phi )\equiv \lambda ^{2}\omega (\phi ). \end{aligned}$$
(12)

We call \(\lambda \) the energy scale parameter of these inflationary QCMs, since the constant \(\lambda ^{2}\) normalizes the values of the scalar field potential \(V(\phi )\), its kinetic energy \(X(\phi ,{\dot{\phi }})\), and non-minimal coupling function \(F(\phi )\).

In addition, taking into account the definitions of slow-roll parameters and corresponding conditions on them

$$\begin{aligned}&\epsilon =-\frac{{\dot{H}}}{H^{2}}\ll 1,\quad \delta =-\frac{{\ddot{H}}}{2H{\dot{H}}}\ll 1, \end{aligned}$$
(13)

one can define the reduced potential and reduced kinetic energy of a scalar field from Eqs. (10)–(11),

$$\begin{aligned}&v\equiv \frac{{\tilde{V}}}{{\tilde{F}}^{2}}=3-6\epsilon +2\epsilon \delta +\epsilon ^{2},\end{aligned}$$
(14)
$$\begin{aligned}&u\equiv \frac{{\tilde{X}}}{{\tilde{F}}^{2}}=2\epsilon \delta +\epsilon ^{2}. \end{aligned}$$
(15)

Defined functions v and u are connected with the class of GST gravity theory, characteristics of the scalar field, and cosmological dynamics as well.

As one can see, the reduced kinetic energy u is represented in terms of second-order slow-roll parameters, while the reduced potential v contains the slow-roll parameters of the first order. Therefore, we have \(u\ll v\) under conditions (13). Thus, the general slow-roll condition \(X\ll V\) is satisfied for these inflationary QCMs when \(\epsilon \ll 1\) and \(\delta \ll 1\).

Considering inflationary QCMs, we have a five-parametric \(\{V,H,F,\omega ,\phi \}\) cosmological model connected by three Eqs. (9)–(11). To investigate such a model, one can consider the scalar field potential \(V=V(\phi )\) and the Hubble parameter \(H=H(t)\) as a priori defined functions. This allows one to seek cosmological solutions for these models for any physical mechanisms of realization of the inflationary scenario and to define the corresponding type of GST gravity theory \(\{F(\phi ),\omega (\phi )\}\) and the type of scalar field evolution \(\phi (t)\) from Eqs. (9)–(11). The exact solutions for GCMs with different cosmological dynamics were considered earlier in [29,30,31,32].

However, one can also consider the inverse problem of determining the Hubble parameter H(t), the evolution of the scalar field \(\phi (t)\), and its potential \(V(\phi )\) for the chosen class of the GST gravity \(\{F(\phi ),\omega (\phi )\}\) on the basis of dynamic equations (9)–(11).

We will now consider the solution of this problem in a general form, passing from a particular case of the Brans–Dicke gravity to other types of GST gravity. Also, we will proceed from the necessity of correspondence between physically motivated potentials [18, 19] and well-known GST gravity theories [22, 23].

3 Reconstruction of cosmological dynamics

In the general case, one can consider models with arbitrary dynamics corresponding to the accelerated expansion of the universe which can be defined by choosing the dependence \(\delta =\delta (\epsilon )\) (or by directly setting the Hubble parameter \(H=H(t)\)) to define the parameters v and u as functions of cosmic time.

Nevertheless, we will define the type of cosmological dynamics in inflationary models under consideration based on the correspondence of the action (1) to well-known GST gravity theories.

For this purpose, we rewrite expressions (11)–(12) as follows

$$\begin{aligned} -\frac{1}{2}{\tilde{\omega }}(\phi )=\frac{1}{{\dot{\phi }}^{2}}\left( {\dot{H}}^{2}+H{\ddot{H}}\right) = \frac{{\tilde{F}}'^{2}}{\dot{{\tilde{F}}}^{2}}\left( {\dot{H}}^{2}+H{\ddot{H}}\right) . \end{aligned}$$
(16)

Further, on the basis of expressions (9) and (13), we obtain

$$\begin{aligned} {\tilde{\omega }}(\phi )= -\frac{1}{2}\left( \frac{{\tilde{F}}'^{2}}{{\tilde{F}}}+\frac{{\ddot{H}}}{H{\dot{H}}^{2}}\right) = -\frac{{\tilde{F}}'^{2}}{{\tilde{F}}}\left( \frac{1}{2}+\frac{\delta }{\epsilon }\right) , \end{aligned}$$
(17)

and using Eqs. (9) and (12), we get

$$\begin{aligned} \omega (\phi )=-\frac{F'^{2}}{F}\left( \frac{1}{2}+\frac{\delta }{\epsilon }\right) . \end{aligned}$$
(18)

To define the relation \(\delta /\epsilon \) in explicit form, we consider the correspondence of GST gravity action (1) to the Brans–Dicke gravity theory [22, 23] which corresponds to

$$\begin{aligned}&F(\phi )=\phi ,\quad \omega (\phi )=\frac{\omega _{\mathrm{BD}}}{\phi }. \end{aligned}$$
(19)

We have the well-known restriction on the Brans–Dicke parameter

$$\begin{aligned} -3/2<\omega _{\mathrm{BD}}<\infty , \end{aligned}$$
(20)

for the scalar field \(\phi \).

Using expressions (18) and (19), we have

$$\begin{aligned} \omega (\phi )=-\frac{1}{\phi }\left( \frac{1}{2}+\frac{\delta }{\epsilon }\right) =\frac{\omega _{\mathrm{BD}}}{\phi }. \end{aligned}$$
(21)

Thus, Eq. (21) leads to the linear connection between slow-roll parameters

$$\begin{aligned} \delta =k\epsilon , \end{aligned}$$
(22)

where k is a constant parameter.

The restriction (20) on the Brans–Dicke gravity parameter \(\omega _{\mathrm{BD}}\) implies the constraint \(k<1\) on the parameter k. Therefore, the kinetic function \(\omega (\phi )\) can be defined as

$$\begin{aligned} \omega (\phi )=-\frac{(1+2k)F'^{2}}{2F},\quad k<1. \end{aligned}$$
(23)

Further, from the expression (22) and the definition of the slow-roll parameters (13), we find the Hubble parameter

$$\begin{aligned} H(t)=\left[ (2k-1)(\alpha t-\lambda )\right] ^{1/(1-2k)}, \end{aligned}$$
(24)

where \(\alpha \) is a constant.

We call k the dynamic parameter of the inflationary models we are talking about, since the constant k determines the rate of accelerated expansion of the universe.

For the special case \(k=1/2\), we have

$$\begin{aligned} H(t)=\lambda \exp (\alpha t),\quad a(t)\propto \exp \left( \frac{\lambda }{\alpha }\exp (\alpha t)\right) , \end{aligned}$$
(25)

corresponding to double exponential expansion of the early universe.

For \(k=0\), the Hubble parameter is

$$\begin{aligned} H(t)=\lambda -\alpha t,\quad a(t)\propto \exp \left( \lambda t-\frac{\alpha }{2}t^{2}\right) . \end{aligned}$$
(26)

It corresponds to the linear deviation from the de Sitter model.

For \(k=0\) and \(\alpha =0\), we have pure exponential expansion

$$\begin{aligned} H(t)=\lambda ,\quad a(t)\propto \exp \left( \lambda t\right) , \end{aligned}$$
(27)

or the de Sitter model corresponding to the minimal coupling, since in the case \(F=1\), Eqs. (9) and (23) lead to \(H=\lambda \) and \(\omega =0\).

For the other values of the constant k, we obtain the intermediate inflation, that is, the regime of accelerated expansion of the universe between pure exponential and power-law evolutions [45,46,47].

4 The connection between the class of GST gravity and the potential

We now turn to considering the connection between the scalar field potential and the parameters of GST gravity for inflationary QCMs.

First, substituting the connection between slow-roll parameters (22) in (14), we obtain

$$\begin{aligned}&v=3-6\epsilon +(1+2k)\epsilon ^{2}. \end{aligned}$$
(28)

In addition, using the expressions (9), (13), and (24), it is not difficult to find the connection between the slow-roll parameter \(\epsilon \) and the coupling function

$$\begin{aligned}&\epsilon =\alpha H^{2(k-1)}=\alpha {\tilde{F}}^{k-1}. \end{aligned}$$
(29)

Substituting (29) into (28) and taking into account (9)–(10), we obtain the exact expression for the potential

$$\begin{aligned}&V(\phi )=V_{0}F^{2}(\phi )+V_{1}F^{k+1}(\phi )+V_{2}F^{2k}(\phi ), \end{aligned}$$
(30)

where

$$\begin{aligned}&V_{0}=3\lambda ^{2}, \quad V_{1}=-6\alpha \lambda ^{2k},\end{aligned}$$
(31)
$$\begin{aligned}&V_{2}=\alpha ^{2}(1+2k)\lambda ^{2(2k-1)}. \end{aligned}$$
(32)

Under the slow-roll condition \(\epsilon \ll 1\), the reduced potential is \(v\simeq 3\), and the scalar field potential \(V(\phi )\) can be considered as the main term only (with negligible second and third terms) in the following form

$$\begin{aligned}&V(\phi )\simeq 3\lambda ^{2}F^{2}(\phi ). \end{aligned}$$
(33)

The kinetic function defined earlier by expression (23) is as follows

$$\begin{aligned} \omega (\phi )=-\left( k+\frac{1}{2}\right) \frac{F'^{2}}{F}. \end{aligned}$$
(34)

Substituting the expression for the Hubble parameter (24) into (9), we obtain

$$\begin{aligned}&F(\phi )=\lambda ^{-2}\left[ (2k-1)(\alpha t-\lambda )\right] ^{2/(1-2k)}. \end{aligned}$$
(35)

The last expression (35) defines a functional connection between the type of a scalar field evolution \(\phi (t)\) and the coupling function \(F(\phi )\).

Thus, Eqs. (30)–(35) completely define the relations between parameters of inflationary models based on GST gravity with quadratic connection (8) and cosmological dynamics (24).

It is important to note that under the conditions \(k=\alpha =0\), from Eqs. (30)–(35), we have \(F=1\), \(\omega =0\), and \(V=3\lambda ^{2}=\Lambda \).

The GST gravity action (1) is reduced to the case of the Einstein gravity and cosmological constantFootnote 1

$$\begin{aligned} S_{\mathrm{E}} = \frac{1}{\kappa }\int \mathrm{d}^4x\sqrt{-g}\left( \frac{1}{2}R - \Lambda \right) , \end{aligned}$$
(36)

if we consider pure exponential expansion (27). It is clear that using (35) where \(k=\alpha =0\), we get \(F(\phi )=1\). Such a situation is considered for Higgs inflation [48] and in modified gravity with higher derivatives [49, 50].

Thus, the non-minimal coupling \(F(\phi )\) between the scalar field and scalar curvature induces the following: (i) a deviation of the scalar field potential from the flat one because \(V\ne const\) in (33); (ii) a deviation of the accelerated expansion regime \({\dot{H}}>-H^2 \) from the de Sitter model, because \(H\ne const\); and (iii) a determination of the evolution of the scalar field itself \(\phi (t)\).Footnote 2

Now, we will analyze the correspondence between physically motivated scalar field potentials and well-known classes of GST gravity theories in the framework of QCMs. Expression (33) in the slow-roll approximation and Eqs. (34)–(35) are the basis of our investigation of QSMs.

We also note that the use of the slow-roll approximation is a common practice for analyzing cosmological inflationary models (see, for example, [18, 19]).

4.1 Chaotic inflation with the massive scalar field

Primarily, we consider the chaotic inflation with massive scalar field [2, 18, 19, 47]

$$\begin{aligned}&V(\phi )=\frac{m^{2}}{2}\phi ^{2}. \end{aligned}$$
(37)

From Eqs. (33)–(34) we have

$$\begin{aligned}&F=\phi ,\quad m^{2}=6\lambda ^{2},\end{aligned}$$
(38)
$$\begin{aligned}&\omega (\phi )=-\frac{1+2k}{2\phi },\quad k<1. \end{aligned}$$
(39)

Thus, we see the correspondence to the Brans–Dicke gravity, where the mass of the scalar field \(m^{2}=6\lambda ^{2}\) defines the energy scale parameter.

From (35) and 38 we obtain the following scalar field evolution

$$\begin{aligned}&\phi (t)=\lambda ^{-2}\left[ (2k-1)(\alpha t-\lambda )\right] ^{2/(1-2k)}, \end{aligned}$$
(40)

corresponding to the inflationary model under consideration.

To realize the transition to pure exponential expansion \(H=\lambda \), under conditions \(k=\alpha =0\), from (37)–(40), one has \(\phi =1\), \(F=1\), \(\omega =-1/2\), \(X=-\frac{\omega }{2}{\dot{\phi }}^{2}=0\), and \(V=3\lambda ^2\) corresponding to Einstein gravity.

4.2 Chaotic inflation with quartic potential

Considering the case of chaotic inflation with quartic potential [18, 19],

$$\begin{aligned} V(\phi )=\frac{\lambda _{\mathrm{C}}}{4}\phi ^{4}, \end{aligned}$$
(41)

where \(\lambda _{\mathrm{C}}\) is a self-coupling constant of a scalar field. From expressions (33)–(34) we have

$$\begin{aligned}&F(\phi )=\xi \phi ^{2},\quad \xi = \frac{1}{2\lambda }\sqrt{\frac{\lambda _\mathrm{C}}{3}}, \end{aligned}$$
(42)
$$\begin{aligned}&\omega (\phi )=-2(1+2k)\xi . \end{aligned}$$
(43)

Thus, we find the correspondence to induced gravity [23], where the energy scale parameter \(\lambda ^{2}\) is defined by the coupling constant \(\xi \) of the scalar field and self-coupling constant \(\lambda _{\mathrm{C}}\) as

$$\begin{aligned}&\lambda ^{2}=\frac{\lambda _{\mathrm{C}}}{12\xi ^{2}}. \end{aligned}$$
(44)

From Eqs. (35) and (42), one has the corresponding evolution of the scalar field

$$\begin{aligned} \phi (t)=\pm \frac{1}{\lambda \sqrt{\xi }}\left[ (2k-1)(\alpha t-\lambda )\right] ^{1/(1-2k)}, \end{aligned}$$
(45)

corresponding to this inflationary model.

To realize the transition to the pure exponential expansion \(H=\lambda \), under conditions \(k=\alpha =0\), from (41)–(45) one has \(\phi =\pm \frac{1}{\sqrt{\xi }}\), \(F=1\), \(\omega =-2\xi \), \(X=-\frac{\omega }{2}{\dot{\phi }}^{2}=0\), and \(V=3\lambda ^2\) corresponding to Einstein gravity.

4.3 Inflation with the Higgs potential

Further, we consider inflation with the Higgs potential [18, 19, 48]

$$\begin{aligned} V(\phi )=\frac{\lambda _{H}}{4}(\phi ^{2}-\sigma ^{2})^{2}, \end{aligned}$$
(46)

where \(\lambda _{H}\) is the self-coupling constant, and \(\sigma \) is the vacuum expectation value of the Higgs field.

From expressions (33)–(34) one has non-minimal coupling [23] and the kinetic function

$$\begin{aligned}&F(\phi )=1-\xi \phi ^{2},\end{aligned}$$
(47)
$$\begin{aligned}&\omega (\phi )=-2(1+2k)\left( \frac{\xi ^{2}\phi ^{2}}{1-\xi \phi ^{2}}\right) , \end{aligned}$$
(48)

where the energy scale constant and non-minimal coupling constant are

$$\begin{aligned}&\lambda ^{2}=\frac{\lambda _{H}\sigma ^{4}}{12},\quad \xi =\sigma ^{-2}. \end{aligned}$$
(49)

The corresponding scalar field is

$$\begin{aligned} \phi (t)=\pm \sqrt{\frac{1}{\xi }-\frac{1}{\xi \lambda ^{2}}\left[ (2k-1)(\alpha t-\lambda )\right] ^{2/(1-2k)}}. \end{aligned}$$
(50)

For the transition to the pure exponential expansion \(H=\lambda \), under conditions \(k=\alpha =0\), from (46)–(50) one has \(\phi =0\), \(F=1\), \(\omega =0\), \(X=-\frac{\omega }{2}{\dot{\phi }}^{2}=0\), and \(V=3\lambda ^2\) corresponding to Einstein gravity.

4.4 Inflation with exponential potential

Now, we consider the case of exponential potential [2, 18, 47]

$$\begin{aligned} V(\phi )=3\lambda ^{2}\exp \left( -2\beta \phi \right) , \end{aligned}$$
(51)

where \(\beta \) is a positive constant. From (33)–(35), we have exponential coupling [23] and the kinetic function

$$\begin{aligned}&F(\phi )=\exp \left( -\beta \phi \right) ,\end{aligned}$$
(52)
$$\begin{aligned}&\omega (\phi )= -\beta ^{2}\left( \frac{1+2k}{2}\right) \exp \left( -\beta \phi \right) . \end{aligned}$$
(53)

From (35) and (52), one can find the scalar field evolution

$$\begin{aligned}&\phi (t)=-\frac{1}{\beta }\ln \left[ \lambda ^{-2}\left[ (2k-1)(\alpha t-\lambda )\right] ^{2/(1-2k)}\right] . \end{aligned}$$
(54)

To realize the transition to the pure exponential expansion \(H=\lambda \), under conditions \(k=\alpha =0\), from (51)–(49) one has \(\phi =0\), \(F=1\), \(\omega =-\beta ^{2}/2\), \(X=-\frac{\omega }{2}{\dot{\phi }}^{2}=0\), and \(V=3\lambda ^2\) corresponding to Einstein gravity.

As one can see, we obtain a good correspondence between the physical potentials and well-known scalar–tensor gravity theories in slow-roll approximation in QCMs. Also, one has a transition to the case of the de Sitter model based on Einstein gravity with a cosmological constant as the source of the pure exponential expansion of the universe.

On the basis of Eqs. (33)–(35), one can define the parameters of the scalar–tensor gravity theories for the other types of the physically motivated potentials [18]. On the other hand, one can reconstruct the type of scalar field potential by using expression (33) for any coupling function \(F=F(\phi )\) and the other corresponding model’s parameters from (34)–(35) as well.

Since the specific type of the inflationary scenario is unknown, we will consider a model-independent verification procedure for an arbitrary type of potential or a type of scalar–tensor gravity, which are connected by relations (33)–(34).

This approach differs from usual verification of the standard inflationary models based on Einstein gravity, in which it is necessary to determine the specific form of the scalar field potential [1, 2, 18, 19].

5 Parameters of cosmological perturbations

Let us consider verification of QCMs, proposed in Sect. 4, onto observational constraints on the cosmological perturbation parameter values.

The parameters of cosmological perturbations in inflationary models based on the action (1) with quadratic connection \(H=\lambda \sqrt{F}\) for arbitrary dynamics were considered in [29,30,31,32].

The constraints on the values of the parameters of cosmological perturbations following from observation of anisotropy of the CMB by Planck [12],

$$\begin{aligned}&A_{\mathrm{S}}=2.1\times 10^{-9},\end{aligned}$$
(55)
$$\begin{aligned}&n_{\mathrm{S}}=0.9663\pm 0.0041,\end{aligned}$$
(56)
$$\begin{aligned}&r<0.065, \end{aligned}$$
(57)

restrict the inflationary model’s parameters.

The expressions of the parameters of cosmological perturbations on the crossing of the Hubble radius were presented in [29,30,31,32] as follows

$$\begin{aligned}&{{\mathcal {P}}}_{\mathrm{S}}=A_{\mathrm{S}}=\frac{\lambda ^{2}}{16\pi ^{2}\epsilon (\epsilon -\delta )},\end{aligned}$$
(58)
$$\begin{aligned}&{{\mathcal {P}}}_{\mathrm{T}}=A_{\mathrm{T}}=\frac{2\lambda ^{2}}{\pi ^{2}},\end{aligned}$$
(59)
$$\begin{aligned}&r=\frac{{{\mathcal {P}}}_{\mathrm{T}}}{{{\mathcal {P}}}_{\mathrm{S}}}=32\epsilon (\epsilon -\delta ),\end{aligned}$$
(60)
$$\begin{aligned}&n_{\mathrm{S}}=1-4\epsilon +2\delta +2\epsilon \delta +(1-\epsilon )\left( \frac{\epsilon \delta -\xi }{\epsilon -\delta }\right) ,\end{aligned}$$
(61)
$$\begin{aligned}&n_{\mathrm{T}}=0, \end{aligned}$$
(62)

where \(A_{\mathrm{S}}\) and \(A_{\mathrm{T}}\) are the values of the power spectra of scalar and tensor perturbations \({{\mathcal {P}}}_{\mathrm{S}}\) and \({{\mathcal {P}}}_{\mathrm{T}}\) on the crossing of the Hubble radius, \(n_{\mathrm{S}}\) and \(n_{\mathrm{T}}\) are the spectral indices of scalar and tensor perturbations, and

$$\begin{aligned} \xi =\epsilon \delta -\frac{1}{H}{\dot{\delta }}\ll 1 \end{aligned}$$
(63)

is the third slow-roll parameter.

In addition, we note that the velocities of scalar and tensor perturbations for such a cosmological model are equal to the speed of light in vacuum \(c_{\mathrm{S}}=c_{\mathrm{T}}=1\) [29, 30], which correspond to the modern observational constraint \(|c_{\mathrm{T}}-1|\le 5\times 10^{-16}\) on the velocity of gravitational waves [24].

For any type of cosmological dynamics, from (58) and (60) we find

$$\begin{aligned}&\lambda ^{2}=\frac{\pi ^{2}}{2}\times A_{\mathrm{S}}\times r=\frac{\pi ^{2}}{9.5}\times 10^{-8}\times r \end{aligned}$$
(64)

for the energy scale parameter.

For the reconstructed type of the Hubble parameter (24), we have

$$\begin{aligned} \delta =k\epsilon ,\quad \xi =k(2k-1)\epsilon ^{2}. \end{aligned}$$
(65)

Substituting these expressions into Eqs. (60)–(61), we obtain

$$\begin{aligned}&r=32(1-k)\epsilon ^{2},\end{aligned}$$
(66)
$$\begin{aligned}&n_{\mathrm{S}}-1=4(k-1)\epsilon . \end{aligned}$$
(67)

Thus, from (66)–(67), one has a dynamic parameter in terms of the parameters of cosmological perturbations

$$\begin{aligned}&k=1-\frac{2}{r}(1-n_{\mathrm{S}})^{2}. \end{aligned}$$
(68)

Finally, from constraints (55)–(57) and expressions (64) and (68), we obtain the following model-independent conditions

$$\begin{aligned}&\lambda ^{2}<6.7\times 10^{-10},\end{aligned}$$
(69)
$$\begin{aligned}&k<0.973, \end{aligned}$$
(70)

on the energy scale parameter \(\lambda ^{2}\) and dynamic parameter k corresponding to verified inflationary models for any potential \(V(\phi )\), any type of the scalar–tensor gravity \(F(\phi )\), and kinetic function \(\omega (\phi )\) connected by Eqs. (33)–(34).

As one can see, the observational constraints (55)–(57) lead to the model-independent condition (70) on the dynamic parameter k corresponding to constraint (23) for the Brans–Dicke gravity.

Fig. 1
figure 1

The dependencies \(r=r(n_{\mathrm{S}})\) for the different values of the parameter k with constraints on the tensor-to-scalar ratio r due to the Planck TT,TE,EE+lowE+lensing+BAO+BICEP2/Keck Array observations [12, 13]

Full size image

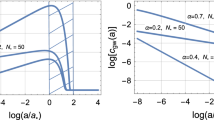
In Fig. 1, the dependence following from (68), namely

$$\begin{aligned}&r=\frac{2}{1-k}(1-n_{\mathrm{S}})^{2}, \end{aligned}$$
(71)

for different values of the dynamic parameter k is represented.

For verifying inflationary models, the values of the tensor-to-scalar ratio r and the spectral index of scalar perturbations \(n_{\mathrm{S}}\) must fall into the outer or inner regions corresponding to 68% and 95% confidence levels  [12, 13].

Also, we note that the future refinement of observational constraints (55)–(57) leads to the refinement of the condition on the constant parameters of the considered cosmological models (64) and (68) only, and it does not eliminate the possibility for the verification of such models.

Nevertheless, we note that compliance with the observational constraints on the values of the parameters of cosmological perturbations is an indirect verification of inflationary models. This statement follows from the fact that relic gravitational waves were not detected directly, and at the moment only indirect estimates of the contribution of tensor perturbations to the anisotropy and polarization of CMB are considered, which lead to an upper bound (57) on the value of tensor-to-scalar ratio [12, 13]. Also, various models of cosmological inflation can satisfy observational constraints (55)–(57); however, they can differ in the spectra of relic gravitational waves (see, for, example, [51,52,53,54, 58]).

Thus, the direct verification of these inflationary models can be carried out by the detection of relic gravitational waves at the present time. To analyze the possibility of direct detection of relic gravitational waves predicted by these models, it is necessary to consider their spectrum taking into account the specific post-inflationary evolution of the universe in the proposed cosmological models compared with standard inflationary models.

6 Stiff energy-dominated era

For the standard inflation based on Einstein gravity, the radiation-dominated (RD) era with a state parameter \(w_{\mathrm{E}}=1/3\) occurs after the end of inflation [1, 2].

The state parameter for the case of standard inflation is defined as follows [1, 2]

$$\begin{aligned} w_{\mathrm{E}}=\frac{X_{\mathrm{E}}-V_{\mathrm{E}}}{X_{\mathrm{E}}+V_{\mathrm{E}}}=-1+\frac{2}{3}\epsilon _{\mathrm{E}}, \end{aligned}$$
(72)

and one has \(w_{\mathrm{E}}\simeq -1\) at the inflationary stage for \(\epsilon _{\mathrm{E}}\ll 1\), \(w_{\mathrm{E}}=-1/3\) at the end of inflation for \(\epsilon _{\mathrm{E}}=1\), and \(w_{\mathrm{E}}=1/3\) for the transition to the radiation-dominated era with \(\epsilon _{\mathrm{E}}=2\).

Now, we consider the state parameter of a scalar field for inflationary models based on GST gravity with connection \(H=\lambda \sqrt{F}\) in terms of the reduced potential and kinetic energy (14)–(15), namely

$$\begin{aligned} w_{\mathrm{S}}=\frac{u-v}{u+v}=\frac{X-V}{X+V}=-\frac{3(1-2\epsilon )}{3-6\epsilon +4\epsilon \delta +2\epsilon ^{2}}. \end{aligned}$$
(73)

On the inflationary stage, under conditions \(\epsilon \ll 1\) and \(\delta \ll 1\), from (73) one has \(w\simeq -1\). At the end of inflation, with \(\epsilon =\delta =1\), one has \(w_{\mathrm{S}}=1\), and for the transition to the radiation-dominated era, one has \(\epsilon =\delta =2\); besides, the state parameter is \(w_{\mathrm{S}}=3/5\).

Thus, for such cosmological models, the intermediate epoch taking place between the end of inflation and the beginning of the radiation-dominated era. These intermediate epoch can be considered as the stiff energy-dominated (SD) era, as discussed in[51,52,53,54].

The generalized analysis of cosmological models implying a stiff energy-dominated era with state parameter \(1/3<w_{\mathrm{S}}\le 1\) was considered in [51,52,53,54]. The quintessential inflation implying an additional kinetic energy-dominant stage with \(w_{\mathrm{S}}=1\) was considered, for example, in [55,56,57]. The spectrum of relic gravitational waves corresponding to \(n_{\mathrm{T}}=0\) and \(w_{\mathrm{S}}>1/3\), similar to the case for the proposed cosmological models, was considered in [51].

Here, in our work, we are not limited to any specific model. We will consider an additional stiff energy-dominated era between the end of inflation and the radiation-dominated era with state parameter

$$\begin{aligned} 3/5\le w_{\mathrm{S}}\le 1 \end{aligned}$$
(74)

for an arbitrary model of cosmological inflation based on the GST gravity with connection \(H=\lambda \sqrt{F}\).

Since cosmological models with an additional SD stage imply the blue-tilted spectrum of relic gravitational waves (see, for example, [51,52,53,54]), one can estimate their maximal energy density taking into account the ultraviolet cutoff frequency of the spectrum due to the Big Bang nucleosynthesis (BBN) constraint [58].

7 Spectrum of relic gravitational waves in QCMs

Direct detection of relic gravitational waves is important for verifying the validity of the inflationary paradigm in describing the evolution of the early universe. According to inflationary cosmology, relic gravitational waves at the present time fill the universe as a stochastic background [51,52,53,54].

The energy density of relic gravitational waves \(\rho _{\mathrm{GW}}\) is usually defined in terms of the following dimensionless quantity [51,52,53,54]

$$\begin{aligned} \Omega _{\mathrm{GW}}(f)=\frac{1}{\rho _{\mathrm{c}}}\frac{d\rho _{\mathrm{GW}}}{d\log f}, \end{aligned}$$
(75)

where \(\rho _{\mathrm{c}}\) is the critical density, and f is the frequency of relic gravitational waves.

The spectrum of relic gravitational waves at the present time for the cosmological models with an additional SD stage can be defined by the expression [53, 54]

$$\begin{aligned} \Omega _{\text {GW}}(f) \simeq \Omega ^{(0)}_{\mathrm{GW}}\times \left\{ \begin{array}{ll} 1, &{}\quad f \ll f_\mathrm{RD}, \\ 1.27\times \left( {f\over f_\mathrm{RD}}\right) ^{\alpha _{\mathrm{S}}}, &{}\quad f \gg f_\mathrm{RD}, \\ \end{array} \right. \end{aligned}$$

where the plateau of the spectrum is

$$\begin{aligned} h^{2}\Omega ^{(0)}_{\mathrm{GW}}\simeq r\times 10^{-15}, \end{aligned}$$
(76)

the parameter \(\alpha _{\mathrm{S}}\) is defined by the state parameter \(w_{\mathrm{S}}\) as follows

$$\begin{aligned} \alpha _{\mathrm{S}}=2\left( \frac{3w_{\mathrm{S}}-1}{3w_{\mathrm{S}}+1}\right) , \end{aligned}$$
(77)

and \(f_{\mathrm{RD}}\) is the present-day frequency corresponding to the horizon scale at the SD-to-RD transition.

The reduced Hubble parameter at the present time is estimated as \(h\simeq 0.68\) [12].

As one can see, for the case \(w_{\mathrm{S}}=1/3\), the parameter \(\alpha _{\mathrm{S}}=0\), and the spectrum of relic gravitational waves closes to the flat one.

Also, we note that for \(f\gg f_{\mathrm{RD}}\) and \(\alpha _{\mathrm{S}}>0\), one has \(\Omega _{\mathrm{GW}}(f)\gg \Omega ^{(0)}_{\mathrm{GW}}\); that is, the energy density of relic gravitational waves can be defined as follows

$$\begin{aligned}&h^{2}\Omega _{\mathrm{GW}}(f)\simeq 1.27\times r \times 10^{-15}\times \left( \frac{f}{f_{\mathrm{RD}}}\right) ^{\alpha _{\mathrm{S}}}. \end{aligned}$$
(78)

Now, we consider the LIGO bound,Footnote 3 which can be obtained from LIGO optimal sensitivity \(\Omega _{\mathrm{GW}}\simeq 10^{-9}\) for the gravitational waves with frequencies \(f\simeq 10^{2}\) Hz [59]; that is, one has the following constraint

$$\begin{aligned}&\Omega _{\mathrm{GW}}(f\simeq 10^{2}\,\mathrm{Hz})<10^{-9}. \end{aligned}$$
(79)

Thus, to match the Planck constraint on the value of the tensor-to-scalar ratio (57) and the LIGO bound on the energy density of gravitational waves (79), we will use expression (78) and obtain

$$\begin{aligned}&f_{\mathrm{RD}}\gtrsim 100\times \exp \left[ -\frac{13.6+\ln \left( \frac{h^{2}}{r}\right) }{\alpha _{\mathrm{S}}}\right] ~\mathrm{Hz}. \end{aligned}$$
(80)

On the basis of the state parameter of stiff energy for the cosmological models under consideration (74) and expressions (77) and (80), we obtain

$$\begin{aligned}&10^{-10}\,\mathrm{Hz}\lesssim f_{\mathrm{RD}}\lesssim 10^{-5} \,\mathrm{Hz},\end{aligned}$$
(81)
$$\begin{aligned}&4/7\le \alpha _{\mathrm{S}}\le 1. \end{aligned}$$
(82)

To find the cutoff frequency of the spectrum of relic gravitational waves \(f_{*}\), one can use the BBN constraint [58]

$$\begin{aligned} \int ^{f_{*}}_{f_{\mathrm{BBN}}}h^{2}\Omega _{\text {GW}}(f)\frac{\mathrm{d}f}{f}\le 1.12\times 10^{-6}, \end{aligned}$$
(83)

where \(f_{\mathrm{BBN}}\simeq 1.41\times 10^{-11} \,\mathrm{Hz}\).

This constraint is derived from the fact that a large gravitational wave energy density at the time of BBN would alter the abundance of the light nuclei produced in this process.

Taking into account that \(f_{*}\gg f_{\mathrm{RD}}\) and \(f_{*}\gg f_{\mathrm{BBN}}\) from (78) and (83), one has

$$\begin{aligned} 1.27\times r\times \left( \frac{f_{*}}{f_{\mathrm{RD}}}\right) ^{\alpha _{\mathrm{S}}} \le 1.12\times 10^{9}\times \alpha _{\mathrm{S}}. \end{aligned}$$
(84)

Thus, from the constraint on the value of the tensor-to-scalar ratio (57) and (81)–(82), one has the following cutoff frequency of the spectrum of relic gravitational waves

$$\begin{aligned} 10^{5} \,\mathrm{Hz}\lesssim f_{*}\lesssim 2\times 10^{7} \,\mathrm{Hz}. \end{aligned}$$
(85)

After substituting (81) and (85) into (78), we obtain the following energy density of gravitational waves at the present era

$$\begin{aligned} \Omega _{\mathrm{GW}}(f_{*})\lesssim 1.3\times 10^{-6}, \end{aligned}$$
(86)

corresponding to cutoff frequency (85).

Fig. 2
figure 2

The spectra of relic gravitational waves \(\Omega _{\mathrm{GW}}=\Omega _{\mathrm{GW}}(f)\) on a logarithmic scale with the BBN constraint and LIGO bound for the stiff energy state parameter \(3/5\le w_{\mathrm{S}}\le 1\) (\(4/7\le \alpha _{\mathrm{S}}\le 1\)) and without the SD stage for \(w=1/3\) (\(\alpha _{\mathrm{S}}=0\))

Full size image

Figure 2 shows the spectra of relic gravitational waves predicted in the proposed inflationary models. The energy density corresponding to the flat part of the spectra is \(\Omega _{\mathrm{GW}}\simeq 1.8\times 10^{-16}\), and the maximum energy density \(\Omega ^{(max)}_{\mathrm{GW}}(f_{*})\simeq 1.3\times 10^{-6}\) due to (86) corresponds to the frequency range (85).

The dimensionless amplitude of relic gravitational waves can be obtained from the expression [58, 62]

$$\begin{aligned} h_{\mathrm{c}}(f)=1.26\times 10^{-18}\left( \frac{\mathrm{Hz}}{f}\right) \sqrt{h^{2}\Omega _{\mathrm{GW}}(f)}. \end{aligned}$$
(87)

Thus, the maximal amplitude of relict gravitational waves with frequencies (85) and energy density (86) is

$$\begin{aligned} 1\times 10^{-26}\lesssim h_{\mathrm{c}}(f_{*})\lesssim 5\times 10^{-29}. \end{aligned}$$
(88)

After estimating the parameters of relic gravitational waves in the proposed cosmological models, we will consider the possibility of detecting them.

As a promising method for registration of low-frequency gravitational waves, the use of the satellite cluster as an interferometric gravitational wave detector can be considered [38,39,40].

For such projected satellite detectors, namely for the Laser Interferometer Space Antenna (LISA) [39] and the Deci-Hertz Interferometer Gravitational-Wave Observatory (DECIGO) [40], the best sensitivities are [41]

$$\begin{aligned}&\Omega ^{(\mathrm{LISA})}_{\mathrm{GW}}(f_{\mathrm{L}}\simeq 10^{-3}\,\mathrm{Hz})\simeq 3\times 10^{-14}, \end{aligned}$$
(89)
$$\begin{aligned}&\Omega ^{(\mathrm{DECIGO})}_{\mathrm{GW}}(f_{\mathrm{D}}\simeq 10^{-1} \,\mathrm{Hz})\simeq 5\times 10^{-17}. \end{aligned}$$
(90)

From expressions (78) and (81)–(82) we obtain the following maximal energy density of relic gravitational waves for the frequencies \(f_{\mathrm{L}}\simeq 10^{-3}\) Hz and \(f_{\mathrm{D}}\simeq 10^{-1}\) Hz predicted in QCMsFootnote 4

$$\begin{aligned}&2\times 10^{-14}\lesssim \Omega _{\mathrm{GW}}(f=f_{\mathrm{L}})\lesssim 2\times 10^{-12},\end{aligned}$$
(91)
$$\begin{aligned}&2\times 10^{-12}\lesssim \Omega _{\mathrm{GW}}(f=f_{\mathrm{D}})\lesssim 2\times 10^{-11}. \end{aligned}$$
(92)

Also, for the standard inflation with \(\alpha _{\mathrm{S}}=0\) from (76), we get

$$\begin{aligned}&\Omega ^{(0)}_{\mathrm{GW}}\simeq 2\times 10^{-16}. \end{aligned}$$
(93)

Thus, the relic gravitational waves predicted in QCMs can in principle be registered by LISA and DECIGO, and for the case of standard inflation, relic GWs with frequency close to \(f\simeq 10^{-1}\) Hz can be registered by DECIGO as well.

Thus, a joint data analysis from the future observations of LISA and DECIGO can make it possible to determine what type of cosmological inflationary model is correct: models with an additional stage of stiff energy domination or standard inflation.

However, it should be noted that the implementation of such projects is expected no earlier than the 2030s [41].

Also, the method of direct verification of the proposed QCMs is the registration of high-frequency relic gravitational waves in a frequency range (85) with amplitudes (88), corresponding to a maximum energy density (86).

Among the existing and prospective detectors of high-frequency gravitational waves [42], part of this frequency range \(f=1{-}13\) MHz is covered by the ground-based Fermilab Holometer with sensitivity \(h_{\mathrm{c}}\simeq 8\times 10^{-22}\) [42,43,44], which consists of two co-located power-recycled Michelson interferometers. On the basis of expression (88), we can conclude that relic gravitational waves predicted by QCMs cannot be registered by this detector.

Thus, a significant improvement in the sensitivity of gravitational wave detectors in frequency range (85) is required for direct verification of these cosmological models by registration of the high-frequency gravitational waves.

8 Conclusion

In this work, we considered the models of cosmological inflation based on the generalized scalar–tensor theory of gravity with a quadratic coupling between the Hubble parameter and the non-minimal coupling function (8). In these QCMs, the de Sitter stage induced by a cosmological constant corresponds to the Einstein gravity, while the non-minimal coupling between the scalar field and the scalar curvature leads to the deviations from the de Sitter stage. Therefore, the correspondence of the theory of gravity at present to the case of general relativity (minimal coupling) leads naturally to the \(\Lambda \)CDM model [63,64,65] to describe the second accelerated expansion of the universe within the framework of the QCMs. It is necessary to note that the \(\Lambda \)CDM model is in good agreement with observational data for the current stage of the universe’s evolution [12].

Obviously, it is necessary to determine the relationship between the physically motivated scalar field potentials and well-known types of GST gravity. Such a relationship was found for a particular type of inflationary dynamics corresponding to the Hubble parameter (24).

In contrast to inflationary models based on general relativity, QCMs are verified by observational constraints on the values of cosmological perturbation parameters for an arbitrary potential of the scalar field, that is, for an arbitrary realization of the inflationary scenario.

Observational constraints on the values of cosmological perturbation parameters (55)–(57) restrict only the values of two constant parameters of QCMs, namely, the inflationary energy scale parameter \(\lambda ^{2}\) and the dynamic parameter k, which determines the expansion rate of the early universe. This result is achieved not by choosing the parameters of the cosmological model, but by means of the certain relationship (8) between the model’s parameters. Obviously, using the relation (8) is not the only way to obtain verifiable cosmological models. However, this approach provides new opportunities to construct phenomenologically correct cosmological models on the basis of certain relations between the model’s parameters regardless of how the inflationary scenario was implemented.

Thus, such an approach differs significantly from the reconstruction procedure of the scalar field potential from the parameters of cosmological perturbations in the framework of GR [14, 15] or from the reconstruction of modified gravity theories from the universe expansion history [3, 4], which also imply different inflationary scenarios.

As an interesting feature of the proposed cosmological models, we note that the restriction on the dynamic parameter \(k<0.973\) which follows from the constraints on the parameters of cosmological perturbations (55)–(57) corresponds to the restriction \(k<1\) following from the constraint on the Brans–Dicke gravity (20) for any type of inflationary models based on STG with relation (8).

Another property of QCMs is the presence of the stiff energy-dominant stage after the end of inflation and before the beginning of the radiation-dominant stage. In these models, the stiff energy state parameter has a fairly wide range of values \(3/5\le w_{\mathrm{S}}\le 1\), which affects the spectrum of relic gravitational waves.

An analysis of the spectrum of relic gravitational waves in the proposed models allowed us to determine the frequency range \(10^{5}~Hz\lesssim f_{*}\lesssim 2\times 10^{7}\) Hz in which their energy density is maximal. However, in this range, the sensitivity of modern detectors of high-frequency gravitational waves is insufficient for direct registration.

Nevertheless, the low-frequency relic gravitational waves predicted in the proposed cosmological models can in principle be registered in future measurements by advanced low-frequency gravitational wave satellite detectors [39,40,41], which is an additional way to verify the proposed cosmological models.