1 Introduction

Dark energy, inflation, and dark matter are examples of much disputed concepts that have been added to Einstein’s General Relativity (GR) in order to explain observations that otherwise would not be accounted for, see e.g. [1,2,3]. The cosmological constant, as its value adjusted to fit the current accelerated expansion of the universe is far at odds with the calculated vacuum energy of matter which it is supposed to represent. Quintessence [4,5,6,7,8,9,10,11,12,13,14,15] – and similar scalar fields invoked to generate an initial explosive inflation of the universe and explain the measured isotropy of cosmic radiation – lack fundamental physical underpinning. Modifications of the gravity are, among other models, hand-crafted just for matching specific observations. The invisible dark matter, finally, necessary to explain the dynamics of galaxies, could not yet been attributed to any field theory, or a known or unknown particle, despite astronomical budgets devoted to its search [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36].

Recently a novel, rigorously derived covariant canonical gauge theory of gravity (CCGG) has been applied to Friedman cosmology. CCGG is based on the covariant version of the canonical transformation theory with which all gauge theories are derived on the same footing. The difference is just the symmetry group under consideration delivering the appropriate minimal coupling scheme for matter fields and the dynamical space-time. Such a “universal” approach must of course be subject to a comprehensive testing against all kinds of experiments, especially as CCGG is its novel application to gravity. In that study [37] CCGG was shown to deliver an explanation of dark energy as a torsion based phenomenon For earlier investigations on the possible cosmological role of torsion see for example [38,39,40,41,42,43, 43,44,45]. There a first analysis of the CCGG-Friedman cosmology was limited to varying the only new parameter beyond \(\Lambda \)CDM. The comparison of the theory with the Hubble diagram indicated that the model can deliver viable scenarios of cosmic evolution.

In this paper that preliminary analysis is extended to Bayesian analysis with the aim to explore further cosmological constraints on the full parameter set, and to compare the results with the standard \(\Lambda \)CDM cosmology. After a brief review of the CCGG theory and the pertinent Friedman equations we first list the observational data considered with focus on low z. A discussion of the numerical analysis and the resulting figures follows. The paper concludes with a discussion of the findings.

2 The CCGG formulation

Rather than following ad-hoc or trial-and-error approaches for modifying GR for compatibility with experiments, we rely ab initio on the powers of proven comprehensive mathematical frameworks. In analogy to point particle physics we apply the covariant, field theoretical version of the canonical transformation theory in the De Donder-Hamiltonian formalism to imprint a given symmetry on a system of covariant fields. In this way a consistent interaction of gravity with matter is derived as laid out in Refs. [46,47,48,49,50,51]. This approach yields the Covariant Canonical Gauge Gravity (CCGG), a Yang-Mills type theory in the spirit of Utiyama, Sciama, Kibble, Hayashi and Shirafuji, and Hehl [52,53,54,55,56], rooted in a few key assumptions. While Einstein’s Principle of General Relativity translates into the requirement of diffeomorphism invariance of the coupled dynamics of matter and space-time, the Equivalence Principle is incorporated by defining at any point of space-time an inertial (observers’) frame of reference. The pertinent mathematical structure is a (“Lorentzian”) frame bundle with fibers spanned by ortho-normal bases fixed up to arbitrary (local) Lorentz transformations. The gauge group underlying the CCGG approach is thus the \(SO(1,3)^{(+)} \times Diff(M)\) group. The emerging gauge fields are the (spin) connection coefficients not restricted to torsion-free and/or metric compatible geometries. The gauge field is a priori independent of the metric tensor, or equivalently of the vierbein fields, which come as fundamental structural elements of the Lorentzian manifold. Minimal couplings are discovered in that way, not postulated a priori. Of course, the structure of the dynamical space-time is dynamically implemented by a specific choice of the Hamiltonian of free gravity, but that remains the only freedom the theory leaves open.

In order to secure the existence of the action integral in the Hamiltonian picture we also postulate non-degeneracy of the Lagrangian and the corresponding Hamiltonian densities, which implies that the Lagrangian must contain an at least quadratic Riemann–Cartan tensor concomitant [57]. A quadratic term is therefore added as a parameter-controlled deformation to Einstein’s linear ansatz, endowing space-time with kinetic energy and thus inertia. In this way the framework delivers a classical, quadratic, first-order (Palatini) field theory where the connection coefficients emerge as independent gauge fields which, in addition to the symmetric metric tensor, determine the space-time geometry and mediate gravitation. The couplings of matter fields and gravity are unambiguously fixed. The so called consistence equation in CCGG is a combination of the canonical (or equivalently Euler–Lagrange) equations of motion, extending the field equation of GR:

$$\begin{aligned} \begin{aligned}&g_1\left( R_{\alpha \beta \gamma \mu }\, {{R}^{\alpha \beta \gamma }_\nu } - {\textstyle \frac{1}{4}}g_{\mu \nu } \, {R}_{\alpha \beta \gamma \delta }\, {R}^{\alpha \beta \gamma \delta }\right) \\&\quad - \frac{1}{8\pi G}\, \left[ {{R}_{(\mu \nu )}} - g_{\mu \nu } \left( {\textstyle \frac{1}{2}}{R} + \lambda _0 \right) \right] = {{T}_{(\mu \nu )}}. \end{aligned} \end{aligned}$$
(1)

Here \(g_1\) is the dimensionless deformation parameter, G Newton’s coupling constant, and \(\lambda _0\) the “bare” cosmological constant.

$$\begin{aligned} {R^{\alpha }_{\beta \mu \nu }} = {\gamma ^{\alpha }_{\beta \nu ,\mu }} - {\gamma ^{\alpha }_{\beta \mu ,\nu }} + {\gamma ^{\alpha }_{\xi \mu }}{\gamma ^{\xi }_{\beta \nu }} - {\gamma ^{\alpha }_{\xi \nu }}{\gamma ^{\xi }_{\beta \mu }} \end{aligned}$$
(2)

is the Riemann–Cartan tensor (in general built from an asymmetric connection), and \({{T}_{(\mu \nu )}}\) the symmetrized stress-energy tensor of matter. (Our conventions are the signature \((+,\,-,\,-,\,-)\) of the metric, and natural units \(\hbar = c = 1\). A comma indicates a partial derivative.)

3 The CCGG-Friedman universe

3.1 Homogenous solution

Our aim is to establish a form of the equations governing the dynamics of the universe that allow for a close comparison with GR. In particular we require that the stress-energy tensor be covariantly conserved. This requirement is here not based on the Bianchi identity for the Einstein tensor. It is invoked independently to retain the standard scaling properties of matter and radiation. As shown in Ref. [37] this leads, in a metric compatible space-time, to the necessity to invoke torsion. For the CCGG version of the Friedman model that promotes the cosmological constant to the time or scale dependent function

$$\begin{aligned} \Lambda (a) =: \lambda _0 + {\textstyle \frac{1}{4}}P(a) =: \Lambda \,f(a). \end{aligned}$$

P(a) is the torsion-dependant portion of the Ricci scalar. \(\Lambda (a)\) reduces to the “bare” cosmological constant \(\lambda _0\) in torsion-free geometries. The Hubble function acquires, in addition, a further geometric correction originating from the quadratic Riemann–Cartan gravity. We ultimately get

$$\begin{aligned} E^2(a)=: & {} \frac{H^2(a)}{H_0^2} = \frac{\rho (a)}{\rho _{crit}} \end{aligned}$$
(3a)
$$\begin{aligned} \rho (a)=: & {} \rho _m + \rho _r + \rho _\Lambda + \rho _{K} + \rho _{geom} \end{aligned}$$
(3b)
$$\begin{aligned} \rho _m(a)=: & {} \rho _{crit} \,\Omega _m \,a^{-3} \end{aligned}$$
(3c)
$$\begin{aligned} \rho _r(a)=: & {} \rho _{crit} \,\Omega _r \,a^{-4} \end{aligned}$$
(3d)
$$\begin{aligned} \rho _{K}(a)=: & {} \rho _{crit} \,\Omega _{K} \,a^{-3} = -\rho _{crit} \,K \,a^{-2} \end{aligned}$$
(3e)
$$\begin{aligned} \rho _\Lambda (a)=: & {} \rho _{crit} \,\Omega _\Lambda \,f(a) = \rho _{crit} \,{\textstyle \frac{1}{3}}\Lambda \, f(a) \end{aligned}$$
(3f)
$$\begin{aligned} \rho _{geom}(a)=: & {} \rho _{crit} \, \Omega _{\text {geom}} \end{aligned}$$
(3g)
$$\begin{aligned}= & {} \rho _{crit} \,\frac{(1/4 \Omega _m + \Omega _\Lambda )(3/4 \Omega _m + \Omega _r)}{\Omega _g - 1/4 \Omega _m -\Omega _\Lambda }, \end{aligned}$$
(3h)

where a is the scale factor and K the curvature parameter of the FLRW metric. \(\Omega _i\) with \(i=m,r,\Lambda , K\) are the standard density constants related respectively to (dark) particle matter, radiation and dark energy. \(H(a) = \dot{a}/a\) is the Hubble function, \(H_0 \equiv H(a = 1)\) the Hubble constant, and \(\rho _{crit} \equiv 3H_0^2/8 \pi G)\). For convenience we use \(\Omega _g =: [32\pi G H_0^2 g_1]^{-1}\). We notice at this point that the various pressure terms combine to

$$\begin{aligned} p(a) =: {\textstyle \frac{1}{3}}\,\rho _r - \rho _\Lambda - {\textstyle \frac{1}{3}}\, \rho _{K} + {\textstyle \frac{1}{3}}\, \rho _{geom}. \end{aligned}$$
(4)

Obviously the cosmological function has the equation of state \(p_\Lambda = -\rho _\Lambda \) of dark energy, and the “geometric fluid” has the equation of state \(p_{geom} = {\textstyle \frac{1}{3}}\, \rho _{geom}\), i.e. it behaves like (dark) radiation.

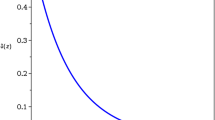
The normalized dark energy function, f(a), is determined from the ordinary first-order, non-linear differential equation

$$\begin{aligned} f'(a) = \frac{3\Omega _m}{4\Omega _\Lambda \, a^4} \frac{ \alpha (a)}{\beta (a) }. \end{aligned}$$
(5)

where:

$$\begin{aligned} \alpha (a)= & {} \Omega _g \left( {\textstyle \frac{3}{4}}\Omega _m a^{-3} + \Omega _r a^{-4}\right) \\&- \left( \Omega _g - {\textstyle \frac{1}{4}}\Omega _m a^{-3} - \Omega _\Lambda \,f \right) \left( {\textstyle \frac{1}{4}}\Omega _m a^{-3} + \Omega _\Lambda \,f \right) , \\ \beta (a)\!= & {} \! \Omega _g \left( {\textstyle \frac{3}{4}}\Omega _m a^{-3} \!\!+\!\! \Omega _r a^{-4}\right) \!+\! \left( \Omega _g \!-\! {\textstyle \frac{1}{4}}\Omega _m a^{-3} \!-\! \Omega _\Lambda \,f \right) ^2\!, \end{aligned}$$

with the boundary condition \(f(1) = 1\). By setting \(g_1 = 0\) (which means \(f'(a) = 0\)) and \(f(a) \equiv 1\) we recover in Eq. (3) the Einstein–Friedman equation for the Hubble function based on General Relativity. There are five independent parameters in the CCGG model that must be optimized, namely \(\Omega _m,\Omega _r,\Omega _\Lambda ,\Omega _K\) and \(\Omega _{\text {geom}} \). By solving \(H_0 = H(a = 1)\), we get the relation for the additional, deformation parameter:

$$\begin{aligned} g_1 = \frac{1}{ 2 \pi G H_0^2 }\frac{ \Omega _K +\Omega _\Lambda +\Omega _m+\Omega _r-1}{(4 \Omega _\Lambda +\Omega _m) ( 4 \Omega _ \Lambda +\Omega _m + 4 \Omega _K - 4 )}. \end{aligned}$$
(6)

Notice that for the standard \(\Lambda \)CDM model (with a spatial curvature \(\Omega _K\)) the sum \(\Omega _K +\Omega _\Lambda +\Omega _m+\Omega _r\) gives 1 and thus from Eq. (6) we get \(g_1 = 0\).

3.2 Stability analysis

In order to test the stability of the model we use the autonomous system method [58, 59]. For simplicity we ignore the spacial curvature and the radiation part and include matter, dark energy and the quadratic term that incorporates the torsional part. In that case the correct definition for the dimensionless parameters reads:

$$\begin{aligned} \begin{aligned} x^2=\frac{\Omega _m}{a^3 E^2},\quad y^2=\frac{\Omega _\Lambda (a)}{E^2},\quad z^2=\frac{\Omega _{geom}}{E^2} \end{aligned} \end{aligned}$$
(7)

with \(x^2 + y^2 + z^2 = 1\). After some algebra, one can define the evaluation equations for the system:

$$\begin{aligned} \frac{dx}{dN}= & {} \frac{x}{2} \left( -x^2-4 y^2+1\right) , \end{aligned}$$
(8a)
$$\begin{aligned} \frac{dy}{dN}= & {} \frac{3 x^2 \left( x^2+y^2-1\right) \left( x^2+4 y^2-2\right) }{y \left( 7 x^4+4 x^2 \left( 8 y^2-5\right) +16 \left( y^2-1\right) ^2\right) }\nonumber \\&-\frac{1}{2} y \left( x^2+4 y^2-4\right) , \end{aligned}$$
(8b)

where \(N = \log (a)\). By setting \(x'(N) = y'(N) = 0\), three solutions for the system are discovered. In order to estimate the stability of those points, we evaluate the matrix that contains the derivatives of the system.

Fig. 1
figure 1

The stream plot for a universe with dark matter, dynamical dark energy \(\Lambda (a)\) and the quadratic term from the CCGG equations. The x refers to the matter part and the y refers to the dark energy density. The figure shows that the matter domination (B) is an unstable point and the dark energy domination (C) is a stable point

Full size image
Table 1 Observational constraints and the corresponding \(\chi ^{2}_\mathrm{min}\) for the CCGG model with uniform prior and with the SH0ES prior, and \(\Lambda \)CDM model. Here we set \(\Omega _K = 0\)
Full size table

Figure 1 shows the stream plot for the system. Point \(A (x=0,y=0)\) describes domination of the quadratic term. The eigenvalues at that point, \(\lambda _{1,2} = 4, 1\), are both positive, which indicates an unstable point. Point \(B (x=1,y=0)\) where matter dominates the universe is also unstable as the eigenvalues of the point are \(\lambda _{1,2} = -3,+3\). In contrast, point \(C (x=0,y=1)\) with dark energy domination and the eigenvalues \(\lambda _{1,2} = -3,-20\) is stable. The solution shows the evolution from point A to C with matter domination during the evolution of the universe.

4 Cosmological probes

4.1 Dataset

In order to constraint our model, we deploy the following data sets: Cosmic Chronometers (CC) exploit the evolution of differential ages of passive galaxies at different redshifts to directly constrain the Hubble parameter [60]. We use uncorrelated 30 CC measurements of H(z) discussed in [61,62,63,64]. As Standard Candles (SC) we use uncorrelated measurements of the Pantheon Type Ia supernova [65] that were collected in [66]. The parameters of the models are adjusted to fit the theoretical \(\mu _{i}^{th}\) value of the distance modulo,

$$\begin{aligned} \mu =m-M=5\log _{10}((1+z) \cdot D_{M})+\mu _{0}, \end{aligned}$$
(9)

to the observed \(\mu _{i}^{obs}\) value. m and M are the apparent and absolute magnitudes and \(\mu _{0}=5\log \left( H_{0}^{-1}/Mpc\right) +25\) is the nuisance parameter that has been marginalized. The luminosity distance is defined by \(D_L = (1+z)\, D_M\), where

$$\begin{aligned} D_M=\frac{c}{H_0} S_k\left( \int _0^z\frac{dz'}{E(z')}\right) , \end{aligned}$$
(10)

and

$$\begin{aligned} S_k(x) = {\left\{ \begin{array}{ll} \frac{1}{\sqrt{-\Omega _K}}\sinh \left( \sqrt{-\Omega _K}x\right) &{}\quad {\text {if }} \Omega _K<0 \\ x &{}\quad {\text {if }} \Omega _K=0 \\ \frac{1}{\sqrt{\Omega _K}}\sin \left( \sqrt{\Omega _K} x\right) \quad &{}\quad {\text {if }} \Omega _K>0. \end{array}\right. } \end{aligned}$$
(11)
Fig. 2
figure 2

The upper panel shows the CCGG best fit vs. the Cosmic Chronometers dataset. The lower panel shows the the CCGG best fit vs. 40 uncorrelated points of the Type Ia supernova dataset. The dataset is presented in red, and the best fit is presented in blue color

Full size image
Fig. 3
figure 3

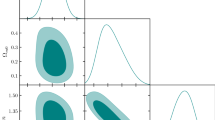
One- (68\(\%\) CI) and two-dimensional (68\(\%\) and 95\(\%\) CI) marginalized posterior distributions for the relevant sampled and derived CCGG parameters. The upper left panel shows the contour for \(\Omega _m\) vs. \(\Omega _\Lambda \) and the right upper panel shows the contour for \(\Omega _m\) vs. \(H_0\). The lower left panel shows the contour for \(g_1\) vs. \(H_0\) and the lower upper panel shows the contour for \(r_d\) vs. \(H_0\). The gray contour describes the CCGG best fit with a uniform prior. The red contour describes the CCGG best fit with the SH0ES measurement as a prior. Finally, the blue contour describes the \(\Lambda \)CDM best fit with a uniform prior

Full size image
Fig. 4
figure 4

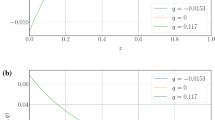
One- (68\(\%\) CI) and two-dimensional (68\(\%\) and 95\(\%\) CI) marginalized posterior distributions for the the deceleration parameter q vs. the Hubble parameter \(H_0\). The gray contour describes the CCGG best fit with a uniform prior. The red contour describes the CCGG best fit with the SH0ES measurement as a prior. Finally, the blue contour describes the \(\Lambda \)CDM best fit with a uniform prior. The lower panel shows a 3D of q and the parameter \(g_1\) vs. the Hubble parameter \(H_0\)

Full size image

In addition, we use the uncorrelated data points from different Baryon Acoustic Oscillations (BAO) collected in [67] from [68,69,70,71,72,73,74,75,76,77,78,79]. Studies of the BAO features in the transverse direction provide a measurement of \(D_H(z)/r_d = c/H(z)r_d\), with the comoving angular diameter distance defined in [80, 81]. In our database we use the parameters \(D_A = D_M/(1+z)\) and

$$\begin{aligned} D_V(z) \equiv [ z D_H(z) D_M^2(z) ]^{1/3}. \end{aligned}$$
(12)

which is a combination of the BAO peak coordinates. \(r_d\) is the sound horizon at the drag epoch. Finally, for very precise “line-of-sight” (or “radial”) observations, BAO can also measure directly the Hubble parameter [82].

We use a nested sampler as it is implemented within the open-source packaged Polychord [83] with the GetDist package [84] to present the results. The prior we choose is with a uniform distributions, where \(\Omega _{r} \in [0;10^{-3}]\), \(\Omega _{m}\in [0.;1.]\), \(\Omega _{\Lambda }\in [0.;1.]\), \(H_0\in [50;100] {\text { km/s/Mpc}}\), \(r_d\in [120;160]\) Mpc. When we include a spatial curvature we extend the prior with \(\Omega _{K} \in [-0.1;0.1]\). The measurement of the Hubble constant yielding \(H_0 = 74.03 \pm 1.42 {\text { (km/s)/Mpc}}\) at \(68\%\) CL by [85] has been incorporated into our analysis as an additional prior (R19). We contrast best-fit parameters and goodness of fit between CCGG and the standard \(\Lambda \)CDM with these datasets. We also compare the Akaike information criteria (AIC) of the two models applied to the data set [86,87,88]. In order to make a complete discussion, we include also the deceleration parameter in our discussion, the dimensionless quantity \(q = - 1 - \dot{H}/H^2\) measuring the acceleration of the cosmic expansion.

Fig. 5
figure 5

One- (68\(\%\) CI) and two-dimensional (68\(\%\) and 95\(\%\) CI) marginalized posterior distributions for the the deceleration parameter \(\Omega _K\) vs. the Hubble parameter \(H_0\). The gray contour describes the CCGG best fit with a uniform prior. The red contour describes the CCGG best fit with the SH0ES measurement as a prior.The table shows Observational constraints and the corresponding \(\chi ^{2}_\mathrm{min}\) for the CCGG model with uniform prior and with the SH0ES prior with spatial curvature

Full size image

4.2 Spatially flat universe

Table 1 summarises the results with \(\Omega _K = 0\). In the CCGG model the quadratic term provides with the deformation parameter an additional degree of freedom. Hence while for \(\Lambda \)CDM we set \(\Omega _r = 1-\Omega _m - \Omega _\Lambda \) for the radiation part, for CCGG we have \(\Omega _{\text {geom}} = 1- \Omega _m - \Omega _\Lambda - \Omega _r\) for the additional geometry term. The Hubble parameter fitted for the CCGG model is \(69.3\pm 1.1 {\text { km/s/Mpc}}\) for a uniform prior or \(71.26\pm 0.75 {\text { km/s/Mpc}}\) with the SH0ES prior. The Hubble parameter for the \(\Lambda \)CDM model is in between these values \(70.18\pm 0.86 {\text { km/s/Mpc}}\) for the uniform prior.

The \(\Omega _m\) matter part in the CCGG model is \(0.29 \pm 0.016\) or \(0.28\pm 0.014\) for the SH0ES prior, which is a bit higher then the \(\Lambda \)CDM fit \(0.25\pm 0.06\). The dark energy \(\Omega _\Lambda \) part is being \(0.71\pm 0.09\) or \(0.72\pm 0.09\) with the SH0ES prior, a bit lower then the \(\Lambda \)CDM fit \(0.74\pm 0.04\).

The BAO scale is set by the redshift at the drag epoch \(z_d \approx 1020\) when photons and baryons decouple [89]. For a flat \(\Lambda \)CDM, the Planck measurements yield \(147.09 \pm 0.26 Mpc\) and the WMAP fit gives \(152.99 \pm 0.97 {\text { Mpc}}\) [90]. Final measurements from the completed SDSS lineage of experiments in large-scale structure provide \(r_d = 149.3 \pm 2.8{\text { Mpc}}\) [91]. The \(\Lambda \)CDM model for the combined data set we use gives \(146.1\pm 1.8{\text { Mpc}}\). However, the CCGG model gives \(147.4\pm 2.4{\text { Mpc}}\). For the SH0ES prior, the distance is \(143.8\pm 1.62{\text { Mpc}}\). The quadratic term thus changes the horizon scale in the early universe, but still in a moderate and reasonable range.

From the AIC we see that \(\Lambda \)CDM is still the better fit to the late universe, since the AIC for \(\Lambda \)CDM model 84.87 is then the CCGG case 88.51 or with SH0ES prior 86.89. However the \(\Lambda \)CDM model does not describe the inflationary epoch, which the quadratic term naturally provides.

4.3 With \(\Omega _K \ne 0\)

The shape of the universe is a fundamental question. The latter can be characterized by measuring the spatial curvature of the universe K, quantifying how much the spatial geometry locally differs from that of flat space. Most models of inflation predict a universe which is extremely close to being spatially flat [90, 92, 93]. Because of the quadratic term the spatial curvature may be larger. Figure 5 shows the spatial curvature vs. the Hubble parameter. For the uniform prior case the spatial curvature turns out to be \(\left( 0.0134 \pm 5.53\right) \cdot 10^{-2}\), while for the SH0ES prior the spatial curvature is \(\left( 2.12 \pm 4.54 \right) \cdot 10^{-2}\). The model predicts a positive value for \(\Omega _K\) but the error bar is sufficient large for the negative values as well. Moreover, from the AIC criteria it seems that the case for absorbing the spatial curvature is better since the AIC for this case is higher: 87.84 for the uniform prior, and 88.61 for the SH0ES prior.

5 Discussion

This paper discusses the cosmological constraints on the CCGG formulation from low-redshift observations. CCGG is a gauge theory of gravity ensuring in a covariant way full diffeomorphism invariance of the system action. Using canonical transformation theory the approach unambiguously fixes how matter fields interact with curved geometry of space-time, and enforces a parameter controlled admixture of a quadratic Riemann–Cartan concomitant to the Einstein–Hilbert linear term. In a preliminary study [37] the cosmological consequence of that quadratic extension were examined in alignment with the \(\Lambda \)CDM model. Here we go a step further and test the CCGG cosmology against a comprehensive database of low-redshift cosmological measurements that include the Pantheon Type Ia supernova, Cosmic Chronometers and Baryon Acoustic Oscillations.

Using the Polychord package we find a good best fit of the CCGG cosmology with data. By the AIC criterium the CCGG fit accuracy is comparable with that of \(\Lambda \)CDM. The key density parameters are in reasonable agreement with the \(\Lambda \)CDM model. The new free parameter of the theory controlling the admixture of quadratic gravity and the inflationary dynamics is of the order \(10^{114}\). However, the statistical error bars do not permit any further conclusions about its value, not even about its sign. Also the non-zero spatial curvature parameter found for the late universe is, within the error bars, consistent with zero. The deceleration parameter q, on the other hand, is predicted to be lower then the \(\Lambda \)CDM best fit: \(-0.57\pm 0.012\) for CCGG and \( -0.62\pm 0.007\) for \(\Lambda \)CDM.

We conclude that the CCGG approach reproduces low-redshift observation with a similar accuracy as the \(\Lambda \)CDM model. The novel features of CCGG, namely the presence of torsion and the influence of quadratic curvature, represented by the additional deformation parameter, turn out to be subdominant in this late era of the cosmic evolution. However, albeit this calculation does not conclusively determine the relative admixture of quadratic gravity to Einsten-Cartan gravity, the data neither excludes a non-zero deformation parameter, nor a deviation from the flat geometry assumed in \(\Lambda \)CDM. This leaves the possibility open that the more complex space-time geometry of CCGG applies, which naturally invokes inflation [94] and substantially alters the Hubble expansion in the early universe [37]. The model’s superiority thus might become obvious only when including the early universe data in the analysis.

The discussion on whether torsion of space-time could be excluded by solar tests have been sparked by the Gravity Probe B (GPB) experiment. While Mao et al. [95] propose to use the high-precision gyroscope for detecting torsion, Hehl et al. [96] conclude, referring to the Poincare Gauge Gravity, that torsion can couple to particle spin only, not to the gyroscope’s angular momentum, and that the accuracy needed for detecting such a coupling is far beyond any currently available technologies. Moreover, they also dismiss possible deviations of test particle trajectories from the geodesic (trajectory of extremal length) by postulating that it is force-free trajectory of particles, rather than the autoparallel (“straightes trajectory”). These discussions indicate that torsion may not be detectable in the solar system, but they so far do not exclude its existence.

While we agree with Hehl’s first conjecture, we advocate the autoparallel to be the correct force-free trajectory as the obvious generalization of Newton’s notion of a straight line to curvilinear space-time. A propagating torsion field that arises naturally in CCGG will also directly interact with spin carrying particles. As in presence of torsion the autoparallel and the geodesic are not identical, a modified connection will in principle be felt by test particles. Direct spin-torsion interactions [97] will in addition affect the trajectories of spin-polarized as compared to spinless test particles. However, if the density of the torsion field is very low in the solar system then we will encounter similar restrictions on the detectability of those spin-torsion interactions. Work along these lines including advanced modeling of the torsion tensor is in progress.

Public Source: The files with the dataset and the fit package can be found in https://github.com/benidav/CCGGcosmology2020.