1 Introduction

At this stage in the development of theoretical investigations of the early universe, cosmological inflation [1,2,3,4,5,6,7] seems to be the most convincing theory. The first models of cosmological inflation were based principally on Einstein gravity and the assumption that there is some scalar field \(\phi \) as an ideal barotropic fluid with negative pressure at the inflationary stage of the evolution of early universe [2,3,4,5,6,7]. Also, according to the theory of cosmological perturbations, quantum fluctuations of a scalar field induce corresponding perturbations of the metric, which give rise to a large-scale structure of the universe and relic gravitational waves [8]. At the moment, a large number of different models of cosmological inflation with canonical scalar fields based on Einstein gravity are considered to describe the inflationary stage of the evolution of universe [9,10,11,12].

Another possibility for constructing the cosmological models of early universe is using modified gravity theories which include the higher-order curvature terms [1, 13,14,15,16,17] which can be associated with quantum effects in the low-energy limit of string theory and supergravity. One such a correction is the Gauss–Bonnet term (scalar) \(R^{2}_\mathrm{GB}= R_{\mu \nu \rho \sigma } R^{\mu \nu \rho \sigma } - 4 R_{\mu \nu }R^{\mu \nu } + R^2\) which arises in the low-energy effective action for the heterotic strings [18,19,20,21,22], and also appears in the second order of Lovelock gravity theory [23].

Cosmological models with the Gauss–Bonnet (GB) term in four-dimensional Friedmann universe was considered earlier in a large number of works (for example, see  [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]). The important property of such a models is that the GB-term affects the cosmological dynamics in four-dimensional space-time only for the case of non-minimal coupling of this term with a scalar field  [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42] that can be defined by some coupling function \(\xi (\phi )\).

The evolution of cosmological perturbations and their corresponding parameters for Einstein–Gauss–Bonnet (EGB) inflationary models were considered in papers [43,44,45,46,47,48,49,50,51,52]. In this case, it should be noted that the non-minimal coupling of a scalar field and the Gauss–Bonnet scalar allows to verify cosmological inflationary models from observational constraints on the values of cosmological perturbation parameters [53, 54], in contrast to some models constructed based on Einstein gravity only due to difference in the evolution of perturbations at the inflationary stage [31, 44, 45, 48, 49].

An important difference between inflationary models based on Einstein–Gauss–Bonnet gravity and ones based on GR is the dependence of the velocities of the propagation of cosmological perturbations on cosmic time [43,44,45,46,47,48,49,50,51,52], that implies the deviations of these velocities from the speed of light in a vacuum for EGB-inflation.

A common method for analyzing cosmological models based on modified gravity theories is conformal transformations of a space-time metric that bring the initial action to the Einstein-Hilbert form with corresponding transformations of the material components [13,14,15,16]. The explicit form of the transformations allows one to compare models based on General Relativity and its modifications. However, for the case of Einstein–Gauss–Bonnet gravity, no such a transformations were found [55].

In papers [56,57,58,59,60] it was proposed to consider the relationship between standard inflationary models and EGB-inflation directly from the equations of cosmological dynamics in flat four-dimensional Friedmann–Robertson–Walker (FRW) space-time, which is sufficient for comparing such a models, since this type of geometry is the basis for constructing phenomenologically correct cosmological of models [53, 54, 61, 62]. Also, this approach was used to analyze cosmological inflationary models based on the other modifications of Einstein gravity [60, 63, 64]. Thus, the application of the approach based on a connection between Einstein–Gauss–Bonnet gravity and General Relativity in relevant cosmological models makes it possible to evaluate the effects of the non-minimal coupling of a scalar field and the Gauss–Bonnet term.

The aim of this work is to develop the method of analysis of Gauss–Bonnet term corrections to standard inflationary models which was proposed in [56,57,58,59,60]. The article is organized as follows. In Sect. 2, the difference between equations of cosmological dynamics for the case of Einstein–Gauss–Bonnet gravity and General Relativity in flat four-dimensional FRW space-time is considered. In Sect. 2.1, this difference is defined in terms of the deviation parameters, and estimates of the influence of the non-minimal coupling of a scalar field and the Gauss–Bonnet term on the main parameters of the background cosmological dynamics are given. It was further obtained that the slow-roll conditions imply a weak effect of such a coupling on cosmological dynamics. This result was applied in Sect. 2.6 for the analysis of EGB-inflationary models with a weak coupling and the parameterization of the Gauss–Bonnet term corrections through a coupling constant. In Sect. 4, different cosmological inflationary models with weak a GB-coupling were considered, and the main effects of such a coupling on the inflationary parameters were determined. In conclusion, the results of this work were discussed.

2 The cosmological models based on the Einstein–Gauss–Bonnet gravity

The models of cosmological inflation with Einstein gravity can be considered on the basis of the action [2,3,4,5,6,7]

$$\begin{aligned} S_{{\text {E}}} = \int _{\mathcal {M}} d^4x\sqrt{-g}\Bigg [\frac{1}{2} R - \frac{1}{2}g^{\mu \nu }\partial _{\mu }\phi _{{\text {E}}} \partial _{\nu } \phi _{{\text {E}}}- V_{{\text {E}}}(\phi _{{\text {E}}})\Bigg ],\nonumber \\ \end{aligned}$$
(1)

and for inflationary models with additional non-minimal coupling of a scalar field and the Gauss–Bonnet term, the action is [24,25,26,27,28,29,30,31,32,33,34,35,36, 38]

$$\begin{aligned} S_{{\text {GB}}}= & {} \int _{\mathcal {M}} d^4x\sqrt{-g}\Bigg [\frac{1}{2} R - \frac{1}{2}g^{\mu \nu }\partial _{\mu }\phi _{{\text {GB}}} \partial _{\nu } \phi _{{\text {GB}}} \nonumber \\&- V_{{\text {GB}}}(\phi _{{\text {GB}}})-\frac{1}{2}\xi (\phi _{{\text {GB}}}) R_\mathrm{GB}^2\Bigg ], \end{aligned}$$
(2)

where \(\phi \) is a scalar field with the potential \(V(\phi )\), R the Ricci scalar curvature of the space-time \(\mathcal {M}\), \(R^{2}_\mathrm{GB}= R_{\mu \nu \rho \sigma } R^{\mu \nu \rho \sigma } - 4 R_{\mu \nu }R^{\mu \nu } + R^2\) the Gauss–Bonnet term and \(\xi (\phi _{{\text {GB}}})\) is a coupling function. Index “E” denotes Einstein gravity, and index “GB” means Einstein–Gauss–Bonnet gravity.

The background dynamic equations corresponding to the action (2) in a spatially flat four-dimensional Friedmann–Robertson–Walker space-time

$$\begin{aligned} {\text {d}}s^2=-{\text {d}}t^2+a^{2}(t)\left( {\text {d}}x^{2}+{\text {d}}y^{2}+{\text {d}}z^{2}\right) , \end{aligned}$$
(3)

in the system of units \(8\pi G=c=1\), are [24,25,26,27,28,29,30,31,32,33,34,35,36, 38]

$$\begin{aligned}&3H^{2}_{{\text {GB}}}=\frac{1}{2}\dot{\phi }^{2}_{{\text {GB}}}+V_{{\text {GB}}}+12\dot{\xi }H^{3}_{{\text {GB}}}, \end{aligned}$$
(4)
$$\begin{aligned}&\dot{\phi }^{2}_{{\text {GB}}}=-2\dot{H}_{{\text {GB}}}+4\ddot{\xi }H^{2}_{{\text {GB}}}+4\dot{\xi }H_{{\text {GB}}}(2\dot{H}_{{\text {GB}}}-H^{2}_{{\text {GB}}}),\end{aligned}$$
(5)
$$\begin{aligned}&\ddot{\phi }_{{\text {GB}}} + 3 H_{{\text {GB}}} \dot{\phi }_{{\text {GB}}} + \frac{\partial V_{{\text {GB}}}(\phi _{{\text {GB}}})}{\partial \phi _{{\text {GB}}}} \nonumber \\&\quad + 12H^2_{{\text {GB}}} \left( \dot{H}_{{\text {GB}}}+H^2_{{\text {GB}}}\right) \frac{\partial \xi (\phi _{{\text {GB}}})}{\partial \phi _{{\text {GB}}}}= 0, \end{aligned}$$
(6)

where a dot represents a derivative with respect to the cosmic time t, \(H \equiv \dot{a}/a\) denotes the Hubble parameter and \(a=a(t)\) is a scale factor.

Since the Eq. (6) can be derived from (4) and (5), one can consider the dynamic Eqs. (4)–(6) in the following form

$$\begin{aligned}&V_{{\text {GB}}}(\phi _{{\text {GB}}})=3H^{2}_{{\text {GB}}}+\dot{H}_{{\text {GB}}}-10H^{3}_{{\text {GB}}}\dot{\xi }-2H^{2}_{{\text {GB}}}\ddot{\xi }\nonumber \\&\quad -4H_{{\text {GB}}}\dot{H}_{{\text {GB}}}\dot{\xi }, \end{aligned}$$
(7)
$$\begin{aligned}&\frac{1}{2}\dot{\phi }^{2}_{{\text {GB}}}=-\dot{H}_{{\text {GB}}}-2H^{3}_{{\text {GB}}}\dot{\xi }+ 4H_{{\text {GB}}}\dot{H}_{{\text {GB}}}\dot{\xi }+2H^{2}_{{\text {GB}}}\ddot{\xi }. \end{aligned}$$
(8)

The transition to the case of Einstein gravity (minimal coupling) is carried out by means of the condition \(\dot{\xi }=0\), when Eqs. (7) and (8) are reduced to

$$\begin{aligned}&V_{{\text {E}}}(\phi _{{\text {E}}})=3H^{2}_{{\text {E}}}+\dot{H}_{{\text {E}}}, \end{aligned}$$
(9)
$$\begin{aligned}&\frac{1}{2}\dot{\phi }^{2}_{{\text {E}}}=-\dot{H}_{{\text {E}}}, \end{aligned}$$
(10)

corresponding to action (1), where the inflationary parameters for EGB-inflation are reduced to ones for the standard inflation under this condition

$$\begin{aligned} V_{{\text {GB}}}^{(\dot{\xi }=0)}=V_{{\text {E}}},~~~\phi _{{\text {GB}}}^{(\dot{\xi }=0)}=\phi _{{\text {E}}},~~~H_{{\text {GB}}}^{(\dot{\xi }=0)}=H_{{\text {E}}}. \end{aligned}$$
(11)

The usual method for analyzing cosmological models based on modified gravity theories is conformal transformations of the metric \(g^{{\text {(E)}}}_{\mu \nu }=\Omega ^{2}(\phi )g_{\mu \nu }\), where \(\Omega ^{2}(\phi )\) is the conformal factor, which lead the action defining the model based on modified gravity to the Einstein-Hilbert action (1) with corresponding transformations of geometric and material components in action [13,14,15,16,17, 46, 47]. However, such a transformations can’t eliminate the non-minimal coupling of a scalar field and the Gauss–Bonnet scalar [55].

Thus, in this case, an approach seems to be relevant in which the connections between inflationary parameters for the case of Einstein–Gauss–Bonnet gravity and General Relativity are determined directly from the equations of cosmological dynamics in the Friedman-Robertson-Walker space-time.

2.1 The deviations between Einstein–Gauss–Bonnet inflation and standard one

As one can see from Eqs. (7)–(8) and (9)–(10), the non-minimal coupling of a scalar field with the Gauss–Bonnet scalar changes the evolution of a field itself, its potential and the dynamics of the universe’s expansion in the Friedman-Robertson-Walker space-time.

To characterize the difference between these inflationary parameters for EGB-inflation and standard inflation in spatially flat FRW space-time one can define following deviation parameters

$$\begin{aligned}&\Delta _{V}\equiv V_{{\text {GB}}}-V_{{\text {E}}}, \end{aligned}$$
(12)
$$\begin{aligned}&\Delta _{X}\equiv X_{{\text {GB}}}-X_{{\text {E}}},\end{aligned}$$
(13)
$$\begin{aligned}&\Delta _{H}\equiv H_{{\text {GB}}}-H_{{\text {E}}}, \end{aligned}$$
(14)

as the functions of cosmic time, where \(X_{{\text {GB}}}\equiv \frac{1}{2}\dot{\phi }^{2}_{{\text {GB}}}\) and \(X_{{\text {E}}}\equiv \frac{1}{2}\dot{\phi }^{2}_{{\text {E}}}\) are the kinetic energies of a scalar field for EGB-inflation and standard one. In general case, the deviation parameters are the some functions of cosmic time, also, under condition \(\dot{\xi }=0\) one has \(\Delta _{V}=\Delta _{X}=\Delta _{H}=0\).

It should be noted, that one can’t define the deviation parameters in explicit form without the connection between inflationary parameters for standard inflation and EGB-inflation.

To find such a connection one can consider the coupling function as follows

$$\begin{aligned} \xi =\int \frac{H_{{\text {GB}}}-F}{2H^{2}_{{\text {GB}}}}{\text {d}}t+{\text {const}},~~~~~\dot{\xi }=\frac{H_{{\text {GB}}}-F}{2H^{2}_{{\text {GB}}}}, \end{aligned}$$
(15)

where \(F=F(t)\) is some arbitrary function of cosmic time.

After substituting (15) into dynamic equations for EGB-inflation (7)–(8) one has

$$\begin{aligned}&V_{{\text {GB}}}=-2H^{2}_{{\text {GB}}}+5FH_{{\text {GB}}}+\dot{F}, \end{aligned}$$
(16)
$$\begin{aligned}&\frac{1}{2}\dot{\phi }^{2}_{{\text {GB}}}=-\dot{F}+FH_{{\text {GB}}}-H^{2}_{{\text {GB}}}. \end{aligned}$$
(17)

To determine the meaning of function F, one can consider the transition to standard inflation \(\dot{\xi }=0\) which can be implemented by the conditions \(H_{{\text {GB}}}=F\) and \(F=H_{{\text {GB}}}\) in expression (15).

Under these conditions, from Eqs. (16)–(17), taking into account (11), one has

$$\begin{aligned}&V_{{\text {E}}}=3F^{2}+\dot{F}=3H^{2}_{{\text {E}}}+\dot{H}_{{\text {E}}},\end{aligned}$$
(18)
$$\begin{aligned}&\frac{1}{2}\dot{\phi }^{2}_{{\text {E}}}=-\dot{F}=-\dot{H}_{{\text {E}}}. \end{aligned}$$
(19)

Therefore, one can conclude that function F is the Hubble parameter for the case of Einstein gravity \(F\equiv H_{{\text {E}}}\), and the condition \(\dot{\xi }=0\) in expression (15) corresponds to \(H_{{\text {GB}}}=H_{{\text {E}}}\).

Thus, the connection between Hubble parameters for standard inflation and EGB-inflation can be obtained from Eq. (15) in following form

$$\begin{aligned} H_{{\text {E}}}=H_{{\text {GB}}}\left( 1-2\dot{\xi }H_{{\text {GB}}}\right) . \end{aligned}$$
(20)

This relation between the Hubble parameters \(H_{{\text {E}}}\) and \(H_{{\text {GB}}}\) was considered earlier in the papers [56,57,58,59,60].

Thus, for \(F=H_{{\text {GB}}}\) one can write dynamic Eqs. (16)–(17) for EGB-inflation as

$$\begin{aligned}&V_{{\text {GB}}}(\phi _{{\text {GB}}})=-2H^{2}_{{\text {GB}}}+5H_{{\text {E}}}H_{{\text {GB}}}+\dot{H}_{{\text {E}}},\end{aligned}$$
(21)
$$\begin{aligned}&\frac{1}{2}\dot{\phi }^{2}_{{\text {GB}}}=-\dot{H}_{{\text {E}}}+H_{{\text {E}}}H_{{\text {GB}}}-H^{2}_{{\text {GB}}}. \end{aligned}$$
(22)

Further, from definitions (12)–(14) and Eqs. (9)–(10), (20)–(22) one can obtain the deviation parameters in explicit form

$$\begin{aligned}&\Delta _{V}=-2H^{2}_{{\text {GB}}}+5H_{{\text {E}}}H_{{\text {GB}}}-3H^{2}_{{\text {E}}}=2H^{3}_{{\text {GB}}}\dot{\xi }(1-6H_{{\text {GB}}}\dot{\xi }), \nonumber \\ \end{aligned}$$
(23)
$$\begin{aligned}&\Delta _{X}=-H_{{\text {GB}}}(H_{{\text {GB}}}-H_{{\text {E}}})=-2H^{3}_{{\text {GB}}}\dot{\xi },\end{aligned}$$
(24)
$$\begin{aligned}&\Delta _{H}=H_{{\text {GB}}}-H_{{\text {E}}}=2H^{2}_{{\text {GB}}}\dot{\xi }, \end{aligned}$$
(25)

These parameters are connected by the relations

$$\begin{aligned} \Delta _{V}=-3\Delta ^{2}_{H}-\Delta _{X},~~~\Delta _{X}=-H_{{\text {GB}}}\Delta _{H}. \end{aligned}$$
(26)

Since the deviation parameters (23)–(25) can be both positive and negative, the character of the influence of non-minimal GB coupling depends on the choice of a specific model of cosmological inflation.

2.2 The influence of GB-term on a scalar field

As the first application of proposed approach, one can determine the change in the characteristics of a scalar field inspired by non-minimal GB coupling.

The influence of such a coupling on the pressure of a scalar field \(p=X-V\) can be found as the difference between pressures for EGB-inflation and standard one

$$\begin{aligned} p_{{\text {GB}}}-p_{{\text {E}}}=X_{{\text {GB}}}-X_{{\text {E}}}-V_{{\text {GB}}}+V_{{\text {E}}}=\Delta _{X}-\Delta _{V}=3\Delta ^{2}_{H}+2\Delta _{X}. \end{aligned}$$
(27)

As one can see, this difference depends on the model’s type of inflation.

However, for the difference between energy densities of a scalar field \(\rho =X+V\) one has

$$\begin{aligned} \rho _{{\text {GB}}}-\rho _{{\text {E}}}=X_{{\text {GB}}}-X_{{\text {E}}}+V_{{\text {GB}}}-V_{{\text {E}}}=\Delta _{X}+\Delta _{V}=-3\Delta ^{2}_{H}<0, \end{aligned}$$
(28)

for any inflationary model.

Therefore, in four-dimensional spatially flat Friedmann–Robertson–Walker space-time the non-minimal coupling of a scalar field with the Gauss–Bonnet term leads to decrease of it’s energy density.

Further, one can write a state parameter of a coupled scalar field as

$$\begin{aligned} w_{{\text {GB}}}= & {} \frac{p_{{\text {GB}}}}{\rho _{{\text {GB}}}}=w_{{\text {E}}}+\frac{3\Delta ^{2}_{H}(p_{{\text {E}}}+\rho _{{\text {E}}})+2\Delta _{X}\rho _{{\text {E}}}}{(\rho _{{\text {E}}}-3\Delta ^{2}_{H})\rho _{{\text {E}}}}\nonumber \\= & {} w_{{\text {E}}}+\frac{2}{3}\left( \frac{\Delta ^{2}_{H}\epsilon _{{\text {E}}}+\Delta _{X}}{H^{2}_{{\text {E}}}-\Delta ^{2}_{H}}\right) \nonumber \\= & {} -1-\frac{2}{3}\left( \frac{\dot{H}_{{\text {E}}}-\Delta _{X}}{H^{2}_{{\text {E}}}-\Delta ^{2}_{H}}\right) , \end{aligned}$$
(29)

where

$$\begin{aligned} w_{{\text {E}}}=\frac{p_{{\text {E}}}}{\rho _{{\text {E}}}}=-1-\frac{2\dot{H}_{{\text {E}}}}{3H^{2}_{{\text {E}}}}=-1+\frac{2}{3}\epsilon _{{\text {E}}}, \end{aligned}$$
(30)

is a state parameter and \(\epsilon _{{\text {E}}}=-\dot{H}_{{\text {E}}}/H^{2}_{{\text {E}}}\) is slow-roll parameter for the case of Einstein gravity.

Thus, in general case, the non-minimal coupling of a scalar field with the Gauss–Bonnet scalar can significantly change the equation of state of a scalar field. Nevertheless, when evaluating such a changes, the condition \(\rho _{{\text {GB}}}>0\) should be taken into account, which will be considered further. Also, for the case \(\dot{\xi }=0\) one has \(\Delta _{X}=\Delta _{H}=0\) and the state parameter \(w_{{\text {GB}}}\) is reduced to \(w_{{\text {E}}}\).

2.3 The influence of GB-term on the background dynamics

The influence of such a coupling on the dynamics can be qualitatively estimated by the sign of \(\dot{\xi }\). In the case of decreasing coupling function \(\xi (t)\) \((\dot{\xi }<0)\) one has \(H_{{\text {GB}}}-H_ {E}<0\), that means a decrease in the rate of expansion of the universe relative to the standard inflationary models and one has the inverse effect (acceleration) in the case of the growth of coupling function \(\xi (t)\) \((\dot{\xi }>0)\).

This effect can be also quantified by the difference in the e-folds numbers which changes as

$$\begin{aligned} N_{{\text {GB}}}-N_{{\text {E}}}=\int ^{t_{{\text {E}}}}_{t_{i}}(H_{{\text {GB}}}-H_{{\text {E}}}){\text {d}}t=\int ^{t_{e}}_{t_{i}}\Delta _{H}{\text {d}}t, \end{aligned}$$
(31)

where \(t_{i}\) and \(t_{e}\) are the times of the beginning and the end of inflationary stage.

From the conditions of positive energy density of a scalar field \(\rho _{{\text {GB}}}>0\), expansion of the universe \(H_{{\text {E}}}>0\), \(H_{{\text {GB}}}>0\) and expression \(\rho _{{\text {E}}}=X_{{\text {E}}}+V_{{\text {E}}}=3H^{2}_{{\text {E}}}\) one has following restriction on the Hubble parameter for EGB-inflation

$$\begin{aligned} \rho _{{\text {GB}}}=\rho _{{\text {E}}}-3\Delta ^{2}_{H}>0,~~~~~0<H_{{\text {GB}}}<2H_{{\text {E}}}, \end{aligned}$$
(32)

and the restrictions on the deviation parameters

$$\begin{aligned} -H_{{\text {E}}}<\Delta _{H}<H_{{\text {E}}},~~~~~-2H^{2}_{{\text {E}}}<\Delta _{X}<2H^{2}_{{\text {E}}}, \end{aligned}$$
(33)

which limits changes in the state parameter of a scalar field (29) as well.

In terms of the slow-roll parameter \(\epsilon \) which characterize the dynamics of the inflationary stage, this restriction can be formulated as

$$\begin{aligned} \frac{1}{2}\epsilon _{{\text {E}}}<\epsilon _{{\text {GB}}}<1, \end{aligned}$$
(34)

since \(\epsilon =1\) is the condition for completing the stage of cosmological inflation.

Also, from (32) one has the following restriction on the increment of e-folds number

$$\begin{aligned} N_{{\text {GB}}}-N_{{\text {E}}}<N_{{\text {E}}},~~~~~N_{{\text {GB}}}<2N_{{\text {E}}}, \end{aligned}$$
(35)

for Einstein–Gauss–Bonnet inflation compared to standard one.

Thus, the results obtained mean that the non-minimal coupling of a scalar field and the Gauss–Bonnet scalar can accelerate the rate of expansion of the Friedmann universe by less than two times.

2.4 The influence of GB-term on the parameters of cosmological perturbations

In accordance with the theory of cosmological perturbations, quantum fluctuations of the scalar field generate the corresponding perturbations of the space-time metric during the inflationary stage. In the linear order of cosmological perturbation theory, the observed anisotropy and polarization of cosmic microwave background radiation (CMB) [53, 54] are explained by the influence of two types of perturbations, namely, scalar and tensor ones. The third type of perturbations (vector perturbations) quickly decay in the process of accelerated expansion of the early universe [8].

The calculation of cosmological perturbation parameters for inflationary models with taking into account the non-minimal coupling of a scalar field and the Gauss–Bonnet scalar was carried out in many works [43,44,45,46,47,48,49,50,51,52] before.

To compare the predictions of the inflationary model with the observational data of CMB anisotropy, it suffices to consider two parameters of cosmological perturbations, namely, the spectral index of scalar perturbations \(n_{{\text {S}}}\) and the tensor-scalar ratio r which is the ratio of the squared amplitudes of tensor and scalar perturbations [43,44,45,46,47,48,49,50,51,52].

The expressions for these parameters on the crossing of the Hubble radius (\(k=aH\)) can be written as follows [43,44,45,46,47,48,49,50,51,52]

$$\begin{aligned}&n_{{\text {S(GB)}}}-1=-2\epsilon _{{\text {GB}}}-\frac{2\epsilon _{{\text {GB}}}(2\epsilon _{{\text {GB}}}-2\delta _{{\text {GB}}})+\Delta _{2}}{2\epsilon _{{\text {GB}}}-\Delta _{1}},\end{aligned}$$
(36)
$$\begin{aligned}&r_{{\text {GB}}}=8\left( 2\epsilon _{{\text {GB}}}-\Delta _{1}\right) , \end{aligned}$$
(37)

where the slow-roll parameters and deviation ones for EGB-inflation are defined as

$$\begin{aligned}&\epsilon _{{\text {GB}}}=-\frac{\dot{H}_{{\text {GB}}}}{H^{2}_{{\text {GB}}}},~~~ \delta _{{\text {GB}}}=-\frac{\ddot{H}_{{\text {GB}}}}{2\dot{H}_{{\text {GB}}}H_{{\text {GB}}}}= \epsilon _{{\text {GB}}}-\frac{\dot{\epsilon }_{{\text {GB}}}}{2\epsilon _{{\text {GB}}}H_{{\text {GB}}}}, \nonumber \\ \end{aligned}$$
(38)
$$\begin{aligned}&\Delta _{1}=4\dot{\xi }H_{{\text {GB}}},\end{aligned}$$
(39)
$$\begin{aligned}&\Delta _{2}=-4\ddot{\xi }+\Delta _{1}\epsilon _{{\text {GB}}}. \end{aligned}$$
(40)

On the basis of expression (20), one can redefine the deviation parameters as

$$\begin{aligned}&\Delta _{1}=2\left( 1-\frac{H_{{\text {E}}}}{H_{{\text {GB}}}}\right) =2\left( 1-\frac{H_{{\text {E}}}}{H_{{\text {E}}}+\Delta _{H}}\right) ,\end{aligned}$$
(41)
$$\begin{aligned}&\Delta _{2}=2\left( \frac{\dot{H}_{{\text {E}}}}{H^{2}_{{\text {GB}}}}-\frac{\dot{H}_{{\text {GB}}}H_{{\text {E}}}}{H^{3}_{{\text {GB}}}}\right) = -\frac{\dot{\Delta }_{1}}{H_{{\text {E}}}+\Delta _{H}}. \end{aligned}$$
(42)

The deviation parameters \(\Delta _{1}\) and \(\Delta _{2}\) are connected with slow-roll parameters \(\delta _{1}\) and \(\delta _{2}\) which are usually used to define the GB-term corrections [48, 49] as followsFootnote 1

$$\begin{aligned}&\Delta _{1}=\delta _{1},\end{aligned}$$
(43)
$$\begin{aligned}&\Delta _{2}=-\delta _{1}\delta _{2}+\delta _{1}\epsilon _{{\text {GB}}},\end{aligned}$$
(44)
$$\begin{aligned}&\delta _{2}=\frac{\ddot{\xi }}{\dot{\xi } H_{{\text {GB}}}}=\epsilon _{{\text {GB}}}-\frac{\Delta _{2}}{\Delta _{1}}. \end{aligned}$$
(45)

The parameters (41) and (42) are considered instead of \(\delta _{1}\) and \(\delta _{2}\), in framework of proposed approach, for the convenience of analyzing the deviations between EGB-inflation and the standard inflationary scenarios, since for \(\xi =const\), parameters \(\delta _{2}\) and \(\tilde{\delta }_{2}\) have an undefined values.

From Eqs. (36)–(42) one has following expressions for the spectral index of scalar perturbations and tensor-to-scalar ratio in the case of EGB-inflation

$$\begin{aligned} n_{S({\text {GB}})}-1&=-2\epsilon _{{\text {GB}}}-\frac{2\dot{\epsilon }_{{\text {GB}}}-\dot{\Delta }_{1}}{(2\epsilon _{{\text {GB}}}-\Delta _{1})H_{{\text {GB}}}}\nonumber \\&= -(\Delta _{1}+\Delta _{3})-\frac{\dot{\Delta }_{3}}{\Delta _{3}H_{{\text {GB}}}},\end{aligned}$$
(46)
$$\begin{aligned} r_{{\text {GB}}}&=8\left( 2\epsilon _{{\text {GB}}}-\Delta _{1}\right) =8\Delta _{3}, \end{aligned}$$
(47)

where

$$\begin{aligned} \Delta _{3}=2\epsilon _{{\text {GB}}}-\Delta _{1}. \end{aligned}$$
(48)

Also, one can define the connection between background deviation parameters \(\{\Delta _{H},\Delta _{X},\Delta _{V}\}\) and ones corresponding to the Gauss–Bonnet term corrections to the parameters of cosmological perturbations \(\{\Delta _{1},\Delta _{2},\Delta _{3}\}\).

Firstly, from Eqs. (23)–(25) one can obtain

$$\begin{aligned}&H_{{\text {GB}}}=-\frac{\Delta _{X}}{\Delta _{H}},\end{aligned}$$
(49)
$$\begin{aligned}&H_{{\text {E}}}=-\frac{\Delta _{X}+\Delta ^{2}_{H}}{\Delta _{H}}. \end{aligned}$$
(50)

Further, from expressions (41), (42) and (48), taking into account (49)–(50), one has

$$\begin{aligned}&\Delta _{1}=-2\frac{\Delta ^{2}_{H}}{\Delta _{X}},\end{aligned}$$
(51)
$$\begin{aligned}&\Delta _{2}=-2\frac{\Delta _{H}}{\Delta _{X}}\frac{{\text {d}}}{{\text {d}}t}\left( \frac{\Delta ^{2}_{H}}{\Delta _{X}}\right) ,\end{aligned}$$
(52)
$$\begin{aligned}&\Delta _{3}=2\frac{\Delta ^{2}_{H}}{\Delta _{X}}-2\frac{{\text {d}}}{{\text {d}}t}\left( \frac{\Delta _{H}}{\Delta _{X}}\right) . \end{aligned}$$
(53)

Also, it as possible to write the relations (51)–(53) in terms of third background deviation parameter \(\Delta _{V}\) on the basis of the connections (26). Thus, the relations (49)–(53) allow one to determine the parameters \(\{\Delta _{1},\Delta _{2},\Delta _{3}\}\) from the background deviation parameters \(\{\Delta _{H},\Delta _{X},\Delta _{V}\}\) that will be used in following analysis of inflationary models.

The expressions (36)–(37) were obtained in [43,44,45,46,47,48,49,50,51,52] taking into account the slow-roll conditions, which can be written as

$$\begin{aligned}&\epsilon _{{\text {GB}}}\ll 1,~~~~\delta _{{\text {GB}}}\ll 1,\end{aligned}$$
(54)
$$\begin{aligned}&\Delta _{1}\ll 1,~~~~\Delta _{2}\ll 1,~~~~\Delta _{3}\ll 1. \end{aligned}$$
(55)

For the case of Einstein gravity \(\dot{\xi }=0\) one has \(H_{{\text {GB}}}=H_{{\text {E}}}\), \(\epsilon _{{\text {GB}}}=\epsilon _{{\text {E}}}\), \(\delta _{{\text {GB}}}=\delta _{{\text {E}}}\) and \(\Delta _{1}=\Delta _{2}=0\), and expressions for the parameters of cosmological perturbations are reduced to

$$\begin{aligned}&n_{{\text {S(E)}}}-1=-4\epsilon _{{\text {E}}}+2\delta _{{\text {E}}},\end{aligned}$$
(56)
$$\begin{aligned}&r_{{\text {E}}}=16\epsilon _{{\text {E}}}, \end{aligned}$$
(57)

that corresponds to the result obtained for the standard inflation [65,66,67] with the slow-roll conditions

$$\begin{aligned} \epsilon _{{\text {E}}}\ll 1,~~~~\delta _{{\text {E}}}\ll 1, \end{aligned}$$
(58)

where the slow-roll parameters for the standard inflation based on Einstein gravity are

$$\begin{aligned} \epsilon _{{\text {E}}}=-\frac{\dot{H}_{{\text {E}}}}{H^{2}_{{\text {E}}}},~~~~~ \delta _{{\text {E}}}=-\frac{\ddot{H}_{{\text {E}}}}{2\dot{H}_{{\text {E}}}H_{{\text {E}}}}= \epsilon _{{\text {E}}}-\frac{\dot{\epsilon }_{{\text {E}}}}{2\epsilon _{{\text {E}}}H_{{\text {E}}}}. \end{aligned}$$
(59)

The parameters of cosmological perturbations must satisfy the following observational constraints [53, 54]

$$\begin{aligned}&n_{{\text {S}}}=0.9663\pm 0.0041,\end{aligned}$$
(60)
$$\begin{aligned}&r<0.065, \end{aligned}$$
(61)

that defines the method of the verification of cosmological inflationary models.

From restrictions (32)–(33) and definition (41) one has the condition \(\Delta _{1}<1\). However, the equation (47) leads to \(\Delta _{1}<2\epsilon _{{\text {GB}}}\ll 1\). Thus, the expressions (36)–(37) are valid only for the case of satisfying conditions (55). A consequence of the conditions (55), taking into account the expressions (41)–(42), is the weak influence of non-minimal coupling of a scalar field and the Gauss–Bonnet scalar on cosmological dynamics \(\Delta _{H}\ll H_{{\text {E}}}\).

Thus, the slow-roll conditions for EGB-inflation correspond to the interpretation of non-minimal coupling of a scalar field and the Gauss–Bonnet scalar as a small quantum corrections to the main dynamical effects determined by Einstein gravity at the inflationary stage of the evolution of early universe, which can be called as a weak GB coupling.

2.5 The influence of GB-term on the velocities of cosmological perturbations

To analyze the influence of non-minimal coupling on the velocities of cosmological perturbations one can use their exact expressions which were considered, for example, in [48, 49].

The velocity of the scalar perturbations can be expressed as follows

$$\begin{aligned} c^{2}_{{\text {S}}}=1-\frac{[4\epsilon _{{\text {GB}}}-\delta _{1}(1-4\epsilon _{{\text {GB}}}-\delta _{2})]\Delta ^{2}}{4\epsilon _{{\text {GB}}}-2\delta _{1}-2\delta _{1}(2\epsilon _{{\text {GB}}}-\delta _{2})+3\delta _{1}\Delta }, \end{aligned}$$
(62)

where \(\Delta =\frac{\delta _{1}}{1-\delta _{1}}\).

In terms of the deviation parameters \(\Delta _{1}\) and \(\Delta _{2}\) the expression (62) can be noted as

$$\begin{aligned} c^{2}_{{\text {S}}}=\frac{7\Delta ^{3}_{1}\epsilon _{{\text {GB}}}+4\Delta ^{3}_{1}+\Delta ^{2}_{1}\Delta _{2}-12\Delta ^{2}_{1} -7\Delta ^{2}_{1}-4\Delta _{1}\Delta _{2}+10\Delta _{1}\epsilon _{{\text {GB}}}+2\Delta _{1}+2\Delta _{2}-4\epsilon _{{\text {GB}}}}{(2\Delta ^{2}_{1}\epsilon _{{\text {GB}}}+5\Delta ^{2}_{1}+2\Delta _{1}\Delta _{2}-6\Delta _{1}\epsilon _{{\text {GB}}}- 2\Delta _{1}-2\Delta _{2}+4\epsilon _{{\text {GB}}})(\Delta _{1}-1)}. \end{aligned}$$
(63)

On the basis of the slow-roll conditions (54)–(55) for a weak GB coupling, after neglecting the small terms second and higher orders, from expression (63) one has \(c^{2}_{{\text {S}}}\simeq 1\).

The expression for the velocity of tensor perturbations (relic gravitational waves) for the case of EGB-gravity is [48, 49]

$$\begin{aligned} c^{2}_{g}=1+\frac{\delta _{1}(1-\delta _{2})}{1-\delta _{1}}= 1+\frac{\Delta _{1}-\Delta _{1}\epsilon _{{\text {GB}}}+\Delta _{2}}{1-\Delta _{1}}. \end{aligned}$$
(64)

After neglecting the second order small term \(\Delta _{1}\epsilon _{{\text {GB}}}\), from expression (64) one has

$$\begin{aligned} c^{2}_{g}\simeq \frac{1+\Delta _{2}}{1-\Delta _{1}}. \end{aligned}$$
(65)

Thus, the parameters \(\Delta _{1}\) and \(\Delta _{2}\) define the small deviations of the velocity of tensor perturbations from the speed of light in vacuum c (in chosen system of units \(c=1\)). It should be noted, that the velocity of gravitational waves \(c_{g}=1\) corresponds to a limited class of gravity theories, including General Relativity [68].

Based on detection of gravitational waves from neutron star merging GW170817 event [69] in modern era of the universe’s evolution one has the following restriction on the value of their velocity

$$\begin{aligned} |c_{g}-1|\le 5\times 10^{-16}. \end{aligned}$$
(66)

In papers [70,71,72] this result was extrapolated to the relic gravitational waves on inflationary stage, and the conditions on the parameters \(\delta _{1}\), \(\delta _{2}\) and corresponding coupling function \(\xi \) were found for the cases \(c^{2}_{g}=1\) and \(c^{2}_{g}\simeq 1\).

One can obtain this result for \(c^{2}_{g}=1\) in terms \(\Delta _{1}\) and \(\Delta _{2}\) from Eq. (64) under condition

$$\begin{aligned} \Delta _{1}-\Delta _{1}\epsilon _{{\text {GB}}}+\Delta _{2}=0. \end{aligned}$$
(67)

Taking into account relations (39)–(40), one has

$$\begin{aligned}&\dot{\xi }=\xi _{0}a_{{\text {GB}}}(t),\end{aligned}$$
(68)
$$\begin{aligned}&\Delta _{1}=4\xi _{0}a_{{\text {GB}}}H_{{\text {GB}}},\end{aligned}$$
(69)
$$\begin{aligned}&\Delta _{2}=-\frac{4\xi _{0}}{a_{{\text {GB}}}}\left[ H_{{\text {GB}}}+\frac{\dot{H}_{{\text {GB}}}}{H_{{\text {GB}}}}\right] , \end{aligned}$$
(70)

where \(\xi _{0}\) is the constant of integration.

For the case \(c^{2}_{g}\simeq 1\) from Eq. (65) one has condition

$$\begin{aligned} \Delta _{1}+\Delta _{2}=0. \end{aligned}$$
(71)

From this condition and relations (39)–(40) one can obtain the following coupling function and corresponding deviation parameters

$$\begin{aligned}&\dot{\xi }=\xi _{0}\frac{a_{{\text {GB}}}}{H_{{\text {GB}}}}, \end{aligned}$$
(72)
$$\begin{aligned}&\Delta _{1}=-\Delta _{2}=4\xi _{0}a_{{\text {GB}}}. \end{aligned}$$
(73)

The conditions (68)–(70) and (72)–(73) significantly limit the possible models of cosmological inflation based on the Einstein–Gauss–Bonnet gravity.

Nevertheless, in the paper [73] it was shown that condition \(|c_{g}-1|\le 5\times 10^{-16}\) is met only for distances corresponding to redshift \(z<0.1\) and on large scales the constraint on the velocity of propagation of gravitational waves can changes. Taking into account the dependence from redshift, this constraint was estimated as follows

$$\begin{aligned} |c_{g}-1|\le 10^{-1}-10^{-2}. \end{aligned}$$
(74)

from \(z=2\) to the CMB scale (\(z\sim 1100\)) [73].

Thus, one can consider the coupling function \(\xi \) which differ from (68) or (72) to analyze the models of cosmological inflation based on EGB gravity, tacking into account restriction (74) on the velocity of relic gravitational waves instead of extrapolation of constraint (66) to the inflationary stage of the evolution of the universe.

2.6 Inflation with a weak coupling of a scalar field and Gauss–Bonnet scalar

The weak influence of non-minimal coupling of the Gauss–Bonnet scalar and a scalar field on cosmological dynamics can be defined in terms of the deviation parameter \(\Delta _{H}\) as

$$\begin{aligned} H_{{\text {GB}}}=H_{{\text {E}}}+\Delta _{H}, ~~~\Delta _{H}\ll H_{{\text {E}}}. \end{aligned}$$
(75)

After substituting expression (75) into (24) and (26) with neglecting the second order terms \({\mathcal O}(\Delta ^{2}_{H})\) one has

$$\begin{aligned}&\Delta _{X}=-H_{{\text {E}}}\Delta _{H}-\Delta ^{2}_{H}\simeq -H_{{\text {E}}}\Delta _{H},\end{aligned}$$
(76)
$$\begin{aligned}&\Delta _{V}=H_{{\text {E}}}\Delta _{H}-2\Delta ^{2}_{H}\simeq H_{{\text {E}}}\Delta _{H}. \end{aligned}$$
(77)

Thus, one can obtain the expressions of the energy density and pressure of a scalar field for a weak GB coupling from (27)–(28) in the following form

$$\begin{aligned} \rho _{{\text {GB}}}&=\rho _{{\text {E}}}+\Delta _{X}+\Delta _{V}\simeq \rho _{{\text {E}}}=3H^{2}_{{\text {E}}},\end{aligned}$$
(78)
$$\begin{aligned} p_{{\text {GB}}}&=p_{{\text {E}}}+2\Delta _{X}+3\Delta ^{2}_{H}\simeq p_{{\text {E}}}+2\Delta _{X}\simeq -3H^{2}_{{\text {E}}}\nonumber \\&\quad -2\dot{H}_{{\text {E}}}+2H_{{\text {E}}}\Delta _{H}. \end{aligned}$$
(79)

The state parameter (30) for a weak GB coupling is

$$\begin{aligned} w_{{\text {GB}}}\simeq -1+\frac{2}{3}\left( \epsilon _{{\text {E}}}+\frac{\Delta _{X}}{H^{2}_{{\text {E}}}}\right) \simeq -1+\frac{2}{3}\left( \epsilon _{{\text {E}}}-\frac{\Delta _{H}}{H_{{\text {E}}}}\right) . \end{aligned}$$
(80)

Therefore, in the case of a weak coupling, a decrease in the energy density of a scalar field is negligible, the pressure and the state parameter changes only slightly on the inflationary stage of accelerated expansion of the universe.

The background dynamic Eqs. (21)–(22) in this case are reduced to expressions

$$\begin{aligned} V_{{\text {GB}}}(\phi _{{\text {GB}}})= & {} 3H^{2}_{{\text {E}}}+\dot{H}_{{\text {E}}}+H_{{\text {E}}}\Delta _{H}-2\Delta ^{2}_{H} \simeq 3H^{2}_{{\text {E}}}+\dot{H}_{{\text {E}}}\nonumber \\&+H_{{\text {E}}}\Delta _{H},\end{aligned}$$
(81)
$$\begin{aligned} \frac{1}{2}\dot{\phi }^{2}_{{\text {GB}}}= & {} -\dot{H}_{{\text {E}}}-H_{{\text {E}}}\Delta _{H}-\Delta ^{2}_{H} \simeq -\dot{H}_{{\text {E}}}-H_{{\text {E}}}\Delta _{H}. \end{aligned}$$
(82)

Also, on the basis of Eq. (20), one can write following expression

$$\begin{aligned} \dot{\xi }= & {} \frac{H_{{\text {GB}}}-H_{{\text {E}}}}{2H^{2}_{{\text {GB}}}}= \frac{1}{2H_{{\text {E}}}}\left[ \frac{x}{(1+x)^{2}}\right] \nonumber \\= & {} \frac{1}{2H_{{\text {E}}}}\left[ x+{\mathcal O}(x^{2})+\cdots \right] \simeq \frac{\Delta _{H}}{2H^{2}_{{\text {E}}}}, \end{aligned}$$
(83)

where \(x\equiv \frac{\Delta _{H}}{H_{{\text {E}}}}\ll 1\).

Further, one can calculate the parameters of cosmological perturbations for the case of a weak GB coupling on the basis of results which were obtained in Sect. 2.5.

The deviation parameters \(\Delta _{1}\), \(\Delta _{2}\) and \(\Delta _{3}\) can be written from equation (76) and (51)–(53) as

$$\begin{aligned}&\Delta _{1}=-2\frac{\Delta ^{2}_{H}}{\Delta _{X}}\simeq 2\frac{\Delta _{H}}{H_{{\text {E}}}}, \end{aligned}$$
(84)
$$\begin{aligned}&\Delta _{2}=-2\frac{\Delta _{H}}{\Delta _{X}}\frac{{\text {d}}}{{\text {d}}t}\left( \frac{\Delta ^{2}_{H}}{\Delta _{X}}\right) \simeq -\frac{2}{H_{{\text {E}}}}\frac{{\text {d}}}{{\text {d}}t}\left( \frac{\Delta _{H}}{H_{{\text {E}}}}\right) ,\end{aligned}$$
(85)
$$\begin{aligned}&\Delta _{3}=2\frac{\Delta ^{2}_{H}}{\Delta _{X}}-2\frac{{\text {d}}}{{\text {d}}t}\left( \frac{\Delta _{H}}{\Delta _{X}}\right) \simeq -2\frac{\Delta _{H}}{H_{{\text {E}}}}-2\frac{\dot{H}_{{\text {E}}}}{H^{2}_{{\text {E}}}}\nonumber \\&\quad =2\epsilon _{{\text {E}}}-2\frac{\Delta _{H}}{H_{{\text {E}}}}. \end{aligned}$$
(86)

Further, after substituting (84) and (86) into (46) one has

$$\begin{aligned} n_{S({\text {GB}})}-1=-2\epsilon _{{\text {E}}}-\frac{2}{H_{{\text {E}}}}\left( 1+\frac{\Delta _{H}}{H_{{\text {E}}}}\right) ^{-1} \frac{{\text {d}}}{{\text {d}}t}\ln \left[ \epsilon _{{\text {E}}}-\frac{\Delta _{H}}{H_{{\text {E}}}}\right] , \end{aligned}$$
(87)

and, taking into account a weak GB coupling condition \(\frac{\Delta _{H}}{H_{{\text {E}}}}\ll 1\), the spectral index of a scalar perturbations can be written in following form

$$\begin{aligned} n_{S({\text {GB}})}-1\simeq -2\epsilon _{{\text {E}}}-\frac{2}{H_{{\text {E}}}}\frac{{\text {d}}}{{\text {d}}t}\ln \left[ \epsilon _{{\text {E}}}-\frac{\Delta _{H}}{H_{{\text {E}}}}\right] . \end{aligned}$$
(88)

Also, after substituting (84) and (86) into (47), one has expression for tensor-to-scalar ratio for a weak GB coupling

$$\begin{aligned} r_{{\text {GB}}}\simeq 16\left[ \epsilon _{{\text {E}}}-\frac{\Delta _{H}}{H_{{\text {E}}}}\right] . \end{aligned}$$
(89)

As one can see, for the case \(\Delta _{H}=0\), expressions (88)–(89) are reduced to (56)–(57) for a standard inflation.

Since the deviation \(\Delta _{H}\) is a free parameter of the theory, it can be considered as a generating function for constructing and analyzing inflationary models of the early universe with a weak coupling of a scalar field and Gauss–Bonnet scalar. Thus, one can consider the specific choice of the deviation parameter \(\Delta _{H}\) in order to satisfy the restriction (74) for any potential of a scalar field coupled with GB scalar. It should also be noted that the choice of the deviation parameter \(\Delta _{H}\) defines a special class of inflationary models based on the Einstein–Gauss–Bonnet gravity.

3 Special class of inflationary models with a weak GB coupling

In general case, one can consider various types of the deviation parameter \(\Delta _{H}\) to construct the models of cosmological inflation with non-minimal GB coupling. In order to consider a special class of EGB inflationary models corresponding to constrain (74), one can define the deviation parameter as follows

$$\begin{aligned} \Delta _{H}=-\alpha _{{\text {GB}}}\frac{\dot{H}_{{\text {E}}}}{H_{{\text {E}}}}, \end{aligned}$$
(90)

where \(|\alpha _{{\text {GB}}}|<1\) is a coupling constant.

For the case of quasi de Sitter expansion (when \(\epsilon _{{\text {E}}}\ll 1\)), after substituting (90) into expressions for deviation parameters (41) and (42) and neglecting the small terms of second order and higher, from (64) one has

$$\begin{aligned} c^{2}_{g}\simeq \frac{1+\alpha _{{\text {GB}}}\epsilon _{{\text {E}}}}{1-\alpha _{{\text {GB}}}\epsilon _{{\text {E}}}},~~~ |c_{g}-1|\simeq |\alpha _{{\text {GB}}}|\epsilon _{{\text {E}}}. \end{aligned}$$
(91)

At the stage of cosmological inflation one can estimate the slow-roll parameter as \(\epsilon _{{\text {E}}}<10^{-2}\) [53, 54], and, therefore, the models with deviation parameter (90) correspond to restriction (74) on the value of the velocity of relic gravitational waves.

The state parameter of a scalar field (30), for the deviation parameter (90), is

$$\begin{aligned} w_{{\text {GB}}}=-1+\frac{2}{3}\left( 1-\alpha _{{\text {GB}}}\right) \epsilon _{{\text {E}}}. \end{aligned}$$
(92)

Thus, on inflationary stage, one has the deviations of the velocity of tensor perturbations from the speed of light in vacuum (in natural units) and deviations of the state parameter \(w_{{\text {GB}}}\) from \(w_{{\text {E}}}\), which are defined by the small factor \(\alpha _{{\text {GB}}}\epsilon _{{\text {E}}}\ll 1\) connected with deviations from pure de Sitter exponential expansion (when \(\epsilon _{{\text {E}}}=0\)).

The background dynamic Eqs. (81)–(82) with the deviation parameter (90) can be written as

$$\begin{aligned}&V_{{\text {GB}}}(\phi _{{\text {GB}}})= 3H^{2}_{{\text {E}}}+(1-\alpha _{{\text {GB}}})\dot{H}_{{\text {E}}}, \end{aligned}$$
(93)
$$\begin{aligned}&\dot{\phi }^{2}_{{\text {GB}}}=-2(1-\alpha _{{\text {GB}}})\dot{H}_{{\text {E}}}. \end{aligned}$$
(94)

As one can see from Eqs. (9)–(10) and (93)–(94), a weak GB-coupling defined by the deviation parameter (90) does not change the shape of the potential.

From Eqs. (75), (90), (9)–(10) and (93)–(94) one has following connections between the potentials, Hubble parameters and scalar fields for standard inflation and EGB-inflation

$$\begin{aligned}&V_{{\text {GB}}}=V_{{\text {E}}}-\alpha _{{\text {GB}}}\dot{H}_{{\text {E}}},\end{aligned}$$
(95)
$$\begin{aligned}&H_{{\text {GB}}}= H_{{\text {E}}}(1+\alpha _{{\text {GB}}}\epsilon _{{\text {E}}}),\end{aligned}$$
(96)
$$\begin{aligned}&\phi _{{\text {GB}}}=\phi _{{\text {E}}}\sqrt{1-\alpha _{{\text {GB}}}}, \end{aligned}$$
(97)

where a weak GB coupling (75) implies that condition \(\alpha _{{\text {GB}}}\epsilon _{{\text {E}}}\ll 1\) is satisfied.

A coupling function can be obtained by integration of expression (83) after substituting the deviation parameter (90) into this expression. As a result, one has

$$\begin{aligned} \xi (\phi _{{\text {GB}}})=\frac{\alpha _{{\text {GB}}}}{4H^{2}_{{\text {E}}}(\phi _{{\text {GB}}})}+\xi _{0}, \end{aligned}$$
(98)

where \(\xi _{0}\) is the integration constant, however, it should be noted, that the constant coupling of a scalar field and the Gauss–Bonnet term \(\xi ={\text {const}}\) does not affect the dynamic of four-dimensional Friedmann universe.

After neglecting the small terms \(-\alpha _{{\text {GB}}}\dot{H}_{{\text {E}}}\ll V_{{\text {E}}}\) and \(\alpha _{{\text {GB}}}\epsilon _{{\text {E}}}\ll 1\) in expressions (95)–(96) one has \(V_{{\text {GB}}}\approx V_{{\text {E}}}\) and \(H_{{\text {GB}}}\approx H_{{\text {E}}}\), that, taking into account Eqs. (93) and (98), gives well known result [33, 36, 45, 48] (with \(\xi _{0}=0\))

$$\begin{aligned} V_{{\text {GB}}}(\phi _{{\text {GB}}})[\xi (\phi _{{\text {GB}}})-\xi _{0}]\approx \frac{3}{4}\alpha _{{\text {GB}}}={\text {const}}, \end{aligned}$$
(99)

therefore, in this approximation one has the changing of a field (97) only.

To determine the difference between results (98) and (99), one can consider a nominal coupling function in the following form

$$\begin{aligned} \xi (\phi _{{\text {GB}}})\simeq & {} \frac{3}{4}\alpha _{{\text {GB}}}\left[ V_{{\text {GB}}}(\phi _{{\text {GB}}})-(1-\alpha _{{\text {GB}}})\dot{H}_{{\text {E}}} +\Lambda \right] ^{-1}+\xi _{0}\nonumber \\= & {} \frac{3}{4}\alpha _{{\text {GB}}}\left[ V_{{\text {GB}}}(\phi _{{\text {GB}}})+X_{{\text {GB}}}+\Lambda \right] ^{-1}+\xi _{0}, \end{aligned}$$
(100)

where potential was redefined as

$$\begin{aligned} V_{{\text {GB}}}(\phi _{{\text {GB}}})\rightarrow V_{{\text {GB}}}(\phi _{{\text {GB}}})+\Lambda , \end{aligned}$$
(101)

and cosmological constant \(\Lambda \) can be associated with non-zero vacuum energy.

From (99) one has expression similar to (100) with \(X_{{\text {GB}}}=0\) after redefinition (101), which was considered in [33, 36] to eliminate the divergence in a value of non-minimal coupling function \(\xi _{{\text {GB}}}(\phi _{{\text {GB}}})\) after completion of inflationary stage.

From expression (100) on the inflationary stage when \(V_{{\text {GB}}}\gg X_{{\text {GB}}}+\Lambda \) one has

$$\begin{aligned} \xi (\phi _{{\text {GB}}})\simeq \frac{3\alpha _{{\text {GB}}}}{4V_{{\text {GB}}}(\phi _{{\text {GB}}})}+\xi _{0}, \end{aligned}$$
(102)

and at the reheating phase when \(X_{{\text {GB}}}\gg V_{{\text {GB}}}+\Lambda \) and energy of a scalar field is transferred to radiation, the coupling function is

$$\begin{aligned} \xi (\phi _{{\text {GB}}})\simeq \frac{3\alpha _{{\text {GB}}}}{4X_{{\text {GB}}}}+\xi _{0}. \end{aligned}$$
(103)

At the following stage, when \(\Lambda \gg X_{{\text {GB}}}+V_{{\text {GB}}}\) one has

$$\begin{aligned} \xi (\phi _{{\text {GB}}})\simeq \frac{3\alpha _{{\text {GB}}}}{4\Lambda }+\xi _{0}={\text {const}}, \end{aligned}$$
(104)

that implies the negligible GB coupling effects after completion of inflationary stage.

Therefore, the difference with results obtained in [33, 36, 45, 48] is the existence of an additional stage of the predominance of a scalar field’s kinetic energy (kination) with corresponding coupling function \(\xi (\phi _{{\text {GB}}})\) which is defined by expression (103).

3.1 Background dynamic equations in terms of a scalar field

To generate the exact solutions for the inflationary models based on Einstein gravity one can use the Eqs. (9)–(10), and, moreover, the method based on the representation of dynamic equations in terms of a scalar field.Footnote 2

In the framework of this approach, one can rewrite the background dynamic equations for standard inflation (9)–(10) on the basis of the relation

$$\begin{aligned} \dot{H}_{{\text {E}}}=\frac{{\text {d}}H_{{\text {E}}}}{{\text {d}}t}=\frac{{\text {d}}H_{{\text {E}}}}{{\text {d}}\phi _{{\text {E}}}}\frac{{\text {d}}\phi _{{\text {E}}}}{{\text {d}}t}= \frac{{\text {d}}H_{{\text {E}}}}{{\text {d}}\phi _{{\text {E}}}}\dot{\phi }_{{\text {E}}}, \end{aligned}$$
(105)

in following form

$$\begin{aligned}&V_{{\text {E}}}(\phi _{{\text {E}}})= 3H^{2}_{{\text {E}}}-2\left( \frac{{\text {d}}H_{{\text {E}}}}{{\text {d}}\phi _{{\text {E}}}}\right) ^{2},\end{aligned}$$
(106)
$$\begin{aligned}&\dot{\phi }_{{\text {E}}}=-2\frac{{\text {d}}H_{{\text {E}}}}{{\text {d}}\phi _{{\text {E}}}}. \end{aligned}$$
(107)

Also, the slow-roll parameters can be determined from expressions (59) as

$$\begin{aligned}&\epsilon _{{\text {E}}}=-\frac{\dot{H}_{{\text {E}}}}{H^{2}_{{\text {E}}}}=2H^{-2}_{{\text {E}}}\left( \frac{{\text {d}}H_{{\text {E}}}}{{\text {d}}\phi _{{\text {E}}}}\right) ^{2}, \end{aligned}$$
(108)
$$\begin{aligned}&\delta _{{\text {E}}}=-\frac{\ddot{H}_{{\text {E}}}}{2\dot{H}_{{\text {E}}}H_{{\text {E}}}}=2H^{-1}_{{\text {E}}}\left( \frac{{\text {d}}H^{2}_{{\text {E}}}}{{\text {d}}\phi _{{\text {E}}}^{2}}\right) . \end{aligned}$$
(109)

In this case, one can generate the exact solutions of Eqs. (106)–(107) by the choice of the Hubble parameter \(H_{{\text {E}}}=H_{{\text {E}}}(\phi _{{\text {E}}})\) as the function of a scalar field \(\phi _{{\text {E}}}\).

For the case of a weak GB coupling, on the basis of relation

$$\begin{aligned} \dot{H}_{{\text {E}}}=\frac{{\text {d}}H_{{\text {E}}}}{{\text {d}}\phi _{{\text {GB}}}}\dot{\phi }_{{\text {GB}}}, \end{aligned}$$
(110)

from Eqs. (93)–(94) one has

$$\begin{aligned}&V_{{\text {GB}}}(\phi _{{\text {GB}}})= 3H^{2}_{{\text {E}}}-2(1-\alpha _{{\text {GB}}})^{2}\left( \frac{{\text {d}}H_{{\text {E}}}}{{\text {d}}\phi _{{\text {GB}}}}\right) ^{2}, \end{aligned}$$
(111)
$$\begin{aligned}&\dot{\phi }_{{\text {GB}}}=-2(1-\alpha _{{\text {GB}}})\frac{{\text {d}}H_{{\text {E}}}}{{\text {d}}\phi _{{\text {GB}}}}, \end{aligned}$$
(112)

where the Hubble parameter \(H_{{\text {E}}}=H_{{\text {E}}}(\phi _{{\text {GB}}})\) is considered as the function of a scalar field \(\phi _{{\text {GB}}}\).

Thus, background dynamic Eqs. (111)–(112) can be considered as the Hamilton–Jacobi type equations [74] or, otherwise, the Ivanov–Salopek–Bond equations [10, 12] by analogy with the case of GR, for a special class of EGB inflationary models with the deviation parameter (90).

The expression for the non-minimal coupling function remains the same

$$\begin{aligned} \xi (\phi _{{\text {GB}}})=\frac{\alpha _{{\text {GB}}}}{4H^{2}_{{\text {E}}}(\phi _{{\text {GB}}})}+\xi _{0}, \end{aligned}$$
(113)

and the connection (96) between Hubble parameters \(H_{{\text {GB}}}\) and \(H_{{\text {E}}}\) can be written as

$$\begin{aligned} H_{{\text {GB}}}=H_{{\text {E}}}(1+\alpha _{{\text {GB}}}\epsilon _{{\text {E}}})= H_{{\text {E}}}\left[ 1+2\alpha _{{\text {GB}}}H^{-2}_{{\text {E}}}\left( \frac{{\text {d}}H_{{\text {E}}}}{{\text {d}}\phi _{{\text {E}}}}\right) ^{2}\,\right] , \end{aligned}$$
(114)

with the same relation (97) between scalar fields \(\phi _{{\text {GB}}}\) and \(\phi _{{\text {E}}}\).

Thus, expressions (93)–(98) or (106)–(114) completely determine the relations between exact inflationary solutions in the case of Einstein gravity (see, for example, in [10, 12, 75, 76]) and approximate ones for a weak GB coupling. The difference between the solutions is determined by a coupling constant \(\alpha _{{\text {GB}}}\).

Also, on the basis of Eqs. (106)–(107) and (111)–(112), one can conclude that a weak GB coupling with the deviation parameter (90) does not change the shape of the potential of a scalar field.

3.2 The parameters of cosmological perturbations for a weak GB coupling

After substituting (90) into Eqs. (88)–(89) one has following expressions for the parameters of cosmological perturbations corresponding to the deviation parameter (90) for a weak GB coupling

$$\begin{aligned}&n_{{\text {S(GB)}}}-1=-4\epsilon _{{\text {E}}}+2\delta _{{\text {E}}}=n_{{\text {S(E)}}},\end{aligned}$$
(115)
$$\begin{aligned}&r_{{\text {GB}}}=16(1-\alpha _{{\text {GB}}})\epsilon _{{\text {E}}}=(1-\alpha _{{\text {GB}}})r_{{\text {E}}}. \end{aligned}$$
(116)

It should be noted that a similar expressions of the parameters of cosmological perturbations for EGB-inflation

$$\begin{aligned}&n_{{\text {S(GB)}}}-1=-2\epsilon _{1}-\epsilon _{2},\end{aligned}$$
(117)
$$\begin{aligned}&r_{{\text {GB}}}=16(1-\lambda )\epsilon _{1}, \end{aligned}$$
(118)

were considered earlier in the paper [36] on the basis of postulated connection \(\delta _{1}=2\lambda \epsilon _{1}\) between slow-roll parameters, where \(\lambda \) is a some constant, \(\delta _{1}=\Delta _{1}\), \(\epsilon _{1}=\epsilon _{{\text {GB}}}\) and \(\epsilon _{2}=2(\epsilon _{{\text {GB}}}-\delta _{{\text {GB}}})\).

The difference between expressions (115)–(116) and (117)–(118) is that the first ones (115)–(116) determine the difference between cosmological perturbations parameters for inflationary models based on General Relativity and Einstein–Gauss–Bonnet gravity, the second expressions (117)–(118) correspond to the case of Einstein–Gauss–Bonnet gravity only where the difference between EGB-inflationary models is defined by the value of the parameter \(\lambda \).

The transition from expressions (117)–(118) to (115)–(116) can be carried out as follows: after neglecting the small term \(\alpha _{{\text {GB}}}\epsilon _{{\text {E}}}\ll 1\) in equation (96) one has \(H_{{\text {GB}}}\approx H_{{\text {E}}}\), which implies the following relations \(\epsilon _{{\text {GB}}}\approx \epsilon _{{\text {E}}}\) and \(\delta _{{\text {GB}}}\approx \delta _{{\text {E}}}\). Further, after substituting these relations into (117)–(118), one has (115)–(116). Also, for the case \(\alpha _{{\text {GB}}}=0\) and \(\lambda =0\), all these expressions are reduced to (56)–(57) corresponding to Einstein gravity.

As one can see, for a weak GB coupling, the corrections to the value of the spectral index of scalar perturbations are negligible \(n_{{\text {S(GB)}}}\simeq n_{{\text {S(E)}}}\). Nevertheless, such a coupling can have a significant effect on the value of the tensor-to-scalar ratio, namely, the positive coupling constant \(0<\alpha _{{\text {GB}}}<1\) leads to decreasing the value of tensor-to-scalar ratio \(r_{{\text {GB}}}<r_{{\text {E}}}\), and the negative one \(\alpha _{{\text {GB}}}<0\) gives a greater contribution of tensor perturbations to the CMB anisotropy than in the case of standard inflation \(r_{{\text {GB}}}>r_{{\text {E}}}\).

Thus, the corrections to Einstein gravity associated with a weak non-minimal coupling of a scalar field and the Gauss–Bonnet term can have a significant effect on the verification of cosmological models from observational constraints on the value of the tensor-to-scalar ratio [53, 54], and in principle, taking into account such corrections can ensure compliance with this observational constraint for any model of cosmological inflation, initially considered on the basis of Einstein gravity only.

Thus, one can consider inflationary models, for which taking into account corrections associated with a weak GB-coupling is critical for verification from observational data, and also other models based on GR that satisfy observational constraints. In both of these cases, one can define an explicit form of the coupling function \(\xi (\phi _{{\text {GB}}})\) and the constraints on the corresponding coupling constant \(\alpha _{{\text {GB}}}\) for a special class of models with the deviation parameter (90).

4 The examples of inflationary models with a weak GB coupling

In order to determine in more detail the influence of a weak GB coupling on the inflationary parameters, one can consider known models of cosmological inflation based on Einstein gravity with corrections (95)–(97).

At the moment, a many models of cosmological inflation with different scalar field potentials and different specifics of its evolution are considered to describe the evolution of the universe. A large number of inflationary models of the early universe based on Einstein gravity was considered in [9,10,11,12].

It should be noted that transformation (101) can be applied to all models under consideration to eliminate the divergence in a value of non-minimal coupling function \(\xi (\phi _{{\text {GB}}})\) after completion of inflationary stage. Condition \(\xi _{0}=0\) will also be considered, since the constant coupling of a scalar field and the Gauss–Bonnet scalar does not affect the dynamics of the universe.

Thus, one can use the observational constraints on the values of cosmological perturbation parameters (60)–(61) to estimate the value of a coupling constant \(\alpha _{{\text {GB}}}\). At the level of qualitative analysis, from expressions (115)–(116), one has that for the case \(\alpha _{{\text {GB}}}\le 0\), the standard inflationary models and corresponding EGB-inflation can be verified, and for \(0<\alpha _{{\text {GB}}}<1\), EGB-inflation only corresponds to the observational constraints. On the other hand, quantitative estimates of the coupling constant \(\alpha _{{\text {GB}}}\) make it possible to determine the influence of a weak GB coupling on the parameters of cosmological inflationary models.

4.1 The inflation with a weak GB coupling based on the double-well potential

This type of cosmological inflation was considered earlier in a large number of works (see, for example, in [7, 77,78,79,80,81]). The specificity of this model is that for a certain choice of parameters, the potential corresponds to the Higgs potential implying realization of the mechanism of spontaneous symmetry breaking [7, 77,78,79]. Also in works [80, 81] it was shown that such a model implies two stages of the accelerated expansion of the universe at small and large times and exit from the first inflation as well. Nevertheless, it should be noted that in the case of Einstein gravity, this model does not correspond to the observational constraints (60)–(61) on the values of the parameters of cosmological perturbations [80,81,82].

For this type of inflation one can consider the Hubble parameter as follows

$$\begin{aligned} H_{{\text {E}}}(\phi )=\beta \left( \frac{2}{3}\mu +\phi ^{2}_{{\text {E}}}\right) , \end{aligned}$$
(119)

and from Eqs. (106)–(107) one has

$$\begin{aligned}&\phi _{{\text {E}}}(t)=\phi _{0}\exp (-4\beta t),\end{aligned}$$
(120)
$$\begin{aligned}&V_{{\text {E}}}(\phi _{{\text {E}}})=\frac{\lambda _{{\text {E}}}}{9}\mu ^{2}+\frac{1}{2}m^{2}_{{\text {E}}}\phi ^{2}_{{\text {E}}}+ \frac{\lambda _{{\text {E}}}}{4}\phi ^{4}_{{\text {E}}},\end{aligned}$$
(121)
$$\begin{aligned}&H_{{\text {E}}}(t)=\beta \left( \frac{2}{3}\mu +\phi ^{2}_{0}e^{-8\beta t}\right) ,\end{aligned}$$
(122)
$$\begin{aligned}&a_{{\text {E}}}(t)\propto \exp \left( \frac{2\mu }{3}\beta t+\frac{\phi ^{2}_{0}}{8}e^{-8\beta t}\right) , \end{aligned}$$
(123)

where \(\beta \) and \(\mu \) are some constants, \(\phi _{0}\) is the initial value of the scalar field, \(\lambda _{{\text {E}}}=12\beta ^{2}\) is the self-coupling constant, and squared mass of the field is \(m^{2}_{{\text {E}}}=\frac{2}{3}\lambda _{{\text {E}}}(\mu -2)\).

For the case \(\mu <2\) one has \(m^{2}_{{\text {E}}}<0\) that corresponds to the spontaneously broken symmetry in this model [7, 77,78,79]. For the case \(\mu >2\) one has a model without the symmetry breaking where squared mass is \(m^{2}_{{\text {E}}}>0\), and the value \(\mu =2\) implies the transition from the Higgs inflation to chaotic one with potential \(V_{{\text {E}}}\sim \phi ^{4}_{{\text {E}}}\) [7].

For EGB-inflation, from Eqs. (111)–(112), one has

$$\begin{aligned} \phi _{{\text {GB}}}(t)= & {} \phi _{0}\sqrt{1-\alpha _{{\text {GB}}}}\exp (-4\beta t),\end{aligned}$$
(124)
$$\begin{aligned} V_{{\text {GB}}}(\phi _{{\text {GB}}})= & {} \frac{\lambda _{{\text {GB}}}}{9}(1-\alpha _{{\text {GB}}})^{2}\mu ^{2}+ \frac{1}{2}m^{2}_{{\text {GB}}}\phi ^{2}_{{\text {GB}}}\nonumber \\&+\frac{\lambda _{{\text {GB}}}}{4}\phi ^{4}_{{\text {GB}}},\end{aligned}$$
(125)
$$\begin{aligned} \xi _{{\text {GB}}}(\phi _{{\text {GB}}})= & {} 27\left( \frac{\alpha _{{\text {GB}}}}{\lambda _{{\text {GB}}}}\right) \left[ 3\phi ^{2}_{{\text {GB}}}-2\mu (1-\alpha _{{\text {GB}}})\right] ^{-2},\nonumber \\ \end{aligned}$$
(126)

where

$$\begin{aligned}&\lambda _{{\text {GB}}}=\frac{12\beta ^{2}}{(1-\alpha _{{\text {GB}}})^{2}}=\frac{\lambda _{{\text {E}}}}{(1-\alpha _{{\text {GB}}})^{2}}, \end{aligned}$$
(127)
$$\begin{aligned}&m^{2}_{{\text {GB}}}=\frac{2}{3}\lambda _{{\text {E}}}\left( \frac{\mu +2\alpha _{{\text {GB}}}-2}{1-\alpha _{{\text {GB}}}}\right) . \end{aligned}$$
(128)

Also, the mass of the Higgs field coupled with Gauss–Bonnet term can be defined as

$$\begin{aligned} m^{2}_{{\text {GB}}}=m^{2}_{{\text {E}}}+\frac{2}{3}\mu \lambda _{{\text {E}}}\left( \frac{\alpha _{{\text {GB}}}}{1-\alpha _{{\text {GB}}}}\right) . \end{aligned}$$
(129)

The condition of spontaneous symmetry breaking also change, namely, taking into account a weak GB coupling, such a condition can be written as

$$\begin{aligned} \mu +2\alpha _{{\text {GB}}}-2<0. \end{aligned}$$
(130)

Also, for the case \(\mu +2\alpha _{{\text {GB}}}-2=0\) one has the transition from the Higgs inflation to chaotic EGB-inflation with corresponding potential \(V_{{\text {GB}}}\sim \phi ^{4}_{{\text {GB}}}\).

The deviation parameter, Hubble parameter and the scale factor for the Higgs inflation with a weak GB coupling are

$$\begin{aligned}&\Delta _{{\text {GB}}}(t)=\frac{24\alpha _{{\text {GB}}}\beta \phi ^{2}_{0}e^{-8\beta t}}{2\mu +3\phi ^{2}_{0}e^{-8\beta t}}, \end{aligned}$$
(131)
$$\begin{aligned}&H_{{\text {GB}}}(t)=H_{{\text {E}}}(t)+\frac{24\alpha _{{\text {GB}}}\beta \phi ^{2}_{0}e^{-8\beta t}}{2\mu +3\phi ^{2}_{0}e^{-8\beta t}}, \end{aligned}$$
(132)
$$\begin{aligned}&a_{{\text {GB}}}(t)\propto a_{{\text {E}}}(t)e^{8\alpha _{{\text {GB}}}\beta t}\left( 3\phi ^{2}_{0}+2\mu e^{8\beta t}\right) ^{-\alpha _{{\text {GB}}}}. \end{aligned}$$
(133)

As one can see, for \(2\mu e^{8\beta t}\gg 3\phi ^{2}_{0}\) one has \(a_{{\text {GB}}}(t)\simeq a_{{\text {E}}}(t)\) up to a constant, that corresponds the condition \(\alpha _{{\text {GB}}}\epsilon _{{\text {E}}}\ll 1\) in expression (96).

For the Hubble parameter (122) from expressions (59) one has \(\epsilon _{{\text {E}}}=-\frac{1}{3}\delta ^{2}_{{\text {E}}}+2\delta _{{\text {E}}}\simeq 2\delta _{{\text {E}}}\), and the connection between tensor-to-scalar ratio and spectral index of scalar perturbations for the Higgs inflation is

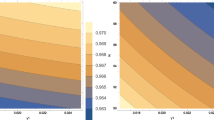
$$\begin{aligned} r=\frac{16}{3}(1-\alpha _{{\text {GB}}})(1-n_{{\text {S}}}). \end{aligned}$$
(134)

From observational constraints (60)–(61) one has the following values of a coupling constant \(0.6<\alpha _{{\text {GB}}}<1\) for the verifiable inflation with the Higgs potential. Thus, the mass of the Higgs field for a weak GB coupling changes as \(m^{2}_{{\text {GB}}}>m^{2}_{{\text {E}}}+\mu \lambda _{{\text {E}}}\) and self-coupling parameter is \(\lambda _{{\text {GB}}}>1.58\lambda _{{\text {E}}}\). The scalar field for this type of inflation with a weak GB coupling can be estimated as \(0<\phi _{{\text {GB}}}<0.63\,\phi _{{\text {E}}}\). The dependence \(r=r(n_{{\text {S}}})\) for inflation with double-well potential is shown on the Fig. 1.

Fig. 1
figure 1

The \(r=r(n_{{\text {S}}})\) diagram for different values of the coupling constant \(\alpha _{{\text {GB}}}\)

Full size image

Now, we consider the behaviour of this model on a large times \(t\rightarrow \infty \), corresponding to the Dark Energy domination era [53, 83, 84].

Firstly, from expression (131) one has \(\Delta _{{\text {GB}}}(t\rightarrow \infty )=0\), i.e. at a large times the non-minimal coupling are negligible, and the gravity theory corresponds to General Relativity.

Secondly, from expressions (122)–(121) for \(t\rightarrow \infty \) one has

$$\begin{aligned}&H_{SI}=\frac{2}{3}\beta \mu ,\end{aligned}$$
(135)
$$\begin{aligned}&a_{SI}(t)\propto \exp \left( \frac{2\mu }{3}\beta t\right) ,\end{aligned}$$
(136)
$$\begin{aligned}&V_{SI}=\Lambda =\frac{4}{3}\beta ^{2}\mu ^{2}, \end{aligned}$$
(137)

therefore, at the large times this models leads to cosmological constant as the source second accelerated expansion on the universe [53, 83, 84].

Consequently, a weak GB coupling defined by the function (126) with a coupling constant \(0.6<\alpha _{{\text {GB}}}<1\) can be taken into account at the inflationary stage to construct a phenomenologically correct models of cosmological inflation based on the double-well potential. At the large times such corrections are negligible, and the gravity theory corresponding to GR.

Another possibility of constructing verified Higgs inflation is to consider the non-minimal coupling of a scalar field with the Ricci scalar, which, however, changes the shape of the potential [82, 85] in contrast to a weak GB coupling.

4.2 Exponential power-law inflation with a weak GB coupling

This type of cosmological inflationary model was considered in papers [60, 86, 87] on the basis of General Relativity and some modified gravity theories as well. Exponential power-law (EPL) inflation also leads to two stages of accelerated expansion of the universe at small and large times with corresponding exit from the initial inflationary stage at small times.

In contrast to the model with double-well potential (121), EPL-inflation corresponds to observational constraints (60)–(61) on the values of the parameters of cosmological perturbations for the case of Einstein gravity [87]. Thus, for this model, the coupling constant \(\alpha _{{\text {GB}}}\) of a scalar field and the Gauss–Bonnet term can be either positive or negative.

For canonical scalar field the Hubble parameter corresponding to EPL-inflation can be written as follows

$$\begin{aligned} H_{{\text {E}}}(\phi _{{\text {E}}})=\mu _{1}\exp (-\mu _{2}\phi _{{\text {E}}})+\mu _{3}, \end{aligned}$$
(138)

where \(\mu _{1}\), \(\mu _{2}\) and \(\mu _{3}\) are some positive constants.

The exact solutions of the Eqs. (106)–(107) are

$$\begin{aligned} V_{{\text {E}}}(\phi _{{\text {E}}})= & {} \mu ^{2}_{1}(3-2\mu ^{2}_{2})\exp (-2\mu _{2}\phi _{{\text {E}}})\nonumber \\&+ 6\mu _{1}\mu _{3}\exp (-\mu _{2}\phi _{{\text {E}}})+3\mu ^{2}_{3},\end{aligned}$$
(139)
$$\begin{aligned} \phi _{{\text {E}}}(t)= & {} \frac{1}{\mu _{2}}\ln \left( 2\mu _{1}\mu ^{2}_{2}t+c\right) ,\end{aligned}$$
(140)
$$\begin{aligned} H_{{\text {E}}}(t)= & {} \frac{\mu _{1}}{2\mu _{1}\mu ^{2}_{2}t+c}+\mu _{3},\end{aligned}$$
(141)
$$\begin{aligned} a_{{\text {E}}}(t)\propto & {} \exp (\mu _{3}t)(2\mu _{1}\mu ^{2}_{2}t+c)^{1/2\mu ^{2}_{2}}, \end{aligned}$$
(142)

where c is the constant of integration.

For ELP-inflation with a weak GB coupling, from Eqs. (111)–(112), one has

$$\begin{aligned} \phi _{{\text {GB}}}(t)&=\frac{1}{\tilde{\mu }_{2}}\ln \left[ 2(1-\alpha _{{\text {GB}}})\mu _{1}\tilde{\mu }^{2}_{2}t+c\right] , \end{aligned}$$
(143)
$$\begin{aligned} V_{{\text {GB}}}(\phi _{{\text {GB}}})&=\mu ^{2}_{1}\left[ 3-2(1-\alpha _{{\text {GB}}})^{3}\tilde{\mu }^{2}_{2}\right] \exp (-2\tilde{\mu }_{2}\phi _{{\text {GB}}})\nonumber \\&\quad + 6\mu _{1}\mu _{3}\exp (-\tilde{\mu }_{2}\phi _{{\text {GB}}})+3\mu ^{2}_{3},\end{aligned}$$
(144)
$$\begin{aligned} \xi _{{\text {GB}}}(\phi _{{\text {GB}}})&=\alpha _{{\text {GB}}}\left( 2\mu _{3}+2\mu _{1}e^{-\tilde{\mu }_{2}\phi _{{\text {GB}}}}\right) ^{-2}, \end{aligned}$$
(145)

where

$$\begin{aligned} \tilde{\mu }_{2}=\frac{\mu _{2}}{\sqrt{1-\alpha _{{\text {GB}}}}}. \end{aligned}$$
(146)

Corresponding deviation parameter, Hubble parameter and the scale factor for ELP-inflation with a weak GB coupling are

$$\begin{aligned}&\Delta _{{\text {GB}}}(t)=\frac{2\mu ^{2}_{2}\mu ^{2}_{2}\alpha _{{\text {GB}}}}{\left( 2\mu _{1}\mu ^{2}_{2}\mu _{3}t+c\mu _{3}+\mu _{1}\right) (2\mu _{1}\mu ^{2}_{2}t+c)},\end{aligned}$$
(147)
$$\begin{aligned}&H_{{\text {GB}}}(t)=H_{{\text {E}}}(t)+\frac{2\mu ^{2}_{2}\mu ^{2}_{2}\alpha _{{\text {GB}}}}{\left( 2\mu _{1}\mu ^{2}_{2}\mu _{3}t+c\mu _{3}+\mu _{1}\right) (2\mu _{1}\mu ^{2}_{2}t+c)}, \nonumber \\ \end{aligned}$$
(148)
$$\begin{aligned}&a_{{\text {GB}}}(t)\propto a_{{\text {E}}}(t)\left( 2\mu _{1}\mu ^{2}_{2}t+c+\frac{\mu _{1}}{\mu _{3}}\right) ^{-\alpha _{{\text {GB}}}} (2\mu _{1}\mu ^{2}_{2}t+c)^{\alpha _{{\text {GB}}}}.\nonumber \\ \end{aligned}$$
(149)

As one can see, for \(c\gg \frac{\mu _{1}}{\mu _{3}}\) one has \(a_{{\text {GB}}}(t)\simeq a_{{\text {E}}}(t)\) up to a constant, that corresponds the condition \(\alpha _{{\text {GB}}}\epsilon _{{\text {E}}}\ll 1\) in expression (96).

For the Hubble parameter (141) from expressions (59) one has \(\epsilon =\frac{1}{2}\left( \frac{\delta }{\mu _{2}}\right) ^{2}\), and the connection between tensor-to-scalar ratio and spectral index of scalar perturbations for EPL-inflation can be written as

$$\begin{aligned} n_{{\text {S}}}=1-\frac{r}{4(1-\alpha _{{\text {GB}}})}-\frac{1}{2\mu _{2}}\left( \frac{2r}{1-\alpha _{{\text {GB}}}}\right) ^{1/2}. \end{aligned}$$
(150)

As one can see, for this type of inflation the observational constraints (60)–(61) can be satisfied by the choice of two constants \(\mu _{2}\) and \(\alpha _{{\text {GB}}}\). Nevertheless, one can define the restriction on the coupling constant \(\alpha _{{\text {GB}}}\) for some certain value of \(\mu _{2}\). Namely, for \(\mu _{2}\ge 12\) one has only positive values of the coupling constant \(0\le \alpha _{{\text {GB}}}<1\) and for \(\mu _{2}<12\) the values of the coupling constant can be both positive or negative \(-1<\alpha _{{\text {GB}}}<1\) for verified EPL-inflation.

Fig. 2
figure 2

The \(r=r(n_{{\text {S}}})\) diagram for \(\mu _{2}=12\) and different values of the coupling constant \(\alpha _{{\text {GB}}}\)

Full size image

On the Fig. 2 the dependence \(r=r(n_{{\text {S}}})\) for EPL-inflation with GB-corrections for \(\mu _{2}=12\) is shown. As one can see, for this case, the model corresponds to observational constraints for \(0\le \alpha _{{\text {GB}}}<1\) and, therefore, taking into account GB-corrections is necessary for verification of EPL-inflation with parameter \(\mu _{2}>12\).

Thus, in this case, the scalar field can be either increased or decreased by means of a non-minimal coipling with the Gauss–Bonnet term, which depends on the value of the parameter \(\mu _{2}\).

At the large times from (147) one has \(\Delta (t\rightarrow \infty )=0\), therefore GR-corrections are negligible at the Dark Energy domination era. The dynamic of the universe’s expansion

$$\begin{aligned} H_{SI}=\mu _{3},~~~a_{SI}\propto \exp (\mu _{3}t), \end{aligned}$$
(151)

is defined by a cosmological constant \(\Lambda =3\mu ^{2}_{3}\). Also, in [86, 87] it was shown that between two these stages, universe expands without acceleration.

Similarly, one can estimate the corrections induced by the non-minimal coupling of a scalar field and the Gauss–Bonnet term for other models of cosmological inflation [9,10,11,12] and obtain the form of the corresponding coupling function as well.

5 Discussion

In this paper, the influence of the non-minimal coupling of a scalar field and the Gauss–Bonnet scalar on the process of cosmological inflation was considered. The basis of the proposed analysis is the presented relations between the parameters of inflationary models for the case of General Relativity and Einstein–Gauss–Bonnet gravity.

The effect of non-minimal GB coupling was determined by means of background deviation parameters \(\{\Delta _{H},\Delta _{X},\Delta _{V}\}\) and ones corresponding to the Gauss–Bonnet term corrections to the parameters of cosmological perturbations \(\{\Delta _{1},\Delta _{2},\Delta _{3}\}\) which are related by Eqs. (26) and (51)–(53).

In general case, two main results were obtained that characterize the influence of the GB-term on the inflationary process. The first result is that in four-dimensional spatially flat Friedmann–Robertson–Walker space-time the non-minimal coupling of a scalar field with the Gauss–Bonnet term leads to decrease of it’s energy density. The second result is that such a coupling can accelerate the rate of expansion of the universe by less than two times.

Nevertheless, the slow-roll conditions correspond to a weak influence of such a coupling on cosmological dynamics. This result leads to the interpretation of non-minimal coupling of a scalar field and the Gauss–Bonnet scalar as a small quantum corrections to the main dynamical effects of General Relativity at the inflationary stage of the evolution of early universe.

Based on this notion, which was called a weak GB coupling, the effect of such a coupling on the background inflationary parameters and cosmological perturbation parameters was evaluated. To satisfy the constraint (74) on the velocity of tensor perturbations at the inflationary stage of the universe’s evolution for any potential of a scalar field, the special class of inflationary models with a weak GB coupling and the deviation parameter (90) was considered. For this class of cosmological models the influence of the Gauss–Bonnet scalar on the inflationary parameters is determined by the value of the coupling constant \(\alpha _{{\text {GB}}}\) only. Also, such a models implying the conservation of the shape of minimal coupled scalar field potential \(V_{{\text {E}}}\). It should also be noted that in the case of exponentially accelerated expansion of the universe, the difference between EGB gravity and General relativity is absent for any value of the parameter \(\alpha _{{\text {GB}}}\) in cosmological models with the deviation parameter (90).

The first effect of such a coupling is a change of a scalar field itself, which decreases for positive values of a coupling constant \(\alpha _{{\text {GB}}}\) and increases for its negative values. The second effect is a change in the mass of a scalar field the Higgs inflation based on Einstein–Gauss–Bonnet gravity compared to General Relativity. Also, the non-minimal coupling of the Higgs field with the Gauss–Bonnet term changes the condition of spontaneous symmetry breaking. The observational constraints on the parameters of cosmological perturbations were used to estimate the value of a coupling constant \(\alpha _{{\text {GB}}}\) for inflationary model with double-well potential and for EPL-inflation as well. In the modern era, a weak GB-corrections for these models are negligible, and the dynamics of the accelerated expansion of the universe is determined by the cosmological constant (prevailing over Dark Matter and the baryonic component [53]) based on Einstein gravity.

Thus, the proposed approach, on the one hand, allows to define the Gauss–Bonnet term corrections for any standard inflationary model based on Einstein gravity; on the other hand, it gives the possibility to verify such a models from observational constraints on the parameters of cosmological perturbations.

It should also be noted that, in the general case, one can consider a wider class of EGB-inflationary models with a deviation parameter which differ from (90). However, in this case, it is necessary to check whether the velocity of relic gravitational waves corresponds to constraint (74) for each specific model.