Magnetic dipole moments of the heavy tensor mesons in QCD

Abstract

The magnetic dipole moments of the $\mathcal{D}_2$, and $\mathcal{D}_{S_2}$, $\mathcal{B}_2$, and $\mathcal{B}_{S_2}$ heavy tensor mesons are estimated in framework of the light cone QCD sum rules. It is observed that the magnetic dipole moments for the charged mesons are larger than that of its neutral counterpart. It is found that the SU(3) flavor symmetry violation is about 10 % in both b and c sectors.

1 Introduction

Recent years were quite productive in field of the particle spectroscopy. Many charmonium and bottomonium like states are observed by BaBar, Belle, LHCb and BES III collaborations [1]. These progresses in experiments stimulated further theoretical studies and experimental investigations on this subject [2–6]. Considerable progress has also been made on spectroscopy of the conventional heavy mesons states containing single charm and bottom quarks such as $\mathcal{D}_{s_I}(2700)$, $\mathcal{D}_{s_J}^*(2860)$, $\mathcal{D}_{s_J}(3040)$, $\mathcal{D}_{J}(2580)$, $\mathcal{D}_{J}(2740)$, $\mathcal{D}_{J}^*(2760)$, $\mathcal{D}_{J}(3000)$, $\mathcal{D}_{J}^*(3000)$, $\mathcal{B}_{1}(5721)$, $\mathcal{B}_{2}^*(5747)$, $\mathcal{B}_{s_1}(5830)$, $\mathcal{B}_{s_2}^*(5840)$, $\mathcal{B}(5970)$, etc [7]. Soon after D0 Collaboration observed the $\mathcal{B}_{1}(5721)$ and $\mathcal{B}_{2}(5747)$ states [8], which were both confirmed by the CDF Collaboration [9]. The CDF Collaboration further observed the $\mathcal{B}_{s_1}(5830)$ and $\mathcal{B}_{s_2}^*(5840)$ states [10] which in turn confirmed by the D0 Collaboration [11]. Moreover, the masses of the $\mathcal{B}_{s_1}(5830)$ and $\mathcal{B}_{s_2}^*(5840)$ states were determined more accurately by the LHCb Collaboration [12].

The masses and decay constants of the heavy tensor meson $\mathcal{D}_{2}^*(2740)$ and $\mathcal{D}_{s_2}^*(2573)$ states were first studied within the framework of the QCD sum rules method in [13–15]. These mesons, as well as the $\mathcal{B}_{2}^*(5747)$ and $\mathcal{B}_{s_2}^*(5840)$ tensor mesons have recently been studied within the same approach in [15]. Note that light tensor mesons without, and with strange quark have also been analyzed in framework of the QCD sum rules method in [16, 17], respectively.

One of the most promising approaches in investigating the properties of mesons and hadrons is the study of the electromagnetic form factors and multipole moments. These studies can provide useful information about their internal structures. The electromagnetic properties of usual mesons, as well as photons and neutrons have comprehensively been studied from theoretical and experimental sides, and at present it is the subject of the growing interest from both sides. However the study of the electromagnetic properties of the tensor mesons has received less interest, and therefore more effort is needed in this respect. The magnetic moments of the light tensor mesons were investigated in framework of the light cone QCD sum rules method (LCSR) in [18]. In the present work we calculate the magnetic dipole moments of the recently discovered heavy tensor mesons in LCSR.

The paper is organized as follows. In Sect. 2, the light cone QCD sum rules are constructed for the magnetic dipole moments of the heavy tensor mesons. In Sect. 3, the numerical analysis is performed for the obtained sum rules.

2 Theoretical framework

Before presenting the light cone sum rules for the magnetic dipole moments of the heavy tensor mesons, let us first introduce the matrix element which corresponds to the transition of the heavy tensor meson with momentum $p+q$ to the heavy tensor meson with momentum p in presence of the electromagnetic field, i.e.,

$$\begin{aligned}&\langle T_Q(p,\varepsilon ) | j_\rho ^{el} | T_Q(p+q,\varepsilon ) \rangle \nonumber \\&\quad = \varepsilon _{\xi \sigma }^*(p) \left\{ 2 p_\rho \left[ g^{\xi \lambda } g^{\sigma \tau } F_1(Q^2) - g^{\sigma \tau } {q^\xi q^\lambda \over 2 m_{T_Q}^2} F_3(Q^2)\right. \right. \nonumber \\&\left. \qquad + {q^\xi q^\lambda \over 2 m_{T_Q}^2}\, {q^\sigma q^\tau \over 2 m_{T_Q}^2} F_5(Q^2) \right] \nonumber \\&\qquad \left. + (g^{\rho \sigma } q^\tau - g^{\rho \tau } q^\sigma ) \left[ g^{\xi \lambda } F_2(Q^2) - {q^\xi q^\lambda \over 2 m_{T_Q}^2} F_4(Q^2) \right] \right\} \nonumber \\&\quad \varepsilon _{\lambda \tau } (p+q), \end{aligned}$$

(1)

where $F_i(Q^2)$ are the form factors, and $T_Q(p,\varepsilon )$ means heavy tensor meson with momentum p and polarization tensor $\varepsilon _{\alpha \beta }$. Since we are interested with the magnetic dipole moments of heavy tensor mesons, the values of the form factors at $Q^2=-q^2=0$ need to be calculated. The transition under consideration can be described by the following correlation function,

$$\begin{aligned}&\Pi ^{\mu \nu \rho \alpha \beta } (p,q)\nonumber \\&\quad = - \int \mathrm{d}^4x \int \mathrm{d}^4y e^{i(px+qy)} \langle 0 | \mathcal{T}\{ j_{\mu \nu } (0) j_\rho ^{el}(y) \bar{j}_{\alpha \beta }(x)\} | 0 \rangle ,\nonumber \\ \end{aligned}$$

(2)

where $j_{\mu \nu }$ is the interpolating current of the heavy tensor meson, and $j_\rho ^{el}$ is the electromagnetic current given as,

$$\begin{aligned} j_\rho ^{el} = e_q \bar{q} \gamma _\rho q + e_Q \bar{Q} \gamma _\rho Q, \end{aligned}$$

with the electric charges $e_q$ and $e_Q$ of the light and heavy quarks, respectively. The coupling of the tensor meson current $j_{\mu \nu }$ to the tensor state is defined as,

$$\begin{aligned} \langle 0 | j_{\mu \nu } | T_Q(p,\varepsilon ) \rangle = m_{T_Q}^3 g_{T_Q} \varepsilon _{\mu \nu }, \end{aligned}$$

(3)

where $m_{T_Q}$ is the mass, and $g_{T_Q}$ is the coupling constant of the tensor meson.

It is more convenient to rewrite the correlator (2) by introducing the electromagnetic background field strength tensor

$$\begin{aligned} F_{\mu \nu } = i (q_\mu \varepsilon _\nu -q_\nu \varepsilon _\mu ) e^{iqx}, \end{aligned}$$

of the plane wave, in the following form

$$\begin{aligned} \Pi _{\mu \nu \rho \alpha \beta } \, \varepsilon ^\rho = i \int \mathrm{d}^4x e^{ipx} \langle 0 | T \{ j_{\mu \nu } (x) \bar{j}_{\alpha \beta } (0) | 0 \rangle _F, \end{aligned}$$

(4)

where F means that all vacuum expectation values are calculated in the background electromagnetic field. The correlation function (2) can be obtained by expanding the correlation function (4) in powers of the background field, and taking into account the terms that are linear in $F_{\mu \nu }$ which corresponds to the single photon radiation. The advantage of using the background field is that it separates the hard and soft photon radiation in an explicitly gauge invariant way (for more about the details of the background field method, see [19, 20]).

After these preliminary remarks, we can now proceed deriving the light cone QCD sum rules for the magnetic dipole moments of the heavy tensor mesons.

These sum rules can be obtained by calculating the correlator function in terms of mesons (physical part) from one side; and calculating the same correlation function in terms of quark-gluon degrees of freedom by using the operator product expansion (OPE) in deep Eucledian region from theoretical side. Matching these two representations of the same correlation function, the sum rules for the magnetic dipole moments of the heavy tensor mesons are obtained.

Calculation of the correlation function from the physical side is performed by inserting the complete set of tensor meson states having the same quantum number as that of the interpolating current, and isolating he ground state, as the result of which we get,

$$\begin{aligned}&\Pi _{\mu \nu \rho \alpha \beta }\, \varepsilon ^\rho = i \varepsilon ^\rho {\langle 0 | j_{\mu \nu } | T_Q(p,\varepsilon ) \rangle \over p^2-m_{T_Q}^2}\nonumber \\&\quad \langle T_Q(p,\varepsilon ) | j_\rho ^{el} | T_Q(p+q,\varepsilon ) \rangle {\langle T_Q(p+q,\varepsilon ) | j_{\alpha \beta }^\dagger | 0 \rangle \over (p+q)^2-m_{T_Q}^2}+ \cdots ,\nonumber \\ \end{aligned}$$

(5)

where dots mean the contribution of the higher states and continuum.

From experimental point of view the multipole form factors are more useful than the form factors given in Eq. (1). The relations between the two sets of the form factors for any arbitrary $q^2$ are derived in [21]. For the real photon $(q^2=0)$ these relations are given as:

$$\begin{aligned}&F_1(0) = G_{E_0}(0), \nonumber \\&F_2(0) = G_{M_1}(0), \nonumber \\&F_3(0) = - 2 G_{E_0}(0) + G_{E_2}(0) + G_{M_1}(0), \nonumber \\&F_4(0) = - G_{M_1}(0) + G_{M_3}(0), \nonumber \\&F_5(0) = G_{E_0}(0)- [ G_{E_2}(0) + G_{M_1}(0) ] \nonumber \\&\quad +\, G_{E_4}(0) + G_{M_3}(0), \end{aligned}$$

(6)

where $G_{E_\ell }(0)$ and $G_{M_\ell }(0)$ are the electric and magnetic multipoles.

Calculation of the correlator function from the physical side is performed by inserting the complete set of tensor meson states in Eqs. (1–4), from which for the hadronic part we get,

$$\begin{aligned}&\Pi _{\mu \nu \rho \alpha \beta } (p,q) \, \varepsilon ^\rho = {m_{T_Q}^6 g_{T_Q}^2 \over (p^2-m_{T_Q}^2) \left[ (p+q)^2-m_{T_Q}^2\right] }\nonumber \\&\quad \times \varepsilon _{\mu \nu }(p) \varepsilon _{\xi \sigma }^*(p) \Bigg \{2 (p\cdot \varepsilon ) \Bigg [ g^{\xi \lambda } g^{\sigma \tau } F_1(Q^2) \nonumber \\&\quad - g^{\sigma \tau } {q^\xi q^\lambda \over 2 m_{T_Q}^2} F_3(Q^2) + {q^\xi q^\lambda \over 2 m_{T_Q}^2}\, {q^\sigma q^\tau \over 2 m_{T_Q}^2} F_5(Q^2) \Bigg ]\nonumber \\&\quad + (\varepsilon ^\sigma q^\tau - \varepsilon ^\tau q^\sigma ) \Bigg [ g^{\xi \lambda } F_2(Q^2) - {q^\xi q^\lambda \over 2 m_{T_Q}^2} F_4(Q^2) \Bigg ] \Bigg \}\nonumber \\&\quad \times \varepsilon _{\lambda \tau } (p+q) \varepsilon _{\alpha \beta }^*(p+q). \end{aligned}$$

(7)

Summation over the polarizations of the heavy tensor mesons can be performed by using the relation,

$$\begin{aligned}&\varepsilon _{\rho \sigma }^*(p) \varepsilon _{\lambda \tau } (p) = {1\over 2} \mathcal{P}_{\rho \lambda }(p) \mathcal{P}_{\sigma \tau }(p)\nonumber \\&\quad + {1\over 2} \mathcal{P}_{\rho \tau }(p) \mathcal{P}_{\sigma \lambda }(p) - {1\over 3} \mathcal{P}_{\rho \sigma }(p) \mathcal{P}_{\lambda \tau }(p), \end{aligned}$$

(8)

where

$$\begin{aligned} \mathcal{P}_{\rho \lambda }(p) = \left( - g_{\rho \lambda } + {p_\rho p_\lambda \over m_{T_Q}^2} \right) . \end{aligned}$$

Using Eqs. (6) and (8) in Eq. (7), for the physical part of the correlation function we get,

$$\begin{aligned}&\Pi _{\mu \nu \rho \alpha \beta } (p,q) \, \varepsilon ^\rho = {m_{T_Q}^6 g_{T_Q}^2 \over (p^2-m_{T_Q}^2) [(p+q)^2-m_{T_Q}^2]}\nonumber \\&\quad \times \left\{ {1\over 2} \mathcal{P}_{\mu \xi }(p) \mathcal{P}_{\nu \sigma }(p) + {1\over 2} \mathcal{P}_{\mu \sigma }(p) \mathcal{P}_{\nu \xi }(p) - {1\over 3} \mathcal{P}_{\mu \nu }(p) \mathcal{P}_{\xi \sigma }(p) \right\} \nonumber \\&\quad \times \Bigg \{2 (p\cdot \varepsilon ) \Bigg [ g^{\xi \lambda } g^{\sigma \tau } G_{E_0}(0) - g^{\sigma \tau } {q^\xi q^\lambda \over 2 m_{T_Q}^2}\nonumber \\&\quad \times \Big ( - 2 G_{E_0}(0)+G_{E_2}(0) + G_{M_1}(0)\Big ) \nonumber \\&\quad + {q^\xi q^\lambda \over 2 m_{T_Q}^2}\, {q^\sigma q^\tau \over 2 m_{T_Q}^2} \Big (G_{E_0}(0) - [G_{E_2}(0) + G_{M_2}(0)]\nonumber \\&\quad + G_{E_4}(0) + G_{M_3}(0)\Big )\Bigg ] + (\varepsilon ^\sigma q^\tau - \varepsilon ^\tau q^\sigma )\nonumber \\&\quad \times \Bigg [ g^{\xi \lambda } G_{M_1}(0) - {q^\xi q^\lambda \over 2 m_{T_Q}^2}\Big ( - G_{M_1}(0) + G_{M_2}(0)\Big ) \Bigg ] \Bigg \} \nonumber \\&\quad \times \left\{ {1\over 2} \mathcal{P}_{\lambda \alpha }(p+q) \mathcal{P}_{\tau \beta }(p+q) + {1\over 2} \mathcal{P}_{\lambda \beta }(p+q) \mathcal{P}_{\alpha \tau }(p+q)\right. \nonumber \\&\quad \left. - {1\over 3} \mathcal{P}_{\lambda \tau }(p) \mathcal{P}_{\alpha \beta }(p+q) \right\} . \end{aligned}$$

(9)

It follows from Eq. (9) that the correlation function $\Pi _{\mu \nu \rho \alpha \beta } \, \varepsilon ^\rho$ contains various independent structures, each of which can be used in determination of the multipole moments of heavy tensor mesons. In the present work we restrict ourselves to the calculation of the magnetic dipole moment $G_{M_1}$, and for this goal we choose the structure $(\varepsilon ^\beta q^\nu - \varepsilon ^\nu q^\beta ) g_{\mu \alpha }$. This structure has advantage over the others since it does not contain contributions coming from the contact terms (for more detail about the contact terms, see for example [22]). As the result we get the following sum rules for the magnetic dipole moment of the heavy tensor mesons,

$$\begin{aligned}&\Pi _{\mu \nu \rho \alpha \beta } \, \varepsilon ^\rho = g_{\mu \alpha } (\varepsilon ^\beta q^\nu - \varepsilon ^\nu q^\beta ) {m_{T_Q}^6 g_{T_Q}^2 \over (p^2-m_{T_Q}^2) [(p+q)^2 - m_{T_Q}^2]}\nonumber \\&\quad {1\over 4} \left[ G_{M_1} + \text{ other } \text{ structures } \right] . \end{aligned}$$

(10)

Denoting the coefficient of the $(\varepsilon ^\beta q^\nu - \varepsilon ^\nu q^\beta ) g_{\mu \alpha }$ structure as the invariant function $\Pi$, we get the following final result for the physical part of the correlator function for the magnetic dipole moment $G_{M_1}$,

$$\begin{aligned} \Pi = {m_{T_Q}^6 g_{T_Q}^2 \over (p^2-m_{T_Q}^2) \left[ (p+q)^2 - m_{T_Q}^2\right] } {1\over 4} G_{M_1}. \end{aligned}$$

(11)

In order to construct the corresponding sum rules the correlation function $\Pi _{\mu \nu \rho \alpha \beta } \, \varepsilon ^\rho$ needs to be calculated from the QCD side in terms of quark and gluon degrees of freedom using the operator product expansion, for which we need the interpolating current $j_{\mu \nu }$. The interpolating current for the ground state heavy tensor meson with the quantum numbers $2^+$ can be chosen as,

(12)

where q and Q denote the light and heavy quark fields, and the derivative operator $\mathop {\mathcal {D}}\limits ^{\leftrightarrow }_\mu$ with respect to $x_\mu$ can be written as,

which acts on the right and left sides, and the covariant derivatives in it are defined as

(13)

where $\lambda ^a$ are the Gell–Mann matrices, and $A_\mu ^a (x)$ is the gluon field. In the present work we use the Fock–Schwinger gauge in which the external field $A_\mu ^a (x)$ satisfies the condition $x^\mu A_\mu ^a (x)=0$.

The correlation function is calculated from the QCD side in deep Eucledian region $p^2 \rightarrow - \infty$, and $(p+q)^2 \rightarrow - \infty$ after contracting the corresponding heavy and light quark fields, as a result of which we get,

$$\begin{aligned}&\Pi _{\mu \nu \rho \alpha \beta } \, \varepsilon ^\rho = {-i \over 16} \int e^{ip\cdot x} e^{-i(p+q)\cdot y} d^4x \nonumber \\&\left\langle 0 \left| \Big \{ S_{q} (y-x) \gamma _\mu \Big [ \mathop {\partial }\limits ^{\rightarrow }_\nu (x) \mathop {\partial }\limits ^{\rightarrow }_\beta (y) - \mathop {\partial }\limits ^{\rightarrow }_\nu (x) \mathop {\partial }\limits ^{\leftarrow }_\beta (y) \right. \right. \nonumber \\&\quad \left. \left. - \mathop {\partial }\limits ^{\leftarrow }_\nu (x) \mathop {\partial }\limits ^{\rightarrow }_\beta (y) + \mathop {\partial }\limits ^{\leftarrow }_\nu (x) \mathop {\partial }\limits ^{\leftarrow }_\beta (y) \Big ] S_{Q} (x-y) \gamma _\alpha \Big \} \right. \right. \nonumber \\&\quad \left. \left. + \{ \beta \leftrightarrow \alpha \} + \{ \nu \leftrightarrow \mu \} + \{ \beta \leftrightarrow \alpha ,~ \nu \leftrightarrow \mu \} \right| 0 \right. \rangle _F, \end{aligned}$$

(14)

where we set $y=0$ after performing derivative with respect to y.

We see from Eq. (14) that, the expressions of the propagators of the light and heavy quarks are needed in order to calculate the correlation function. The light quark propagator in presence of the external field is calculated in [23], whose expression is given as:

$$\begin{aligned}&S_q(x-y) = S_q^{free} (x-y) - {\langle \bar{q} q \rangle \over 12} \Bigg [1 -i {m_q \over 4} (\not \!{x}-\not \!{y}) \Bigg ]\nonumber \\&\quad + {(x-y)^2 \over 192} m_0^2 \langle \bar{q} q \rangle \Bigg [1 - i {m_q \over 6} (\not \!{x}-\not \!{y}) \Bigg ] \nonumber \\&\quad - i g_s \int _0^1 \mathrm{d}u \Bigg \{ {\not \!x - \not \!{y} \over 16 \pi ^2 (x-y)^2} G_{\mu \nu }(u(x-y)) \sigma ^{\mu \nu }\nonumber \\&\quad - u (x^\mu -y^\mu ) G_{\mu \nu }(u(x-y)) \gamma ^\nu \nonumber \\&\quad \times {i \over 4 \pi ^2 (x-y)^2} - i {m_q \over 32 \pi ^2} G_{\mu \nu }(u(x-y)) \sigma ^{\mu \nu }\nonumber \\&\quad \times \Bigg [\ln \left( -{(x-y)^2 \Lambda ^2 \over u} + 2 \gamma _E \right) \Bigg ] \Bigg \}, \end{aligned}$$

(15)

where $\Lambda$ is the scale parameter separating the perturbative and nonperturbative domains. This parameter is estimated in [24] to have the value $\Lambda =(0.5 \div 1.0)$ GeV; and $S^\mathrm{free}(x-y)$ is the free quark operator whose expression is given as:

$$\begin{aligned} S_q^\mathrm{free} (x-y) = {i (\not \!x-\not \!y) \over 2 \pi ^2 (x-y)^4} - {m_q \over 4 \pi ^2 (x-y)^2}. \end{aligned}$$

(16)

The propagator for the heavy quark have the following form in coordinate space:

$$\begin{aligned} S_Q(x-y)= & {} S_Q^{free} - {g_s \over 16 \pi ^2} \int _0^1 \mathrm{d}u G_{\mu \nu }(u(x-y))\nonumber \\&\times \Bigg ( i [\sigma ^{\mu \nu } (\not \!{x}-\not \!{y}) + (\not \!{x}-\not \!{y})\sigma ^{\mu \nu }]\nonumber \\&\times {K_1 (m_Q\sqrt{-(x-y)^2})\over \sqrt{-(x-y)^2}}\nonumber \\&+ 2 \sigma ^{\mu \nu } K_0(m_Q\sqrt{-(x-y)^2})\Bigg )\Bigg \} +\cdots , \end{aligned}$$

(17)

where $K_i(m_Q\sqrt{-x^2})$ are the modified Bessel functions, and

$$\begin{aligned}&S_Q^\mathrm{free} = {m_Q^2 \over 4 \pi ^2} \\&\quad \times \Bigg \{ {K_1(m_Q\sqrt{-(x-y)^2}) \over \sqrt{-(x-y)^2}} + i {(\not \!{x}-\not \!{y}) \over -(x-y)^2} K_2(m_Q\sqrt{-(x-y)^2}) \Bigg \}. \end{aligned}$$

Few words about the expression of the quark propagator are in order. The complete light cone expansion of the light quark propagator in presence of the external field is calculated in [23], which includes the contributions coming from nonlocal three $\bar{q}G q$, and four-particle $\bar{q}q\bar{q}q$, $\bar{q}G^2 q$ operators. Using the expansion in conformal spin, one can show that aforementioned contributions are small (for more detail see [25]), therefore we shall neglect them in further analysis.

There are three type of contributions to the correlation function: (1) perturbative part, when photon interacts perturbatively with the quark propagator (light or heavy). (2) “Mixed” contributions, which take place when heavy quark propagator interacts with the photon field perturbatively, and light quark fields form quark condensate. (3) “Long distance” contribution. It takes place when photon is radiated at long distance.

The perturbative contribution is calculated from Eq. (14) by replacing heavy or light propagator with,

$$\begin{aligned} S_{\mu \nu }^{ab}(x-y) \rightarrow -{1\over 4} \bar{q}^a (x) \Gamma _\rho q^b (y) (\Gamma _\rho )_{\mu \nu }, \end{aligned}$$

(18)

where $\Gamma _\rho$ are the full set of Dirac matrices. As has already been noted, when a photon interacts with the light quark fields matrix elements of the nonlocal operators such as $\bar{q}(x) \Gamma q(y)$ and $\bar{q}(x) G_{\mu \nu } \Gamma q(y)$ appear between vacuum and photon states. These matrix elements are parametrized in terms of the photon distribution amplitudes (DAs), which are the key nonperturbative parameters in light cone sum rules, whose explicit expressions are given below,

$$\begin{aligned}&\langle \gamma (q) \vert \bar{q}(x) \sigma _{\mu \nu } q(0) \vert 0 \rangle = -i e_q \langle \bar{q} q \rangle (\varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu )\nonumber \\&\qquad \times \int _0^1 \mathrm{d}u e^{i \bar{u} qx} \left( \chi \varphi _\gamma (u) + \frac{x^2}{16} \mathbb {A} (u) \right) \nonumber \\&\qquad -\frac{i}{2(qx)} e_q \langle \bar{q} q \rangle \left[ x_\nu (\varepsilon _\mu - q_\mu \frac{\varepsilon x}{qx}) - x_\mu \left( \varepsilon _\nu - q_\nu \frac{\varepsilon x}{q x}\right) \right] \nonumber \\&\qquad \times \int _0^1 \mathrm{d}u e^{i \bar{u} q x} h_\gamma (u) \nonumber \\&\qquad \times \langle \gamma (q) \vert \bar{q}(x) \gamma _\mu q(0) \vert 0 \rangle \nonumber \\&\quad = e_q f_{3 \gamma } \left( \varepsilon _\mu - q_\mu \frac{\varepsilon x}{q x} \right) \int _0^1 \mathrm{d}u e^{i \bar{u} q x} \psi ^v(u) \nonumber \\&\qquad \times \langle \gamma (q) \vert \bar{q}(x) \gamma _\mu \gamma _5 q(0) \vert 0 \rangle \nonumber \\&\quad = - \frac{1}{4} e_q f_{3 \gamma } \epsilon _{\mu \nu \alpha \beta } \varepsilon ^\nu q^\alpha x^\beta \int _0^1 \mathrm{d}u e^{i \bar{u} q x} \psi ^a(u) \nonumber \\&\qquad \times \langle \gamma (q) | \bar{q}(x) g_s G_{\mu \nu } (v x) q(0) \vert 0 \rangle \nonumber \\&\quad = -i e_q \langle \bar{q} q \rangle (\varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu ) \int \mathcal{D}\alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) q x} \mathcal{S}(\alpha _i) \nonumber \\&\qquad \times \langle \gamma (q) | \bar{q}(x) g_s \tilde{G}_{\mu \nu } i \gamma _5 (v x) q(0) \vert 0 \rangle \nonumber \\&\quad = -i e_q \langle \bar{q} q \rangle (\varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu ) \int \mathcal{D}\alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) q x} \tilde{\mathcal{S}}(\alpha _i) \nonumber \\&\qquad \times \langle \gamma (q) \vert \bar{q}(x) g_s \tilde{G}_{\mu \nu }(v x) \gamma _\alpha \gamma _5 q(0) \vert 0 \rangle \nonumber \\&\quad = e_q f_{3 \gamma } q_\alpha (\varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu ) \int \mathcal{D}\alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) q x} \mathcal{A}(\alpha _i) \nonumber \\&\qquad \times \langle \gamma (q) \vert \bar{q}(x) g_s G_{\mu \nu }(v x) i \gamma _\alpha q(0) \vert 0 \rangle \nonumber \\&\quad = e_q f_{3 \gamma } q_\alpha (\varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu ) \int \mathcal{D}\alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) q x} \mathcal{V}(\alpha _i) \nonumber \\&\qquad \times \langle \gamma (q) \vert \bar{q}(x) \sigma _{\alpha \beta } g_s G_{\mu \nu }(v x) q(0) \vert 0 \rangle \nonumber \\&\quad = e_q \langle \bar{q} q \rangle \left\{ \left[ (\varepsilon _\mu - q_\mu \frac{\varepsilon x}{q x})\left( g_{\alpha \nu } - \frac{1}{qx} (q_\alpha x_\nu + q_\nu x_\alpha )\right) \right. \right. q_\beta \nonumber \\&\qquad - \left( \varepsilon _\mu - q_\mu \frac{\varepsilon x}{q x}\right) \left( g_{\beta \nu } - \frac{1}{qx} (q_\beta x_\nu + q_\nu x_\beta )\right) q_\alpha \nonumber \\&\qquad - \left( \varepsilon _\nu - q_\nu \frac{\varepsilon x}{q x}\right) \left( g_{\alpha \mu } - \frac{1}{qx} (q_\alpha x_\mu + q_\mu x_\alpha )\right) q_\beta \nonumber \\&\qquad + \left. \left( \varepsilon _\nu - q_\nu \frac{\varepsilon x}{q.x}\right) \left( g_{\beta \mu } - \frac{1}{qx} (q_\beta x_\mu + q_\mu x_\beta )\right) q_\alpha \right] \nonumber \\&\qquad \times \int \mathcal{D}\alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) qx} \mathcal{T}_1(\alpha _i) \nonumber \\&\qquad + \left[ \left( \varepsilon _\alpha - q_\alpha \frac{\varepsilon x}{qx}\right) \left( g_{\mu \beta } - \frac{1}{qx}(q_\mu x_\beta + q_\beta x_\mu )\right) \right. q_\nu \nonumber \\&\qquad - \left( \varepsilon _\alpha - q_\alpha \frac{\varepsilon x}{qx}\right) \left( g_{\nu \beta } - \frac{1}{qx}(q_\nu x_\beta + q_\beta x_\nu )\right) q_\mu \nonumber \\&\qquad - \left( \varepsilon _\beta - q_\beta \frac{\varepsilon x}{qx}\right) \left( g_{\mu \alpha } - \frac{1}{qx}(q_\mu x_\alpha + q_\alpha x_\mu )\right) q_\nu \nonumber \\&\qquad + \left. \left( \varepsilon _\beta - q_\beta \frac{\varepsilon x}{qx}\right) \left( g_{\nu \alpha } - \frac{1}{qx}(q_\nu x_\alpha + q_\alpha x_\nu ) \right) q_\mu \right] \nonumber \\&\qquad \times \int \mathcal{D} \alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) qx} \mathcal{T}_2(\alpha _i) \nonumber \\&\qquad + \frac{1}{qx} (q_\mu x_\nu - q_\nu x_\mu ) (\varepsilon _\alpha q_\beta - \varepsilon _\beta q_\alpha ) \int \mathcal{D} \alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) qx} \mathcal{T}_3(\alpha _i) \nonumber \\&\qquad + \left. \frac{1}{qx} (q_\alpha x_\beta - q_\beta x_\alpha ) (\varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu ) \int \mathcal{D} \alpha _i e^{i (\alpha _{\bar{q}} + v \alpha _g) qx} \mathcal{T}_4(\alpha _i) \right\} ,\nonumber \\ \end{aligned}$$

(19)

where $\varphi _\gamma (u)$ is the leading twist-2, $\psi ^v(u)$, $\psi ^a(u)$, $\mathcal{A}$ and $\mathcal{V}$ are the twist-3, and $h_\gamma (u)$, $\mathbb {A}$, $\mathcal{T}_i$ ($i=1,~2,~3,~4$) are the twist-4 photon DAs, and $\chi$ is the magnetic susceptibility. The photon DAs are calculated in [20] and their explicit expressions are given in Appendix A. The measure $\mathcal{D} \alpha _i$ is defined as

$$\begin{aligned} \int \mathcal{D} \alpha _i = \int _0^1 \mathrm{d} \alpha _{\bar{q}} \int _0^1 \mathrm{d} \alpha _q \int _0^1 \mathrm{d} \alpha _g \delta (1-\alpha _{\bar{q}}-\alpha _q-\alpha _g). \end{aligned}$$

Separating out the coefficient of the structure $(\varepsilon ^\beta q^\nu - \varepsilon ^\nu q^\beta ) g_{\mu \alpha }$ from the QCD and the phenomenological parts of the correlation function and equating them, we get the magnetic moments of the heavy tensor mesons. In order to suppress the contributions of the higher states and continuum, we apply double Borel transformation with respect to the variables $p^2$ and $(p+q)^2$. As the result of these calculations we obtain the following sum rules for the magnetic dipole moment of the heavy tensor mesons,

$$\begin{aligned}&{m_{T_Q}^6 g_{T_Q}^2 \over 4} e^{-m_{T_Q}^2/M^2} G_{M_1}(q^2=0) \nonumber \\&\quad =-{1 \over 1152 \pi ^2} \Big [e_u \langle g_s^2 G^2 \rangle M^2 \left( -2 m_b^2 \mathcal{I}_2 + m_b^4 \mathcal{I}_3\right) \Big ]\nonumber \\&\qquad - {e^{-m_b^2/M^2}\over 3456 m_b \pi ^2} M^2 \Big \{9 m_b \left( e_u \langle g_s^2 G^2 \rangle + 96 e_b m_b \pi ^2 \langle \bar{u} u \rangle \right) \nonumber \\&\qquad + 4 e_u \pi ^2 \Big [18 m_b^2 \langle \bar{u} u \rangle \left( \mathbb {A} (u_0) + 2 \widetilde{j}_1(h_\gamma ) + 4 \widetilde{j}_2(h_\gamma )\right) \nonumber \\&\qquad + \langle g_s^2 G^2 \rangle \langle \bar{u} u \rangle \chi \varphi _\gamma (u_0) + 36 f_{3\gamma } m_b^3 \psi ^a (u_0)\Big ]\Big \} \nonumber \\&\qquad + {1\over 32 \pi ^2} e_b m_b^4 M^4 \left( \mathcal{I}_2 - m_b^2 \mathcal{I}_3\right) + {e^{-m_b^2/M^2}\over 96} e_u M^4\nonumber \\&\qquad \times \Big \{8 f_{3\gamma } \widetilde{j}_1(\psi ^v) + 8 m_b \langle \bar{u} u \rangle \chi \varphi _\gamma (u_0) \nonumber \\&\qquad - f_{3\gamma } \Big [6 \psi ^a (u_0) - 4 \psi ^v(u_0) + \psi ^{a\prime }(u_0)\Big ]\Big \} + {e^{-m_b^2/M^2}\over 16 \pi ^2} e_u M^6 \nonumber \\&\qquad - {1\over 32\pi ^2} m_b^2 M^6\nonumber \\&\qquad \times \Big [-2 e_b \mathcal{I}_2 + 3 e_b m_b^2 \mathcal{I}_3 + 4 e_b m_b^4 \mathcal{I}_4 + 2 e_u m_b^4 \mathcal{I}_4 + 2 (e_b - e_u) m_b^6 \mathcal{I}_5 \Big ] \nonumber \\&\qquad + {e^{-m_b^2/M^2}\over 6912 M^2} m_b \Big \{432 e_b m_0^2 m_b^2 \langle \bar{u} u \rangle + e_u \langle g_s^2 G^2 \rangle \nonumber \\&\qquad \times \Big [-4 \langle \bar{u} u \rangle \mathbb {A} (u_0) + 4 (5 - 4 u) \langle \bar{u} u \rangle \widetilde{j}_1(h_\gamma ) \nonumber \\&\qquad + 40 \langle \bar{u} u \rangle \widetilde{j}_2(h_\gamma ) + m_b \Big (-8 m_b \langle \bar{u} u \rangle \chi \varphi _\gamma (u_0) + f_{3\gamma } (-8 \widetilde{j}_1(\psi ^v)\nonumber \\&\qquad + 6 \psi ^a (u_0) - 4 \psi ^v(u_0) + \psi ^{a\prime }(u_0))\Big )\Big ]\Big \} \nonumber \\&\qquad + {e^{-m_b^2/M^2}\over 3456 M^4} e_u \langle g_s^2 G^2 \rangle m_b^3\nonumber \\&\qquad \times \Big [\langle \bar{u} u \rangle \Big (\mathbb {A} (u_0) + 2 \widetilde{j}_1(h_\gamma ) + 4 \widetilde{j}_2(h_\gamma )\Big ) + 2 f_{3\gamma } m_b \psi ^a (u_0) \Big ] \nonumber \\&\qquad + {e^{-m_b^2/M^2}\over 3456 M^6} e_u \langle g_s^2 G^2 \rangle m_b^5 \langle \bar{u} u \rangle \mathbb {A} (u_0)\nonumber \\&\qquad + {e^{-m_b^2/M^2}\over 3456 m_b \pi ^2} e_u \Big \{4 (\langle g_s^2 G^2 \rangle - 18 m_b^4) \pi ^2 \langle \bar{u} u \rangle \mathbb {A} (u_0) \nonumber \\&\qquad + \langle g_s^2 G^2 \rangle \Big [-3 m_b^3 + \pi ^2 \Big (4 (2 + u) \langle \bar{u} u \rangle \widetilde{j}_1(h_\gamma )\nonumber \\&\qquad + 16 \langle \bar{u} u \rangle \widetilde{j}_2(h_\gamma ) + m_b \left\{ -12 m_b \langle \bar{u} u \rangle \chi \varphi _\gamma (u_0) \right. \nonumber \\&\left. \qquad + f_{3\gamma } \left[ -12 \widetilde{j}_1(\psi ^v) - 2 \psi ^a (u_0) + (-2 + u) (4 \psi ^v(u_0) - \psi ^{a\prime }(u_0))\right] \right\} \Big )\Big ] \Big \},\nonumber \\ \end{aligned}$$

(20)

where

$$\begin{aligned} u_0={M_1^2 \over M_1^2 +M_2^2},\quad M^2={M_1^2 M_2^2 \over M_1^2 +M_2^2}. \end{aligned}$$

The functions $i_n~(n=1,2)$, and $\widetilde{j}_1(f(u))$ are defined as:

$$\begin{aligned}&\widetilde{j}_1(f(u)) = \int _{u_0}^1 \mathrm{d}u f(u), \\&\widetilde{j}_2(f(u)) = \int _{u_0}^1 \mathrm{d}u (u-u_0) f(u), \\&\mathcal{I}_n = \int _{m_b^2}^{s_0} \mathrm{d}s\, {e^{-s/M^2} \over s^n}, \end{aligned}$$

where $s_0$ is the continuum threshold.

Since we have the same heavy tensor mesons in the initial and final states, we can set $M_1^2=M_2^2=2 M^2$, as the result of which we have,

$$\begin{aligned} u_0={M_1^2 \over (M_1^2+M_2^2)}={1\over 2}. \end{aligned}$$

Physically this means that each quark and antiquark carries the half the photon momentum.

3 Numerical analysis

This section is devoted to the numerical analysis of the sum rules for the magnetic dipole moments of the heavy tensor mesons obtained in the previous section. The values of the input parameters entering into sum rules are, $\langle \bar{u} u \rangle (\mu =1~\mathrm{GeV}) = \langle \bar{d} d \rangle (\mu =1~\mathrm{GeV}) = -(0.243)^3~\mathrm{GeV}^3$, $^\vert _{\mu =1~\mathrm{GeV}} = (0.8 \pm 0.2) \langle \bar{u} u \rangle (\mu =1~\mathrm{GeV})$, $m_0^2=(0.8\pm 0.2)~\mathrm{GeV}^2$ which are obtained from the mass sum rule analysis for the light baryons [26, 27], and B, $B^*$ mesons [28]. For the heavy quark masses we have used their $\overline{MS}$ values, which are given as: $\bar{m}_b(\bar{m}_b)=(4.16\pm 0.03)~\mathrm{GeV}$ and $\bar{m}_c(\bar{m}_c)=(1.28\pm 0.03)~\mathrm{GeV}$ [29–35]. The magnetic susceptibility of quarks was estimated in [36–38] in framework of the QCD sum rules. As we have noted earlier, the residues and masses of the heavy tensor mesons were calculated within the QCD sum rules method in [13–15], and their values are $g_{\mathcal{D}_2} = 0.0228 \pm 0.0068$, $g_{\mathcal{D}_{S_2}} = 0.023 \pm 0.011$, $g_{\mathcal{B}_2} = 0.0050 \pm 0.0005$, $g_{\mathcal{B}_{S_2}} = 0.0060 \pm 0.0005$.

Having decided the values of the input parameters, we are ready now to perform numerical analysis of the sum rules for the magnetic dipole moment of the heavy tensor mesons.The sum rule contains two unphysical parameters: a) The Borel mass parameter $M^2$, and continuum threshold $s_0$. It is known that the physical results should be independent of the these parameters. Therefore, our primary goal is to find such domain of these parameters for which the magnetic dipole moment is practically independent of them. The “working region” of $M^2$ is determined as follows: The upper bound of $M^2$ can be found by requiring that the contributions coming from higher states constitutes about 40 % of the perturbative part. The lower bound of $M^2$ could be fixed by demanding that the higher twist contributions are less than that of the leading twist contributions. In other words, the light cone expansion with increasing twist should be convergent. These requirements leads us to the following domains for the Borel mass parameter:

$$\begin{aligned}&2.0~\mathrm{GeV}^2 \le M^2 \le 4.0~\mathrm{GeV}^2, \text{ for } \mathcal{D}_2 \hbox { and } \mathcal{D}_{S_2} \hbox {mesons},\\&4.5~\mathrm{GeV}^2 \le M^2 \le 7.0~\mathrm{GeV}^2, \text{ for } \mathcal{B}_2 \hbox { and } \mathcal{B}_{s_2} \hbox {mesons}. \end{aligned}$$

The second parameter entering to the sum rules is the continuum threshold $s_0$. Generally speaking, this parameter is not arbitrary and it is related to the energy of the first excited state. The energy necessary for the transition of the meson from ground state to first excited state is $\sqrt{s_0}-m_\mathrm{ground}$. This difference varies, usually, from 0.3 to $0.8~\mathrm{GeV}$, where in our numerical analysis we have used their average value, i.e., $\sqrt{s_0}-m_\mathrm{ground}=0.5~\mathrm{GeV}$.

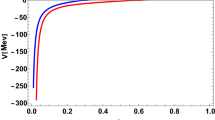
In Figs. 1, 2 and 3 we present the dependence of the magnetic dipole moments of $\mathcal{D}_2^+$, $\mathcal{D}_2^0$ and $\mathcal{D}_{S_2}$ tensor mesons on $M^2$, at various fixed values of the continuum threshold. From these figures we get the following results,

$$\begin{aligned} G_{M_1}(q^2=0) = \left\{ \begin{array}{l} 0.75 \pm 0.25,~\text{ for }~\mathcal{D}_2^0 \\ -2.10 \pm 0.20,~\text{ for }~\mathcal{D}_2^-\\ -2.20 \pm 0.20,~\text{ for }~\mathcal{D}_{S_2}^- \end{array} \right. \end{aligned}$$

in units of $e/2 m_{T_Q}$.

Fig. 1

The dependence of the magnetic dipole moment of the $\mathcal{D}_2^0$ tensor meson on $M^2$, at two fixed values of $s_0=9.0~\mathrm{GeV}^2$, and $s_0=9.5~\mathrm{GeV}^2$

Fig. 2

The same as Fig. 1, but for the $\mathcal{D}_2^-$ tensor meson

Fig. 3

The same as Fig. 1, but for the $\mathcal{D}_{S_2}^-$ tensor meson

Similar analysis performed for heavy tensor mesons containing b-quark, whose results are presented in Figs. 4, 5 and 6, respectively. From the analysis of these figures we obtain,

$$\begin{aligned} G_{M_1}(q^2=0) = \left\{ \begin{array}{l} 3.8 \pm 0.7,~\text{ for }~\mathcal{B}_2^+ \\ -1.3 \pm 0.3,~\text{ for }~\mathcal{B}_2^0\\ -1.4 \pm 0.3,~\text{ for }~\mathcal{B}_{S_2}^0 \end{array} \right. \end{aligned}$$

in units of $e/2 m_{T_Q}$.

Fig. 4

The same as Fig. 1, but for the $\mathcal{B}_2^+$ tensor meson, at two fixed values of $s_0=37.5~\mathrm{GeV}^2$, and $s_0=40.0~\mathrm{GeV}^2$

Fig. 5

The same as Fig. 4, but for the $\mathcal{B}_2^0$ tensor meson

Fig. 6

The same as Fig. 4, but for the $\mathcal{B}_{s_2}^0$ tensor meson

In conclusion, The magnetic dipole moments of the heavy tensor mesons are calculated in framework of the light cone QCD sum rules. It is observed that the magnetic moments of the charged tensor mesons are larger compared to the neutral ones. The SU(3) symmetry breaking in heavy tensor mesons containing beauty quarks is about 10 %, while in the charmed meson sector it is quite large.

Appendix A: Photon distribution amplitudes

Explicit forms of the photon DAs [20]:

$$\begin{aligned} \varphi _\gamma (u)= & {} 6 u \bar{u} \Big [ 1 + \varphi _2(\mu ) C_2^{\frac{3}{2}}(u - \bar{u}) \Big ], \\ \psi ^v(u)= & {} 3 [3 (2 u - 1)^2 -1 ]\\&+\frac{3}{64} (15 w^V_\gamma - 5 w^A_\gamma ) [3 - 30 (2 u - 1)^2\\&+ 35 (2 u -1)^4], \\ \psi ^a(u)= & {} [1- (2 u -1)^2] [ 5 (2 u -1)^2 -1 ]\\&\times \frac{5}{2} \Bigg (1 + \frac{9}{16} w^V_\gamma - \frac{3}{16} w^A_\gamma \Bigg ), \\ \mathcal{A}(\alpha _i)= & {} 360 \alpha _q \alpha _{\bar{q}} \alpha _g^2 \Bigg [ 1 + w^A_\gamma \frac{1}{2} (7 \alpha _g - 3)\Bigg ], \\ \mathcal{V}(\alpha _i)= & {} 540 w^V_\gamma (\alpha _q - \alpha _{\bar{q}}) \alpha _q \alpha _{\bar{q}} \alpha _g^2,\\ h_\gamma (u)= & {} - 10 (1 + 2 \kappa ^+ ) C_2^{\frac{1}{2}}(u - \bar{u}),\\ \mathbb {A}(u)= & {} 40 u^2 \bar{u}^2 (3 \kappa - \kappa ^+ +1 )\\&+ 8 (\zeta _2^+ - 3 \zeta _2) [u \bar{u} (2 + 13 u \bar{u})\\&+ 2 u^3 (10 -15 u + 6 u^2) \ln (u) \\&+ 2 \bar{u}^3 (10 - 15 \bar{u} + 6 \bar{u}^2) \ln (\bar{u}) ], \\ \mathcal{T}_1(\alpha _i)= & {} -120 (3 \zeta _2 + \zeta _2^+)(\alpha _{\bar{q}} - \alpha _q) \alpha _{\bar{q}} \alpha _q \alpha _g,\\ \mathcal{T}_2(\alpha _i)= & {} 30 \alpha _g^2 (\alpha _{\bar{q}} - \alpha _q) [(\kappa - \kappa ^+) \\&+ (\zeta _1 - \zeta _1^+)(1 - 2\alpha _g) + \zeta _2 (3 - 4 \alpha _g)],\\ \mathcal{T}_3(\alpha _i)= & {} - 120 (3 \zeta _2 - \zeta _2^+)(\alpha _{\bar{q}} -\alpha _q) \alpha _{\bar{q}} \alpha _q \alpha _g, \\ \mathcal{T}_4(\alpha _i)= & {} 30 \alpha _g^2 (\alpha _{\bar{q}} - \alpha _q) [(\kappa + \kappa ^+) \\&+ (\zeta _1 + \zeta _1^+)(1 - 2\alpha _g) + \zeta _2 (3 - 4 \alpha _g)],\\ \mathcal{S}(\alpha _i)= & {} 30\alpha _g^2\{(\kappa + \kappa ^+)(1-\alpha _g)\\&+(\zeta _1 + \zeta _1^+)(1 - \alpha _g)(1 - 2\alpha _g)\\&+\zeta _2 [3 (\alpha _{\bar{q}} - \alpha _q)^2-\alpha _g(1 - \alpha _g)]\},\\ \widetilde{\mathcal{S}}(\alpha _i)= & {} -30\alpha _g^2\{(\kappa - \kappa ^+)(1-\alpha _g)\\&+(\zeta _1 - \zeta _1^+)(1 - \alpha _g)(1 - 2\alpha _g)\\&+\zeta _2 [3 (\alpha _{\bar{q}} - \alpha _q)^2-\alpha _g(1 - \alpha _g)]\}. \end{aligned}$$

The parameters entering the above DA’s are borrowed from [20] whose values are $\varphi _2(1~\mathrm{GeV}) = 0$, $w^V_\gamma = 3.8 \pm 1.8$, $w^A_\gamma = -2.1 \pm 1.0$, $\kappa = 0.2$, $\kappa ^+ = 0$, $\zeta _1 = 0.4$, $\zeta _2 = 0.3$, $\zeta _1^+ = 0$, and $\zeta _2^+ = 0$.