1 Introduction

Einstein–Aether theory is a Lorentz-violating theory in which a unitary timelike vector field, called the æther, is introduced into the Einstein–Hilbert action [1,2,3,4]. The introduction of the timelike vector field in the action integral is also a specific selection of preferred frame at each point in the spacetime, and so this modification spontaneously breaks the Lorentz symmetry [5]. The gravitational field equations are of second-order and correspond to variations of the action with respect to the metric tensor and the æther field. At this point we recall that the unitarity of the timelike vector field is guaranteed by introducing a lagrange multiplier. The Einstein–Aether theory can describe various cosmological phases, including those of early inflationary expansion and late dark-energy domination [6,7,8,9]. It is important to mention here that the Einstein–Aether approach also describes the classical limit of Hořava gravity [10].

One of the ways to study a cosmological model is to perform a dynamical analysis by studying its critical points in order to connect them to the different observed eras, with their respective dynamical behaviours and characteristics[11,12,13,14,15,16,17,18,19,20,21]. For the Einstein–Aether cosmologies there have been several such studies [22,23,24,25,26,27,28].

For Einstein–Aether cosmologies [29] provided exact solutions for specific forms of the scalar field potential in the framework of Friedmann–Lemaître–Robertson–Walker (FLRW) spacetime. There has been further study of the dynamical evolution and stability of those inflationary solutions in homogeneous and isotropic Einstein–Aether cosmologies containing a self interacting scalar field which interacts with the aether [27]. Similar dynamical analysis can by found in [30], where it was shown that for isotropic expansion the dynamics are independent of the aether parameters, but this is not the case for anisotropic expansion. In all cases there is a period of slow-roll inflation at intermediate times and, in some cases, accelerated expansion at late times.

Apart from the FLRW background scenario, there have been more wideranging studies. One such work, investigating the dynamical equations of the Einstein–Aether theory for the cases of FLRW as well as in an locally rotationally symmetric Bianchi Type III geometry [31]. There, it was found that the existence or the non-existence of the solutions to the reduced equations depends on the values of combinations of the initial parameters that enter the action integral. Results of this type have also been found elsewhere [32,33,34]. For other dynamical studies in the context of the Einstein–Aether scenario we refer the reader the articles of [28, 35,36,37,38,39].

The plan of this paper is as follows. In Sect. 2 we present the model to be studied, which is an Einstein–Aether scalar field cosmology with spatially flat FLRW spacetime, where the scalar field lagrangian has been modified so that the scalar field potential is non-minimally coupled to the aether field, as proposed in [1]. The dimensionless dynamical analysis and the corresponding critical points are presented in Sect. 3. The absence of the matter in the action integral implies that the dimension of the dynamical system can be either one or two, while adding a pressureless fluid raises the dimension of the system to two or three. Furthermore, the critical points are classified into three families. Sections 4 and 5 include the main results of the current analysis, where we present the allowed critical points, It is interesting to mention that the case of general relativity (GR) with a minimally coupled scalar field is fully recovered, while new critical points are found which describe either power-law or de Sitter solutions. Finally, we draw our conclusions in Sect. 7.

2 Einstein–Aether cosmology

First, we consider a spatially flat FLRW spacetime with line element

$$\begin{aligned} ds^{2}=-dt^{2}+a^{2}\left( t\right) \left( dr^{2}+r^{2}d\theta ^{2} +r^{2}\sin ^{2}\theta d\phi ^{2}\right) , \end{aligned}$$
(1)

and as an aether field we consider the timelike vector field \(u^{\mu } =\delta _{t}^{\mu }\). In Einstein–Aether Models the gravitational action is given by [40]

$$\begin{aligned} S_{EA}= & {} \int \sqrt{-g}dx^{4}\left( R+\frac{c_{\theta }}{3}\theta ^{2}+c_{\sigma }\sigma ^{2}+c_{\omega }\omega ^{2}+c_{\alpha }\alpha ^{2}\right) \nonumber \\&+S_{\phi }, \end{aligned}$$
(2)

where the action integral of the scalar field is assumed to be [1]

$$\begin{aligned} S_{\phi }=\int \sqrt{-g}dx^{4}\left( \frac{1}{2}g^{\mu \nu }\phi _{,\mu }\phi _{,\nu }-V\left( \theta ,\phi \right) \right) . \end{aligned}$$
(3)

Parameters \(\theta ,~\sigma ,~\omega \) and \(\alpha \) describe the kinematic quantities of the unitary vector field \(u^{\mu },\) and correspond to the volume expansion rate, shear, vorticity and fluid acceleration. Following the notations of [1] for the line element (1), the field equations are written as (with units \(8\pi G=c=1\))

$$\begin{aligned}&\frac{1}{3}\theta ^{2}=\frac{1}{2}{\dot{\phi }}^{2}+V-\theta V_{\theta }, \end{aligned}$$
(4)
$$\begin{aligned}&\frac{2}{3}{\dot{\theta }}=-{\dot{\phi }}^{2}-{\dot{\theta }}V_{\theta \theta }-\dot{\phi }V_{\theta \phi }, \end{aligned}$$
(5)
$$\begin{aligned}&\ddot{\phi }+\theta {\dot{\phi }}+V_{\phi }=0. \end{aligned}$$
(6)

Barrow [29] previously found that for

$$\begin{aligned} V\left( \phi ,\theta \right) =V_{0}e^{-\lambda \theta }+ {\displaystyle \sum \limits _{r=0}^{n}} V_{r}\theta ^{r}e^{\frac{r-2}{2}\lambda \phi }, \end{aligned}$$
(7)

where \(V_{0},~V_{r}\) and \(\lambda \) are constants, the field equations (4)–(6) admit exact power-law solutions \(\phi \left( t\right) =\frac{2}{\lambda }\ln t~\), \(\theta \left( t\right) =3Bt^{-1}\), i.e. \(a\left( t\right) \simeq t^{B}\) where \(B=B\left( V_{0},V_{r},\lambda \right) \). The detailed dynamical analysis of (7) was performed in [27].

In this work we consider the potential function \(V\left( \phi ,\theta \right) \) to be

$$\begin{aligned} V\left( \phi ,\theta \right) =U\left( \phi \right) +Y\left( \phi \right) \theta , \end{aligned}$$
(8)

where \(U\left( \phi \right) \) now denotes the scalar field potential and \(Y\left( \phi \right) \) is the coupling term between the scalar and aether fields. It is straightforward to observe that for \(U\left( \phi \right) =U_{0}e^{-\lambda \theta }\) and \(Y\left( \phi \right) \simeq \sqrt{U\left( \phi \right) }\) potential (7) is recovered for \(n=1,V_{0}=0\).

With the aid of (8) the field equations (4)–(6) simplify to

$$\begin{aligned}&\frac{1}{3}\theta ^{2}=\frac{1}{2}{\dot{\phi }}^{2}+U\left( \phi \right) , \end{aligned}$$
(9)
$$\begin{aligned}&\frac{2}{3}{\dot{\theta }}+\frac{1}{3}\theta ^{2}=-\frac{1}{2}{\dot{\phi }} ^{2}+U\left( \phi \right) -{\dot{\phi }}Y_{,\phi }, \end{aligned}$$
(10)
$$\begin{aligned}&\ddot{\phi }+\theta {\dot{\phi }}+U_{,\phi }+Y_{,\phi }\theta =0. \end{aligned}$$
(11)

from which we can rewrite them as

$$\begin{aligned} G_{ab}=T_{ab}, \end{aligned}$$
(12)

where \(G_{ab}\) is the Einstein tensor, and \(T_{ab}\) describes the effective Einstein–Aether fluid source with the scalar field, where in the \(1+3\) decomposition is written as

$$\begin{aligned} T_{ab}=\rho _{\phi }u_{a}u_{b}+p_{\phi }h_{ab}, \end{aligned}$$
(13)

in which \(h_{ab}=g_{ab}+u_{a}u_{b}\) is the projective tensor and \(\rho _{\phi }~\)and \(p_{\phi }\) are given by

$$\begin{aligned} \rho _{\phi }=\frac{1}{2}{\dot{\phi }}^{2}+U\left( \phi \right) ~,~p_{\phi } =\frac{1}{2}{\dot{\phi }}^{2}-U\left( \phi \right) +{\dot{\phi }}Y_{,\phi }. \end{aligned}$$
(14)

We observe that for this specific potential, (8), the energy density \(\rho _{\phi }\) is defined as in Einstein’s GR, while in the pressure term \(p_{\phi }\) a new part is introduced due to the coupling between the scalar field and the aether field.

If a minimally coupled matter source is introduced with energy density \(\rho _{m}\), pressure \(p_{m}\), and constant parameter for the equation of state, \(w_{m}=p_{m}/\rho _{m},\) the field equations (9), (10) are modified as follows:

$$\begin{aligned}&\frac{1}{3}\theta ^{2}=\frac{1}{2}{\dot{\phi }}^{2}+U\left( \phi \right) +\rho _{m} \end{aligned}$$
(15)
$$\begin{aligned}&\frac{2}{3}{\dot{\theta }}+\frac{1}{3}\theta ^{2}=-\frac{1}{2}{\dot{\phi }} ^{2}+U\left( \phi \right) -{\dot{\phi }}Y_{,\phi }-w_{m}\rho _{m} \end{aligned}$$
(16)

where, for the perfect fluid \(\rho _{m}\), the conservation law is

$$\begin{aligned} {\dot{\rho }}_{m}+\theta \left( 1+w_{m}\right) \rho _{m}=0. \end{aligned}$$
(17)

We carry out our analysis by writing the field equations (15)–(17) in dimensionless variables by using expansion-normalised variables.

3 Dynamical system

In this section we present the main features of the dynamical analysis by using the method of critical points. This method is powerful because it provides information concerning the general evolution of the dynamical system. Hence, from such an analysis the overall cosmological viability of the model can be discussed.

The new dimensionless variables are defined as follows [41]

$$\begin{aligned} x= & {} \sqrt{\frac{3}{2}\frac{{\dot{\phi }}^{2}}{\theta ^{2}}}~,~y=\sqrt{\frac{3U}{\theta ^{2}}}~,~\lambda =\frac{U_{,\phi }}{U}~,\xi =\sqrt{2}\frac{Y_{,\phi } }{\sqrt{U}}~,~\nonumber \\ \Omega _{m}= & {} \frac{3\rho _{m}}{\theta ^{2}}. \end{aligned}$$
(18)

After some calculations, the system of the field equations is written in these variables as

$$\begin{aligned} \Omega _{m}= & {} 1-x^{2}-y^{2}, \end{aligned}$$
(19)
$$\begin{aligned} \frac{dx}{dN}= & {} -3x(1+J\left( x,y,\xi ,\Omega _{m}\right) )\ -\frac{1}{2}\left( \sqrt{6}\lambda y+3\xi \right) y, \end{aligned}$$
(20)
$$\begin{aligned} \frac{dy}{dN}= & {} \sqrt{\frac{3}{2}}\lambda xy-3yJ, \end{aligned}$$
(21)
$$\begin{aligned} \frac{d\lambda }{dN}= & {} \sqrt{6}x\lambda ^{2}(\Gamma _{\lambda }\left( \lambda \right) -1),\ \end{aligned}$$
(22)
$$\begin{aligned} \frac{d\xi }{dN}= & {} \sqrt{3}\xi x\left( \Gamma _{\xi }\left( \xi \right) -\frac{\lambda }{\sqrt{2}}\right) , \end{aligned}$$
(23)

where \(N=\ln \left( a\right) \), function \(J\left( x,y,\xi ,\Omega _{m}\right) \) is expressed as

$$\begin{aligned} 2J\left( x,y,\xi ,\Omega _{m}\right) =-1-x^{2}+y^{2}-\xi xy-w_{m}\Omega _{m}. \end{aligned}$$
(24)

and

$$\begin{aligned} \Gamma _{\lambda }\left( \lambda \right) =\frac{U_{,\phi \phi }U}{(U_{,\phi } )^{2}},~\Gamma _{\xi }\left( \xi \right) =\sqrt{2}\frac{Y_{,\phi \phi } }{Y_{,\phi }} \end{aligned}$$
(25)

In general, Eqs. (19)–(23) form a three-dimensional system. Specifically, Eqs. (22), (23) do not coexist, because parameters \(\lambda \) and \(\xi \) are not independent. Locally, the condition \(\frac{\partial \lambda }{\partial \phi }\ne 0\) implies that the inverse function of \(\lambda \left( \phi \right) \) exists so that \(\phi =\phi \left( \lambda \right) \). Hence the function \(\xi \left( \phi \right) \) depends on \(\lambda \); indeed, \(\xi =\xi \left( \phi \left( \lambda \right) \right) \), so \(\xi =\xi \left( \lambda \right) \). In that case the only independent variables which survive are the \(\left\{ x,y,\lambda \right\} \).

On the other hand, if locally \(\lambda =const\), then \(\frac{d\lambda }{dN} \equiv 0\), and \(\xi =\xi \left( \phi \right) \); hence, the only independent variables that survive are \(\left\{ x,y,\xi \right\} ,\) since \(\phi =\phi \left( \xi \right) \). Consequently, there are three large families of potentials which we will study, that admit different dynamical systems:

Family (A) with \(\lambda =const\). and \(\xi =cons\not t ,\) which corresponds to the potentials

$$\begin{aligned} U\left( \phi \right) =U_{0}e^{\lambda \phi }~,~Y\left( \phi \right) =Y_{0}+Y_{1}e^{-\frac{\lambda }{2}\phi }, \end{aligned}$$
(26)

Family (B) where \(U\left( \phi \right) =U_{0}e^{\lambda \phi }\), \(\lambda =const\) with \(\xi =\xi \left( \phi \right) ,\) and

Family (C) where the potential \(U\left( \phi \right) \) is different from the exponential potential and so \(\xi =\xi \left( \lambda \right) .\)

We observe from Eq. (19) that the variables x, y obey the inequalities \(0\le x^{2}+y^{2}\le 1\), where in the special case of \(\Omega _{m}=0\), this reduces to \(x^{2}+y^{2}=1.\) At this point we mention that the equation of state parameter for the perfect fluid is now

$$\begin{aligned} w_{\phi }\left( x,y,\lambda ,\xi ,\Omega _{m}\right) =-1+\frac{2x^{2}+\xi xy}{x^{2}+y^{2}}, \end{aligned}$$
(27)

while the deceleration parameter is

$$\begin{aligned} q\left( x,y,\lambda ,\xi ,\Omega _{m}\right) =-1-2J, \end{aligned}$$
(28)

and the equation of state parameter for the effective fluid is

$$\begin{aligned} w_{\mathrm {tot}}\left( x,y,\lambda ,\xi ,\Omega _{m}\right) =\frac{1}{3}\left( q-1\right) \text {.} \end{aligned}$$
(29)

We continue our study with the analysis of the critical points of the system (19)–(23) for the aforementioned three families of potentials.

4 Scalar field without matter source

In this section we consider the case where the cosmic fluid does not include matter, namely \(\Omega _{m}=0\). In this case our results are summarized as follows.

4.1 Family A

For the first family of potentials the constraint (19) implies that the dynamical system (20), (21) is reduced to a one-dimensional system. In this case we derive four critical points \(\left( x_{P},y_{P}\right) \):

  1. a.

    Points \(A_{1\left( \pm \right) }\) with coordinates \(A_{1\left( \pm \right) }=\left( \pm 1,0\right) \). These points describe a universe where \(\rho _{\phi }=p_{\phi }={\dot{\phi }}^{2}/2\), hence \(w_{\phi }=\frac{p_{\phi }}{\rho _{\phi }}=1\). For the stability of the points we need to calculate the corresponding eigenvalues, which in this case are given by \(e_{1}\left( A_{1\left( \pm \right) }\right) =3\pm \sqrt{\frac{3}{2}}\lambda .\) Therefore, point \(A_{1\left( +\right) }\) is stable for \(\lambda <-\sqrt{6}\) while point \(A_{1\left( -\right) }\) is stable for \(\lambda >\sqrt{6}\).

Fig. 1
figure 1

Region plot in the space \(\left\{ \lambda ,\xi \right\} \) for \(w_{\phi }\) in the case of critical points \(A_{2}\) and \(A_{3}\). The stable critical points are represented by shaded regions. Shaded regions define the areas where the critical points are stable

Full size image
  1. b.

    Point \(A_{2}\) with coordinates \(A_{2}=\left( -\frac{2\sqrt{2}\lambda +\xi \sqrt{3\left( 4+\xi ^{2}\right) -2\lambda ^{2}}}{\sqrt{3}\left( 4+\xi ^{2}\right) },\frac{-\sqrt{2}\lambda \xi +2\sqrt{3\left( 4+\xi ^{2}\right) -2\lambda ^{2}}}{\sqrt{3}\xi \left( 4+\xi ^{2}\right) }\right) ~\)exists for \(\left\{ \lambda <-\sqrt{6},~\xi \ge \sqrt{\frac{2\left( \lambda ^{2}-6\right) }{3}}\right\} ~\)or \(\left\{ \lambda >\sqrt{6}~,~\xi \le -\sqrt{\frac{2\left( \lambda ^{2}-6\right) }{3}}\right\} \) or \(\left\{ -\sqrt{6}\le \lambda \le \sqrt{6},~\xi \ne 0\right\} .\) The equation of state parameter is written as

    $$\begin{aligned} w_{\phi }\left( \lambda ,\xi \right) =-1+\lambda \frac{4\lambda +\xi \sqrt{6\left( 4+\xi ^{2}\right) -4\lambda ^{2}}}{3\left( 4+\xi ^{2}\right) }.~ \end{aligned}$$
    (30)

    Point \(A_{2}\) describes an accelerated universe when \(w_{\phi }<-\frac{1}{3}\); that is, the parameters \(\lambda ,\xi \) are constrained by the following conditions  \(\left\{ \lambda <-\sqrt{2}~,~\xi >\sqrt{2}\frac{\lambda ^{2} -2}{\sqrt{3\lambda ^{2}-2}}\right\} ~\)or  \(\left\{ \lambda >\frac{\sqrt{6}}{3}~,~0<\xi <-\sqrt{2}\frac{\lambda ^{2}-2}{\sqrt{3\lambda ^{2}-2}}\right\} ~\)or \(\Big \{ -\sqrt{2}\le \lambda \le \frac{\sqrt{6}}{3}~,~\xi >0\Big \} \) or \(\Big \{ \lambda \ge \sqrt{6}~,~\xi <-\sqrt{2}\frac{\lambda ^{2}-2}{\sqrt{3\lambda ^{2}-2}}\Big \} .\) As far as the stability is concerned we find that \(A_{2}\) is stable when \(\left\{ 0<\lambda \le \sqrt{6} ~,~\xi >0\right\} ~\)or \(\left\{ \lambda =\sqrt{6}~,~\xi <0\right\} \) or \(\left\{ \lambda >\sqrt{6}~,~\xi \le -\sqrt{\frac{2}{3}\left( \lambda ^{2}-6\right) }\right\} .~\) Moreover, if \(A_{2}\) is an attractor describing cosmic acceleration, then the parameters \(\lambda ,\xi \) obey the inequalities \(\Big \{ -\sqrt{2}<\lambda \le \sqrt{\frac{2}{3}}~,~\xi >0\Big \} ~\)or \(\left\{ \lambda<-\sqrt{2}~,~0<\xi <\sqrt{2}\frac{\lambda ^{2}-2}{\sqrt{3\lambda -2}}\right\} \) or \(\left\{ \lambda \ge \frac{\sqrt{6}~}{3},0<~\xi <-\sqrt{2}\frac{\lambda ^{2}-2}{\sqrt{3\lambda -2}}\right\} \) or \(\Big \{ \lambda \ge \sqrt{6}~,~\xi <-\sqrt{2}\frac{\lambda ^{2}-2}{\sqrt{3\lambda -2}}~\Big \}. \)

  2. c.

    Point \(A_{3}\)\(=\Big ( \frac{-2\sqrt{6}\lambda +\sqrt{9\xi ^{4}-6\left( \lambda ^{2}-6\right) \xi ^{2}}}{3\left( 4+\xi ^{2}\right) }, \frac{-\sqrt{6}\xi ^{2}\lambda +\sqrt{9\xi ^{4}-6\left( \lambda ^{2}-6\right) \xi ^{2}}}{3\xi \left( 4+\xi ^{2}\right) }\Big ) \) exists when \(\Big \{ \lambda <-\sqrt{6}~,~\xi \ge \sqrt{6\left( \lambda ^{2}-6\right) }\Big \} \) or \(\left\{ \lambda =-\sqrt{6}~,~\xi \ne 0\right\} ~\) or \(\Big \{ -\sqrt{6}<\lambda<\sqrt{6},~\xi <0\Big \} \) or \(\left\{ \lambda >\sqrt{6}~,~\xi <-\frac{1}{3}\sqrt{6\left( \lambda ^{2}-6\right) }\right\} \). The parameter of the equation of state is

    $$\begin{aligned} w_{\phi }\left( \lambda ,\xi \right) =-1+\lambda \frac{4\lambda -\sqrt{6\xi ^{4}-4\left( \lambda ^{2}-6\right) }}{3\left( 4+\xi ^{2}\right) }, \end{aligned}$$
    (31)

    where \(w_{\phi }<-\frac{1}{3}\) when \(\Bigg \{ -\sqrt{2}<\lambda<-\sqrt{\frac{2}{3}},-\sqrt{\frac{2\left( 2-\lambda ^{2}\right) ^{2}}{3\lambda ^{2}-2}}<\xi <0\Bigg \} \) or \(\ \left\{ -\sqrt{\frac{2}{3}}\le \lambda \le \sqrt{2}~,~\xi <0\right\} \) or \(\Big \{ \lambda >\sqrt{2},~\xi <-\sqrt{\frac{2\left( 2-\lambda ^{2}\right) ^{2}}{3\lambda ^{2}-2}}\Big \} \). Point \(A_{3}\) describes a stable solution only for \(\xi <0\) and more specifically \(\Big \{ 0<\lambda<\sqrt{6}~,~-\xi _{1}<\xi <0\Big \} \) or \(\left\{ -\sqrt{6}\le \lambda \le \sqrt{6}~,~\xi <0\right\} \) or \(\left\{ \lambda >\sqrt{6}~,~\xi _{2}<\xi <0\right\} \), where \(\xi _{1},\xi _{2}\) are the solutions of the algebraic equation

    $$\begin{aligned} 8\left( 6-\lambda ^{2}\right) -\left( 120+50\lambda ^{2}\right) \xi ^{2}+75\xi ^{4}=0. \end{aligned}$$
    (32)

In Fig. 1 we present the contour plots of the equation of state parameter \(w_{\phi }\left( \lambda ,\xi \right) \) for points \(A_{2}\) and \(A_{3}\). Notice that the stable critical points are represented by shaded regions. We observe that points with \(\lambda >0\) and \(\xi <0\) describe stable accelerated solutions, while it is possible for the EoS parameter to cross the phantom line, namely \(w_{\phi }<-1\).

4.2 Family B

We continue our analysis with the second family of critical points, namely Family B. Here the dynamical system is formed by Eqs. (20), (21) and (23). By including the constraint, the dimension of the system is reduced by one, i.e. from three to two dimensions. We study the general evolution of the dynamical system by considering a general function \(\Gamma _{\xi }\left( \xi \right) \) [42,43,44].

Fig. 2
figure 2

Phase space portrait in the variables \(\left\{ x,\xi \right\} \) for the dynamical system (20), (21) and (23) and for \(Y\left( \phi \right) =Y_{1}e^{\left( \nu +\frac{\lambda }{2}\right) \phi }~\)without a matter source. Left-hand figure is for \(\lambda =-2\) and \(\nu =1\) where we see that point \(B_{5}\) is the attractor of the system. \(\backslash \)Right-hand figure is for \(\lambda =-\sqrt{3}\) and \(\nu =-\frac{1}{2}\) where the attractor is point \(B_{4}\) ,which describes the tracking solution. Solid lines describe real trajectories

Full size image
Fig. 3
figure 3

Region plots for the variables \(\left\{ \lambda _{0},\xi \left( \lambda _{0}\right) \right\} \) in which points \(C_{2}\) and \(C_{3}\) have eigenvalues with negative real parts. Left-hand figures are for \(\Gamma _{\lambda }^{\prime }\left( \lambda _{0}\right) >0,\) while right-hand figures are for \(\Gamma _{\lambda }^{\prime }\left( \lambda _{0}\right) \,<0\)

Full size image

The critical points \(\left( x_{p},y_{p},\xi _{p}\right) ~\)of the dynamical system are:

  1. a.

    Points \(B_{1\left( \pm \right) }=\left( A_{1\left( \pm \right) },\xi _{0}\right) \) for which \(\xi _{0}\) is a solution of the algebraic equation \(\Gamma _{\xi }\left( \xi _{0}\right) =\frac{\lambda }{\sqrt{2}},~\)or \(\xi _{0}=0.\) The points describe the same physical solution as those for \(A_{1\left( \pm \right) }\), hence the existence of the critical points is given in Sect. 4.1, however the stability conditions change Specifically, the two eigenvalues are \(e_{1}\left( B_{1\left( \pm \right) }\right) =6\pm \sqrt{6}\lambda \) and \(e_{2}\left( B_{1\left( \pm \right) }\right) =\pm \sqrt{3}\xi _{0}\Gamma _{\xi }^{\prime }\left( \xi _{0}\right) .\) Therefore, \(B_{1\left( +\right) }\) is stable when \(\lambda<-\sqrt{6},~\xi _{0} \Gamma _{\xi }^{\prime }\left( \xi _{0}\right) <0\), while \(B_{1\left( -\right) }\) is stable as long as \(\lambda>\sqrt{6},~\xi _{0}\Gamma _{\xi }^{\prime }\left( \xi _{0}\right) >0\).

  2. b.

    Point \(B_{2}=\left( A_{2}\left( \xi _{0}\right) ,\xi _{0}\right) \) with \(\Gamma _{\xi }\left( \xi _{0}\right) =\frac{\lambda }{\sqrt{2}}\). Again the properties of \(B_{2}\) are similar with those of \(A_{2}\) (see Sect. 4.1). Concerning stability conditions \(B_{2}\), describes an attractor solution when \(\xi _{0}\Gamma _{\xi }^{\prime }\left( \xi _{0}\right) >0:\) \(\left\{ \lambda <0~,\xi _{0}>\frac{\sqrt{6}}{3}\left| \lambda \right| \right\} \) or \(\left\{ 0<\lambda \le \sqrt{6}~,~\xi _{0}>0\right\} \).

  3. c.

    Point \(B_{3}=\left( A_{3}\left( \xi _{0}\right) ,\xi _{0}\right) \) with \(\Gamma _{\xi }\left( \xi _{0}\right) =\frac{\lambda }{\sqrt{2}}\). The physical properties of \(B_{3}\) are those of point \(A_{3}\) (see previous section). \(B_{3}\) describes a stable solution for \(\xi _{0}\Gamma _{\xi }^{\prime }\left( \xi _{0}\right)<0:\left\{ -\sqrt{6}<\lambda \le 0,~\xi _{0}<0\right\} \) or \(\left\{ \lambda >0,\xi <-\frac{\sqrt{6}}{3}\lambda \right\} \).

  4. d.

    Point \(B_{4}\) with coordinates \(B_{4}=\left( -\frac{\lambda }{\sqrt{6} },\sqrt{1-\frac{\lambda ^{2}}{6}},0\right) \) exists for \(\left| \lambda \right| <\sqrt{6}\). This situation describes a tracking solution of the exponential potential with \(\xi =0\). The equation of state parameter reads \(w_{\phi }\left( \lambda ,\xi \right) =-1+\frac{\lambda ^{2}}{3}\), hence we have acceleration when \(\left| \lambda \right| <\sqrt{2}\). The eigenvalues of the linearized system are determined to be \(e_{1}\left( B_{4}\right) =-3+\lambda ^{2}~,~e_{2}\left( B_{4}\right) =\frac{\lambda }{2}\left( \lambda -\sqrt{2}\Gamma _{\xi }\left( 0\right) \right) ,\) where \(e_{1}\left( B_{4}\right)<0,\ e_{2}\left( B_{4}\right) <0\) for \(\left| \lambda \right| <\sqrt{3}\), and \(\left| \Gamma _{\xi }\left( 0\right) \right| >\frac{\sqrt{2}}{2}\lambda \).

  5. e.

    Finally, point \(B_{5}\) with coordinates \(B_{5}=\left( 0,1,\xi _{0}\right) ,~\xi _{0}=-\sqrt{\frac{2}{3}}\lambda \) describes a de Sitter solution for which \(w_{\phi }=-1\). The eigenvalues of the linearized system are \(e_{1}\left( B_{5}\right) =-\frac{3+\sqrt{3\left( 3-2\lambda ^{2}+2\sqrt{2}\lambda \Gamma _{\xi }\left( \xi _{1}\right) \right) }}{2},~e_{1}\left( B_{5}\right) =-\frac{3-\sqrt{3\left( 3-2\lambda ^{2}+2\sqrt{2}\lambda \Gamma _{\xi }\left( \xi _{1}\right) \right) }}{2}~\)and thus point \(B_{5}\) is an attractor when \(\left| \Gamma _{\xi }^{\prime }\left( \xi _{0}\right) \right| <\frac{\lambda }{\sqrt{2}}\). Notice that the de Sitter solution does not exist for the exponential case in the context of the scalar field cosmology which reduces to GR.

4.2.1 Application

Consider \(Y\left( \phi \right) =Y_{1}e^{\left( \nu +\frac{\lambda }{2}\right) \phi },~\nu \ne 0\); we calculate that \(\phi =\frac{1}{2}\ln \left( \frac{2\xi ^{2}}{Y_{1}^{2}\left( 2\nu +\lambda \right) ^{2}}\right) \) and \(\Gamma \left( \xi \right) =\left( \sqrt{2}v+\frac{\lambda }{\sqrt{2}}\right) \).

Therefore, Eq. (23) is simplified to

$$\begin{aligned} \frac{d\xi }{dN}=\ \sqrt{6}\nu \xi x, \end{aligned}$$
(33)

while the possible critical points are now only points \(B_{1\left( \pm \right) }~\)with \(\xi _{0}=0\), \(B_{4}\) and \(B_{5}\). Points \(B_{4}\) and \(B_{5}\) are attractors when \(\left\{ \left| \lambda \right| <\sqrt{6},\nu \lambda >0\right\} \) and \(\left\{ \nu<0~,~0<\lambda \le -\frac{3}{2\nu }\right\} \cup \left\{ \nu >0~,~-\frac{3}{2\nu }<\lambda \le 0\right\} ,\) respectively.

In Fig. 2 we present the phase space diagram for the dynamical system in the variables \(\left\{ x,\xi \right\} \) for two sets of the variables \(\lambda ~\)and \(\nu \). For \(\lambda =-2\) and \(\nu =1\) it is clear that the de Sitter universe \(B_{5}~\)is an attractor while for \(\lambda =-\sqrt{3}\), \(\nu =-\frac{1}{2}\) the unique attractor is the scaling solution \(B_{4}\).

In a similar way we continue with the third family of critical points that we considered.

4.3 Family C

The third family of critical points correspond to the dynamical system (20), (21) and (22) with the constraint condition (19). Recall that in this case \(\xi =\xi \left( \lambda \right) \).

The critical points are:

  1. a.

    Points \(C_{1\left( \pm \right) }=\left( A_{1\left( \pm \right) } ,\lambda _{0}\right) \) with \(\Gamma \left( \lambda _{0}\right) =1\) or \(\lambda _{0}=0.\) The physical descriptions of the points are those of \(A_{1\left( \pm \right) }\). The eigenvalues of the linearized system are calculated to be \(e_{1}\left( C_{1\left( \pm \right) }\right) =6-\sqrt{6}\lambda _{0},~e_{2}\left( C_{1\left( \pm \right) }\right) =-\sqrt{6}\lambda _{0}^{2}\Gamma ^{\prime }\left( \lambda _{0}\right) \). We observe that at least of one of the points \(C_{1\left( \pm \right) }\) is stable only for \(\Gamma ^{\prime }\left( \lambda _{0}\right) >0\) and \(\left| \lambda _{0}\right| >\sqrt{6}\).

  2. b.

    Point \(C_{2,3}=\left( A_{2,3},\lambda _{0}\right) \) with \(\Gamma \left( \lambda _{0}\right) =1\). The existence conditions and the physical description are the same as those of \(A_{2,3}\) (see Sect. 4.1). Because of the nonlinearity of the eigenvalues, the map of \(\lambda _{0},\xi \left( \lambda _{0}\right) \) in which the points are stable is presented in Fig. 3.

  3. c.

    Point \(C_{4}=\left( -\frac{\xi }{\sqrt{4+\xi ^{2}}},\frac{2}{\sqrt{4+\xi ^{2}}},\lambda _{0}\right) \) with \(\lambda _{0}=0,\) describes a de Sitter solution, \(w_{\phi }\left( C_{4}\right) =-1\), and actually reduces to points \(C_{2}\), \(C_{3}\), with \(\lambda _{0}=0\) respectively. The eigenvalues of the linearized system are given by \(e_{1}\left( C_{4}\right) =0~,~e_{2}\left( C_{4}\right) =-3.~\) Since \(e_{1}=0\) we apply the central manifold theorem in order to decide the stability and we find that \(C_{4}\) is always an attractor.

  4. d.

    Point \(C_{5}=\left( B_{5},\lambda _{0}\right) \) with \(\lambda _{0} =-\sqrt{\frac{3}{2}}\xi \) is found to be stable when the following condition holds \(\left( \Gamma _{\lambda }\left( 0\right) -1\right) \Big ( 2+\sqrt{6}\xi ^{\prime }\left( 0\right) \Big ) >0\,\). The physical description of \(C_{5}\) is the same as that of \(B_{5}\).

Fig. 4
figure 4

Phase space portrait for in the variables \(\left\{ x,\lambda \right\} \) for the dynamical system (20), (21) and (24) and for \(U\left( \phi \right) =U_{0}\phi ^{n}\) and \(Y\left( \phi \right) =Y_{0}\phi ^{1+\frac{2}{n}}~\)without matter source. Left figure is for \(n=-2\) and \(\xi =\sqrt{\frac{2}{3}}\) from where points \(C_{4}\) and \(C_{5}\) are attractor of the system. Right figure is for \(n=-2\) and \(\xi =-\sqrt{\frac{2}{3}}\) where again \(C_{4}\) and \(C_{5}\) are attractor of the system. Solid lines describe real trajectories

Full size image
Fig. 5
figure 5

Phase space portrait for in the variables \(\left\{ x,\lambda \right\} \) for the dynamical system (20), (21) and (24) and for \(U\left( \phi \right) =U_{0}\phi ^{n}\) and \(Y\left( \phi \right) =Y_{0}\phi ^{1+\frac{2}{n}}\) without matter source. Left figure is for \(n=-0.1\) and \(\xi =\sqrt{\frac{2}{3}}\) while right figure is for \(n=-0.1\) and \(\xi =-\sqrt{\frac{2}{3}}\). It is clear that the only attractor is \(C_{4}\) while \(C_{5}\) is a source point. Solid lines describe real trajectories

Full size image
Fig. 6
figure 6

Region plots for the parameters \(\left\{ \lambda ,\xi \right\} \) in which the critical points \(A_{2},~A_{3}\) and \(A_{4}\) are stable. The lower right-hand figure shows the common regions where we observe that there is not any common intersection. Hence, there is only one possible stable point for the dynamical system

Full size image
Fig. 7
figure 7

Phase space diagrams for the dynamical system (20), (21) with three different sets of the free parameters \(\lambda ,\xi \) where one of the critical points \({\bar{A}}_{2},~{\bar{A}}_{3}\) and \({\bar{A}}_{4}\) is stable. For \(\left( \lambda ,\xi \right) =\left( -2,\frac{3}{2}\right) \) point \(A_{2}\) is the unique attractor; for \(\left( \lambda ,\xi \right) =\left( 2,-2\right) \) point \({\bar{A}}_{3}\) is the unique attractor, while point \({\bar{A}}_{4}\) is an attractor for the plot with \(\left( \lambda ,\xi \right) =\left( 2,1\right) \). Solid lines correspond to real trajectories

Full size image

4.3.1 Application

Let us consider \(U\left( \phi \right) =U_{0}\phi ^{n}\) and \(Y\left( \phi \right) =Y_{0}\phi ^{1+\frac{2}{n}}\) from where we calculate \(\phi =\frac{n}{\lambda }\), \(\xi =\frac{Y_{0}}{\sqrt{2U_{0}}}\left( 2+n\right) =const\) and \(\Gamma _{\lambda }\left( \lambda \right) =\frac{n-1}{n}\). Therefore, Eq. (22) reduces to

$$\begin{aligned} \frac{d\lambda }{dN}=-\frac{\sqrt{6}}{n}x\lambda ^{2}. \end{aligned}$$
(34)

Therefore, the critical points are \(C_{1\left( \pm \right) },~C_{4}\) and \(C_{5}\). As far as stability is concerned we find that points \(C_{1\left( \pm \right) }\) are always unstable and point \(C_{5}~\)is stable only when \(n\le -2\xi ^{2}\). For the latter case using various values of the free parameters \(n,~\xi \) we plot in Figs. 4 and 5 the phase space diagram \(\left\{ x,\lambda \right\} \).

5 Scalar field in the presence of matter

In this section we include in our analysis a pressureless matter component with \(w_{m}=\frac{p_{m}}{\rho _{m}}=0\). In this case since \(0\le \Omega _{m} \le 1\), the constraint equation  (19) yields \(x^{2}+y^{2}\le 1\). Following the lines of the previous section we study the same family of potentials, namely A, B and C.

5.1 Family A

  1. a.

    The first Point is \({\bar{A}}_{0}=\left( 0,0\right) \) and the arbitrary parameters \(\lambda ,~\xi \) describe a universe for which \(\Omega _{m}=1\), \(w_{\mathrm {tot}}=0\). The eigenvalues of the linearized system are determined to be \(e_{1}\left( {\bar{A}}_{0}\right) =-\frac{3}{2}\), \(e_{2}\left( \bar{A}_{0}\right) =\frac{3}{2}\), hence the point is always unstable.

  2. b.

    Points \({\bar{A}}_{1\left( \pm \right) }\) with eigenvalues \(e_{1}\left( {\bar{A}}_{1\left( \pm \right) }\right) =3\pm \sqrt{\frac{3}{2}}\lambda ,~e_{2}\left( {\bar{A}}_{1\left( \pm \right) }\right) =3\), from which we infer that points \({\bar{A}}_{1\left( \pm \right) }\) are unstable points.

  3. c.

    Point \({\bar{A}}_{2}\) with eigenvalues \(e_{1}\left( {\bar{A}}_{2}\right) =-3+\frac{4\lambda ^{2}+\lambda \sqrt{6\xi ^{4}-4\left( \lambda ^{2}-6\right) } }{4+\xi ^{2}},~e_{2}\left( {\bar{A}}_{2}\right) {=}-3+\frac{2\lambda ^{2} +\lambda \sqrt{6\xi ^{4}-4\left( \lambda ^{2}-6\right) }}{2\left( 4+\xi ^{2}\right) }\) describes a stable solution when \(\left\{ \lambda <-\sqrt{3}~,~\xi >\frac{2\left( \lambda ^{2}-3\right) }{\sqrt{6\lambda ^{2}-9} }\right\} ~\)or \(\left\{ -\sqrt{3}\le \lambda {\le }\frac{\sqrt{6}}{2} ~,~\xi {>}0\right\} \) or \(\left\{ \lambda >\frac{\sqrt{6}}{2}~,~\xi <\frac{6-2\lambda ^{2}}{\sqrt{6\lambda ^{2}-9}}\right\} \) or \(\left\{ \lambda =-\sqrt{6},~\xi >\frac{2\sqrt{3}}{3}\right\} \).

  4. d.

    Point \({\bar{A}}_{3}\) with eigenvalues \(e_{1}\left( {\bar{A}}_{3}\right) =-3+\frac{4\lambda ^{2}-\lambda \sqrt{6\xi ^{4}-4\left( \lambda ^{2}-6\right) } }{4+\xi ^{2}}~,~e_{2}\left( {\bar{A}}_{3}\right) =-3+\frac{2\lambda ^{2} -\lambda \sqrt{6\xi ^{4}-4\left( \lambda ^{2}-6\right) }}{2\left( 4+\xi ^{2}\right) }\) describes a stable solution when \(\Big \{ \lambda<-\frac{\sqrt{6}}{2}~,~\frac{2\left( \lambda ^{2}-3\right) }{\sqrt{6\lambda ^{2}-9}}<\xi <0\Big \} ~\)or \(\left\{ -\frac{\sqrt{6}}{2}\le \lambda \le \sqrt{3}~,~\xi <0\right\} \) or \(\Big \{ \lambda >\sqrt{3},~\xi <-\frac{2\left( \lambda ^{2}-3\right) }{\sqrt{6\lambda ^{2}-9}}\Big \} \) or \(\left\{ \lambda =\sqrt{6}~,~\xi <-\frac{2\sqrt{3}}{3}\right\} \).

  5. e.

    Point \({\bar{A}}_{4}\) with coordinates \({\bar{A}}_{4}=\Big (-\sqrt{\frac{3}{2}}\frac{1}{\lambda },\sqrt{\frac{3}{2}}\frac{\sqrt{\lambda ^{2}\left( 4+\xi ^{2}\right) }-\lambda \xi }{2\lambda ^{2}}\Big ) \) describes a universe where the scalar field mimics the pressureless fluid, i.e. \(w_{\phi }=0\). The effective parameter is \(w_{\mathrm {tot}}=0\), where \(\Omega _{m}=1-\frac{3}{\lambda ^{2}}-\frac{3\xi ^{2}}{4\lambda ^{2}}+\frac{3}{4}\frac{\xi }{\lambda ^{3}}\sqrt{\lambda ^{2}\left( 4+\xi ^{2}\right) }\). The point exists when \(\left\{ \lambda <-\frac{\sqrt{6}}{2}~,~\xi \le \frac{2\left( \lambda ^{2}-3\right) }{\sqrt{6\lambda ^{2}-9}}\right\} \) or\(~\Big \{ \sqrt{\frac{3}{2}}<\lambda <\sqrt{3}~,~\xi \ge \frac{2\left( \lambda ^{2}-3\right) }{\sqrt{6\lambda ^{2}-9}}\Big \} \) or \(\left\{ \lambda \ge \sqrt{3}~,~\xi \ge -\frac{2\left( \lambda ^{2}-3\right) }{\sqrt{6\lambda ^{2}-9}}\right\} \).

In Fig. 6 we show \(\left\{ \lambda ,\xi \right\} \) diagrams for where the critical points \({\bar{A}}_{2}~,~{\bar{A}}_{3}\) and \({\bar{A}}_{4}\) exist and have negative eigenvalues, namely we have stable solutions. Moreover, from Fig. 6 we observe that only one of the critical points \({\bar{A}}_{2} \), \({\bar{A}}_{3}\) and \({\bar{A}}_{4}\) can be stable points of the system.

In Fig. 7 we present the phase space diagrams for the dynamical variables \(\left\{ x,y\right\} \), using different values of the free parameters \(\lambda ,\xi \). In particular, we provide three diagrams where in each case one of the critical points \({\bar{A}}_{2},~{\bar{A}}_{3}\) and \({\bar{A}}_{4}\) is stable. The dynamical evolution of the cosmological parameters \(\Omega _{m}\left( a\right) \) and \(w_{tot}\left( a\right) \) are demonstrated in Fig. 8 for the real trajectories presented in Fig. 7.

Fig. 8
figure 8

Qualitative evolution of the energy density \(\Omega _{m}\) and of the parameter of the equation of state for the effective fluid for the real trajectories presented in Fig. 7

Full size image
Fig. 9
figure 9

Region plots for the variables \(\left\{ \lambda ,\xi \right\} \) in which point \({\bar{B}}_{2}\) (left-hand figure) is an attractor and \(\xi _{0}\Gamma _{\xi }^{\prime }\left( \xi _{0}\right) >0\) and point \({\bar{B}}_{3}\) (right-hand figure) describe a stable solution with \(\xi _{0}\Gamma _{\xi }^{\prime }\left( \xi _{0}\right) <0\)

Full size image

5.2 Family B

The critical points which correspond to family B are the following:

  1. a.

    Point \({\bar{B}}_{0}=\left( {\bar{A}}_{0},\xi \right) \) where \(\xi \) is arbitrary: since \(\xi \) is arbitrary, point \(B_{0}\) describes a line in the space \(\left\{ x,y,\xi \right\} \). The physical description is that of point \(A_{0}\). The eigenvalues of the linearized system are determined to be \(e_{1}\left( {\bar{B}}_{0}\right) =-\frac{3}{2}~,~e_{2}\left( {\bar{B}} _{0}\right) =\frac{3}{2}\) and \(e_{3}\left( {\bar{B}}_{0}\right) =0\), from which we conclude that \(B_{0}\) describes an unstable solution and \(B_{0}\) is a source point.

  2. b.

    Points \({\bar{B}}_{1\left( \pm \right) }\) with eigenvalues \(e_{1}\left( {\bar{B}}_{1\left( \pm \right) }\right) =3~\), \(e_{2}\left( {\bar{B}}_{1\left( \pm \right) }\right) =3\pm \sqrt{6}\lambda ~, e_{3}\left( {\bar{B}}_{1\left( \pm \right) }\right) =\pm \sqrt{3}\xi _{0}\Gamma _{\xi }^{\prime }\left( \xi _{0}\right) \), hence the solutions at points \(B_{1\left( \pm \right) }\) are unstable.

  3. c.

    Point \({\bar{B}}_{2}\) which is found to describe a stable solution if and only if \(\xi _{0}\Gamma _{\xi }^{\prime }\left( \xi _{0}\right) >0\). Notice that the parameters \(\left\{ \lambda ,\xi _{0}\right\} \) can be viewed in Fig. 9.

  4. d.

    Point \({\bar{B}}_{3}\) which is found to describe a stable solution if and only if \(\xi _{0}\Gamma _{\xi }^{\prime }\left( \xi _{0}\right) <0\), while the parameters \(\left\{ \lambda ,\xi _{0}\right\} \) are given in Fig. 9.

  5. e.

    Point \({\bar{B}}_{4}\) with eigenvalues \(e_{1}\left( {\bar{B}}_{4}\right) =-3+\frac{\lambda ^{2}}{2}\), \(e_{2}\left( {\bar{B}}_{4}\right) =-3+\lambda ^{2}\) and \(e_{3}\left( {\bar{B}}_{3}\right) =\frac{\lambda ^{2}}{2}-\frac{\sqrt{2}\lambda }{2}\Gamma _{\xi }\left( 0\right) .\)It describes a stable power-law solution when \(\Big \{ -\sqrt{3}<\lambda<0~,~\Gamma _{\xi }\left( 0\right) <\frac{\lambda }{\sqrt{2}}\Big \} \) or \(\left\{ 0<\lambda <\sqrt{3} ~,~\Gamma _{\xi }\left( 0\right) >\frac{\lambda }{\sqrt{2}}\right\} \).

  6. f.

    Point \({\bar{B}}_{5}\) describes a stable de Sitter universe when \(\left| \Gamma _{\xi }^{\prime }\left( \xi _{0}\right) \right| <\frac{\lambda }{\sqrt{2}}.\)

  7. g.

    Point \({\bar{B}}_{6}\) with coordinates \({\bar{B}}_{6}=\left( {\bar{A}}_{4} ,\xi _{0}\right) \) with \(\xi _{0}=0\) or \(\Gamma _{\xi }\left( \xi _{0}\right) =0\). Because of the nonlinearity of the eigenvalues, the regions of the parameter space, \(\left\{ \lambda ,\xi _{0}\right\} \), for which point \({\bar{B}}_{6}\) is an attractor, are shown in Fig. 10.

Fig. 10
figure 10

Region plots for the variables \(\left\{ \lambda ,\xi \right\} \) in which point \({\bar{B}}_{5}\) is an attractor. The blue area is for \(\xi _{0}\Gamma _{\xi }^{\prime }\left( \xi _{0}\right) \ge 0\) while the grey area is for \(\xi _{0}\Gamma _{\xi }^{\prime }\left( \xi _{0}\right) \le 0\)

Full size image
Fig. 11
figure 11

Region plots for the variables \(\left\{ \lambda ,\xi \left( \lambda \right) \right\} \) in which points \({\bar{C}}_{2}\) and \({\bar{C}}_{3}\) are attractors. Left-hand figures are for\(~\Gamma _{\lambda }^{\prime }\left( \lambda _{0}\right) >0\) while right-hand figures are for \(\Gamma _{\lambda }^{\prime }\left( \lambda _{0}\right) <0\)

Full size image

5.3 Family C

We complete our analysis with the third family of critical points which correspond to the case where \(\lambda _{,\phi }\ne const\) and \(\xi =\xi \left( \lambda \right) \). Using the dynamical system (20), (21), (22) we find the following critical points \(\left( x_{p} ,y_{p},\lambda _{p}\right) \):

  1. a.

    Point \({\bar{C}}_{0}=\left( {\bar{A}}_{0},\lambda \right) \) where \(\lambda \) is arbitrary. This point describes a line of points in the space \(\left\{ x,y,\lambda \right\} \). The eigenvalues of the linearized system are \(e_{1}\left( {\bar{C}}_{0}\right) =-\frac{3}{2}~,~e_{2}\left( {\bar{C}} _{0}\right) =\frac{3}{2}\) and \(e_{3}\left( {\bar{C}}_{0}\right) =0\), from which we infer that the current point is a source “line”.

  2. b.

    Points \({\bar{C}}_{1\left( \pm \right) }=\left( {\bar{A}}_{1\left( \pm \right) },\lambda _{0}\right) \) with \(\lambda _{0}=0\) or \(\Gamma _{\lambda }\left( \lambda _{0}\right) =1\). These points are always sources, because they always have a positive eigenvalue. Indeed, the corresponding eigenvalues are \(e_{1}\left( {\bar{C}}_{1\left( \pm \right) }\right) =3~,~e_{2}\left( {\bar{C}}_{1\left( \pm \right) }\right) =3+\sqrt{\frac{3}{2}}\lambda _{0}\) and \(e_{3}\left( {\bar{C}}_{1\left( \pm \right) }\right) =\sqrt{6}\lambda ^{2}\Gamma _{\lambda }^{\prime }\left( \lambda _{0}\right) \).

  3. c.

    Points \({\bar{C}}_{2,3}\) describes a power-law solution with \(\Omega _{m}\left( {\bar{C}}_{2,3}\right) =0\). Due to the nonlinearity of the eigenvalues in Fig. 11 we present the region of the parameters \(\left\{ \lambda _{0},\xi \left( \lambda _{0}\right) \right\} \) for which \({\bar{C}}_{2,3}\) are stable.

  4. d.

    Point \({\bar{C}}_{4}\) describes a de Sitter universe and the eigenvalues for the linearized system are \(e_{1}\left( {\bar{C}}_{4}\right) =-3~,~e_{2}\left( {\bar{C}}_{4}\right) =-3\) and \(e_{3}\left( {\bar{C}}_{4}\right) =0\). Since \(e_{3}=0\) means that we need to use central manifold theorem: it implies that \({\bar{C}}_{4}\) is always a future attractor of the dynamical system.

  5. e.

    Point \({\bar{C}}_{5}\) with eigenvalues \(e_{1}\left( {\bar{C}}_{5}\right) =-3\), \(e_{2,3}\left( {\bar{C}}_{5}\right) =-\frac{3}{2}\left( 1\pm \sqrt{1+\left( \Gamma _{\lambda }\left( 0\right) -1\right) \left( \sqrt{6}\right) \xi ^{\prime }-2}\right) \) describes a stable de Sitter solution when \(\left\{ \Gamma _{\lambda }\left( 0\right) <1,\xi ^{\prime }>\sqrt{\frac{2}{3}}\right\} \) or \(\left\{ \Gamma _{\lambda }\left( 0\right) >1,\xi ^{\prime }<\sqrt{\frac{2}{3}}\right\} \).

  6. f.

    Point \({\bar{C}}_{6}=\left( {\bar{A}}_{4},\lambda _{0}\right) \,\ \)with \(\lambda _{0}=0\) or \(\Gamma \left( \lambda _{0}\right) =0\), is stable when \(\left\{ \sqrt{\frac{3}{2}}<\lambda ~,~\xi >\frac{6-2\lambda ^{2}}{\sqrt{6\lambda ^{2}-9}}\right\} \) or \(\Big \{ \lambda<\frac{\sqrt{6}}{2}~,~\xi <\frac{6-2\lambda ^{2}}{\sqrt{6\lambda ^{2}-9}}\Big \} \).

Overall, from the aforementioned analysis, we conclude that in the case of matter there are two possible de Sitter solutions which can act as attractors for the expansion dynamics.

6 Exact solutions

In the above analysis we have shown that the evolution of the dimensionless dynamical system is always in a three-dimensional phase space, and there is an extra free function which must satisfy constraints in order for the critical point, that is, the solution at the critical point, to exist. In order to understand this more fully let us consider the field equations (15), (16) and assume that there is no matter source other than the scalar field, i.e. \(\rho _{m}=p_{m}=0\).

From system (15), (16) we find

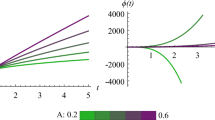
$$\begin{aligned} U\left( \phi \right) =\frac{\theta ^{2}}{3}-\frac{{\dot{\phi }}^{2}}{2},~Y\left( \phi \right) =-\frac{2}{3}\frac{{\dot{\theta }}}{{\dot{\phi }}} -3{\dot{\phi }}. \end{aligned}$$
(35)

Assume now that \(\theta =\theta _{0}t^{-1},~\)which describes a perfect fluid solution, and for \(\phi =t^{-1}\) we find that

$$\begin{aligned} U\left( \phi \right) =\frac{\phi ^{2}}{2}\left( \frac{2}{3}\theta _{0} ^{2}-\phi ^{2}\right) ,~Y\left( \phi \right) =\phi ^{2}-\frac{2}{3}\theta _{0}. \end{aligned}$$
(36)

Hence, this solution is described by a point in family C. In order to study the stability of the solution we substitute in (15), (16) \(\theta =\theta _{0}t^{-1}+\varepsilon \Theta \left( t\right) ,~\phi =t^{-1}+\varepsilon \Phi \left( t\right) \) for the latter potentials and the solution of the linearized system reveals that functions \(\Theta \) and \(\Phi \) decay when\(~\theta _{0}>3\).

However, this it is not the unique power-law solution as is the case in GR. Indeed, by selecting the same expansion rate \(\theta =\theta t^{-1}\), but now \(\phi =\ln t^{\frac{1}{\alpha }}\), we find

$$\begin{aligned} U(\phi )= & {} \left( \frac{\theta _{0}^{2}}{3}-\frac{1}{2\alpha ^{2} }\right) e^{-2\alpha \phi }~,~\nonumber \\ Y(\phi )= & {} \left( \frac{2}{3} \alpha \theta -\frac{1}{\alpha }\right) e^{-\alpha \phi }, \end{aligned}$$
(37)

and this is a solution that is now described by a critical point of family B.

Moreover, when \(\theta =\frac{2}{3}\coth \left( \theta _{0}\tau \right) \) and \(\phi =\frac{1}{\alpha t}\) we find

$$\begin{aligned} U(\phi )= & {} \frac{4}{27}\coth ^{2}\left( \alpha \theta _{0} \phi \right) -\frac{1}{2\alpha ^{2}}~,~\nonumber \\ Y(\phi )= & {} -\frac{8}{27}\alpha \theta _{0}\frac{\cosh \left( \alpha \theta _{0}\phi \right) }{\sinh ^{3}\left( \alpha \theta _{0}\phi \right) }. \end{aligned}$$
(38)

In a similar way we can construct other kinds of solutions for the scalar field with the aether field and other kinds of matter sources. For instance, the latter solution is that of GR with cosmological constant term and a perfect fluid source.

7 Conclusions

In this paper we have performed a detailed analysis of the dynamical evolution of an Einstein–Aether scalar field cosmology in the framework of a spatially-flat FLRW background universe, where the scalar field is coupled to the aether field. The model that we analysed depends on two unknown functions, the first, \(U\left( \phi \right) ,\) corresponds to the scalar field potential, while the second function \(Y\left( \phi \right) \) defines the coupling between the scalar field and the aether field. The Friedmann equation is the same with that of Einstein’s GR, while the Raychaudhuri acceleration equation is modified, since the effective pressure term of the scalar field fluid differs from that in GR.

We use expansion-normalised variables to rewrite the field equations as a system of algebraic-differential equations, which contains at most three independent variables. The possible critical points correspond to three different families of solutions. In family A the scalar field potential is exponential \(U\left( \phi \right) =U_{0}e^{\lambda \phi }~\)while the coupling function is given by \(~Y\left( \phi \right) =Y_{0}+Y_{1}e^{-\frac{\lambda }{2}\phi }\). Family B corresponds to the exponential potential for \(U\left( \phi \right) ,\) while \(Y\left( \phi \right) \) is arbitrary, while in family C the scalar field potential \(U\left( \phi \right) \) is arbitrary.

When we assume there is no other fluid source in the universe, we find that family A admits four-critical points, while families B and C admit six critical points. On the other hand, when a pressureless matter source is introduced, the maximum number of possible critical points is increased by two for the three families. At this point it is important to mention that family A corresponds to a specific case of the function \(V\left( \phi ,\theta \right) \) which is determined in [29] and for which the the field equations admit exact power-law solutions. Moreover, we found that in family B, power-law solutions exist only when \(Y\left( \phi \right) \) is approximated locally by the exponential function \(Y\left( \phi \right) \simeq e^{-\frac{\lambda }{2}\phi }\). On the other hand, we found that for family C there is a critical point which describes a de Sitter universe as a future attractor. Additionally, the critical points of families A and C reduce to solutions of GR when \(Y\left( \phi \right) \ \)is constant.

Finally, in order to demonstrate the evolution of the dynamical system, we presented some phase-space diagrams for specific cases as well as a qualitative evolution for the respective cosmological parameters. From the latter it is clear that this specific scalar field type of cosmology approach can describe some key epochs in cosmological evolution.