1 Introduction

It has been over 40 years since Bekenstein and Hawking first disclosed that black hole can be considered as a thermodynamic system, with characteristic temperature and entropy [1,2,3,4]. Taking into account the fact that black holes have no hair, there are no classical degrees of freedom to account for such thermodynamic properties. It is a general belief that thermodynamic properties of a system may reflect the statistical mechanics of underlying relevant microscopic degrees of freedom. But the detailed nature of these microscopic gravitational states has remained a mystery. The Bekenstein–Hawking entropy, \(S=A/(4\hbar G)\), depends on both Planck’s constant and Newtonian gravitational constant, implying that the thermodynamics of black holes may relate quantum mechanics and gravity. Recently, there has been some progress in understanding the microscopic degrees of freedom of the black hole entropy, for example in string theory [5,6,7] as well as loop quantum gravity [8,9,10]. But the accounts of the black hole entropy are not complete and they only work within some particular models and some special domains where string theory and loop quantum gravity can apply. Besides, despite counting very different states, many inequivalent approaches to quantum gravity obtain identical results and it is not clear why any counting of microstates should reproduce the same Bekenstein–Hawking entropy [11]. The statistical mechanical description of the black hole entropy is still not elegant.

On the other side, black hole can be heated or cooled through absorption and evaporation processes. According to Boltzmann’s insight, if a system can be heated, it must have microscopic structures. Recently, in [12], possible microscopic structures of a charged anti-de Sitter black hole have been studied and some kind of interactions between possible micromolecules have been investigated by an interesting physical tool, the Ruppeiner geometry. Derived from the thermodynamic fluctuation theory, the Ruppeiner geometry [13, 14] is considered a powerful tool in exploring the possible interactions between black hole microscopic structures. The sign of the Ruppeiner invariant \(\mathfrak {R}\) (the Ricci scalar of the Ruppeiner geometry) was argued to be useful for identifying the physical systems similar to the Fermi (Bose) ideal gas when \(\mathfrak {R}>0\) (\(\mathfrak {R}<0\)) or the classical ideal gas when \(\mathfrak {R}=0\) [15]. Besides, the sign of the Ruppeiner invariant \(\mathfrak {R}\) can further be used to interpret the type of dominant interaction between molecules of a thermodynamic system. When \(\mathfrak {R}>0\), there is a repulsive interaction between molecules, when \(\mathfrak {R}<0\) the interaction is attractive, and for \( \mathfrak {R}=0\) there is no interaction in the microstates [16,17,18]. Moreover, the magnitude of the Ruppeiner invariant \( \left| \mathfrak {R}\right| \) measures the average number of correlated Planck areas on the event horizon for a black hole system [19]. For a review of the description of the Ruppeiner geometry in black hole systems, we refer to [20, 21] and the references therein. Further studies of molecular interactions of black holes, based on the Ruppeiner geometry, have been carried out in [12, 22, 23].

The phase transition is another interesting topic in black holes thermodynamics. Davies discussed the thermodynamic phase transition of the black holes by looking at the behavior of the heat capacity [24,25,26]. He claimed that the discontinuity of the heat capacity marks a second order phase transition in black holes. However, it was argued that physical properties do not show any particularity at this discontinuity point if compared with other heat capacity values; for example the regularity of the event horizon is not lost and the black hole internal state remains uninfluenced [27]. Thus, it is hard to accept the discontinuity point of the heat capacity as a true physical point of the phase transition. Employing the Landau–Lifshitz theory of thermodynamic fluctuations [28, 29], Pavon and Rubi gave a deep understanding of the black hole phase transition [30, 31]. They found that some second moments in the fluctuation of relevant thermodynamic quantities diverge when the black hole becomes extreme. This divergence shows that the thermodynamic fluctuation is tremendous and the rigorous meaning of the thermodynamical quantities is broken down. This is exactly the characteristic of the thermodynamic phase transition point. At this phase transition point, the Hawking temperature is zero which indicates that for the extreme black hole there is only super-radiation but no Hawking radiation, which is in sharp difference from that of the non-extreme black holes. Black holes phase transition in the context of Landau–Lifshitz theory have been investigated in [32, 33]. Recently, further differences in dynamical properties before and after the black hole thermodynamical phase transition has been disclosed in [34,35,36]. Also, in [37,38,39,40,41,42], black hole phase transitions have been studied from holographic point of view. A question now arises: how we can further understand this macroscopic thermodynamic phase transition in black hole physics? for example whether there is a microscopic explanation of this thermodynamic phase transition. The Ruppeiner geometry is a possible tool we can use to investigate the thermodynamic phase transitions from microscopic point of view. This method is safer to determine true phase transitions than other methods since, regardless of the microscopic model, \(\mathfrak {R}\) has a unique status in identifying microscopic order (which is at the foundation of phase transitions at microscopic level) from thermodynamics [20, 21]. Some attempts in this direction have been reported in [43,44,45,46,47,48,49,50,51,52,53,54]. In a recent work [46], it was found that the divergence of the Ruppeiner invariant coincides with the critical point in the phase transition in a holographic superconductor model. It is interesting to investigate whether the Ruppeiner geometry [20, 21] can present us further reason to determine which of the thermodynamical discussions mentioned above is valid for describing the thermodynamical phase transition. In particular, we would like to explore whether the Davies phase transition conjecture can reflect some special properties in microstructures and be in consistence with the Ruppeiner geometry description. If the Davies conjecture does not have the microscopic explanation, we will further think about how to improve the Davies conjecture to describe the black hole phase transition.

We will employ the black hole in Lifshitz spacetime as a configuration to study our physical problems mentioned above. This spacetime was first introduced in [55], which respects the anisotropic conformal transformation \(t\rightarrow \lambda ^{z}t\), \(\vec {\mathbf {x}}\rightarrow \lambda \vec {\mathbf {x}}\), where z is dynamical critical exponent. For the Lifshitz spacetime, it is necessary to include some matter sources such as massive gauge fields [56,57,58,59,60] or higher-curvature corrections [61] to guarantee the asymptotic behavior of the Lifshitz black hole. It is difficult to find an analytic Lifshitz black hole solution for arbitrary z, although some attempts have been performed [62]. This makes the discussion of thermodynamics for such a black hole difficult. Fortunately, in Einstein–dilaton gravity with a massless gauge field, it is possible to find an exact Lifshitz black solution for arbitrary z [63, 64]. This model is suggested in the low energy limit of string theory [65]. While thermodynamical behaviors of uncharged and charged Einstein–dilaton–Lifshitz black holes have been revealed in [63, 66] and [64], respectively, thermodynamics of uncharged Gauss–Bonnet–dilaton–Lifshitz solution has been studied in [67]. It is also interesting to study Lifshitz black hole solutions in the presence of other gauge fields such as the power-law Maxwell field [68], the logarithmic [69] and exponential [70] nonlinear electrodynamics. For example, thermodynamics and thermal and dynamical stabilities of Einstein–dilaton–Lifshitz solutions in the presence of power-law Maxwell field have been studied in [71]. In the context of AdS/CFT [72,73,74] application, the electrical conductivity were explored for exponentially [75] and logarithmic [76] charged Lifshitz solutions. In the present work, we shall consider the Born–Infeld (BI) nonlinear electrodynamics in the context of Einstein–dilaton–Lifshitz black holes. The motivation for considering the BI-dilaton action comes from the fact that the dynamics of D-branes and some soliton solutions of supergravity are governed by the BI action [77,78,79,80,81,82]. Besides, the low energy limit of open superstring theory suggest the BI electrodynamic action to be coupled to a dilaton field [77,78,79]. It is surprising that many years before the appearance of the BI action in superstring theory, in the 1930s, this nonlinear electrodynamics was introduced for the first time, with the aim of solving the infinite self-energy problem of a point-like charged particle by imposing a maximum strength for the electromagnetic field [83].

In this paper, we will first look for a general (\(n+1\))-dimensional Lifshitz black hole solution in the context of Einstein–dilaton gravity in the presence of BI electrodynamics. We will show that the general metric function has different solutions for \(z=n+1\) and \(z\ne n+1\) cases. It is important to note that the difference in the metric function has not been observed in the previous studies on Lifshitz–dilaton black holes [71, 75, 76]. Based on this general solution, we will study the thermodynamics of Lifshitz–dilaton black holes coupled to a linear Maxwell field and BI nonlinear electrodynamics. We will show that the Hawking–Page phase transition [84] exists both in the presence of linear and nonlinear electrodynamics. There are some attempts to study phase transitions of uncharged Lifshitz solutions for fixed z [85] or in three [86] and four [87] dimensions. The Hawking–Page phase transition revealed in this paper is interesting, since it depends on different values of z in different spacetime dimensions in the presence of linear Maxwell and nonlinear BI electrodynamic fields. We will further concentrate our attention on understanding the thermodynamic phase transition from microstructures. We shall examine the relation between the Ruppeiner geometry and thermodynamical descriptions of the phase transition such as the Davies conjecture and the Landau–Lifshitz method. We try to give more microscopic understanding of the thermodynamical phase transitions in the black hole system. We explore the thermodynamic geometry (Ruppeiner geometry) for linearly and nonlinearly charged Lifshitz solutions separately and show the properties of interactions between possible black hole molecules. To the best of our knowledge, there is no study of thermodynamic geometry on Lifshitz solutions in the literature. Interestingly enough, by studying Ruppeiner geometry, we have found that our solutions show the Van der Waals like behavior near critical point in some cases.

The layout of the paper is as follows. In the next section, we give the basic field equations and obtain the BI charged Lifshitz–dilaton black hole solutions. In Sect. 3, we first explore the satisfaction of the first law of thermodynamics for Lifshitz–dilaton black holes in the presence of BI electrodynamics. Then we study different phase transitions including the Hawking–Page phase transition and phase transition at zero temperature for linearly and BI charged cases. In Sect. 4, we investigate thermodynamic geometry of the obtained solutions for linearly and nonlinearly BI charged cases by adopting the Ruppeiner approach. We finish with a summary and closing remarks in Sect. 5.

2 Action and asymptotic Lifshitz solutions

In this section, we intend to obtain exact \((n+1)\)-dimensional dilaton–Lifshitz black holes in the presence of BI nonlinear electrodynamics. Our ansatz for the line elements of the spacetime is [64, 88]

$$\begin{aligned} \mathrm{d}s^{2}=-\frac{r^{2z}f(r)}{l^{2z}}\mathrm{d}t^{2}+{\frac{l^{2}\mathrm{d}r^{2}}{r^{2}f(r)}} +r^{2}\mathrm{d}\mathbf {\Omega }_{n-1}^{2}, \end{aligned}$$
(1)

where \(z(\ge 1)\) is the dynamical critical exponent and

$$\begin{aligned} \mathrm{d}\mathbf {\Omega }_{n-1}^{2}=\mathrm{d}\theta _{1}^{2}+\sum \limits _{i=2}^{n-1}\mathrm{d}\theta _{i}^{2}\prod \limits _{j=1}^{i-1}\sin ^{2}\left( \theta _{j}\right) \end{aligned}$$

is an (\(n-1\))-dimensional hypersurface with constant curvature \((n-1)(n-2)\) and volume \(\omega _{n-1}\). As \(r\rightarrow \infty \), the line elements ( 1) reduce asymptotically to the Lifshitz spacetime,

$$\begin{aligned} \mathrm{d}s^{2}=-\frac{r^{2z}\mathrm{d}t^{2}}{l^{2z}}+{\frac{l^{2}\mathrm{d}r^{2}}{r^{2}}}+r^{2}\mathrm{d} \mathbf {\Omega }_{n-1}^{2}. \end{aligned}$$
(2)

On the other side, as pointed out above, we would like to consider BI nonlinear electrodynamics. In the absence of the dilaton field, the BI Lagrangian density is written as [83]

$$\begin{aligned} L=4\beta ^{2}\left( 1-\sqrt{1+\frac{F}{2\beta ^{2}}}\right) , \end{aligned}$$
(3)

where \(\beta \) is the Born–Infeld parameter related to the Regge slope \( \alpha ^{\prime }\) as \(\beta =1/\left( 2\pi \alpha ^{\prime }\right) \). \( F=F_{\mu \nu }F^{\mu \nu }\) is Maxwell invariant in which \(F_{\mu \nu }=\partial _{[\mu }A_{\nu ]}\) where \(A_{\mu }\) is electromagnetic potential. One of the effects of the presence of a dilaton field is its coupling with the electromagnetic field. Thus, in the presence of the dilaton field we deal with a modified form for the BI Lagrangian density including its coupling with the dilaton scalar field \(\Phi \) [89, 90],

$$\begin{aligned} L(F,\Phi )=4\beta ^{2}e^{4\lambda \Phi /(n-1)}\left( 1-\sqrt{1+\frac{ e^{-8\lambda \Phi /(n-1)}F}{2\beta ^{2}}}\right) , \end{aligned}$$
(4)

where \(\lambda \) is a constant. The Lagrangian density of the string-generated Einstein–dilaton model [65] with two Maxwell gauge fields [64] in the presence of BI electrodynamics can be written in an Einstein frame as

$$\begin{aligned} \mathcal {L}= & {} \frac{1}{16\pi }\bigg \{ \mathcal {R}-\frac{4}{n-1}(\nabla \Phi )^{2}-2\Lambda \nonumber \\&-\sum \limits _{i=1}^{2}e^{-4\Phi \lambda _{i}/(n-1)}H_{i}+L(F,\Phi )\bigg \} , \end{aligned}$$
(5)

where \(\mathcal {R}\) is the Ricci scalar and \(\Lambda \) and the \(\lambda _{i}\) are some constants. In Lagrangian (5), \(H_{i}=\left( H_{i}\right) _{\mu \nu }\left( H_{i}\right) ^{\mu \nu }\) where \(\left( H_{i}\right) _{\mu \nu }=\partial _{[\mu }\left( B_{i}\right) _{\nu ]}\) and \(\left( B_{i}\right) _{\mu } \) is gauge potential. In the large \(\beta \) limit, \( \mathcal {L}\) recovers the Einstein–dilaton–Maxwell Lagrangian in its leading order [64, 71]

$$\begin{aligned} \lim _{\beta \rightarrow \infty }16\pi \mathcal {L}= & {} \cdots -e^{-4\lambda \Phi /(n-1)}F\nonumber \\&+\frac{e^{-12\lambda \Phi /(n-1)}F^{2}}{8\beta ^{2}}+O\left( \frac{1 }{\beta ^{4}}\right) . \end{aligned}$$
(6)

Varying the action \(S=\int _{\mathcal {M}}d^{n+1}x\sqrt{-g}\mathcal {L}\) with respect to the metric \(g_{\mu \nu }\), the dilaton field \(\Phi \) and electromagnetic potentials \(A_{\mu }\) and \(\left( B_{i}\right) _{\mu }\) leads to the following field equations:

$$\begin{aligned} \mathcal {R}_{\mu \nu }- & {} \frac{g_{\mu \nu }}{n-1}\bigg \{ 2\Lambda +2L_{F}F-L(F,\Phi )\nonumber \\- & {} \sum \limits _{i=1}^{2}e^{-4\Phi \lambda _{i}/(n-1)}H_{i}\bigg \} \nonumber \\- & {} \frac{4}{n-1}\partial _{\mu }\Phi \partial _{\nu }\Phi +2L_{F}F_{\mu \lambda }F_{\nu }^{ \lambda }\nonumber \\- & {} 2\sum \limits _{i=1}^{2}e^{-4\lambda _{i}\Phi /(n-1)}\left( H_{i}\right) _{\mu \lambda }\left( H_{i}\right) _{\nu }^{ \lambda }=0, \end{aligned}$$
(7)
$$\begin{aligned}&\nabla ^{2}\Phi +\frac{n-1}{8}L_{\Phi }+\sum \limits _{i=1}^{2}\frac{{ \lambda }_{i}}{2}e^{-{4{\lambda }_{i}\Phi }/({n-1})}H_{i}=0, \end{aligned}$$
(8)
$$\begin{aligned}&\triangledown _{\mu }\left( L_{F}F^{\mu \nu }\right) =0, \end{aligned}$$
(9)
$$\begin{aligned}&\triangledown _{\mu }\left( e^{-{4\lambda }_{i}{\Phi }/({n-1})}\left( H_{i}\right) ^{\mu \nu }\right) =0, \end{aligned}$$
(10)

where we use the convention \(X_{Y}=\partial X/\partial Y\). Using the metric ansatz (1), electromagnetic field equations (9) and (10) can be solved immediately as

$$\begin{aligned} F_{rt}= & {} \frac{q\beta e^{4\lambda \Phi /(n-1)}r^{z-n}}{\Upsilon }, \end{aligned}$$
(11)
$$\begin{aligned} \left( H_{i}\right) _{rt}= & {} q_{i}r^{z-n}e^{4\lambda _{i}\Phi /(n-1)}, \end{aligned}$$
(12)

where \(\Upsilon =\sqrt{1+q^{2}l^{2z-2}/(\beta ^{2}r^{2n-2})}\), and \(\Phi (r)\) can be obtained by subtracting (tt) and (rr) components of Eq. (7 ) and solving the resulting equation. We find

$$\begin{aligned} \Phi (r)=\frac{(n-1)\sqrt{z-1}}{2}\ln \left( \frac{r}{b}\right) . \end{aligned}$$
(13)

Substituting Eqs. (11), (12) and (13) in the field equations (7) and (8), one can solve the equations for f(r) to obtain

$$\begin{aligned} f(r)=\left\{ \begin{array}{ll} 1-\frac{m}{r^{n+z-1}}+\frac{(n-2)^{2}l^{2}}{(n+z-3)^{2}r^{2}}+\frac{4\beta ^{2}l^{2}{b}^{2z-2}}{{r}^{2z-2}(n-1)(n-z+1)}-\frac{4\beta ^{2}l^{2}b^{2z-2}}{ (n-1)r^{n+z-1}}\int \Upsilon r^{n-z}{\mathrm{d}r,} &{} \quad \text {for }z\ne n+1, \\ &{} \\ 1-\frac{m}{r^{2n}}+\frac{(n-2)^{2}l^{2}}{4(n-1)^{2}r^{2}}-\frac{4\beta ^{2}b^{2n}l^{2}}{(n-1)^{2}r^{2n}}\left[ 1-\Upsilon +\ln \left( \frac{ 1+\Upsilon }{2}\right) \right] , &{} \quad \text {for }z=n+1, \end{array} \right. \end{aligned}$$
(14)

where we should set

$$\begin{aligned} \lambda= & {} -\sqrt{z-1}, \lambda _{1}=\frac{n-1}{\sqrt{z-1}}, \lambda _{2}=\frac{n-2}{\sqrt{z-1}}, \nonumber \\ q_{1}^{2}= & {} \frac{-\Lambda \left( z-1\right) b^{2(n-1)}}{\left( z+n-2\right) l^{2(z-1)}}, q_{2}^{2}=\frac{(n-1)(n-2)(z-1)b^{2(n-2)}}{ 2(z+n-3)l^{2(z-1)}}, \nonumber \\ \Lambda= & {} -\frac{(n+z-1)(n+z-2)}{2l^{2}}, \end{aligned}$$
(15)

so that the field equations are fully satisfied. In the solution (14), m is a constant which is related to the total mass of black brane as we will see in next section. The integral of the last term of f(r) for \(z\ne n+1\) can be done in terms of hypergeometric function. Thus, f(r) can be written as

$$\begin{aligned} f(r)&=1-\frac{m}{r^{n+z-1}}+\frac{(n-2)^{2}l^{2}}{(n+z-3)^{2}r^{2}}+\frac{ 4b^{2z-2}l^{2}\beta ^{2}(1-\Upsilon )}{(n-1)(n-z+1)r^{2z-2}} \nonumber \\&\quad +\frac{4q^{2}b^{2z-2}l^{2z}\Upsilon }{(n+z-3)(n-z+1)r^{2\left( n+z-2\right) }}\nonumber \\&\quad \times \mathbf {F}\left( 1,\frac{2n+z-4}{2n-2},\frac{3n+z-5}{2n-2} ,1-\Upsilon ^{2}\right) . \end{aligned}$$
(16)

Note that solution (16) obviously satisfies the fact that \( f(r)\rightarrow 1\) as \(r\rightarrow \infty \) (note that \(\mathbf {F}\left( a,b,c,0\right) =1\)). The behavior of f(r) for large \(\beta \) is

$$\begin{aligned} f(r)=\left\{ \begin{array}{ll} 1-\frac{m}{r^{n+z-1}}+\frac{(n-2)^{2}l^{2}}{(n+z-3)^{2}r^{2}}+\frac{ 2q^{2}b^{2z-2}l^{2z}}{\left( n-1\right) \left( n+z-3\right) r^{2n+2z-4}}- \frac{q^{4}b^{2z-2}l^{4z-2}}{4\left( n-1\right) \left( 3n+z-5\right) \beta ^{2}r^{4n+2z-6}}+O\left( \frac{1}{\beta ^{4}}\right) {,} &{} \text {for }z\ne n+1, \\ &{} \\ 1-\frac{m}{r^{2n}}+\frac{(n-2)^{2}l^{2}}{4(n-1)^{2}r^{2}}+\frac{ q^{2}b^{2n}l^{2n+2}}{\left( n-1\right) ^{2}r^{4n-2}}-\frac{ q^{4}b^{2n}l^{4n+2}}{8\left( n-1\right) ^{2}\beta ^{2}r^{6n-4}}+O\left( \frac{1}{\beta ^{4}}\right) , &{} \text {for }z=n+1. \end{array} \right. \end{aligned}$$
(17)

which reproduces the result of [71] for every z in linear Maxwell case. The behaviors of the metric function for \(z=n+1\) and \(z\ne n+1\) have been depicted in Fig. 1a and b, respectively. It is notable to mention that in the case of \(z=n+1\), there is no Schwartzschild-like black hole since in this case f(r) goes to positive infinity as r goes to zero. However, for \(z\ne n+1\), we may have Schwartzschild-like black hole (dash-dotted line in Fig. 1a) in addition to non-extreme (solid line) and extreme (dotted line) black holes and naked singularity (dashed line). For non-extreme case, there are two inner (Cauchy) and outer (event) horizons. In both Fig. 1a and b, we see that the larger the nonlinearity parameter \(\beta \) is, the smaller the distance between two inner and outer horizons is so that, for large enough \(\beta \), we have just one horizon (extreme case) or naked singularities. The Schwartzschild-like case occurs for lower \(\beta \)’s in the case of \(z\ne n+1\) as Fig. 1a shows.

Fig. 1
figure 1

The behavior of f(r) versus r for \(l=1\), \(b=0.8\) and \(q=1.3\)

Full size image

As one can see in (17), the fourth term in expansions for both \( z=n+1\) and \(z\ne n+1\) cases reproduce the charge term of [71] in linear Maxwell case as one expects. The temperature of the black hole horizon can be obtained via

$$\begin{aligned} T=\frac{1}{2\pi }\left. \sqrt{-\frac{1}{2}\nabla _{b}\chi _{a}\nabla ^{b}\chi ^{a}}\right| _{r=r_{+}}, \end{aligned}$$
(18)

where \(\chi =\partial _{t}\) is the Killing vector and \(r_{+}\) is the radius of event horizon. Using (18), one can calculate the Hawking temperature as

$$\begin{aligned} T= & {} \left. \frac{r^{z+1}f^{\prime }}{4\pi l^{z+1}}\right| _{r=r_{+}} \nonumber \\= & {} \frac{{(n+z-1){r}_{+}^{z}}}{4\pi l^{z+1}}+\frac{(n-2)^{2}l^{1-z}}{4\pi (n+z-3)r_{+}^{2-z}}\nonumber \\&+\frac{\beta ^{2}b^{2z-2}r_{+}^{2-z}\left( 1-\Upsilon _{+}\right) }{\pi (n-1)l^{z-1}}, \end{aligned}$$
(19)

where prime denotes the derivative with respect to r and \(\Upsilon _{+}=\Upsilon \left( r=r_{+}\right) \). For the temperature one has the same formula as (19) for the two cases \(z=n+1\) and \(z\ne n+1\). One can check that, for large \(\beta \), (19) reduces to the temperature of Einstein–Maxwell–dilaton–Lifshitz black holes [71], namely

$$\begin{aligned} T= & {} \frac{(n+z-1)r_{+}^{z}}{4\pi l^{z+1}}+\frac{(n-2)^{2}l^{1-z}}{ 4\pi (n+z-3)r_{+}^{2-z}}\nonumber \\&-\frac{q^{2}l^{z-1}b^{2z-2}}{2\pi (n-1)r_{+}^{2n+z-4} }+\frac{q^{4}l^{3z-3}b^{2z-2}}{8\pi (n-1)r_{+}^{4n+z-6}\beta ^{2}}+O\left( \frac{1}{\beta ^{4}}\right) .\nonumber \\ \end{aligned}$$
(20)

The entropy of the black holes can be calculated by using the area law of the entropy [2, 91, 92] which is applied to almost all kinds of black holes in Einstein gravity including dilaton black holes [93,94,95,96]. Therefore, the entropy of the black brane per unit volume \(\omega _{n-1}\) becomes

$$\begin{aligned} S=\frac{r_{+}^{n-1}}{4}. \end{aligned}$$
(21)

Having Eqs. (11), (13) and (15) at hand, we can find electromagnetic gauge potential \(A_{t}=\int F_{rt}\mathrm{d}r\) in terms of hypergeometric function as

$$\begin{aligned} A_{t}\left( r\right) =-\frac{qb^{2z-2}}{(n+z-3)r^{n+z-3}}\mathbf {F}\left( \frac{1}{2},\frac{n+z-3}{2n-2},\frac{3n+z-5}{2n-2},1-\Upsilon ^{2}\right) . \end{aligned}$$
(22)

The large \(\beta \) behavior of gauge potential is in agreement with [71]

$$\begin{aligned} A_{t}\left( r\right) =-\frac{qb^{2z-2}}{(n+z-3)r^{n+z-3}}\mathbf {+}\frac{ q^{3}b^{2z-2}l^{2z-2}}{\left( 3n+z-5\right) r^{3n+z-5}\beta ^{2}}+O\left( \frac{1}{\beta ^{4}}\right) . \end{aligned}$$
(23)

      In next section, we will study thermodynamics of dilaton Lifshitz black holes in the presence of BI electrodynamics by seeking for satisfaction of thermodynamics first law through calculation of conserved and thermodynamic quantities. We also show that our Lifshitz solutions can exhibit the Hawking–Page phase transition. Then we discuss the inside phase transitions of our Lifshitz black holes.

3 Thermodynamics of Lifshitz black holes

3.1 First law of thermodynamics

This subsection is devoted to a study of the first law of thermodynamics for Lifshitz–dilaton black hole solutions in the presence of BI nonlinear electrodynamics. As the first step, we calculate the fundamental quantity for thermodynamics discussions namely mass. For this purpose, we apply the modified subtraction method of Brown and York (BY) [97,98,99]. In order to use this method, the metric should be written in the form

$$\begin{aligned} \mathrm{d}s^{2}=-X(R)\mathrm{d}t^{2}+\frac{\mathrm{d}R^{2}}{Y(R)}+R^{2}\mathrm{d}\mathbf {\Omega }_{n-1}^{2}. \end{aligned}$$
(24)

For our case, it is clear that \(R=r\) and thus

$$\begin{aligned} X(R)=\frac{r(R)^{2z}f(r(R))}{l^{2z}},\quad Y(R\mathcal {)}=\frac{ r(R)^{2}f(r(R))}{l^{2}}. \end{aligned}$$
(25)

The metric of background is chosen to be the Lifshitz metric (24) i.e.

$$\begin{aligned} X_{0}(R)=\frac{r(R)^{2z}}{l^{2z}}, \quad Y_{0}(R)=\frac{r(R)^{2}}{ l^{2}}. \end{aligned}$$
(26)

The quasilocal conserved mass can be obtained through

$$\begin{aligned} M= & {} \frac{1}{8\pi }\int _{\mathcal {B}}d^{2}\varphi \sqrt{\sigma }\bigg \{ \left( K_{ab}-Kh_{ab}\right) \nonumber \\&-\left( K_{ab}^{0}-K^{0}h_{ab}^{0}\right) \bigg \} n^{a}\xi ^{b}, \end{aligned}$$
(27)

where \(\sigma \) is the determinant of the boundary \(\mathcal {B}\) metric, \( K_{ab}^{0}\) is the background extrinsic curvature, \(n^{a}\) is the timelike unit normal vector to the boundary \(\mathcal {B}\) and \(\xi ^{b}\) is a timelike Killing vector field on the boundary surface. Applying the above modified BY formalism, the mass of the space-time per unit volume \({\omega _{n-1}}\) can be calculated as

$$\begin{aligned} M=\frac{(n-1)m}{16\pi l^{z+1}}, \end{aligned}$$
(28)

where the mass parameter m can be obtained from the fact that \(f(r_{+})=0\) as

$$\begin{aligned} m{(r_{+})=}\left\{ \begin{array}{ll} \begin{array}{l} r_{+}^{n+z-1}+\frac{(n-2)^{2}l^{2}r_{+}^{n+z-3}}{(n+z-3)^{2}}+\frac{ 4b^{2z-2}l^{2}\beta ^{2}(1-\Upsilon _{+})}{(n-1)(n-z+1)r_{+}^{z-n-1}} \\ +\frac{4q^{2}b^{2z-2}l^{2z}\Upsilon _{+}}{(n+z-3)(n-z+1)r_{+}^{n+z-3}} \mathbf {F}\left( 1,\frac{2n+z-4}{2n-2},\frac{3n+z-5}{2n-2},1-\Upsilon _{+}^{2}\right) \end{array} &{} \text {for }z\ne n+1 ,\\ &{} \\ r_{+}^{2n}+\frac{(n-2)^{2}l^{2}r_{+}^{2n-2}}{4(n-1)^{2}}-\frac{4\beta ^{2}b^{2n}l^{2}}{(n-1)^{2}}\left[ 1-\Upsilon _{+}+\ln \left( \frac{ 1+\Upsilon _{+}}{2}\right) \right] &{} \text {for }z=n+1. \end{array} \right. \end{aligned}$$
(29)

Now, we turn to a calculation of the electric charge of the solution. Using the Gauss law, we can calculate the electric charge via

$$\begin{aligned} Q=\frac{\,{1}}{4\pi }\int r^{n-1}L_{F}F_{\mu \nu }n^{\mu }u^{\nu }\mathrm{d}{\Omega }, \end{aligned}$$
(30)

where

$$\begin{aligned}&n^{\mu }=\frac{1}{\sqrt{-g_{tt}}}\mathrm{d}t=\frac{l^{z}}{r^{z}\sqrt{f(r)}}\mathrm{d}t, \\&u^{\nu }=\frac{1}{\sqrt{g_{rr}}}\mathrm{d}r=\frac{r\sqrt{f(r)}}{l}\mathrm{d}r, \end{aligned}$$

are, respectively, the unit spacelike and timelike normals to the hypersurface of radius r. Using (30), the charge per unit volume \(\omega _{n-1} \) can be computed as

$$\begin{aligned} Q=\frac{ql^{z-1}}{4\pi }. \end{aligned}$$
(31)

The electrostatic potential difference (U) between the horizon and infinity is defined as

$$\begin{aligned} U=A_{\mu }\chi ^{\mu }\left| _{r\rightarrow \infty }-A_{\mu }\chi ^{\mu }\right| _{r=r_{+}}. \end{aligned}$$
(32)

Using Eqs. (22) and (32), one can obtain the electric potential

$$\begin{aligned} U=\frac{qb^{2z-2}}{(n+z-3)r_{+}^{n+z-3}}\mathbf {F}\left( \frac{1}{2},\frac{ n+z-3}{2n-2},\frac{3n+z-5}{2n-2},1-\Upsilon _{+}^{2}\right) , \end{aligned}$$
(33)

which is the same for the cases \(z=n+1\) and \(z\ne n+1\). In order to investigate the first law of black hole thermodynamics, we should obtain the Smarr-type formula for mass (28). With Eqs. (29), (31) and (21) at hand, the mass can be written as a function of the extensive thermodynamic quantities S and Q in the form of

$$\begin{aligned} M\left( S,Q\right) {=}\left\{ \begin{array}{ll} \begin{array}{l} \frac{(n-1)\left( 4S\right) ^{(n+z-1)/(n-1)}}{16\pi l^{z+1}}+\frac{\left( n-1\right) (n-2)^{2}(4S)^{(n+z-3)/(n-1)}}{16\pi l^{z-1}\left( n+z-3\right) ^{2}}+\frac{\beta ^{2}\left( 4S\right) ^{(n-z+1)/(n-1)}( 1-\Gamma ) }{4\pi {l}^{z-1}{b}^{2(1-\,z)}(n-z+1)} \\ +\frac{4(n-1)\pi Q^{2}{b}^{2z-2}l^{1-z}\Gamma }{(n+z-3)(n-z+1)\left( 4S\right) ^{\left( n+z-3\right) /(n-1)}}{}\mathbf {F}\left( 1,\frac{2n+z-4}{ 2n-2},\frac{3n+z-5}{2n-2},1-\Gamma ^{2}\right) , \end{array} &{} \text {for }z\ne n+1, \\ &{} \\ \frac{(n-1)\left( 4S\right) ^{2n/(n-1)}}{16\pi l^{n+2}}+\frac{(n-2)^{2}S^{2} }{4\pi (n-1)l^{n}}-\frac{\beta ^{2}b^{2n}}{4\pi (n-1)l^{n}}\left[ 1-\Gamma +\ln \left( \frac{1+\Gamma }{2}\right) \right] , &{} \text {for }z=n+1, \end{array} \right. \end{aligned}$$
(34)

where \(\Gamma =\sqrt{1+\pi ^{2}Q^{2}/(\beta ^{2}S^{2})}\). Calculations show that intensive quantities

$$\begin{aligned} T=\left( \frac{\partial M}{\partial S}\right) _{Q}\quad \text {and} \quad U=\left( \frac{\partial M}{\partial Q}\right) _{S}, \end{aligned}$$
(35)

coincide with those computed by Eqs. (19) and (33). Therefore, the thermodynamics quantities satisfy the first law of thermodynamics,

$$\begin{aligned} \mathrm{d}M=T\mathrm{d}S+U\mathrm{d}Q, \end{aligned}$$
(36)

for the two solutions \(z=n+1\) and \(z\ne n+1\).

In the next part of this section, we will discuss the Hawking–Page and inside black hole phase transitions for our Lifshitz solutions.

3.2 Black hole phase transitions

3.2.1 Hawking–Page phase transition

Fig. 2
figure 2

The behavior of T versus S for \(l=1\), \(b=1\)

Full size image
Fig. 3
figure 3

The behavior of G versus T for linearly charged case with \(l=1\), \(b=1\) and \(n=3\)

Full size image
Fig. 4
figure 4

The behavior of G versus T for nonlinearly charged case with \( l=1\), \(b=1\) and \(n=3\)

Full size image

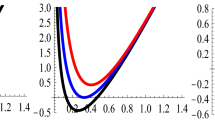
As it is clear from Fig. 1, there are some parameter choices for which we have extreme black holes and therefore zero temperature. In addition, as one can see from Fig. 2, there are some other choices of the parameters that show a non-zero positive minimum for temperature \(T_{\min }\). The influences of different parameters on \(T_{\min }\) can be seen from Fig. 2. When we increase the dimension n, \(T_{\min }\) increases too, while it decreases with increasing z. Comparing Fig. 2a and b, one finds that the effect of nonlinearity implies increasing in \(T_{\min }\). The behaviors illustrated in Fig. 2 show a Hawking–Page phase transition for the obtained solutions. Let us have a closer look on Fig. 2. In the first part of the T–S curves where we have small black holes (note that \(S=r_{+}^{n-1}/4\)), \(\partial T/\partial S<0\), which implies negative heat capacity and therefore small black holes are thermally unstable. But in the large black hole part of the curves we have a positive heat capacity and therefore large black holes are thermally stable. In addition to small and large black holes, we have a thermal Lifshitz or radiation solution too. Since small black holes are thermally unstable, the system has a choice between large black hole and thermal Lifshitz solutions and chooses one of them according to the Gibbs free energy. The Gibbs free energy,

$$\begin{aligned} G\left( T,U\right) =M-TS-QU, \end{aligned}$$
(37)

can be obtained by using (19), (21), (28), (31) and (33). Figures 3 and 4 show the behavior of the Gibbs free energy for some choices of the parameters. The two up and bottom branches correspond to small and large black holes, respectively. The positive Gibbs free energy shows that the system is in a radiation phase, while there is a Hawking–Page phase transition at the intersection point of the bottom branch and \(G=0\). This fact that the Gibbs free energy of large black holes always has the lower energy in comparison to small ones confirms the above arguments as regards their thermal stability. As one moves rightward on the temperature axis in the G–T diagram, first one has the radiation regime or the thermal Lifshitz solution for which \(G>0\). At \(G=0\), the Hawking–Page phase transition between the thermal Lifshitz case and large black holes occurs, and for \( G<0 \) we are at the large black hole phase. The temperature at which the phase transition occurs is called the Hawking–Page temperature \(T_\mathrm{HP}\). The effects of a change in the electric potential U, the critical exponent z and the nonlinearity parameter \(\beta \) can be seen from Figs. 3 and 4. Increasing the electric potential U and the critical exponent z makes \(T_\mathrm{HP}\) lower. Also, the lower the nonlinearity parameter \(\beta \) is, the lower the Hawking–Page temperature \(T_\mathrm{HP}\) is. Note that a lower \(\beta \) makes the electrodynamics more affected by nonlinearity.

3.2.2 Phase transitions inside the black hole

There are at least three well-known ways to discuss the phase transitions inside the black hole. Two of these ways are based on the macroscopic point of view and one of them is based on the microscopic viewpoint. The two macroscopic ways are Davies [24] and Landau–Lifshitz [28, 29] methods, which discuss, respectively, the behavior of heat capacities and thermodynamic fluctuations. Thermodynamic geometry or Ruppeiner geometry [16, 20, 21] is the microscopic way; it discusses the phase transitions in addition to type and strength of interactions. In what follows, we discuss the relation between the phase transitions predicted by Ruppeiner geometry and the Davies method. Next, we will turn to the Landau–Lifshitz theory of thermodynamic fluctuations.

3.2.3 Ruppeiner and Davies phase transitions

In order to discuss thermodynamic geometry, one should study the divergences, sign and magnitude of Ricci scalar corresponding to Ruppeiner metric (usually called Ruppeiner invariant) to determine phase transitions and strength and type of dominated interaction between possible black hole molecules [16, 20, 21]. To do that, we define the Ruppeiner metric in (M, Q) space where the entropy S is the thermodynamic potential,

$$\begin{aligned} g_{\alpha \beta }=-\frac{\partial ^{2}S}{\partial X^{\alpha }\partial X^{\beta }}, \quad X^{\alpha }=(M,Q). \end{aligned}$$
(38)

The above metric can also be rewritten in the Weinhold form,

$$\begin{aligned} g_{\alpha \beta }=\frac{1}{T}\frac{\partial ^{2}M}{\partial Y^{\alpha }\partial Y^{\beta }}, \quad Y^{\alpha }=(S,Q). \end{aligned}$$
(39)

The Ruppeiner invariant corresponding to (39) can be expressed in a general form as

$$\begin{aligned} \mathfrak {R}=\frac{\mathfrak {N}(S,Q)}{\mathfrak {D}(S,Q)}, \end{aligned}$$
(40)

where \(\mathfrak {N}\) and \(\mathfrak {D}\) stand for the numerator and the denominator of \(\mathfrak {R}\). The divergences of the Ruppeiner invariant is determined by the roots of \(\mathfrak {D}\), equal to \(T\left[ \mathbf {H}_{S,Q}^{M} \right] ^{2}\) where \(\mathbf {H}_{S,Q}^{M}=M_{SS}M_{QQ}-M_{SQ}^{2}\) is the determinant of the Hessian matrix and \(X_{YZ}=\partial ^{2}X/\partial Y\partial Z \). Of course, at these divergence points the numerator \(\mathfrak {N}\) should be finite. These divergences show both zero temperature and vanishing \(\mathbf {H}_{S,Q}^{M}\). The root of \(\mathbf {H}_{S,Q}^{M}\) may show the boundary between thermal stability and instability. For thermal stability, in addition to positivity of the determinant of the Hessian, \(M_{QQ}\) and \( M_{SS}\) should be positive too [100, 101].

It is remarkable that at the point where \(M_{SS}\) vanishes or equivalently heat capacity at constant charge \(C_{Q}\) diverges, we have a thermally unstable system due to negativity of \(\mathbf {H}_{S,Q}^{M}\) if \( M_{SQ}\ne 0\) (which occurs in many black hole systems). Thus, the heat capacity at constant charge \(C_{Q}\) cannot be a suitable thermodynamic quantity to show the phase transition of such systems when we have two changing thermodynamic parameters, for instance S and Q. There is some work in the literature (for instance [102]) in which the correctness of the Ruppeiner method for recognizing the phase transitions has been judged by comparing the Ruppeiner and \(C_{Q}\) transition points. This procedure of course seems to be incorrect according to what we pointed out above. Also, as we discussed in the introduction, the divergences of \(\mathfrak {R}\) are safer if we determine phase transitions. On the other hand, in [43, 48], the authors have suggested some suitable thermodynamic quantities to show the phase transitions predicted by the Ruppeiner invariant. These quantities are the specific heat at constant electrical potential, \(C_{U}\), the analog of the volume expansion coefficient, \(\alpha \), and the analog of the isothermal compressibility coefficient \(\kappa _{T}\) defined as

$$\begin{aligned} C_{U}=T\left( \frac{\partial S}{\partial T}\right) _{U}\text {, } \quad \alpha = \frac{1}{Q}\left( \frac{\partial Q}{\partial T}\right) _{U},\ \ \ \kappa _{T}=\frac{1}{Q}\left( \frac{\partial Q}{\partial U}\right) _{T}\text {.} \end{aligned}$$
(41)

As one can see in the Appendix, these thermodynamic quantities have the forms

$$\begin{aligned} C_{U}=T\frac{M_{SS}}{\mathbf {H}_{S,Q}^{M}}, \quad \alpha =-\frac{1}{ Q}\frac{M_{SQ}}{\mathbf {H}_{S,Q}^{M}},\ \ \ \kappa _{T}=-\alpha \left. \frac{ \partial T}{\partial U}\right| _{Q}. \end{aligned}$$
(42)

It is obvious that these quantities show the same phase transitions as the Ruppeiner geometry because all of them diverge at roots of \(\mathbf {H} _{S,Q}^{M}\) and \(C_{U}\) vanishes at zero temperature where \(\mathfrak {R}\) diverges. To show the coincidence of the Ruppeiner phase transitions and \(C_{U}\) divergences, some proofs have been presented in [50, 54]. The above quantities can be considered as improved Davies quantities [24] which show the phase transitions to coincide with the Ruppeiner ones. In the next part, we study the Landau–Lifshitz theory of thermodynamic fluctuations to explore the possible signature of black hole phase transitions and the properties of black hole radiance.

3.2.4 Landau–Lifshitz theory (non-extreme/extreme phase transition)

Here, we seek any possible effect of a transition on black hole radiance by using the Landau–Lifshitz theory of thermodynamic fluctuations [28, 29]. We focus on the (\(3+1\))-dimensional linearly charged case. The extension to higher-dimensional or nonlinearly charged cases is trivial and gives no novel result. Based on Landau–Lifshitz theory [28, 29], in a fluctuation–dissipative process, the flux \(\dot{X}_{i}\) of a given thermodynamic quantity \(X_{i}\) is given by

$$\begin{aligned} \dot{X}_{i}=-\sum _{j}\Gamma _{ij}\chi _{j}, \end{aligned}$$
(43)

where a dot shows the temporal derivative and \(\chi _{i}\) and \(\Gamma _{ij}\) are, respectively, the thermodynamic force conjugate to the flux \(\dot{X}_{i}\) and the phenomenological transport coefficients. In addition, the rate of entropy production is expressed by

$$\begin{aligned} \dot{S}=\sum _{i}\pm \chi _{i}\dot{X}_{i}, \end{aligned}$$
(44)

where “\(+\)” (“−”) holds for the entropy rate contributions which come from the non-concave (concave) parts of S. The second moments corresponding to the flux fluctuations are (we set \(k_{B}=1\))

$$\begin{aligned} \left\langle \delta \dot{X}_{i}\delta \dot{X}_{j}\right\rangle =\left( \Gamma _{ij}+\Gamma _{ji}\right) \delta _{ij}, \end{aligned}$$
(45)

where the mean value with respect to the steady state is denoted by the angular brackets and the fluctuations \(\delta \dot{X}_{i}\) are the spontaneous deviations from the value of steady state \(\left\langle \dot{X} _{i}\right\rangle \). To guarantee that the correlations are zero when two fluxes are independent, the Kronecker \(\delta _{ij}\) is put in Eq. (45).

According to [71], the mass M, electric potential energy U and temperature T can be obtained for (\(3+1\))-dimensional linearly charged case as

$$\begin{aligned} M=\frac{(4S)^{(z+2)/2}}{8\pi l^{z+1}}+\frac{(4S)^{z/2}}{8\pi z^{2}l^{z-1}}+ \frac{2\pi Q^{2}b^{2z-2}}{zl^{z-1}(4S)^{z/2}}, \end{aligned}$$
(46)
$$\begin{aligned} U=\frac{\pi b^{2z-2}Q}{z2^{z-2}l^{z-1}S^{z/2}}\quad \text {and} \quad T=\frac{2^{z-4}\Xi }{\pi zl^{z-1}S^{z/2+1}}, \end{aligned}$$
(47)

where

$$\begin{aligned} \Xi =S^{z}+4z(z+2)S^{z+1}l^{-2}-4^{2-z}z\pi ^{2}b^{2z-2}Q^{2}. \end{aligned}$$

We know that in extreme black hole case, the Hawking temperature on the event horizon vanishes and therefore in this case we have \(\Xi =0\). Using Eq. (46), we can obtain the entropy production rate as

$$\begin{aligned} \dot{S}(M,Q)=\chi _{M}\dot{M}-\chi _{Q}\dot{Q}, \end{aligned}$$
(48)

where

$$\begin{aligned} \chi _{M}=\frac{\pi zl^{z-1}S^{z/2+1}}{2^{z-4}\Xi }\quad \text {and}\quad \chi _{Q}= \frac{\pi ^{2}b^{2z-2}QS}{4^{z-2}\Xi }. \end{aligned}$$

The mass loss rate is given by [103]

$$\begin{aligned} \frac{\mathrm{d}M}{\mathrm{d}t}=-b\alpha \sigma T^{4}+U\frac{\mathrm{d}Q}{\mathrm{d}t}. \end{aligned}$$
(49)

The first term on the right side of Eq. (49) is the thermal mass loss corresponding to Hawking radiation, which is just the Stefan–Boltzmann law, with \(b=\pi ^{2}/15\) (we set \(\hbar =1\)) as the radiation constant. The constant \(\alpha \) depends on the number of species of massless particles and the quantity \(\sigma \) is the cross-section of geometrical optics. The second term on the right side of Eq. (49) is responsible for the loss of mass corresponding to charged particles. In fact, it is the \(U\mathrm{d}Q\) term which arises in the first law of black hole mechanics.

With references to what was explained and computed above, one can calculate the second moments or correlation functions of the thermodynamical quantities,

$$\begin{aligned} \left\langle \delta \dot{M}\delta \dot{M}\right\rangle= & {} -\frac{2^{z-3}\Xi }{ \pi zl^{z-1}S^{z/2+1}}\dot{M},\quad \left\langle \delta \dot{Q} \delta \dot{Q}\right\rangle =\frac{2^{2z-5}b^{2-2z}\Xi }{\pi ^{2}SQ}\dot{Q}, \nonumber \\ \left\langle \delta \dot{M}\delta \dot{Q}\right\rangle= & {} U\left\langle \delta \dot{Q}\delta \dot{Q}\right\rangle , \end{aligned}$$
(50)
$$\begin{aligned} \left\langle \delta \dot{S}\delta \dot{S}\right\rangle= & {} \frac{\pi ^{2}z^{2}l^{2z-2}S^{z+2}}{4^{z-4}\Xi ^{2}}\left[ \left\langle \delta \dot{M} \delta \dot{M}\right\rangle +\frac{\pi ^{2}b^{4z-4}Q^{2}}{ 4^{z-2}z^{2}l^{2z-2}S^{z}}\right. \nonumber \\&\times \left. \left\langle \delta \dot{Q}\delta \dot{Q} \right\rangle -\frac{\pi b^{2z-2}Q}{2^{z-3}zl^{z-1}S^{z/2}}\left\langle \delta \dot{M}\delta \dot{Q}\right\rangle \right] \nonumber \\= & {} -\frac{\pi zl^{z-1}S^{z/2+1}}{2^{z-5}\Xi }\left[ \dot{M}+\frac{\pi b^{2z-2}Q}{z2^{z-2}l^{z-1}S^{z/2}}\dot{Q}\right] , \end{aligned}$$
(51)
$$\begin{aligned} \left\langle \delta \dot{T}\delta \dot{T}\right\rangle= & {} \frac{\left[ (z-2)S^{z}+4z^{2}(z+2)l^{-2}S^{z+1}+\pi ^{2}z(z+2)4^{2-z}b^{2z-2}Q^{2}\right] ^{2}}{4S^{2}\Xi ^{2}}\nonumber \\&\left\langle \delta \dot{M}\delta \dot{M}\right\rangle \nonumber \\&+\frac{4^{2-z}\pi ^{2}b^{4z-4}Q^{2}\left[ (z-1)S^{z}+4z^{2}(z+2)l^{-2}S^{z+1}+\pi ^{2}z4^{2-z}b^{2z-2}Q^{2}\right] ^{2} }{z^{2}l^{2z-2}S^{z+2}\Xi ^{2}}\nonumber \\&\left\langle \delta \dot{Q}\delta \dot{Q} \right\rangle \nonumber \\&-\frac{\pi b^{2z-2}Q\left[ (z-1)S^{z}+4z^{2}(z+2)l^{-2}S^{z+1}+\pi ^{2}z4^{2-z}b^{2z-2}Q^{2}\right] \left[ (z-2)S^{z}+4z^{2}(z+2)l^{-2}S^{z+1}+ \pi ^{2}z(z+2)4^{2-z}b^{2z-2}Q^{2}\right] }{z2^{z-2}l^{z-1}S^{z/2+2}\Xi ^{2}}\nonumber \\&\left\langle \delta \dot{M}\delta \dot{Q}\right\rangle \nonumber \\= & {} -\frac{2^{z-5}}{\pi zl^{z-1}S^{z/2+3}\Xi }\left\{ \left[ (z-2)S^{z}+4z^{2}(z+2)l^{-2}S^{z+1}\right. \right. \nonumber \\&+\left. \left. \pi ^{2}z(z+2)4^{2-z}b^{2z-2}Q^{2}\right] ^{2}\dot{M}\right. \nonumber \\&\left. -\frac{\pi b^{2z-2}Q}{2^{z-4}zl^{z-1}S^{z/2}}\left[ (z-1)S^{z}+4z^{2}(z+2)l^{-2}S^{z+1}\right. \right. \nonumber \\&+\left. \left. \pi ^{2}z4^{2-z}b^{2z-2}Q^{2}\right] \left[ S^{z}-16\pi ^{2}4^{-z}Q^{2}b^{2z-2}z(z+1)\right] \dot{Q}\right\} , \end{aligned}$$
(52)
$$\begin{aligned} \left\langle \delta \dot{S}\delta \dot{T}\right\rangle= & {} \frac{\pi zS^{z/2} \left[ (z-2)S^{z}+4z^{2}(z+2)l^{-2}S^{z+1}+\pi ^{2}z(z+2)4^{2-z}b^{2z-2}Q^{2} \right] }{2^{z-3}l^{z-1}\Xi ^{2}}\nonumber \\&\left\langle \delta \dot{M}\delta \dot{M} \right\rangle \nonumber \\&+\frac{\pi ^{3}b^{4z-4}Q^{2}\left[ (z-1)S^{z}+4z^{2}(z+2)l^{-2}S^{z+1}+\pi ^{2}z4^{2-z}b^{2z-2}Q^{2}\right] }{z2^{3z-8}l^{z-1}S^{z/2}\Xi ^{2}}\nonumber \\&\left\langle \delta \dot{Q}\delta \dot{Q}\right\rangle \nonumber \\&-\frac{\pi ^{2}b^{2z-2}Q\left[ (3z-4)S^{z}+12z^{2}(z+2)l^{-2}S^{z+1}+\pi ^{2}z(z+4)4^{2-z}b^{2z-2}Q^{2}\right] }{2^{2z-5}\Xi ^{2}}\nonumber \\&\left\langle \delta \dot{M}\delta \dot{Q}\right\rangle \nonumber \\= & {} -\frac{\left[ (z-2)S^{z}+4z^{2}(z+2)l^{-2}S^{z+1}+\pi ^{2}z(z+2)4^{2-z}b^{2z-2}Q^{2}\right] }{l^{2z-2}S\Xi }\nonumber \\&\times \left[ \dot{M}+\frac{ \pi b^{2z-2}l^{z-1}Q}{2^{z-2}zS^{\frac{1}{2}z}}\dot{Q}\right] . \end{aligned}$$
(53)

It is clear that the second moments \(\left\langle \delta \dot{S}\delta \dot{S} \right\rangle \), \(\left\langle \delta \dot{T}\delta \dot{T}\right\rangle \) and \(\left\langle \delta \dot{S}\delta \dot{T}\right\rangle \) diverge for the extreme black hole case where \(\Xi \) vanishes (see Eq. 47). It means that there is a phase transition in this case. This phase transition is between extreme and non-extreme black holes for which we have a sudden change in emission properties. In the non-extreme case, the black hole can give off particles and radiation through both spontaneous Hawking emission and superradiant scattering, whereas in the extreme case, the black hole can just radiate via superradiant scattering.

As one can see from Eq. (49), \(\dot{M}\) and \(\dot{Q}\) are related. Therefore, all of the above second moments can be reexpressed in terms of \( \dot{Q}\). Let us calculate \(\dot{Q}\) for our case. The rate of charge loss can be stated as

$$\begin{aligned} -\frac{\mathrm{d}Q}{\mathrm{d}t}=e\int _{r_{+}}^{\infty }\int _{0}^{2\pi }\int _{0}^{\pi }\sqrt{-g }\Gamma \mathrm{d}\theta \mathrm{d}\phi \mathrm{d}r, \end{aligned}$$
(54)

where \(\Gamma \) is the rate of electron–positron pair creation per four-volume and e is charge of electron. According to Schwinger’s theory [104] for (\(3+1\)) dimensions, the rate of electron–positron pair creation in a constant electric field E is

$$\begin{aligned} \Gamma =\frac{4e^{2}b^{4z-4}}{\pi l^{2z-2}}E^{2}\exp \left( -\frac{1}{EQ_{0}} \right) \left[ 1+O\left( \frac{e^{3}E}{m^{2}}\right) +\cdots \right] , \end{aligned}$$
(55)

where \(Q_{0}=4\pi eb^{2z-2}/\pi m^{2}l^{z-1}\) and m is the mass of electron. In the presence of linear Maxwell electrodynamics, the electric field is \(E=Q/r^{z+1}\) and therefore

$$\begin{aligned} \Gamma= & {} \frac{4e^{2}b^{4z-4}Q^{2}}{\pi l^{2z-2}r^{2z+2}}\exp \left( -\frac{ r^{z+1}}{QQ_{0}}\right) \nonumber \\&\times \left[ 1+O\left( \frac{e^{3}Q}{m^{2}r^{z+1}}\right) +\cdots \right] . \end{aligned}$$
(56)

Combining Eqs. (55) and (56), we arrive at

$$\begin{aligned} \frac{\mathrm{d}Q}{\mathrm{d}t}=-\frac{16e^{3}b^{4z-4}Q^{(z+2)/(z+1)}}{ (z+1)l^{3z-3}Q_{0}^{z/(z+1)}}\Gamma \left[ -\frac{z}{z+1},\frac{r_{+}^{z+1}}{ QQ_{0}}\right] , \end{aligned}$$
(57)

where \(\Gamma \left[ a,b\right] \) is incomplete gamma function. When \( r_{+}\gg Q\), Eq. (57) reduces to

$$\begin{aligned} \frac{\mathrm{d}Q}{\mathrm{d}t}\approx -\frac{64e^{4}b^{6z-6}Q^{3}}{ (z+1)m^{2}l^{4z-4}r_{+}^{2z+1}}\exp \left( -\frac{r_{+}^{z+1}}{QQ_{0}} \right) +\cdots , \end{aligned}$$
(58)

where we have used

$$\begin{aligned} \Gamma \left[ -\frac{z}{z+1},x\right]\approx & {} \exp \left( -x\right) x^{1/(z+1)}\nonumber \\&\times \left[ \frac{1}{x^{2}}+O\left( \frac{1}{x^{3}}\right) +\cdots \right] , \end{aligned}$$
(59)

in which \(x^{-1}\ll 1\).

In the following section, we turn to the study of thermodynamic geometry of our black hole solutions to figure out the behavior of the black hole’s possible molecules and phase transitions.

4 Ruppeiner geometry

In this section we study thermodynamic geometry of the Lifshitz–dilaton black holes for linearly Maxwell and nonlinearly BI gauge fields, separately. We have introduced this method in Sect. 3.2.2 with focus on the study of the phase transitions which occur at divergence of the Ruppeiner invariant \(\mathfrak {R}\). In addition to divergences, \(\mathfrak {R} \) has other properties which give us information about thermodynamic of the system. The sign of \(\mathfrak {R}\) gives us the information about the dominated interaction between possible black hole molecules, while its magnitude measures the average number of correlated Planck areas on the event horizon [16, 19,20,21]. \(\mathfrak {R}>0\) means the domination of repulsive interaction, \(\mathfrak {R}<0\) shows the attraction dominated regime and when \(\mathfrak {R}\) vanishes the system behaves like an ideal gas i.e. there is no interaction. In the following, we first study thermodynamic geometry in the presence of linear Maxwell electrodynamics. Then we extend our study to nonlinearly charged black holes where BI electrodynamics has been employed. There is just a necessary comment. As we stated before in Sect. 3.2.2, for thermal stability, \(M_{QQ}\), \(M_{SS}\) and \(\mathbf {H} _{S,Q}^{M}=M_{SS}M_{QQ}-M_{SQ}^{2}\) should be positive [100, 101]. One can show that the positivity of \(\mathbf {H} _{S,Q}^{M}\) and \(M_{QQ}\) (\(M_{SS}\)) imposes the positivity of \( M_{SS}\) (\(M_{QQ}\)). Therefore, we just turn to the study of the signs of \(\mathbf {H} _{S,Q}^{M}\) and \(M_{QQ}\) in the following discussions to guarantee the thermal stability.

4.1 Linear Maxwell case

The mass and Hawking temperature of black holes in the presence of linear Maxwell (LM) electrodynamics are

$$\begin{aligned} T_{LM}= & {} \frac{(n+z-1)r_{+}^{z}}{4\pi l^{z+1}}+\frac{ (n-2)^{2}l^{1-z}}{4\pi (n+z-3)r_{+}^{2-z}}\nonumber \\&-\frac{q^{2}l^{z-1}b^{2z-2}}{2\pi (n-1)r_{+}^{2n+z-4}}, \end{aligned}$$
(60)
$$\begin{aligned} M_{LM}(S,Q)= & {} \frac{(n-1)(4S)^{(n+z-1)/(n-1)}}{16\pi l^{z+1}}\nonumber \\&+\frac{ (n-1)(n-2)^{2}(4S)^{(n+z-3)/(n-1)}}{16\pi (n+z-3)^{2}l^{z-1}}\nonumber \\&+\frac{2\pi Q^{2}b^{2z-2}(4S)^{(3-n-z)/(n-1)}}{(n+z-3)l^{z-1}}. \end{aligned}$$
(61)

As we mentioned above, for investigating thermal stability we need to check the signs of \(M_{QQ}\) and \(\mathbf {H}_{S,Q}^{M}\). In our case

$$\begin{aligned} M_{QQ}=\frac{\pi b^{2z-2}S^{-\left( n+z-3\right) /\left( n-1\right) }}{ \left( n+z-3\right) l^{z-1}2^{2\left( z-2\right) /\left( n-1\right) }}>0. \end{aligned}$$
(62)

Thus, in order to disclose the thermal stability of system, we need to study the sign of the determinant of the Hessian matrix. We find

$$\begin{aligned} \mathbf {H}_{S,Q}^{M}=\left\{ \begin{array}{ll} \frac{(z-2)(n-2)^{2}b^{2z-2}S^{-2\left[ 2+(z-2)/(n-1)\right] }}{ 4(n-1)(n+z-3)^{2}l^{2z-2}}\mathfrak {F}(S,Q) &{} z\ne 2 \\ &{} \\ \frac{(n+1)b^{2}2^{(n-5)/(1-n)}S^{2(n-2)/(1-n)}}{(n-1)^{2}l^{4}} &{} z=2 \end{array} \right. , \end{aligned}$$
(63)

where

$$\begin{aligned} \mathfrak {F}(S,Q)\equiv & {} \bigg [ S^{2[1+(z-2)/(n-1)]}\nonumber \\&+\frac{ z(n+z-3)(n+z-1)S^{2[1+(z-1)/(n-1)]}}{2^{-4/(n-1)}(z-2)(n-2)^{2}l^{2}}\nonumber \\&-\frac{ \pi ^{2}(n+z-3)Q^{2}2^{(n-4z+7)/(n-1)}}{(n-1)(n-2)^{2}b^{2(1-z)}}\bigg ]. \end{aligned}$$
(64)

The numerator \(\mathfrak {N}\) of (40) is a complicated finite function of S and Q in this case, including long terms that we do not express explicitly for brevity. However, as mentioned in Sect. 3.2.2, one can find the denominator \(\mathfrak {D}\) in the form of

$$\begin{aligned} \mathfrak {D}(S,Q)=T_{LM}\left[ \mathbf {H}_{S,Q}^{M}\right] ^{2}, \end{aligned}$$
(65)

where \(T_{LM}\) and \(\mathbf {H}_{S,Q}^{M}\) have been give in (60) and (63), respectively.

Having Eqs. (63) and (65) at hand, we are in a position to investigate the divergences of \(\mathfrak {R}\), which play the central role in thermodynamic geometry discussions, and also thermal stability of system. As one can see from Eqs. (63) and (65), for \(z=2\), the divergences occur just in the case of the extremal black holes where \( T_{LM}=0\). For \(z\ne 2\), in addition to extremal black hole case, \( \mathfrak {R}\) diverges in zeros of (63). In the latter case, we can calculate the corresponding temperature by solving \(\mathfrak {F}=0\) for Q and then putting this Q in Eq. (60) to arrive at

$$\begin{aligned} \mathcal {T}=\frac{(n+z-1)2^{(2z-n+1)/(n-1)}S^{z/(n-1)}}{\pi (2-z)l^{z+1}}. \end{aligned}$$
(66)
Fig. 5
figure 5

The behavior of \(\mathbf {H}_{S,Q}^{M}\) versus T for the linear Maxwell case with \(l=b=1\)

Full size image
Fig. 6
figure 6

The behavior of the Ruppeiner invariant \(\mathfrak {R}\) versus T for the linear Maxwell case with \(l=b=1\)

Full size image

The above temperature is negative for \(z>2\) i.e. there is no black hole at this diverging point and therefore the divergences of \(\mathfrak {R}\) occur just for extremal black hole case when \(z>2\). However, for \(z<2\) when \( \mathcal {T}>0\), we can see an upper limit in entropy and charge of system. The largest entropy S for which \(\mathfrak {F}=0\) (which we call it critical entropy \(S_{c}\)) can be calculated by finding the extremum point where \(\partial \mathfrak {F/}\partial S=0\) as

$$\begin{aligned} S_{c}^{2/(1-n)}=\frac{z(n+z-1)(n+z-2)2^{4/(n-1)}}{(2-z)(n-2)^{2}l^{2}}, \end{aligned}$$
(67)

at which

$$\begin{aligned} Q_{c}^{2}= & {} \frac{(n-2)^{2(n+z-2)}}{l^{-2(n+z-3)}b^{2(z-1)}\pi ^{2}}\nonumber \\&\times \frac{ (n-1)(n+z-2)^{2-n-z}(n+z-1)^{3-n-z}}{2^{5}(n+z-3)}\nonumber \\&\times \left( \frac{2}{z} -1\right) ^{n+z-3} \end{aligned}$$
(68)

and

$$\begin{aligned} \left. \frac{\partial ^{2}\mathfrak {F}}{\partial S^{2}}\right| _{S=S_{c}}= & {} -\frac{\left( n+z-3\right) 4^{\left( n-2z+3\right) /\left( n-1\right) }}{\left( n-1\right) ^{2}}\nonumber \\&\times \left[ \frac{\left( n+z-1\right) \left( n+z-2\right) z}{\left( 2-z\right) \left( n-2\right) ^{2}l^{2}}\right] ^{2-z}<0. \end{aligned}$$
(69)

One should note that the absolute value of \(Q_{c}\) is also the largest charge value which satisfies \(\mathfrak {F}=0\). Another remark to be mentioned is that (67) imposes an upper limit on the size of black hole too (see (21)). At this point, the corresponding temperature can be obtained:

$$\begin{aligned} T_{c}=\frac{(n-2)^{z}}{2\pi l\sqrt{\left( z(n+z-2)\right) ^{z}}}\left( \frac{ n+z-1}{2-z}\right) ^{(2-z)/2}. \end{aligned}$$
(70)

For charges greater than \(Q_{c}\), the Ruppeiner invariant diverges only in the case of extremal black holes. For \(Q=Q_{c}\), in addition to \(T_{LM}=0\), we have one other divergence in \(\mathfrak {R}\) specified by (67) and (70). For \(Q<Q_{c}\), in addition to \(T_{LM}=0\), we have at most two other divergences, since the order of the polynomial in terms of S is always lower than 3 for \(n\ge 3\) and \(z<2\). One should note that, in the latter case, the temperature region between two divergences is not allowed since \( \mathbf {H}_{S,Q}^{M}<0\) (Fig. 5).

Fig. 7
figure 7

The behavior of the Ruppeiner invariant \(\mathfrak {R}\) versus T for the linear Maxwell case with \(l=b=1\)

Full size image

We have summarized the above discussion in Figs. 6 and 7. These figures also show the sign of the Ruppeiner invariant for different choices of the parameters that determines the type of interaction between black hole molecules [16, 20, 21]. Figure 6a is depicted for RN-AdS case (\(n=3\), \(z=1\)). In this case, it can be seen that, for \(Q>Q_{c}\), the Ruppeiner invariant diverges only for extremal black holes. As Fig. 6a shows, there is also a range of T for which \(\mathfrak {R}<0\), namely the dominated interaction between black hole molecules is attractive. Furthermore, the interactions near zero temperature is the same as interactions of Fermi gas molecules near zero temperature [16]. According to Fig. 5a, for \(Q>Q_{c}\), \(\mathbf {H}_{S,Q}^{M}\) is positive (also \(M_{QQ}>0\) (see (62))), and therefore the system is stable for all T region. For \(Q=Q_{c}\), in addition to the zero temperature, we have another temperature (\(T_{c}\)), where a divergence of \(\mathfrak {R}\) occurs (see Fig. 6a). At zero temperature, the Ruppeiner invariant goes to \(+\infty \), while at \(T_{c}\) it goes to \(-\infty \). The latter case is similar to the Van der Waals gas phase transition at the critical point in the sense that at the phase transition temperature, \( \mathfrak {R}\) goes to \(-\infty \) [14, 21]. For \(Q=Q_{c}\), \(\mathfrak { R}\) becomes positive when we go away from the second divergence (\(T_{c}\)) on the temperature axis. In \(Q=Q_{c}\) case, \(\mathbf {H}_{S,Q}^{M}\) is positive and just vanishes at \(T_{c}\) (Fig. 5a), so, the system is always thermally stable. For \(Q<Q_{c}\), there are three divergences; one at \(T=0\), one at \(T<T_{c}\) and one at \(T>T_{c}\). In this case, according to Fig. 5a, \(\mathbf {H}_{S,Q}^{M}\) is negative in the temperature region between two roots and show instability. This not-allowed region is equivalent to the temperature region between two divergences of the Ruppeiner invariant for \(Q<Q_{c}\) (Fig. 6a). Figures 5b and 6b show the same properties for black holes with different parameters. In this case, \(T_{c}\) is greater than one of previous case while \(Q_{c}\) is lower. Figure 7 shows the behavior of the Ruppeiner invariant for \(z\ge 2\). As this figure shows, there are just divergences at \(T=0\). The properties of black hole molecular interactions (\(\mathfrak {R}>0\): Repulsion, \(\mathfrak {R}=0\): No interaction and \(\mathfrak {R}<0\): Attraction) depend on parameters such as the dimension of space time and the charge, in this case. According to Eq. (63), for \(z=2\), \(\mathbf {H} _{S,Q}^{M}\) is always positive. For \(z>2\), we can find Q from \( T_{LM}=0\) and put it in \(\mathbf {H}_{S,Q}^{M}\) to obtain

$$\begin{aligned} \mathbf {H}_{S,Q,T=0}^{M}=\frac{(n+z-1)b^{2z-2}2^{(n-5)/(1-n)}}{ (n-1)(n+z-3)l^{2z}S^{(n-2)/(n-1)}}>0. \end{aligned}$$
(71)

Thus, since \(\mathbf {H}_{S,Q}^{M}\) nowhere vanishes for \(z>2\) (see discussions below (66)) and is positive at \(T=0\) according to above equation, it is positive throughout the temperature region and therefore the system is always thermally stable for \(z>2\).

Fig. 8
figure 8

The behavior of the Ruppeiner invariant \(\mathfrak {R}\) versus T for the Born–Infeld case with \(l=b=1\)

Full size image
Fig. 9
figure 9

The behavior of the determinant of the Hessian matrix \(\mathbf {H}_{S,Q}^{M}\) versus T for the Born–Infeld case with \(l=b=1\)

Full size image

Regarding the nature of the phase transition occurring at zero temperature where the Ruppeiner invariant diverges, we discussed in previous section via Landau–Lifshitz theory of thermodynamic fluctuations. However, regarding the phase transitions occurred at divergences of \(\mathfrak {R}\) at finite temperatures, we can give some comments here. We have seen two kinds of phase transitions here for \(z<2\) (see Fig. 6) namely continuous (for \(Q=Q_{c}\) where \(\mathfrak {R}\) diverges at just one finite temperature or entropy) and discontinuous (for \(Q<Q_{c}\) where \(\mathfrak {R}\) diverges at two finite temperatures or entropies and we have a jump between these two points since there is no thermally stable black hole between them). Both of these phase transitions can be considered as small/large black holes phase transitions. The first reason for this argument is that as temperature increases, entropy or equivalently size of black hole increases (note that \( \partial S/\partial T=M_{SS}^{-1}>0\)). Therefore,on the left side of phase transition points where the temperature is lower, we have small size black holes and the right side where the temperature is higher we have large size ones. This fact can also be seen from the behavior of the Ruppeiner invariant magnitude at the two sides of the phase transitions. For small black holes, we expect a finite correlation between possible black hole molecules (of course far from phase transition points) because those are close to each other. For large black holes, we expect the correlation between possible molecules to tend to a small value near zero since molecules become approximately free. These expected behaviors can be seen in Fig. 6.

4.2 Born–Infeld case

Fig. 10
figure 10

The behavior of \(M_{QQ}\) versus T for Born–Infeld case with \( l=b=1 \)

Full size image
Fig. 11
figure 11

The behavior of the Ruppeiner invariant \(\mathfrak {R}\), \(\mathbf {H} _{S,Q}^{M}\) and \(M_{QQ}\) versus T for the Born–Infeld case with \(b=0.9\), \( l=0.76\), \(n=6\), \(z=3\) and \(Q=0.018\)

Full size image

For the Born–Infeld case, we can calculate the Ruppeiner invariant by using Eqs. (19), (34) and (39). The Ruppeiner invariant in this case is very complicated due to the presence of hypergeometric functions. Therefore, in this case we discuss the thermodynamic geometry non-analytically and by looking at plots. We study the cases \(z<2\), \(z>2\), \(z=2\) and \( z=n+1\) separately. First, we study the case \(z<2\). Figure 8a shows that changing \(\beta \) can cause a change in the dominant interaction. For instance, in a range of T, we have negative \(\mathfrak {R}\) (attraction) for \(\beta =1\) (note that in this range the system is thermally stable as one can see from Figs. 9a and 10a). For \(\beta =1\), the system behaves like a Fermi gas at zero temperature, namely \(\mathfrak {R}\) goes to positive infinity at zero temperature [16]. For \(\beta =0.82\), the Ruppeiner invariant diverges at two points; one of them is the zero temperature. According to Fig. 9a, for temperatures lower than the second divergence point, \(\mathbf {H}_{S,Q}^{M}\) is negative and therefore the system is thermally unstable. Since \(M_{QQ}>0\) (Fig. 10a), the system is thermally stable just for temperatures greater than the temperature of second divergence for \(\beta =0.82\). Figure 8a shows that there is no extremal black hole for \(\beta =0.5\) i.e. we have a black hole with just a single horizon. The allowed temperatures are greater than the temperature of divergence according to Figs. 9a and 10a. In Figs. 8b, 9b and b, respectively, the Ruppeiner invariant, \(\mathbf {H}_{S,Q}^{M}\) and \( M_{QQ} \) are depicted for different choices of the parameters. It is remarkable that, in the case of \(\beta =0.046\), Fig. 8b shows that the behavior of system looks like Van der Waals gas at phase transition temperature i.e. \(\mathfrak {R}\) goes to negative infinity at this point [14, 21]. For \(z>2\), the behavior of \(\mathfrak {R}\) is depicted in Fig. 11a. It can be seen that the type of dominated interaction changes for different \(\beta \) and we have negative \(\mathfrak {R}\) for some cases. In this case, we have a behavior like a Fermi gas at zero temperature for extremal black holes. For \(\beta =0.13\), there is a divergence at non-zero temperature; for lower temperatures, the system is unstable (Fig. 11b, c). In the case of \(z=2\), \(\mathbf {H} _{S,Q}^{M}\) and \(M_{QQ}\) are

$$\begin{aligned} \left. \mathbf {H}_{S,Q}^{M}\right| _{z=2}=\frac{(n+1)b^{2}}{ 2^{(n-5)/(n-1)}l^{4}(n-1)^{2}S^{2n/(n-1)}\Gamma }, \end{aligned}$$
(72)

and

$$\begin{aligned} \left. M_{QQ}\right| _{z=2}=\frac{b^{2}\pi }{(n-1)lS\Gamma }, \end{aligned}$$
Fig. 12
figure 12

The behavior of the Ruppeiner invariant \(\mathfrak {R}\) versus T for the Born–Infeld case with \(z=2\) and \(l=b=1\)

Full size image

which are always positive and therefore the system is always stable and \( \mathfrak {R}\) experiences no divergence (Fig. 12). In this case, for different values of nonlinear parameter \(\beta \), we have different dominated interaction. For this case, possible molecules of black hole behave like Fermi gas at zero temperature. The last case is \(z=n+1\). In this case \(M_{QQ}\) is

$$\begin{aligned} \left. M_{QQ}\right| _{z=n+1}=\frac{b^{2n}\beta ^{2}\left( \Gamma -1\right) }{4\pi (n-1)Q^{2}l^{n}\Gamma }, \end{aligned}$$
(73)

which is positive for all temperatures. The behavior of the Ruppeiner invariant and \(\mathbf {H}_{S,Q}^{M}\) are depicted in Fig. 13a and b for this case, respectively. As one can see the type of interaction is \(\beta \)-dependent for some temperatures. For \(\beta =0.04\), \(\mathbf {H} _{S,Q}^{M}\) is positive just for temperatures greater than the finite temperature of divergence (Fig. 13b) and therefore the system is thermally stable for this range of temperatures.

Most of the phase transitions discovered above in the presence of BI electrodynamics at finite temperatures cannot be interpreted as small/large black hole phase transitions because in these cases small size black holes are unstable. Further studies to disclose the nature of these phase transitions are called for.

Fig. 13
figure 13

The behavior of the Ruppeiner invariant \(\mathfrak {R}\) and \(\mathbf {H} _{S,Q}^{M}\) versus T for the Born–Infeld case with \(b=0.91\), \(l=0.72\), \(n=3\), \( z=4\) and \(Q=0.012\)

Full size image

5 Summary and closing remarks

In many condensed matter systems, fixed points governing the phase transitions respect dynamical scaling, \(t\rightarrow \lambda ^{z}t\), \(\vec { \mathbf {x}}\rightarrow \lambda \vec {\mathbf {x}}\) where z is the dynamical critical exponent. The gravity duals of such systems are Lifshitz black holes. In this paper, we first sought for the (\(n+1\))-dimensional Born–Infeld (BI) charged Lifshitz black hole solutions in the context of dilaton gravity. We found that these solutions are different for the cases \(z=n+1\) and \(z\ne n+1\). We found that both solutions and showed that the solution for the case \(z=n+1\) can never be Schwartzschild-like. Then we studied the thermodynamics of both cases by calculating conserved and thermodynamical quantities and checking the satisfaction of the first law of thermodynamics. After that, we looked for the Hawking–Page phase transition for our solutions, both in the cases of linearly and BI charged black holes. We studied this phenomenon and the effects of different parameters on it by presenting the behaviors of temperature T with respect to entropy S at fixed electrical potential energy U and also Gibbs free energy G with respect to T. Then we turned to discuss the phase transitions inside the black holes. In this part, we first presented the improved Davies quantities that show the phase transition points coincided with the ones of the Ruppeiner geometry. This coincidence has been proved directly in the Appendix. All of our solutions, provided that those are thermally stable at zero temperature, show the divergence at this point both from the Ruppeiner and the Davies points of view. Using the Landau–Lifshitz theory of thermodynamic fluctuations, we showed that this phase transition is a transition of the radiance properties of black holes. At zero temperature, an extreme black hole can just radiate through superradiant scattering whereas a non-extreme black hole at finite temperature can give off particles and radiation via both spontaneous Hawking radiation and superradiant scattering.

Next, we turned to study Ruppeiner geometry for our solutions. We investigated thermal stability, interaction type of possible black hole molecules and phase transitions of our solutions for linearly and nonlinearly BI charged cases separately. For the linearly charged case, we showed that there are no diverging points for Ricci scalar of the Ruppeiner geometry (Ruppeiner invariant) at finite temperature for the case \(z\ge 2\). For \(z<2\), it was found that the number of divergences (which show the phase transitions) at finite temperatures depend on the value of the charge Q. We introduced a critical value for the charge, \(Q_{c}\); for greater values there is no divergence at finite temperature, for values lower than it there are at most two divergences and for \(Q=Q_{c}\), there is just one diverging point for the Ruppeiner invariant. For the case of \(Q<Q_{c}\), there is a thermally unstable region for systems between two divergences at finite temperatures. So, this phase transition can be claimed as a discontinuous phase transition between small and large black holes. For small black holes not close to the transition point, we observed a finite magnitude for the Ruppeiner invariant \(\mathfrak {R}\). This is reasonable since the magnitude of \( \mathfrak {R}\) shows the correlation of possible black hole molecules. Also, for large black holes the magnitude of the Ruppeiner invariant tends to a very small value as expected. For \(Q=Q_{c}\), the solutions show a continuous small/large black holes phase transition at finite temperature. In the case of BI charged solutions, we investigated the Ruppeiner geometry and thermal stability for \(z<2\), \(z>2\), \(z=2\) and \(z=n+1\) separately. In some of these cases, small black holes were thermally unstable. So, more studies are called for to discover the nature of phase transitions at diverging points of \(\mathfrak {R}\). In both the linearly and nonlinearly charged cases, for some choices of the parameters, the black hole system behaves like a Van der Waals gas near the transition point.

Finally, we would like to suggest some related interesting issues which can be considered for future studies. It is interesting to repeat the studies such as regards the Hawking–Page phase transition, Ruppeiner geometry and Landau–Lifshitz theory for black branes to discover the effect of different constant curvatures of the (\(n-1\))-dimensional hypersurface on those phenomena. One can also seek for any signature of different phase transitions discovered here such as the Hawking–Page phase transition, and phase transitions determined by the Ruppeiner geometry, in dynamical properties of solutions by investigating quasi-normal modes. Some of this work is in progress by the authors.