Abstract
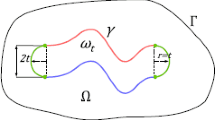
An optimal control problem is studied for the elliptic system of equations describing the equilibrium of the Kirchhoff-Love plate with an delaminated thin rigid inclusion. It is required to minimize the mean-square integral deviation of the bending moment from a function defined on the exterior boundary. The shape of the inclusion is chosen as the control function. The solvability of this problem is established.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A.M. Khludnev and V.A. Kovtunenko, Analysis of Cracks in Solids (WIT Press, Southampton and Boston, 2000).
A. M. Khludnev and G. Leugering, “On Elastic Bodies with Thin Rigid Inclusions and Cracks,” Math.Meth. Appl. Sci. 33(16), 1955–1967 (2010).
A. M. Khludnev and M. Negri, “Optimal Rigid Inclusion Shapes in Elastic Bodies with Cracks,” Z. Angew. Math. Phys. 64(1), 179–191 (2013).
V. V. Shcherbakov, “On an Optimal Control Problem for the Shape of Thin Inclusions in Elastic Bodies,” Sibirsk.Zh. Industr. Mat. 16(1), 138–147 (2013) [J. Appl. Indust.Math. 7 (3), 435–443 (2013)].
V. V. Shcherbakov, “Control for the Rigidity of Thin Inclusions in Elastic Bodies with Curvilinear Cracks,” Vestnik Novosib. Gos. Univ. Mat. Mekh. Inform. 13(1), 135–149 (2013).
E. M. Rudoi, “Invariant Integrals in a Planar Problem of Elasticity Theory for Bodies with Rigid Inclusions and Cracks,” Sibirsk. Zh. Industr. Mat. 15(1), 99–109 (2012). [J. Appl. Indust. Math. 6 (3), 371–380 (2012)].
V. A. Kovtunenko, “Variation and Boundary Value Problem in the Presence of Friction on the Inner Boundary,” SibirskMat. Zh. 39(5), 1060–1073 (1998) [SiberianMath. J. 39 (5), 913–926 (1998)].
V. A. Kovtunenko, “Solution of the Problem of the Optimal Cut in Elastic Beam,” Zh. Priklk. Mekh. i Tekhn. Fiz. 40(5), 149–157 (1999) [Appl.Mech. Tech. Phys. 40 (5), 908–915 (1999)].
A. M. Khludnev, “Thin Rigid Inclusions with Delaminations in Elastic Plates,” Europ. J. Mech. A/Solids 32(1), 69–75 (2012).
N. P. Lazarev, “An Equilibrium Problem for the Timoshenko-Type Plate Containing a Crack on the Boundary of a Rigid Inclusion,” J. Siberian Federal Univ. Math. & Phys. 6(1), 53–62 (2013).
N. P. Lazarev, “The Griffith Formula for a Timoshenko-Type Plate with a Curvilinear Crack,” Sibirsk. Zh. Industr. Mat. 16(2), 98–108 (2013).
L. T. Berezhnitskii, V. V. Panasyuk, and N. G. Stashchuk, Interaction of Rigid Linear Inclusions and Cracks in a Deformable Body (Naukova Dumka, Kiev, 1983) [in Russian].
S. Agmon, A. Douglis, and L. Nirenberg, “Estimates near the Boundary for Solutions of Elliptic Partial Differential Equations SatisfyingGeneral Boundary Conditions. II,” Comm. Pure Appl.Math. 17(1), 35–92 (1964).
F. Browder, “On the Regularity Properties of Solutions of Elliptic Differential Equations,” Comm. Pure Appl. Math. 19(3), 351–361 (1956).
J.-L. Lions and E. Magenes, Non-Homogeneous Boundary Value Problems and Applications (Springer, Berlin, 1972; Mir, Moscow, 1971).
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © V.V. Shcherbakov, 2013, published in Sibirskii Zhurnal Industrial’noi Matematiki, 2013, Vol. XVI, No. 4, pp. 142–151.
Rights and permissions
About this article
Cite this article
Shcherbakov, V.V. Existence of an optimal shape of the thin rigid inclusions in the Kirchhoff-Love plate. J. Appl. Ind. Math. 8, 97–105 (2014). https://doi.org/10.1134/S1990478914010116
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1990478914010116