Modeling and Analysis of Output Processes of Linear Continuous Stochastic Systems Based on Orthogonal Expansions of Random Functions

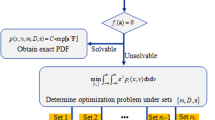
Abstract

The problem of modeling and analyzing output processes of linear continuous stochastic systems is considered and the method for its solution based on the spectral form of mathematical description of the control systems is proposed. The proposed approach provides an explicit representation of the output signal of the system in the form of functional series with random coefficients or in the form of a partial sum in the approximate solution, which distinguishes this method from other approaches when the result of the solution are the deterministic characteristics of the output signal: the first two moments or the probability density function. As an application, the problem of modeling the action of wind is considered using the Dryden shaping filter.

SPECTRAL FORM OF MATHEMATICAL DESCRIPTION OF LINEAR NONSTATIONARY CONTROL SYSTEMS

Appendix A. Description of Functions (Signals)

Suppose that the system of functions $\{ q(i,t)\} _{{i = 0}}^{\infty }$ is defined in the segment $\mathbb{T} = [0,T]$ with values in $\mathbb{R}$ and is complete and orthonormal; i.e., it is the basis system

$${{\left( {q(i,t),q(j,t)} \right)}_{{{{L}_{2}}(\mathbb{T})}}} = \int\limits_\mathbb{T} {q(i,t)q(j,t)dt} = {{\delta }_{{ij}}},\quad i,j = 0,1,2,\; \ldots ,$$

(A.1)

where δ_ij is the Kronecker delta, ${{(\;\cdot\;,\;\cdot\;)}_{{{{L}_{2}}(\mathbb{T})}}}$ means the scalar product of elements of the space of square-integrable functions ${{L}_{2}}(\mathbb{T})$ and $x(t):\mathbb{T} \to \mathbb{R}$ is the square integrable function

$$\int\limits_\mathbb{T} {{{x}^{2}}(t)dt} < \infty \quad \left( {x(t) \in {{L}_{2}}(\mathbb{T})} \right).$$

Then, the function x(t) is represented by the generalized Fourier series

$$x(t) = \sum\limits_{i = 0}^\infty {{{X}_{i}}q(i,t)} ,$$

(A.2)

where the expansion coefficients X_i are computed by the formula

$${{X}_{i}} = {{\left( {q(i,t),x(t)} \right)}_{{{{L}_{2}}(\mathbb{T})}}} = \int\limits_\mathbb{T} {q(i,t)x(t)dt} ,\quad i = 0,1,2,\; \ldots ,$$

and the functional series converges to x(t) in the norm ${{L}_{2}}(\mathbb{T})$ and

$$\sum\limits_{i = 0}^\infty {X_{i}^{2}} < \infty .$$

The ordered set X of the expansion coefficients X_i of the function x(t) in the basis system $\{ q(i,t)\} _{{i = 0}}^{\infty }$ is represented as an infinite column matrix and is called the nonstationary spectral characteristic of the function x(t). This term was introduced in [1], and its nonstationary character consisted of the fact that the boundaries of segment $\mathbb{T}$ are in general functions of time; however, we restrict ourselves by the fixed segment and will call X and the characteristics similar to it the spectral characteristics. The representation of the function x(t) in the form of series Eq. (A.2) is called the inversion formula. We also may consider the segment $[{{t}_{0}},T]$ in place of $\mathbb{T}$; however, here it is convenient to set t₀ = 0.

For the functions of two variables $h(t,\tau ):{{\mathbb{T}}^{2}} \to \mathbb{R}$, ${{\mathbb{T}}^{2}} = \mathbb{T} \times \mathbb{T}$, we also introduce the spectral characteristic, following the terminology of [1], the two-dimensional nonstationary spectral characteristic (TNSC), that is, the infinite matrix H with the elements

$${{H}_{{ij}}} = {{\left( {q(i,t)q(j,\tau ),h(t,\tau )} \right)}_{{{{L}_{2}}({{\mathbb{T}}^{2}})}}} = \int\limits_\mathbb{T} {\int\limits_\mathbb{T} {q(i,t)q(j,\tau )h(t,\tau )dtd\tau } } ,\quad i,j = 0,1,2,\; \ldots ,$$

and, hence,

$$h(t,\tau ) = \sum\limits_{i = 0}^\infty {\sum\limits_{j = 0}^\infty {{{H}_{{ij}}}q(i,t)q(j,\tau )} } .$$

The last relation for the representation of the function $h(t,\tau )$ in the form of a series is also called the inversion formula.

The definition of the spectral characteristics may be extended to random functions $x(t)$ satisfying the condition

$$\int\limits_\mathbb{T} {\int\limits_\mathbb{T} {R_{x}^{2}(t,\tau )dtd\tau } } < \infty ,$$

where

$${{R}_{x}}(t,\tau ) = {\text{cov}}\left( {x(t),x(\tau )} \right) = {\text{E}}\left[ {(x(t) - {{m}_{x}}(t))(x(\tau ) - {{m}_{x}}(\tau ))} \right],\quad {{m}_{x}}(t) = {\text{E}}x(t).$$

In these relations, E is the expected value and ${\text{cov}}$ is the covariance (${{R}_{x}}(t,\tau )$ is the covariance function).

Thus, if

$$x(t) = \sum\limits_{i = 0}^\infty {{{X}_{i}}q(i,t)} ,\quad {{X}_{i}} = \int\limits_\mathbb{T} {q(i,t)x(t)dt} ,\quad i = 0,1,2,\; \ldots ,$$

where X_i are the random variables, then we also represent the ordered set X of these random variables in the form of an infinite column matrix and call it the spectral characteristic of the random function x(t). Here, the functional series converges to x(t) in the mean-square sense and

$${\text{E}}\sum\limits_{i = 0}^\infty {X_{i}^{2}} < \infty .$$

(A.3)

To indicate the correspondence of functions and their spectral characteristics, we will use the following notations $\mathbb{S}$ is the spectral transform and ${{\mathbb{S}}^{{ - 1}}}$ is the inverse spectral transform:

$$\mathbb{S}[x(t)] = X,\quad x(t) = {{\mathbb{S}}^{{ - 1}}}[X];\quad \mathbb{S}[h(t,\tau )] = H,\quad h(t,\tau ) = {{\mathbb{S}}^{{ - 1}}}[H].$$

(A.4)

Note that the definition of the spectral characteristic of a function may be extended to the generalized functions, for instance, to the Dirac delta function and its derivatives. Thus, the spectral characteristic of the function $\delta (t - \tau )$ at fixed $\tau \in \mathbb{T}$ is the ordered set Δ_τ of the values of functions of the basis system $\{ q(i,t)\} _{{i = 0}}^{\infty }$ at point t = τ. Similarly, we may extend the class of random functions for which the definition of the spectral characteristic is introduced; however, property (A.3) is not valid for them.

We consider the standard Wiener process, or the Brownian motion, w(t) (the Gaussian random process with zero expected value and covariance function ${{R}_{w}}(t,\tau ) = \min \{ t,\tau \}$) and represent it in the form of the series [8, 9, 26]

$$w(t) = \sum\limits_{i = 0}^\infty {{{\xi }_{i}}Q(i,t)} ,\quad Q(i,t) = \int\limits_0^t {q(i,\tau )d\tau } ,$$

(A.5)

where the coefficients ξ_i are independent random variables with the normal distribution. We formally differentiate the left and right sides and obtain the expression for the standard Gaussian white noise (of the unitary intensity)

$${v}(t) = \sum\limits_{i = 0}^\infty {{{\xi }_{i}}q(i,t)} ,$$

(A.6)

that is, the spectral characteristic $\mathcal{V}$ of the standard Gaussian white noise is the infinite column matrix whose elements are independent random variables ξ_i with the standard normal distribution for any basis system $\{ q(i,t)\} _{{i = 0}}^{\infty }$.

Appendix B. Relation with Description of Random Functions in the Correlation Theory

We report how the spectral characteristic X of a random function is related to the first and second nonstationary spectral densities (NSDs), which are the spectral characteristics of the expected value and covariance function of x(t). By definition [1], the first NSD $^{1}{{S}^{x}}$ is the spectral characteristic of the expected value ${{m}_{x}}(t) = {\text{E}}x(t)$,

$$^{1}{{S}^{x}} = \mathbb{S}\left[ {{{m}_{x}}(t)} \right],{{\quad }^{1}}S_{i}^{x} = {{\left( {q(i,t),{{m}_{x}}(t)} \right)}_{{{{L}_{2}}(\mathbb{T})}}} = \int\limits_\mathbb{T} {q(i,t){{m}_{x}}(t)dt} ,\quad i = 0,1,2,\; \ldots ,$$

and, consequently,

$$\begin{gathered} ^{1}S_{i}^{x} = \int\limits_\mathbb{T} {q(i,t){\text{E}}x(t)dt} = \int\limits_\mathbb{T} {q(i,t){\text{E}}\left[ {\sum\limits_{j = 0}^\infty {{{X}_{j}}q(j,t)} } \right]dt} \\ = \;\sum\limits_{j = 0}^\infty {{\text{E}}\left[ {{{X}_{j}}\int\limits_\mathbb{T} {q(i,t)q(j,t)dt} } \right]} = \sum\limits_{j = 0}^\infty {{{\delta }_{{ij}}}{\text{E}}{{X}_{j}}} = {\text{E}}{{X}_{i}}. \\ \end{gathered} $$

The second NSD S^x is the spectral characteristic of the covariance function ${{R}_{x}}(t,\tau ) = {\text{cov}}(x(t),x(\tau ))$,

$$\begin{gathered} {{S}^{x}} = \mathbb{S}\left[ {{{R}_{x}}(t,\tau )} \right],\quad S_{{ij}}^{x} = {{\left( {q(i,t)q(j,\tau ),{{R}_{x}}(t,\tau )} \right)}_{{{{L}_{2}}({{\mathbb{T}}^{2}})}}} \\ = \;\int\limits_\mathbb{T} {\int\limits_\mathbb{T} {q(i,t)q(j,\tau ){{R}_{x}}(t,\tau )dtd\tau } } ,\quad i,j = 0,1,2,\; \ldots \\ \end{gathered} $$

By analogy with the first NSD, we may show that

$$S_{{ij}}^{x} = \int\limits_\mathbb{T} {\int\limits_\mathbb{T} {q(i,t)q(j,\tau ){\text{cov}}\left( {x(t),x(\tau )} \right)dtd\tau } } = {\text{cov}}({{X}_{i}},{{X}_{j}}).$$

Thus, $^{1}{{S}^{x}} = {\text{E}}X$ and ${{S}^{x}} = {\text{cov}}(X) = {\text{E}}(X{{ - }^{1}}{{S}^{x}}){{(X{{ - }^{1}}{{S}^{x}})}^{{\text{T}}}}$. For instance, for the standard Gaussian white noise ${v}(t)$, $^{1}{{S}^{{v}}}$ is the infinite zero column matrix and ${{S}^{{v}}} = E$ is the infinite identity matrix.

Appendix C. Relation with Karhunen–Loeve Expansion

The Karhunen–Loeve expansion [13] is the expansion of the random function x(t) in terms of eigenfunctions of the linear integral operator with the kernel ${{R}_{x}}(t,\tau )$. That is, the system of functions $\{ q(i,t)\} _{{i = 0}}^{\infty }$ is generated from the condition

$$\int\limits_\mathbb{T} {{{R}_{x}}(t,\tau )q(i,\tau )d\tau } = {{\lambda }_{i}}q(i,t),\quad {{\lambda }_{i}} > 0,\quad i = 0,1,2,\; \ldots $$

With this choice of the basis system, the second NSD S^x is the diagonal matrix generated by the eigenvalues λ_i and the spectral characteristic X is formed based on the values $\sqrt {{{\lambda }_{i}}}$ and on the uncorrelated random variables with unitary variance. However, the Karhunen–Loeve expansion is associated with the determination of eigenfunctions and eigenvalues of the linear operator; therefore, it is not used further. As the basis systems, we propose to use the universal system of functions, for instance, the Legendre polynomials, the trigonometric functions (cosinusoids), and the system of functions generated by wavelets [3].

Appendix D. Relation with Canonical Representations of Random Functions

If we represent a random function x(t) as the sum ${{m}_{x}}(t) + \mathop {x}\limits^{ \circ} (t)$, where ${\text{E}}\mathop {x}\limits^{\circ} (t)= 0$, then it is easy to find the relation with the canonical representation of the random function [14, 15]

$$x(t) = {{m}_{x}}(t) + \sum\limits_{i = 0}^\infty {\mathop {{{X}_{i}}}\limits^ \circ q(i,t)} ,$$

where $\mathop {{{X}_{i}}}\limits^ \circ$ are the uncorrelated random variables with zero expected value whose ordered set $\mathop X\limits^ \circ$ generates the spectral characteristic of the random function $\mathop x\limits^ \circ (t)$: $\mathbb{S}[\mathop x\limits^ \circ (t)] = \mathop X\limits^ \circ$, $\mathop x\limits^ \circ (t) = {{\mathbb{S}}^{{ - 1}}}[\mathop X\limits^ \circ ]$. Consequently, X = $^{1}{{S}^{x}} + \mathop X\limits^ \circ$ and $x(t) = {{m}_{x}}(t) + {{\mathbb{S}}^{{ - 1}}}[\mathop X\limits^ \circ ]$.

Appendix E. Description of Linear Systems

We proceed to the description of linear control systems [2, 4]. Such systems may be characterized by linear differential equations with constant (for stationary systems) or variable (for nonstationary systems) coefficients. The description of linear systems by transfer functions has become widely used in the control theory; for instance, the pulse transfer function (PTF) $k(t,\tau )$ is used, which is the reaction of the system to the pulse input excitation $\delta (t - \tau )$ at zero initial conditions. In the spectral form of mathematical description for linear system, the two-dimensional nonstationary transfer function (TNTF) is applied, the TNSC PTF $k(t,\tau )$, that is, the infinite matrix W whose elements are computed by the formula

$$\begin{gathered} {{W}_{{ij}}} = {{\left( {q(i,t)q(j,\tau ),k(t,\tau )} \right)}_{{{{L}_{2}}({{\mathbb{T}}^{2}})}}} = \int\limits_\mathbb{T} {\int\limits_\mathbb{T} {q(i,t)q(j,\tau )k(t,\tau )dtd\tau } } \\ = \;\int\limits_\mathbb{T} {q(i,t)\int\limits_0^t {k(t,\tau )q(j,\tau )d\tau } dt} ,\quad i,j = 0,1,2,\; \ldots , \\ \end{gathered} $$

(E.1)

taking into account the physical realizability: $k(t,\tau ) = 0$ for $t \leqslant \tau$.

In [5] the equivalent definition of the matrix W was applied,

$${{W}_{{ij}}} = {{\left( {q(i,t),\mathcal{A}q(j,t)} \right)}_{{{{L}_{2}}(\mathbb{T})}}} = \int\limits_\mathbb{T} {q(i,t)\mathcal{A}q(j,t)dt} ,\quad i,j = 0,1,2,\; \ldots ,$$

(E.2)

where $\mathcal{A}$ is the linear operator corresponding to the linear system with the PTF $k(t,\tau )$. In [5] the matrix W is called the spectral characteristic of the linear operator $\mathcal{A}$, and in [14] it is called the matrix operator.

The input–output relation for the linear system with the PTF $k(t,\tau )$ under deterministic excitation is equal to

$$x(t) = \int\limits_0^t {k(t,\tau )g(\tau )d\tau } ,$$

where g(t) and x(t) are the input and output signals, respectively; in the spectral form of mathematical description it is characterized by the relation $X = WG$ [1, 3, 4], where $G = \mathbb{S}[g(t)]$ and $X = \mathbb{S}[x(t)]$.

Under random excitations

$${{m}_{x}}(t) = \int\limits_0^t {k(t,\tau ){{m}_{g}}(\tau )d\tau } ,\quad ~{{R}_{x}}(t,\tau ) = \int\limits_0^t {\int\limits_0^\tau {k(t,\theta )k(\tau ,\vartheta ){{R}_{g}}(\theta ,\vartheta )d\theta d\vartheta } } ,$$

where ${{m}_{g}}(t)$, ${{m}_{x}}(t)$, ${{R}_{g}}(t,\tau )$, and ${{R}_{x}}(t,\tau )$ are the expected values and covariance functions of the input and output signals, respectively, we have $^{1}{{S}^{x}} = W{{{\mkern 1mu} }^{1}}{{S}^{g}}$ and ${{S}^{x}} = W{{S}^{g}}{{W}^{{\text{T}}}}$ [1, 3, 4]. Here, $^{1}{{S}^{g}} = \mathbb{S}[{{m}_{g}}(t)]$, ¹S^x = $\mathbb{S}[{{m}_{x}}(t)]$, ${{S}^{g}} = \mathbb{S}[{{R}_{g}}(t,\tau )]$, and ${{S}^{x}} = \mathbb{S}[{{R}_{x}}(t,\tau )]$.

In the paper we use the proportional ($k(t,\tau ) = a(t)\delta (t - \tau )$, where $a(t)$ is the amplifying factor), differential ($k(t,\tau ) = \delta '(t - \tau )$), and integrational ($k(t,\tau ) = 1(t - \tau )$ is the unity step function) elements. For each of these elements, the TNTF [1, 3] or the spectral characteristic of the corresponding linear operator is determined: the operator of multiplication, differentiation, or integration [5], that is, the matrices A, $\mathcal{P}$, and P^–1 with the elements

$$\begin{gathered} {{A}_{{ij}}} = \int\limits_\mathbb{T} {a(t)q(i,t)q(j,t)dt} ,\quad {{\mathcal{P}}_{{ij}}} = \int\limits_\mathbb{T} {q(i,t){\mkern 1mu} \frac{{dq(j,t)}}{{dt}}{\mkern 1mu} dt} , \\ P_{{ij}}^{{ - 1}} = \int\limits_\mathbb{T} {q(i,t)\int\limits_0^t {q(j,\tau )d\tau } dt} ,\quad i,j = 0,1,2,\; \ldots , \\ \end{gathered} $$

(E.3)

according to (E.8).

Using the introduced notations, we may write the representation of the spectral characteristic $\mathcal{W}$ of the standard Wiener process w(t) with the spectral characteristic P^–1 of the integrational operator and the spectral characteristic $\mathcal{V}$ of the standard Gaussian white noise

$$\mathcal{W} = {{P}^{{ - 1}}}\mathcal{V},$$

(E.4)

which is a consequence of the relation

$$w(t) = \int\limits_0^t {{v}(t)dt} ,$$

that is, the Wiener process w(t) is the output signal of the integrational element whose input signal is the Gaussian white noise ${v}(t)$.

We establish the relation between formulas (A.4) and (E.4). We represent the function $Q(i,t)$ as a series in the basis system $\{ q(i,t)\} _{{i = 0}}^{\infty }$. Then, taking into account the definition of elements $P_{{ij}}^{{ - 1}}$, we have

$$w(t) = \sum\limits_{j = 0}^\infty {{{\xi }_{j}}Q(j,t)} = \sum\limits_{j = 0}^\infty {{{\xi }_{j}}\sum\limits_{i = 0}^\infty {P_{{ij}}^{{ - 1}}q(i,t)} } = \sum\limits_{i = 0}^\infty {\left( {\sum\limits_{j = 0}^\infty {P_{{ij}}^{{ - 1}}{{\xi }_{j}}} } \right)q(i,t)} .$$

We denote the expression in parentheses by ${{\mathcal{W}}_{i}}$ and obtain the ordered set $\mathcal{W}$ of the expansion coefficients ${{\mathcal{W}}_{i}}$.

In addition, we use the input–output relations for the linear system under random excitation in the spectral form of mathematical description and take into account that ${{S}^{{v}}} = E$, thus obtaining that S^w = ${{P}^{{ - 1}}}{{[{{P}^{{ - 1}}}]}^{{\text{T}}}}$, where S^w are the spectral characteristics of the covariance function of the Wiener process ${{R}_{w}}(t,\tau )$. Thus, ${{S}^{w}} = {\text{cov}}({{\mathcal{W}}_{i}}) = {\text{E}}(\mathcal{W}{{\mathcal{W}}^{{\text{T}}}})$ and the matrix P^–1 determines the linear transform of column $\mathcal{V}$ whose result is the column with the covariance matrix S^w.