The Optimal Pair of Rydberg Alkali-Metal Atoms in the Nonsymmetric Penning Ionization Processes

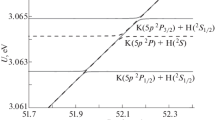
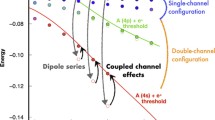
Abstract

Features of Penning ionization in cold gaseous media of Rydberg alkali-metal atoms have been investigated. In contrast to the hydrogen atom, the corresponding autoionization widths exhibit a strong (by orders of magnitude) dependence on the orbital quantum numbers of the atoms involved in the long-range dipole–dipole interaction. An important feature of Penning ionization is the nontrivial dependence of its efficiency on the Rydberg particle size. For all types of alkali-metal atoms, the optimal highly nonsymmetric configurations of Rydberg pairs have been found that lead to the explosive (by several orders of magnitude) intensification of the free electron formation by means of the Penning ionization processes. This property makes Penning ionization an important means of forming primary charged particles during the cold Rydberg plasma formation. The numerical data for pairs of potassium atoms are reported that demonstrate a significant effect of the Förster resonance on the values of the Penning ionization rate constants.

APPENDIX

1.1 Quasi-Classical Representations of Radial Integrals

The quasi-classical representations of the dipole matrix elements at optical transitions $nl \to n'l'$ are based on the Bohr–Heisenberg correspondence principles [20]. For the close Rydberg ($n \gg 1$) quantum states (${\text{|}}n'{\text{*}} - n{\text{*|}} < 10$), radial matrix elements $R_{{nl}}^{{n'l'}}$ are determined by the coefficients of the Fourier expansion of the classical electron orbit, which is associated with bound quantum state $nl$. The corresponding representations $R_{{nl}}^{{n'l'}}$ for alkali atoms were obtained in [22, 23, 29]:

$$R_{{nl}}^{{n'l'}} = \frac{{l_{{\max }}^{2}}}{{\Delta \varepsilon \sqrt {n{{{\text{*}}}^{3}}n'{{{\text{*}}}^{3}}} }}{{G}_{{\Delta l}}}(\gamma ),\quad \gamma = n'{\text{*}} - n{\text{*}},$$

((A.1))

$$\begin{gathered} {{G}_{{\Delta l}}}(\gamma ) = \frac{{{{{( - 1)}}^{{\Delta n}}}n_{a}^{{*2}}}}{{l_{{\max }}^{2}}}\left\{ {\frac{{\sin (\pi \gamma )}}{{\pi \gamma }}[\gamma (1 - {{e}_{a}}) - \Delta l\sqrt {{\text{1/}}e_{a}^{2} - 1} ]} \right. \\ \left. { - \;\tilde {\Im }_{\gamma }^{{^{{^{{^{{}}}}}}}}( - \gamma {{e}_{a}}) + \Delta l\sqrt {{\text{1/}}e_{a}^{2} - 1} {{\Im }_{\gamma }}( - \gamma {{e}_{a}})} \right\}. \\ \end{gathered} $$

((A.2))

Symbol Δ suggests a difference between the physical quantities corresponding to the final ($n{\kern 1pt} 'l{\kern 1pt} '$) and initial ($nl$) states; for example, $\Delta n{\text{*}} = n{\kern 1pt} '{\text{*}} - \;n{\text{*}} \equiv \gamma$, Δl = $l{\kern 1pt} '\; - l$. Index а indicates the ${{n}_{a}}{{l}_{a}}$ level intermediate with respect to the states nl; $n{\kern 1pt} 'l{\kern 1pt} '$. The quasi-classical parameters of this level were obtained in [22, 23]:

$$\begin{gathered} {{l}_{a}} = l_{{\max }}^{{}} = \max \{ l,l'\} ,\quad n_{a}^{{{\text{*}}3}} = \frac{{2{{n}^{{{\text{*}}2}}}{{n}^{{{\text{*}}2}}}}}{{n{\text{*}} + n'{\text{*}}}}, \\ e_{a}^{{}} = \sqrt {1 - l_{a}^{2}{\text{/}}n_{a}^{{{\text{*}}2}}} . \\ \end{gathered} $$

((A.3))

The functions from Eq. (A.2) are the Anger function and its derivative:

$$\begin{gathered} {{\Im }_{\gamma }}(x) = \frac{1}{\pi }\int\limits_0^\pi {d\xi \cos } (\gamma \xi - x\sin \xi ), \\ {{{\tilde {\Im }}}_{\gamma }}(x) = \frac{d}{{dx}}{{\Im }_{\gamma }}(x). \\ \end{gathered} $$

((A.4))

Comparison of the $R_{{nl}}^{{n'l'}}$ values calculated using formula (A.1) with the quantum-mechanical data shows that the error of (A.1) is fractions of percent at ${{n}_{a}} \geqslant 10$ and several percent at ${{n}_{a}} \approx 3$ [22, 29].

Equations (A.1) and (A.2) are inconvenient when working with “long” $\left| \gamma \right| \gg 1$ transitions. At the same time, the presence of a large parameter $\gamma$ makes it possible to obtain the asymptotic representation for the ${{G}_{{\Delta l}}}(\gamma )$ function (A.2) [23], which reduces Eq. (A.1) to the form

$$R_{{nl}}^{{n'l'}} = \frac{{l_{{\max }}^{2}}}{{\Delta \varepsilon \sqrt {n{{{\text{*}}}^{3}}n'{{{\text{*}}}^{3}}} }}G_{{\Delta l}}^{{({\text{as}})}}(x),\quad x = {{(\Delta \varepsilon l_{{\max }}^{3}{\text{/2}})}^{{2/3}}}.$$

((A.5))

The $G_{{\Delta l}}^{{{\text{(as)}}}}$ asymptotic is a function of the new argument $x$ (the reduced frequency of the investigated transition)

$$\begin{gathered} G_{{\Delta l}}^{{({\text{as}})}}(x) = - \frac{{\sin (\pi \Delta \delta )}}{\pi }\left( {\frac{1}{2} + \frac{{\Delta l}}{{{{l}_{{\max }}}}}\left( {{{\Lambda }_{q}} + 1} \right)} \right) \\ + \;\frac{1}{{x\sqrt \pi }}{{{\tilde {\Phi }}}_{{\Delta \delta }}}(x) + \left( {\Delta l + \frac{{{{\Lambda }_{q}}}}{{5l_{{\max }}^{{}}}}} \right)\sqrt {\frac{1}{{\pi x}}} {{\Phi }_{{\Delta \delta }}}(x) \\ \end{gathered} $$

((A.6))

and expressed via modified Airy function ${{\Phi }_{{\Delta \delta }}}(x)$ and its derivative ${{\tilde {\Phi }}_{{\Delta \delta }}}(x)$

$$\begin{gathered} {{\Phi }_{{\Delta \delta }}}(x) = \frac{1}{{\sqrt \pi }}\int\limits_0^\infty {\cos \left( {x\xi + \frac{{{{\xi }^{3}}}}{3} + \pi \Delta \delta } \right)} d\xi , \\ {{{\tilde {\Phi }}}_{{\Delta \delta }}}(x) = - \frac{d}{{dx}}{{\Phi }_{{\Delta \delta }}}(x). \\ \end{gathered} $$

((A.7))

Equation (A.6) contains the difference between quantum defects $\Delta \delta = {{\delta }_{{l'}}} - {{\delta }_{l}}$ and quantum factor ${{\Lambda }_{q}} = (\varepsilon ' + \varepsilon ){\text{/}}\Delta \varepsilon$, which takes into account the higher-order quantum corrections in the quasi-classical approximation [30, 31].

Note that the derivation of asymptotic (A.5) suggests that there is a positive value of the difference $\gamma = n'{\text{*}} - n{\text{*}}$; i.e., transitions with a finite level always higher than the initial one are investigated. Since the matrix elements are self-conjugated, the situation with $\gamma < 0$ is reduced to the case of $\gamma > 0$ by replacing the levels: $R_{{nl}}^{{n'l'}} = R_{{n'l'}}^{{nl}}$.

An important feature of asymptotic formulas (A.5) is the possibility of obtaining radial integrals (A1) with a satisfactory (~5%) accuracy even near parameter $\gamma$ ~ 1. In the numerical calculation of the Penning widths, we use representation (A1) for $R_{{nl}}^{{n'l'}}$ in Eq. (4) if in the individual transition $N \to N'$ the parameter is $\left| \gamma \right| \leqslant 4$ and representation (A.5) in the opposite case, i.e., at $\left| \gamma \right| > 4$.

Under typical conditions of laboratory experiments with cold Rydberg atoms, the principle quantum numbers are $n \cong 50$, whereas $l$ is only several units. This means that parameter $x$ ~ $l_{{\max }}^{{}}{\text{/}}{{n}^{{4/3}}}$ in (A.5) is small, which significantly simplifies the Airy functions:

$${\lim_{x \to 0}}{{\Phi }_{{\Delta \delta }}}(x) = \frac{{\Gamma ({\text{1/3}})}}{{\sqrt \pi {{3}^{{2/3}}}}}\sin \left( {\frac{\pi }{3} - \pi \Delta \delta } \right),$$

((A.8))

$${\lim_{x \to 0}}{{\tilde {\Phi }}_{{\Delta \delta }}}(x) = \frac{{\Gamma ({\text{2/3}})}}{{\sqrt \pi {{3}^{{1/3}}}}}\sin \left( {\frac{\pi }{3} + \pi \Delta \delta } \right).$$

((A.9))

Here, $\Gamma (x)$ is the Airy Γ function. At small $x$, the second term in $G_{{\Delta l}}^{{{\text{(as)}}}}(x)$ function (A.6) becomes dominant and Eqs. (A.5) and (5) for the radial matrix element and photoionization cross sections take the form

$$R_{{{{n}_{d}}{{l}_{d}}}}^{{n_{d}^{'}l_{d}^{'}}} \cong \frac{{{{2}^{{2/3}}}\Gamma ({\text{2/3}})}}{{{{3}^{{1/3}}}\pi }}\frac{{\sin \left( {\pi {\text{/3}} - \pi \Delta \delta } \right)}}{{\omega _{d}^{{5/3}}\sqrt {n_{d}^{{*3}}n_{d}^{{'*3}}} }},$$

((A.10))

$$\begin{gathered} {{\sigma }_{{ph}}}({{n}_{i}} \to \varepsilon _{i}^{'}) \\ \cong \frac{{{{2}^{{10/3}}}{{\Gamma }^{2}}({\text{2/3}})}}{{{{3}^{{5/3}}}c}}\frac{{{{l}_{{i\max }}}}}{{2{{l}_{i}} + 1}}\frac{{{{{\sin }}^{2}}\left( {\pi {\text{/3}} + \pi \Delta \delta } \right)}}{{\omega _{d}^{{7/3}}n_{i}^{{*3}}}}, \\ \end{gathered} $$

((A.11))

which is convenient for the analytical estimation of the rate constants of many physical processes.