Approximate Calculation of Equilibria in the Nonlinear Stackelberg Oligopoly Model: A Linearization Based Approach

Abstract

The game-theoretic problem of choosing optimal strategies for oligopoly market agents with linear demand functions and nonlinear cost functions is considered. Necessary conditions for the existence of a solution of a system of nonlinear equations with power functions are established. The system of equations for the optimal responses of agents is linearized by expanding the power functions in Taylor series. As a result, the linearized system depends on the vector of linearization parameters, and the calculation of game equilibria is reduced finding fixed points of nonlinear mappings. The deviations of the approximate equilibrium from the exact solution are investigated. Analytical formulas for calculating equilibria in the game of oligopolists under an arbitrary level of Stackelberg leadership are derived. Analysis of duopoly and tripoly demonstrates that the game equilibrium is determined by two factors as follows. First, the concavity of the agent’s cost function (the positive scale effect) leads to an increase in his payoff compared to the agents with convex cost functions (the negative scale effect). Second, the agent’s payoff increases if he is a Stackelberg leader; however, the advantage of his environment by the type of cost function reduces the effect of the second factor.

Appendix

Proof of Proposition 1. For ensuring the condition ${q}_{i}\ \in \left(0,1\right)$, normalize the action vector of agents by the formula

$${q}_{i}=\frac{{Q}_{i}}{{Q}_{\rm{max}}},\quad i\in N,\quad {Q}_{\rm{max}}>{Q}_{i},\quad i\in N.$$

(A.1)

The value ${Q}_{\rm{max}}=\frac{a-M{C}_{\min }}{b}$, $M{C}_{\rm{min}}=\mathop{\rm{min}}\limits_{i\in N}\left({B}_{i}{\beta }_{i}{Q}_{i}^{{\beta }_{i}-1}\right)$, is given by the market volume formula for an oligopoly with infinitely many firms; for details, see [18]. Find the coefficients of Eqs. (7) for the normalized action vector by equating the values of the utility function (1) for the action vectors q_i, i ∈ N, and Q_i, i ∈ N:

$$\left(\hat{a}-\hat{b}q\right){q}_{i}-{C}_{Fi}-{\hat{B}}_{i}{q}_{i}^{{\beta }_{i}}=\left(a-bQ\right){Q}_{i}-{C}_{Fi}-{B}_{i}{Q}_{i}^{{\beta }_{i}},\quad i\in N.$$

(A.2)

Substitute (A.1) into this expression, and compare the coefficients at the same powers of the actions vector to arrive in formulas (9c). Therefore, (7) can be written as

$${\hat{F}}_{i}=\hat{a}-\hat{b}q-\hat{b}{q}_{i}\left(1+\sum _{j\in N\backslash i}{x}_{ij}^{r}\right)-{\hat{B}}_{i}{\beta }_{i}{q}_{i}^{{\beta }_{i}-1}=0,\quad i\in N.$$

(A.3)

The nonlinear component of Eqs. (A.3) is the function $f({q}_{i})={\hat{B}}_{i}{\beta }_{i}{q}_{i}^{{\beta }_{i}-1}$. In the neighborhood of a number ν_i such that ${\nu }_{i}\in \left(0,1\right)$ and ν_i < q_i, this function is expanded in the Taylor series

$$\bar{f}\left({q}_{i}\right)=f\left({\nu }_{i}\right)+f^{\prime} \left({\nu }_{i}\right)\left({q}_{i}-{\nu }_{i}\right)+\frac{f^{\prime\prime} \left({\nu }_{i}\right)}{2!}{\left({q}_{i}-{\nu }_{i}\right)}^{2}+\ldots .$$

If there exists a number ${\Omega }_{i}={\nu }_{i}+{\theta }_{i}\left({q}_{i}-{\nu }_{i}\right)$ such that ν_i < Ω_i < q_i (i.e., $\theta \in \left(0,1\right)$), this series has the remainder in the Lagrangian form [20] calculated by

$${R}_{k}\left({q}_{i}\right)=\frac{1}{k!}{f}^{\left(k\right)}\left({\Omega }_{i}\right){\left({q}_{i}-{\nu }_{i}\right)}^{k}=\frac{{\left({q}_{i}-{\nu }_{i}\right)}^{k}}{k!}\frac{{\Omega }_{i}^{{\beta }_{i}}}{{\Omega }_{i}^{k+1}}{\hat{B}}_{i}{\beta }_{i}\mathop{\prod }\limits_{j = 1}^{k}\left({\beta }_{i}-j\right).$$

(A.4)

The series is convergent if $\left|{q}_{i}-{\nu }_{i}\right|<{r}_{i}$ and $\mathop{\rm{lim}}\limits_{k\to \infty }{R}_{k}\left({q}_{i}\right)=0$. Hence, take a small number r_i such that 0 < r_i < Ω_i, and establish the existence of the limit of the remainder sequences. Since ${r}_{i}\in \left(0,{\Omega }_{i}\right)$, it follows that Ω_i > q_i − ν_i, and consequently $\frac{{\left({q}_{i}-{\nu }_{i}\right)}^{k}}{{\Omega }_{i}^{k}}>\frac{{\left({q}_{i}-{\nu }_{i}\right)}^{k+1}}{{\Omega }_{i}^{k+1}}$, with $k!={\prod}_{j = 1}^{k}j$ and $j\ge \left|{\beta }_{i}-j\right|$. This means that $\frac{{\prod}_{j = 1}^{k}\left|{\beta }_{i}-j\right|}{{\prod}_{j = 1}^{k}j}>\frac{{\prod}_{j = 1}^{k+1}\left|{\beta }_{i}-j\right|}{{\prod}_{j = 1}^{k+1}j}$. Therefore, $\mathop{\rm{lim}}\limits_{k\to \infty }{R}_{k}\left({q}_{i}\right)=0$, and the Taylor series with the remainder (A.4) converges to the function $f\left({q}_{i}\right)={\hat{B}}_{i}{\beta }_{i}{q}_{i}^{{\beta }_{i}-1}$.

Up to the first term only, the Taylor expansion of the function $f\left({q}_{i}\right)$ has the form $\bar{f}\left({q}_{i}\right)={\hat{B}}_{i}{\beta }_{i}{\nu }_{i}^{{\beta }_{i}-1}+{\hat{B}}_{i}{\beta }_{i}\left({\beta }_{i}-1\right){\nu }_{i}^{{\beta }_{i}-2}\left({q}_{i}-{\nu }_{i}\right)$. Hence, (A.3) can be written as (9b), and the remainder (A.4) is

$${R}_{2}\left({q}_{i}\right)=\frac{{\left({q}_{i}-{\nu }_{i}\right)}^{2}}{2}{\hat{B}}_{i}{\beta }_{i}\left({\beta }_{i}-1\right)\left({\beta }_{i}-2\right){\Omega }_{i}^{{\beta }_{i}-3}.$$

(A.5)

Now estimate the error generated by replacing the solution of the original system (7) by the solution of the linearized system (9b). The functions F_i that describe the left-hand sides of Eqs. (7) are decreasing in Q_i in the neighborhood of the local maximum of the utility function (1), because $F_{i{Q_i}}^\prime = {u_i} - S_i^r < 0$ under condition (8). The functions ${\hat{F}}_{i}$ corresponding to the left-hand sides of Eqs. (9b) are decreasing as well due to the inequality

$$\hat F_{i{q_i}}^\prime = - 2\hat b - \hat bS_i^r - {\hat B_i}{\beta _i}\left( {{\beta _i} - 1} \right)\nu _i^{{\beta _i} - 2} < 0,$$

(A.6)

which holds under condition (8). Note that in formula (A.6), $\frac{\partial {S}_{i}^{r}}{\partial {q}_{i}}=\frac{\partial {S}_{i}^{r}}{\partial {Q}_{i}}\frac{\partial {Q}_{i}}{\partial {q}_{i}}=0$; for details, see [17].

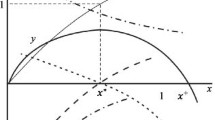
In accordance with Fig. 1, the deviation of the solution ${q}_{i}^{* }$ of system (9b) from the exact solution ${Q}_{i}^{* }$ of system (7) reduced to the units of measurement Q_i using the normalization procedure (A.1), i.e., the deviation $\Delta {Q}_{i}^{* }={Q}_{i}^{* }-{\hat{Q}}_{i}^{* }$, is

$$\left|\Delta {Q}_{i}^{* }\right|={Q}_{\rm{max}}\frac{\left|{R}_{2}\left({q}_{i}^{* }\right)\right|}{\left|{\hat{F}^{\prime} }_{i{q}_{i}}\right|}.$$

(A.7)

In view of the coefficients calculated by formulas (9c), the expression (A.6) takes the form

$$\begin{array}{rcl}\hat F_{i{q_i}}^\prime &=&-2{Q}_{\rm{max}}^{2}b-{Q}_{\rm{max}}^{2}b{S}_{i}^{r}-{Q}_{\rm{max}}^{{\beta }_{i}}{B}_{i}{\beta }_{i}\left({\beta }_{i}-1\right){\nu }_{i}^{{\beta }_{i}-2}\\ &=&-b{Q}_{\rm{max}}^{2}\left(2+{S}_{i}^{r}+\frac{{B}_{i}{\beta }_{i}\left({\beta }_{i}-1\right)}{b}{Q}_{\rm{max}}^{{\beta }_{i}-2}{\nu }_{i}^{{\beta }_{i}-2}\right).\end{array}$$

Due to (8a), this expression is equal to $\hat F_{i{q_i}}^\prime =-b{Q}_{\rm{max}}^{2}\left[2-({u}_{i{\rm{max}}}+2){\nu }_{i}^{{\beta }_{i}-2}+{S}_{i}^{r}\right]$, where ${u}_{i{\rm{max}}}={u}_{i}\left({Q}_{\rm{max}}\right)$. Substituting this expression and (A.5) into (A.7) gives

$$\begin{array}{rcl}\left|\Delta {Q}_{i}^{* }\right|&=&{Q}_{\rm{max}}\frac{{\left({q}_{i}-{\nu }_{i}\right)}^{2}}{2}\frac{{B}_{i}{Q}_{\rm{max}}^{{\beta }_{i}}{\beta }_{i}\left|{\beta }_{i}-1\right|\left|{\beta }_{i}-2\right|{\Omega }_{i}^{{\beta }_{i}-3}}{b{Q}_{\rm{max}}^{2}\left|2-\left({u}_{i{\rm{max}}}+2\right){\nu }_{i}^{{\beta }_{i}-2}+{S}_{i}^{r}\right|}\\ &=&{Q}_{\rm{max}}\frac{{\left({q}_{i}-{\nu }_{i}\right)}^{2}}{2}\frac{\left|{u}_{i{\rm{max}}}+2\right|\left|{\beta }_{i}-2\right|{\Omega }_{i}^{{\beta }_{i}-3}}{\left|2-\left({u}_{i{\rm{max}}}+2\right){\nu }_{i}^{{\beta }_{i}-2}+{S}_{i}^{r}\right|}.\end{array}$$

As was demonstrated in [17], $\left|{S}_{i}^{r}\right|<{S}_{\rm{max}}=\frac{m}{m-1-{\upsilon }_{\rm{max}}}$, where ${\upsilon }_{\rm{max}}=\frac{{\psi }_{\rm{max}}{\left(1+\sqrt{{\psi }_{\rm{max}}}\right)}^{2}}{m\sqrt{{\psi }_{\rm{max}}}}$, ψ_max ≈ 1, ψ_max < 1, and m denotes the number of environmental agents for agent i, m ≥ 2. Then, letting ψ_max = 1 − ε, where 0 < ε ≪ 1, yields the approximate formula ${\upsilon }_{\rm{max}}\approx \frac{1-\varepsilon }{m}{\left(2-\frac{\varepsilon }{2}\right)}^{2}{\left(1-\frac{\varepsilon }{2}\right)}^{-1}$. Therefore, in the general case,

$$\left|\Delta {Q}_{i}^{* }\right|\le {Q}_{\rm{max}}\frac{{\left({q}_{i}-{\nu }_{i}\right)}^{2}}{2}\frac{\left|{u}_{i{\rm{max}}}+2\right|\left|{\beta }_{i}-2\right|{\Omega }_{i}^{{\beta }_{i}-3}}{\left|2-\left({u}_{i{\rm{max}}}+2\right){\nu }_{i}^{{\beta }_{i}-2}+{S}_{\rm{max}}\right|}.$$

Since u_imax is bounded due to (8a), S_max is also bounded [17] for m ≥ 2. This means that if r_i → 0, then $\left|{q}_{i}-{\nu }_{i}\right|\to 0$, and consequently $\mathop{\rm{lim}}\limits_{r\to 0}\left|\Delta {Q}_{i}^{* }\right|=0$.

To proceed, study the existence of a solution of system (7). Consider the following system of equations, which obviously has the same solution as system (7):

$${f}_{i}^{r}=-{F}_{i}^{r}=-a+bQ+b{Q}_{i}\left(1+\sum _{j\in N\backslash i}{x}_{ij}^{r}\right)+{B}_{i}{\beta }_{i}{Q}_{i}^{{\beta }_{i}-1}=0,\quad {Q}_{i}>0,\quad i\in N.$$

(A.8)

Use the conditions formulated in Theorem 3 of the paper [21] for the vector function ${{\bf{f}}}^{r}=\left\{{f}_{i}^{r},i\in N\right\}$: if the Jacobian matrix ${\bf{J}} = \left\{ {f_{i{Q_j}}^\prime ,i,j \in N} \right\}$ of system (7) has diagonal dominance, i.e.,

$$f_{i{Q_i}}^\prime - \mathop \sum \limits_{j = 1,j \ne i}^N \left| {f_{i{Q_j}}^\prime } \right| > 0,\quad i \in N,$$

(A.9)

then system (A.8) has a unique solution. (Hereinafter, the superscript r is omitted.)

Since $f_{i{Q_i}}^\prime = - b\left( {{u_i} - {S_i}} \right)$, $f_{i{Q_j} = b\left( {1 + S_{i{Q_j}}^{r/}} \right)}^\prime$, and ${lim}_{{Q}_{j}\to \infty }\frac{\partial {S}_{i}^{r}}{\partial {Q}_{j}}=0$ (for details, see [17]), for sufficiently large Q_i the nth order Jacobian matrix J_n for system (A.8) has the form

$${{\bf{J}}}_{n}=\left[\begin{array}{cccc}-b\left({u}_{1}-{S}_{1}\right)&b&\ldots &b\\ b&-b\left({u}_{2}-{S}_{2}\right)&\ldots &b\\ \ldots &\ldots &\ldots &\ldots \\ b&b&\ldots &-b\left({u}_{n}-{S}_{n}\right)\end{array}\right]=b\left[\begin{array}{cccc}-{g}_{1}&1&\ldots &1\\ 1&-{g}_{2}&\ldots &1\\ \ldots &\ldots &\ldots &\ldots \\ 1&1&\ldots &-{g}_{n}\end{array}\right],$$

where g_i = u_i − S_i < 0, i ∈ N, due to (8). The inverse ${{\bf{J}}}_{n}^{-1}$ exists if the determinant of the Jacobian matrix is ΔJ_N ≠ 0; this determinant can be calculated [17] using the formula

$$\Delta {{\bf{J}}}_{n}=b\left(\mathop{\prod}\limits_{i = 1}^{n}\left(-{g}_{i}-1\right)+\mathop{\sum }\limits_{\gamma =1}^{n}\mathop{\prod}\limits_{j = 1\backslash \gamma }^{n}\left({g}_{i}-1\right)\right).$$

Therefore, the condition ΔJ_n ≠ 0 is equivalent to $\sum _{i\in N}\frac{1}{{g}_{i}+1}\ne 1$ and g_i ≠ 0 ∀ i ∈ N;  see [17]. In this case, condition (A.9) has the form $-{g}_{i}-\left(n-1\right)>0$, i ∈ N, which gives

$$n<\left|{u}_{i}-{S}_{i}^{r}\right|+1,\quad i\in N.$$

(A.10)

Note that system (7) does not satisfy the hypotheses of Theorems 1 and 2 of the paper [21]. (More specifically, the derivatives $F_{i{Q_i}}^\prime$ and $F_{i{Q_j}}^\prime$ do not have different signs.) Hence, the existence of a nonnegative solution cannot be guaranteed. This issue was considered in [22].

However, condition (A.10) is not necessary: if it does not hold, system (7) may still have a solution. Formulate a necessary condition for the existence of a solution of system (7), resting on its geometrical interpretation as the intersection point of the optimal response lines in the case n = 2. Assume that there exist functions ${\bar{F}}_{i}$ obtained by expressing the actions of agent i via the actions of his environmental agents (denoted by  − i) from Eqs. (7), i.e., the optimal response functions are ${Q}_{i}={\bar{F}}_{i}\left({Q}_{-i}\right)$. Introduce the deviations of the responses of agents i and j in the form ${G}_{ij}\left({Q}_{i},{Q}_{j}\right)={\bar{F}}_{i}-{\bar{F}}_{ij}^{-1}$, where ${\bar{F}}_{ij}^{-1}$ is the inverse of the function ${\bar{F}}_{j}$, obtained by expressing Q_i from F_j. If the solution $\left\{{Q}_{i}^{* },i\in N\right\}$ of system (7) exists, then

$${G}_{ij}\left({Q}_{i}^{* },{Q}_{j}^{* }\right)=0\,\forall i,j\in N.$$

(A.11)

Since $\bar F_{i{Q_j}}^\prime \frac{{\partial {Q_i}}}{{\partial {Q_j}}} = {x_{ji}}$ and ${\left({\bar{F}}_{ij}^{-1}\right)^{\prime} }_{{Q}_{j}}={u}_{i}-{S}_{i}$, where x_ji < 0 due to [17] and u_i − S_i < 0 by (8), the functions ${\bar{F}}_{i}$ and ${\bar{F}}_{ij}^{-1}$ are monotonically decreasing in Q_j on the corresponding interval where these conditions hold. Therefore, for ${Q}_{i}^{* }$ the functions ${G}_{ij}\left({Q}_{i}^{* },{Q}_{j}\right)$ are monotonically increasing in Q_j on the interval $\left({\bar{Q}}_{j},{Q}_{\rm{max}}\right)$ (or monotonically decreasing with an alternative form ${G}_{ij}={\bar{F}}_{ij}^{-1}-{\bar{F}}_{i}$), i.e.,

$$G_{ij{Q_j}}^\prime = \bar F_{i{Q_j}}^\prime - {\left( {\bar F_{ij}^{ - 1}} \right)^\prime }_{{Q_j}} > 0,$$

if ∣x_ji∣ < ∣u_i − S_i∣ (or ∣x_ji∣ > ∣u_i − S_i∣ under ${G}_{ij}={\bar{F}}_{ij}^{-1}-{\bar{F}}_{i}$). In other words, the monotonicity condition of the function G_ij has the form

$$\left|{x}_{ji}\right|\ne \left|{u}_{i}-{S}_{i}\right|.$$

(A.12)

In view of (8a), the boundary ${\bar{Q}}_{j}$ of this interval can be calculated from condition (8) using the formula

$${\bar{Q}}_{j}={\left(\frac{{B}_{j}{\beta }_{j}\left|{\beta }_{j}-1\right|}{b\left(2+{S}_{j}^{r}\right)}\right)}^{\frac{1}{2-{\beta }_{j}}}\quad {\rm{for}}\quad {\beta }_{j}<1,\quad {\bar{Q}}_{j}=0\quad {\rm{for}}\quad {\beta }_{j}>1.$$

The monotonic function is bounded on the closed interval ${A}_{j}=\left[{\bar{Q}}_{j},{Q}_{\rm{max}}\right]$, i.e., by the Weierstrass theorem,

$$m\le {G}_{ij}\left({Q}_{i}^{* },{Q}_{j}\right)\le M,\quad {\rm{where}}\quad m=\mathop{\rm{inf}}\limits_{{Q}_{j}\in {A}_{j}}{G}_{ij},\quad M=\mathop{\rm{sup}}\limits_{{Q}_{j}\in {A}_{j}}{G}_{ij}.$$

Due to condition (A.11), it follows that m ≤ 0 ≤ M. In accordance with the intermediate value theorem (also known as the Bolzano–Cauchy theorem), ${\bar{Q}}_{j}\le {Q}_{j}^{* }\le {Q}_{\rm{max}}$. Hence, the joint fulfillment of (A.12) and $0\le {\bar{Q}}_{j}\le {Q}_{\rm{max}}$ is a necessary condition for (A.11) on the interval $\left({\bar{Q}}_{j},{Q}_{\rm{max}}\right)$.

This condition becomes sufficient if, in addition, m and M have opposite signs:

$${G}_{ij}\left({Q}_{i}^{* },{\bar{Q}}_{j}\right){G}_{ij}\left({Q}_{i}^{* },{Q}_{\rm{max}}\right)<0.$$

(A.13)

(Under (A.12) the function G_ij is monotonic, and due to (A.13) the monotonicity interval includes the point ${G}_{ij}\left({Q}_{i}^{* },{Q}_{j}\right)=0.$) Derive a convenient form of condition (A.13): for the equations of system (7), ${\bar{F}}_{ij}^{-1}$ can be written as

$${\bar{F}}_{ij}^{-1}={Q}_{i}=\frac{a}{b}-\sum _{k\in N\backslash \left(i,j\right)}{Q}_{k}-{Q}_{j}-b{Q}_{j}\left(1+{S}_{j}\right)-\frac{{B}_{j}{\beta }_{j}{Q}_{j}^{{\beta }_{j}-1}}{b}.$$

(A.14)

Since conditions (A.13) must hold for all values of the actions, consider the case in which the actions of all agents, except for agents i and j, are equal to ${\bar{Q}}_{k}$. Then from the expression (A.14) it follows that

$${\bar{F}}_{ij}^{-1}\left({Q}_{\rm{max}}\right)\equiv {{\boldsymbol{\kappa }}}_{j}=\frac{a}{b}-\sum _{k\in N\backslash \left(i,j\right)}{\bar{Q}}_{k}-{Q}_{\rm{max}}-{Q}_{\rm{max}}\left(1+{S}_{j}\right)-\frac{{B}_{j}{\beta }_{j}{Q}_{\rm{max}}^{{\beta }_{j}-1}}{b}.$$

Let ${\bar{F}}_{i}\left({\bar{Q}}_{j}\right)<{\bar{F}}_{ij}^{-1}\left({\bar{Q}}_{j}\right)$, i.e., ${G}_{ij}\left({Q}_{i}^{* },{\bar{Q}}_{j}\right)<0;$ then, due to the monotonic decrease of ${\bar{F}}_{i}\left({Q}_{j}\right)$, the condition ${\bar{F}}_{i}\left({Q}_{\rm{max}}\right)>{\bar{F}}_{ij}^{-1}\left({Q}_{\rm{max}}\right)$, i.e., ${G}_{ij}\left({Q}_{i}^{* },{Q}_{\rm{max}}\right)>0$, holds for $\left|{x}_{ji}\right|<\left|{u}_{i}-{S}_{i}\right|$. Substituting Q_j = Q_max and ${\bar{Q}}_{k}$ into the ith equation of system (7) yields

$${F}_{i}\left({{\boldsymbol{\kappa }}}_{i}\right)=a-b\left({Q}_{\rm{max}}+\sum _{k\in N\backslash \left(i,j\right)}{\bar{Q}}_{k}+{{\boldsymbol{\kappa }}}_{i}\right)-b{{\boldsymbol{\kappa }}}_{i}\left(1+{S}_{i}\right)-{B}_{i}{\beta }_{i}{{\boldsymbol{\kappa }}}_{i}^{{\beta }_{i}-1}=0,$$

where κ_i denotes the solution of this equation. Since the functions F_i are monotonically decreasing under condition (8), the inequality ${F}_{i}\left({{\boldsymbol{\kappa }}}_{j}\right)>0$ implies κ_j < κ_i, and vice versa. Hence, condition (A.13) can be written as follows: if ${F}_{i}\left({{\boldsymbol{\kappa }}}_{j}\right)>0$ and $\left|{x}_{ji}\right|<\left|{u}_{i}-{S}_{i}\right|$ for all i, j ∈ N, then m and M have opposite signs. ■

Proof of Proposition 2. From Eqs. (9a) it follows that

$$\begin{array}{cccc}\hat{a}-\hat{b}{q}_{-i}-\hat{b}{q}_{i}-\hat{b}{q}_{i}\left(1+\mathop{\sum }\limits _{j\in N\backslash i}{x}_{ij}^{r}\right)-{\hat{B}}_{i}{\beta }_{i}{\nu }_{i}^{{\beta }_{i}-1}-{\hat{B}}_{i}{\beta }_{i}({\beta }_{i}-1){\nu }_{i}^{{\beta }_{i}-2}{q}_{i}+{\hat{B}}_{i}{\beta }_{i}({\beta }_{i}-1){\nu }_{i}^{{\beta }_{i}-2}{\nu }_{i}=0,\\ -\hat{b}\left(2+\frac{{\hat{B}}_{i}{\beta }_{i}\left({\beta }_{i}-1\right)}{\hat{b}}{\nu }_{i}^{{\beta }_{i}-2}+\mathop{\sum }\limits _{j\in N\backslash i}{x}_{ij}^{r}\right){q}_{i}-\hat{b}{q}_{-i}+\hat{a}-{\hat{B}}_{i}{\beta }_{i}{\nu }_{i}^{{\beta }_{i}-1}+{\hat{B}}_{i}{\beta }_{i}\left({\beta }_{i}-1\right){\nu }_{i}^{{\beta }_{i}-1}=0,\\ -\hat{b}\left(2+\frac{{\hat{B}}_{i}{\beta }_{i}\left({\beta }_{i}-1\right)}{\hat{b}}{\nu }_{i}^{{\beta }_{i}-2}+\mathop{\sum }\limits _{j\in N\backslash i}{x}_{ij}^{r}\right){q}_{i}-\hat{b}{q}_{-i}+\hat{a}-{\hat{B}}_{i}{\beta }_{i}\left(2-{\beta }_{i}\right){\nu }_{i}^{{\beta }_{i}-1}=0,\\ \left(2+\frac{{\hat{B}}_{i}{\beta }_{i}\left({\beta }_{i}-1\right)}{\hat{b}}{\nu }_{i}^{{\beta }_{i}-2}+\mathop{\sum }\limits _{j\in N\backslash i}{x}_{ij}^{r}\right){q}_{i}+{q}_{-i}-\frac{\hat{a}-{\hat{B}}_{i}{\beta }_{i}\left(2-{\beta }_{i}\right){\nu }_{i}^{{\beta }_{i}-1}}{\hat{b}}=0,\end{array}$$

which gives (10a).

System (10a) can be solved using Cramer’s rule. Also, take advantage of the materials includes in the Appendix of the paper [17]. The left-hand sides of system (10a) are analogous to system (A.2) from [17]. Therefore, the principal determinant has the form

$$\Delta =\mathop{\prod }\limits_{j = 1}^{n}\left({\delta }_{j}-1\right)+\mathop{\sum }\limits_{j=1}^{n}\mathop{\prod }\limits_{\gamma = 1\backslash j}^{n}\left({\delta }_{\gamma }-1\right).$$

The existence of a unique solution of system (10a) is established by the Cramer theorem [20]: a linear system of equations has a unique solution if the principal determinant is Δ ≠ 0. From the principal determinant formula it follows that

$$\frac{\Delta }{\mathop{\sum }\limits_{j=1}^{n}\left({\delta }_{j}-1\right)}=1+\mathop{\sum }\limits_{j=1}^{n}\frac{1}{{\delta }_{j}-1}\quad {\rm{for}}\quad {\delta }_{j}-1\ne 0\,\forall j\in N.$$

Therefore, the solution of system (10a) exists if

$$\mathop{\sum }\limits_{j=1}^{n}\frac{1}{{\delta }_{j}\,-\,1}\ne -1\wedge {\delta }_{j}-1\ne 0\,\forall j\in N.$$

The auxiliary determinant of system (10a) corresponding to the ith unknown is calculated via the following transformations:

• 1) The factor α_i is taken from the ith row.

• 2) Zeros are created in the ith column.

• 3) The determinant is expanded with respect to the elements of the ith column with decreasing order.

• 4) The resulting determinant is sequentially expanded into the sums of determinants for each row.

• 5) In this expansion the determinants having the same rows (columns) are equal to zero, and the other determinants correspond to either the principal determinant or the auxiliary determinant of system (A.2) from the paper [17].

For example, for i = 2 these transformations have the form

$$\begin{array}{ccc}{\Delta }_{2}=\left|\begin{array}{ccc}{\delta }_{1}&{\alpha }_{1}&1\\ 1&{\alpha }_{2}&1\\ 1&{\alpha }_{3}&{\delta }_{3}\end{array}\right|={\alpha }_{2}\left|\begin{array}{ccc}{\delta }_{1}&\frac{{\alpha }_{1}}{{\alpha }_{2}}&1\\ 1&1&1\\ 1&\frac{{\alpha }_{3}}{{\alpha }_{2}}&{\delta }_{3}\end{array}\right|={\alpha }_{2}\left|\begin{array}{ccc}{\delta }_{1}-\frac{{\alpha }_{1}}{{\alpha }_{2}}&0&1-\frac{{\alpha }_{1}}{{\alpha }_{2}}\\ 1&1&1\\ 1-\frac{{\alpha }_{3}}{{\alpha }_{2}}&0&{\delta }_{3}-\frac{{\alpha }_{3}}{{\alpha }_{2}}\end{array}\right|={\alpha }_{2}\left|\begin{array}{cc}{\delta }_{1}-\frac{{\alpha }_{1}}{{\alpha }_{2}}&1-\frac{{\alpha }_{1}}{{\alpha }_{2}}\\ 1-\frac{{\alpha }_{3}}{{\alpha }_{2}}&{\delta }_{3}-\frac{{\alpha }_{3}}{{\alpha }_{2}}\end{array}\right|\\ ={\alpha }_{2}\left|\begin{array}{cc}{\delta }_{1}&1\\ 1&{\delta }_{3}\end{array}\right|-{\alpha }_{2}\frac{{\alpha }_{3}}{{\alpha }_{2}}\left|\begin{array}{cc}{\delta }_{1}&1\\ 1&1\end{array}\right|-{\alpha }_{2}\frac{{\alpha }_{1}}{{\alpha }_{2}}\left|\begin{array}{cc}1&1\\ 1&{\delta }_{3}\end{array}\right|+\frac{{\alpha }_{3}}{{\alpha }_{2}}\frac{{\alpha }_{3}}{{\alpha }_{2}}\left|\begin{array}{cc}1&1\\ 1&1\end{array}\right|\\ ={\alpha }_{2}{\Delta }_{-2}-{\alpha }_{3}\left({\delta }_{1}-1\right)-{\alpha }_{1}\left({\delta }_{2}-1\right),\end{array}$$

where Δ_−i is the principal determinant of system (10a) without the ith equation and without the ith unknown. For the auxiliary determinant of a fourth-order system (e.g., for i = 1), these transformations have the form

$$\begin{array}{cccc}{\Delta }_{1}=\left|\begin{array}{cccc}{\alpha }_{1}&1&1&1\\ {\alpha }_{2}&{\delta }_{2}&1&1\\ {\alpha }_{3}&1&{\delta }_{3}&1\\ {\alpha }_{4}&1&1&{\delta }_{4}\end{array}\right|={\alpha }_{1}\left|\begin{array}{cccc}1&1&1&1\\ 0&{\delta }_{2}-\frac{{\alpha }_{2}}{{\alpha }_{1}}&1-\frac{{\alpha }_{2}}{{\alpha }_{1}}&1-\frac{{\alpha }_{2}}{{\alpha }_{1}}\\ 0&1-\frac{{\alpha }_{3}}{{\alpha }_{1}}&{\delta }_{3}-\frac{{\alpha }_{3}}{{\alpha }_{1}}&1-\frac{{\alpha }_{3}}{{\alpha }_{1}}\\ 0&1-\frac{{\alpha }_{4}}{{\alpha }_{1}}&1-\frac{{\alpha }_{4}}{{\alpha }_{1}}&{\delta }_{4}-\frac{{\alpha }_{4}}{{\alpha }_{1}}\end{array}\right|={\alpha }_{1}\left|\begin{array}{ccc}{\delta }_{2}-\frac{{\alpha }_{2}}{{\alpha }_{1}}&1-\frac{{\alpha }_{2}}{{\alpha }_{1}}&1-\frac{{\alpha }_{2}}{{\alpha }_{1}}\\ 1-\frac{{\alpha }_{3}}{{\alpha }_{1}}&{\delta }_{3}-\frac{{\alpha }_{3}}{{\alpha }_{1}}&1-\frac{{\alpha }_{3}}{{\alpha }_{1}}\\ 1-\frac{{\alpha }_{4}}{{\alpha }_{1}}&1-\frac{{\alpha }_{4}}{{\alpha }_{1}}&{\delta }_{4}-\frac{{\alpha }_{4}}{{\alpha }_{1}}\end{array}\right|\\ ={\alpha }_{1}\left|\begin{array}{ccc}{\delta }_{2}&1&1\\ 1&{\delta }_{3}&1\\ 1&1&{\delta }_{4}\end{array}\right|-{\alpha }_{1}\frac{{\alpha }_{4}}{{\alpha }_{1}}\left|\begin{array}{ccc}{\delta }_{2}&1&1\\ 1&{\delta }_{3}&1\\ 1&1&1\end{array}\right|-{\alpha }_{1}\frac{{\alpha }_{3}}{{\alpha }_{1}}\left|\begin{array}{ccc}{\delta }_{2}&1&1\\ 1&1&1\\ 1&1&{\delta }_{4}\end{array}\right|\\ +\,{\alpha }_{1}\frac{{\alpha }_{3}}{{\alpha }_{1}}\frac{{\alpha }_{4}}{{\alpha }_{1}}\left|\begin{array}{ccc}{\delta }_{2}&1&1\\ 1&1&1\\ 1&1&1\end{array}\right|-{\alpha }_{1}\frac{{\alpha }_{2}}{{\alpha }_{1}}\left|\begin{array}{ccc}1&1&1\\ 1&{\delta }_{3}&1\\ 1&1&{\delta }_{4}\end{array}\right|+{\alpha }_{1}\frac{{\alpha }_{2}}{{\alpha }_{1}}\frac{{\alpha }_{4}}{{\alpha }_{1}}\left|\begin{array}{ccc}1&1&1\\ 1&{\delta }_{3}&1\\ 1&1&1\end{array}\right|\\ ={\alpha }_{1}{\Delta }_{-1}-{\alpha }_{2}\left({\delta }_{3}-1\right)\left({\delta }_{4}-1\right)-{\alpha }_{3}\left({\delta }_{2}-1\right)\left({\delta }_{4}-1\right)-{\alpha }_{4}\left({\delta }_{2}-1\right)\left({\delta }_{3}-1\right).\end{array}$$

The induction-based generalization of these expressions to the class of arbitrary order systems leads to the formula

$${\Delta }_{i}={\alpha }_{i}{\Delta }_{-i}-\mathop{\sum }\limits_{j=1\backslash i}^{n}\left[{\alpha }_{j}\mathop{\prod }\limits_{\gamma = 1\backslash i,j}^{n}\left({\delta }_{\gamma }-1\right)\right],$$

which in turn gives formula (10b).

Demonstrate in which cases the roots (10c) satisfy conditions (10d), i.e.,

$$\left|{q}_{i}-{\nu }_{i}\right|<{r}_{i},\quad {\Omega }_{i}={\nu }_{i}+{\theta }_{i}\left({q}_{i}-{\nu }_{i}\right),\quad {\theta }_{i},{\nu }_{i}\in \left(0,1\right),\quad {r}_{i}\in \left(0,{\Omega }_{i}\right),\quad {\nu }_{i}<{q}_{i},\quad i\in N.$$

(A.15)

The conditions $\left|{q}_{i}-{\nu }_{i}\right|<{r}_{i}$ and ν_i < q_i jointly hold if for the roots (10c) there exists a function ${G}_{i}={q}_{i}^{* }\left({\nu }_{i}\right)-{\nu }_{i}$ such that ${G}_{i}\in \left(0,{r}_{i}\right)$ on the interval ${\nu }_{i}\in \left(0,1\right)$. In this case, the condition ${r}_{i}\in \left(0,{\Omega }_{i}\right)$ is true if ${\Omega }_{i}={\nu }_{i}+{\theta }_{i}\left({q}_{i}^{* }-{\nu }_{i}\right)>{r}_{i}$, i.e., ${\theta }_{i}>\frac{{r}_{i}-{\nu }_{i}}{{q}_{i}^{* }-{\nu }_{i}}>\frac{{r}_{i}-{\nu }_{i}}{{r}_{i}}$. Hence, $1>{\theta }_{i}>\frac{{r}_{i}-{\nu }_{i}}{{r}_{i}}$. Note that in this inequality, the case r_i − ν_i < 0 is possible for small values ν_i. Therefore, in this case condition (A.15) holds for any ${\theta }_{i}\in \left(0,1\right)$.

Since the function G_i is continuous under condition (10b), the inclusion G_i ∈ (0, r_i) holds if on the interval ${\nu }_{i}\in \left(0,1\right)$ the function G_i has at least one zero. In the sequel, the subscript i will be omitted, because conditions (A.15) must hold for all i ∈ N. From (10c) it follows that

$${q}^{* }=\frac{\alpha \left({\chi }^{n-1}+\left(n-1\right){\chi }^{n-2}\right)-\left(n-1\right)\alpha {\chi }^{n-2}}{{\chi }^{n}+n{\chi }^{n-1}}=\frac{\alpha }{\chi +n},\quad {\rm{where}}\quad \chi =\delta -1.$$

Finally analyze the behavior of the function G_i at the boundaries of the interval $\nu \in \left(0,1\right)$. For this purpose, find the right-hand limits of the coefficients $\alpha \left(\nu \right),\delta \left(\nu \right)$ as ν → 0 + 0:

$$\begin{array}{rcl}\mathop{\rm{lim}}\limits_{\nu \to 0+0}\alpha &=&\left\{\begin{array}{ll}{\mu }_{1}&{\rm{for}}\,\beta >1\\ -\infty &{\rm{for}}\,\beta <1,\end{array}\right.\\ \mathop{\rm{lim}}\limits_{\nu \to 0+0}\delta &=&\left\{\begin{array}{ll}\infty &{\rm{for}}\,\beta >1\\ -\infty &{\rm{for}}\,\beta <1,\end{array}\right.\end{array}\quad {\rm{where}}\,{\mu }_{1}=\frac{a}{b{Q}_{\rm{max}}}.$$

Hence, lim_ν→0+0q* = 0, which means that lim_ν→0+0G = − 0. In other words, as ν → 0 on the right the function G → 0 from below, i.e., $G\left(\nu \to 0+0\right)<0$. Find the left-hand limits of the coefficients $\alpha \left(\nu \right),\delta \left(\nu \right)$ as ν → 1 − 0:

$$\mathop{\rm{lim}}\limits_{\nu \to 1-0}\alpha =\frac{\hat{a}-{\hat{B}}_{i}{\beta }_{i}\left(2-{\beta }_{i}\right)}{\hat{b}}=\frac{a}{b{Q}_{\rm{max}}}+\frac{\beta }{\beta -1}\left({u}_{\rm{max}}+2\right)\approx \frac{a}{b{Q}_{\rm{max}}},$$

since $\mathop{\rm{lim}}\limits_{Q\to {Q}_{\rm{max}}}\left({u}_{i}+2\right)=0$ by (8a);

$$\mathop{\rm{lim}}\limits_{\nu \to 1-0}\delta =2+\frac{{\hat{B}}_{i}{\beta }_{i}\left({\beta }_{i}-1\right)}{\hat{b}}+{S}_{i}^{r}=-\left({u}_{\rm{max}}-{S}_{i}^{r}\right)>0$$

due to (8). Therefore,

$$\mathop{\rm{lim}}\limits_{\nu \to 1-0}{q}^{* }=\frac{a}{b{Q}_{\rm{max}}}\frac{1}{-\left({u}_{\rm{max}}-{S}_{i}^{r}\right)-1+n}.$$

In accordance with [17], $\left|{S}_{i}^{r}\right|\le 1$, which gives

$$\mathop{\rm{lim}}\limits_{\nu \to 1-0}{q}^{* }\ge \frac{a}{b{Q}_{\rm{max}}}\frac{1}{-{u}_{\rm{max}}+n}.$$

This number exceeds 1, i.e.,

$$\mathop{\rm{lim}}\limits_{\nu \to 1-0}G=+0,$$

under the condition

$$\frac{a}{b{Q}_{\rm{max}}}\frac{1}{-{u}_{\rm{max}}+n}>1\Rightarrow n<\frac{a}{b{Q}_{\rm{max}}}+{u}_{\rm{max}}.$$

The function G_i changes sign on the interval ${\nu }_{i}\in \left(0,1\right)$. Hence, by the Cauchy theorem [20] it has at least one zero on this interval. ■