-
PDF
- Split View
-
Views
-
Cite
Cite
John B Carlin, Lyle C Gurrin, Jonathan AC Sterne, Ruth Morley, Terry Dwyer, Regression models for twin studies: a critical review, International Journal of Epidemiology, Volume 34, Issue 5, October 2005, Pages 1089–1099, https://doi.org/10.1093/ije/dyi153
Close - Share Icon Share
Abstract
Twin studies have long been recognized for their value in learning about the aetiology of disease and specifically for their potential for separating genetic effects from environmental effects. The recent upsurge of interest in life-course epidemiology and the study of developmental influences on later health has provided a new impetus to study twins as a source of unique insights. Twins are of special interest because they provide naturally matched pairs where the confounding effects of a large number of potentially causal factors (such as maternal nutrition or gestation length) may be removed by comparisons between twins who share them. The traditional tool of epidemiological ‘risk factor analysis’ is the regression model, but it is not straightforward to transfer standard regression methods to twin data, because the analysis needs to reflect the paired structure of the data, which induces correlation between twins. This paper reviews the use of more specialized regression methods for twin data, based on generalized least squares or linear mixed models, and explains the relationship between these methods and the commonly used approach of analysing within-twin-pair difference values. Methods and issues of interpretation are illustrated using an example from a recent study of the association between birth weight and cord blood erythropoietin. We focus on the analysis of continuous outcome measures but review additional complexities that arise with binary outcomes. We recommend the use of a general model that includes separate regression coefficients for within-twin-pair and between-pair effects, and provide guidelines for the interpretation of estimates obtained under this model.
Epidemiological data analysis concerning risk factors relies heavily on regression models, which seek to ‘explain’ the variation in an outcome of interest in terms of differences in one or more risk factors (which we may refer to more generally as covariates). Regression modelling provides a flexible set of tools for examining such associations while allowing either for potentially confounding effects of other factors or for interaction effects (effect modification). Epidemiologists are well aware that despite the use of terms such as ‘effect’ for a regression coefficient, regression modelling only describes associations among variables, so that inferences about causation must be made with extreme caution.1 A prominent example of the use of regression models in epidemiological studies of the early life origins of disease has been in relating cardiovascular outcomes in later childhood or adulthood to birth weight. Several studies have shown that people with lower birth weight tend to have slightly higher risk of coronary heart disease.2,3
The paired structure of data arising from twins presents a number of challenges in the construction, estimation, and interpretation of regression models. Although there has been an explosion of statistical literature on methods for modelling correlated data, there has been relatively little discussion of these methods in the epidemiological literature, and, so far as we are aware, none in the specific context of twins. At the same time, interest in using data from twins to illuminate aetiological questions in life-course epidemiology continues to grow. For example, a recent systematic review identified 10 studies of twins, which examined the association between birth weight and later blood pressure.4 This review failed to define clearly the meanings of ‘unpaired’ and ‘paired’ analyses, and statistical methods used under each of these names differed among these studies.
In this paper, we aim to explain in non-technical terms the distinctions and connections among different regression modelling approaches that may be adopted for twin data, and provide recommendations on how they should be used and interpreted. We focus primarily on the analysis of a continuous outcome measure where the covariate of interest is also continuous, for several reasons. First, this type of analysis has been especially prominent in recent epidemiological studies of twins.4–10 Second, outcomes of this kind support a more detailed unpacking of associations that may differ when examined within twin pairs and between twin pairs compared with binary or ordinal outcomes. Third, the statistical issues associated with fitting some of the models of interest (using so-called random effects) become more complex with binary outcomes.
For expository purposes, we use an example in which we investigated shared (maternal) and individual (twin) factors that may be predictive of birth weight: thus birth weight is the outcome of interest, rather than a potential predictor of later cardiovascular outcomes as in much of the recent literature. In particular, there is interest in factors that may be associated with growth restriction and/or pre-term delivery. Twin pregnancies offer a unique opportunity to study the contributions of and interactions between shared and individual factors, for example, between maternal factors (common to both twins) and ‘supply line’ factors (e.g. placental, which may differ between twins). In the present example, we examined the association between cord blood erythropoietin (EPO) and birth weight.11
We begin by introducing the dataset, and then we provide a detailed description of three different regression-based approaches to the data, exploring the rationale for the models that underlie the methods. All three approaches have been used and recommended in various combinations in order to investigate the extent to which associations may reflect factors shared by two twins in a pair [e.g. fixed maternal factors such as diet and socioeconomic background, genes for monozygotic (MZ) twins] vs factors that could differ between twins [e.g. fetal nutrient supply line, genes for dizygotic twins (DZ)].5,7–9 After discussing the results of these three analytic approaches for the example, extensions of the methods to handle a dichotomous outcome are considered. Finally, some general discussion and recommendations for practice are offered, along with further comments on other issues such as the potential use of zygosity information for assessing the importance of genetic effects.
Example: birth weight and EPO
In a recently published analysis,11 we examined the association between birth weight standard deviation score (or ‘Z-score’, the birth weight standardized to a reference distribution for gestational age and sex), as outcome, and cord blood EPO, as independent variable. The rationale for modelling birth weight in terms of EPO was that the latter is a marker for hypoxic stress in utero, and the investigators were interested in the hypothesis that higher levels of EPO would be associated with growth restriction and, thus, lower birth weight for gestational age. All analyses used log2 EPO, so that regression coefficients can be interpreted as the mean difference in outcome per doubling of EPO concentration.
In Table 1 we present a range of results from various regression analyses of the birth weight–EPO data, from 110 DZ twin pairs. Initially we ignore the presence of several covariates of interest, although the full analysis focused on possible effect modification by some of these covariates. We checked that it was reasonable to assume a linear relationship between birth weight and log EPO.
Estimates of regression coefficients representing linear association between birth weight Z-score and log2 EPO level for 220 DZ twin infants, under alternative regression approaches as described in the text
| Parameter . | Estimation method . | Estimate . | SE . | P-value . | 95% CI . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model (1) | ||||||||||
| βC | Standard OLS | −0.194 | 0.0440 | <0.001 | (−0.281 to −0.107) | |||||
| OLS + ‘robust’ SE | −0.194 | 0.0396 | <0.001 | (−0.273 to −0.116) | ||||||
| GLS/REML | −0.236 | 0.0454 | <0.001 | (−0.325 to −0.147) | ||||||
| GLS/MLE | −0.235 | 0.0467 | <0.001 | (−0.327 to −0.144) | ||||||
| GLS/GEE | −0.235 | 0.0413 | <0.001 | (−0.284 to −0.122) | ||||||
| Model (2) | ||||||||||
| βW | GLS/REML | −0.379 | 0.0691 | <0.001 | (−0.515 to −0.244) | |||||
| βB | −0.133 | 0.0588 | 0.024 | (−0.248 to −0.018) | ||||||
| βW | GLS/MLE | −0.379 | 0.0688 | <0.001 | (−0.514 to −0.247) | |||||
| βB | −0.133 | 0.0583 | 0.022 | (−0.247 to −0.019) | ||||||
| βW | GLS/GEE | −0.379 | 0.0573 | <0.001 | (−0.492 to −0.267) | |||||
| βB | −0.133 | 0.0453 | 0.003 | (−0.222 to −0.044) | ||||||
| Model (3) | ||||||||||
| βW | OLS through origin | −0.379 | 0.0691 | <0.001 | (−0.516 to −0.243) | |||||
| Parameter . | Estimation method . | Estimate . | SE . | P-value . | 95% CI . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model (1) | ||||||||||
| βC | Standard OLS | −0.194 | 0.0440 | <0.001 | (−0.281 to −0.107) | |||||
| OLS + ‘robust’ SE | −0.194 | 0.0396 | <0.001 | (−0.273 to −0.116) | ||||||
| GLS/REML | −0.236 | 0.0454 | <0.001 | (−0.325 to −0.147) | ||||||
| GLS/MLE | −0.235 | 0.0467 | <0.001 | (−0.327 to −0.144) | ||||||
| GLS/GEE | −0.235 | 0.0413 | <0.001 | (−0.284 to −0.122) | ||||||
| Model (2) | ||||||||||
| βW | GLS/REML | −0.379 | 0.0691 | <0.001 | (−0.515 to −0.244) | |||||
| βB | −0.133 | 0.0588 | 0.024 | (−0.248 to −0.018) | ||||||
| βW | GLS/MLE | −0.379 | 0.0688 | <0.001 | (−0.514 to −0.247) | |||||
| βB | −0.133 | 0.0583 | 0.022 | (−0.247 to −0.019) | ||||||
| βW | GLS/GEE | −0.379 | 0.0573 | <0.001 | (−0.492 to −0.267) | |||||
| βB | −0.133 | 0.0453 | 0.003 | (−0.222 to −0.044) | ||||||
| Model (3) | ||||||||||
| βW | OLS through origin | −0.379 | 0.0691 | <0.001 | (−0.516 to −0.243) | |||||
βC = common (‘twins-as-individuals’) regression coefficient; βW = within-pair regression coefficient; and βB = between-pair regression coefficient.
Estimates of regression coefficients representing linear association between birth weight Z-score and log2 EPO level for 220 DZ twin infants, under alternative regression approaches as described in the text
| Parameter . | Estimation method . | Estimate . | SE . | P-value . | 95% CI . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model (1) | ||||||||||
| βC | Standard OLS | −0.194 | 0.0440 | <0.001 | (−0.281 to −0.107) | |||||
| OLS + ‘robust’ SE | −0.194 | 0.0396 | <0.001 | (−0.273 to −0.116) | ||||||
| GLS/REML | −0.236 | 0.0454 | <0.001 | (−0.325 to −0.147) | ||||||
| GLS/MLE | −0.235 | 0.0467 | <0.001 | (−0.327 to −0.144) | ||||||
| GLS/GEE | −0.235 | 0.0413 | <0.001 | (−0.284 to −0.122) | ||||||
| Model (2) | ||||||||||
| βW | GLS/REML | −0.379 | 0.0691 | <0.001 | (−0.515 to −0.244) | |||||
| βB | −0.133 | 0.0588 | 0.024 | (−0.248 to −0.018) | ||||||
| βW | GLS/MLE | −0.379 | 0.0688 | <0.001 | (−0.514 to −0.247) | |||||
| βB | −0.133 | 0.0583 | 0.022 | (−0.247 to −0.019) | ||||||
| βW | GLS/GEE | −0.379 | 0.0573 | <0.001 | (−0.492 to −0.267) | |||||
| βB | −0.133 | 0.0453 | 0.003 | (−0.222 to −0.044) | ||||||
| Model (3) | ||||||||||
| βW | OLS through origin | −0.379 | 0.0691 | <0.001 | (−0.516 to −0.243) | |||||
| Parameter . | Estimation method . | Estimate . | SE . | P-value . | 95% CI . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model (1) | ||||||||||
| βC | Standard OLS | −0.194 | 0.0440 | <0.001 | (−0.281 to −0.107) | |||||
| OLS + ‘robust’ SE | −0.194 | 0.0396 | <0.001 | (−0.273 to −0.116) | ||||||
| GLS/REML | −0.236 | 0.0454 | <0.001 | (−0.325 to −0.147) | ||||||
| GLS/MLE | −0.235 | 0.0467 | <0.001 | (−0.327 to −0.144) | ||||||
| GLS/GEE | −0.235 | 0.0413 | <0.001 | (−0.284 to −0.122) | ||||||
| Model (2) | ||||||||||
| βW | GLS/REML | −0.379 | 0.0691 | <0.001 | (−0.515 to −0.244) | |||||
| βB | −0.133 | 0.0588 | 0.024 | (−0.248 to −0.018) | ||||||
| βW | GLS/MLE | −0.379 | 0.0688 | <0.001 | (−0.514 to −0.247) | |||||
| βB | −0.133 | 0.0583 | 0.022 | (−0.247 to −0.019) | ||||||
| βW | GLS/GEE | −0.379 | 0.0573 | <0.001 | (−0.492 to −0.267) | |||||
| βB | −0.133 | 0.0453 | 0.003 | (−0.222 to −0.044) | ||||||
| Model (3) | ||||||||||
| βW | OLS through origin | −0.379 | 0.0691 | <0.001 | (−0.516 to −0.243) | |||||
βC = common (‘twins-as-individuals’) regression coefficient; βW = within-pair regression coefficient; and βB = between-pair regression coefficient.
The regression models
To describe the models we introduce some notation. We use Y to denote the outcome and X the covariate of immediate interest, with i used to index twin pairs and j =1, 2 to index individual twins within pairs, so Yij, Xij, represent, respectively, the outcome and covariate value for the jth twin of the ith pair. The expected value of Yij, given the value of Xij, is denoted by E(Yij).
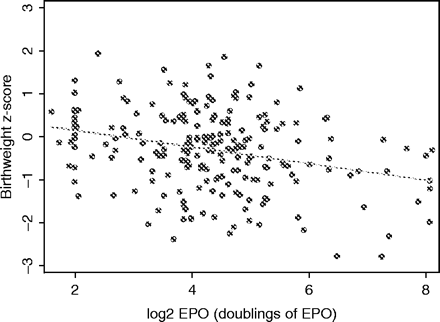
(1) Regression on X alone (treating twins ‘as individuals,’ ignoring paired nature of data)
Scatter plot of birth weight Z-scores vs log2 EPO level, for 220 DZ twins, treating all twins as unrelated individuals, with OLS regression line superimposed
First, the standard method for calculating standard errors when using OLS is not correct in the context of twin data. Assuming independence wrongly treats each observation as providing the same information about the regression slope. This may lead to standard errors that are either too large or too small (depending on the underlying correlation structure) and, hence, to confidence intervals (CIs) and P-values that are invalid. Methods of estimation that explicitly allow for the correlation structure, such as the generalized least squares (GLS) approaches described below, will produce valid standard errors. For completeness, however, we note that it is possible to produce ‘robust’ (information-sandwich) standard errors and CIs for OLS estimates, where the correlation structure is acknowledged in calculating standard errors but not used in estimating the regression parameters12 (see Table 1 for illustration).
The second problem relates to the properties of the OLS estimates of the regression coefficients, not just the standard error estimation. In large samples the OLS estimates are unbiased, so the method is not strictly invalid, if the robust standard error calculation is used. However, it can be improved upon, since the paired structure of the data provides additional information that can contribute to finding a better straight-line fit. Formalization of this argument underlies the GLS method of estimation, which applies differential weighting to the data points in a manner that reflects the correlation structure. A simple model allowing a common correlation within each pair of twins and independence between unrelated individuals is the natural starting point. We use the term GLS to refer to the weighted estimation of regression parameters using particular values for the error variance and correlation—the parameters required to describe the variability and correlation around the mean values determined by Equation (1); see below. These variance–covariance parameters need to be estimated from the data, and particular implementations of ‘GLS’ differ according to how this estimation is performed, although the practical differences are minimal for twin data.
(2) Multiple regression: including the co-twin X value in the model
The third problem with OLS regression goes beyond issues relating to the methods used for fitting the model: it may be that the specification for the expected value of Yij is inadequate. Model (1) assumes that the average difference between outcome (Y) values for a given difference between covariate (X) values is the same whether we are comparing two unrelated individuals or two twins. This assumption may be untrue, and to investigate it we need to fit a more general regression model that allows the covariate effect to differ within and between twin pairs. Another way of expressing this is to say that there may be information about the value of Yij in the co-twin's X value as well as in the subject's own X. Note that this issue, concerning the appropriate specification of the model for the expected value (mean) of Yij given the X values, is quite distinct from the matter of the statistical technique used to obtain estimates of the model parameters.
Some insight into the interpretation of formulation (2) may be obtained by considering alternative possible values of the two coefficients, βW and βB. To begin with, suppose that βW = βB. In this case the model reduces to model (1) since the effect of the twin-pair mean cancels out, and thus the expected difference in Y for a given difference in X is the same whether we compare within or between twin pairs.
We illustrate this model and other possibilities with a diagram using a small number of ‘randomly generated’ hypothetical twin pairs, with X and Y distributions similar to those of X = log EPO and Y = birth weight Z-score in the example (except that the strength of the linear trends has been increased to make the distinctions between models clearer). The first row of Figure 2 illustrates model (1), which is the special case of model (2) where βW and βB are identical. In the row labelled 2a, the between-pair coefficient βB is zero and the only systematic source of variation in Yij is within-pair variation in X: an individual's outcome can be predicted by how different their X value is from their co-twin's, but once this is accounted for the outcome does not depend on the value of X. If this model were to hold it would appear to rule out hypotheses that involve X representing common causal factors (maternal, environmental, and genetic) shared between twins. Row 2b illustrates the other extreme possibility, where the within-pair coefficient βW is zero and the only systematic variation relates to the ‘common’ factor represented by the average X value of the two twins. If this model were true, then it would suggest that outcome variation is explained only by between-pair variation in X, although it is important to note that there could well be other within-pair factors operating through pathways unrelated to X. Row 2c illustrates a general case, where both coefficients are non-zero and of the same sign, but not equal.
Graphs of expected Y vs X for 6 hypothetical twin pairs, with a fixed set of X values. In each row, the left-hand panel shows expected (mean) value of Y according to regression model: (1) simple linear decline with X, βC = −0.4 [model (1), with jitter added so the lines for each twin can be distinguished from each other]; (2a) βW = −0.8, βB = 0; (2b) βW = 0, βB = −0.4; (2c) βW = −0.8, βB = −0.4. Right-hand panel for each case shows hypothetical (simulated) data where correlated random errors with between-subject and within-subject standard deviation both 0.5 has been added to the mean values in the left-hand panel. To maximize comparability between panels, the same simulated errors are used in each case. Note that by chance some twin pairs have very similar X values (e.g. pair 4) while others have quite different values (pairs 2, 3)
Given a set of (X, Y) data on twin pairs, there is again a variety of estimation methods that could be applied to fit model (2) and obtain estimates of the two parameters βW and βB, along with a test statistic to assess the null hypothesis that βW and βB are equal. It turns out that all of the standard methods, including OLS, lead to the same (point) estimates for these regression coefficients.14 Again, however, valid standard errors are only obtained by methods that respect the paired structure of the data, for instance MLE under a model allowing correlation within pairs, or the robust sandwich variance method. Before trusting the results of any such analysis one should check that the usual assumptions of linear regression are satisfied, in particular that the scale of measurement of Y is such that the additive model specification for between-pair and within-pair effects is reasonable.
(3) Regression using twin-pair difference values
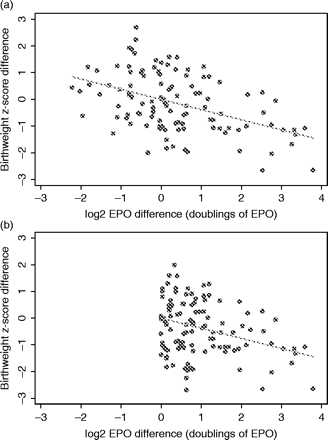
Scatter plot of difference values for birth weight Z-score vs log2 EPO, where difference values were obtained (a) as first-born twin minus second-born twin, and (b) ordered according to EPO value (so the difference in EPO values is always positive). Despite the apparently different scatter, the estimated regression slope, for the line constrained through the origin, is the same from both sets of difference values
Results and interpretation for the example
We display estimates using the three approaches for the EPO-birth weight data from 110 DZ twin pairs in Table 1. In this example the estimated value of βW is considerably larger (more negative) than that of βB. A test that the two coefficients are equal reveals strong evidence against the null hypothesis (P = 0.007 by likelihood ratio or Wald test), so the adjustment for pair-level factors (by way of the pair mean term) clearly improves the fit of the model. Further insight can be gained from the fact that the twin-specific deviation from the pair mean,
In summary, fitting model (1) for the expected value of Y essentially ignores the pairing between the twins, fitting a standard linear regression that treats the twins ‘as individuals’. In this example we find an estimated regression coefficient
Inclusion of other covariates, effect modification
In many twin studies the research question of interest relates not simply to the strength of linear association between outcome and covariate considered across all twins, but to whether a linear association is modified by twin characteristics, including environmental and genetic factors. For example, Morley et al.11 examined whether the negative birth size–EPO association was stronger in infants delivered by elective Caesarean section than by other delivery modes. They focussed on the within-pair association measured by βW since this is free of any confounding due to shared maternal, genetic, or environmental factors. These analyses can be performed by including interaction terms involving other covariates in model (2) or in the paired-difference approach of model (3), but the more general model (2) approach allows examination of between-pair effects and related interactions as well.
Models for dichotomous outcomes
Many epidemiological studies use dichotomous outcomes rather than continuous measures. We have concentrated most of this paper on continuous outcomes because this has been the focus of most of the recent interest in this type of twin study regression modelling. One reason for this may be that there is more scope to distinguish between different sources of variation when examining a continuously varying measure than a simple dichotomy. In addition, however, although the same general considerations carry over from the previous discussion to fitting logistic regression models to binary outcomes, there is an important additional complication. We will outline this briefly in the context of a further illustrative analysis involving the association of EPO level with the risk of the baby being born at low birth weight. For the purpose of this illustration we define low birth weight as being >1 SD below expected weight, based on gender and gestational age at birth; 47/220 (21%) of twins met this definition.
Results for the EPO example are displayed in Table 2. The standard logistic regression and GEE approaches produce only slightly different estimates of the common odds ratio parameter [exp(βC)], while the ML estimate of
Estimates of odds ratios from logistic regression models for the association between risk of low birth weight (defined as Z-score < −1) and log2 EPO level for 220 DZ twin infants, under alternative regression approaches as described in the text
| Parameter . | Estimation method . | Estimate . | P-value . | 95% CI . | ||||
|---|---|---|---|---|---|---|---|---|
| Model (1) | ||||||||
| βC | Standard GLM | 1.41 | 0.005 | (1.11–1.79) | ||||
| βC | GLM + ‘robust’ SE | 1.41 | 0.008 | (1.09–1.82) | ||||
| \({\beta}_{\mathrm{C}}^{{\ast}}\) | MLE (pair-specific) | 1.66 | 0.010 | (1.13–2.44) | ||||
| βC | GEE | 1.48 | 0.002 | (1.15–1.91) | ||||
| Model (2) | ||||||||
| \({\beta}_{\mathrm{W}}^{{\ast}}\) | MLE (pair-specific) | 3.00 | 0.002 | (1.49–6.05) | ||||
| \({\beta}_{\mathrm{B}}^{{\ast}}\) | 1.27 | 0.255 | (0.84–1.92) | |||||
| βW | GEE | 2.29 | <0.001 | (1.52–3.44) | ||||
| βB | 1.21 | 0.249 | (0.88–1.66) | |||||
| Model (3) | ||||||||
| \({\beta}_{\mathrm{W}}^{{\ast}}\) | Conditional ML | 3.20 | 0.020 | (1.21–8.50) | ||||
| Parameter . | Estimation method . | Estimate . | P-value . | 95% CI . | ||||
|---|---|---|---|---|---|---|---|---|
| Model (1) | ||||||||
| βC | Standard GLM | 1.41 | 0.005 | (1.11–1.79) | ||||
| βC | GLM + ‘robust’ SE | 1.41 | 0.008 | (1.09–1.82) | ||||
| \({\beta}_{\mathrm{C}}^{{\ast}}\) | MLE (pair-specific) | 1.66 | 0.010 | (1.13–2.44) | ||||
| βC | GEE | 1.48 | 0.002 | (1.15–1.91) | ||||
| Model (2) | ||||||||
| \({\beta}_{\mathrm{W}}^{{\ast}}\) | MLE (pair-specific) | 3.00 | 0.002 | (1.49–6.05) | ||||
| \({\beta}_{\mathrm{B}}^{{\ast}}\) | 1.27 | 0.255 | (0.84–1.92) | |||||
| βW | GEE | 2.29 | <0.001 | (1.52–3.44) | ||||
| βB | 1.21 | 0.249 | (0.88–1.66) | |||||
| Model (3) | ||||||||
| \({\beta}_{\mathrm{W}}^{{\ast}}\) | Conditional ML | 3.20 | 0.020 | (1.21–8.50) | ||||
βC,
Estimates of odds ratios from logistic regression models for the association between risk of low birth weight (defined as Z-score < −1) and log2 EPO level for 220 DZ twin infants, under alternative regression approaches as described in the text
| Parameter . | Estimation method . | Estimate . | P-value . | 95% CI . | ||||
|---|---|---|---|---|---|---|---|---|
| Model (1) | ||||||||
| βC | Standard GLM | 1.41 | 0.005 | (1.11–1.79) | ||||
| βC | GLM + ‘robust’ SE | 1.41 | 0.008 | (1.09–1.82) | ||||
| \({\beta}_{\mathrm{C}}^{{\ast}}\) | MLE (pair-specific) | 1.66 | 0.010 | (1.13–2.44) | ||||
| βC | GEE | 1.48 | 0.002 | (1.15–1.91) | ||||
| Model (2) | ||||||||
| \({\beta}_{\mathrm{W}}^{{\ast}}\) | MLE (pair-specific) | 3.00 | 0.002 | (1.49–6.05) | ||||
| \({\beta}_{\mathrm{B}}^{{\ast}}\) | 1.27 | 0.255 | (0.84–1.92) | |||||
| βW | GEE | 2.29 | <0.001 | (1.52–3.44) | ||||
| βB | 1.21 | 0.249 | (0.88–1.66) | |||||
| Model (3) | ||||||||
| \({\beta}_{\mathrm{W}}^{{\ast}}\) | Conditional ML | 3.20 | 0.020 | (1.21–8.50) | ||||
| Parameter . | Estimation method . | Estimate . | P-value . | 95% CI . | ||||
|---|---|---|---|---|---|---|---|---|
| Model (1) | ||||||||
| βC | Standard GLM | 1.41 | 0.005 | (1.11–1.79) | ||||
| βC | GLM + ‘robust’ SE | 1.41 | 0.008 | (1.09–1.82) | ||||
| \({\beta}_{\mathrm{C}}^{{\ast}}\) | MLE (pair-specific) | 1.66 | 0.010 | (1.13–2.44) | ||||
| βC | GEE | 1.48 | 0.002 | (1.15–1.91) | ||||
| Model (2) | ||||||||
| \({\beta}_{\mathrm{W}}^{{\ast}}\) | MLE (pair-specific) | 3.00 | 0.002 | (1.49–6.05) | ||||
| \({\beta}_{\mathrm{B}}^{{\ast}}\) | 1.27 | 0.255 | (0.84–1.92) | |||||
| βW | GEE | 2.29 | <0.001 | (1.52–3.44) | ||||
| βB | 1.21 | 0.249 | (0.88–1.66) | |||||
| Model (3) | ||||||||
| \({\beta}_{\mathrm{W}}^{{\ast}}\) | Conditional ML | 3.20 | 0.020 | (1.21–8.50) | ||||
βC,
Finally, it is worth noting that the conditional likelihood method may be used to fit the analogue of model (3) for a dichotomous outcome: see last line of Table 2. Unlike the continuous paired-difference method, the analogy is not exact, and this method is not as efficient as likelihood estimation of model (2D).23
Discussion
How should regression analysis be applied in twin studies? Although some authors have recently recommended the use of the within-pairs and between-pairs model (2),9,16 practice in the twin literature has generally followed the paired-difference approach (3), which we have shown can be subsumed under model (2).
A prominent recent strand of the literature has fitted the ‘twins-as-individuals’ model (1), and suggested that substantive conclusions should be based on comparing the results with those from within-pair analysis, i.e. comparing estimates of βC and βW.5,7,8,24 However, if the more general model (2) holds, i.e. if βW ≠ βB, then it will be difficult to interpret the estimated value of βC. In this regard, it can be shown that the GLS estimate of βC is a weighted average of the estimates of βW and βB where the weights depend on the within-pair correlation in both the outcome and the covariate.17,25 Model (1) may be seen as addressing the question: how does Y vary with X (in the twin population) when one treats each twin separately? If we ignore the co-twin and ask how predictable is the outcome simply on the basis of the current twin's covariate value, then fitting model (1) may be appropriate. It may be, however, that the resulting association is wholly or partially confounded by factors that we know about, at least indirectly, because of the data we have on the co-twin.
To investigate an association after removing all confounding by factors shared between twins, one should examine the within-pair effect βW. We have shown how this can be done either by performing the traditional paired-differences analysis [approach (3)], or by fitting the more general model (2). Advantages of fitting model (2) are that it allows (i) direct examination of whether a common-effect model (βW = βB) fits the data and (ii) simultaneous examination of other confounding effects due to factors that may be constant or variable within twin pairs. (Constant confounders will not affect βW but may affect βB while variable confounders may affect both.)
How then do we interpret the results of fitting model (2)? The within-pair effect βW is quite readily interpretable: the equivalence with the paired-difference analysis reflects the fact that this parameter represents an association that is free of confounding due to factors that are common to the two twins. As pointed out elsewhere,24,26 this supports interpretation in terms of possible causal mechanisms related to individual-specific factors such as different fetal nutrient supply lines: large values indicating for instance that whatever fetal factors underlie within-pair differences in X may also be driving the associated differences in Y.
This duality of possible interpretations between regression parameters occurs whenever covariates in a multiple regression specification are functionally related to each other. Another example is in the fitting of models for later-life outcomes such as blood pressure using standardized body size measures at birth and at current age, where the model can be interpreted either in terms of parameters for birth weight and current weight or in terms of parameters for birth weight and growth or change in weight between the two points.28,29
The primary attraction of the original parameterization used in (2) may be the technical feature that the covariates
So far we have considered only the regression of Y on X, that is, we have tried to explain variation in Y conditional on the observed pattern of X values, which was assumed to be fixed or ‘given’ in the usual sense of regression analysis. However, there may be little variation in X, especially within pairs, in which case there will be little scope for discerning related variation in Y and the corresponding estimated regression coefficient will have a large standard error. In order to explain the joint variation of two measures it is possible to develop a joint or bivariate model for X and Y, rather than relying on the regression approach of pretending that one variable is ‘given’ and that we are only interested in modelling the variation of the other one given the first. A natural approach is to build a variance components models for each of X and Y, where different components are included to represent sources of variation common to either or both the measurements on X and Y within a twin pair.15,30 Such a model is capable of representing a range of underlying biological sources of variability, and in particular can be used in the manner of traditional twin study analysis to address the question of whether the within-pair correlations of either X or Y, and the regression relationship between them, appear to be explicable by genetic factors.
Conclusion
If the investigator is only interested in within-pair effects, that is, in the association of Y with X after removing all shared factors (covariates that are constant between twins), then the simple paired-difference analysis is sufficient. If one wishes to estimate an average relationship across the twin population without specifically using information on twin's shared characteristics, then model (1) provides an appropriate approach, except that the model should be fitted using a GLS method that allows for the correlation between twins. However, the more general model (2) is recommended since it allows simultaneous examination of both within-pair and between-pair effects, and if these effects are different then the results for model (1) are of less interest. We, therefore, recommend fitting model (2) using GLS (‘mixed model’ estimation or GEE), with the following general interpretations of the possible results:
If βB ≈ 0 then we conclude that the only association is a dependence of the outcome on within-pair difference in covariate, not on the absolute level of the covariate. This would be consistent with causal mechanisms that relate to individual-specific factors that vary between twins in a pair, reflected in differences in the covariate and related differences in the outcome.
If βW ≈ 0 we conclude that any association of Y with X, which would then only appear in the form of a non-zero βB, can be explained by shared twin-pair factors. Once these are adjusted for, the association disappears, so an association found in a crude (unpaired) association between Y and X [an analysis assuming model (1)] could be explained as being due to confounding by these shared factors.
If βB ≈ βW we may conclude that expected change in the outcome for a given change in the covariate is the same irrespective of whether the comparison is made between two twins or between two unrelated individuals in the twin population. It seems reasonable to infer from this that if there is a causal mechanism underlying the association then it cannot rely entirely on shared, twin-pair level (e.g. maternal), factors. For one thing, such factors are by definition similar if not constant within twin pairs and so should not lead to differences in X, let alone to related differences in Y. On the other hand, given a non-zero βB, the effect cannot be purely due to within-pair mechanisms.
If both coefficients are non-zero but not equal, the interpretation becomes more complex—a compromise between the previously described three extremes.
Most of this paper has concentrated on continuous outcome measures, for which direct linear modelling of the mean, with normal error terms, is a natural approach (possibly after transformation of the outcome variable). Much epidemiological analysis is concerned with dichotomous outcomes, where the standard approach of logistic regression is to model the log-odds of the parameter of interest (the risk or probability of the outcome), with a binomial error distribution. As we have outlined, many of the concepts discussed in this paper carry over to the logistic regression framework, but there are some important further complications, in particular the fact that the ML and GEE approaches to model estimation diverge, as commonly applied—the GEE method is used to estimate marginally specified models while ML is used for a conditionally specified random-effects model. These two types of models involve different parameter definitions that require different interpretations.19,20
A further issue that requires comment is handling dichotomous covariates. These provide a special case, since the deviation from the pair mean, or half the difference between twins, can be only −½ or ½, when the twins are discordant, or 0 when the twins are concordant (assuming the dichotomous X is coded 0/1). The pair mean can only take the values 0, ½, or 1. With dichotomous covariates the concept of between-pair regression effects may not be useful and it appears best to analyse such covariates by examining within-pair differences amongst discordant pairs.
Returning to the application of the continuous normal linear model, many studies seek to draw conclusions about possible causal pathways by comparing regression parameters between various strata in the twin population, with the classic example being the comparison between MZ and DZ twins. These inferences need to be approached with caution, for reasons discussed in the previous section, but certain cases may be reasonably compelling. For instance, in the birth weight–EPO example, the comparison of the estimated value of βW between twin pairs born by elective Caesarean section and those born vaginally indicated a stronger within-pair association in the Caesarean-born twins. This suggests that the twin-specific factors underlying this association may be blunted by various extraneous changes in EPO levels related to exposure to labour, which one would not expect to be predictive of birth weight.
Similarly, one might argue that a smaller within-pair regression coefficient for MZ twins than for DZ twins should be taken as evidence that the association is due to genetic factors, which are ‘matched out’ for the MZ pairs. It is possible, however, for the within-pair regression coefficients for MZ and DZ pairs to be similar even if the observed within-pair correlation structure for the outcome and exposure is consistent with a genetic influence.15 More work is needed to clarify these issues but we believe it is not feasible to use regression methods to derive conclusions about the role of genetic factors in explaining associations.
As always, epidemiologists need to keep in mind the limitations of regression methodology,31 remembering that it is fundamentally only a tool for assessing patterns of variation in an outcome conditional on one or more covariates. With twin data, the difficulties are increased, since one needs to consider whether the modelling should be conditional just on the individual's covariate(s) or on their correlated twin's as well. Explaining the causes of systematic variation identified by the regression model will in general require information from beyond the data, especially in the absence of randomization to control unknown confounders.
Appendix
We display commands used in the Stata package (Release 9, Stata Corporation, College Station, TX, 2005) to obtain the results shown in Tables 1 and 2.
/* Variables used are
bwtsds birth weight SD-score or z-score
lowbwt low birth weight indicator (=1 if SD-score < −1, 0 otherwise)
epolog2 log(base 2)of EPO concentration in cord blood
pair_no unique identifier for each twin pair
twin_no birth order of twins(1,2) */
* first create mean and difference variables:
by pair_no: egen epolmn=sum(epolog2)
replace epolmn=epolmn/2
generate epold=epolog2-epolmn
sort pair_no twin_no
by pair_no: generate epoldif=epolog2[_n]-epolog2[_n-1]
by pair_no: generate bwtdif=bwtsds[_n]-bwtsds[_n-1]
* TABLE 1
* model (1)
* standard OLS:
regress bwtsds epolog2
* OLS with “robust” SEs:
regress bwtsds epolog2, cl(pair_no)
* GLS estimation (REML method for variance parameters):
xtmixed bwtsds epolog2 ‖ pair_no:, reml
* GLS estimation (ML method for variance parameters):
xtmixed bwtsds epolog2 ‖ pair_no:, mle
est store A
* GEE estimation
xtgee bwtsds epolog2, i(pair_no) robust
* model (2)
* GLS estimation (REML method for variance parameters):
xtmixed bwtsds epold epolmn ‖ pair_no:, reml
* GLS estimation (ML method for variance parameters):
xtmixed bwtsds epold epolmn ‖ pair_no:, reml
est store B
* LR test for difference between beta_W and beta_B:
lrtest A B
* Wald test for difference between beta_W and beta_B:
lincom epolmn-epold
* GEE estimation
xtgee bwtsds epold epolmn, i(pair_no) rob
lincom epolmn-epold
* model (3)
reg bwtdif epoldif, nocons
* TABLE 2
* model (1D)
* standard GLM fit ignoring pairing:
logit lowbwt epolog2, or
* standard GLM fit with “robust” SEs
* (= GEE with independence working correlation):
logit lowbwt epolog2, cl(pair) or
* ML estimation of random effects model (pair-specific ORs)
xtlogit lowbwt epolog2, i(pair) or quad(24) nolog
est store A
* GEE estimation (i.e. with non-zero working correlation):
xtgee lowbwt epolog2, fam(binom) i(pair) eform robust nolog
* model (2)
* ML estimation of random effects model (pair-specific ORs)
xtlogit lowbwt epold epolmn, i(pair) or quad(24) nolog
est store B
quadchk
* LR test for difference between beta*_W and beta*_B:
lrtest A B
* Wald test for difference between beta*_W and beta*_B:
lincom epolmn-epold
* GEE estimation (i.e. with non-zero working correlation):
xtgee lowbwt epold epolmn, fam(binom) i(pair) eform robust nolog
* Wald test for difference between beta_W and beta_B:
lincom epolmn-epold
* model (3)
* conditional logistic regression estimation of beta*_W:
clogit lowbwt epold, group(pair) or
References
Greenland S, Brumback B. An overview of relations among causal modelling methods.
Leon DA, Lithell HO, Vagero D et al. Reduced fetal growth rate and increased risk of death from ischaemic heart disease: cohort study of 15 000 Swedish men and women born 1915–29.
Rich-Edwards JW, Stampfer MJ, Manson JE et al. Birth weight and risk of cardiovascular disease in a cohort of women followed up since 1976.
McNeill G, Tuya C, Smith W. The role of genetic and environmental factors in the association between birthweight and blood pressure: evidence from meta-analysis of twin studies.
Dwyer T, Blizzard L, Morley R, Ponsonby A. Within pair association between birth weight and blood pressure at age 8 in twins from a cohort study.
Zhang J, Brenner RA, Klebanoff MA. Differences in birth weight and blood pressure at age 7 years among twins.
Nowson CA, MacInnis RJ, Hopper JL et al. Association of birth weight and current body size to blood pressure in female twins.
Christensen K, Stovring H, McGue M. Do genetic factors contribute to the association between birth weight and blood pressure?
Johansson-Kark M, Rasmussen F, De Stavola B, Leon DA. Fetal growth and systolic blood pressure in young adulthood: the Swedish Young Male Twins Study.
McNeill G, Tuya C, Campbell DM et al. Blood pressure in relation to birth weight in twins and singleton controls matched for gestational age.
Morley R, Moore VM, Dwyer T, Owens JA, Umstad MP, Carlin JB. Association between erythropoietin in cord blood of twins and size at birth: does it relate to gestational factors or to factors during labor or delivery?
Carlin JB, Wolfe R, Coffey C, Patton GC. Analysis of binary outcomes in longitudinal studies using weighted estimating equations and discrete-time survival methods: prevalence and incidence of smoking in an adolescent cohort.
Hanley JA, Negassa A, Edwardes MD, Forrester JE. Statistical analysis of correlated data using generalized estimating equations: an orientation.
Scott AJ, Holt D. The effect of two-stage sampling on ordinary least squares methods.
Gurrin LC, Carlin JB, Sterne JAC, Dite GS, Hopper JL. Using bivariate models to understand between- and within-cluster regression coefficients, with application to twin data.
Iliadou A, Cnattingius S, Lichtenstein P. Low birthweight and type 2 diabetes: a study on 11 162 Swedish twins.
Mann V, De Stavola BL, Leon DA. Separating within and between effects in family studies: an application to the study of blood pressure in children.
Hopper JL, Seeman E. The bone density of female twins discordant for tobacco use.
Hu FB, Goldberg J, Hedeker D, Flay BR, Pentz MA. Comparison of population-averaged and subject-specific approaches for analyzing repeated binary outcomes.
Carlin JB, Wolfe R, Brown CH, Gelman A. A case study on the choice, interpretation and checking of multilevel models for longitudinal binary outcomes.
Zeger SL, Liang K-Y, Albert PS. Models for longitudinal data: a generalized estimating equation approach.
Neuhaus JM. Statistical methods for longitudinal and clustered designs with binary responses.
Neuhaus JM, Lesperance ML. Estimation efficiency in a binary mixed-effects model setting.
Dwyer T, Morley R, Blizzard L. Twins and fetal origins hypothesis: within-pair analyses.
Neuhaus JM, Kalbfleisch JD. Between- and within-cluster covariate effects in the analysis of clustered data.
Leon DA. The foetal origins of adult disease: interpreting the evidence from twin studies.
Begg MD, Parides MK. Separation of individual-level and cluster-level covariate effects in regression analysis of correlated data.
Lucas A, Fewtrell MS, Cole TJ. Fetal origins of adult disease—the hypothesis revisited.
Cole TJ. Modeling postnatal exposures and their interactions with birth size.
Neale MC, Cardon LR. Methodology for Genetic Studies of Twins and Families. Dordrecht: Kluwer,



![Graphs of expected Y vs X for 6 hypothetical twin pairs, with a fixed set of X values. In each row, the left-hand panel shows expected (mean) value of Y according to regression model: (1) simple linear decline with X, βC = −0.4 [model (1), with jitter added so the lines for each twin can be distinguished from each other]; (2a) βW = −0.8, βB = 0; (2b) βW = 0, βB = −0.4; (2c) βW = −0.8, βB = −0.4. Right-hand panel for each case shows hypothetical (simulated) data where correlated random errors with between-subject and within-subject standard deviation both 0.5 has been added to the mean values in the left-hand panel. To maximize comparability between panels, the same simulated errors are used in each case. Note that by chance some twin pairs have very similar X values (e.g. pair 4) while others have quite different values (pairs 2, 3)](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ije/34/5/10.1093/ije/dyi153/2/m_dyi153f2.gif?Expires=1716347535&Signature=Sv5OtiFmaD9h9lON8BIrhKqacadS9tNo8JLqnyjdfeMQY34bJbyERb3CNowymyB9yXkKugbb5Iaxsgoegm4OYFpbjNavABuBKNKChwxzlHHd9cfqjSQ1TpHIUqOnB0fqiEdkUq49A6DPde2ilvhT~NO731h4gUi39IsKlBnyFnK1YbKZlAmsQ7o9oO-5ciITJiVIrLldX-X7r3fsC5QxnXk3QN7MRMz~Uqh8OAgv5luQAS91cIDaY9zWbRCL0tntlmTSddQFklDllD4w~bBO5roRU8W61QZhUR7dulxToHfZeUEZC8qVT8G0LTaikB4of~W6GBI9P8YRqlZqsBbZ3g__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)