-
PDF
- Split View
-
Views
-
Cite
Cite
Lev A. Zhivotovsky, David B. Goldstein, Marcus W. Feldman, Genetic Sampling Error of Distance (δμ)2 and Variation in Mutation Rate Among Microsatellite Loci, Molecular Biology and Evolution, Volume 18, Issue 12, December 2001, Pages 2141–2145, https://doi.org/10.1093/oxfordjournals.molbev.a003759
Close - Share Icon Share
Abstract
An expression is obtained for the time-dependent variance of the microsatellite genetic distance (δμ)2 when the mutation rate is allowed to vary randomly among loci. An estimator is presented for the coefficient of variation, Cw, in the mutation rate. Estimated values of Cw from genetic distances between African and non-African populations were less than 100%. Caveats to this conclusion are discussed.
Introduction
In order to estimate the time of divergence of two contemporary populations from a single ancestral lineage, a genetic distance that is a known function of this time is desirable. When the populations are assayed for microsatellite polymorphism, the genetic distance (δμ)2, based on the average squared differences in the sizes of alleles sampled in pairs, one from each population, has an expectation that increases linearly with time at a rate equal to twice the mutation rate in the case of one-step mutations (Goldstein et al. 1995 ). For multistep mutations, the rate of increase is twice the effective mutation rate, which is the product of the mutation rate and the variance of changes in allele size due to mutation (Zhivotovsky and Feldman 1995 ).
The usual way to analyze a set of microsatellite loci from individuals sampled in two populations is to compute (δμ)2 for each locus and average across loci. If the mutation rate (or the effective mutation rate) is the same at all loci, and is known, then simple division gives an estimate of the expected time since separation of the populations. Variation across loci in the mutation rate affects the variance of (δμ)2 (but not its expectation).
The evolutionary process involves genetic sampling error due to random genetic drift and mutation, and thus the variance among the possible evolutionary replicates of the distance is an important issue. Zhivotovsky and Feldman (1995) implied that among replicates, the distance follows a chi-square distribution. In fact, the variance of the distance does asymptotically satisfy the most important property of the chi-square distribution, namely, that its variance approaches twice the square of its expectation as time increases (Zhivotovsky, Feldman, and Grishechkin 1997 ), but the actual distribution is not exactly chi-square.
From their analysis of properties of (δμ)2 in a study of more than 200 human microsatellite loci, Cooper et al. (1999) found strong evidence for variation among loci in the mutation rate. Our purpose with this paper is to obtain an analytical expression for the variance of (δμ)2 when the mutation rate is variable. An important application of this analytical expression could be estimation of the extent of variation in mutation rate among microsatellite loci. Our analysis also allows us to compute the time-dependent dynamics of the variance of (δμ)2 and to assess how sensitive these dynamics are to the assumption of a fixed mutation rate that is constant across loci.
Results
Consider a randomly mating diploid population of constant size N with nonoverlapping generations and an autosomal microsatellite locus undergoing multiple-step mutation with mutation rate μ and, possibly, constant mutation bias, as measured by the difference between the mean size of mutations and the size of the parental allele. (There is no bias if the difference is zero). Let η(2)m be the expectation of the square of mutational gains and losses (Di Rienzo et al. 1998 ), which in the case of no average mutation bias becomes the variances in mutation changes, σ2m (Slatkin 1995 ). We call w = μη(2)m the effective mutation rate. Also, introduce k = μη(4)m, where η(4)m is the fourth noncentral moment of mutational changes in repeat score; w = k = μ in the case of one-step symmetric mutation. Assume for a while that the mutation parameters do not vary between loci.
The within-population variation at a microsatellite locus can be characterized by the mean allele size (r), the variance of allele size (the second central moment) (V), and the unnormalized kurtosis (the fourth central moment) (K) (Zhivotovsky and Feldman 1995 ). The between-population variation can be measured by analogs of FST (Slatkin 1995 ; see also Michalakis and Excoffier 1996 ; Rousset 1996 ; Feldman, Kumm, and Pritchard 1999 ). For two populations, the (δμ)2 distance is defined as the squared difference of the mean values of their repeat scores: (δμ)2 = (r1 − r2)2 (Goldstein et al. 1995 ).
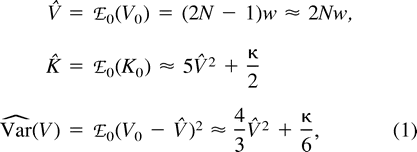
After τ generations of divergence, the expected distance, ℰ0ℰr((δμ)2), equals 2wτ (Zhivotovsky and Feldman 1995 ; see also Feldman, Kumm, and Pritchard 1999 ; Zhivotovsky 2001 ), which becomes 2μτ with one-step symmetric mutation (Goldstein et al. 1995 ).
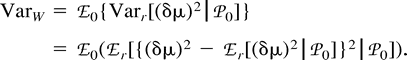
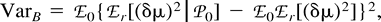
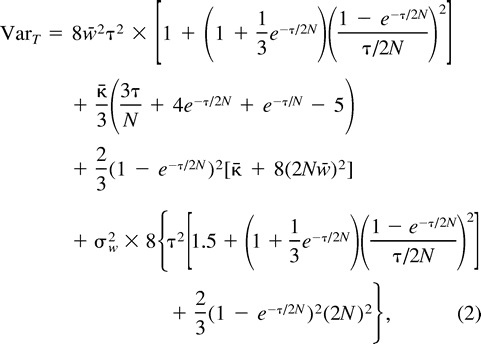
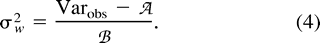
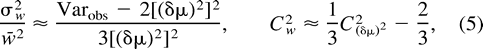
Discussion
We can use expression (5) to estimate Cw from data. Table 1 shows the estimates for different sets of di- and tetranucleotide loci based on genetic distances between African and non-African human populations. Two of three sets show substantial values of Cw. However, probably not more than 10,000 generations have passed since the divergence of Africans and non-Africans, and thus the values of Cw in table 1 are overestimated (see fig. 1 ). Therefore, on average, variation in mutation rate does not seem to be very extensive, although it is not excluded that some microsatellite loci can show much higher or lower mutation rates than an average locus. For example, Forster et al. (2000) found that the average mutation rate at the Y-chromosome loci could be taken as 0.26 × 10−3 if locus DYS392 was omitted because of its unusual behavior; otherwise, it was about 10 times as high. However, we should emphasize that our findings concern the effective mutation rate, i.e., the product of mutation rate and the variance in the number of repeats due to mutation, while Forster et al. (2000) considered only the mutation rate.
Two caveats should be noted in connection with the above remarks on the size of Cw. First, our estimates were made under the assumption of constant population size, which is surely erroneous for humans in the last 4,000 generations. Second, since the variance of Cw is likely to be large over this time range and with the number of loci considered here, our confidence that Cw is indeed small cannot be great.
Earlier, Zhivotovsky and Feldman (1995) pointed out that hundreds of loci are required to estimate the genetic distance (δμ)2 with reasonable accuracy, and with variable mutation rates, the number of loci must be even greater. Indeed, as follows from equation (5) , the coefficient of variation of genetic distance (δμ)2 averaged over L loci, which can be used as a measure of the relative accuracy (R) of estimation of the genetic distance, is approximated by [(2 + 3C2w)/L]½, or L = (2 + 3C2w)/R2. For instance, if the relative accuracy is 10%, i.e., R = 0.1, then 200 loci with identical mutation rates would be needed, whereas 500 loci are required to estimate genetic distance with the same precision if the relative variation in mutation rates is 100%, i.e., if Cw = 1. As an example, using combined data on 131 di-, tri-, and tetranucleotide microsatellite loci, Zhivotovsky (2001,table 1 ) estimated approximately 14% for the accuracy of genetic distances between African and non-African populations. It should be noted, however, that in the analyses of Jin et al. (2000) , (δμ)2 was not able to reliably distinguish continental groups in trees made using the 28 loci of Bowcock et al. (1994) , although its performance was comparable with other distance measures with 64 microsatellite loci. Again, this reinforces our view that several hundred loci would be needed to produce satisfactory estimates of (δμ)2 and Cw.
It should be strongly emphasized that expression (2) , as well as expressions (4) and (5) , derived from it, are only valid for reproductively isolated populations of constant size at mutation-drift equilibrium. Otherwise, if we consider a process of subdivision of a parental population into two populations that subsequently evolve under mutation and genetic drift, the genetic distance (δμ)2 becomes a nonlinear function of time; in particular, it underestimates the divergence time if the two populations are growing in size and/or are connected by gene flow (Zhivotovsky 2001 ). Therefore, our estimates in table 1 have to be regarded with caution.
Appendix
A Case of Constant Mutation Bias
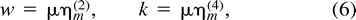
The Within-Locus Variance of (δμ)2
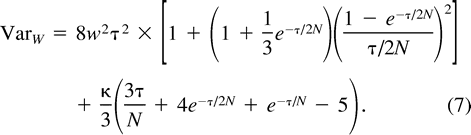
The Between-Locus Variance of (δμ)2
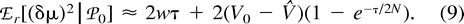
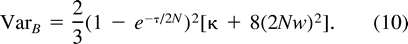
Variation in Mutation Rate
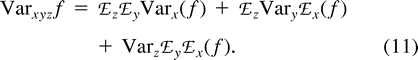
Now, consider ℰx, ℰy, and ℰz, respectively, as ℰr, ℰ0, and the expectation operator averaging over varying values of the mutation parameters, ℰm, and take the distance (δμ)2 as function f. The first two terms in the right-hand side of equation (11) represent the expectation ℰm of VarW in equation (7) and VarB in equation (10) , respectively. The third term is Varm(ℰ0((δμ)2)), the variance of the expected distance in equation (9) with respect to mutation parameters. Taking the expectations and summing in equation (11) , we obtain equation (2) .
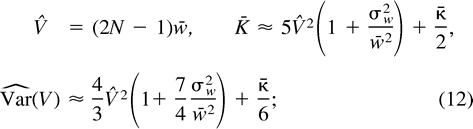
Di Rienzo et al. (1998) obtained the same expression for Var(V).
Keith Crandall, Reviewing Editor
Keywords: microsatellite loci mutation rate genetic distance
Address for correspondence and reprints: Marcus W. Feldman, Department of Biological Sciences, Stanford University, Stanford, California 94305. marc@charles.stanford.edu .
Table 1 Estimates of the Coefficient of Variation Among Loci of the Effective Mutation rate, Cw, Based on Genetic Distances Between African and Non-African Populations for Different Sets of Data
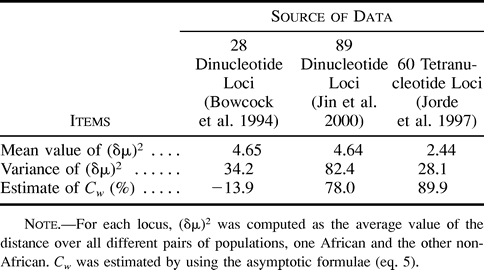
Table 1 Estimates of the Coefficient of Variation Among Loci of the Effective Mutation rate, Cw, Based on Genetic Distances Between African and Non-African Populations for Different Sets of Data

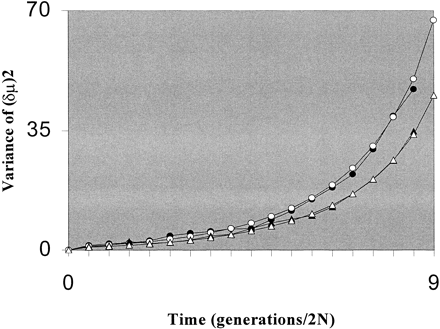
Fig. 1.—To evaluate the accuracy of equation (2) , we ran coalescent simulations following the algorithm of Hudson (1990) including the stepwise mutation process with and without rate variation. Separation times are given in units of 2N. In the case of a constant mutation rate, 𝛉 is set to 3.5. For rate variation, the average 𝛉 is again 3.5, but the thetas are now drawn from a gamma distribution with a variance of 10. Each of 200 replications involves 30 loci and 30 sampled alleles at each locus. White triangles and circles represent analytical results for no variation in mutation and for variation in mutation among loci, respectively. Black triangles and circles are the corresponding simulated values
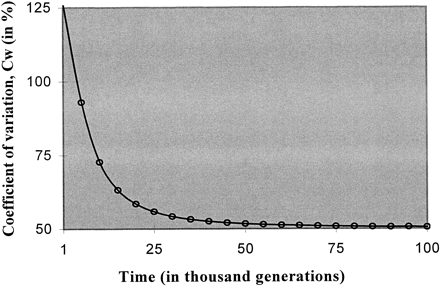
Fig. 2.—Dynamics of the coefficient of variation (%) of the effective mutation rate Cw (equation 5 ). The parameters are w = 0.001, σw = 0.0005 (hence, Cw = 0.5), and 2N = 5,000. Mutation is single-step and symmetric
We are indebted to two anonymous reviewers for helpful comments and constructive suggestions. This research was supported in part by the National Institutes of Health (grants GM 28016, GM 28428, and 1 R03 TW005540), the Russian Foundation of Basic Research (grants 01-04-48441 and 01-07-90197), and the Russian State Program “Human Genome” (grant 26/01).
References
Bowcock A. M., A. Ruiz-Linares, J. Tomfohrde, E. Minch, J. R. Kidd, L. L. Cavalli-Sforza,
Cooper G., W. Amos, R. Bellamy, M. R. Siddiqui, A. Frodsham, A. V. S. Hill, D. C. Rubinsztein,
Di Rienzo A., P. Donnelly, C. Toomajian, B. Sisk, A. Hill, M. L. Petzl-Erler, G. K. Haines, D. H. Barch,
Feldman M. W., J. Kumm, J. K. Pritchard,
Forster P., A. Rohl, P. L. Lunnermann, C. Brinkmann, T. Zerjal, C. Tyler-Smith, B. Brinkmann,
Goldstein D. B., A. R. Linares, L. L. Cavalli-Sforza, M. W. Feldman,
Jin L., M. L. Baskett, L. L. Cavalli-Sforza, L. A. Zhivotovsky, M. W. Feldman, N. A. Rosenberg,
Jorde L. B., A. R. Rogers, M. Bamshad, W. S. Watkins, P. Krakowiak, S. Sung, J. Kere, H. Harpending,
Kimmel M., R. Chakraborty,
Michalakis Y., L. A. Excoffier,
Rice J. A.,
Rousset F.,
Slatkin M.,
Weir B. S.,
Zhivotovsky L. A.,
Zhivotovsky L. A., M. W. Feldman,