Multifunctional composites: a metamaterial perspective

Metamaterials that influence the behaviour of EM waves fall under the category of electrodynamic. Two key material properties (electrical permittivity, , and magnetic permeability, μ) can be derived to be frequency dependent [10]. With these frequency equations, the properties of the metamaterial can be tailored at given frequency ranges.

One example of a very recent multifunctional metamaterial that affects EM rays is the pyroelectric infrared (IR) detectors conceptualised and demonstrated by Suen et al [26]. Pyroelectric materials, such as lithium niobate enable detection of IR radiation through a temperature differential that induces a change in potential used to generate a signal [26]. Whereas other pyroelectric detectors must have at least a filter, sensor and electrode, all three functions have been met in the pyroelectric metamaterial detector. The filter function is enabled through the geometry and material of the top section of the detector. Depending on the size of the unit cell, a different absorption wavelength can be realised through a small range of 8.3–10.7 μm. The sensor and electrode function are from the metallic layer. The unit cell can be seen in figure 3(a) and repeating pattern in figure 3(b).

Zoom In Zoom Out Reset image size

There are a number of benefits to a multifunctional detector made from composite metamaterials. Firstly, the 'detector itself is spectrally selective but can be tuned by simply changing the dimensions of the top metal structure' [26], greatly simplifying the system (no moving parts). Additionally, the electrical time constant is reduced by a small capacitance footprint, which reduces noise losses. The detector has a narrow bandwidth, which can be seen as an advantage (results over a specific range) or a disadvantage (little flexibility in the operational frequencies). This characteristic of a narrow, inflexible bandwidth is common within electrodynamic metamaterials as the metamaterial properties are a function of a geometry which cannot change.

This metamaterial sensor has found use in CO₂ detectors that outperforms the current state-of-the-art by displaying a 250 times greater sensitivity and a size seven times smaller than comparative work [27].

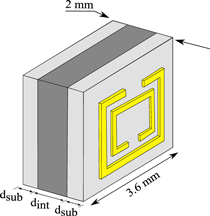
A macro-scale (i.e. between 1 and 100 mm in size) multifunctional metamaterial sensor that has the capability to sense changes at the macro scale in moisture content, density of a silica aerogel or temperature of seawater was presented by Ekmekci et al [28]. This paper is an example of the frequency dependent permittivity of a material being used in reverse in order to sense changes in quantities of interest by measuring resonant frequencies. An intermediate layer (d_int) is sandwiched between two substrates (d_sub) on which split ring resonators (SRR) are placed. This set-up, shown in figure 4, causes the resonant frequency of the double-sided split ring resonator (DSRR) to be a function of the permittivity and thickness of the intermediate layer.

Zoom In Zoom Out Reset image size

To find the variations in environmental factors (such as humidity, density and temperature as mentioned previously), a relationship between permittivity of the intermediate layer (_int), capacitance of SRR and resonant frequency is found. As the _int increases from the environment, SRR capacitance increases causing a decrease in resonance frequency. The same applies vice versa. Very good sensitivity is seen in moisture content, density and temperature sensing with resolution of 0.07%, 2 mg cm⁻³ and 0.21 °C, respectively, for a frequency resolution (Δf) of 1 MHz. This Δf is reasonable considering the sensor works in the microwave region (in this instance, 10–12 GHz). The application of these sensors is directed towards biological and chemical sensing, across a range of frequencies. One can imagine by having an array of these sensors, different properties within a single structure could be simultaneously measured. This avenue appears not be have been pursued at the present time.

The intermediate layer was changed based on the environmental factor wanting to be measured, but the choice of intermediate layer is restricted as the variation in permittivity must complement the frequency range being used. For example, for a given change in temperature within seawater, there must be data about the permittivity of seawater as a function of salinity and temperature. This requirement means the list of usable intermediate materials is a short one. Similar to the narrow bandwidth issue found in pyroelectric IR sensors, the selective nature of metamaterials is an advantage and disadvantage, depending on the application. Future work could investigate the possibility of incorporating more substances in these intermediate layers and characterisation of their permittivity as a function of the substance properties to enable a broader range of material use.

An experimental illustration of a broad-ranged electrodynamic metamaterial is proposed by Liu et al [29], where a hybrid metamaterial is able to be tuned based on an electric current. A layered structure is used to create a self-contained device, shown in figure 5. The bottom Au layer is a ground plane, whereas the top cross pattern provides two functions. First, the structure aids resonant absorption modes and second, by being connected to an external circuit it heats up because of current flow. The thermal conductivity characteristics of Au also enable it to heat the VO₂ layers easily through the Al₂O₃ layers. The Al₂O₃ layers create sharper absorption resonance at room temperature and act as diffusion layers between Au and VO₂.

Zoom In Zoom Out Reset image size

By combining these materials in the designed structure, electrical control of the permittivity in the mid-IR range is demonstrated experimentally. When the applied current is 0 A, the metamaterial is reflective at 2.67 μm, whereas when the applied current is 2.03 A, the metamaterial is completely invisible at 2.67 μm. When the current is further increased, the metamaterial appears to be completely absorptive. This phenomenon can be exploited to generate 'electrically switchable reflection' [29] at resonant wavelengths. This clearly has application in cloaking devices, where objects behind a perfectly reflective device are deemed invisible. However, the physical use of these objects for such applications is not expanded on in the paper and would be a critical area of future work. In order for practical cloaking devices to be created, the frequency to be cloaked from must be known. In medical situations (where specific frequencies are used) this is possible. However, in more dynamic environments (e.g. military applications) a broadband, tunable metamaterial would be necessary.

Fan et al show a tunable metamaterial that has been experimentally and numerically proven to 'yield a transmission modulation depth of 60%' [30] between 1.1 THz and 1.8 THz. At the resonant frequency of 0.98 THz, transmission is as low as 25%. Whilst these modulation and transmission percentages are not as large as other experiments, the metamaterials (shown in figure 6) are thin and flexible: they can be placed on nonplanar surfaces. This drastically increases the adaptability of these metamaterials.

Zoom In Zoom Out Reset image size

The unit cell has dimensions of 68 μm by 68 μm. The metamaterial has dimensions of 8 mm by 8 mm. With a total thickness of the metamaterial of 4.7 μm, it can easily be wrapped around a cylinder and still exhibit tunable performance. In order to tune the metamaterial, optical-pump THz-probe spectroscopy is used. By changing the pump power by a few mW, large transmission amplitude changes are seen at various frequencies. At 0 mW and resonant frequency, transmission is at 25%, whereas at 1 mW and resonant frequency, transmission is at 40%. The pumping power applied in these experiments is 'approximately two orders of magnitude smaller' [30] when compared to previously reported experiments. The manufacturing process is briefly mentioned by Fan et al, including the possibility that the transfer process used to achieve the thin layer of the GaAs semiconductor can be used for other semiconductors. This would open up new avenues of future work and a larger field of flexible metamaterials could be researched.

Shin et al [31] present a broadband, inexpensive lattice-type metamaterial comprised of silicon circular unit cells. This is shown in figure 7.

Zoom In Zoom Out Reset image size

The experimental and simulation results show a broadband (10–12 GHz) and lossless smart cloak. Due to the size and shape of the unit cell there is broadband operation (as there is no electromagnetic resonance) and the two materials utilized, silicon and air, are 'virtually lossless and dispersion-free at microwave frequencies' [31]. The construction of the lattice-type structure is from off-the-shelf injection-moulded silicon tubes, arranged in a right-angle triangle. As can be seen in figure 7(b), there is a small right angled triangle along the bottom surface. This is necessary to produce varied density of silicon and air across the bottom region when compressed. A given density profile is necessary to produce the required variation in effective refractive index. In terms of manufacturability and tunability, this metamaterial performs better than previous architectures. One reason for this could be the approach used to generate the appropriate refractive index distribution: transformation optics. By starting from the fundamental principle that a variation in EM properties can warp an EM wave, Shin et al present an elegant solution to change the EM properties by physically changing the material stress and strain profile.

The metamaterial only operates in two-dimensional space, and authors do not indicate how the structure could be extended to three dimensions. However, the approach taken could be investigated in order to produce a 3D lattice structure that is able to direct/reflect/absorb based on changes in mechanical structure. Additionally, further investigation into material choice could reveal a material that has a much higher dielectric constant than air (a necessary feature for the shape change to produce the correct refractive index variation). This design approach shows great promise and could be employed at various length scales theoretically and with advances in manufacturing this is a possibility.

Metamaterials that affect the response of a wave through a fluid are classed as acoustic metamaterials. In an analogous manner to electrodynamic metamaterials, there are two essential properties that influence an acoustic metamaterials response: ρ, mass density and κ, bulk modulus [32]. The following section discusses multifunctional metamaterials that have constitutive properties not found in nature.

Mikoshiba presents an acoustic metamaterial that can absorb acoustic waves and generate electricity [33]. By adapting a mass-in-mass spring model, a unit cell can be created that has electrical generation capabilities whilst sustaining the resonance frequency absorption ability, shown in figure 8.

Zoom In Zoom Out Reset image size

These unit cells are combined in sequence. Through harmonic excitation, given conditions of wave attenuation can be achieved for different mass ratios and spring constant ratios. The condition of interest is where all external masses (M₁) oscillate at the natural frequency of the system, close to local resonant frequency. At close to local resonant frequency, the internal masses have amplitude greater than the driving frequency, which continues propagation of the wave through the system. At this condition efficient electricity generation is possible as at greater amplitudes of displacement voltage generation is increased.

The combination of frequencies and amplitudes that drive the mass-in-mass spring model are usually impractical for producing sufficient electricity. Thus, this metamaterial can be used as a sound block where high frequency noise is available, i.e.—most high power engines, to generate electricity and dampen noise. Additionally, this metamaterial can measure the resonant frequency of a location by seeing where voltage generation is largest. Whilst experimental data is shown in this paper, the possible applications were not explored. A damping feedback system could be imagined where resonant frequency generates electricity, which in turn powers an active damping system to reduce resonant frequency.

Chen et al aim to combat acoustic metasurfaces that are passive, have narrow operative band and are monofunctional by designing a magnetically-tuned multifunctional acoustic metamaterial [34]. It is important to note that the use of magnetics in metamaterials is well established. Examples of metamaterial lattices capitalising on pure magnetic attraction-repulsion and shape change can be found in references [35–37] and active control with particulates dispersed in elastomers to provide shape change can be found in references [38–40]. Chen et al [34] use active control through a magnetic force that enables tuning of the transmission spectrum. An additional function can be created added by 'switching the magnetic force distribution' [34]. By doing this, acoustic wave manipulation is possible without changing the structure of the metamaterial. Active control is designed into the membrane-type structure by allowing nonlinear geometric changes to the structure. A thin polyamide elastic membrane is supported with aluminium rings either side, and a magnetic mass is placed in the centre of the membrane, shown in figure 9(a).

Zoom In Zoom Out Reset image size

By changing the distance between electromagnet and mass (positioned below unit cell, shown in figure 9(b)), out-of-plane magnetic forces can vary. This causes a change in tension in the membrane and therefore a shift in phase modulation and transmission loss. This process is repeated at each unit cell, and an overall system response can be customised depending on the magnetic force distribution. This system response has the ability to redirect or focus waves, depending on this distribution. Low-frequency acoustic cloaking is an application of this. By changing the reflective properties of the acoustic metamaterial and arranging the metamaterial in a closed shape, an 'invisible' region within the closed shape can be created.

Tang et al demonstrate theoretically and through finite element analysis an acoustic metamaterial that has 'low-frequency sound absorption, excellent stiffness/strength and impact energy absorption' [41]. A honeycomb-corrugated (HC) hybrid core sandwich with top panel and bottom facesheet is shown in figure 10.

Zoom In Zoom Out Reset image size

Both the top panel and corrugated core have micro-perforations. These are introduced in order to allow sound into the structure without compromising its structural integrity. Unity absorption is shown at given frequencies, depending on the height of the structure. At 60 mm total height, unity absorption is at 580 Hz, with 0.5 or greater absorption seen between 290 and 1000 Hz. A parametric study was carried out to investigate the influence of geometry on the absorption of the metamaterial, though each study was carried out independently. An optimisation loop of the most influential parameters could be an interesting area of work, especially if the absorption frequency could be included in this. Additionally, as the work by Tang et al was only theoretical and numerical, a physical demonstrator would be a logical next step. An investigation into types of material this structure could be made of whilst still achieving desirable absorption qualities could lead to many applications where honeycomb type structures are already used. Honeycomb structures for a diaphragm in a loudspeaker could eliminate low-frequency noise interference. Honeycomb structures are already prolific within the aerospace industry as floor and side panels. Using the design features outlined by Tang et al the honeycomb sandwich panels could become multifunctional acoustic metamaterials. Pursuing this as an avenue of future work would open up many opportunities for large-scale acoustic dampening for use in the aerospace, construction and music industry. In addition, the paper by Tang et al only considers a square cross-section; mechanical and acoustic characterisation of different cross-sections could open up a greater area of applications.

Popa et al [42] present a real-time configurable acoustic metamaterial made of piezoelectric membranes unit cells. The unit cells are arranged horizontally to act as a slab that is able to change both the focal length and direction of the wave within milliseconds. An example of the unit cell and slab are shown in figure 11.

Zoom In Zoom Out Reset image size

To test the functionality of this slab, three modulated pulses were sent with a gap of 13 ms. The results show that each pulse, via electronic manipulation of the circuit, has a different focal position and focal direction. To add to this multifunctionality, further experiments were completed to show the metamaterial can perform two functions at the same time: it is able to steer an incoming wave in a different direction and focus an incoming wave, simultaneously. An interesting feature of this design is the simplicity and availability of the materials. The piezoelectric membrane is available commercially and the housing is acrylic glass. This means future experimental work can be easily carried out, and variations in the set-up could be tested. Applications of this metamaterial ranges from nonlinear imaging to acoustic cloaking. Nonlinear imaging has applications in the medical field, for ultrasonic testing, and also in nondestructive testing of composites.

Yu et al [43] extend this tuneability to three dimensions by creating magnetoactive acoustic metamaterial responsive to external physical stimuli. A 3D lattice structure embedded with ferromagnetic nanoparticles within a polymer substrate (created via stereolithography-based manufacturing technique) enable a 'magnetically triggered structural buckling of [the] elastomer to achieve controlled negative-modulus within design acoustic frequency regimes' [43]. The lattice structure is shown as a 3D model and in real life in figure 12.

Zoom In Zoom Out Reset image size

By modulating the magnetic field, the Young's modulus and effective density of the lattice can switch between positive and negative. This occurs due to a change in structural configuration (the buckling of individual trusses) and induces the low frequency absorption desired in metamaterials. It is observed in both experiment and simulation that between 3450 and 2500 Hz, the transmission is far below 50%, finding a minimum (in experiments) of approximately 8% at 3000 Hz. However, the magnetic field required to induce these is in the order of 0.1 to 0.5 Tesla, which is considered reasonably strong (100 times stronger than a typical fridge magnet). Therefore the applicability of such a structure is limited to very specific acoustic transmission opportunities. However, the proof of concept is promising, as the materials and manufacturing are highly accessible.

Elastic bodies that undergo deformations through static or dynamic waves can been designed so that fundamental properties such as Poisson's ratio, ν, dynamic mass density, ρ_eff, coefficient of thermal expansion (CTE), α, can respond in a manner never seen before. These materials are called mechanical metamaterials. Whilst electrodynamic and acoustic are often distinctly frequency-dependent, and so have a bandwidth in which they perform in a given way, mechanical metamaterials are sometimes not frequency dependent.

Ai et al [44] present an example of this non-frequency dependent behaviour by running finite element simulations on a lattice structure in order to determine a combination of parameters that creates a material with negative ν and α. The authors compare four metamaterials with slightly different lattice structures, and perform a parametric study on seven variables that affect the properties of the metamaterial designed. A designed metamaterial, with geometric parameters labelled, is shown in figure 13.

Zoom In Zoom Out Reset image size

The geometric design is 'based on star-shaped re-entrant lattice structures... [r]e-entrant structures are known to be one class of auxetic structures' [44]. Three material combinations are used, aluminium-Invar (Al-Invar), aluminium-stainless steel (Al-St), and stainless steel-Invar (St-Invar). Only one of the metamaterials studied is able to show negative Poisson's ratio and CTE at the same time, using the Al-Invar material combination. The achieved properties are: ν = −0.0186 and α = −0.0366. Clearly, these values are not large deviations from materials seen in nature, but they do represent the possibility of increased functionality that is often not available to single-material systems.

The article by Ai et al [44] highlights a number of key scientific advancements. Firstly, the study extends the boundaries of mechanical metamaterials as it does not involve joints that are welded, pinned, or pressure-fitted. Secondly, it is able to be created via additive manufacturing. In this way, this metamaterial offers a scale of manufacturing not previously seen in multifunctional, metamaterial composites. The authors also benefit from a vast amount of work carried out on auxetic structures (negative Poisson's ratio), whereas electrodynamic and acoustic metamaterials do not have this luxury.

An example of a frequency-dependent mechanical metamaterial is one characterised by Harne et al [45]. An on-demand controllable magnetoelastic metamaterial (MM) is characterised in terms of its stress–strain relationship under a magnetic field. Four materials are compared—two isotropic MMs and two anisotropic MMs—with control and test specimens, shown in figure 14.

Zoom In Zoom Out Reset image size

An isotropic MM was made by curing iron particles within an elastomer without a magnetic field being present. An anisotropic MM was made in the same way, but with a magnetic field applied during curing to polarise it. The paper aims to provide experimental evidence of a MM that can be controlled and understanding of the extent to which it can be controlled. This tunability was compared between a non-cellular and cellular topology, clearly seen by comparing figures 14(a)–(b) and figures 14(c)–(d). When a magnetic field was applied, it was found that both isotropic and anisotropic cellular structures exhibited a larger frequency-shift for the frequency at which the softening behaviour was displayed. This softening behaviour is also seen in the 'double-negative' metamaterials exhibited by Hewage et al [46].

In order to test the tunability of the samples, tests were repeated with and without a magnetic field. A dramatic increase in overall stiffness was seen with an anisotropic cellular structure when a magnetic field was applied, with a 100% increase in maximum stiffness for a 15% reduction in maximum strain. This stiffness increase is attributed to the collapsing of the cells and self-contact effects. Interestingly, beyond approximately 13% strain in the isotropic cellular structure, a sharp decrease in stiffness is seen. A local negative Young's modulus is shown by the material between 13% and 19% strain without field applied. With a magnetic field applied, this range decreases to be between 12% and 16% strain. The shown tunability offers many applications in vibration damping, impact resistance and noise management. Variable stiffness applications in soft robotics are also an avenue of future work, though the interaction between tuning magnetic field and electronics may cause a problem. A larger sample regime, with more parameters would also be of interest, as only four samples were tested. This would validate the conclusions from the paper and allow for further research to take place.

Chen et al [47] present a metamaterial that absorbs wave propagation whilst keeping its function as a sandwich beam by using a modified mass-in-mass spring system. Multiple mass-spring-dashpots are used to form a dissipative multi-resonator structure that is placed within the sandwich beam, shown in figure 15.

Zoom In Zoom Out Reset image size

By changing the damping ratios of the outside and inside dashpot, strong wave attenuation can be achieved at given frequencies (analytically calculated to be between 49 and 371 Hz). The system is optimised to a threshold of less than 5% transmissibility. A large design region is found that satisfies these requirements, showing that the system can theoretically provide enough wave attenuation. A numerical example of the blast resistance of such a system is shown, with the blast location, sensor locations and dissipater locations as indicated by figure 15. The dissipative resonators show a large decrease in amplitude and velocity of the incoming wave. Predicted wave attenuation bandwidth was confirmed: between 40 and 350 Hz, the amplitude is decreased to near zero. The velocity without resonators peaks at $20\,{\rm{m}}\,{{\rm{s}}}^{-1},$ whereas with resonators it peaks at $5.5\,{\rm{m}}\,{{\rm{s}}}^{-1}$.

The mechanism is clearly effective, but the length over which it happens is large and further optimisation could lead to a shorter beam. Additionally, it was not reported how the wave changes across the beam, which could indicate how many resonators are actually needed in order to achieve the response desired. Further work could also look at tuning and extending the wave attenuation band to beyond the 40–350 Hz gap, by adjusting the ratio between spring coefficient and mass.

Zhang et al [48] present tunability within mechanical metamaterials by introducing a soft metamaterial with a negative swelling ratio and tunable stress–strain curve. A three part design is used for the unit cell, shown in figure 16.

Zoom In Zoom Out Reset image size

The stress–strain curves of various hydration and dehydration states were experimentally measured and compared against FE simulation. Very good correlation between the two is found and it is clear that various stiffness levels can be achieved by having different concentrations of saturation. A study on the influence of initial arc angle was carried out, with results showing that either a negative or positive swelling ratio is possible. A negative swelling ratio means a structure will get smaller the more hydration it receives. The manufacturing process of this metamaterial is carried out solely with a 3D printer. This manufacturing process seems to be becoming more common as 3D printing technology advances.

Applications of such materials can vary from soft robotics to molecular sieves. By reacting to ambient conditions the metamaterial could form a portion of a smart system, where actuation is enabled through this distinct swelling behaviour. As the process shows little hysteresis when expanding/compressing, it could easily be introduced into a detector system that is sensitive to hydration levels. Such applications have not been considered within the paper and could be an area of future work.

Zhao et al [49] detail another controllable mechanical metamaterial, but one that uses thermal tuning for Poisson's ratio modification. This thermally controllable lattice structure combines a low elastic modulus material with high elastic modulus material, arranged in node and element structure, shown in figure 17.

Zoom In Zoom Out Reset image size

By utilizing current 3D printing technology, multiple materials can be printed into 2D and 3D structures. Thus, the Poisson's ratios can be tuned. This, with the addition of using materials that respond to temperature, multiple behaviours can be programmed into the structure. For example, a combination of low-stiffness nodes and high-stiffness elements results in a near-zero Poisson's ratio at 25 °C compared with a highly negative Poisson's ratio at 70 °C for both experimental and finite element analysis. Whilst an interesting result in itself, the design space expands greatly when considering that these lattice structures can be hybridised to combine any number of Poisson's ratios across the entire lattice structure at various temperatures. 3D lattice structures are simulated by the authors and show expected auxetic behaviour at a range of temperatures, but 'the hollow nature of the lattice makes it difficult to fabricate a 3D lattice using current multi-material 3D printers' [49]. However, the thermal tuneability and ease of manufacturing indicates these lattice structures are promising and can be applied in soft robotics for programmable responses.

Metamaterials were initially discovered by manipulating EM radiation, where given frequencies of waves caused 'backward' behaviour in a specially designed structure. This meant that by definition, a metamaterial had a bandwidth (only worked at given frequencies). This is especially true of electrodynamic and acoustic metamaterials. A more recent push to tunable metamaterials is evidenced that designers are trying to expand the range over which the metamaterials work. The bandwidth of a metamaterial isn't inherently a downside however, if the functionality of the metamaterial is designed to be at that frequency. Further work in making a multifunctional metamaterial tunable, such as those presented by Fan et al [30], Yu et al [43] and Zhao et al [49], is crucial.

The bandwidth of a multifunctional metamaterial is directly linked with the tunability of the structure. If one can change the metamaterial composite/shape/structure/geometry, then the inherent characteristics change (mainly due to Bragg scattering—where the spacing between objects changes the wavelength of wave influenced.) Many types of external stimuli can be employed, including electricity, hydration, heat, pressure, EM frequency, etc. This external stimuli is inherently limited however as a material can only adapt (shrink/swell/deform) within certain material, structural, geometric and temporal limits.

In light of the above point, a metamaterial with hierarchically structured lattices (i.e. one that has many 'sizes' within it) could be promising as it can affect the wavelength at a variety of scales—a multifunctional, multi-scale metamaterial. However, these lattice-type hierarchical metamaterials are a work in progress with published papers being sparse.

3D printing offers the most flexibility with metamaterials as the requirements (generally low stiffness/strength and a different materials) suit this method. Both polymer (Zhang et al [48]) and non-polymer (Ai et al [44]) additive manufacturing have shown promise and further work into large volume manufacturing of metamaterials may prove fruitful. Sadeqi et al [50] successfully showed the potential of coupling 2D etching and deposition processes, with nanoscale stereolithography 3D printing to create frequency selective optical metamaterials. The fabrication approach proposed promises a consolidation of metamaterial and optical elements with significant potential for reducing size, weight and complexity of instruments. The authors believe that with the ongoing resolution improvements in 3D printing, a new breed of metamaterial devices will be able to reach terahertz and optical frequencies in the near future. Lei et al [51] also showed the potential of 3D printing for generating auxetic metamaterial, where a flat two-dimensional elastic sheet design can readily be translated into a cylindrical shell through optimisation of the digital pattern and consideration of the rotational symmetry. New advances in 3D printing software and hardware offers the possibility of a step-change in metamaterial fabrication with the potential to yield more complex solutions in the future.

An interesting addition to 3D printing is the introduction of a printed smart material, with a time dependent attribute (commonly referred to as 4D printing [52]). A metamaterial with an active material has the potential to move beyond an architecture with fixed properties and gains the ability to adapt and adjust. Similar concepts have been explored in the past when building auxetic lattices or porous solids with smart material components (such as shape memory alloys, shape memory polymers and magnetorheological fluids) [53–56]. In the work by Yang et al [57], the authors demonstrated geometrically reconfigurable, functionally deployable, and mechanically tunable lightweight lattice metamaterials using a shape memory polymer constructed through a digital micro 3D printer. They noted the effective stiffness of the printed lattices changed by over two orders of magnitude when operated within a temperature range of 30 °C to 90 °C. Similarly, Lei et al [51] also considered the potential of a shape memory polymer as a 4D printing material for reversible change in the stiffness, geometry, and functions of their metamaterial constructs. In this particular case, they designed a 4D cylindrical shell where the control of the moduli, Poisson's ratios, and fracture strains of the structure can be programmed and reprogrammed to realise complex shape changes. Clearly, this research using shape memory polymers opens up the potential for geometrically reconfigurable and functionally deployable mechanical metamaterials; it will now be interesting to see if 4D printing can also realise reconfigurable electrodynamic and acoustic metamaterials.

These examples illustrate the potential of novel design and material strategies in the development of metamaterials for the future. However, some metamaterial designs do not readily lend themselves to this methodology since the scale at which they operate is beyond the resolution of current 3D printers. The authors accept these limits are constantly being revised but fundamental there is a lower manufacturing limit beyond which metamaterials will not reside.

Metamaterials aim to add functionality to a composite structure through their 'beyond nature' behaviour. As the field is relatively new, working examples of application are few, especially among multifunctional metamaterials. Whilst the discussed application space is broad, there are not many physical examples of multifunctional metamaterials applied to solve problems as of yet. Future research into metamaterials that demonstrate their application in real life would establish their functionality and increase the use of these appealing composite structures.

One key area of application of EM metamaterials is the field of 5G communication. Naqvi et al [58] showed, through simulation, a 95%–100% absorption of EM waves from 20 to 60 GHz (the range at which 5G operates) at a range of incidence angles. A symmetric, novel G-shape absorber is used that absorbs Ku, K-, Ka-, Q- and U- bands. Another area where EM metamaterials show great promise is in flexible electronics. A wearable, metamaterial antenna designed and simulated by Ali et al [59] shows greater than 69% radiation efficiency when placed on an simulated human arm. With reasonable gain (6.29 dB) across a 74 MHz band gap centred around 2.42 GHz the metamaterial opens up a large number of opportunities for electronics to integrate with biological systems in a more functional and less invasive manner.

A promising avenue for acoustic metamaterials is energy harvesting. Wang et al [60] present an excellent example of a simple, diaphragm-based acoustic metamaterial that is able to output up to 70 mV at a resonant frequency (318 Hz). This translates to a 0.073 1 μW maximum power output. Whilst not a large power output, when arranged in tandem and larger transducers are used, low-frequency energy absorption would be a viable avenue of metamaterial application. A natural extension of this is in the aerospace industry, where low frequency engine noise is very prevalent. A similar investigation and structure was developed by Sun et al [61] that was able to produce 0.346 μW of power at 600 Hz, and due to the resonant frequency driving the piezoelectric plate an output voltage '6.32 times higher than that of [a] conventional piezoelectric harvesting plate' [61].

An analytical and numerical proof-of-concept for a practical use of mechanical metamaterials is laid out by La Salandra et al [62]. Drawing on inspiration from phononic lattice structures for low-frequency vibration attenuation, a 3D structured optimized foundation made of concrete and rubber. Results show that acceleration of the tank can be halved with a 'smart foundation' at key frequencies. A second application area for mechanical metamaterials is soft robotics. Rafsanjani et al [63] present a selection of soft robotic architectures in three themes: beam-based structures, folding and cutting systems, reinforced systems. These features increase the functionality and programmability of soft robotics far beyond the single function philosophy currently used. Rafsanjani et al point towards artificial intelligence as the main future tool for capturing the design space and honing in on an optimized solution.

Lattice structures are extremely promising when considering the broad range of issues found in multifunctional composite metamaterials. The manufacturing techniques available (3D printing and stereolithography-based techniques) enable prototypes and experimental coupons to be easily manufactured. Multimedia 3D printing and 4D printing adds extra levels of functionality and (if required) bandwidth to combat single-use and adaptive multi-use metamaterials.

Additionally, lattice structures are found in all three areas of multifunctional metamaterials (electrodynamic, acoustic and mechanical). Whilst not pursued at the present time, a 3D multimedia lattice capable of influencing all three types of waves would be a structure worth developing.

The identification of the metamaterial applications above is neither exclusive nor exhaustive and there are likely to be many topics not listed that are equally important for future development. However, it is imperative that multidisciplinary or transdisciplinary teams are created to develop the next generation of metamaterials.