Abstract
An empirical model for small circular electron fields was developed. This can be of great help in the treatment planning process for small circular electron fields. A complete dosimetric analysis of the circular fields defined by electron cutouts diameters (2 cm–9 cm) was done for nominal electron energies ranging between 6 MeV and 20 MeV using a 3D water phantom and a pin-point ion chamber. Properties studied included depth dose, in-air inverse-square fall-off, and beam profiles. The Varian Clianc 2100 C accelerator was modelled, benchmarked and Monte Carlo simulations were performed using the EGSnrc/BEAMnrc code for the small circular cutouts. A simple exponential model was found to accurately predict the very important therapeutic depth (90% of Dmax) for the small circular field size within an accuracy of better than 2 mm in most cases. The model has only two parameters (d90 and 'b'). Also, the penumbra widths (90% of the off-axis profiles) of these small circular electron fields were studied and least square fitted to a simple quadratic model. Full dosimetric profiles of these small circular electron fields were further studied using the benchmarked Monte Carlo simulations. This study presents a simple model to predict the very important therapeutic depth (90% of Dmax) and a recipe to develop such an electron treatment model for any linear accelerator system. Such predictions can be extremely valuable and time saving prior to treatment planning involving not only small circular shaped electron fields but also irregularly shaped electron fields.
Export citation and abstract BibTeX RIS
1. Introduction
The surge in commercial development and applications of the linear accelerators during the seventies for cancer therapy also led to a surge in use of electrons for therapy. Work carried out at some of the premier institutions during this time, showed that in some common situations, there was no alternative treatment to the electron beam therapy. Electrons are charged particle with a finite range and therefore are suitable for treatment of superficial and shallow targets. Electron beam therapy offers some distinct advantages over megavoltage photon beam therapy [1, 2]. Electrons deliver a reasonably uniform dose from the surface to a specific depth, after which the dose falls off rapidly to a near zero value unlike the megavoltage photon beams. Electrons are useful in treating cancer of the skin and lips, head and neck, breast, upper respiratory and digestive tract. Small electron fields, shaped using circular cutouts made of Cerrobend are frequently used for treating superficial tumors, which are not too deep in the body. Clinically it is extremely important to know the depth dose characteristics and off-axis profiles of these small circular electron cutouts as they can vary to a great extent with the electron energy and the diameter of the circular cutouts [3]. A lot of laborious measurements in this regard may need to be performed before deciding upon the right electron energy and the circular cutout size for a particular case. Previous studies have been performed in this respect to get Output Factors using the Monte Carlo method [4]. Prediction of Output Factors have also been obtained using a parametric form [5] and pencil beam algorithm [6]. Several studies have been done on measuring dosimetric properties of small electron fields. However most of the studies are missing on estimating a very important parameter for electron treatment that is the therapeutic depth (90% of Dmax). The therapeutic depth, which is the 80% to 90% of the depth of the depth dose curve coming after Dmax is the most useful range for any electron field. The therapeutic depth (90% of Dmax) is given by the depth of the 90% depth dose coming after Dmax, for that particular field size. This is very important as the dose decreases abruptly beyond the 90% dose level after Dmax. The therapeutic depth (90% of Dmax) and the required electron energy must be chosen very carefully. In this study we have characterized the dosimetric properties of small electron cutouts with diameter ranging from 2 cm to 9 cm for a Varian Clinac 2100 C. We have arrived at a simple analytical model, which using a single curve fitted coefficient : 'b' can be used for predicting the very important: therapeutic depth (90% of Dmax) for small circular cutouts made of Cerrobend. Also, we have measured and fitted equations to the 90% field width at SSD of 110 cm, which can be very useful to decide the energy and cutout size based on the intended target coverage area. The empirical formation developed in this study can be used effectively for deciding the right electron energy and the right circular cutout diameter after deciding upon the right therapeutic depth (90% of Dmax). Similar measurements may be performed for any linear accelerator system to use the simple exponential expression with machine specific parameters including the fitting parameter 'b'. This approach can be used for making optimal and swift treatment planning for cases involving small circular electron fields and shallow targets.
2. Methods
A set of circular electron cutouts, made of Cerrobend with physical diameters from 2 cm to 9 cm were constructed in the usual clinical manner (figure 1). A full dosimetric analysis of the circular fields defined by each cutout was done for nominal electron energies ranging from 6 MeV to 20 MeV for a Varian Clinac 2100 C. The dosimetric data was collected using a pinpoint chamber and 3D water phantom as the same equipment/process was used in the commissioning process of the linear accelerator. Properties studied included depth dose, in-air inverse-square fall-off, and beam profiles. A linear accelerator model was built in EGSnrc/BEAMnrc [7] for the Varian Clinac 2100 C. The geometry of the linear accelerator (position of scattering foil, x-y jaws, applicators etc) was obtained directly from Varian Medical Systems of Palo Alto, California. After appropriate benchmarking, these properties were further studied with Monte Carlo model of the accelerator developed using the EGSnrc/BEAMnrc code [7]. From the physical data and simulations, the following parameters were determined for each cutout/energy combination: R50, R90, widths of 90% and 95% isodose surfaces, effective SSD, and dose output factor. Selected parameters were then correlated with collimator size to arrive at an exponential model, which accurately predicts the therapeutic depth (90% of Dmax). For projected circular cutout sizes smaller than 2 cm, the measurements are very hard to perform, therefore the results from benchmarked Monte Carlo simulations were used to fill in the points in order to develop the complete empirical model. This set of crucial data points (x < 2 cm) are necessary to arrive at the functional form of equation (1).
Figure 1. Circular Cerrobend Electron Cutouts of diameter ranging from 2 cm to 9 cm.
Download figure:
Standard image High-resolution image3. Results
The following simple exponential model (equation (1)) had been found to accurately predict the commonly used the therapeutic depth (90% of Dmax) for the circular field size with projected diameter x (at SSD = 100 cm), within an accuracy of better than 2 mm in most cases.
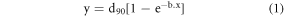
Here y is the 90% depth for the circular cutout with projected diameter: x, d90 is the 90% therapeutic or prescription depth (90% of Dmax) for the open cutout (10 × 10 cm2 field), which is normally measured during the commissioning process. This d90 can also be estimated approximately by E/3.2 cm, where E is the most probable energy in MeV of the electron beam at the patient/phantom surface [8]. Figure 2 shows the plot of measured values and also those obtained from Monte Carlo modelling for projected diameter: x < 2 cm. The predicted curves are plotted as well by curve fitting the functional form using least square method for electron beam energies ranging from 6 MeV to 20 MeV. The only real unknown in this model here is the parameter 'b', to be determined using least curve fitting. The coefficient of determination for the curve fitting (R2 value) was close to 0.99 for all the electron energies [9].
Figure 2. 90% Depth (y) beyond Dmax versus projected circular cutout diameter (x) for SSD of 100 cm. For x < 2 cm, the data points were generated through benchmarked Monte Carlo accelerator model.
Download figure:
Standard image High-resolution imageTable 1 shows the values of the least square fitted parameter 'b', d90 for all the nominal electron energies for the therapeutic depth (90% of Dmax). These values can be easily obtained for any particular linear accelerator by performing measurements for a few circular electron cutouts and a few Monte Carlo simulations. The parameter 'b' depends on the beam energy and has been least square fitted to a quadratic model (cubic term coefficient is close to zero) as shown in figure 3 with coefficient of determination : R2 = 0.998. This model can be developed for any accelerator system and used to predict the 'b' parameter for a particular energy to be used the main modeled equation (1) for calculating the therapeutic depth (90% of Dmax).
Table 1. Values of fitted parameters evaluated using least square regression analysis.
| Parameters | Energy = 6 MeV | Energy = 9 MeV | Energy = 12 MeV | Energy = 16 MeV | Energy = 20 MeV |
|---|---|---|---|---|---|
| d90 | 1.846 | 3.005 | 4.247 | 5.475 | 6.061 |
| b | 0.7517 | 0.5086 | 0.4105 | 0.3536 | 0.3759 |
Figure 3. The parameter 'b' of the equation (1) as a function of electron energy along with a least square fitted quadratic model for predicting it for any console energy: E.
Download figure:
Standard image High-resolution imagePenumbra widths, which are defined as the 90% field width at the depth of maximum dose were evaluated and are presented in figure 4. These are plotted as a function of electron cutout size (x) and nominal electron energy at 110 cm SSD. The data was least square curve fitted to set of quadratic expressions (shown in figure 4) for each electron energy. The coefficient of determination (R2 value), which is a measure of how good the fitting [10] has been calculated and in almost all cases are very close to the ideal number of one.
Figure 4. Measured and fitted quadratic equations for 90% penumbra widths at 110 cm SSD.
Download figure:
Standard image High-resolution imageFigure 5 shows the measured and Monte Carlo generated data for 12 MeV central axis, percent depth doses for all the small circular cutouts of diameters ranging from 2 cm to 10 cm. Figure 6 shows a comparison of the measured and the Monte Carlo generated data for off-axis profiles of 9 MeV electron beams again for all the circular cutouts of diameter ranging from 2 cm to 10 cm. The simulations were done using 100 million histories to give error bars of sizes less than ±1%. The simulation time taken for each cutout was around 2 to 3 hours on an Intel i5-4570@3.2 GHz processor with 4GB RAM.
Figure 5. Measured and Monte Carlo data for 12 MeV, central axis percent depth dose profiles.
Download figure:
Standard image High-resolution imageFigure 6. Measured and Monte Carlo data for 9 MeV off-axis profiles for circular cutouts with diameters ranging from 2 cm to 5 cm.
Download figure:
Standard image High-resolution imageThe Monte Carlo method needs to be able to predict a dose distribution in agreement with the measurement within clinically acceptable tolerance level [11, 12]. A commonly accepted accuracy level is ±2% or ±2 mm as stated in ICRU Report 42. [13]. Great agreements (differences less than 2%) between the measurements and the Monte Carlo data have been found in both the cases studied in figures 5 and 6. The agreement for very small circular sizes of 2 cm and 3 cm is not as great as the agreement for field sizes higher than 3 cm. This slight disagreement may be due the uncertainties involved in measurement for very small field sizes. The bench marked Monte Carlo data for percent depth dose may be trusted more in these cases.
4. Discussion and conclusions
The formulation developed in this work accurately describes the clinical dosimetric properties of small circular electron fields. It can be used to select the circular cutout diameter needed to provide the desired coverage (using 90% field widths) at the very important therapeutic depth (90% of Dmax), beyond which the dose falls off very rapidly. This can be done without relying on usually used approximate rules i.e. estimating it as E/3.2 cm, where E is the most probable energy in MeV of the electron beam at the patient/phantom surface [8] or trying various combinations of energy and cutout size in a treatment planning system. This formulation can greatly help in providing adequate dose at the right target depth under the skin and have intended target coverage.
Equation (1) can be effectively used for predicting the depth (90% of Dmax), represented as: y for small circular cutouts with projected diameter: x and greatly help in the decision of choosing the right circular cutout size and energy. Once a set of relevant cutout sizes and energies have been narrowed down, the fitted equations of the measured data for penumbra widths can be used to close the search for the right cutout and the right energy. Modelled equation (1) has only two parameters that of d90 for the open 10 × 10 field (which is usually measured during the commissioning process) and the independent parameter 'b'. The possible values of parameter 'b' (shown in table 1) were determined using the empirical data and nonlinear regression method [9]. It may be noted that the parameter 'b' does not vary much for higher energies ranging from 12 MeV to 20 MeV. Parameter 'b' may be related to the scattering power of the electron beam, which is higher for lower energies. This parameter can easily be obtained by doing measurements for all the available circular cutouts and filling in the points for cutout diameter for x < 2 cm, using the benchmarked Monte Carlo simulations. Finally, this 'b' parameter can be predicted using the least curve fitted quadratic function shown in figure 3. A similar functional form can be easily developed for any accelerator system.
The Monte Carlo method relies on fundamental physics principles governing interaction of particles in media and has been proved to be capable of accurately modeling electron beams in radiation therapy [11, 12]. A lot of improvement has been attained in this regard [9]. Final choice of the circular cutout size and energy can be used as input into the benchmarked Monte Carlo model to get the full dosimetric properties of the cutout: percent depth dose (figure 5) and off axis profiles (figure 6) at the chosen energy. Processing time may be saved in performing benchmarked Monte Carlo simulations by using phase-space files. A phase-space file is a collection of data specifying properties such as the position, direction, energy and the type for each particle crossing a plane defined as a phase-space plane. These phase-space files are usually compatible with the International Atomic Energy Agency (IAEA) format for clinical electron energies just above the jaws. These are provided for some of the new systems such as the Trubeam Linacs from Varian. Complete studies of small electron fields using such a phase space file approach has been demonstrated [14]. This recipe may be followed for any of the commercial linear accelerator, thereby greatly cutting down the treatment planning time and effort without compromising on the optimization of the planning process. Similar studies and modelling may be designed to be carried out for other symmetrically shaped small electron cutouts such as triangular, square or rectangular shaped. This study was specially carried for small circular electron cutouts but can be useful for irregularly shaped electron fields as well. The benchmarked Monte Carlo models (tested for small circular cutouts) may be relied upon to get the full dosimetric properties of any irregularly shaped field.








