Tuning the band gap and effective mass of black arsenic phosphide monolayer by in-plane strain

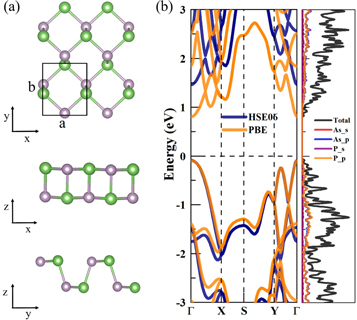
The black AsP monolayer has an orthorhombic lattice with a space group of Pmna2, which is similar to that of phosphorene, a unit cell containing four atoms with alternating P atoms and As atoms (see figure 1).

Zoom In Zoom Out Reset image size

Furthermore, the optimized lattice constants of the monolayer are a = 3.50 Å, b = 4.69 Å, which are consistent with previous DFT calculations [33]. The band structure and projected density of states (PDOS) are presented in figure 1(d). The band structure calculations are performed using the PBE method and HSE06 method, which yield band gap values of 0.90 eV and 1.55 eV, respectively. These results are consistent with previous reported findings [33]. From the PDOS image, we observe that the contributions of the valence band maximum (VBM) and the conduction band minimum (CBM) arise mainly from the 3p state of the P atom and the 4p state of the As atom. This similarity results from the similar electronegativities of the P atom and As atom as well as the strong hybridization of the 3p orbital comprising the P atom and the 4p orbital comprising the As atom.

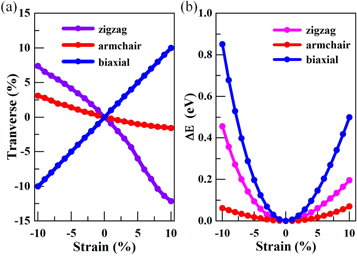
Generally, for 2D materials stretched in the axial direction, shrinkage deformation occurs along the direction perpendicular to the material. Poisson's ratio, which is given as $v=-\tfrac{d{\varepsilon }_{tranverse}}{d{\varepsilon }_{axial}},$ reflects the elastic constant of transverse deformation in the material. The relationship between the transverse strain and the axial strain is plotted in figure 2(a) (Poisson's ratio values for the zigzag and armchair directions are 0.23 and 1.01, respectively). The significant difference between the ratios indicates the anisotropy of the black AsP monolayer. The Poisson's ratio of the monolayer is slightly lower than that of phosphorene along the zigzag direction, and slightly greater than that of phosphorene along the armchair direction [47]. The axial-strain-induced changes in the total energy of the monolayer are plotted in figure 2(b). As shown in the figure, the applied axial strain along the zigzag direction results in greater changes than the strain applied along the armchair direction, indicating that the zigzag direction is more resistant to elastic deformation. That is, the strain applied along the zigzag direction has the least effect on the structural stability of the material.

Zoom In Zoom Out Reset image size

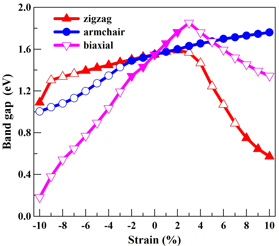
To obtain more accurate band gap results (than those previously reported), a hybrid functional HSE06 method is used in our calculations. The relationship between the band gap and strain is revealed in figure 3. For strain applied along the zigzag direction, the band gap decreases linearly with increasing compressive strain until a strain value of −9% is reached. The gap value decreases sharply when a strain of −10% is reached. However, for increasing tensile strain, the value increases slightly at first, and then occurs either under compressive strain or tensile strain. For strain (−10% to 10%) applied along the armchair direction, the value of band gap increases monotonically. Furthermore, the band gap of black AsP monolayer exhibits a decreases linearly with increasing compressive strain. In contrast, the band gap is monotonous increasing along with the increasing tensile strain. A direct-indirect conversion in band gap is occur for strain values less than −2%. For the applied biaxial strain, the band gap value decreases substantially with increasing compressive strain. The value increases linearly, however, with increasing tensile strain until a strain value of 3% is reached, and decreases rapidly thereafter. The maximum gap value of 1.85 eV is obtained at a strain value of 3%. The direct band gap is maintained for compressive and tensile strain values of ≤2%, and the indirect band gap occurs for strains of >2%. In order to reveal the variation trend of CBM and VBM of black AsP monolayer in black AsP monolayer along with the applied tensile or compressive strain, in figure S1 (available online at stacks.iop.org/MRX/9/025009/mmedia) of the supplementary material, we show the CBM and VBM of black AsP monolayer under the applied strain. It implies that the band gap of black AsP monolayer exhibits anisotropy character under the applied uniaxial strain, which is decided by the relative energy level of CBM and VBM. This is induced by the different structural deformation of the AsP monolayer induced by the applied strain along different directions or by applying biaxial strain.

Zoom In Zoom Out Reset image size

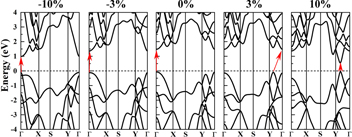
The influence of strain on the electronic properties of monolayer black AsP is further explored by plotting the band structure at some specific strain (see figure 4). For intrinsic monolayer black AsP, we observe a direct band gap resulting from the CBM and VBM located on the Γ point. Consider a strain applied along the zigzag direction. When the applied compressive strain increases to −3%, we found that the CBM and VBM are still located on this point but the band gap decreases to 1.47 eV. Moreover, the CBM moves slowly toward the Fermi level. The band gap decreases to 1.09 eV when the material is subjected to a compressive strain of −10%, and the CBM moves further toward the Fermi level. When a tensile strain of 3% is applied, the VBM moves from the Γ point to a k point on the Γ-Y path, and the distance between the CBM and the Fermi level changes only slightly. Considering an applied tensile strain of up to 10%, owing to this strain, the CBM moves from the Γ point to the Γ-Y path, a direct band gap of 0.57 eV is formed, and the energy between the CBM and the Fermi level decreases further. These results indicate that the CBM is more sensitive to tensile strain than to compressive strain. Furthermore, monolayer black AsP exhibits semiconductor characteristics over the strain range (−10% to 10%) considered (for strain applied along the y axis and xy axis, see figure S2 for more details). To better understand the change of VBM and CBM in the band structure under different applied strain, we give a more detailed analysis on the variation of VBM and CBM tuned by in-plane strain along x, y and biaxial directions, which can be found in figures S3 and S4 in supplementay material.

Zoom In Zoom Out Reset image size

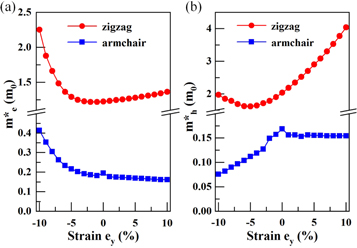
Previous studies have demonstrated that strain has a significant impact on the transport properties of 2D materials. The carrier mobility plays a critical role in the performance of measurement devices, and the carrier mobility is inversely proportional to the effective mass of electrons and holes. Therefore, we explore the effective mass of electrons and holes under both axial strain and biaxial strain. The effective mass is calculated as follows: ${m}^{* }={\hslash }^{2}{\left(\tfrac{{d}^{2}{\rm{{\rm E}}}}{{d}^{2}k}\right)}^{-1}.$ For intrinsic monolayer black AsP, along the zigzag (Γ-X) direction, effective mass values of 1.226 m₀ and 2.040 m₀ are obtained for the electrons and holes, respectively. However, in the armchair (Γ-Y) direction, mass values of 0.179 m₀ and 0.157 m₀ are obtained for the electrons and holes, respectively. These results are consistent with those of a previous study [30]. In figure 5, the relationship between the effective mass of electrons and holes and the strain is illustrated for strain applied along the x direction.

Zoom In Zoom Out Reset image size

We observe from figure 5(a) that the effective mass of electrons along the zigzag direction changes only slightly under compressive strains, indicating that the mass insensitive to strain in this case. However, along the armchair direction, the effective mass increases initially and then decreases with increasing tensile strain, with a sudden drop resulting from the CBM jumping from the Γ point to the Γ-Y path. A detailed band structure showing all the effective mass sharp jump/drop points is presented in figure S5. In figure 5(b), the effective mass of the holes along the zigzag direction changes significantly under compressive strain, demonstrating that this mass is sensitive to strain. Moreover, the jump occurs at −10% compressive strain and −9% compressive strain along the zigzag direction and the armchair direction, respectively. This considerable change results from the fact that the band dispersion is weak along the Γ-Y direction around VBM. For strains of up to −9%, the dispersion is enhanced along the Γ-X direction around VBM when the strain reaches −10%.

For strain applied along the y direction, with increasing compressive strain, the effective mass of electrons exhibits the same trend along the zigzag direction and the armchair direction (figure 6(a)). However, the mass is insensitive to the tensile strain along these directions. Due to the strain-dependent sensitivity of the VBM, the effective mass of the holes exhibits irregular variation

Zoom In Zoom Out Reset image size

along the zigzag direction (figure 6(b)). The effective mass of electrons along the armchair direction is an order of magnitude smaller than that along the zigzag direction, for strain ranging from −10% to 10%. This indicates that electron transport will occur preferentially along the armchair direction.

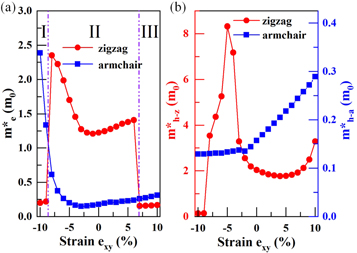
Considering the application of strain in biaxial directions, at a compressive strain of −9% and a tensile strain of 7%, the effective mass of electrons decreases sharply along the zigzag direction (see figure 7(a)). This results from the jump of CBM from the Γ point to the Γ-X path and enhanced band dispersion in the Γ-X direction around CBM. In addition, the effective mass of electrons along the armchair direction is more sensitive to larger compressive strains than to smaller compressive strains. These results indicate that the electrons in region I and region II are mainly transported along the zigzag direction and the armchair direction, respectively. The effective mass of holes is sensitive to compressive strain along the zigzag direction and a sudden drop occurs at a compressive strain of −9% (see figure 7(b)). This drop results from enhancement of the band dispersion in the Γ-X direction around VBM (the corresponding band structure is presented in the supplementary material (figure S2)). This change leads to a competition between the hole transport along the armchair and that along the zigzag direction. However, for strains ranging from −9% to 10%, this transport occurs preferentially along the zigzag direction. In the literature, carrier effective mass in many other 2D materials were reported. For example, in black phosphorene, it was reported that its carrier effective mass is anisotropic with an hole/electron mass of 11.16m0/1.24m0 close to the Γ point (VBM) and a hole/electron mass of 0.14m0/0.15m0 along the Γ-Y direction [48]. Similar anisotropic behavior was also found in 2D semiconductor GeP by first-principles prediction [49]. Some of them were also sensitive to the applied external strain. For example, in MSb (M = C, Si, Ge and Sn) monolayers, it was found that the effective mass can be tuned by applying strain [50]. In our recent study of 2D PbSe [51], we also found that the effective mass of both electron and hole can be tuned by biaxial strain. In table S1 in supplementary material, we list some values of effective mass of electron and hole under some particular applied strains. It implies that the external in-plane strain is an efficient way to tune the effective mass of electron and hole in 2D AsP.

Zoom In Zoom Out Reset image size