Abstract
We have proposed a topological carbon allotrope, named Hopfene, which has three-dimensional (3D) arrays of Hopf-links to bind 2D Graphene layers both horizontally and vertically without forming strong σ bonds between layers. Tight-binding calculations show unique band structures of this crystal, which predicts semi-metal characteristics with the existence of both Weyl and Dirac Fermions depending on the Fermi energy. Here, we have theoretically examined superconductivity of Hopfene based on the attractive Hubbard model. Regardless of its simplicity of the model, we found non-trivial competitions between Hartree–Fock mean-field contributions and Cooper-paring interactions to open semiconductor and superconducting energy gaps, respectively. Consequently, the superconducting order parameters are significantly reduced at every quarterly doping concentration, where the system is in the close vicinity of the quantum critical point, and we found superconductor-insulator transition in the strong coupling limit. Upon doping, we confirmed a classical scenario of a smooth crossover from weak coupling Bardeen-Cooper-Schrieffer (BCS) superconductivity to strong coupling Bose–Einstein Condensation (BEC) of preformed pairs by increasing the interaction strength. We think the proposed Hopfene is a useful platform to investigate the impacts of the topological nature of the Fermi surfaces on the superconductivity and other orders, including charge-density-waves and magnetic orders, and possible quantum phase transitions among them.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The discovery of superconductivity by Onnes [1, 2] was a mystery for a long time and it was finally solved by Bardeen, Cooper, and Schrieffer (BCS) after a half century from the discovery based on quantum-mechanical many-body field theory [3–6]. Besides its technological significance of superconductivity, the mechanism was astonishing: the broken U(1) gauge symmetry led to the formation of the energy gap, Δ, leading to the macroscopic coherent state, which allows the persistent currents and Meissner effect [3–7]. Nambu was inspired by the BCS theory and generalised the concept of broken symmetry [8] to explain the emergence of mass in elementary particles. He compared the quasi-particle dispersion, 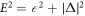 , after the onset of the superconductivity with the energy spectrum obtained by Einstein's special theory of relativity, E2 = (cp)2 + (m c2)2, where c is the speed of light and m is the mass of the particle. He suggested that the original massless particle with the energy,
, after the onset of the superconductivity with the energy spectrum obtained by Einstein's special theory of relativity, E2 = (cp)2 + (m c2)2, where c is the speed of light and m is the mass of the particle. He suggested that the original massless particle with the energy,  = cp, and the momentum of p would acquire the mass by the formation of the energy gap
= cp, and the momentum of p would acquire the mass by the formation of the energy gap 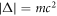 . He also established the generation of new Bosons, known as Nambu-Anderson-Goldstone-Higgs modes [4, 8–10], which recover the broken symmetry by using the phase degree of freedom,
. He also established the generation of new Bosons, known as Nambu-Anderson-Goldstone-Higgs modes [4, 8–10], which recover the broken symmetry by using the phase degree of freedom, 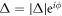 , in low energy excitation to circulate around the minimum of Ginzburg-Laudau free energy with the shape of a Mexican hat [11–13]. These theories [4, 8–10] saved the apparent contradiction of the variational BCS wavefunction [3, 4, 6] with the unfixed number of electrons, regardless of the definite number of electrons in a material, because the inclusion of the collective modes ensures the conservation law of charge under the current flow as a vertex correction of the Ward-Takahashi identity [4, 8]. It is also interesting to note that a fully analytic exact solution of a superconducting ground state with a fixed number of electrons, describing the vacuum state of collective modes, beyond the BCS wavefunction is still unknown even for a simplified BCS Hamiltonian. Nevertheless, the essential mechanism of superconductivity is considered to be understood based on the BCS theory. This statement would be mostly true even after the discoveries of new superconducting materials [14–17], including copper-oxides with d-wave paring symmetries [14, 18], although the source of the attractive interaction would be required to be reconsidered from phonon-mediated mechanism to spin-correlated one. It is considered that the normal states of the copper-oxides [18, 19] are even more anomalous than the superconducting states, since the strong Coulomb repulsion in two-dimensional (2D) leads the Mott-Hubbard metal-insulator transition and the validity of the Fermi liquid theory is marginal [11, 12, 18]. It is certainly beyond the authors abilities to grasp the entire recent progress on superconductivity. The subject of superconductivity is huge and still expanding significantly across interdisciplinary areas, and superconductivity is deeply linked to the forefront of fundamental physics on broken symmetries and the emergence of mass.
, in low energy excitation to circulate around the minimum of Ginzburg-Laudau free energy with the shape of a Mexican hat [11–13]. These theories [4, 8–10] saved the apparent contradiction of the variational BCS wavefunction [3, 4, 6] with the unfixed number of electrons, regardless of the definite number of electrons in a material, because the inclusion of the collective modes ensures the conservation law of charge under the current flow as a vertex correction of the Ward-Takahashi identity [4, 8]. It is also interesting to note that a fully analytic exact solution of a superconducting ground state with a fixed number of electrons, describing the vacuum state of collective modes, beyond the BCS wavefunction is still unknown even for a simplified BCS Hamiltonian. Nevertheless, the essential mechanism of superconductivity is considered to be understood based on the BCS theory. This statement would be mostly true even after the discoveries of new superconducting materials [14–17], including copper-oxides with d-wave paring symmetries [14, 18], although the source of the attractive interaction would be required to be reconsidered from phonon-mediated mechanism to spin-correlated one. It is considered that the normal states of the copper-oxides [18, 19] are even more anomalous than the superconducting states, since the strong Coulomb repulsion in two-dimensional (2D) leads the Mott-Hubbard metal-insulator transition and the validity of the Fermi liquid theory is marginal [11, 12, 18]. It is certainly beyond the authors abilities to grasp the entire recent progress on superconductivity. The subject of superconductivity is huge and still expanding significantly across interdisciplinary areas, and superconductivity is deeply linked to the forefront of fundamental physics on broken symmetries and the emergence of mass.
The effective mass [20–22] in a material is also very important for various practical electronic applications, especially for Metal-Oxide-Semiconductor (MOS) Field-Effect-Transistors (FETs), because the mobility is larger if the mass is smaller [20, 22–25] suitable for high speed operations. Novel strain-engineering technologies [25–27] are introduced in Si MOFETs to reduce the effective mass. Graphene [28–32] is especially promising for high-speed RF applications in this sense, because the effective mass vanishes at the 2D Dirac point [29, 33]. The band structure of the Graphene [34] was known for a long time, however, it was not considered to be able to isolate as a complete 2D layer, because the long-range order is not expected to realise at any finite temperature due to thermal and quantum fluctuations [35–37]. It was a great discovery that the Graphene monolayer was exfoliated by a sticky tape [30, 31], which was a modern innovation like an Egg of Columbus. It is now considered that the ripples of Graphene are ensuring to stabilise its 2D crystalline structure without violating Mermin-Wagner's theorem [35–37]. Again, the dimensionality and the symmetry are closely linked to the massless character of Dirac Fermions [29, 33]. These Dirac Fermions can be considered to be generated from magnetic monopoloes located at the Dirac points [29, 38, 39], which are topologically protected due to the conservation of geometrical Pancharatnam-Berry phase factors [40, 41]. Thus, the features of Dirac Fermions are robust against perturbations, if the external fields are conserving space and time reversal symmetries and the state is continuously changing without an occurrence of a phase transition, including superconductivity, which leads to the emergence of mass in quasi-particles, as outlined above [4, 8]. The idea of exfoliation and its transfer was successfully expanded to wider materials beyond Graphene with multi-layered structures weakly stacked via van-der Walls force [42, 43]. This will allow us to create a completely new material with various combinations of stacked layers, which was not possible to fabricate based on conventional superlattice fabricated by traditional epitaxial growth technologies, so that 2D materials are revolutionising material science and technologies.
We have recently proposed a new family of carbon allotropes with topologically non-trivial structures [44]. Topology is a mathematical concept to distinguish an isolated ring from a linked chain, for example, and it allows us to classify structures by continuous deformation of a structure. From topological points of views, Graphene with ripples is obviously equivalent to that without a ripple, and stacked 2D materials are categorised as topologically trivial, which means there is neither a link nor a knot. On the the other hand, we can consider various topologically nontrivial structures with links and knots in carbon allotropes [44], which include Hopf-link [45], Whitehead-link, Trefoil-knots, Mebius ring, Bborromean rings, and so on. In particular, we think Hopf-links are very useful to extend the topologically non-trivial network in the form of a chain (1D), a chainmail (2D), and a crystal (3D). The Hopf-links can change spacial configuration without topologically changing the structure, so that it is strong against deformation. A Hopf-linked Carbon-Nano-Chain (CNC) can be stretched to change its length orders of magnitude, depending on whether it is relaxed or tensile-strained, similar to a macroscopic chain. The CNC does not have to maintain the rigid crystalline structure like a conventional crystal, while the topological feature is maintained as far as strong σ bonds are preserved, so that we can consider that the CNC possesses a topological-long-range order [44, 46–53]. By making arrays of Hopf-links, we can consider a new 3D crystalline carbon-allotrope, which links horizontal Graphene layers with vertical Graphene layers (figure 1). We have named this Hopf-linked Graphene layers as Hopfene, and the details of the structures are shown in [44]. Hopfene is classified by the way to insert Graphene layers against available slots, and (1,1)-Hopfene is the most closely packed structure with AB-stacks between adjacent layers, while (2,2)-Hopfene is made by AA-stacking with every other slot empty [44]. The crystal is tetragonal and the lattice constants are a = 3a0, b = 3a0 = a, and 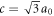 with the bond length of carbon atoms a0 [44]. The unit cell of the structure is shown in figures 1(b)–(d). We have included supplementary video available online at stacks.iop.org/MRX/6/106004/mmedia to show the stability of Hopfene (Supplementary video). In this simulation, 5 horizontal Graphene layers were intersected with another 5 vertical Graphene layers, and the structure was optimised by a commercial software of Chem3D. We confirmed that the structure is stable after the optimisation by using molecular dynamic simulations. After the structural optimisation, we found that the Graphene layers are optimised at the centres of the inter-penetrating Graphene layers to minimise the total energy. The σ bonds of Graphene layers were preserved, such that the optimum positions were determined by the van-der-Waals force between Graphene layers. We have found that massless Dirac and Weyl Fermions exist in Hopfene and the observed flat-band features would be favourable for the appearance of superconductivity and other magnetic orders [54, 55].
with the bond length of carbon atoms a0 [44]. The unit cell of the structure is shown in figures 1(b)–(d). We have included supplementary video available online at stacks.iop.org/MRX/6/106004/mmedia to show the stability of Hopfene (Supplementary video). In this simulation, 5 horizontal Graphene layers were intersected with another 5 vertical Graphene layers, and the structure was optimised by a commercial software of Chem3D. We confirmed that the structure is stable after the optimisation by using molecular dynamic simulations. After the structural optimisation, we found that the Graphene layers are optimised at the centres of the inter-penetrating Graphene layers to minimise the total energy. The σ bonds of Graphene layers were preserved, such that the optimum positions were determined by the van-der-Waals force between Graphene layers. We have found that massless Dirac and Weyl Fermions exist in Hopfene and the observed flat-band features would be favourable for the appearance of superconductivity and other magnetic orders [54, 55].
Figure 1. Hopf-linked Graphene layers: Hopfene. (a) Graphene layers are linked both horizontally and vertically through Hopf-links without forming σ bonds between layers. Colours of carbon atoms are just guide to the eyes, representing A, B, C, and D-sublattices. The crystal structure of Hopfene is tetragonal. (b) Hopfene, seen from the bottom. The unit cell is shown as a box. The lattice constants are a = b = 3a0. (c) Hopfene, seen from the top of the vertical graphene layers. The lattice constant along z-axis is 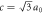 , which is shorter than a. (d) Hopfene, seen from the side of the horizontal graphene layers. (e) An example of a topological defect, breaking the long-range order of the translational symmetry, while preserving bonds.
, which is shorter than a. (d) Hopfene, seen from the side of the horizontal graphene layers. (e) An example of a topological defect, breaking the long-range order of the translational symmetry, while preserving bonds.
Download figure:
Standard image High-resolution imageIn this paper, we theoretically discuss superconductivity in (2,2)-Hopfene for the future, since various carbon allotropes exhibit superconductivity such as intercalated graphites [56, 57], K3C60 [15], carbon-nano-tube [58, 59], Q-Carbon [16], and twisted bilayer Graphene [60]. In particular, we discuss the notion of the crossover [61–63] and possible quantum phase transitions [19, 64] from weak coupling BCS limit to strong coupling Bose–Einstein Condensation (BEC) of preformed pairs in Hopfene, because the attractive interaction is not know a priori, so that it is reasonable to assume the interaction strength as a free theoretical parameter. According to the conventional wisdom [61, 62], the evolution from BCS to BEC is rather continuous upon hypothetical increase of the attractive interaction strength, while the pictures are completely different between weak coupling Cooper paring in momentum space and strong coupling BEC of bipolarons in the real space [61, 62]. The formation of pre-formed pairs [65] might also be relevant to the pseudo-gap phenomena found in copper-oxides [18, 65] or excitonic condensation in graphite under high magnetic fields at the quantum limit [66]. More recently, it was theoretically identified that there exists a quantum critical point [19, 67–70] in 2D Graphene, so that the impact of vanishing the Density-Of-State (DOS) at the Dirac points is significant on superconductivity [67–69]. The requirement of the finite critical attractive interaction strength at half-filling is a significant deviation from the BCS picture, which predicted the superconducting instability at the infinitely weak attractive interaction, while the BCS theory is still valuable to explain the superconductivity [68]. Our motivation of this study is to explore how the topological feature of the complicated band structure of Hopfene affects the BCS-BEC evolution scenario. We found non-trivial competitions between the formations of the semiconductor band gap and the superconducting gap near the quarterly fillings, where the superconducting order parameter is severely reduced and the system is close to a quantum critical point, where the superconducting transition temperature is reduced to be zero.
2. Model
2.1. Attractive Hubbard model
We employ the attractive Hubbard Hamiltonian [61]
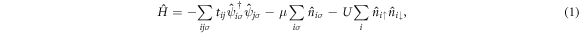
where 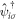 and
and 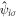 are creation and annihilation operators at the atomic lattice site i for spin σ, respectively, tij is the transfer energy between the lattice sites i and j, μ is chemical potential,
are creation and annihilation operators at the atomic lattice site i for spin σ, respectively, tij is the transfer energy between the lattice sites i and j, μ is chemical potential, 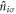 is the number operator, and U is the attractive interaction strength. The real crystal of Hopfene would contain defects and disorder of impurities. In particular, we think it is important to consider new type of defects, named topological defects, which break translational long-range order, while preserving the strong σ-bonds (figure 1 (e)), because Hopfene is made of soft Graphene layers against deformations. The structure will be maintained as far as the topological long-range order is preserved, even if the perfect translational symmetry is broken. These topological defects would not affect s-wave superconductivity, as far as the radius of the Cooper pair is much larger than the size of the topological defects. In this paper, we focus on (2,2)-Hopfene (figure 1) and restrict the electron transfers within the nearest neighbour sites [44, 54]. In (2,2)-Hopfene, the numbers of sub-lattice atoms for all sublattices are the same
is the number operator, and U is the attractive interaction strength. The real crystal of Hopfene would contain defects and disorder of impurities. In particular, we think it is important to consider new type of defects, named topological defects, which break translational long-range order, while preserving the strong σ-bonds (figure 1 (e)), because Hopfene is made of soft Graphene layers against deformations. The structure will be maintained as far as the topological long-range order is preserved, even if the perfect translational symmetry is broken. These topological defects would not affect s-wave superconductivity, as far as the radius of the Cooper pair is much larger than the size of the topological defects. In this paper, we focus on (2,2)-Hopfene (figure 1) and restrict the electron transfers within the nearest neighbour sites [44, 54]. In (2,2)-Hopfene, the numbers of sub-lattice atoms for all sublattices are the same 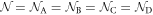 , so that it is convenient to split the sum over all lattice sites into the sum within sub-lattices as
, so that it is convenient to split the sum over all lattice sites into the sum within sub-lattices as
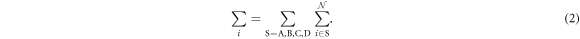
This means that we can assign a number from 1 to  for each atom with a sublattice index from A to D to describe the lattice coordinate of an atom. The total number of lattice sites is
for each atom with a sublattice index from A to D to describe the lattice coordinate of an atom. The total number of lattice sites is 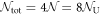 with the total number of the unit cell,
with the total number of the unit cell,  , and the number of sub-lattice atoms for each sublattice in the unit cell is 2 and the total number of atoms in the unit cell is 8. Similarly, it is convenient to describe
, and the number of sub-lattice atoms for each sublattice in the unit cell is 2 and the total number of atoms in the unit cell is 8. Similarly, it is convenient to describe 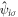 with a sublattice index as
with a sublattice index as 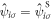 , and consequently we can define Fourier transformation and its inverse as
, and consequently we can define Fourier transformation and its inverse as
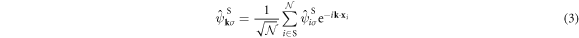
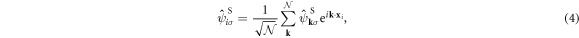
respectively. We will describe the wave number vectors, k, equivalent to the momentum p = ℏk, in the unit of 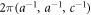 and ℏ is the Dirac constant, which is the Plank constant divided by 2π.
and ℏ is the Dirac constant, which is the Plank constant divided by 2π.
Alternatively, we can also define the field-vector operator, 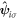 , with a sub-lattice index similar to a spinor description as
, with a sub-lattice index similar to a spinor description as  , and its Fourier transform is
, and its Fourier transform is 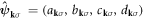 . This simplification was possible because of the same number of lattice sites among sub-lattices. If this was not the case, it is required to define two coordination vectors: one for the unit cell and the other for the relative vectors inside the cell.
. This simplification was possible because of the same number of lattice sites among sub-lattices. If this was not the case, it is required to define two coordination vectors: one for the unit cell and the other for the relative vectors inside the cell.
Below, we will examine the 1st term of  as the kinetic energy Hamiltonian
as the kinetic energy Hamiltonian  , the 2nd term as the chemical potential Hamiltonian
, the 2nd term as the chemical potential Hamiltonian  , and the last term as the interaction Hamiltonian
, and the last term as the interaction Hamiltonian  in more details.
in more details.
2.2. Tight-binding Hamiltonian
 represents delocalised π-electrons in the carbon network, and we expect 1 electron per atom without doping. The other 3 electrons among 4 electrons in the outer shell of a carbon atom are forming strong σ bonds. We assume the nearest neighbour transfer energy of −t within Graphene layers and that of −tH for Hopf-links. Then, we obtain
represents delocalised π-electrons in the carbon network, and we expect 1 electron per atom without doping. The other 3 electrons among 4 electrons in the outer shell of a carbon atom are forming strong σ bonds. We assume the nearest neighbour transfer energy of −t within Graphene layers and that of −tH for Hopf-links. Then, we obtain
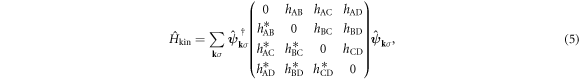
where we have defined
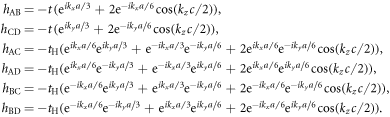
If we define the Hamiltonian matrix for Graphene as

and that of Hopf-links as
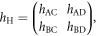
then, it can be summarised as
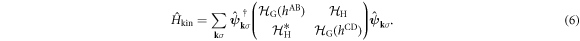
In the limit of the absence of the Hopf-link transfer, 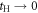 , the energy dispersion reduces to that of Graphene for Dirac Fermions
, the energy dispersion reduces to that of Graphene for Dirac Fermions
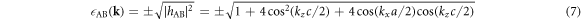
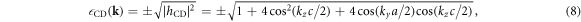
with t = 2.8 eV [29, 33, 34]. In general,  , we need to diagonalise
, we need to diagonalise 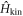 numerically at each k, and we can obtain the band diagram with 4 energy dispersions,
numerically at each k, and we can obtain the band diagram with 4 energy dispersions,  1 (k) −
1 (k) −  4 (k), labelled from the bottom. After the diagonalisation, the state will carry the band index, α, instead of S, and we obtain
4 (k), labelled from the bottom. After the diagonalisation, the state will carry the band index, α, instead of S, and we obtain
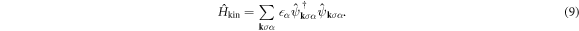
Figure 2 shows examples of calculated tight-binding band structures. At tH = 0, electrons in Graphene layers cannot transfer from each other through Hopf-links, so that electrons are confined within Garphene layers. In this case, the band dispersions are flat against the directions perpendicular to the Graphene layers, so that we have flat-bands along kx, from (0,0.5,1) to (0.5,0.5,1), and ky, from (0,0,1) to (0,0.5,1) (figure 2 (a)). There are 10 Dirac points at (±1, 0, ±1/3), (0, ±1, ±1/3), and (0,0, ±2/3). Among these points, at (0,0, ±2/3), Dirac points coming from horizontal and vertical Graphene layers are degenerate (figure 2(a)). Therefore, we can recognise 2 dispersion curves are completely overlapping around the Dirac point (figure 2(a)). At 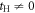 , Dirac point at (0, 0, 2/3) split into 2 Dirac points (figures 2(b) and (c)) due to the formation of bonding and anti-bonding states through Hopf-links. We have compared these tight-binding results with the first-principle calculations [55] and confirmed reasonable agreements and extracted tH = 1.5 eV. All calculations below are based on this parameter with t = 2.8 eV [29, 33, 34] and tH = 1.5 eV.
, Dirac point at (0, 0, 2/3) split into 2 Dirac points (figures 2(b) and (c)) due to the formation of bonding and anti-bonding states through Hopf-links. We have compared these tight-binding results with the first-principle calculations [55] and confirmed reasonable agreements and extracted tH = 1.5 eV. All calculations below are based on this parameter with t = 2.8 eV [29, 33, 34] and tH = 1.5 eV.
Figure 2. Tight-binding band structures of (2,2)-Hopfene at (a) tH = 0, (b) tH = 1 eV, and (c) tH = 2 eV. The original Dirac point at (0,0,2/3) was degenerate at tH = 0, and it splits into 2 Dirac points with the introduction of 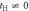 due to the hybridisation. Flat-bands also exist due to the original 2D character of Graphene, showing weak dispersion along the directions perpendicular to the Graphene layers, which remained with
due to the hybridisation. Flat-bands also exist due to the original 2D character of Graphene, showing weak dispersion along the directions perpendicular to the Graphene layers, which remained with 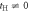 .
.
Download figure:
Standard image High-resolution image2.3. Dirac points and nodal lines
Due to its analytic nature of the tight-binding model, it is easy to calculate energy band dispersions,  α =
α =  α(kx, ky, kz). However, we must fix 1 component in order to describe in a 3D form (figure 3). We can recognise Dirac points in the (kx, kz) plot at fixed ky = 0 (figure 3(a)), and the dispersion is symmetric under the exchange of kx and ky, so that exactly the same energy dispersion is obtained in the (ky, kz) plot at kx = 0 (not shown). At kz = 0, we do not see Dirac points, and a simple band interception was found at the zone edge of (1, 1, 0). We also found the broken particle-hole symmetry, which means
α(kx, ky, kz). However, we must fix 1 component in order to describe in a 3D form (figure 3). We can recognise Dirac points in the (kx, kz) plot at fixed ky = 0 (figure 3(a)), and the dispersion is symmetric under the exchange of kx and ky, so that exactly the same energy dispersion is obtained in the (ky, kz) plot at kx = 0 (not shown). At kz = 0, we do not see Dirac points, and a simple band interception was found at the zone edge of (1, 1, 0). We also found the broken particle-hole symmetry, which means  α (kx, ky, kz) is symmetric against
α (kx, ky, kz) is symmetric against  = 0 by the change of the sign. The particle-hole symmetries were found in Graphene layers, as seen in
= 0 by the change of the sign. The particle-hole symmetries were found in Graphene layers, as seen in  AB and
AB and  CD of equations (7) and (8) while it was broken at
CD of equations (7) and (8) while it was broken at 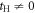 . This could be understood simply by diagonalising 2 and 3 sites models as shown in table 1. The simplest 2 sites model will give two energy states, corresponding to particle and hole state with the energy of t and −t, respectively. If we introduce 1 more site allowing equivalent transfers to these 2 sites, mimicking Hopf-links, we obtain the asymmetric eigenstates,
. This could be understood simply by diagonalising 2 and 3 sites models as shown in table 1. The simplest 2 sites model will give two energy states, corresponding to particle and hole state with the energy of t and −t, respectively. If we introduce 1 more site allowing equivalent transfers to these 2 sites, mimicking Hopf-links, we obtain the asymmetric eigenstates, 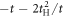 ,
, 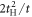 , and t, in the limit of
, and t, in the limit of  . Therefore, the energy levels depend on the sign of t and the particle-hole symmetry is broken. On the other hand, the sign change of tH does not break the particle-hole symmetry. This comes from the fact that 2 transfers through Hopf-link are required to come back to the original Graphene sites, so that the sign change of tH cannot contribute. More generally in Hopfene, even number of transfers thorough Hopf-links are required to come back, so that the obtained energy bands
. Therefore, the energy levels depend on the sign of t and the particle-hole symmetry is broken. On the other hand, the sign change of tH does not break the particle-hole symmetry. This comes from the fact that 2 transfers through Hopf-link are required to come back to the original Graphene sites, so that the sign change of tH cannot contribute. More generally in Hopfene, even number of transfers thorough Hopf-links are required to come back, so that the obtained energy bands  α (kx, ky, kz) did not change by
α (kx, ky, kz) did not change by 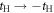 . Please also note that the spacial reflection symmetry
. Please also note that the spacial reflection symmetry 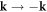 (
( α (k) =
α (k) =  α (−k)) and the time reversal symmetry
α (−k)) and the time reversal symmetry 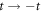 are still maintained without applying magnetic fields. It is also symmetric with the exchange of kx and ky in (2,2)-Hopfene, due to the symmetry between horizontal and vertical directions, but it would not be the case in (n, m)-Hopfene with
are still maintained without applying magnetic fields. It is also symmetric with the exchange of kx and ky in (2,2)-Hopfene, due to the symmetry between horizontal and vertical directions, but it would not be the case in (n, m)-Hopfene with 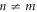 .
.
Figure 3. Bend structures of (2,2)-Hopfene at (a) ky = 0 and (b) kz = 0, calculated at tH = 1.5 eV.
Download figure:
Standard image High-resolution imageTable 1. Two and three sites models for the impacts of signs in transfer energies.
| Model | Hamiltonian | Eigenvalues | Eigenvalues (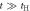 ) ) |
|---|---|---|---|
| 2 sites |
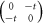
|
±t | ±t |
| 2 sites + Hopf-link |
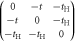
|
t, 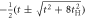
|
 , , 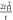 , t , t |
| Negative transfer |
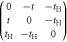
|
−t, 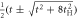
|
−t, 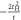 , , 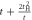
|
| Negative Hopf-link |
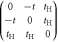
|
t, 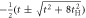
|
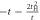 , ,  , t , t |
Another interesting feature of the band diagram of Hopfene is the existence of nodal lines [39] (figure 4). This is coming from the original flat dispersion relationships of  AB and
AB and  CD against ky and kx, which are directions perpendicular to horizontal AB-layers and vertical CD-layers, respectively. Therefore, the bands close to the Dirac points are also dispersionless along these directions, so that Dirac points are connected as nodal lines. Once nodal lines were formed, they cannot be eliminated upon the adiabatic introduction of tH, since nodal lines are topologically protected. In the example of figure 3, nodal lines have dispersion along kx = ky − 1 at kz = 1/2 but the lines are in perfect agreement with the adjacent bands (figure 3(b)), confirming the degeneracies and topological features of band diagrams.
CD against ky and kx, which are directions perpendicular to horizontal AB-layers and vertical CD-layers, respectively. Therefore, the bands close to the Dirac points are also dispersionless along these directions, so that Dirac points are connected as nodal lines. Once nodal lines were formed, they cannot be eliminated upon the adiabatic introduction of tH, since nodal lines are topologically protected. In the example of figure 3, nodal lines have dispersion along kx = ky − 1 at kz = 1/2 but the lines are in perfect agreement with the adjacent bands (figure 3(b)), confirming the degeneracies and topological features of band diagrams.
Figure 4. Dirac points and nodal lines at kz = 1/2. (a) Energy dispersions along kx and ky. (b) Energy dispersions along kx = ky − 1 to show the nodal lines.  4 (dotted blue) and
4 (dotted blue) and  3 (dashed cyan) are completely overlapping, and
3 (dashed cyan) are completely overlapping, and  2 (dotted magenta) and
2 (dotted magenta) and  1 (dashed red) are also overlapping.
1 (dashed red) are also overlapping.
Download figure:
Standard image High-resolution image2.4. Fermi surface
In the presence of tH, electronic states between horizontal and vertical Graphene layers are hybridised to form topologically unique Fermi surfaces [54]. The band structures can be highlighted by the existence of 3D, 2D, and 1D Weyl and Dirac Fermions [54] with flat-band features (figure 2). The Fermi energy of the non-doped (2,2)-Hopfene was EF = 1.1 eV, but this could be changed by doping alkali-atoms [15, 56, 57] or NH3 [71] at interstitial sites due to the large spacing in the unit cell [44, 54]. Here, we describe typical structures of Fermi surfaces in (2,2)-Hopfene.
3D Weyl Fermions exist around at the Dirac point with the energy of Ed = −1.0 eV, where  3 and
3 and  2 have linear dispersions along all 3 directions, kx, ky, and kz, and therefore, the spatial quantum confinements are strongest [54]. Figure 5 shows the Fermi surface of 3D Weyl Fermions below (EF = −0.8 eV, figures 5(a) and (c)) and above (EF = −1.2 eV, figures 5(b) and (d)) this point at Ed = −1.0 eV. Fermi surfaces of 3D Weyl Fermions are small, because of the limited DOS due to strong confinements and linear dispersions. The reduced DOS is not favourable for superconductivity [67–70], as we shall see in the following sections for Hopfene. The Fermi surface of
2 have linear dispersions along all 3 directions, kx, ky, and kz, and therefore, the spatial quantum confinements are strongest [54]. Figure 5 shows the Fermi surface of 3D Weyl Fermions below (EF = −0.8 eV, figures 5(a) and (c)) and above (EF = −1.2 eV, figures 5(b) and (d)) this point at Ed = −1.0 eV. Fermi surfaces of 3D Weyl Fermions are small, because of the limited DOS due to strong confinements and linear dispersions. The reduced DOS is not favourable for superconductivity [67–70], as we shall see in the following sections for Hopfene. The Fermi surface of  1 in figure 5(d) is particularly unique, because the 2 edges of the Fermi surface are connected to the Fermi surfaces of
1 in figure 5(d) is particularly unique, because the 2 edges of the Fermi surface are connected to the Fermi surfaces of  2 by point-contacts. This is originated from the nodal lines, shown in figure 4. Due to the close proximity of the Dirac point to the nodal lines, the Fermi surfaces of
2 by point-contacts. This is originated from the nodal lines, shown in figure 4. Due to the close proximity of the Dirac point to the nodal lines, the Fermi surfaces of  1 were terminated on the nodal lines, so that Fermi surfaces of
1 were terminated on the nodal lines, so that Fermi surfaces of  1 and
1 and  2 were connected by points without overlapping each other. This topological feature is maintained to a certain extent, and the filling of these bands were competing: as we increase EF,
2 were connected by points without overlapping each other. This topological feature is maintained to a certain extent, and the filling of these bands were competing: as we increase EF,  1 is eventually occupied completely, leading to the reduction of the size of the Fermi surface of lower valley (Figure 5(d)) for 3D Weyl Fermions, and the flat-bands of
1 is eventually occupied completely, leading to the reduction of the size of the Fermi surface of lower valley (Figure 5(d)) for 3D Weyl Fermions, and the flat-bands of  2 is taking over the area, while further increase of EF induces the reduction of the volume of Fermi surfaces of
2 is taking over the area, while further increase of EF induces the reduction of the volume of Fermi surfaces of  2, and the Fermi surface of the upper valley (figure 5(c)) starts to take over.
2, and the Fermi surface of the upper valley (figure 5(c)) starts to take over.
Figure 5. 3D Weyl Fermions in Hopfene. Fermi surfaces of the bands  3,
3,  2, and
2, and  1 are shown in colours of cyan, magenta, and red, respectively. Fermi surfaces at (a) EF = −0.8 eV and (b) EF = −1.2 eV. Flat-bands if
1 are shown in colours of cyan, magenta, and red, respectively. Fermi surfaces at (a) EF = −0.8 eV and (b) EF = −1.2 eV. Flat-bands if  2 were dominated, while the small Fermi surfaces for 3D Weyl Fermions are found around edges. 3D Weyl Fermions in (c) upper valleys at EF = −0.8 eV and (d) lower valley at EF = −1.2 eV.
2 were dominated, while the small Fermi surfaces for 3D Weyl Fermions are found around edges. 3D Weyl Fermions in (c) upper valleys at EF = −0.8 eV and (d) lower valley at EF = −1.2 eV.
Download figure:
Standard image High-resolution imageWe also found the weaker confinements at the 1D Dirac point of Ed = 2.7 eV, where the confinement is strong only along kx direction (figure 6). The Fermi surfaces located these valleys are more spreading along vertical and diagonal directions, since band dispersions along these directions are flat (figures 6(b) and (c)). We can also recognise that the close proximity of nodal lines near Ed due to the point contacts of the Fermi surfaces of  4 with
4 with  3, at (0, 0, 1), which is equivalent to (0, 0, −1).
3, at (0, 0, 1), which is equivalent to (0, 0, −1).
Figure 6. 1D Dirac Fermions at (0.19, 0.19, 0.74). (a) Horizontal kx at fixed ky = 0.19 and kz = 0.74, (b) diagonal kx = kyat fixed kz = 0.74, and (c) vertical dependences of band dispersions. Fermi surfaces of (c) lower valley ( 3, cyan) and (d) upper valley (
3, cyan) and (d) upper valley ( 4, blue). Energy band structures at (f) kz = 0.74 and (g) its extended view.
4, blue). Energy band structures at (f) kz = 0.74 and (g) its extended view.
Download figure:
Standard image High-resolution imageA similar point-contacts of the Fermi surfaces were also found at Ed = −4.3 eV (figure 7), where 4 Dirac points are found and each Fermi surface of the upper valleys ( 2) have 4 point contacts to the Fermi surfaces of the lower band (
2) have 4 point contacts to the Fermi surfaces of the lower band ( 1). As we increase EF, the flat-bands of
1). As we increase EF, the flat-bands of  1 (figure 7(a)) are gradually filled, leading to the reduced Fermi surfaces, and eventually the Fermi surfaces of another flat-bands of
1 (figure 7(a)) are gradually filled, leading to the reduced Fermi surfaces, and eventually the Fermi surfaces of another flat-bands of  2 (figure 7(b)) start to grow. These changes of the Fermi surfaces upon increasing EF will give important consequences on the evolutions of superconductivity using these valleys, and the larger DOS is favourable for larger superconducting order parameters, as expected from the BCS theory [3, 4, 6, 61, 62].
2 (figure 7(b)) start to grow. These changes of the Fermi surfaces upon increasing EF will give important consequences on the evolutions of superconductivity using these valleys, and the larger DOS is favourable for larger superconducting order parameters, as expected from the BCS theory [3, 4, 6, 61, 62].
Figure 7. Flat-bands near Dirac points. Fermi surfaces for (a) lower valleys at EF = −4.5 eV and (a) upper valleys at EF = −4.0 eV.
Download figure:
Standard image High-resolution image2.5. Density of states
The DOS per unit volume per spin for the band α is given by

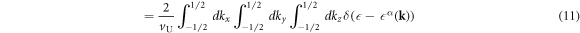
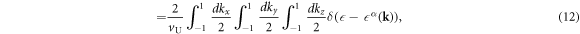
where V is the volume of the system, vU = abc is the volume of the unit cell, a factor of 2 in equation (11) is coming from the number of each sub-lattice atoms in the unit cell, and equation (12) is described by the integration in the extended Brillouin zone of kx ∈ (−2π/a, 2π/a), ky ∈ (−2π/a, 2π/a), and kz ∈ (−2π/c, 2π/c). The DOS per unit cell per spin for the band α is
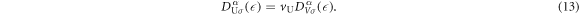
The total number of atoms per unit cell is 4 × 2 = 8, so that the DOS per atom per spin for the band α is given by
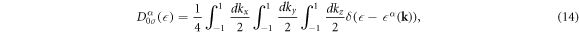
and the total DOS per atom per spin is
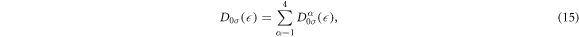
which satisfies the sum rule
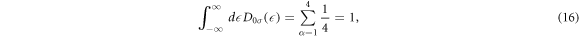
meaning that each atom can accommodate 1 electron per spin, so that the maximum number of 2 electrons can occupy an atom including spin.
Figure 8 shows the calculated DOS of non-interacting electrons at tH = 1.5 eV. The band structure predicts semi-metal characteristics with peaks, coming from flat-bands. The point contact of  1 and
1 and  3 bands at
3 bands at  = −1.0 eV is showing 3D Dirac point, where the peak of DOS of the band
= −1.0 eV is showing 3D Dirac point, where the peak of DOS of the band  2 is coming from the flat-band feature (figure 5).
2 is coming from the flat-band feature (figure 5).
Figure 8. Density of states calculated for (2,2)-Hopfene at tH = 1.5 eV.
Download figure:
Standard image High-resolution image2.6. Mean-field theory
Finally, we will focus on the impact of the attractive interaction Hamiltonian,
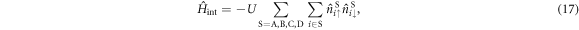
where 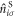 is the number operator at the site i in the sub-lattice S. We introduce Fourier transformation and its inverse of
is the number operator at the site i in the sub-lattice S. We introduce Fourier transformation and its inverse of 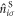 as
as
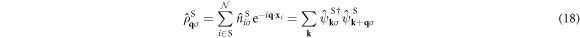
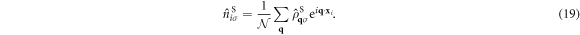
Inserting these into  , we obtain
, we obtain
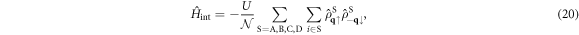
which shows the interaction works within the sub-lattice, because of the local nature of the Hubbard interaction. We examine how the interaction works among sub-bands after the diagonalisation of the kinetic Hamiltonian as
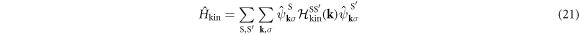
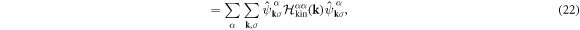
where the Hamiltonian matrix
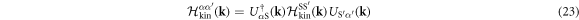
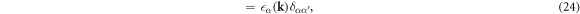
was diagonalised by the unitary matrix US α . It is not trivial whether the interaction is still within the intra-bands, because US α is included in the Fourier transform of the density operator as
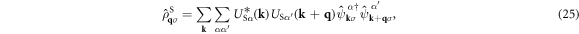
and we obtain

We show the products of unitary matrices do not contribute in the end. We utilise the fundamental character of the Unitary matrix, 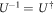 , namely
, namely
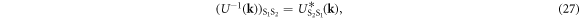
and the reflection symmetry of the system
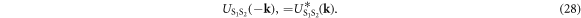
In the Cooper channel, the contribution from the zero center-of-mass momentum of the Cooper pair dominates due to BEC nature of superconductivity, so that the pairing of k' = k within the sub-babnds in  dominates. Then, we consider
dominates. Then, we consider
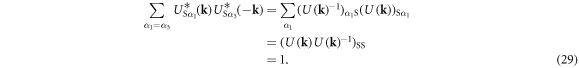
Similarly, we confirm
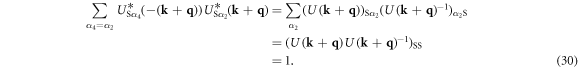
Therefore, the dominant interaction would be the paring within sub-bands
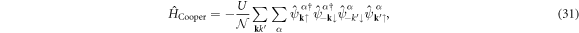
and the factor of unitary matrices become unity.
Another dominant source of interaction is the Hartree–Fock channel at q = 0
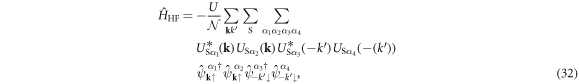
for which the main contribution is coming from the intra-band interaction to conserve the number of electrons in each sub-band. Then, we consider
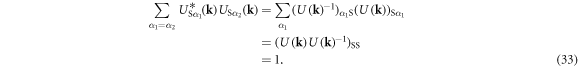
Similarly, we confirm
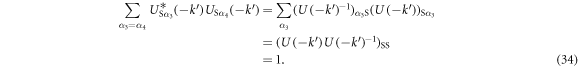
Therefore, we obtain
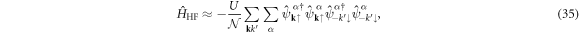
and the unitary matrix US α(k) does not contribute to expectation values.
The unitary transformation does not change the total number of electrons
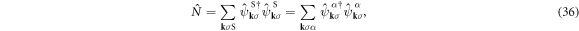
either. We can also define the average number of electrons per atom for each sub-lattice
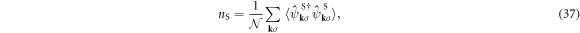
which is nS ∈ (0,2) and the filling fraction is defined by nS/2∈ (0,1). The average total number of electrons per site among all 4 sub-lattices is
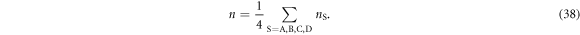
At zero temperature, T = 0, we use the BCS wavefunction [3, 4, 6, 7, 61]
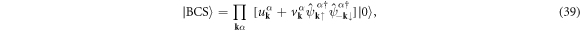
where 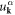 and
and 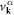 are described as
are described as
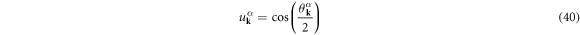
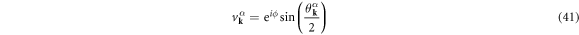
with the superconducting U(1) phase, ϕ, to satisfy the normalisation condition
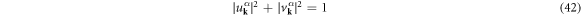
for 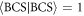 . Then, we can calculate the thermodynamic potential energy [3, 4, 6, 7, 61, 72]
. Then, we can calculate the thermodynamic potential energy [3, 4, 6, 7, 61, 72]
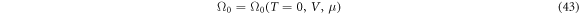
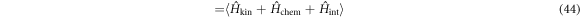
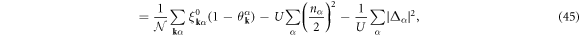
where 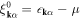 . The electron density, nα, and the superconducting energy gap, Δα, for the band α are self-consistently determined by the density equation
. The electron density, nα, and the superconducting energy gap, Δα, for the band α are self-consistently determined by the density equation
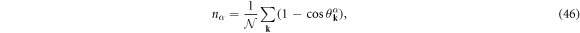
and the gap equation
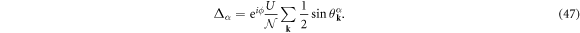
By calculating the functional derivative of Ω0, the saddle-point solution is given by
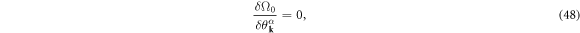
which yields
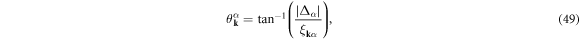
where 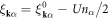 . By using the gapped quasi-particle energy spectrum
. By using the gapped quasi-particle energy spectrum
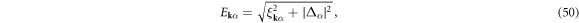
the density and gap equations become
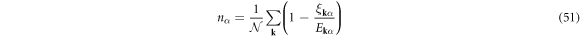
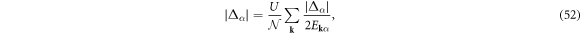
respectively, and we obtain the saddle-point free energy
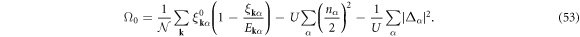
The gap equation always has a normal state solution of 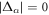 , while a superconducting solution has none-zero gap energy,
, while a superconducting solution has none-zero gap energy,  . It is not always obvious whether a superconducting solutions has a lower energy, as discovered in Graphene [67–69], due to vanishing DOS at Dirac points. In the grand canonical ensemble with variable number of electrons, the state with the lowest thermodynamic potential energy Ω0(T = 0, V, μ) will be realised at the given chemical potential, μ. For the fixed number of electrons, Ne, or equivalently, at the fixed density,
. It is not always obvious whether a superconducting solutions has a lower energy, as discovered in Graphene [67–69], due to vanishing DOS at Dirac points. In the grand canonical ensemble with variable number of electrons, the state with the lowest thermodynamic potential energy Ω0(T = 0, V, μ) will be realised at the given chemical potential, μ. For the fixed number of electrons, Ne, or equivalently, at the fixed density, 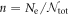 , on the other hand, we need to find out a state with the lowest Helmholtz free energy, whose zero-temperature form is given by the internal energy
, on the other hand, we need to find out a state with the lowest Helmholtz free energy, whose zero-temperature form is given by the internal energy
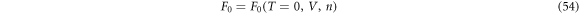
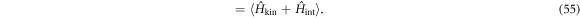
The difference between Ω0(T = 0, V, μ) and F0(T = 0, V, n) was crucial to identify the correct ground state.
At finite temperature, 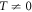 , we can use a standard Bogoliubov transformations [3, 4, 6, 7, 61, 72] to obtain the self-consistency conditions
, we can use a standard Bogoliubov transformations [3, 4, 6, 7, 61, 72] to obtain the self-consistency conditions
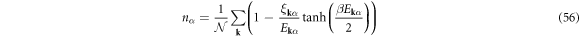
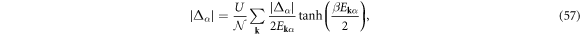
where β = 1/(kBT) with the Boltzmann constant of kB, and the thermodynamic potential becomes
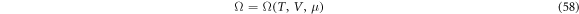
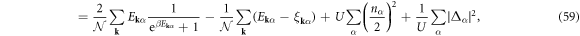
whose first term vanishes towards T = 0, corresponding to the disappearance of a quasi-particle, which is the main reason for zero resistivity and the Meissner effect, because the absence of single particle excitation leads to the macroscopic coherence, characterised by the current proportional to the vector potential [3–6].
3. Results and discussions
3.1. Ground state solutions and quantum critical behaviours
Numerical solutions of self-consistency equations at T = 0 are shown in figure 9. The non-doped (2, 2)-Hopfene is half-filled (n = 1), and it is semi-metal at U = 0 (figures 8 and 9(a)). With the introduction of 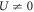 , Δ3 developed with the peak at U ∼ 3 eV (figure 9(b)) and it decreased upon increasing U. This was attributed to the reduction of the filling fraction of n3 due to the decrease of the effective lower band energy of ξk2 =
, Δ3 developed with the peak at U ∼ 3 eV (figure 9(b)) and it decreased upon increasing U. This was attributed to the reduction of the filling fraction of n3 due to the decrease of the effective lower band energy of ξk2 =  k2 − Un2/2 by the Hartree–Fock interaction. Consequently, the
k2 − Un2/2 by the Hartree–Fock interaction. Consequently, the  k3 band becomes empty at U > UMI ∼ 4 eV, and Δ3 vanishes, and we expect a Metal-Insulator transition in the normal state at UMI due to the opening of the semiconductor gap. With sufficient doping, such significant changes in the filling fractions were not found in a system (figure 9(b)). On the other hand, Δ2 remained to be zero at n = 1 until Uc ∼ 1 eV, showing that the system is very close to the quantum critical point [67–69]. At U < Uc, the free energy is lower by reducing ξk2 without opening Δ2, which is similar to the finding of the quantum critical behaviour in 2D Graphene. However, in Hopfene, the DOS is finite at μ ∼ 1 eV (figures 8 and 9(e)) and the reduction in the mean-field Hartree–Fock energy overcame the emergence of superconducting order. Surprisingly, further increase of U > UMI allowed the increase of Δ2, although the increase is significantly smaller than that in the doped case at n = 1.25 (figure 9(d)). This increase of Δ2 at n = 1 is similar to the pioneering work found in [65], where the superconducting order is expected in a semiconductor with a small band gap, if the attractive interaction between electrons in conduction band and holes in valence band is strong enough to overcome the semiconductor gap. An excitonic strong pairing and condensation were experimentally found in Graphite under extremely high magnetic fields in the quantum limit [66]. In our case, the attractive interaction is working within the sub-bands, and the opening of the superconducting gap Δ2 is smaller than the semiconductor gap ∼U. Consequently, the energy gain by the superconducting order at n = 1 was significantly limited.
k3 band becomes empty at U > UMI ∼ 4 eV, and Δ3 vanishes, and we expect a Metal-Insulator transition in the normal state at UMI due to the opening of the semiconductor gap. With sufficient doping, such significant changes in the filling fractions were not found in a system (figure 9(b)). On the other hand, Δ2 remained to be zero at n = 1 until Uc ∼ 1 eV, showing that the system is very close to the quantum critical point [67–69]. At U < Uc, the free energy is lower by reducing ξk2 without opening Δ2, which is similar to the finding of the quantum critical behaviour in 2D Graphene. However, in Hopfene, the DOS is finite at μ ∼ 1 eV (figures 8 and 9(e)) and the reduction in the mean-field Hartree–Fock energy overcame the emergence of superconducting order. Surprisingly, further increase of U > UMI allowed the increase of Δ2, although the increase is significantly smaller than that in the doped case at n = 1.25 (figure 9(d)). This increase of Δ2 at n = 1 is similar to the pioneering work found in [65], where the superconducting order is expected in a semiconductor with a small band gap, if the attractive interaction between electrons in conduction band and holes in valence band is strong enough to overcome the semiconductor gap. An excitonic strong pairing and condensation were experimentally found in Graphite under extremely high magnetic fields in the quantum limit [66]. In our case, the attractive interaction is working within the sub-bands, and the opening of the superconducting gap Δ2 is smaller than the semiconductor gap ∼U. Consequently, the energy gain by the superconducting order at n = 1 was significantly limited.
Figure 9. Superconducting ground state of (2,2)-Hopfene. (a) (b) Filling fractions, (c) (d) energy gap, and (e) (f) chemical potential at n = 1 and n = 1.25, respectively. Reentrant behaviour was found in Δ3 in (c) due to the opening of the semiconductor gap by the Hartree–Fock interaction.
Download figure:
Standard image High-resolution imageThe condensation energies were calculated by the difference of the Helmholtz free energy between superconducting and normal state, Δ F = Fsuper − Fnormal (figure 10). At n = 1, we estimated solely from the BCS theory (figure 10(a)), because the band is almost completely filled and the impact of strong correlation is limited. In fact, Δ F was order of magnitude smaller than that in the doped case (figure 10(b)), so that the system at n = 1 is closer to a band insulator. In particular, Δ F ∼ 0 at U ∼ UMI, where Δ3 is also close to zero. On the other hand, the BCS theory overestimates Δ F for n = 1.25 at the strong coupling limit. It is beyond the scope of this paper to include the impact of strong correlation precisely, because it is quite challenging to include small energy scale of the order t2/U, which is similar to the problem of Mott transition [61]. Here, we roughly estimate the impact of strong correlation by considering a Gutzwiller-BCS variational wavefunction [64, 73, 74]
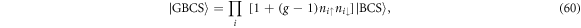
by which local spatial correlation is included in the limit of 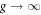 [64, 74]. In this limit, the electrons are spreading completely in the momentum space to form local singlet of preformed electrons. The impact of the correlation on the free energy in a superconducting state is actually not significant, while the change in the normal state is significant [64]. Therefore, we estimated the normal state free energy simply by assuming all electrons to form locally singlet pairs with the interaction energy of −Un/2, while the kinetic energy was calculated by assuming local paring corresponds to the spreading in the entire sub-band in momentum space [64, 74]. The calculated condensation energy is considered to be a simplified BEC model, which is shown in figure 10(b). We could somehow include the energy scale of t2/U, and the true condensation energy would show a crossover from BCS to BEC.
[64, 74]. In this limit, the electrons are spreading completely in the momentum space to form local singlet of preformed electrons. The impact of the correlation on the free energy in a superconducting state is actually not significant, while the change in the normal state is significant [64]. Therefore, we estimated the normal state free energy simply by assuming all electrons to form locally singlet pairs with the interaction energy of −Un/2, while the kinetic energy was calculated by assuming local paring corresponds to the spreading in the entire sub-band in momentum space [64, 74]. The calculated condensation energy is considered to be a simplified BEC model, which is shown in figure 10(b). We could somehow include the energy scale of t2/U, and the true condensation energy would show a crossover from BCS to BEC.
Figure 10. Superconducting condensation energies at (a) n = 1 and (b) n = 1.25. (a) Superconducting order is significantly limited by the opening of the semiconductor gap. (b) Smooth crossover from weak coupling BCS to strong coupling BEC.
Download figure:
Standard image High-resolution imageWe have also examined the filling dependence of superconductivity in (2,2)-Hopfene (figure 11). We found significant decreases of superconducting order parameters at every quarterly fillings (figures 11(a), (c), and (e)), because of the complete filling of the lower sub-bands. These observations are consistent with the filling fractions found in figures 11(b), (d), and (f), which show the subsequent completion of filling at n = 0.5, 1, 1.5 and 2, so that the system is close to quantum critical points towards a semiconductor or an insulator. At n = 1, it was quite marginal whether the superconducting order remains, as we have seen in figures 9 and 10, and according to our numerical calculations, the system remains to be superconducting at T = 0. The robust superconductivity at n = 1 was coming from the sharp peak of the sub-band  3 at the bottom edge of the band, because of the flat-band (figure 5(c)). At n = 0.5, the superconducting order parameters are reduced even further, which was coming from the stronger confinement of 3D Weyl Fermions at the top edge of the sub-band
3 at the bottom edge of the band, because of the flat-band (figure 5(c)). At n = 0.5, the superconducting order parameters are reduced even further, which was coming from the stronger confinement of 3D Weyl Fermions at the top edge of the sub-band  1 (figure 5(d)). Therefore, the system at n = 0.5 in the strong coupling is very close to the situation of the reduced superconductivity found in 2D Dirac Fermions [67–69]. In our case, the system is semi-metal with the finite DOS from sub-bands
1 (figure 5(d)). Therefore, the system at n = 0.5 in the strong coupling is very close to the situation of the reduced superconductivity found in 2D Dirac Fermions [67–69]. In our case, the system is semi-metal with the finite DOS from sub-bands  1 and
1 and  2 at the weak coupling, so that the superconducting order is still finite and there is no finite critical attractive interaction strength to induce the superconductivity. In that sense, from fundamental point of view, superconductivity in 3D Hopfene is less significant compared with the case in 2D Graphene. This is consistent with the common understanding, that order parameters are more robust against quantum and thermal fluctuations in higher dimensions, where mean-field pictures are validated [11, 13, 35, 37]. Nevertheless, at strong coupling, the Hartree–Fock interaction reduces the sub-band energy, effectively, leading to an isolation of
2 at the weak coupling, so that the superconducting order is still finite and there is no finite critical attractive interaction strength to induce the superconductivity. In that sense, from fundamental point of view, superconductivity in 3D Hopfene is less significant compared with the case in 2D Graphene. This is consistent with the common understanding, that order parameters are more robust against quantum and thermal fluctuations in higher dimensions, where mean-field pictures are validated [11, 13, 35, 37]. Nevertheless, at strong coupling, the Hartree–Fock interaction reduces the sub-band energy, effectively, leading to an isolation of  1 and opening of a semiconductor gap.
1 and opening of a semiconductor gap.
Figure 11. Impact of carrier doping on superconducting order parameters. (a), (c), (e) energy gaps and (b), (d), (f) filling fractions were calculated at U = 5, 3, and 1 eV, respectively. (e) The energy gaps reflects the shape of the density-of-states at weak coupling, while (a), (c) they become smooth function against filling at strong coupling due to the spreading of the states in momentum space due to local spatial correlation.
Download figure:
Standard image High-resolution imageThe superconducting energy gaps were significantly affected by DOS (figures 11(e) and 8) at weak coupling, as expected from the BCS theory. On the other hand, in the strong coupling, the gaps are smooth functions of fillings (figures 11(a) and (c)), showing the states are spreading to the entire Brillouin zone of the momentum space in order to form local singlet pairs, so that the system is close to BEC.
3.2. Crossover from BCS to BEC and superconductor-insulator phase transition
We have also examined the temperature dependence of superconducting order parameters by solving the self-consistency conditions, equations (56) and (57) simultaneously (Figure 12). We found continuous reductions of order parameters as we increase the temperature, so that the phase transitions are of the second order. This is expected in a 3D material, for which the mean field theory should be appropriate. Superconductivity is considerably reduced at n = 1, while it is order of magnitude larger at n = 1.25, consistent with previous results. Obviously, the superconducting transition temperatures are too large if we assume U > 2 eV. In practice, superconductivity in carbon allotropes [15, 16, 56, 57, 60] were found only at temperatures much lower than room temperature. Therefore, a weak coupling condition U < 1 eV is appropriate, when we consider realistic experiments. Nevertheless, it would be valuable to consider a crossover [61] or a possible quantum phase transition [19, 64] at least theoretically. Stronger coupling would be expected to excitonic systems [66], for which the model needs to be modified to allow the inter-band interactions.
Figure 12. Temperature dependence of order parameters at (a) n = 1 and (b) n = 1.25. They show the second order phase transition.
Download figure:
Standard image High-resolution imageFinally, we have made phase diagrams of (2, 2)-Hopfene based on an attractive Hubbard model (figure 13). At n = 1, which would be expected for non-doped Hopfene, we expect BCS superconductivity with reduced transition temperatures. In the weak coupling limit, only Δ3 opens up. At moderate interaction strengths, 1 eV < U < 4 eV, both Δ2 and Δ3 open at low temperature. At strong coupling limit U > 4 eV, we expect insulator to superconductor transition at high temperature, because of the opening of a semiconductor gap, solely from the attractive Hartree–Fock interaction, which is different from Mott transition coming from strong correlation. Obviously, the transition temperature of the order 1000 K is not realistic at all, since Hopfene would be burned out. Nevertheless, we hope there is some theoretical implications of this result, since our results suggest competitions of a semiconductor band gap and a superconducting energy gap with an increase of attractive interaction strength, which is similar to a problem suggested by Nozières and Pistolesi [65]. At n = 1.25 with sufficient doping, we confirmed a smooth crossover from BCS to BEC (figure 13(b)). The transition temperature of BEC was simply estimated from the condensation energy, so that it is not accurate quantitatively. Nevertheless, the result suggests the existence of the optimum interaction strength at around U ∼ 2 eV, so that the infinitely strong attraction would not help to increase transition temperature, which is consistent with previous publications [61]. The gap formation is important at weak coupling to expect superconductivity, while the phase coherence is required to expect BEC of local singlet pairs. The sharp increase in DOS by a flat-band will also help to increase the transition temperature at practical weak coupling, while it is less effective due to the spreading in momentum space at strong coupling. The impact of doping on superconductivity in Hopfene is significant and the system is located to the close proximity of the quantum critical point, where the transition temperature is reduced to zero, due to the competition between the opening of semiconductor and superconducting gaps.
Figure 13. Phase diagrams of attractive Hubbbard model for (2,2)-Hopfene at (a) n = 1 and (b) n = 1.25. (a) Standard BCS superconductivity is expected at weak coupling, while superconductor to insulator phase transition is expected at strong coupling. (b) Smooth crossover is expected from BCS to BEC. Preformed pairs would behave as Bose-gas at strong coupling at high temperature, and BEC is expected at lower temperature due to the phase coherence. The transition temperature was estimated from the condensation energy.
Download figure:
Standard image High-resolution image4. Conclusion
In conclusion, we have proposed a 3D carbon allotrope named Hopfene, which has a topologically nontrivial structure with arrays of Hopf-links to link 2D Graphne layers, and examined possible superconductivity based on an attractive Hubbard model. We found topologically unique Fermi surfaces with Dirac and Weyl Fermisons and flat-band features, which affected significantly on the nature of superconductivity especially at practical weak coupling limit. We also found the superconductivity is significantly reduced at every quarterly fillings, due to the opening of semiconductor band gaps, so that the system is in the vicinity of the quantum critical point. As we increase the interaction strength, we confirmed smooth crossover from weak coupling BCS superconductivity to BEC in a doped system. At the half-filling without doping, the superconductivity is significantly reduced and a superconductor-insulator transition was found at the strong coupling limit.
We think unique topological features of Hopfene are valuable to investigate impacts of topology and Fermi surfaces on the emergence of various order parameters including superconductivity, charge-density-waves, magnetisms, and so on. For magnetisms, e.g. we expect ferro-magnetism [7] due to the flat-bands and the peaks in DOS by the introduction of Coulomb repulsive interaction. We also expect introduction of frustration of anti-ferro-magnetic orders through Hopf-links. The impacts of topological structures on magnetism would be quite interesting to explore. Our theoretical analysis in this paper is quite primitive, and we would like to encourage researchers to explore Hopfene and other topologically unique carbon allotropes towards the paradigm-shift of material science and innovation.
Acknowledgments
This work is supported by EPSRC Manufacturing Fellowship (EP/M008975/1). We would like to thank Prof. H. Mizuta, Dr M Muruganathan, Prof. Y Oshima, Prof. S Matsui, Prof. S Ogawa, Prof. S Kurihara, and Prof. H. N. Rutt for stimulating discussions. S S also would like to thank JAIST for their hospitalities during his stay at the Center for Single Nanoscale Innovative Devices. The data from the paper can be obtained from the University of Southampton ePrint research repository: https://doi.org/10.5258/SOTON/D0955.















