Abstract
Chiral nanocrystalline cellulose (NCC) free-standing films were prepared through slow evaporation of aqueous suspensions of cellulose nanocrystals in a nematic chiral liquid crystal phase. Mueller matrix (MM) spectroscopic ellipsometry is used to study the polarization and depolarization properties of the chiral films. In the reflection mode, the MM is similar to the matrices reported for the cuticle of some beetles reflecting near circular left-handed polarized light in the visible range. The polarization properties of light transmitted at normal incidence for different polarization states of incident light are discussed. By using a differential decomposition of the MM, the structural circular birefringence and dichroism of a NCC chiral film are evaluated.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Helicoidal structures of cellulose, chitin or collagen microfibrils are commonly found in nature [1, 2]. These helicoidal arrangements are often referred to as twisted lamellae (Bouligand) structures. Depending on rotation direction the helical structure is defined as right- or left-handed. The characteristic length to complete a rotation of 360° defines the helix pitch (Λ). In some plants, the helicoidal structure of cellulose microfibrils produces iridescent colors in leaves and fruits [3]. Some beetles exhibit circular polarization features and in some cases also with metallic shine due to chitin-protein fibrils arranged in parallel lamellae comprising a Bouligand structure in the exoskeleton (cuticle) [4]. Both for plants and beetles, unpolarized incident light is selectively reflected with the same handedness as the chiral structure producing the bright colors observed. This is due to the circular Bragg phenomenon commonly referred to as selective Bragg reflection [5]. At normal incidence, selective reflection takes place in a spectral band centered at wavelength λ0 = navΛ, where nav is the in-plane average refractive index. Thus, an analogy with the cholesteric (chiral nematic) phase of some liquid crystals is straightforward.
Since decades, natural helicoidal structures have inspired the development of processes for optical biomimetics leading to the discovery of the helicoidal self-ordering of cellulose microfibrils in aqueous suspensions [6]. At that time, slow evaporation of the suspensions produced chiral films with pitch of a few microns mimicking the left-handed helicoidal arrangement of natural systems. Over the years, the research on nanocrystalline cellulose (NCC) chiral films showing iridescent colors progressed and nowadays it is an intense field of research carried out by several groups around the world [7–16]. In those works, the effect of the diverse processing parameters on the microstructure and optical properties of the NCC chiral films have been investigated. The complexity of the process involves many physicochemical phenomena occurring during film formation. Among them, the competition between glass formation and liquid crystal self-assembly has been identified as a source of film inhomogeneity [9]. The lack of uniformity in the films produces a mosaic texture with domains in the micrometer scale. The optical performance of NCC chiral films has been studied by several groups by measuring the reflected or transmitted irradiance for unpolarized, right-and left-handed circularly polarized (LHCP) incident light, as well as characterization of their circular dichroism (CD) [7, 14, 15]. Although these techniques account for the selective Bragg reflection of near-circular polarized light, a more extensive study of the polarization and depolarization properties of light reflected or transmitted by NCC chiral films has not been performed yet. Recently, we have used variable angle Mueller-matrix spectroscopic ellipsometry for a complete characterization of light reflected from the cuticle of several species of beetles [17–22]. We have then used a multiple angle of incidence approach to account for the angular and spectral shift characteristic of these all-dielectric reflective systems. Moreover, the knowledge of the Mueller matrix of an optical system allows determination of the polarization and depolarization capabilities of the system for any polarization state of the incident beam. These capabilities have not been investigated for NCC chiral films and a comparison with those exhibited by the cuticle of beetles could offer an opportunity to explore possible optical applications.
In this work, we study the polarization and depolarization properties of NCC free-standing chiral films in reflection and transmission modes using Mueller-matrix spectroscopic ellipsometry. In section 2, the experimental details are described. In section 3.1, the properties of the Mueller matrix of NCC chiral films in reflection mode for oblique incidence are discussed and compared with those of beetle cuticle. Also, the polarization properties of light reflected for incident unpolarized light are determined. In section 3.2, the Mueller matrix of NCC chiral films in transmission mode at normal incidence is reported. The polarization properties of transmitted light for unpolarized and circularly polarized incident beams are determined in section 3.3. The case of linearly polarized incident light is discussed in section 3.4. In section 3.5, application of the differential decomposition of the transmission Mueller matrix measured at normal incidence is analyzed. In the last section, some concluding remarks are presented.
2. Experimental details
2.1. Sample preparation
Dried bacterial cellulose membranes were milled to pass through a 0.5 mm screen to ensure uniform particle size and to increase the surface area. The milled pulp was hydrolyzed in 8.75 ml of a sulfuric acid solution per gram of pulp at a concentration of 64 wt% at 50 °C for 0.5 h under vigorous stirring. The bacterial cellulose suspension was then diluted with cold water (10 times the volume of the acid solution) to stop the hydrolysis, and allowed to settle overnight. The clear top layer was decanted, and the remaining cloudy layer was centrifuged at 6000 rpm for 10 min (Jouan C3i-CR3i multifunction centrifuge). The supernatant was decanted, and the resulting thick white suspension was washed three times with water to remove water soluble cellulose materials. The thick white suspension was dialyzed against water for one to four days in cellulose membrane tubes (12 000–14 000 molecular weight cut-off). The suspension was diluted to the desired concentration and then dispersed by ultrasound treatment in a sonicator (Sonics Vibra-Cell VC 505 500 W 20 kHz) with a 6 mm diameter probe. Typically, 50 ml of a 3.0 wt% NCC suspension was placed in a 100 ml plastic tube and sonicated at 60% of the maximum power (300 W). Prolonged sonication (to an energy input of over 700 J g−1 of NCC) was performed in an ice bath to prevent desulfation caused by the suspension heating. The suspension (8 ml) was transferred to a polystyrene Petri dish (diameter of 45 mm) and allowed to evaporate under ambient conditions until yielding solid films with chiral nematic organization.
2.2. Basics of Mueller matrix
The most general description of the polarization and depolarization capabilities of a sample requires the use of Stokes vectors and Mueller matrices [23]. A Stokes vector has four components (I, Q, U, V) which are expressed in terms of the irradiances of six basic polarization states: Ip, Is, I+45°, and I−45° corresponding to linear polarization parallel (p), perpendicular (s), at +45° and at −45° relative to the plane of incidence, respectively; and the other two corresponding to right- and LHCP light IR and IL, respectively. The explicit form of the Stokes vectors is
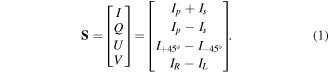
In the Mueller–Stokes description, the light-sample interaction is accounted for by a linear relationship between the Stokes vectors of incident (Si) and outgoing (So) light beams, through a 4 × 4 Mueller matrix (M),

In this work, normalized Mueller matrices (m11 = 1) and Stokes vectors Si (Ip + Is = 1) are used.
After interaction with the sample, the light beam (reflected or transmitted) in general will emerge partially polarized with a degree of polarization P given by [23],

The polarized component of the emerging beam in general will be elliptically polarized with ellipticity e [17],
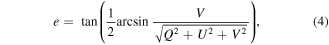
where −1 ≤ e ≤ +1. The extrema correspond to left- and right-handed circularly polarized (RHCP) light, respectively; for linearly polarized light, e = 0, and other values of e are for elliptical polarization. The major axis of the polarization ellipse is located at an azimuthal angle φ measured from the plane of incidence and is given by [23],
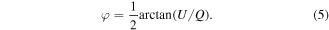
2.3. Characterization techniques
The Mueller matrix measurements were performed with a dual rotating compensator ellipsometer (RC2, J. A. Woollam Co., Inc.) in the wavelength (λ) range 245–1000 nm. Since the films are inhomogeneous and not flat, focusing probes were used to achieve a beam spot with size below 100 μm. Images of the area measured were acquired with a CCD camera attached to the RC2 system. More details about the instrument can be found in [17–22]. Measurements in transmission mode were done at normal incidence whereas in reflection mode, measurements were performed at angles of incidence (θ) between 20° and 75° in steps of 5°. The transmitted irradiance of unpolarized light at normal incidence on areas of 2 mm in diameter was measured in the spectral range of 240–840 nm using a FilmTek 3000 system (SCI, Inc.). The transmittance of circular right- and left-handed polarized light was also measured using commercial plastic-sheets filters (Edmund Optics), which show good performance in the 400–700 nm wavelength range as evaluated with the RC2 system. The thickness of the film was determined from cross-section scanning electron microscopy (SEM) images using a JXA-8530F system (JEOL).
3. Results and discussion
3.1. Mueller matrix and polarization properties of NCC chiral films in reflection mode
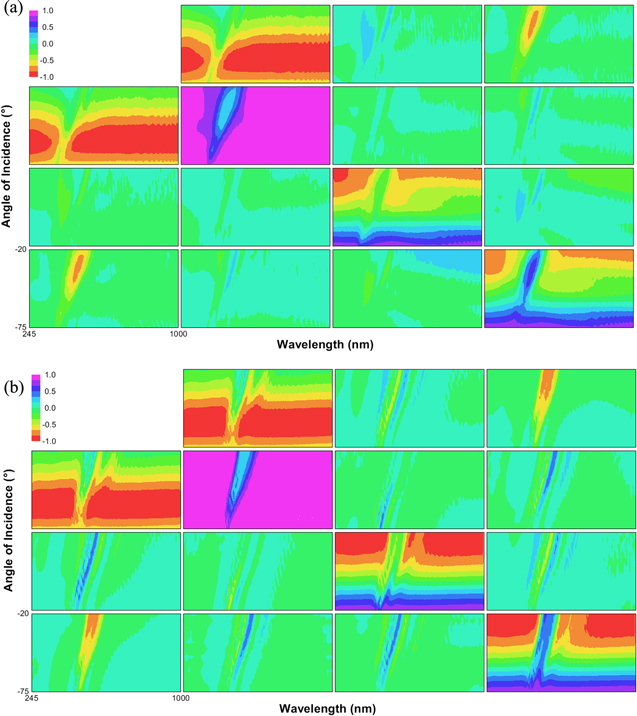
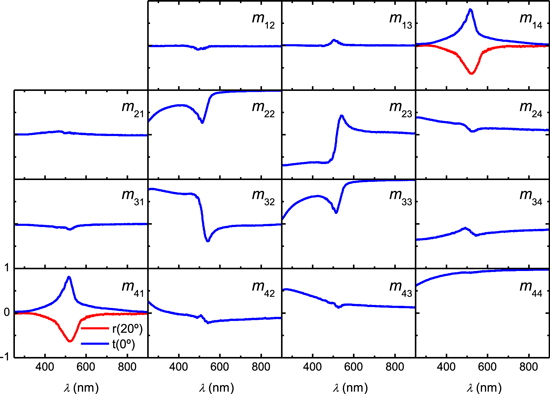
The Mueller-matrix spectroscopic ellipsometry data of an NCC chiral film are shown as function of wavelength and angle of incidence in the contour map in figure 1(a). A careful inspection provides the following relationships for all angles of incidence: m12 = m21, m13 = −m31, m14 = m41, m23 =−m32, m24 = m42, and m34 = −m43. As was earlier reported for beetle cuticles [20], these symmetries in M result from the constraint for cross polarization coefficients in chiral systems rps = −rsp. The band of selective reflection of left-handed polarized light is identified by the negative values of m41 (yellow–red regions). At θ = 20°, this band is centered at 516 nm and shifts to shorter wavelengths at larger angles of incidence. It is known that at oblique incidence the wavelength of selective reflection is given by  where θt is the angle of wave propagation inside the helicoidal structure determined from Snell's law
where θt is the angle of wave propagation inside the helicoidal structure determined from Snell's law  [24]. Therefore, taking na = 1 and nav = 1.54 [25] the corresponding pitch is 343 nm. At wavelengths outside the band of selective reflection, M shows a behavior typical for dielectric materials [20]. For comparison, the data of M from the cuticle of the beetle C. mutabilis [21] is shown in figure 1(b). It can be noticed the similarities between the contour maps in figure 1 which shows that the polarization and depolarization properties of NCC chiral films and beetle cuticles are qualitatively similar.
[24]. Therefore, taking na = 1 and nav = 1.54 [25] the corresponding pitch is 343 nm. At wavelengths outside the band of selective reflection, M shows a behavior typical for dielectric materials [20]. For comparison, the data of M from the cuticle of the beetle C. mutabilis [21] is shown in figure 1(b). It can be noticed the similarities between the contour maps in figure 1 which shows that the polarization and depolarization properties of NCC chiral films and beetle cuticles are qualitatively similar.
Figure 1. Contour maps of Mueller matrices in reflection mode as function of wavelength and angle of incidence of (a) a nanocrystalline cellulose free-standing film and (b) the cuticle of the scarab beetle Cotinis mutabilis.
Download figure:
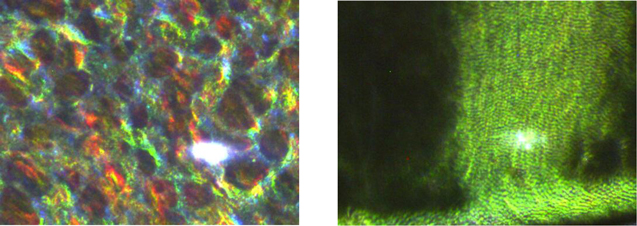
Standard image High-resolution imageAs was mentioned above, NCC chiral films are characterized by a mosaic-like texture as can be observed in the image on the left in figure 2. This texture identifies the multidomain type and is characterized by both, random helix direction and pitch length distribution. Single-domain structures are characterized by the presence of a single helical structure selectively reflecting a well-defined band of wavelengths. In the image of the NCC chiral film in figure 2, we can see domains of different colors (blue, green, red), which define it as the multidomain type. Therefore, measurements at different places show selective reflection bands with different spectral characteristics. On the other hand, the image on the right in figure 2 corresponds to the cuticle of the beetle C. mutabilis where a more uniform color is seen. From the latter observation, it can be tempting to assume that the cuticle of beetles is of the single-domain type. However, the cuticle of C. mutabilis is comprised of chiral layers of different pitch, being larger near the surface.
Figure 2. Optical images (4×) of a nanocrystalline cellulose film (left) and cuticle of C. mutabilis beetle (right). The white elliptic areas correspond to the spot of light beam probe.
Download figure:
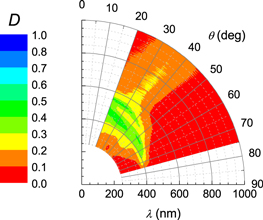
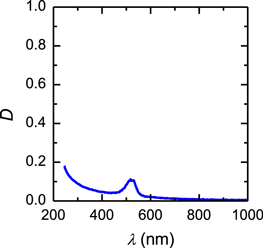
Standard image High-resolution imageIn order to be physically meaningful, any experimentally determined Mueller matrix must fulfill several requirements. Among others, the system must not over-polarize incident polarized light. In quantitative terms, this means that the depolarizance (D) given by [26],
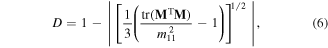
shall be in the range 0 ≤ D ≤ 1. In equation (6), T and tr stand for transpose and trace, respectively and m11 = 1 in our case. Thus, D gives the average measure of the depolarization produced by a system for all incident pure states. For a pure depolarizer D = 1 and D = 0 for a non-depolarizing pure system. Figure 3 shows D of the NCC chiral film in a contour polar representation where the radial and angular coordinates correspond to the wavelength λ and angle of incidence θ, respectively. As can be noticed, D ≤ 1 and M is thus not over-polarizing. The largest values of D are found in the band of selective reflection, which is similar to the observation in the data measured on the cuticle of beetles [20, 21]. However, NCC chiral films are more depolarizing than beetle cuticle.
Figure 3. Depolarizance of the Mueller matrix of an NCC chiral film.
Download figure:
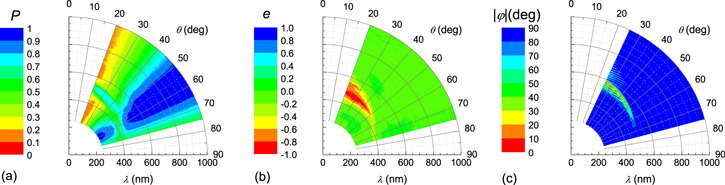
Standard image High-resolution imageOf particular interest are the polarization properties of light reflected for unpolarized incident light with Stokes vector ![${{\bf{S}}}_{{\rm{i}}}={[\mathrm{1,0,0,0}]}^{{\rm{T}}}.$](https://content.cld.iop.org/journals/2040-8986/20/2/024001/revision2/joptaa9e7dieqn3.gif) In this case and according to equation (2), the reflected light is given by
In this case and according to equation (2), the reflected light is given by ![${{\bf{S}}}_{{\rm{r}}}\,={[1,{m}_{21},{m}_{31},{m}_{41}]}^{{\rm{T}}},$](https://content.cld.iop.org/journals/2040-8986/20/2/024001/revision2/joptaa9e7dieqn4.gif) i.e. the first column of M. The elements of Sr can then be used in equations (3)–(5) to calculate the quantities defining the polarization properties of the reflected light as is shown in figure 4. As can be noticed at small angles of incidence, P is high in the spectral range of selective reflection and this polarized part of the reflected beam is left-handed because e < 0. For angles of incidence near 55° and outside the Bragg band, the reflected light is almost totally polarized P ≈ 1, with a linear character e ≈ 0 and s-type φ ≈ 90°, which is typical of a dielectric material as in the case of beetle cuticle [20–22].
i.e. the first column of M. The elements of Sr can then be used in equations (3)–(5) to calculate the quantities defining the polarization properties of the reflected light as is shown in figure 4. As can be noticed at small angles of incidence, P is high in the spectral range of selective reflection and this polarized part of the reflected beam is left-handed because e < 0. For angles of incidence near 55° and outside the Bragg band, the reflected light is almost totally polarized P ≈ 1, with a linear character e ≈ 0 and s-type φ ≈ 90°, which is typical of a dielectric material as in the case of beetle cuticle [20–22].
Figure 4. Polarization properties of light reflected from an NCC chiral film with unpolarized incident light: (a) degree of polarization, (b) ellipticity, and (c) azimuth.
Download figure:
Standard image High-resolution image3.2. Mueller matrix and depolarization of NCC chiral films in transmission mode
Figure 5 shows the Mueller matrix measured in transmission mode at normal incidence. First, we note that m41 = m14 > 0 indicating that right-handed polarized light is transmitted. This is expected because as was discussed in figure 1, the films reflect left-handed polarized light. This complementarity is illustrated by including the elements m41 and m14 measured in reflection mode at angle of incidence 20°. It should be noticed that diagonal and anti-diagonal elements show appreciable values, whereas the remaining ones have values close to zero with some deviations at short wavelengths in m24, m34, m42, and m43 probably due to multiple scattering.
Figure 5. Transmission Mueller matrix of an NCC chiral film measured at normal incidence (0°). The elements m14 and m41 of the Mueller matrix in reflection mode (20°) are included.
Download figure:
Standard image High-resolution imageThe depolarizance of the Mueller matrix measured in transmission mode is shown in figure 6. It can be noticed that 0 ≤ D ≤ 0.2 meaning that the M shown in figure 5 is physically meaningful. In addition, at wavelengths larger than 550 nm D is close to zero and the NCC chiral film could be considered as a non-depolarizing pure system. The increasing values of D in the band of selective reflection might be related to the multidomain texture (helicoidal axis orientation and pitch distribution) across the film. On the other hand, at wavelengths shorter than 450 nm D monotonically increases probably due to scattering.
Figure 6. Depolarizance of the Mueller matrix of a chiral NCC film measured in transmission mode at normal incidence.
Download figure:
Standard image High-resolution image3.3. Polarization properties of the transmitted light for unpolarized and circularly polarized incident light
It is instructive to investigate the polarization properties of light transmitted by the NCC chiral film for different polarization states of the incident beam. Using the Mueller matrix formalism, this implies straightforward calculations using equation (2). We first consider three cases of incident light: unpolarized ![${{\bf{S}}}_{{\rm{i}}{\rm{U}}}={[\mathrm{1,0,0,0}]}^{{\rm{T}}},$](https://content.cld.iop.org/journals/2040-8986/20/2/024001/revision2/joptaa9e7dieqn5.gif) LHCP
LHCP ![${{\bf{S}}}_{{\rm{i}}{\rm{L}}{\rm{H}}}={[\mathrm{1,0,0},-1]}^{{\rm{T}}}$](https://content.cld.iop.org/journals/2040-8986/20/2/024001/revision2/joptaa9e7dieqn6.gif) and RHCP
and RHCP ![${{\bf{S}}}_{{\rm{i}}{\rm{R}}{\rm{H}}}={[\mathrm{1,0,0,1}]}^{{\rm{T}}}.$](https://content.cld.iop.org/journals/2040-8986/20/2/024001/revision2/joptaa9e7dieqn7.gif) As was noted above for SiU, the Stokes vector of the transmitted beam is given by the first column of M, whereas for LHCP incident light it is
As was noted above for SiU, the Stokes vector of the transmitted beam is given by the first column of M, whereas for LHCP incident light it is ![${{\bf{S}}}_{t}={[1-{m}_{14},{m}_{21}-{m}_{24},{m}_{31}-{m}_{34},{m}_{41}-{m}_{44}]}^{{\rm{T}}}$](https://content.cld.iop.org/journals/2040-8986/20/2/024001/revision2/joptaa9e7dieqn8.gif) and for RHCP incident light the out coming beam has Stokes vector
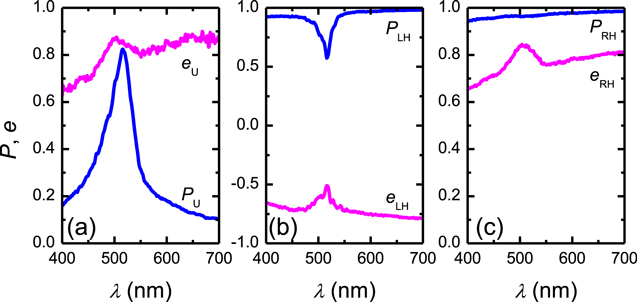
and for RHCP incident light the out coming beam has Stokes vector ![${{\bf{S}}}_{t}={[1+{m}_{14},{m}_{21}+{m}_{24},{m}_{31}+{m}_{34},{m}_{41}+{m}_{44}]}^{{\rm{T}}}.$](https://content.cld.iop.org/journals/2040-8986/20/2/024001/revision2/joptaa9e7dieqn9.gif) The degree of polarization and ellipticity of the transmitted beam calculated with equations (3) and (4) for each case of incident polarization state are shown in figure 7. In figure 7(a), it can be noticed that unpolarized incident light at 515 nm emerges with a relatively high degree of polarization (P = 0.82) and this polarized part of the transmitted beam has a near circular right-handed character (e = 0.85). In figure 7(b) for LHCP incident light, the degree of polarization appreciably decreases at wavelengths in the band of selective reflection, whereas for RHCP incident light in figure 7(c) the transmitted beam is highly polarized in most of the spectral range. In both cases, the handedness of the incident beam is retained although for LHCP the ellipticity (e = −0.55) considerably deviates from the incident polarization state. For RHCP incident light, the ellipticity of transmitted beam is relatively high (e = 0.84).
The degree of polarization and ellipticity of the transmitted beam calculated with equations (3) and (4) for each case of incident polarization state are shown in figure 7. In figure 7(a), it can be noticed that unpolarized incident light at 515 nm emerges with a relatively high degree of polarization (P = 0.82) and this polarized part of the transmitted beam has a near circular right-handed character (e = 0.85). In figure 7(b) for LHCP incident light, the degree of polarization appreciably decreases at wavelengths in the band of selective reflection, whereas for RHCP incident light in figure 7(c) the transmitted beam is highly polarized in most of the spectral range. In both cases, the handedness of the incident beam is retained although for LHCP the ellipticity (e = −0.55) considerably deviates from the incident polarization state. For RHCP incident light, the ellipticity of transmitted beam is relatively high (e = 0.84).
Figure 7. Degree of polarization (P) and ellipticity (e) of light transmitted through a NCC chiral film for incident light: (a) U-unpolarized, (b) LH-left-handed circularly polarized, and (c) RH-right-handed circularly polarized. Notice the different scale in (b).
Download figure:
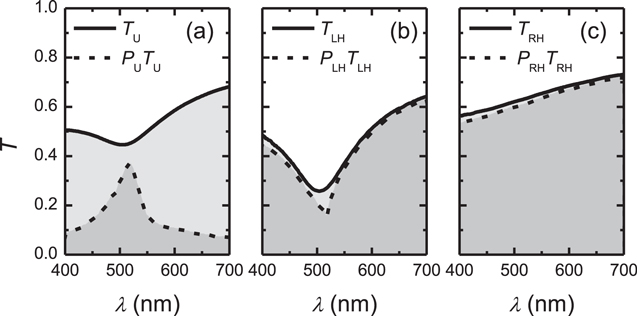
Standard image High-resolution imageFurther insight into the optical response of the NCC chiral films is gained when the actual transmittance for each incident polarization state is considered. Figure 8 shows the transmittance measured in the visible range for unpolarized incident light (TU), LHCP (TLH), and RHCP (TRH) incident light. As can be noticed, for unpolarized and LHCP incident light the band of selective reflection is evident. In contradistinction, RHCP incident light is freely transmitted. Also in figure 8 is included the polarized part of the transmittance for each case of incident light, that is, the product of the polarization degree according to equation (3) and the corresponding transmittance PjTj (j = U, RH, LH). Thus, the polarized and unpolarized parts are represented by the light-gray and dark-gray areas, respectively. It should be mentioned that in the ideal case of monodomain chiral nematic ordering, the baseline of Tj is expected at about 0.9 for an average refractive index of 1.54 for cellulose with a slight decrease to shorter wavelengths due to the dispersion of the refractive index. Therefore, smaller values of transmittance are indicative of light scattering. In addition, for the ideal case the minima in TU and TLH (at λmin = 505 nm) are expected to be 0.5 and 0, respectively. The larger values obtained result from the multidomain texture. An LHCP incident light of wavelength λmin will propagate through domains with pitch larger or smaller than Λ = λmin/nav with an attenuation decreasing with the distance to λmin. Also, the LHCP wave will only be partially attenuated in domains with pitch Λ if the number of turns in the helicoids is so small that the domain thickness is less than attenuation length. These two mechanisms may contribute to the non-zero value of TLH. As a side result, the partial incoherent superposition of these types of contributions depolarizes the transmitted light modifying the ellipticity as well.
Figure 8. Transmittance of a NCC chiral film for incident light: (a) U-unpolarized, (b) LH-left-handed circularly polarized, and (c) RH-right-handed circularly polarized.
Download figure:
Standard image High-resolution image3.4. Polarization properties of the transmitted beam for linearly polarized incident light
Another case of interest is when the incidence is linearly polarized. As an example, we consider an incident Stokes vector ![${{\bf{S}}}_{{\rm{i}}}={[\mathrm{1,}\mathrm{1,}\mathrm{0,}0]}^{{\rm{T}}}.$](https://content.cld.iop.org/journals/2040-8986/20/2/024001/revision2/joptaa9e7dieqn10.gif) In this particular case, the Stokes vector of the transmitted light is
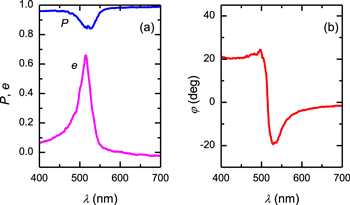
In this particular case, the Stokes vector of the transmitted light is ![${{\bf{S}}}_{{\rm{t}}}\,={[1+{m}_{12},{m}_{21}+{m}_{22},{m}_{31}+{m}_{32},{m}_{41}+{m}_{42}]}^{{\rm{T}}}.$](https://content.cld.iop.org/journals/2040-8986/20/2/024001/revision2/joptaa9e7dieqn11.gif) The polarization properties of the transmitted beam calculated with equations (3)–(5) are shown in figure 9. As can be noticed in figure 9(a), the degree of polarization is relatively high with a minimum in the band of selective reflection. The polarized part of the transmitted beam is right-handed elliptically polarized in the band of selective reflection and near linearly polarized light e ≈ 0 at larger wavelengths.
The polarization properties of the transmitted beam calculated with equations (3)–(5) are shown in figure 9. As can be noticed in figure 9(a), the degree of polarization is relatively high with a minimum in the band of selective reflection. The polarized part of the transmitted beam is right-handed elliptically polarized in the band of selective reflection and near linearly polarized light e ≈ 0 at larger wavelengths.
Figure 9. (a) Degree of polarization and ellipticity, and (b) azimuth angle of transmitted light for linearly polarized incident light.
Download figure:
Standard image High-resolution imageAnother property of interest is the optical rotation dispersion (ORD) which results from the difference in the refractive indices for left- and right-handed circularly polarized light. In this case, ORD can be evaluated from the azimuth of the transmitted beam shown in figure 9(b) which shows the change in azimuth for linearly polarized incident light. The maximum rotation is around +20° and −20° at wavelengths slightly smaller than and larger than the selective Bragg resonance wavelength. With a film thickness of 28 μm as determined by SEM we then get a maximum specific rotation of +20/0.028 ≈ +700° mm−1 which is comparable to that found in the cuticle of the beetle Cetonia aurata [27]. Nevertheless, the transmitted light in the spectral band of selective reflection is right-handed ellipticaly polarized as shown in figure 9(a).
3.5. Mueller matrix differential decomposition
In chiral systems, CD is the differential absorption of LHCP and RHCP and is thus a measure of the difference between the absorption coefficients for LHCP (αL) and RHCP (αR) incident light. These are determined by assuming a Lambert–Beer dependence of the transmitted irradiances IL ∼ exp(−αL d) and IR ∼ exp(−αR d), where d is the sample thickness of homogenous materials with natural optical activity where LHCP and RHCP are eigenmodes of propagation [28]. In that case, for LHCP and RHCP incident light the total irradiance of the transmitted light is proportional to the first component of the Stokes vector, that is, IL = (1 − m14) and IR = (1 + m14), respectively, and CD can be quantified as,
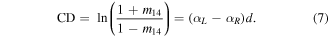
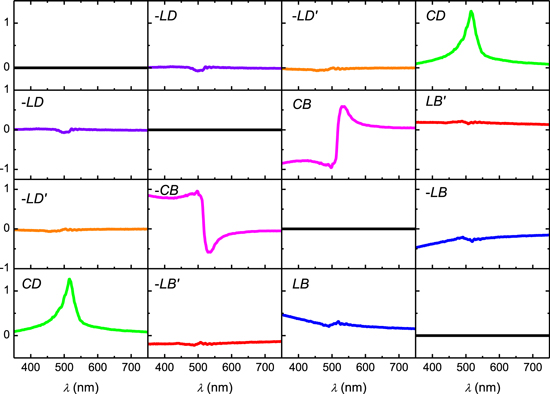
However, in anisotropic depolarizing media, equation (7) is not suitable to use for CD computation because LHCP and RHCP are not propagation eigenmodes. Recently, a differential decomposition was proposed to determine the elementary properties for homogeneous media [29, 30]. That formalism establishes that M and its spatial variation along the direction of wave propagation z are related as dM/dz = mM where m is the z-independent differential matrix. Direct integration gives L = lnM where L = md being d the sample thickness. The matrix L is split into symmetric and asymmetric parts L = Lm + Lu where Lm = (L − GLTG)/2 and Lu =(L + GLTG)/2, respectively, and G = diag[1, −1, −1, −1]. Thus, Lm is a non-depolarizing matrix containing six elementary properties [30],
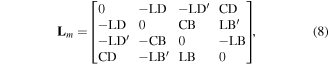
where LB (LD) and LB' (LD') are the linear birefringence (dichroism) along the x–y and ±45° axes, CD is the circular dichroism and CB the circular birefringence. On the other hand, Lu is given by [30],

where LDP, LDP', and CDP describe selective depolarization of linearly horizontal, linearly 45°, and circularly polarized light, respectively. The Δpj elements are related to inhomogeneity in the sample or time non-reversal events [30]. Although the NCC chiral film shows a multidomain texture i.e. a non-homogeneous media, it is interesting to explore the differential decomposition of its Mueller matrix to evaluate not the intrinsic properties given in equation (8) but their equivalent effective structural parameters.
Figure 10 shows the non-depolarizing matrix Lm corresponding to the transmission Mueller matrix measured at normal incidence shown in figure 5. It is clear that CB and CD are the dominant elementary properties of the NCC chiral film. It should be mentioned that the off-diagonal elements in Lu (not shown) are Δpj ≈ 0. It is worth mentioning that Δpj = 0 is a necessary condition for homogeneity in depolarizing media with time-reversal symmetry [30]. Introducing Δα = CD/d, the differential absorption per unit length attains a maximum of 45.22 mm−1 at wavelength 516 nm. On the other hand, diagonal elements of Lu have a similar wavelength dependence as the depolarizance shown in figure 6.
Figure 10. Matrix of elementary parameters Lm (equation (8)) corresponding to the transmission Mueller matrix shown in figure 5 of an NCC chiral film. The vertical scale for each row is given on the left.
Download figure:
Standard image High-resolution imageCurrent equipment routinely used to quantify CD (known as spectropolarimeters) measure only a few elements of the Mueller matrix (sometimes only one), and often anisotropic artifacts in the system affect the measurements making their interpretation difficult. Also, those equipments are limited to measure samples with low values of CD because in molecular systems the difference between the absorption coefficients αL and αR is very small. These limitations are overcome when the Mueller matrix approach is used in chiral films to determine the strong CD signal.
4. Conclusions
NCC chiral films were processed from bacterial cellulose. The films are iridescent and have a multidomain texture. The Mueller matrices of the films exhibit the same symmetries as those found in the cuticle of beetles having chiral structures. For unpolarized light at small angles of incidence, the films reflect partially polarized light of the left-handed type in the spectral range from 420 to 560 nm. The depolarization of NCC chiral films in reflection mode is larger compared to that observed in beetle´s cuticle. For unpolarized light at normal incidence, the films transmit right-handed polarized light. In the band of selective reflection, the depolarization depends on the state of polarization of the incident light but right-handed polarized light is not largely affected. The depolarization increases at short wavelengths probably due to multiple scattering. For longer wavelengths, the depolarization is almost zero. Large values of structural circular birefringence and dichroism were determined using a differential decomposition of the transmission Mueller matrix at normal incidence.
Acknowledgments
The Knut and Alice Wallenberg foundation, the Swedish Research Council, Carl Tryggers foundation and the Swedish Government Strategic Research Area in Materials Science on Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU # 2009-00971) are acknowledged for financial support. Brazilian agencies FAPESP and CNPq are acknowledged for financial support. Moliria Vieira dos Santos acknowledges FAPESP for a doctoral fellowship (grants #2014/12424-2).