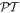Abstract
We study transport properties of an array created by alternating (a, b) layers with balanced loss/gain characterized by the key parameter γ. It is shown that for non-equal widths of (a, b) layers, i.e., when the corresponding Hamiltonian is non-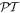 -symmetric, the system exhibits the scattering properties similar to those of truly
-symmetric, the system exhibits the scattering properties similar to those of truly 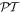 -symmetric models provided that without loss/gain the structure presents the matched quarter stack. The inclusion of the loss/gain terms leads to an emergence of a finite number of spectral bands characterized by real values of the Bloch index. Each spectral band consists of a central region where the transmission coefficient
-symmetric models provided that without loss/gain the structure presents the matched quarter stack. The inclusion of the loss/gain terms leads to an emergence of a finite number of spectral bands characterized by real values of the Bloch index. Each spectral band consists of a central region where the transmission coefficient 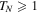 , and two side regions with
, and two side regions with 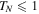 . At the borders between these regions the unidirectional reflectivity occurs. Also, the set of Fabry–Perot resonances with TN = 1 are found in spite of the presence of loss/gain.
. At the borders between these regions the unidirectional reflectivity occurs. Also, the set of Fabry–Perot resonances with TN = 1 are found in spite of the presence of loss/gain.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Introduction
The possibility of deliberately intermixing loss and gain in optical structures as a means to attain physical properties that are otherwise out of reach in standard arrangements has recently been explored in a number of studies [1–8]. In general, such non-conservative configurations can display surprising behavior resulting from the possible presence of exceptional points [9, 10] and mode bi-orthogonality. A particular class of non-Hermitian systems that has recently attracted considerable attention is that respecting parity-time ( ) symmetry [1–5]. Such a symmetry emerges if a Hamiltonian is symmetric under the combined action of space reflection
) symmetry [1–5]. Such a symmetry emerges if a Hamiltonian is symmetric under the combined action of space reflection 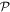 and time reversal
and time reversal 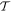 operators. In this case the spectrum happens to be real in spite of the fact that the potential involved is complex [9, 10]. Once however a loss/gain parameter exceeds a critical value, this symmetry can spontaneously break and consequently the eigenvalue spectrum ceases to be real and hence enters the complex domain [9].
operators. In this case the spectrum happens to be real in spite of the fact that the potential involved is complex [9, 10]. Once however a loss/gain parameter exceeds a critical value, this symmetry can spontaneously break and consequently the eigenvalue spectrum ceases to be real and hence enters the complex domain [9].
The availability of optical attenuation and amplification makes optics an ideal ground where 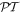 -symmetric effects can be experimentally observed and investigated [3, 4, 11]. In the paraxial regime, a necessary (but not sufficient) condition to impose this symmetry in photonics is that the complex refractive index distribution obeys
-symmetric effects can be experimentally observed and investigated [3, 4, 11]. In the paraxial regime, a necessary (but not sufficient) condition to impose this symmetry in photonics is that the complex refractive index distribution obeys  [1, 2]. This latter condition directly implies that the real part of the refractive index potential must be an even function of position while its imaginary component must be antisymmetric. On the other hand, in the case of scattering problems,
[1, 2]. This latter condition directly implies that the real part of the refractive index potential must be an even function of position while its imaginary component must be antisymmetric. On the other hand, in the case of scattering problems, 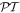 -symmetric effects can be investigated based on scattering matrix formalisms or transfer matrices—avenues that have remained so far relatively unexplored.
-symmetric effects can be investigated based on scattering matrix formalisms or transfer matrices—avenues that have remained so far relatively unexplored.
Thus far, the ramifications of parity-time symmetry on optical transport have been systematically considered in several theoretical and experimental investigations. Processes emerging from 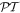 -symmetry, like double refraction, band merging, unidirectional invisibility, abrupt phase transitions and nonreciprocal wave propagation have been predicted and observed [1, 3, 11–14]. In addition this same symmetry was recently utilized to enforce single-mode behavior in laser micro-cavities as well as to judiciously control wave dynamics around exceptional points and photonic crystals [15]. Finally, similar concepts are nowadays used in other fields, like for example opto-mechanics, acoustics, nonlinear optics, plasmonics, metamaterials, and imaging to mention a few [16]. In view of these developments, the following question naturally arises. To which extent could a system depart from an exact parity-time symmetry and still exhibit
-symmetry, like double refraction, band merging, unidirectional invisibility, abrupt phase transitions and nonreciprocal wave propagation have been predicted and observed [1, 3, 11–14]. In addition this same symmetry was recently utilized to enforce single-mode behavior in laser micro-cavities as well as to judiciously control wave dynamics around exceptional points and photonic crystals [15]. Finally, similar concepts are nowadays used in other fields, like for example opto-mechanics, acoustics, nonlinear optics, plasmonics, metamaterials, and imaging to mention a few [16]. In view of these developments, the following question naturally arises. To which extent could a system depart from an exact parity-time symmetry and still exhibit 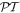 -symmetric characteristics? Recently, a possibility of synthesizing complex potentials that support entirely real spectra despite the fact that they violate the necessary condition for
-symmetric characteristics? Recently, a possibility of synthesizing complex potentials that support entirely real spectra despite the fact that they violate the necessary condition for 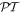 -symmetry has been discussed in [17] within the context of optical supersymmetry (see, also, [18]).
-symmetry has been discussed in [17] within the context of optical supersymmetry (see, also, [18]).
In this paper we show that it is indeed possible to observe 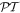 -scattering behavior even in systems that strictly speaking lack this symmetry. This is explicitly demonstrated in perfectly matched multilayer non-Hermitian arrangements having unequal layer widths. In this case, the incorporation of loss/gain domains leads to a finite number of bands—all associated with a real Bloch index that is reminiscent of actual
-scattering behavior even in systems that strictly speaking lack this symmetry. This is explicitly demonstrated in perfectly matched multilayer non-Hermitian arrangements having unequal layer widths. In this case, the incorporation of loss/gain domains leads to a finite number of bands—all associated with a real Bloch index that is reminiscent of actual 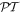 -symmetric lattices [12]. Special attention has been paid to an emergence of unidirectional reflectivity. Our results indicate that a
-symmetric lattices [12]. Special attention has been paid to an emergence of unidirectional reflectivity. Our results indicate that a 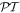 -symmetric response can be quite robust and therefore can be observed in more involved structures even in the absence of a strict
-symmetric response can be quite robust and therefore can be observed in more involved structures even in the absence of a strict 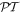 -symmetry.
-symmetry.
The model
We consider the propagation of an electromagnetic wave of frequency ω through a regular array of N identical unit (a, b) cells embedded in a homogeneous 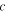 -medium, see figure 1. Each cell consists of two dielectric a and b layers with the thicknesses da and db, respectively, so that
-medium, see figure 1. Each cell consists of two dielectric a and b layers with the thicknesses da and db, respectively, so that 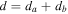 is the unit-cell size. The a and b layers are made of the materials absorbing and amplifying the electromagnetic waves, respectively. The loss and gain in the layers are incorporated via complex permittivities, while the magnetic permeabilities
is the unit-cell size. The a and b layers are made of the materials absorbing and amplifying the electromagnetic waves, respectively. The loss and gain in the layers are incorporated via complex permittivities, while the magnetic permeabilities 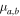 are assumed to be real and positive constants. The refractive indices
are assumed to be real and positive constants. The refractive indices 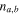 , impedances
, impedances 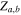 and wave phase shifts
and wave phase shifts 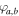 of a and b layers are presented as follows,
of a and b layers are presented as follows,
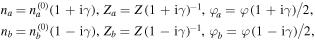
where
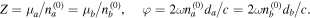
Here the parameter 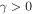 measures the strength of balanced loss and gain inside a and b layers, respectively, and
measures the strength of balanced loss and gain inside a and b layers, respectively, and 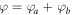 is the purely real phase shift of the wave passing each of the unit cells. In the case of no loss/gain (
is the purely real phase shift of the wave passing each of the unit cells. In the case of no loss/gain ( ) the structure is known as the matched quarter stack for which the a and b layers are perfectly matched and have equal optic paths,
) the structure is known as the matched quarter stack for which the a and b layers are perfectly matched and have equal optic paths, 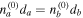 . As one can see, for
. As one can see, for 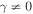 and
and 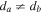 the corresponding Hamiltonian has no
the corresponding Hamiltonian has no 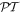 -symmetry. A particular
-symmetry. A particular 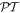 -symmetric realization is achieved only when da = db with
-symmetric realization is achieved only when da = db with 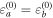 , and
, and 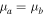 .
.
Figure 1. A sketch of the model.
Download figure:
Standard image High-resolution imageWithin any layer an electromagnetic wave propagates along the 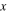 -direction (figure 1) perpendicular to the stratification according to the 1D Helmholtz equation. Its general solution inside every unit cell can be presented as a superposition of traveling forward and backward plane waves. By combining these solutions with the boundary conditions for the wave at the interfaces between a and b layers, one can obtain the unit-cell transfer matrix
-direction (figure 1) perpendicular to the stratification according to the 1D Helmholtz equation. Its general solution inside every unit cell can be presented as a superposition of traveling forward and backward plane waves. By combining these solutions with the boundary conditions for the wave at the interfaces between a and b layers, one can obtain the unit-cell transfer matrix 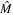 relating the wave amplitudes of two adjacent unit cells (see, e.g., [19]). For our model the elements of the M-matrix read
relating the wave amplitudes of two adjacent unit cells (see, e.g., [19]). For our model the elements of the M-matrix read
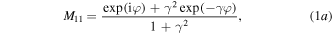
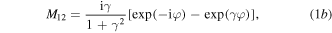

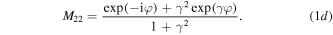
Note that 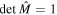 in accordance with the general condition inherent for transfer matrices. On the other hand, the transfer matrix
in accordance with the general condition inherent for transfer matrices. On the other hand, the transfer matrix 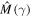 has specific symmetry,
has specific symmetry,
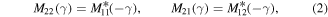
where '∗' stands for the complex conjugation. This symmetry can be compared with that emerging for various 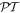 -symmetric Hamiltonians [7, 20–22]. Clearly, it differs from the standard one,
-symmetric Hamiltonians [7, 20–22]. Clearly, it differs from the standard one, 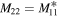 ,
, 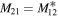 , that originates from time-reversal symmetry.
, that originates from time-reversal symmetry.
Frequency band structure
The dispersion relation for the Bloch index 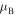 determined through the eigenvalues
determined through the eigenvalues 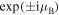 of the transfer
of the transfer 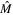 -matrix, is defined by the matrix trace,
-matrix, is defined by the matrix trace, 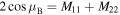 . Thus, one obtains
. Thus, one obtains
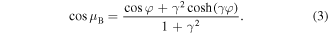
This relation determines the dependence of the Bloch wave number 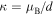 on the frequency ω (or, on the phase shift
on the frequency ω (or, on the phase shift 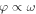 ) for the wave inside the scattering region. One of the important conclusions that follows from equation (3), is a finite number Nband of spectral bands defined by the condition
) for the wave inside the scattering region. One of the important conclusions that follows from equation (3), is a finite number Nband of spectral bands defined by the condition 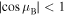 . This number Nband depends on the parameter γ only, and for
. This number Nband depends on the parameter γ only, and for 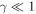 can be estimated as
can be estimated as
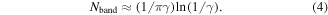
Within these bands the Bloch index  is real in spite of the presence of loss and gain. This property has been widely discussed in view of the nature of
is real in spite of the presence of loss and gain. This property has been widely discussed in view of the nature of  -symmetric systems. As is known, the real-valued solutions
-symmetric systems. As is known, the real-valued solutions 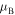 to the dispersion equation
to the dispersion equation  can exist only when the trace
can exist only when the trace  of the transfer
of the transfer 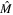 -matrix is real-valued, i.e. if
-matrix is real-valued, i.e. if
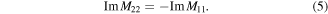
In our model this determinative condition is provided not due to the 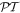 -symmetry but merely due to the balance between loss and gain.
-symmetry but merely due to the balance between loss and gain.
Outside the bands, where 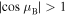 , the index
, the index 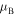 is purely imaginary, thus creating spectral gaps. Here the waves are known as the evanescent Bloch states, attenuated on the scale of the order of
is purely imaginary, thus creating spectral gaps. Here the waves are known as the evanescent Bloch states, attenuated on the scale of the order of 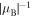 . Therefore, for a sufficiently long structure,
. Therefore, for a sufficiently long structure, 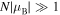 , the transmission is exponentially small. It should be noted that in the absence of loss/gain (
, the transmission is exponentially small. It should be noted that in the absence of loss/gain ( ), there are no spectral gaps since all spectral bands are touching.
), there are no spectral gaps since all spectral bands are touching.
When γ exceeds the critical value 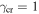 , there are no spectral bands since the Bloch index
, there are no spectral bands since the Bloch index 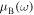 becomes imaginary for any frequency ω. Two examples of the dependence
becomes imaginary for any frequency ω. Two examples of the dependence 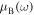 are shown in figure 2 for different values of γ. It is quite instructive that within any spectral band the maximal value of the Bloch index
are shown in figure 2 for different values of γ. It is quite instructive that within any spectral band the maximal value of the Bloch index 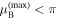 for any nonzero γ. The smaller the parameter γ, the closer to π can be the Bloch index
for any nonzero γ. The smaller the parameter γ, the closer to π can be the Bloch index 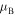 . On the other hand, for any given γ from the interval
. On the other hand, for any given γ from the interval 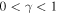 the higher the band the smaller the value of
the higher the band the smaller the value of 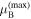 .
.
Figure 2. The dependence (3) of the Bloch index 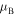 on the phase shift
on the phase shift 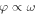 for two values of γ. Spectral bands and gaps are shown by shaded areas.
for two values of γ. Spectral bands and gaps are shown by shaded areas.
Download figure:
Standard image High-resolution imageTransmittance
With the standard transfer matrix approach we derived an analytical expression for the transmittance TN of our model consisting of N unit (a, b) cells and connected to perfect 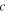 -leads by the impedance Z,
-leads by the impedance Z,
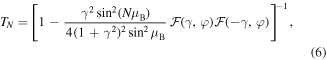
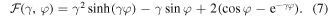
Here 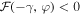 for any value of ϕ, unlike
for any value of ϕ, unlike 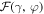 that can be either positive or negative as a function of φ. Two examples of dependence
that can be either positive or negative as a function of φ. Two examples of dependence 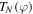 are given in figure 3.
are given in figure 3.
Figure 3. The logarithm of TN defined by equation (6) as a function of φ for 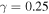 and different values N of unit cells. Shaded regions correspond to spectral bands, and circles stand for the borders between the regions with
and different values N of unit cells. Shaded regions correspond to spectral bands, and circles stand for the borders between the regions with 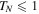 and
and 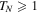 .
.
Download figure:
Standard image High-resolution imageThe analysis shows that a distinctive property of the transmittance is that every spectral band consists of the central region with  and those with
and those with 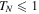 , see figures 3 and 4. At the borders between these regions (circles in figure 3) the transmission is perfect, TN = 1, and this happens due to vanishing the function
, see figures 3 and 4. At the borders between these regions (circles in figure 3) the transmission is perfect, TN = 1, and this happens due to vanishing the function 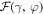 . The corresponding values
. The corresponding values 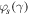 for which
for which 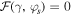 can be compared with exceptional points emerging in the
can be compared with exceptional points emerging in the 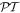 -symmetric models (see, e.g., [23] and references therein). However, in our case the Bloch index
-symmetric models (see, e.g., [23] and references therein). However, in our case the Bloch index  does not vanish, in contrast to truly exceptional points for which both conditions, TN = 1 and
does not vanish, in contrast to truly exceptional points for which both conditions, TN = 1 and 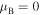 , are fulfilled. These conditions are known as that providing invisibility of a model in the scattering process. The only situation for the invisibility to occur in our setup is when two conditions,
, are fulfilled. These conditions are known as that providing invisibility of a model in the scattering process. The only situation for the invisibility to occur in our setup is when two conditions, 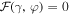 and
and 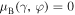 , meet. As one can see in figure 4, the sequence of exceptional points
, meet. As one can see in figure 4, the sequence of exceptional points 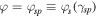 emerges for the corresponding sequence of
emerges for the corresponding sequence of 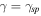 for which two curves
for which two curves 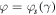 and
and 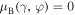 touch each other. Note that at every fixed value of
touch each other. Note that at every fixed value of 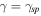 the corresponding exceptional point
the corresponding exceptional point  is located on the top of the highest band.
is located on the top of the highest band.
Figure 4. Spectral bands and gaps in dependence on the loss/gain parameter γ. The full curve shows the border 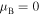 above which
above which 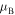 is imaginary (gaps). Below this curve
is imaginary (gaps). Below this curve 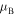 is real. Between full and dashed curve
is real. Between full and dashed curve 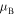 is real and
is real and 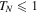 . Inside dashed regions
. Inside dashed regions 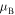 is real and
is real and 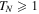 . The dependence
. The dependence 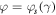 is depicted by the dashed curve on which TN = 1. The horizontal dash-dotted line is shown for
is depicted by the dashed curve on which TN = 1. The horizontal dash-dotted line is shown for 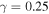 .
.
Download figure:
Standard image High-resolution imageApart from the specific points 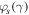 , the perfect transmission, TN = 1, occurs due to Fabry–Perot resonances located within spectral bands. They are defined by the condition
, the perfect transmission, TN = 1, occurs due to Fabry–Perot resonances located within spectral bands. They are defined by the condition 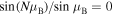 specifying the resonant values
specifying the resonant values 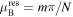 (
(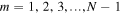 ) of the Bloch index
) of the Bloch index 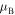 . Since the spectrum
. Since the spectrum 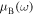 is restricted by
is restricted by 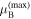 , the total number of such resonances in a given spectral band can vary from zero to
, the total number of such resonances in a given spectral band can vary from zero to 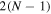 , depending on the band number and loss/gain parameter γ. Specifically, for a fixed γ the higher spectral band contains the smaller number of Fabry–Perot resonances. This result is principally different from what happens in an array of bi-layers with real and positive optical parameters, where
, depending on the band number and loss/gain parameter γ. Specifically, for a fixed γ the higher spectral band contains the smaller number of Fabry–Perot resonances. This result is principally different from what happens in an array of bi-layers with real and positive optical parameters, where  number of Fabry–Perot resonances emerge in any spectral band.
number of Fabry–Perot resonances emerge in any spectral band.
Unidirectional reflectivity
The expressions for the left and right reflectances, 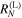 and
and 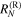 , read
, read
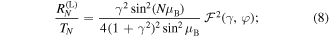
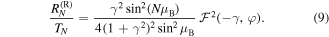
Note that 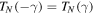 and
and 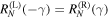 . It is remarkable that
. It is remarkable that 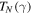 and
and  satisfy the famous relation,
satisfy the famous relation,
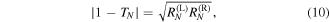
that is known to occur in 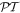 -symmetric models (see, e.g., [24]).
-symmetric models (see, e.g., [24]).
Since at the specific points 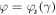 the function
the function 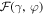 vanishes, the left reflectance (8) also vanishes, however, the right one (9) remains finite. For
vanishes, the left reflectance (8) also vanishes, however, the right one (9) remains finite. For 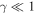 and
and 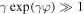 it can be estimated as follows,
it can be estimated as follows,
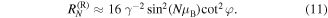
This effect is known as the unidirectional reflectivity [12]. It is one of the most important properties of scattering in the 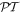 -symmetric systems. The ratio between right and left reflectances,
-symmetric systems. The ratio between right and left reflectances,
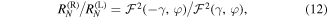
is shown in figure 5 in dependence on φ for 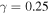 . Remarkably, this ratio is N-independent, whereas at the Fabry–Perot resonances where
. Remarkably, this ratio is N-independent, whereas at the Fabry–Perot resonances where  , both reflectances expectedly vanish,
, both reflectances expectedly vanish, 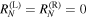 .
.
Figure 5. Ratio right-to-left reflectances (full curve) versus φ for 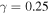 . Dashed regions are those where
. Dashed regions are those where 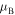 is real and
is real and 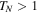 , see figure 4.
, see figure 4.
Download figure:
Standard image High-resolution imageAs for the exceptional points 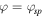 (
(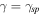 ) where our setup can be treated as invisible, the left reflectance vanishes,
) where our setup can be treated as invisible, the left reflectance vanishes,  , while the right one is very large,
, while the right one is very large,
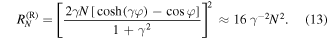
The estimate is given for  . Since
. Since 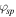 is located at the top of the highest band, one can see that for
is located at the top of the highest band, one can see that for 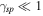 this condition is easily satisfied.
this condition is easily satisfied.
Within the spectral gaps where the Bloch index is purely imaginary (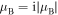 ), for a sufficiently long structure,
), for a sufficiently long structure, 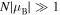 , the transmittance (6) is exponentially small. In such a situation the left reflectance (8) is larger than TN, however smaller than 1. The right reflectance (9) can be shown to exceed unity. Summarizing, one can write,
, the transmittance (6) is exponentially small. In such a situation the left reflectance (8) is larger than TN, however smaller than 1. The right reflectance (9) can be shown to exceed unity. Summarizing, one can write, 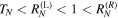 . Both reflectances increase and eventually saturate inside the gaps for
. Both reflectances increase and eventually saturate inside the gaps for 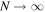 . However, both
. However, both 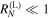 and
and 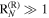 remain to be valid. Thus, the ratio
remain to be valid. Thus, the ratio 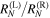 can reach extremely small values of the order of 10−7.
can reach extremely small values of the order of 10−7.
Conclusions
We have analytically studied the model that reveals the 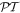 -symmetric transport although its Hamiltonian, in general, is not the
-symmetric transport although its Hamiltonian, in general, is not the 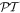 -symmetric one. Our analysis exhibits that such a situation emerges in the bi-layer optical setup which without loss/gain is known as the quarter stack, provided all layers are perfectly matched (no reflections due to boundary conditions).
-symmetric one. Our analysis exhibits that such a situation emerges in the bi-layer optical setup which without loss/gain is known as the quarter stack, provided all layers are perfectly matched (no reflections due to boundary conditions).
In the absence of loss/gain terms, all spectral bands are touched thus creating a perfect transmission for any wave frequency. When the balanced loss and gain are alternatingly included in all layers, the spectral gaps emerge between the bands, and the total number of bands is defined by the loss/gain parameter γ only.
Inside the spectral bands the Bloch index 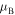 appears to be real as it happens in the known models with the
appears to be real as it happens in the known models with the 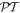 -symmetric Hamiltonians. The analysis shows that each of the spectral bands consists of a central region where the transmission coefficient is greater than one,
-symmetric Hamiltonians. The analysis shows that each of the spectral bands consists of a central region where the transmission coefficient is greater than one, 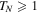 , and two side regions with
, and two side regions with 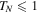 . At the borders between these regions the transmission is perfect, TN = 1, however,
. At the borders between these regions the transmission is perfect, TN = 1, however, 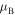 does not typically vanish as happens in the known
does not typically vanish as happens in the known 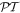 -symmetric models. These borders are of specific interest since one of the reflectances vanishes, thus leading to the so-called 'unidirectional reflectivity', the effect which is important both from theoretical and experimental points of view. The ratio between left and right reflectances is specified by the loss/gain parameter γ and the wave frequency ω, being independent of the number N of cell units. It is important that a strong difference between left and right reflectances occurs in a relatively large wave-propagation region where the Bloch index
-symmetric models. These borders are of specific interest since one of the reflectances vanishes, thus leading to the so-called 'unidirectional reflectivity', the effect which is important both from theoretical and experimental points of view. The ratio between left and right reflectances is specified by the loss/gain parameter γ and the wave frequency ω, being independent of the number N of cell units. It is important that a strong difference between left and right reflectances occurs in a relatively large wave-propagation region where the Bloch index 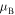 is real.
is real.
The analytical expressions display that inside the spectral bands the Fabry–Perot resonances emerge in spite of the presence of loss and gain. These resonances exist both in the regions with 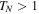 and
and 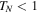 . It is also worthwhile that the invisibility (when both relations, TN = 1 and
. It is also worthwhile that the invisibility (when both relations, TN = 1 and 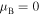 hold) is realized only for a quite specific values
hold) is realized only for a quite specific values 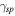 and for the corresponding wave frequencies located in the highest spectral bands.
and for the corresponding wave frequencies located in the highest spectral bands.
In conclusion, our study unexpectedly manifests that the 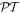 -symmetric properties may occur in non-
-symmetric properties may occur in non-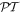 -symmetric systems, a fact that may be important in view of experimental realizations of matched quarter stacks, as well as for the theory of the
-symmetric systems, a fact that may be important in view of experimental realizations of matched quarter stacks, as well as for the theory of the 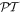 -symmetric transport.
-symmetric transport.
Acknowledgments
The authors are thankful to L Deych, T Kottos and A Lisyansky for fruitful discussions. This work was supported by the CONACYT (México) grant No. CB-2011-01-166382 and by the VIEP-BUAP grant IZF-EXC15-G. DNC acknowledges the support by NSF (Grant No. ECCS-1128520), and AFOSR (Grant No. FA9550-14-1-0037).