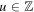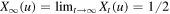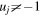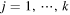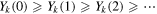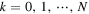Abstract
Complex systems in the real world often operate through multiple kinds of links connecting their constituents. In this paper we propose an opinion formation model under bounded confidence over multiplex networks, consisting of edges at different topological and temporal scales. We determine rigorously the critical confidence threshold by exploiting probability theory and network science when the nodes are arranged on the integers,  , evolving in continuous time. It is found that the existence of 'multiplexity' impedes the convergence, and that working with the aggregated or summarized simplex network is inaccurate since it misses vital information. Analytical calculations are confirmed by extensive numerical simulations.
, evolving in continuous time. It is found that the existence of 'multiplexity' impedes the convergence, and that working with the aggregated or summarized simplex network is inaccurate since it misses vital information. Analytical calculations are confirmed by extensive numerical simulations.
Export citation and abstract BibTeX RIS
1. Introduction
Much work has been done over the past few decades to probe varied social contagion processes underpinning voting behaviors as well as innovation diffusion [1–4]. At the heart of such processes are the opinion formation models characterizing a wide range of collective social phenomena, including adoption of a belief, collective decision making, minority opinion survival, emergence of extremism or fads, rise and fall of political parties, etc In a model of opinion formation, each agent holds an opinion which can change when she becomes aware of the opinions of her neighbors in a social network. According to whether the variable that represents the opinion of an agent is discrete or continuous, opinion formation models are classified into two types. In the discrete case, most established examples include the voter model [5], the Galam majority-rule model [6], and the Sznajd model [7]. A unifying frame for discrete opinion dynamics was proposed in [8]. Among continuous models, two models presented by Hegselmann and Krause [9, 10] (HK model) and Deffuant et al [11, 12] (Deffuant model) have raised significant attention. In these two models, each agent is only willing to adjust her opinion towards those opinions that differ less than a certain bound of confidence d from her own opinion. An excellent survey for such continuous opinion dynamics under bounded confidence can be found in [13].
The assumption of bounded confidence in opinion interaction may find its origin in the psychological concept of selective exposure, where people are inclined to perceive their environment in favor of their own opinions. In the initial studies of bounded confidence models, agents in a network are assumed to be homogeneous and have the same confidence level. For example, it was shown in [11, 14] that there exists a universal critical confidence threshold dc for the homogeneous Deffuant model, above which complete consensus is reached (namely, a single opinion cluster emerges) while below which opinions diverge (namely, two or more opinion clusters are observed) through simulations on diverse networks, be them complete graphs, lattices, or scale-free networks. Later on, the idea of agent-dependent confidence bounds is introduced to interpret the heterogeneity/disparity of people's knowledge, experience, and personality, etc [15–20]; agents are thereby divided into open-minded, closed-minded, and stubborn, according to their confidence levels. The effects of heterogeneous bounds of confidence were analyzed experimentally for a group of open-minded and closed-minded agents in both HK and Deffuant models [16]. Other more sophisticated models, for example, incorporating competitive influence of social media [21], have also been reported.
In all the aforementioned work, the opinion negotiation processes take place on networks containing edges of the same type and at the same temporal and topological scale. However, several papers showed that the presence of temporal co-evolving network structures can drastically change the convergence threshold; see e.g. [22–24]. Moreover, the real agents usually simultaneously engage in multiple types of interactions, which can make a non-additive effect on network dynamics [25]. People in a society, for example, interact through a variety of relationships: friendship, partnership, kinship, work-related acquaintanceship, collaboration and colocation, to name just a few. Admittedly, a natural and more appropriate description of such systems is in terms of multiplex networks [26–28], the networks made up of different layers containing the same nodes and a given type of edges in each layer (see figure 1 for an illustration). A considerable amount of effort has been devoted recently to the modeling and structure of multiplex networks in the sociophysics community, with the aim to understand emergent properties ranging from epidemics [29, 30] to cooperation [33], from diffusion [31, 32] to synchronization [34] to cascades [35, 36].
Figure 1. An example scenario of multiplex network as a duplex network consisting of  layers. The two layers indicate two different types of intralayer connections, while the interlayer connections (dashed links) map each node to itself.
layers. The two layers indicate two different types of intralayer connections, while the interlayer connections (dashed links) map each node to itself.
Download figure:
Standard image High-resolution imageThe goal of this paper is to investigate analytically the Deffuant model of opinion formation in multiplex networks. Due to the essential nonlinearity rooted in the action of confidence bound, the Deffuant model has mostly been studied using the tools borrowed from statistical physics and through agent-based simulations [1]. Remarkably, when the underlying interaction network is modeled as an infinite one-dimensional lattice, rigorous analyses based on probability theory have been performed and the critical confidence bounds have been identified by several mathematicians recently [37–40]. The current work can be viewed as an extension in this direction from a single-layer (or simplex) network to a multiplex one. In particular, we are able to identify the critical confidence threshold as a function of interaction rates and parameters capturing confidence bounds in multiple layers capitalizing on the marked Poisson process theory. Our results reveal that working with a simplex aggregated network, ignoring the existence of multiple edges in topological and temporal scales, is inaccurate. Similar observation that the aggregation procedure tends to lose important information has also been shared in recent studies of structure and dynamics of complex systems [29, 41, 42], highlighting the significance of exploring multilayer networks.
We mention that some work of bounded confidence model on multilayer networks has been done very recently. For example, in [21] the authors address the media competition and social influence issues by involving an inner dynamics of the multiple actors of social media. A coupled network of two layers is considered therein: one is the layer of gossipers and the other is that of media. Such networks are conventionally called as interdependent systems, which fall in a different category of ours (see [25] for more backgrounds). Another work similar in spirit is [43], where the effect of multiple communities on opinion formation is investigated. It is shown that increasing the multiple layers is similar to promoting coupling between different communities. Unfortunately, this model is not amenable to rigorous analytical treatment due to its involved community complications.
The remainder of the paper is organized as follows. In section 2, we introduce the opinion model on general multiplex networks. For clarity, we first focus on the case of one-dimensional duplex model and present our main results for the critical confidence threshold in section 3. The results are then extended in section 4 to the one-dimensional multiplex networks. Section 5 is devoted to numerical simulations illustrating the theoretical results. Finally, we conclude the paper in section 6 with some remarks.
2. Multiplex opinion dynamics model
Given an integer  , a multiplex network is a pair
, a multiplex network is a pair  , made of ℓ layers
, made of ℓ layers  such that each layer is a simple graph
such that each layer is a simple graph  with node set V and edge set
with node set V and edge set  (
( ). The edge set of G consists of ℓ types of edges:
). The edge set of G consists of ℓ types of edges:  . We assume that each layer Gi has bounded degrees, namely, the set of node degrees is bounded. Thus, each agent in the network G has a bounded number of neighbors and at most ℓ types of relationship.
. We assume that each layer Gi has bounded degrees, namely, the set of node degrees is bounded. Thus, each agent in the network G has a bounded number of neighbors and at most ℓ types of relationship.
In the Deffuant model, two agents compromise as per the following rules. Initially at time t = 0, each agent  is assigned an opinion
is assigned an opinion  uniformly distributed on the interval
uniformly distributed on the interval ![$[0,1]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn12.gif) independent of others. Independent of this, each edge
independent of others. Independent of this, each edge  is independently assigned a Poisson process with rate (or intensity)
is independently assigned a Poisson process with rate (or intensity)  with
with  and
and  for
for  . We assume that
. We assume that  without loss of generality. Let Xt(u) represent the opinion value of agent u at time
without loss of generality. Let Xt(u) represent the opinion value of agent u at time  , which remains unchanged as long as no Poisson event happens for any of the edges incident to u. Let
, which remains unchanged as long as no Poisson event happens for any of the edges incident to u. Let  ,
,  and
and  for
for  . (Here,
. (Here,  implies that
implies that  is the largest one in
is the largest one in  after a possible normalization without loss of generality.) When at some time t the Poisson event occurs at edge
after a possible normalization without loss of generality.) When at some time t the Poisson event occurs at edge  for some i, such that the pre-meeting opinions of the two agents are
for some i, such that the pre-meeting opinions of the two agents are  and
and  , we set
, we set
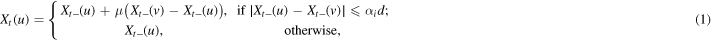
and
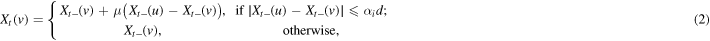
where ![$\mu \in (0,1/2]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn30.gif) is the so-called convergence parameter. Hence, two meeting agents adjust their opinions by moving towards each other by a relative amount μ (
is the so-called convergence parameter. Hence, two meeting agents adjust their opinions by moving towards each other by a relative amount μ ( implies that the two agents meet halfway) if their difference of opinion is smaller in magnitude than a threshold. Note that our assumption of bounded degrees guarantees that none of the Poisson events will be simultaneous for any node set V, be it finite or infinite. Indeed, for a finite node set V, there will be only finitely many Poisson events in any finite time interval; while for an infinite V, the prevention of simultaneous events can be shown following a standard denseness argument (see [44, p 28]). Therefore, the model is well-defined.
implies that the two agents meet halfway) if their difference of opinion is smaller in magnitude than a threshold. Note that our assumption of bounded degrees guarantees that none of the Poisson events will be simultaneous for any node set V, be it finite or infinite. Indeed, for a finite node set V, there will be only finitely many Poisson events in any finite time interval; while for an infinite V, the prevention of simultaneous events can be shown following a standard denseness argument (see [44, p 28]). Therefore, the model is well-defined.
The multiplexity in the above opinion model lies in two aspects. First, the interaction rates  in each layer can be different. Second, the confidence bounds
in each layer can be different. Second, the confidence bounds  in each layer can be different too. We might as well consider distinct convergence parameters, for example,
in each layer can be different too. We might as well consider distinct convergence parameters, for example,  for the ith layer. However, it has been confirmed that μ plays no role in the qualitative behavior of the opinion dynamics; it only affects the convergence time (see e.g. [11, 13, 38]).
for the ith layer. However, it has been confirmed that μ plays no role in the qualitative behavior of the opinion dynamics; it only affects the convergence time (see e.g. [11, 13, 38]).
In what follows, we will consider the opinion model on the real line  following [37–40]. More specifically, we take
following [37–40]. More specifically, we take  with
with  and
and  for
for  . When
. When  , G becomes a simplex network with only one type of edges. For this interaction network, the critical confidence threshold for opinion formation is identified to be
, G becomes a simplex network with only one type of edges. For this interaction network, the critical confidence threshold for opinion formation is identified to be  in [38]. This can be viewed as a special case of theorems 1 and 2 below.
in [38]. This can be viewed as a special case of theorems 1 and 2 below.
3. Critical confidence bound in one-dimensional duplex networks
For simplicity, in this section we first present the results in the case of  . Namely, we take
. Namely, we take  ,
,  , and
, and  . With these notations the main result concerning the critical confidence threshold for the one-dimensional duplex model reads as follows.
. With these notations the main result concerning the critical confidence threshold for the one-dimensional duplex model reads as follows.
Theorem 1. Consider the above continuous opinion model on  with parameters
with parameters  ,
, ![$\mu \in (0,1/2]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn48.gif) , and
, and  . Suppose
. Suppose  . Then
. Then ![${d}_{c}={[2(p+\alpha (1-p))]}^{-1}$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn51.gif) is the critical confidence threshold in the following sense
is the critical confidence threshold in the following sense
- If
 , then with probability 1, the limiting value
, then with probability 1, the limiting value  exists and
exists and ![$\{| {X}_{\infty }(u)-{X}_{\infty }(u+1)| \}\in \{0\}\cup [d,1]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) for every
for every  ;
; - If
 , then with probability 1,
, then with probability 1,  for every
for every  .
.
Several remarks are in order. First, the result indicates that when  , the opinions of all agents will converge to 1/2, the average of the initial opinion distribution. This reproduces the results for simplex network (i.e.,
, the opinions of all agents will converge to 1/2, the average of the initial opinion distribution. This reproduces the results for simplex network (i.e.,  ) [37, 38], and also agrees with the results for general initial opinion distributions [39, 40]. Second, when
) [37, 38], and also agrees with the results for general initial opinion distributions [39, 40]. Second, when  , the limiting configuration is piecewise constant interrupted by jumps of size at least d. This is nontrivial and essentially different from the situation in [45], where the random confidence bound D is set once and for all. In our setup, the two bounds d and
, the limiting configuration is piecewise constant interrupted by jumps of size at least d. This is nontrivial and essentially different from the situation in [45], where the random confidence bound D is set once and for all. In our setup, the two bounds d and  take effect alternatively as time t tends to infinity. Third, the assumption
take effect alternatively as time t tends to infinity. Third, the assumption  is for technical reason (see the proof of proposition 3), which does not have counterpart in the case of simplex network where μ only influences the convergence time of negotiation process. It would be interesting to sort out whether this condition can be dropped, which is the case suggested by our numerical simulations.
is for technical reason (see the proof of proposition 3), which does not have counterpart in the case of simplex network where μ only influences the convergence time of negotiation process. It would be interesting to sort out whether this condition can be dropped, which is the case suggested by our numerical simulations.
In the following we show theorem 1 in two regimes  and
and  separately. Our proof heavily relies on the technique called sharing a drink (SAD) proposed in [38]. We briefly review the SAD process in the appendix for completeness.
separately. Our proof heavily relies on the technique called sharing a drink (SAD) proposed in [38]. We briefly review the SAD process in the appendix for completeness.
3.1. Subcritical regime 
Given  and the initial opinion configuration
and the initial opinion configuration  , a node
, a node  is said to be an
is said to be an  -flat point to the right if for all
-flat point to the right if for all  ,
,
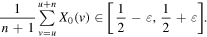
By analogy,  is said to be an
is said to be an  -flat point to the left if for all
-flat point to the left if for all  ,
,
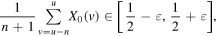
and two-sidedly  -flat if for all
-flat if for all  ,
,

If u is  -flat to the right, the Kolmogorov strong law of large numbers indicates that
-flat to the right, the Kolmogorov strong law of large numbers indicates that  Employing the translation invariance of the configuration
Employing the translation invariance of the configuration  and a coupling argument, we can show that all the following three events occur with positive probability; see [38].
and a coupling argument, we can show that all the following three events occur with positive probability; see [38].
Define a Boolean random variable A by A = 1 with probability p and  with probability
with probability  . It follows from the decomposition of the Poisson stream that the Poisson events in our opinion model constitute a marked Poisson process with rate λ. Recall that a marked Poisson process
. It follows from the decomposition of the Poisson stream that the Poisson events in our opinion model constitute a marked Poisson process with rate λ. Recall that a marked Poisson process  is composed of a Poisson stream
is composed of a Poisson stream  and a sequence of associate random variables
and a sequence of associate random variables  [46]. (More precisely, we should write At explicitly as a function of t when a Poisson event occurs at time t. We can safely omit t by using an independent coupling when necessary.) Suppose that
[46]. (More precisely, we should write At explicitly as a function of t when a Poisson event occurs at time t. We can safely omit t by using an independent coupling when necessary.) Suppose that  . Take
. Take  . For
. For  , define the following events
, define the following events  ,
,  ,
,  ,
,  , and
, and  .
.
Proposition 1. Under the assumption of theorem 1, if  , then for any
, then for any  ,
,  .
.
Proof. For  , define
, define  . It follows from lemma 1 that
. It follows from lemma 1 that  The proposition will follow if we can show that
The proposition will follow if we can show that

Suppose that  and
and  hold. Let
hold. Let  be the first time that opinion adjustment happens across any of the four edges
be the first time that opinion adjustment happens across any of the four edges  and
and  (i = 1,2). Obviously,
(i = 1,2). Obviously,  for any
for any  . We will show by contradiction that T does not exist. Indeed, on one hand, there must exist some
. We will show by contradiction that T does not exist. Indeed, on one hand, there must exist some  such that either (i)
such that either (i)  , or (ii)
, or (ii)  takes place.
takes place.
On the other hand, for any  we obtain from lemma A2, by replacing 0 with
we obtain from lemma A2, by replacing 0 with  using translation invariance,
using translation invariance,  and
and  for all
for all  . Lemma A1 gives
. Lemma A1 gives  for some integer N with
for some integer N with  . Set
. Set  for
for  . Arguing as in [38, equations (19) and (20)], we have
. Arguing as in [38, equations (19) and (20)], we have  and
and
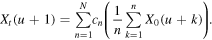
Since  holds, it follows that
holds, it follows that

Similarly, ![${X}_{t}(u-1)\in [1/2-\delta ,1/2+\delta ]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn121.gif) . These contradict with (i) and (ii). Hence,
. These contradict with (i) and (ii). Hence,  is concluded.
is concluded.
The events  and
and  in conjunction with (4) yield, for all
in conjunction with (4) yield, for all  ,
,
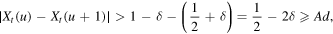
and  holds. Hence, (3) is established, which completes the proof.
holds. Hence, (3) is established, which completes the proof.
Due to the ergodicity of the indicator processes  and
and  , we are led to the following corollary (see [47, theorem 1.3] and [38, lemma 5.2]).
, we are led to the following corollary (see [47, theorem 1.3] and [38, lemma 5.2]).
Corollary 1. With probability 1, there are infinitely many nodes u to the left (and right) of 0 such that  happens. The same thing holds for
happens. The same thing holds for  .
.
Proposition 2. Under the assumption of theorem 1, if  , then with probability 1 the limiting value
, then with probability 1 the limiting value  exists and
exists and ![$\{| {X}_{\infty }(u)-{X}_{\infty }(u+1)| \}\in \{0\}\cup [d,1]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn133.gif) for all
for all  .
.
Proof. Given the initial opinion configuration  , let u1 be a node such that
, let u1 be a node such that  happens, and let
happens, and let  . It follows from (3) that the opinions in the interval
. It follows from (3) that the opinions in the interval  will not be influenced by nodes outside and vice versa. Corollary 1 indicates that every node
will not be influenced by nodes outside and vice versa. Corollary 1 indicates that every node  is located in some such interval. Therefore, it suffices to prove the proposition for every
is located in some such interval. Therefore, it suffices to prove the proposition for every  .
.
Define the energy of the interval  at time t as
at time t as
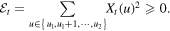
If two nodes u and  in the interval exchange opinions at time t,
in the interval exchange opinions at time t,  drops by an amount of
drops by an amount of  . Therefore,
. Therefore,  is a decreasing function of t. We claim that
is a decreasing function of t. We claim that
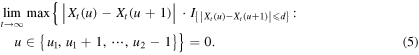
Indeed, the maximum value in (5) should be larger than some  for all sufficiently large t if (5) is not true. But for such large t that a Poisson event occurs, with probability at least
for all sufficiently large t if (5) is not true. But for such large t that a Poisson event occurs, with probability at least  some edge
some edge  with
with ![$| {X}_{t}(u)-{X}_{t}(u+1)| \in (\sigma ,d]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn149.gif) will exchange opinions. Then,
will exchange opinions. Then,  will decrease by at least
will decrease by at least  , and this will happen infinitely often almost surely in view of the conditional version of the Borel–Cantelli lemma [47, corollary 3.2]. This yields
, and this will happen infinitely often almost surely in view of the conditional version of the Borel–Cantelli lemma [47, corollary 3.2]. This yields  , a contradiction, which establishes (5).
, a contradiction, which establishes (5).
For any edge  in the interval
in the interval  , a single opinion adjustment can only increase
, a single opinion adjustment can only increase  by at most
by at most  . In the light of (5), we have either
. In the light of (5), we have either  for all sufficiently large t or
for all sufficiently large t or  . To see this, just note that otherwise there would exist some
. To see this, just note that otherwise there would exist some  so that
so that  jumps back and forth between
jumps back and forth between ![$[0,\sigma ]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn161.gif) and
and ![$(d,1]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn162.gif) infinitely often for arbitrarily small σ. However,
infinitely often for arbitrarily small σ. However,  for small σ, which leads to a contradiction.
for small σ, which leads to a contradiction.
Now, arguing as in [38, theorem 5.3], the fact that the quantity  remains unchanged over time readily implies the existence of
remains unchanged over time readily implies the existence of  . The proof is complete.
. The proof is complete.
3.2. Supercritical regime 
The following result informs us what values can be achieved for a two-sidedly flat node regardless of all future Poisson events. It can be proved exactly as [33, lemma 6.3].
Lemma 2. Given  and the initial configuration
and the initial configuration  . If
. If  is two-sidedly
is two-sidedly  -flat, then
-flat, then ![${X}_{t}(u)\in [1/2-6\varepsilon ,1/2+6\varepsilon ]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn170.gif) for all
for all  .
.
Define the energy at node  as
as  . Define an auxiliary continuous-time step function
. Define an auxiliary continuous-time step function  by
by  with
with  increasing by an amount of
increasing by an amount of  if and only if opinion exchange occurs on the edge
if and only if opinion exchange occurs on the edge  at time t. The following lemma can be shown exactly as [38, lemma 6.2].
at time t. The following lemma can be shown exactly as [38, lemma 6.2].
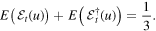
In other words, the expected sum of  is constant over time. The following proposition holds for all
is constant over time. The following proposition holds for all  .
.
Proposition 3. With probability 1, for any  , either
, either  for all sufficiently large t, or
for all sufficiently large t, or  .
.
Proof. Given a node  and a sufficiently small σ with
and a sufficiently small σ with  , we claim that, with probability 1,
, we claim that, with probability 1,

for all sufficiently large t.
Indeed, when a Poisson event occurs on any of the edges  ,
,  or
or  , the next Poisson event will occur at
, the next Poisson event will occur at  with probability 1/3. If
with probability 1/3. If ![$| {X}_{t}(u)-{X}_{t}(u+1)| \in (\sigma ,{Ad}]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn192.gif) , then
, then  will increase at least
will increase at least  if a Poisson event occurs at
if a Poisson event occurs at  . In view of the conditional Borel–Cantelli lemma as before, this will happen infinitely often with probability 1. Hence,
. In view of the conditional Borel–Cantelli lemma as before, this will happen infinitely often with probability 1. Hence,  , contradicting lemma 3. Equation (6) is established.
, contradicting lemma 3. Equation (6) is established.
What remains to show is that for small enough  ,
,  cannot jump back and forth between
cannot jump back and forth between ![$[0,\sigma ]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn199.gif) and
and ![$({Ad},1]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn200.gif) infinitely often. This is true because a single Poisson event cannot increase
infinitely often. This is true because a single Poisson event cannot increase  by more than
by more than  , which for small enough σ, is always less than the span of the gap
, which for small enough σ, is always less than the span of the gap ![$(\sigma ,{Ad}]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn203.gif) that needs to be crossed since
that needs to be crossed since  .
.
Proposition 4. Under the assumptions of theorem 1, if  , then with probability 1,
, then with probability 1,  for every
for every  .
.
Proof. Choose an  such that
such that  . We first show that with probability 1,
. We first show that with probability 1,

for any  . In the light of proposition 3, we only need to show that for each node u,
. In the light of proposition 3, we only need to show that for each node u,
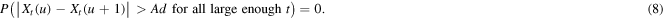
Suppose for contradiction that the probability in (8) is strictly positive. Then the event in (8) happens for infinitely many u on  and
and  with probability 1 by using the ergodicity again. We will show that the limit
with probability 1 by using the ergodicity again. We will show that the limit

exists for any  .
.
Fix a node  . Note that we can always pick two nodes
. Note that we can always pick two nodes  with
with  such that
such that  are the nodes locating between edges
are the nodes locating between edges  and
and  which never exchange opinions for any
which never exchange opinions for any  with some
with some  . To show (9) we consider two scenarios: (a) no edge
. To show (9) we consider two scenarios: (a) no edge  in
in  gets stuck with the event
gets stuck with the event  happening for any
happening for any  ; and (b) some edge
; and (b) some edge  in
in  gets stuck with this event at some time
gets stuck with this event at some time  . If (a) happens, we obtain
. If (a) happens, we obtain  for all v in this interval by proposition 3. Since
for all v in this interval by proposition 3. Since  remains constant over time,
remains constant over time,  must all converge to the average value
must all converge to the average value  . If (b) happens, u will still belong to some subinterval
. If (b) happens, u will still belong to some subinterval  such that
such that  for all v in this subinterval and that no opinion adjustment will occur on
for all v in this subinterval and that no opinion adjustment will occur on  and
and  from some time
from some time  onwards. Here we allow that
onwards. Here we allow that  . Likewise, we obtain that the opinion of any node in the subinterval converges to the average value
. Likewise, we obtain that the opinion of any node in the subinterval converges to the average value  . Equation (9) is established.
. Equation (9) is established.
Lemma 1 plus ergodicity implies that with probability 1 there exists a node w which is two-sidedly  -flat. We know from (9) and lemma 2 that
-flat. We know from (9) and lemma 2 that ![${X}_{\infty }(w)\in [1/2-6\varepsilon ,1/2+6\varepsilon ]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn240.gif) . Proposition 3 implies either
. Proposition 3 implies either  or
or  . However, the first option leads to (i)
. However, the first option leads to (i)  , or (ii)
, or (ii)  . Since
. Since  , it follows from (i) that the event
, it follows from (i) that the event  happens with positive probability. This of course is impossible. Likewise, (ii) gives rise to the event
happens with positive probability. This of course is impossible. Likewise, (ii) gives rise to the event  happening with positive probability, which is impossible either. Consequently, we deduce that
happening with positive probability, which is impossible either. Consequently, we deduce that  . In an iterative manner, we have
. In an iterative manner, we have  for all
for all  . This, however, contradicts the assumption that the event in (8) holds with positive probability. Therefore, (8) is proved and (7) follows.
. This, however, contradicts the assumption that the event in (8) holds with positive probability. Therefore, (8) is proved and (7) follows.
For the node w chosen above, we obtain by using lemma 2 that ![${X}_{t}(w)\in [1/2-6\varepsilon ,1/2+6\varepsilon ]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn251.gif) for all
for all  . For any
. For any  , we obtain with probability 1 that
, we obtain with probability 1 that ![${X}_{t}(u)\in [1/2-7\varepsilon ,1/2+7\varepsilon ]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn254.gif) for sufficiently large t invoking (7), as there are only finitely many edges between u and w. We conclude the proof by taking
for sufficiently large t invoking (7), as there are only finitely many edges between u and w. We conclude the proof by taking  .
.
Combining propositions 2 and 4 we finally complete the proof of theorem 1.
4. Generalization to multiplex networks
The techniques developed in the previous section can be used to cope with a more general interaction network, a multiplex network  with ℓ layers. The following theorem can be proved in the same way as in the previous section but the details are left to the reader.
with ℓ layers. The following theorem can be proved in the same way as in the previous section but the details are left to the reader.
Theorem 2. Consider the continuous opinion model on  with parameters
with parameters  ,
, ![$\mu \in (0,1/2]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn259.gif) ,
,  for
for  ,
,  for
for  , and
, and  . Suppose
. Suppose  ,
,  . Then
. Then  is the critical confidence threshold in the following sense
is the critical confidence threshold in the following sense
- If
 , then with probability 1, the limiting value
, then with probability 1, the limiting value  exists and
exists and ![$\{| {X}_{\infty }(u)-{X}_{\infty }(u+1)| \}\in \{0\}\cup [d,1]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) for every
for every  ;
; - If
 , then with probability 1,
, then with probability 1,  for every
for every  .
.
We give a couple of comments here. First, recall that we assume  , and therefore
, and therefore  unless the underlying network is simplex, i.e.,
unless the underlying network is simplex, i.e.,  . This suggests that it is more difficult to reach agreement in multiplex networks, going some way to explaining the commonly seen nonconsensus or polarization in real-life social systems [48]. This also seems to resonate with the recent finding in [36] that response heterogeneity in multiplex networks may slow down the cascade progress.
. This suggests that it is more difficult to reach agreement in multiplex networks, going some way to explaining the commonly seen nonconsensus or polarization in real-life social systems [48]. This also seems to resonate with the recent finding in [36] that response heterogeneity in multiplex networks may slow down the cascade progress.
Second, if there exists some k such that  for all
for all  , then
, then  . This means that, if a frequently interaction layer exists, the critical threshold, in line with intuition, will be dominated by its confidence bound. Third, if we consider an aggregated simplex network based on average confidence bound, we would have
. This means that, if a frequently interaction layer exists, the critical threshold, in line with intuition, will be dominated by its confidence bound. Third, if we consider an aggregated simplex network based on average confidence bound, we would have  , which is not equivalent to dc in general. Indeed, the aggregation procedure missed important information in inherent multiplex systems leading to inaccurate results.
, which is not equivalent to dc in general. Indeed, the aggregation procedure missed important information in inherent multiplex systems leading to inaccurate results.
5. Simulation results
In this section, we conduct agent-based simulations on large rings to illustrate and test our obtained theoretical results.
To start with, we show the time evolution of opinions among a population of n = 1000 agents distributed on a duplex ring, namely, a ring with perimeter 1000 and  layers. Take
layers. Take  ,
,  ,
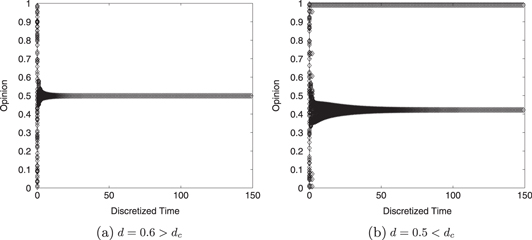
,  , and p = 0.8. By theorem 1, we deduce the critical threshold dc = 0.54. The opinion dynamics is performed by monitoring 2000 independent Poisson processes, each of which determines the meeting time of a pair of agents as described in the model. For the sake of clarity, we plot in figure 2 the opinion behavior of a randomly selected subset of 100 agents, and discretize the time axis by compressing 40000 times of Poisson jumps into one time unit.
, and p = 0.8. By theorem 1, we deduce the critical threshold dc = 0.54. The opinion dynamics is performed by monitoring 2000 independent Poisson processes, each of which determines the meeting time of a pair of agents as described in the model. For the sake of clarity, we plot in figure 2 the opinion behavior of a randomly selected subset of 100 agents, and discretize the time axis by compressing 40000 times of Poisson jumps into one time unit.
Figure 2. Evolution of opinions with  ,
,  ,
,  , p = 0.8 on a duplex ring consisting of n = 1000 agents. Only a subset of 100 agents out of 1000 is displayed. Each opinion is represented by a diamond. Each plot corresponds to one realization of the simulation.
, p = 0.8 on a duplex ring consisting of n = 1000 agents. Only a subset of 100 agents out of 1000 is displayed. Each opinion is represented by a diamond. Each plot corresponds to one realization of the simulation.
Download figure:
Standard image High-resolution imageFrom figure 2 we observe that the opinions converge to 1/2, the average of the initial opinions, when  (see figure 2(a)); while they diverge when
(see figure 2(a)); while they diverge when  with a gap of opinion clusters at least d (see figure 2(b)). These are in line with our theoretical predictions of theorem 1. We performed extensive tests by using different parameters α and p, and different size n of nodes varying from 1000 to 5000, and they confirm the theoretical results. Here, we mention that the shape of the envelop of opinions' trajectories has a relatively large change from one simulation to another. It is sensitive to the initial opinion distribution and the underpinning Poisson process.
with a gap of opinion clusters at least d (see figure 2(b)). These are in line with our theoretical predictions of theorem 1. We performed extensive tests by using different parameters α and p, and different size n of nodes varying from 1000 to 5000, and they confirm the theoretical results. Here, we mention that the shape of the envelop of opinions' trajectories has a relatively large change from one simulation to another. It is sensitive to the initial opinion distribution and the underpinning Poisson process.
Next, we determine the critical confidence bound dc through Monte Carlo simulations. Choose  ,
,  and
and  as above. Given parameters α, p and the number n of agents, we run the duplex opinion model algorithm on 1000 samples. The algorithm proceeds until no agent changes her opinion by more than 10−4 for 106 times of consecutive Poisson events. We qualify this regime as quasi-steady state. Once the system evolves into the quasi-steady state, we examine whether all agents belong to the same cluster or not. Define Pc as the fraction of samples which reaches a compete consensus at one-half. In figure 3 we show Pc as a function of confidence bound d for different α, p and n.
as above. Given parameters α, p and the number n of agents, we run the duplex opinion model algorithm on 1000 samples. The algorithm proceeds until no agent changes her opinion by more than 10−4 for 106 times of consecutive Poisson events. We qualify this regime as quasi-steady state. Once the system evolves into the quasi-steady state, we examine whether all agents belong to the same cluster or not. Define Pc as the fraction of samples which reaches a compete consensus at one-half. In figure 3 we show Pc as a function of confidence bound d for different α, p and n.
Figure 3. Fraction of samples with complete consensus as a function of confidence bound d in a quasi-steady state regime. Three different numbers of individuals located on rings are considered: n = 5000 (red squares), 10 000 (blue circles), and 20 000 (green triangles). We fix  ,
,  and
and  . (a)
. (a)  ; (b)
; (b)  ; (c)
; (c)  . The critical threshold dc is indicated by a vertical dotted line in each plot.
. The critical threshold dc is indicated by a vertical dotted line in each plot.
Download figure:
Standard image High-resolution imageWe observe from figure 3 that Pc increases gradually for  and then saturated to 1 for
and then saturated to 1 for  in each plots. A further look into the growth of Pc for different population size n shows that it will converge to a step function in the large size limit
in each plots. A further look into the growth of Pc for different population size n shows that it will converge to a step function in the large size limit  , implying a folding point at dc. This is in line with our theorem 1. Analogous qualitative results for simplex rings have been reported previously in [39]. Moreover, comparing figures 3(a), (b), and (c), we find that the sharpness of phase transition increases with respect to α but remains insensitive to p; for example, the increase of Pc from 0 to 1 in the case of n = 20 000 requires a raise of d by around 0.025 for
, implying a folding point at dc. This is in line with our theorem 1. Analogous qualitative results for simplex rings have been reported previously in [39]. Moreover, comparing figures 3(a), (b), and (c), we find that the sharpness of phase transition increases with respect to α but remains insensitive to p; for example, the increase of Pc from 0 to 1 in the case of n = 20 000 requires a raise of d by around 0.025 for  (figure 3(a)) while only around 0.015 for
(figure 3(a)) while only around 0.015 for  (figure 3(c)). We contend that this correlation may find its origin in the higher level of homophily resulting from the more homogeneous confidence bounds, namely, larger α, as observed in wealthy social behaviors [45, 49].
(figure 3(c)). We contend that this correlation may find its origin in the higher level of homophily resulting from the more homogeneous confidence bounds, namely, larger α, as observed in wealthy social behaviors [45, 49].
Finally, we perform extensive simulations to examine the relationship between the critical confidence bound and the number of layers. Recall the comment below theorem 2 that the critical value  as long as
as long as  . In figure 4 we pictorially show the evolution of dc with respect to the number of layers ℓ. We consider multiplex rings with perimeter
. In figure 4 we pictorially show the evolution of dc with respect to the number of layers ℓ. We consider multiplex rings with perimeter  and
and  . Fix
. Fix  and
and  . For each given ℓ and a confidence bound d, we run the multiplex opinion model algorithm with the following parameters
. For each given ℓ and a confidence bound d, we run the multiplex opinion model algorithm with the following parameters
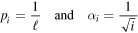
for  . We first put
. We first put  and run the algorithm until the system enters the quasi-steady state. Repeat this process for 1000 times to obtain the fraction of complete consensus Pc as before. We then start over by increasing d gradually and repeating the entire process until
and run the algorithm until the system enters the quasi-steady state. Repeat this process for 1000 times to obtain the fraction of complete consensus Pc as before. We then start over by increasing d gradually and repeating the entire process until  . The corresponding value of d is regarded as dc.
. The corresponding value of d is regarded as dc.
Figure 4. The critical confidence bound dc as a function of the number ℓ of layers. Theoretical estimates (green crosses) are derived from theorem 2. The green line is drawn to aid the eye. Numerical results (upper and lower red bars) indicate the ranges of dc obtained from an ensemble of 100 independent samples.
Download figure:
Standard image High-resolution imageAccording to our choice of parameters, all the conditions in theorem 2 are satisfied. The simulation results reported in figure 4 agree with the prediction of dc in theorem 2. With the growth of ℓ, the critical threshold dc also increases, implying, as expected, a tougher situation for reaching consensus. For example, for a randomly selected  , the possibility of consensus for
, the possibility of consensus for  is almost cut in half as compared to that for
is almost cut in half as compared to that for  .
.
6. Conclusion
In this paper, we have studied a continuous opinion dynamics model of Deffuant et al under bound confidence. The underlying interaction network is modeled by an one-dimensional multiplex network,  , with arbitrary ℓ layers. Based on the SAD process and probability theory, we obtained analytically the critical threshold dc for the opinion consensus, extending the previous results for simplex networks, i.e., the case of
, with arbitrary ℓ layers. Based on the SAD process and probability theory, we obtained analytically the critical threshold dc for the opinion consensus, extending the previous results for simplex networks, i.e., the case of  . Our key findings, that the increase of 'multiplexity' hinders the opinion formation and the aggregated simplex network loses essential information, suggests a vital topological factor in opinion formation and further deepens our understanding of the multilayer impact on network dynamics. Our theoretical derivations are confirmed by extensive numerical simulations.
. Our key findings, that the increase of 'multiplexity' hinders the opinion formation and the aggregated simplex network loses essential information, suggests a vital topological factor in opinion formation and further deepens our understanding of the multilayer impact on network dynamics. Our theoretical derivations are confirmed by extensive numerical simulations.
For future research, we note that the question put forward in [38] regarding the critical case  remains open. Moreover, we believe it is hopeful to deal with the higher-dimensional lattice
remains open. Moreover, we believe it is hopeful to deal with the higher-dimensional lattice  for
for  by extending the framework developed here. However, the case of D = 1 with one or two boundaries, e.g.,
by extending the framework developed here. However, the case of D = 1 with one or two boundaries, e.g.,  or
or  , may pose much greater challenges with exact confidence threshold being difficult to obtain. Towards more realistic network structure of populations, such as random networks and scale-free networks, a plausible intermediate step is to consider tree networks (Notice that the key SAD process has been studied in the case of Cayley tree in [39]).
, may pose much greater challenges with exact confidence threshold being difficult to obtain. Towards more realistic network structure of populations, such as random networks and scale-free networks, a plausible intermediate step is to consider tree networks (Notice that the key SAD process has been studied in the case of Cayley tree in [39]).
Acknowledgments
This work has been supported by the Program for Young Excellent Talents in Tongji University (2014KJ036) and by Shanghai Pujiang Program (15PJ1408300). The author would like to thank the anonymous referees and the editor who provided valuable comments and advices resulting in improvements of this paper.
Appendix
In the appendix, we review the SAD process proposed in [38], which turns out to be closely related with the Deffuant model on  .
.
Let  be an integer. The SAD process, denoted by
be an integer. The SAD process, denoted by  , is a deterministic process defined iteratively as follows. Set
, is a deterministic process defined iteratively as follows. Set

For a given sequence of nodes  and
and ![$\mu \in (0,1/2]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn328.gif) , we obtain the configuration
, we obtain the configuration  for
for  by setting
by setting
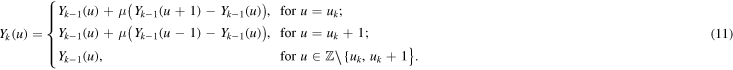
This procedure can be delineated as a liquid exchanging process on  . A glass is put at each site
. A glass is put at each site  . At k = 0 only the glass located at the origin is full (signified by 1) while all others are empty (signified by 0). At each subsequent step k, one picks two neighboring glasses at uk and
. At k = 0 only the glass located at the origin is full (signified by 1) while all others are empty (signified by 0). At each subsequent step k, one picks two neighboring glasses at uk and  , and pouring liquids from the glass with higher level to that with lower level by a relative amount μ. This leads to the SAD process. The following lemma can be easily shown.
, and pouring liquids from the glass with higher level to that with lower level by a relative amount μ. This leads to the SAD process. The following lemma can be easily shown.
Fix  and consider our opinion model on
and consider our opinion model on  . Note that there exists a finite interval
. Note that there exists a finite interval ![$[{u}_{\alpha },{u}_{\beta }]\subseteq {\mathbb{Z}}$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn339.gif) containing 0 such that the Poisson events on the boundary edges
containing 0 such that the Poisson events on the boundary edges  and
and  for all
for all  have not happened yet up to time t. Let N be the number of opinion adjustments occur in
have not happened yet up to time t. Let N be the number of opinion adjustments occur in ![$[{u}_{\alpha },{u}_{\beta }]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn343.gif) up to time t. The times of these adjustments are arranged in the chronological order as
up to time t. The times of these adjustments are arranged in the chronological order as
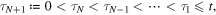
where we set  for convenience. For
for convenience. For  , we write uk as the left endpoint of the edge
, we write uk as the left endpoint of the edge  for which uk and
for which uk and  adjust opinions at time
adjust opinions at time  . Given the sequence
. Given the sequence  (in this order) and
(in this order) and ![$\mu \in (0,1/2]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn350.gif) , we obtain a SAD process
, we obtain a SAD process  as defined by (10) and (11).
as defined by (10) and (11).

In particular,  .
.
Lemma A2 can be proved through induction over k similarly as [38, lemma 3.1]. It unveils that the opinion at the origin can be expressed as a linear combination of initial opinions over nodes of  , with coefficients given by the associated SAD process.
, with coefficients given by the associated SAD process.



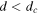

![$\{| {X}_{\infty }(u)-{X}_{\infty }(u+1)| \}\in \{0\}\cup [d,1]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn54.gif)
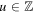
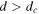
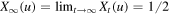
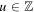
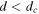
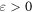
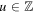
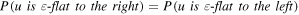


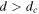
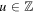
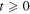

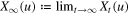
![$\{| {X}_{\infty }(u)-{X}_{\infty }(u+1)| \}\in \{0\}\cup [d,1]$](https://content.cld.iop.org/journals/1751-8121/48/39/395101/revision1/jpa518916ieqn270.gif)