Reply to 'No correction for the light propagation within the cube: Comment on Relativistic theory of the falling cube gravimeter'^*

The phase of the reflected signal derived in [1] comes from a detailed relativistic analysis of signal phase arriving at the point of recombination of the test and reference beams in an absolute gravimeter, and provides an alternative to the currently used or 'standard' approach [3]. The 'corrections' calculated in [1] represent differences between two models of the retroreflector: one model characterized by parameters 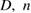$D, \ n$, and d, which are respectively the cube depth, refractive index, and distance of the face from the center of mass (COM), and a model with D  =  d  =  0 corresponding to reflection from the face. The difference arises when these two models are used to fit the same data—other conditions remaining unchanged—and the results quoted are large enough to show that the index of refraction and other retroreflector properties should be accounted for in fitting data from absolute gravimeters.

The comment states that the correction translates the gravity value to the point above the cube's COM by the distance Dn  −  d. However, such a point would be in motion, would not give a unique value for g, and is inconsistent with the definition of g used in [1]. The gravity value referred to in the original paper [1]is the value at Z  =  0, the point of recombination. This can be seen from the form of the gravitational potential as a function of the vertical coordinate Z, in equation (1) of [1].

After quoting the phase of the signal at the beamsplitter from the paper [1], the comment multiplies the interference signal by 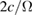$2 c/\Omega$ where Ω is the angular frequency of reference beam light, thus deriving a quantity called 'the position of the cube at the moment 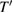$T'$ (equation (3) of [2]). This is a fictitious position, since the interference signal is generated at the origin Z  =  0. The calculation is based on the idea that successive interference fringes correspond to changes in position of the point of reflection by a half wavelength. The times T are times of arrival at the reference origin Z  =  0, whereas the fictitious retroreflector position is at some height 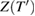$Z(T')$ above the beamsplitter at which there is no reference beam to generate an interference signal. If this cube position had meaning, the position would have to be related to the COM position by no more than an added constant. This is not so, as can be seen by comparing the COM position, used repeatedly in [1]—

$$\begin{align} \newcommand{\bi}{\boldsymbol} \newcommand{\e}{{\rm e}} \displaystyle \label{composition} Z_{cm}(T)=Z_0+V_0T-\frac{1}{2}g T^2+\gamma \bigg(\frac{1}{2} Z_0 T^2+\frac{1}{6}V_0 T^3-\frac{1}{24} g T^4\bigg) \nonumber \end{align} \tag{ 1 }$$

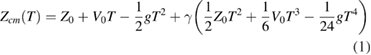
—with equation (2) of [2], which has additional time-dependent terms. The main conclusion of the comment, as expressed in its title, is thus without justification.

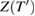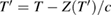However, following this line of argument leads to an interesting result. Let us account for retardation by assuming that at moving position $Z(T')$ a wavefront of phase $\phi(T')$ is emitted and travels with speed c through vacuum to the detector, where it arrives at time T later. The retarded time is determined implicitly by $T'=T-Z(T')/c$. Let the interference phase at the detector be the function $\phi_0(T)$ as provided in equation (33) of [1] and quoted in the comment [2], equation (1) with the reference phase removed. The phase at emission would be

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \phi(T') = \phi_0(T)=\phi_0(T'+Z(T')/c). \nonumber \end{align} \tag{ 2 }$$

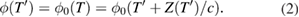
Proceeding as in the comment, we identify the position $Z(T')$ as

$$\begin{align} \newcommand{\bi}{\boldsymbol} \newcommand{\e}{{\rm e}} \displaystyle Z(T')=\frac{c \phi(T')}{2\Omega} =\frac{c}{2\Omega}\bigg(\phi_0(T')+\frac{{\rm d}\phi_0(T')}{{\rm d}T'}\frac{Z(T')}{c}\bigg). \nonumber \end{align} \tag{ 3 }$$

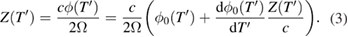
This leads to

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle Z(T')=\frac{c}{2\Omega}\frac{\phi_0(T')}{1-\frac{1}{2 \Omega}\frac{{\rm d}\phi_0(T')}{{\rm d}T'}}. \nonumber \end{align} \tag{ 4 }$$

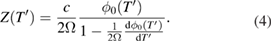
Carrying out this calculation, we obtain for the fictitious position

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \label{fictitiousposition} Z(T')=Z_{cm}(T')+D n-d+O(c^{-2}). \nonumber \end{align} \tag{ 5 }$$

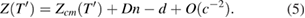
This result would have been obtained in the comment [2], if retardation had been included. The form of equation (5), above, fully supports the conclusion in [1] that properties of the retroreflector are important in absolute gravimeters. Equation (5) suggests there is a hypothetical surface at distance 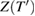$Z(T')$ above the COM, from which the phase at the detector can be obtained by application of a simple retardation calculation with light speed c. The hypothetical phase at this surface at time 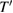$T'$ would be

$$\begin{align} \newcommand{\bi}{\boldsymbol} \newcommand{\e}{{\rm e}} \displaystyle \phi(T')=\frac{2 \Omega}{c}\bigg(Z_{cm}(T')+D n -{\rm d}\bigg) \nonumber \end{align} \tag{ 6 }$$

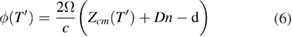
and, if transferred to the origin at Z  =  0 with speed c using retarded time, yields 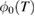$\phi_0(T)$. This compact characterization of the interference signal in [1] works very well. The fictitious position is above the COM and in fact, above the cube.

The constant in equation (5) contains all the corrections discussed in [1], and provides a useful example of the problem of matching two polynomials in the present context. We ask, in a model based on equation (5), what corrections 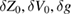$\delta Z_0, \delta V_0, \delta g$ arise compared to simply using a model based on the uncorrected COM position, equation (1)? This leads to the condition

$$\begin{align} \newcommand{\bi}{\boldsymbol} \newcommand{\e}{{\rm e}} \displaystyle \label{correctionconditions} &Dn -d+\delta Z_0+\delta V_0 T-\frac{1}{2}\delta g T^2 \nonumber \\ & +\frac{\gamma}{24} \big(12 \delta Z_0 T^2+4 \delta V_0 T^3-\delta g T^4\big)=0. \nonumber \end{align} \tag{ 7 }$$

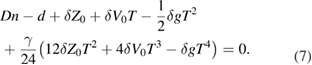
This is a polynomial of order four involving five coefficients, while only three quantities are being determined. However, 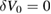$\delta V_0=0$ removes the two terms in equation (7) that are odd in T; the constant term gives 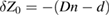$\delta Z_0=-(Dn-d)$, and the quadratic term gives 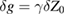$\delta g=\gamma \delta Z_0$. The residual quartic term is 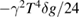$-\gamma^2 T^4 \delta g/24$. This term is of second order in γ and is extremely small; even for $T=1\ {\rm s}$, it is less than 10⁻¹⁴ meters. Such terms have been systematically neglected throughout [1]. This explains how two fourth-order polynomials can be matched, with more than adequate precision, with only three quantities. The issue was already discussed near the end of section 7 in [1]. Thus, there is no basis for the suggestion in the comment, that a mistake was made in the fitting routines; this is extremely unlikely anyway because of the agreement between the fitting of data for thousands of drops and the algebraic calculations carried out independently.

In sum, the suggestion in the comment that it is not necessary to consider retroreflector properties in fitting data from absolute gravimeters has been shown to be invalid. Other statements in the comment have been responded to; in particular, it has been explained how for this theory only three parameters are precisely determined by matching fourth-order polynomials. A compact characterization of the interference signal has been presented. No errors or substantive criticisms of the original paper [1] as claimed in the comment [2] are justified.