Abstract
A simple and effective fiber implementation of the BB84 protocol is proposed, which does not use phase modulators at the receiving side and do not require adjustment of the polarization state at the output of the communication channel. The implementation of the protocol permits to prove of the secrecy of keys based on the fundamental entropic uncertainty relations. The secret key length is expressed only in terms of the values observed on the reception side, with various detector parameters, such as quantum efficiency and the probability of dark counts, are taken into account automatically for the secret key length, but implicitly in terms of the observed parameters.
Export citation and abstract BibTeX RIS
1. Introduction
To date, a large number of quantum cryptography protocols and their experimental implementations have been proposed. The most commonly used protocol is BB84 [1]. The main requirement for quantum cryptography systems is provable or unconditional secrecy of distributed keys, which should be based only on the fundamental limitations of quantum theory. Evidence claiming unconditional secrecy of keys should not be based on demonstrating the secrecy of keys regarding specific attacks, but on demonstrating secrecy regarding all attacks. For the case of a strictly single-photon source of quantum states, the proofs that guarantee unconditional secrecy of keys are based on the fundamental entropy uncertainty relations. These ratios take into account all sorts of attacks and allow us to estimate the upper limit for information leaks to the eavesdropper without going through various attacks. However, not for all protocols of quantum key distribution, even in the single-photon case, is it possible to use the entropy uncertainty relations.
The use of entropic uncertainty relations implicitly implies the possibility of reducing the protocol to the so-called EPR (Einstein–Podolsky–Rosen) version (see, for example, [2]), which is not possible for all protocols.
In a real world, quantum states are quasi-single photon ones, or more precisely, strongly attenuated coherent states of laser light. In the case of coherent states, the reduction of the protocol to the EPR version turns out to be impossible. In this case, in the presence of inevitable losses in the communication channel and using not a strict single-photon source, a number of attacks occur, which were absent in the single-photon case. Such attacks are PNS attacks (photon number splitting) [3], which uses Poisson statistics on the number of photons in measuring coherent states, and attacks with UM measurements (unambiguous measurements, often called the USD attack—unambiguous states discrimination). This attack uses the fact of linear independence of coherent information states.
Protocols have been proposed that would be robust with respect to the attacks mentioned. These are protocols DPS [4], COW [5], decoy state method [6, 7], and protocol with a reference state [8], which were supposed to ensure the secrecy of keys in the presence of large losses in the channel.
However, for a number of protocols, due to the distributed coding method, it has not yet been possible to find proof of unconditional secrecy even in the single-photon case, since these protocols cannot be reduced to the EPR version.
The most commonly used is the so-called decoy state method for detecting a portion of the attacks mentioned. However, as was shown in [9], this method is also not universal, since it is not sensitive to the BS (beam split) attack, which limits the transmission distance of secret keys compared to PNS attacks. Note that the BS attack is applicable to all protocols using attenuated coherent states.
The decoy state method, which is reduced to random modulation of the intensity of coherent states, is used in a number of protocols. The secrecy of the keys is 'recruited' from the fraction of the single-photon component in coherent states, the value of which is estimated from the change in the statistics of samples on the receiving side for states with different average number of photons. Parcels with multi-photon components are considered known to the eavesdropper and do not contribute to the secret key.
Thus, in order to prove the secrecy of keys, it is necessary to have an exact proof of unconditional secrecy for single-photon states, which is based on fundamental principles—on the entropy uncertainty relations. The lack of evidence of unconditional secrecy reduces the value of the protocol.
The next important condition is the simplicity of the technical implementation of the protocol. Communication channels use standard single-mode fiber, which does not maintain polarization. Almost all systems use phase coding, in which Mach–Zander or Michelson interferometers are inevitably present on the receiving side. The use of active elements on the receiving side, such as phase modulators that are polarization sensitive, leads to the fact that one needs to adjust the polarization state at the output of the communication channel.
In paper [10], implementations of the QKD system were proposed in which the interferometer was made with Faraday mirrors and in which there are no polarization-sensitive phase modulators, therefore, no adjustment of the polarization state [10] at the output of the communication channel is required.
However, the 'price' for the lack of adjustment of the polarization state and phase modulators is a reduced version of the BB84 protocol. Such a reduced version of the BB84 protocol exploits three states instead of four, as it was suggested in the original version of BB84. Namely, two states are informational, and one state is control one [10]1.
For a reduced version of the BB84 protocol with three, instead of four states in two bases, it is impossible to use the entropy uncertainty relations, so the secrecy of keys in the single-photon case has to be proved by explicitly constructing specific attacks [2]. Building explicit attacks does not guarantee the absolute secrecy of the protocol, since one can never be sure that there are no other attacks even in the single-photon case, which allows the eavesdropper to get more information with the same observed error.
The next requirement for the protocol is that the estimation of the length of the secret key should not explicitly include such system parameters as quantum efficiency and dark counts from avalanche detectors. The secret key length should depend only on the observed parameters—i.e. from the total number of counts and the number of erroneous counts measured in each basis. Of course, the number of erroneous and correct counts depends on the parameters of the detectors, but obviously the parameters themselves should not be included in the formula for the secret key length, and even more so, the counts due to dark counts cannot be subtracted from the total number of counts.
This paper proposes a simple and effective implementation of the BB84-based protocol, which does not require the following.
- (1)Adjustment the state of polarization at the exit of the communication channel.
- (2)Does not use active elements (phase modulators, polarization controllers) at the receiving side.
- (3)Implements the complete, but not reduced version of the BB84 protocol.
- (4)It is fundamentally important that the protocol, when proving secrecy in a single-photon case, can be reduced to the EPR version, which makes it possible to use the fundamental entropy uncertainty relations, which guarantees unconditional secrecy regarding any attacks.
- (5)As a consequence of the using the entropy uncertainty relations, the estimate of the length of the secret key includes only the observed parameters of the classical Alice–Bob channel, which takes place after the measurements of Bob. Estimation of the the secret key length automatically takes into account the fact that avalanche detectors have different parameters—quantum efficiencies and dark counts rate, and explicitly these parameters are not included in the length of the key.
2. Informational states
To prove the secrecy of a protocol using entropy uncertainty relations, it is necessary to use the EPR version of the protocol. In this version, the information states are obtained by measuring over the EPR pair. Alice is preparing an ESR pair. Alice retains her subsystem, and sends the second subsystem to Bob through a quantum communication channel. This subsystem is available to attack the eavesdropper. Next, Alice performs measurements in one of two bases, which are chosen randomly and equiprobably. As a result of measurements, the subsystems of Alice and Bob are in the same states. One of the two states depends on the choice of the basis of measurements. The basis of measurements on the receiving side is chosen by Bob irrespective of the choice of basis by Alice. Alice's measurement basis is reported to Bob only after his measurements. Reduction of the protocol to the EPR version is an exclusively formal technique that allows us to use the entropy uncertainty relations. The EPR version of the protocol is equivalent to the version with preparation and sending of states by Alice to Bob. However, not every protocol can be reduced to the EPR version, and then the entropy uncertainty relations can be used. The protocol must have two bases, the states in which can be obtained from a single EPR pair.
The representation of the same EPR state of a pair in different bases is
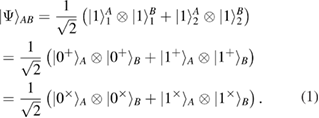
Two measurement bases are used. Information states in the two bases + and  are
are

here we have introduced the notation 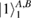 and
and 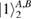 Fock single-photon states localized in time windows 1 and 2 (see figure 1(a)). As can be seen from (2), the states within each basis are orthogonal, the states between the bases are pairwise nonorthogonal.
Fock single-photon states localized in time windows 1 and 2 (see figure 1(a)). As can be seen from (2), the states within each basis are orthogonal, the states between the bases are pairwise nonorthogonal.
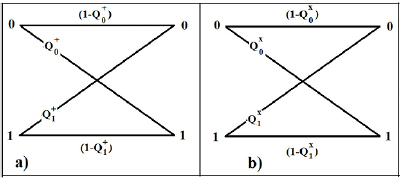
Figure 1. Figure (a) experimental implementation of the protocol. L—laser, MI—intensity modulator, PM—phase modulator, Circ—circulator, SPAD1,2—single-photon avalanche detectors, FM—Faraday mirrors, PZ—controlled piezoelectric element. Informational states in different bases are also shown. The calculation of the optical scheme is given in [11]. Figure (b) shows the state in different time slots after conversion on the interferometer. If the basis + is randomly selected, information states are recorded by gating both detectors in time window 2. When choosing the base  , the information states are recorded by gating both detectors equally likely in time slots 1 or 3.
, the information states are recorded by gating both detectors equally likely in time slots 1 or 3.
Download figure:
Standard image High-resolution imageEve is only available subsystem B. After Eve's attack, the state (1) becomes equal
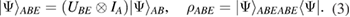
Here we emphasize that, precisely, this choice of information states provides a simple and effective experimental implementation of the quantum key distribution protocol, which does not require active elements on the receiving side and does not require adjustment of the polarization state at the output of the communication channel (see figure 1(a)).
The measurements are given by the identity resolution in one of two bases. Thus we have

The measurements (4) of Alice over the density matrix (3) in the bases (2) lead to a reduced density matrix. So one can find
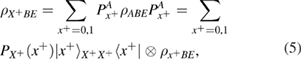
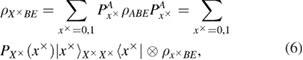
where
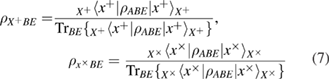
in formulas (5)–(7) the following notation is entered

Expressions (8) have the meaning of a priori probabilities at the entrance to the quantum communication channel for symbols 0 and 1 in the corresponding bases.
3. Measurements at the receiving side
Before the Bob measurement at the receiving side, the input states are transformed on the Mach–Zander interferometer (although this interferometer is often called the Michelson interferometer), made using Faraday mirrors. It was previously shown that in such an interferometer interference is provided without adjusting the polarization state at the output of the communication channel (see details of the calculation of the optical receiving part in [11]).
After the input states are transformed, detection occurs by gating the detectors in a specific time slot, depending on the choice of basis by Bob (see figure 1(b)) and an explanation for it).
The Bob measurements lead to the following density matrices in the + basis
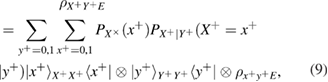
similarly in basis 
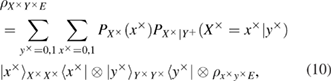
in formulas (9) and (10) we introduced the following notation
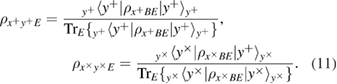
After measurements on the receiving side, Alice and Bob are connected by a binary, generally asymmetrical, classical communication channel (see figure 2) with transition probabilities
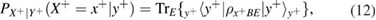
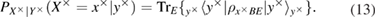
Figure 2. A schematic representation of the binary classical communication channels that arise between Alice and Bob after measuring Bob and disclosing the bases. Transient probabilities (a)—basis +, (b)—basis 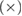 are also shown, which are associated with the observed errors on the receiving side.
are also shown, which are associated with the observed errors on the receiving side.
Download figure:
Standard image High-resolution imageThe asymmetry of the Alice–Bob communication channel arises, among other things, due to the different characteristics of avalanche single-photon detectors.
Finally, for density matrices in different bases, we find
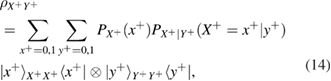
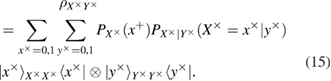
Transition probabilities in f-las (12)–(15) are expressed through the observed errors in the Alice–Bob communication channel (see figure 2)
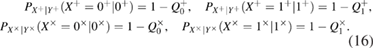
The summation rule for conditional (transitional) probabilities is
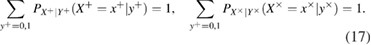

4. Entropy uncertainty relations, asymptotic limit
The entropy uncertainty relations link the conditional entropies of Alice–Eve and Alice–Bob in different bases. In the asymptotic limit of long sequences, the parameters of the classical Alice–Bob channel are known exactly, therefore the conditional Shannon entropies of Alice–Bob after the measurements of Bob are also known precisely. We have (see details in [12])
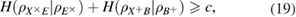
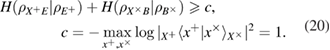
As usual
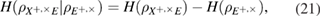
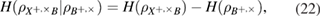
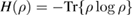 —,
—,
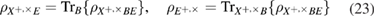
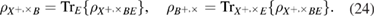
5. Estimation of the secret key length in the asymptotic limit
We write the expression for estimating the key length in the basis of +, taking into account (19) and (20), we have (see details in [13])

where n is the number of registered parcels in the basis of +. A similar expression holds for the key length 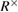 in the basis
in the basis 
It is important to note that in (25) it is implicitly implied that the number of registered n parcels in each basis is the same. Note that in the formula (25) inequality was used
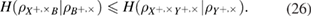
The length of the secret key in the asymptotic limit turns out to be the same in both bases + and  . Informally,
. Informally,  in (25) has the meaning of a lack of information in the bits of Bob's Alice bit string, provided that Bob has at his disposal a quantum system correlated with Alice's string.
in (25) has the meaning of a lack of information in the bits of Bob's Alice bit string, provided that Bob has at his disposal a quantum system correlated with Alice's string.
Errors can be different in different bases, and the channel, in general, within a single basis is asymmetric with respect to 0 and 1 (figure 2).
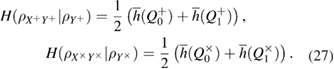
Finally, to estimate the total length of the secret key in two bases in terms of each registered package, we get
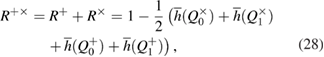
where notation is entered

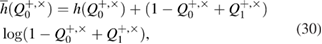
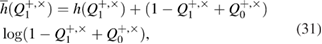
in the case of a binary symmetric classical communication channel Alice–Bob, 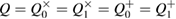 , the estimate for the secret key length is reduced to the known formula
, the estimate for the secret key length is reduced to the known formula
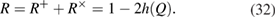
Note that in formulas (28) and (32) it is assumed that the number of registered n packages in different bases is the same. If the number of registered parcels is different, then as n you need to take the smallest value.
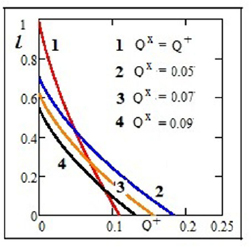
An example of the dependences of the length of the secret key as a function of the error is shown in figure 3.
Figure 3. Dependencies of the of secret bits per position as a function of 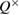 error in one of the bases. The error Q+ in another basis is taken as a parameter, the parameter values are shown in figure Channels in each basis were considered to be symmetrical.
error in one of the bases. The error Q+ in another basis is taken as a parameter, the parameter values are shown in figure Channels in each basis were considered to be symmetrical.
Download figure:
Standard image High-resolution imageIt is interesting to estimate at what value of the average number of photons in the coherent state the critical error (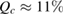 ) in the symmetric case (
) in the symmetric case (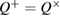 ) is achieved. The error on receiving side
) is achieved. The error on receiving side 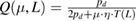 , where
, where 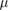 —for a single-photon component, the typical quantum efficiency of the detector is
—for a single-photon component, the typical quantum efficiency of the detector is 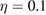 , and the probability of dark counts per strobe is
, and the probability of dark counts per strobe is 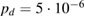 ,
,  —single-mode fiber channel transmission, typical single-mode fiber loss factor
—single-mode fiber channel transmission, typical single-mode fiber loss factor 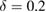 dB km−1, L—the length of the communication channel. Under a channel length of L = 100 km the critical error value is reached when
dB km−1, L—the length of the communication channel. Under a channel length of L = 100 km the critical error value is reached when 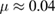 ,
, 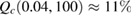 .
.
6. Estimation of the length of the secret key with finite sequences
According to [13], the key secrecy criterion is formulated in terms of the trace distance. Let n the length of the raw key be the length of the bit sequence after matching the bases.
It was previously shown [13] that the trace distance is limited from above
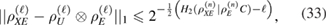
where C is the totality of classical information used in error correction,  —second-order Renyi entropy [13],
—second-order Renyi entropy [13],  is the density matrix of Eve's quantum system before error correction.
is the density matrix of Eve's quantum system before error correction.
Formula (33) implies that the density matrix 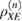 is known exactly. For legitimate users, the only value from which the density matrix can be estimated is the observed number of errors
is known exactly. For legitimate users, the only value from which the density matrix can be estimated is the observed number of errors 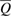 . Based on the observed number of errors, it is possible to estimate the density matrix with only some variation. By these words, it is actually understood that the accuracy of determining the density matrices is fixed by some set of them. All that can be guaranteed is that the observed number of errors occurred from the measurement of density matrices from a given set with a probability of at least
. Based on the observed number of errors, it is possible to estimate the density matrix with only some variation. By these words, it is actually understood that the accuracy of determining the density matrices is fixed by some set of them. All that can be guaranteed is that the observed number of errors occurred from the measurement of density matrices from a given set with a probability of at least 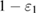 . The required probability (accuracy) of
. The required probability (accuracy) of 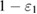 is given by legitimate users.
is given by legitimate users.
The min entropy contains all the information about the attacks of Eve, by definition [13], we have
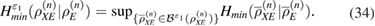
Here, 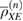 is a set of density matrices that ensure that an observable number of errors occur in their measurement with a probability of at least
is a set of density matrices that ensure that an observable number of errors occur in their measurement with a probability of at least 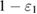 .
.
Smooth max entropy is directly related to the number of errors on the receiving side, and gives the minimum number of bits that are required to correct errors with a probability of success of at least  . By definition [13]
. By definition [13]
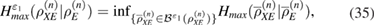
where the upper and lower faces are taken from the  density matrices—close in the sense of trace distance,
density matrices—close in the sense of trace distance, 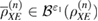 ,
, 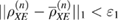 .
.
Further, in view of (34), using a chain of inequalities [13], we have
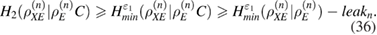
In fact, this means that a maximum is reached on the density matrix 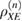 , since the space is finite-dimensional and compact, then
, since the space is finite-dimensional and compact, then  . Further, C is the entire set of classical information used in error correction, where
. Further, C is the entire set of classical information used in error correction, where 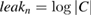 is information in bits output through the open channel during error correction. If you include information in the leak, information to verify the identity of Alice's and Bob's cleaned keys, leakn is replaced by
is information in bits output through the open channel during error correction. If you include information in the leak, information to verify the identity of Alice's and Bob's cleaned keys, leakn is replaced by 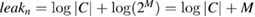 , where M is the number of bits output by Alice and Bob through an open communication channel when verifying the identity of cleared keys.
, where M is the number of bits output by Alice and Bob through an open communication channel when verifying the identity of cleared keys.
Taking (36) into account, one can pass from the second-order Renyi entropy to the minimum entropy (see details in [13] section 5.6), we have
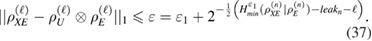
If the length of the secret key 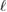 is
is

This fulfills the secrecy criteria (33). Keys that satisfying condition (33) are usually called  —secret2.
—secret2.
7. Entropy uncertainty relations for smooth quantum conditional min and max entropies
The entropy uncertainty relations for smooth entropies eliminate the finding of the optimal eavesdropper attack, but do not eliminate the need to know the density matrix itself. 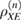 . Evaluation of information leakage to Eve is made through the evaluation of the smooth conditional classical max entropy Alice–Bob, which is estimated from the observed number of errors. The lower bound for
. Evaluation of information leakage to Eve is made through the evaluation of the smooth conditional classical max entropy Alice–Bob, which is estimated from the observed number of errors. The lower bound for 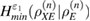 can be obtained only from the number of errors at the receiving using the entropy uncertainty relations [14], we have
can be obtained only from the number of errors at the receiving using the entropy uncertainty relations [14], we have
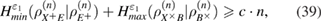
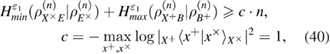
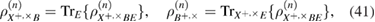
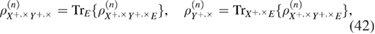
where 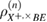 —the joint density matrix Alice–Bob–Eve in the corresponding basis before the measurements of Bob, and
—the joint density matrix Alice–Bob–Eve in the corresponding basis before the measurements of Bob, and 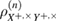 —the density matrix Alice–Bobs after Bob's measurement. The bob bit string containing errors
—the density matrix Alice–Bobs after Bob's measurement. The bob bit string containing errors 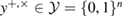 in the corresponding basis. In the same way as in (19) and (20) there are inequalities
in the corresponding basis. In the same way as in (19) and (20) there are inequalities
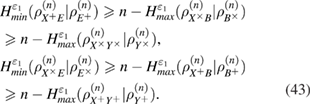
Once again, we note that the number of registered packages n in (43) is assumed to be the same in different bases.
8. Estimation of the probability of error by observable parameters
Usually, to estimate the probability of error, a part of the registered sequence is disclosed and the observed number of errors is calculated in the opened part, from which an estimate is made about the true probability of errors. Further, according to this estimate of the error probability, the smooth max entropy is estimated.
We will follow a slightly different logic on estimating the probability of error. Adaptive error correction procedures based on LDPC codes [15, 16] allow you to immediately begin error correction without first estimating the error probability, i.e. without actually disclosing part of the registered parcels.
Alice sends the states corresponding to 0 and 1 in different bases with equal probability. Due to the different quantum efficiency of two avalanche detectors, different numbers of 0 and 1 can be registered. We denote these numbers as 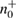 ,
, 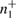 ,
,  ,
, 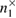 , inside each basis. At the same time, the uncertainty ratios (39), (40) and (43) include the same number of recorded parcels in different bases, so it is inevitable that the number of registered parcels must be equalized.
, inside each basis. At the same time, the uncertainty ratios (39), (40) and (43) include the same number of recorded parcels in different bases, so it is inevitable that the number of registered parcels must be equalized.
The alignment procedure is as follows. After the transmission of a series of states, Bob informs Alice of the position of the parcels, where he registered the counts and which measurement basis he chose. The values of the bits in each position are kept secret. Further, knowing the number of registered positions in each basis for 0 and 1 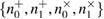 , Alice determines the number of positions
, Alice determines the number of positions 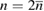 to be used to get the key
to be used to get the key 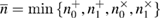 .
.
Extra positions are randomly discarded by Alice during the alignment, and the numbers of the positions being discarded are reported to Bob. After this stage, the number of packages in each basis is the same. After that, Alice and Bob correct the errors. As a result, the sequence length remains 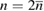 in each basis, namely, this sequence length appears in the formulas below.
in each basis, namely, this sequence length appears in the formulas below.
After error correction, a procedure is performed to verify the identity of the cleared keys between Alice and Bob. For example, the M multiplication rounds of the cleared key with the public random common bit string of Alice and Bob, which is transmitted through the open classical communication channel, and the subsequent calculation of the parity bit in each round, guarantee that the parity bits match if the cleared keys match 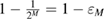 .
.
After error correction, Bob knows the number of corrected positions, as well as the number of corrections 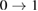 and the number of corrections
and the number of corrections  in each of the bases. Knowing the number of corrections, Bob can get an estimate of transition probabilities in the Alice–Bob channel, which allows him to get an estimate of the parameters of the Alice–Bob channel
in each of the bases. Knowing the number of corrections, Bob can get an estimate of transition probabilities in the Alice–Bob channel, which allows him to get an estimate of the parameters of the Alice–Bob channel 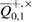 (see figure 2).
(see figure 2).
Under the approach used, the observed number of errors 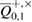 on the receiving side allows Alice and Bob to obtain an estimate of the parameter
on the receiving side allows Alice and Bob to obtain an estimate of the parameter  , which appears in the entropy uncertainty relations (39), (40) and (43).
, which appears in the entropy uncertainty relations (39), (40) and (43).
Let uss keep the designation for the number of registered parcels in each basis after alignment: 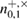 —the number of registered packages on the receiving side, for example,
—the number of registered packages on the receiving side, for example, 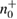 is the number of registered packages by Bob on the basis of +, when Alice sent the states 0+ . After the error correction stage, Bob knows the total number of registered packages
is the number of registered packages by Bob on the basis of +, when Alice sent the states 0+ . After the error correction stage, Bob knows the total number of registered packages 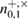 for each bit, respectively, knows the number of corrected positions in each sequence
for each bit, respectively, knows the number of corrected positions in each sequence 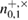 parcels, i.e. can find an estimate of the magnitude of the error
parcels, i.e. can find an estimate of the magnitude of the error 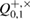 in each sequence. This information is enough for Bob to get an estimate of the error probability
in each sequence. This information is enough for Bob to get an estimate of the error probability 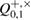 with an accuracy of the width of the confidence interval
with an accuracy of the width of the confidence interval ![$Q^{+,\times}_{0,1}\in [\overline{Q}^{+,\times}_{0,1}-\delta, \overline{Q}^{+,\times}_{0,1}+\delta]$](https://content.cld.iop.org/journals/1612-202X/16/7/075203/revision1/lplab189bieqn067.gif) . The width of the confidence interval
. The width of the confidence interval 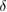 is chosen by Alice and Bob.
is chosen by Alice and Bob.
Fixing the width of the confidence interval 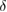 ensures that the probability of an event
ensures that the probability of an event ![$ \overline{Q}^{+, \times}_{0,1} \in [Q^{+, \times}_{0,1} - \delta, Q^{+, \times}_{0,1} + \delta] $](https://content.cld.iop.org/journals/1612-202X/16/7/075203/revision1/lplab189bieqn070.gif) not less than
not less than 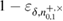 . Accordingly, the probability of occurrence of a larger (or smaller) number of errors will be no more than
. Accordingly, the probability of occurrence of a larger (or smaller) number of errors will be no more than 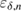 , when calculating the conditional probability for a given parameter
, when calculating the conditional probability for a given parameter 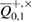 used inequality [17], we find,
used inequality [17], we find,

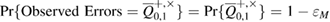 —the probability that the observed number of errors in Bob's error correction is
—the probability that the observed number of errors in Bob's error correction is 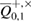 really coincides with the true number of errors. Since the correction code may not completely correct the errors, but the identity verification procedure will not notice this with a probability of no more than
really coincides with the true number of errors. Since the correction code may not completely correct the errors, but the identity verification procedure will not notice this with a probability of no more than 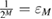 . Do not confuse the observed number of errors in Bob
. Do not confuse the observed number of errors in Bob 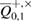 with the true number of errors in this series, as well as with true parameters of the channel Alice and Bob
with the true number of errors in this series, as well as with true parameters of the channel Alice and Bob 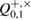 .
.
Then 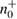 ,
, 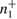 ,
, 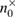 ,
, 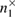 —registered sequences 0 and 1 in different bases,
—registered sequences 0 and 1 in different bases,  true values of Alice–Bob channel parameters, and
true values of Alice–Bob channel parameters, and 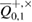 are the observed parameters of the Alice–Bob channel (figure 2) that Bob receives after error correction, and
are the observed parameters of the Alice–Bob channel (figure 2) that Bob receives after error correction, and  ,
, 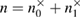 ,
, 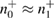 ,
, 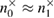 .
.
The estimation of the error probability in the Alice–Bob channel (figure 2) is performed separately in each basis and separately for each sequence of bits from 0 and 1.
Knowing the error probability estimate makes it possible to calculate the lower bound for smooth max entropy,
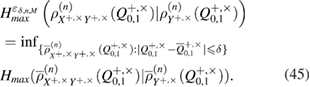
9. Calculation of min and max entropy, secret key length
We use the statistical interpretation (44) as applied to density matrices. Calculation of max entropy in (45) implies minimization of density matrices, which give the observed number of errors on the receiving side ![$ \overline{Q}^{+, \times}_{0,1} \in [Q^{+, \times}_{0,1} - \delta, Q^{+, \times}_{0,1} + \delta] $](https://content.cld.iop.org/journals/1612-202X/16/7/075203/revision1/lplab189bieqn089.gif) with a probability of at least
with a probability of at least 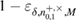 . Accordingly, the likelihood that the observed number of errors will come from
. Accordingly, the likelihood that the observed number of errors will come from ![$ \overline{Q}^{+, \times}_{0,1} \overline{\in} [Q^{+, \times}_{0,1} - \delta, Q^{+, \times}_{0,1} + \delta] $](https://content.cld.iop.org/journals/1612-202X/16/7/075203/revision1/lplab189bieqn091.gif) , no more than
, no more than 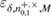 .
.
In fact, this means that any density matrix with the 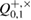 parameter from the confidence interval will give the observed number of errors
parameter from the confidence interval will give the observed number of errors ![$ \overline{Q}^{+, \times}_{0,1} \in [Q^{+, \times}_{0,1} - \delta, Q^{+, \times}_{0,1} + \delta] $](https://content.cld.iop.org/journals/1612-202X/16/7/075203/revision1/lplab189bieqn094.gif) with probability at least
with probability at least 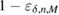 . At this point, a homogeneous estimate of the parameter
. At this point, a homogeneous estimate of the parameter 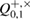 is important—the independence of the probability from the observed number of errors
is important—the independence of the probability from the observed number of errors 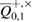 . Accordingly, in the opposite direction, the homogeneity of the assessment ensures that the probability the appearance of
. Accordingly, in the opposite direction, the homogeneity of the assessment ensures that the probability the appearance of 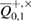 errors from the interval
errors from the interval ![$ \overline{Q}^{+, \times}_{0,1} \in [Q^{+ , \times}_{0,1} - \delta, Q^{+, \times}_{0,1} + \delta] $](https://content.cld.iop.org/journals/1612-202X/16/7/075203/revision1/lplab189bieqn099.gif) depends only on its width.
depends only on its width.
It was previously shown [18] that equality in entropy uncertainty relations in the asymptotic limit is achieved on density matrices that have the structure of a tensor product. An eavesdropping attack was also clearly built, respectively, the density matrix, on which the lower limit of the uncertainty relations is reached. There is a Bernoulli test scheme between Alice and Bob with parameters ![$Q^{+,\times}_{0,1}\in [\overline{Q}^{+,\times}_{0,1} - \delta, \overline{Q}^{+,\times}_{0,1}+\delta]$](https://content.cld.iop.org/journals/1612-202X/16/7/075203/revision1/lplab189bieqn100.gif) in the corresponding branches of the Alice–Bob channel. In this case, the calculation of max entropy on density matrices having the structure of a tensor product makes it possible to obtain more accurate estimates. When calculating the min entropy in (45) and (48), you can use the immediate estimate for the smooth max entropy. Conservatively, we assume that the parameter
in the corresponding branches of the Alice–Bob channel. In this case, the calculation of max entropy on density matrices having the structure of a tensor product makes it possible to obtain more accurate estimates. When calculating the min entropy in (45) and (48), you can use the immediate estimate for the smooth max entropy. Conservatively, we assume that the parameter 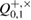 lies on the upper boundary of the confidence interval
lies on the upper boundary of the confidence interval 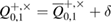 . Since the density matrices from this set have the structure of a tensor product, (see, details in [18])
. Since the density matrices from this set have the structure of a tensor product, (see, details in [18])

The reduced Bob's density matrix
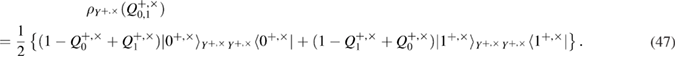
Conditional smooth max entropy is classic one
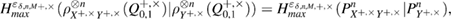
where distrubutions  —of sequences
—of sequences 
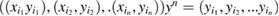 .
.
For calculations, it is more convenient to use the equivalent definition of smooth max entropy [19]

where the probability of the event is ![$ {{\rm Pr}} [\Omega]> 1 \,- $](https://content.cld.iop.org/journals/1612-202X/16/7/075203/revision1/lplab189bieqn106.gif)
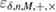 . The
. The 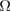 event is itself the intersection of events.
event is itself the intersection of events. 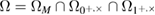 , where
, where 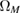 is an event that passed the test for verifying the identity of the cleared keys.
is an event that passed the test for verifying the identity of the cleared keys.
Event probability ![$ {{\rm Pr}} [\Omega_M]> 1 - \varepsilon_{M} $](https://content.cld.iop.org/journals/1612-202X/16/7/075203/revision1/lplab189bieqn111.gif) —passing the test means that the observed error rates
—passing the test means that the observed error rates 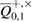 is really equal to the number of errors in Bob, i.e. all errors are fixed.
is really equal to the number of errors in Bob, i.e. all errors are fixed.
The events 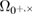 and
and 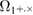 mean that the distributions with parameters from the confidence interval around the error rate
mean that the distributions with parameters from the confidence interval around the error rate 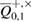 will give the number of errors not more than
will give the number of errors not more than 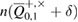 with probability at least
with probability at least ![$ {{\rm Pr}} [\Omega_{0^{+, \times}, 1^{+, \times}}]> 1- \varepsilon^{+, \times}_{0,1} $](https://content.cld.iop.org/journals/1612-202X/16/7/075203/revision1/lplab189bieqn117.gif) . As a result, the probability of an event
. As a result, the probability of an event 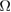
![${{\rm Pr}}[\Omega]>1 - \varepsilon_M-\varepsilon_{0^{+,\times}}-\varepsilon_{1^{+,\times}} = 1-\varepsilon_{\delta,n,M,+,\times} $](https://content.cld.iop.org/journals/1612-202X/16/7/075203/revision1/lplab189bieqn119.gif) .
.
The value (48) is the logarithm of the number of sequences, which with probability at least  give the observed error rate in sequences 0 and 1 in the bases + and
give the observed error rate in sequences 0 and 1 in the bases + and  .
.
In fact, the smoothing procedure is reduced to discarding unlikely events—sequences that can give a greater number of observed errors with a probability of no more than 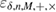 .
.
As a result, for smooth conditional max entropy, we obtain (see also [13])
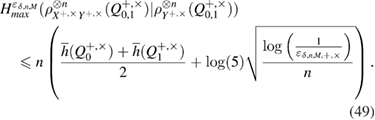
In view of (43) we find
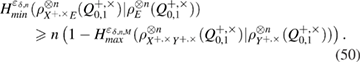
All functions in (49) and (50) are expressed in terms of the observed number of errors.  and the value of the confidence interval
and the value of the confidence interval  , which is selected by legitimate users and the secrecy parameter is determined
, which is selected by legitimate users and the secrecy parameter is determined 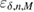 .
.
Taking into account (29)–(31), (49) and (50), we obtain an estimate for the total length of the secret key in both bases (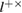 )
)

where 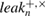 is the actual number of bits opened through the classical communication channel between Alice and Bob with error correction in the + and
is the actual number of bits opened through the classical communication channel between Alice and Bob with error correction in the + and  bases.
bases.
10. Conclusion
In conclusion, we note one important feature of the implementation of this protocol. Since the measurement of states in the  basis is not related to interference (see figure 1), there is no error in the measurement in this basis, which can occur due to inaccurate balancing of the interferometer. The error in this basis in the absence of an eavesdropper is associated only with dark counts of the detectors. For this reason, an error in this basis may exceed a critical value in
basis is not related to interference (see figure 1), there is no error in the measurement in this basis, which can occur due to inaccurate balancing of the interferometer. The error in this basis in the absence of an eavesdropper is associated only with dark counts of the detectors. For this reason, an error in this basis may exceed a critical value in 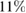 , which occurs in the symmetric case. For example, if the error is
, which occurs in the symmetric case. For example, if the error is 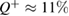 in the basis of + (which corresponds to the visibility of the interferometer only
in the basis of + (which corresponds to the visibility of the interferometer only 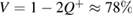 ), and if there is an error in the basis
), and if there is an error in the basis  in
in 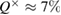 , it is still possible to get the secret key that the protocol does more sustainable when implemented.
, it is still possible to get the secret key that the protocol does more sustainable when implemented.
Acknowledgments
We thank our colleagues from the Academy of Cryptography of the Russian Federation for discussions and support. The author also thanks I M Arbekov, K A Balygin, S P Kulik and A N Klimov for numerous discussions. The work was supported by a grant from the the RSF (no. 16-12-00015; continuation).
Footnotes
- 1
The logic of using three states instead of 4 is clear. The Mach–Zander or Michelson interferometer can distinguish (without active elements—phase modulators) only two orthogonal states at different outputs. In the standard BB84 protocol, where four states are used (a pair of orthogonal states in each basis), it is impossible to reliably distinguish all four states without changing the relative phase of states, since they all belong to a two-dimensional space tied to two time windows. In our version of the protocol, the problem of distinguishing between four states was solved in a simple and effective way (figure 1).
- 2