Abstract
The intensities of two types of Cherenkov waves arising at the motion of a solitary vortex along a Josephson sandwich are compared. These waves arise in the tail part of the vortex or are emitted deep into the medium surrounding the sandwich. The vortex velocities at which one of these two types of waves excited by the Cherenkov mechanism dominates are determined.
Export citation and abstract BibTeX RIS
1. Introduction
Radiation emitted by various systems with Josephson interaction has long been actively studied both theoretically and experimentally (see, e.g., the reviews [1–3]). In recent years, interest in the radiative properties of Josephson junctions has been associated with the development of the terahertz frequency range (see, e.g., [4–9] and references herein). In doing so, one of the important reasons for the interest in Josephson systems is the study of fluxons—solitary Josephson vortices, which can produce Cherenkov radiation [10]. In [11] the possibility of Cherenkov emission of waves by vortices in a system consisting of two Josephson junctions was theoretically predicted. Since then, a lot of analytical, numerical and experimental studies have been carried out, in which the manifestation of the Cherenkov effect in a variety of systems with Josephson interaction has been found. The general property of the systems studied is that their dispersion properties allow resonant interaction of traveling Josephson vortices and electromagnetic waves. Such resonant Cherenkov interaction can be realized due to different features of the studied systems: due to the electromagnetic coupling of the distributed junction with a dispersive spatially periodic transmission stripline in linear or annular geometry, due to the essentially two-dimensional consideration of the Josephson junction of annular geometry, which has a finite radius [12], due to the presence of a lateral passive (non-Josephson) dielectric-filled region leading to a 'geometric' dispersion [13], due to the fact that the characteristic frequencies of the electromagnetic field created by a lattice of vortices in a layered superconducting system with Josephson interaction, fall into the region of frequencies of 'plasma' oscillations of superconducting electrons [14, 15], due to the discreteness of linear or annular arrays of small Josephson junctions [16–18].
The first example of such radiation was detected experimentally when the vortex velocity exceeded one of the Swihart velocities in a structure with two Josephson junctions [19]. More than 20 years ago, it became clear that a correct description of the electrodynamics of long distributed Josephson structures can be based on a nonlocal approach [20–22]. Within this approach, Mints and Snapiro described the Cherenkov 'tail' of a solitary vortex in a Josephson junction with bulk electrodes [23]. On the other hand, it was shown that a vortex traveling along the Josephson sandwich can emit electromagnetic waves into the surrounding decelerating medium [24, 25]. This radiation also has a Cherenkov origin.
In the present communication the intensity of the Cherenkov wave in the tail part of the vortex travelling inside the Josephson sandwich is found for the first time, and a comparison of this value with the intensity of the Cherenkov radiation into the external medium is given. This allowed us to show that, for most admissible velocities, the Cherenkov vortex losses caused by wave emission into the external decelerating medium are dominant.
2. Main equations
Consider a Josephson sandwich consisting of two superconducting electrodes of thickness L separated by a thin tunneling layer of thickness 2d (see figure 1). The electrodes are symmetrically positioned with respect to the yOz plane. When studying Josephson vortices in a sandwich, it is sufficient to consider an electromagnetic field that has components E = (Ex , 0, Ez ) and H = (0, H, 0), which do not depend on the coordinate y. The fields Ex , Ez and H in the tunnel layer, superconducting electrodes and external dielectric are found from Maxwell's equations. When considering the fields in the tunnel layer, the Josephson current is taken into account. When analyzing the fields in the electrodes, the London equation is taken into account. When considering Ex , Ez and H in an external dielectric, the solution of Maxwell's equations is sought as a field decreasing away from the sandwich, or as a wave moving away from the sandwich. It is assumed that in the frequency range ∼ 1011 − 1012 s−1 the frequency dispersion of the dielectric permittivity of the external dielectric can be neglected. The continuity conditions for the tangential field components Ez and H at the boundaries of the electrodes are used to obtain a general solution in the entire solid-state structure. Using this method of field description makes it possible to determine the relationship between the magnetic field HJ (z, t) in the tunnel layer and the phase difference φ(z, t) of the superconducting order parameters on different sides of the tunnel layer [24, 25]. Generally speaking, this relationship is nonlocal. First, the effective penetration depth of the electromagnetic field in superconducting electrodes depends on the characteristic spatial scales of field change along the Oz axis, which leads to spatial nonlocality [26]. Second, taking into account the dependence of the electromagnetic field structure in the medium surrounding the sandwich on the characteristic frequencies of this field leads to the appearance of temporal nonlocality as well.
Figure 1. Schematic illustration of the cross section of a Josephson sandwich in the plane xz. The vortex is shown as an ellipse. Behind the vortex is a Cherenkov wave due to spatial nonlocality. To the left and right of the sandwich are shown electromagnetic waves going deep into the external dielectric.
Download figure:
Standard image High-resolution imageIn the simplest case, when the influence of the field in the external dielectric can be neglected, we have:
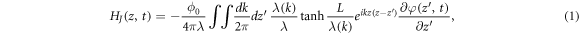
where ϕ0 is magnetic flux quantum, λ is the London penetration depth, 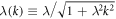 is the effective penetration depth of the inhomogeneous field into the electrodes. The formula (1) allows us to find the current at the boundary of the superconductor and the tunnel layer. This current is ∝ ∂HJ
/∂z. On the other hand, the current passing through the tunnel layer consists of the Josephson current
is the effective penetration depth of the inhomogeneous field into the electrodes. The formula (1) allows us to find the current at the boundary of the superconductor and the tunnel layer. This current is ∝ ∂HJ
/∂z. On the other hand, the current passing through the tunnel layer consists of the Josephson current 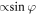 and the displacement current ∝ ∂2
φ/∂t2. The continuity condition for the x-component of the current at the boundary of the tunnel layer leads to the equation for the phase difference. If the characteristic distances 1/k at which the field changes along the axis Oz are large compared to λ, then, as seen from (1), the relationship between HJ
(z, t) and ∂φ(z, t)/∂z becomes local and the continuity requirement for x-component current leads to the well-known equation for the phase difference:
and the displacement current ∝ ∂2
φ/∂t2. The continuity condition for the x-component of the current at the boundary of the tunnel layer leads to the equation for the phase difference. If the characteristic distances 1/k at which the field changes along the axis Oz are large compared to λ, then, as seen from (1), the relationship between HJ
(z, t) and ∂φ(z, t)/∂z becomes local and the continuity requirement for x-component current leads to the well-known equation for the phase difference:
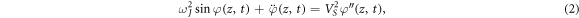
where 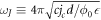 is the Josephson plasma frequency, jc
is the Josephson critical current density,
is the Josephson plasma frequency, jc
is the Josephson critical current density,  is the permittivity of the tunnel layer,
is the permittivity of the tunnel layer, 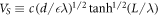 is the Swihart velocity of the sandwich, a dot over the function denotes derivative with respect to t, a prime mark denotes derivative with respect to z. If L → ∞ , then (2) turns into the sine-Gordon equation describing the junction formed by semi-infinite electrodes. At finite values of L the redistribution of magnetic fields and currents inside the electrodes leads to VS
in the right-hand side of (2).
is the Swihart velocity of the sandwich, a dot over the function denotes derivative with respect to t, a prime mark denotes derivative with respect to z. If L → ∞ , then (2) turns into the sine-Gordon equation describing the junction formed by semi-infinite electrodes. At finite values of L the redistribution of magnetic fields and currents inside the electrodes leads to VS
in the right-hand side of (2).
This nonlinear equation has a well-known solution describing a solitary vortex (2π-kink) traveling with constant velocity v:
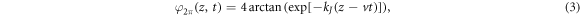
where 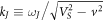 . (2) does not take into account the effect of spatial nonlocality and the effect of electromagnetic waves emitting from the side surfaces of the sandwich, which lead to a complex integral operator in the right-hand side of (2) instead of
. (2) does not take into account the effect of spatial nonlocality and the effect of electromagnetic waves emitting from the side surfaces of the sandwich, which lead to a complex integral operator in the right-hand side of (2) instead of 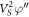 , namely
, namely 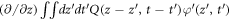 [24, 25]. (2) corresponds to the kernel
[24, 25]. (2) corresponds to the kernel
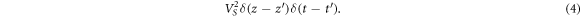
Assuming that effect of nonlocality and emission is finite but small, the kernel Q can be written as the sum of the kernel (4) and the corrections. This will lead to the corresponding additional terms in the right-hand side of (2).
To determine these corrections, it is convenient to represent the Fourier transform Q(k, ω) of the kernel Q (see [25]) as a sum of real and imaginary parts. Since further we will consider a uniformly traveling vortex, it is necessary to assume that ω = vk, and instead of Q(k, ω) we analyze the value Q(k, vk). In the case when a traveling vortex can radiate electromagnetic waves into the dielectric medium surrounding the sandwich, using expressions (11) and (14) from [25] we obtain the following Fourier transform of the kernel:
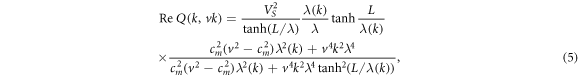
where 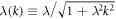 , cm
is the speed of light in the medium surrounding the sandwich, v > cm
. It is assumed that cm
is independent of the frequency of radiated waves. When writing (5), it is assumed that the thickness of the tunnel layer, usually a few nanometers, is small compared to
, cm
is the speed of light in the medium surrounding the sandwich, v > cm
. It is assumed that cm
is independent of the frequency of radiated waves. When writing (5), it is assumed that the thickness of the tunnel layer, usually a few nanometers, is small compared to 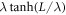 . From (5) it follows that in order to obtain in the coordinate representation of (4) with small corrections, the following conditions must be met:
. From (5) it follows that in order to obtain in the coordinate representation of (4) with small corrections, the following conditions must be met:

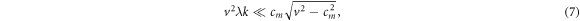
which leads to
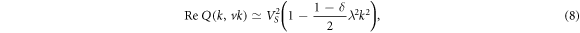
where  . Below we consider the conditions when δ is less than unity. Note that in the case of bulk electrodes, δ is equal to 0. As this takes place, the Fourier transform (8) of the kernel corresponds to the well-studied weak spatial nonlocality limit.
. Below we consider the conditions when δ is less than unity. Note that in the case of bulk electrodes, δ is equal to 0. As this takes place, the Fourier transform (8) of the kernel corresponds to the well-studied weak spatial nonlocality limit.
Under the conditions (6) and (7), the small imaginary part Q(k, vk) can be obtained from expression (17) of [24]:
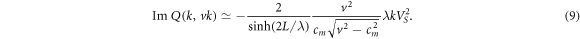
Turning back to the coordinate representation, the equation for the phase difference for a vortex traveling with constant velocity v can be approximately written in the following form:
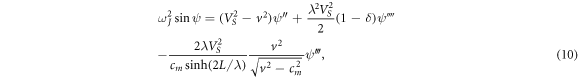
where ψ(ζ) ≡ φ(z, t), ζ = z − vt. We emphasize that it is precisely the conditions (6) and (7) that allowed us to write (10) as an equation that refines (2) by taking into account two new effects—weak spatial nonlocality and emission of electromagnetic waves deep into the medium surrounding the sandwich.
The second term in the right-hand side of (10) describes the so-called weak nonlocality. This phenomenon is due to the fact that taking into account small, but finite values of the parameter λ
k leads to taking into account the field components with characteristic lengths smaller than λ, which, in turn, leads to a nonlocal relationship (1) between the magnetic field inside the tunnel layer and 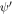 . Note that at L ≫ λ this term obviously coincides with the corresponding term arising in the theory of Josephson junctions with bulk electrodes.
. Note that at L ≫ λ this term obviously coincides with the corresponding term arising in the theory of Josephson junctions with bulk electrodes.
The third term in the right-hand side of (10) is related to the Cherenkov emission of electromagnetic waves by the vortex, which moves with velocity v > cm , from the side surfaces of the sandwich into the depth of the medium surrounding the sandwich. This term is generated by (9) and therefore contains the third order derivative of the phase difference. In the next two sections, we will briefly describe how these new terms manifest themselves in the structure of the electromagnetic field created by the vortex (3).
Because the effective penetration depth of the field into the electrodes depends on the characteristic scale of the field change along the vortex propagation direction, its structure changes. Under the conditions of weak spatial dispersion considered here, this change is small and manifests itself as the formation of a surface wave field with the wave number k0 in the vortex tail. As shown in [23], this is possible if, due to the weak spatial dispersion, the possibility of Cherenkov interaction between the vortex and the surface wave appears. This allows us to consider the Cherenkov losses of the vortex for excitation of the surface wave. In the case of a finite electrode thickness and when the vortex velocity exceeds the speed of light cm in the external medium, another mechanism of Cherenkov losses appears. Namely, the vortex loses energy to emission of electromagnetic waves into the external dielectric. Under the considered conditions, if the vortex losses for both generation mechanisms are small compared to the vortex energy and do not lead to significant distortion of its form, both mechanisms can be considered without taking into account their mutual influence on each other.
3. Intensity of the Cherenkov wave in the tail part of the vortex
Let us discuss the effect of spatial nonlocality on the structure of electromagnetic field. This effect is described by the second term in the right-hand side of (10). The phase difference in the tail part of the vortex (3) (in the notation [23]—at ζ ≪ 0) will be written as ψ = φ2π + δ ψ. Then from (10) we obtain approximately:
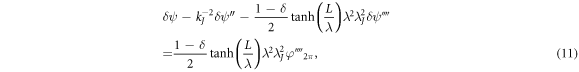
where λJ is the Josephson length. Using the Fourier transform, the solution of this equation can be represented as δ ψ = δ ψ0 + δ ψ1, where
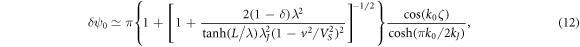
and δ ψ1 is an exponentially decreasing function with a characteristic scale of 1/k1,
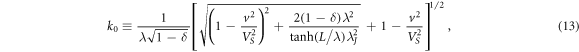

Note that the wave contribution δ ψ0 to δ ψ occurs only at δ < 1. From the mathematical point of view, the fulfillment of the condition δ < 1 provides a negative sign of the coefficient at the fourth derivative in the equation for δ ψ and, thus, determines the type of its solutions. The nonwave contribution δ ψ1 describes a small change in the vortex shape (3) due to taking into account spatial nonlocality. Since our consideration is aimed at the analysis of the Cherenkov radiation, the detailed structure of the δ ψ1 function is not described below.
It follows from (12) that the vortex (3) creates a traveling electromagnetic wave behind itself, propagating along the Oz axis. Under the considered conditions, the electromagnetic field has three components: Ex , Ez and Hy ≡ H. Therefore, the Poynting vector has two components: Sx and Sz . When calculating the energy loss due to the appearance of a wave in the vortex tail, it is necessary to average the values of Sx and Sz over the period of the wave. In the electrodes, the period average of Sx is zero, since the field components Ez and H are phase-shifted by π/2. Therefore, when calculating the energy loss in the vortex tail, it is sufficient to calculate the period average of the component Sz = (c/4π)Ex H.
Let us briefly describe this procedure. Inside the tunnel layer ( − d < x < d) for the x-component of the electric field of this wave, from the Josephson relation follows that  . At the same time, for the y-component of the magnetic field of the wave in the tunnel layer, we have:
. At the same time, for the y-component of the magnetic field of the wave in the tunnel layer, we have: 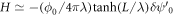 . According to the London equation in the electrodes (∣x∣ > d + L) the magnetic field of the wave changes according to the law
. According to the London equation in the electrodes (∣x∣ > d + L) the magnetic field of the wave changes according to the law ![$H\sinh [(-| x| +d+L)/\lambda ]/\sinh (L/\lambda )$](https://content.cld.iop.org/journals/1402-4896/97/5/055817/revision2/psac6546ieqn14.gif) [26], at the same time, according to the London equation the electric field of the wave in the electrodes
[26], at the same time, according to the London equation the electric field of the wave in the electrodes ![${E}_{x}\propto (v/c){\left(\lambda {k}_{0}\right)}^{2}H\sinh [(-| x| +d+L)/\lambda ]/\sinh (L/\lambda )$](https://content.cld.iop.org/journals/1402-4896/97/5/055817/revision2/psac6546ieqn15.gif) . By integrating Sz
over x, we obtain the energy that the wave transports per unit time through a unit length in the direction Oy:
. By integrating Sz
over x, we obtain the energy that the wave transports per unit time through a unit length in the direction Oy:
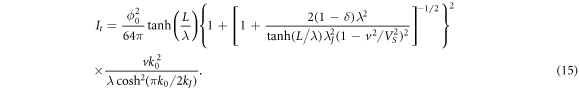
In the last expression, the averaging over the period 2π/vk0 is made. When deriving (15), it is taken into account that the condition λ
k0 ≪ 1 is satisfied due to (6), which leads to the main contribution to It
arising from the tunnel layer, while the contribution from electrodes is  times smaller.
times smaller.
4. The Cherenkov losses from the lateral surfaces
The third term in the right-hand part of (10) allows finding the radiation losses of the vortex for the emission of electromagnetic waves from the lateral surfaces of the sandwich into the surrounding medium [24]:

This expression corresponds to the vortex energy loss per unit time per unit length of the Josephson junction in the Oy direction. This radiation is also due to the Vavilov-Cherenkov effect. It is emitted from the outer surfaces of the electrodes, and for typical sandwich parameters its frequencies lie in the terahertz range. We emphasize that a necessary condition for the existence of this radiation is that the velocity of the vortex exceeds the speed of light in the external medium, v > cm , while the velocity of the vortex itself cannot exceed VS . Therefore, the Cherenkov radiation of the vortex (3) is possible if the condition cm < VS is fulfilled.
5. Comparison of two radiation mechanisms
In the previous sections, two mechanisms of emergence of the Cherenkov radiation when a vortex travels in a Josephson sandwich have been described. To compare them, let us consider the ratio of expressions (16) and (15):
The penultimate factor in (17), containing the speed of light cm , obviously, reflects the fact that the power (15) of the Cherenkov radiation into the medium is determined by the coupling strength of the Swihart wave and the electromagnetic wave in the medium.
The consideration is carried out under the assumption that the imaginary part of the kernel Q is small. This requires that the interaction between the Swihart wave and the electromagnetic wave in the medium is relatively small. This condition can be met if L ≳ λ and the vortex velocity v is not too close to cm
. Therefore, further analysis will be carried out under the assumption that δ is not close to unity. From the condition (6) and the definition of the wave number k0 (13), the following limitation on the vortex velocity follows:  . First, consider the narrow region of vortex velocities near the Swihart velocity of the sandwich:
. First, consider the narrow region of vortex velocities near the Swihart velocity of the sandwich:
where the left hand side of the inequality follows from the condition λ
kJ
≪ 1. The velocity region exists only at λ ≪ λJ
. In this region from (13) we have: 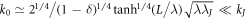 . Then (17) takes the following form:
. Then (17) takes the following form:
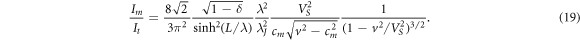
Below is a qualitative analysis of formula (19) at L ∼ λ and at λ ≪ λJ
. According to (18), value Im
/It
can be either less or greater than one. This is determined by the velocity 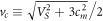 , at which the derivative of the function (19) over velocity turns to zero.
, at which the derivative of the function (19) over velocity turns to zero.
If cm
≪ VS
, the value 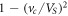 lies to the right of the region (18). In this case, if the parameter
lies to the right of the region (18). In this case, if the parameter  is not small, then in the entire velocity region (18) the Cherenkov radiation of the vortex (3) goes mainly into the external medium. If the parameter
is not small, then in the entire velocity region (18) the Cherenkov radiation of the vortex (3) goes mainly into the external medium. If the parameter 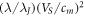 is small, then exists two intervals. When
is small, then exists two intervals. When 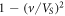 is less than
is less than  , then the Cherenkov losses to the external medium are dominating. Contra, if the inverse inequality is fulfilled, then the Cherenkov losses in the tail dominate.
, then the Cherenkov losses to the external medium are dominating. Contra, if the inverse inequality is fulfilled, then the Cherenkov losses in the tail dominate.
When cm
is increased to values at which 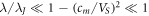 , the considered velocity region is again divided into parts, whose boundary is located at
, the considered velocity region is again divided into parts, whose boundary is located at 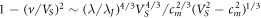 . When
. When  lies to the left of the boundary, the losses to the medium dominate. Contra, when
lies to the left of the boundary, the losses to the medium dominate. Contra, when 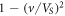 lies to the right of the boundary, the losses in the tail part of the vortex are greater.
lies to the right of the boundary, the losses in the tail part of the vortex are greater.
When cm
is further increased, when 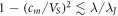 , we obtain that in the entire velocity region (18) the Cherenkov emission of the vortex (3) goes mainly into the external medium.
, we obtain that in the entire velocity region (18) the Cherenkov emission of the vortex (3) goes mainly into the external medium.
At even larger values of cm
, such that 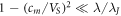 , the velocity vc
falls inside the region (18) and, still, the Cherenkov radiation of the vortex (3) is mostly carried into the external medium.
, the velocity vc
falls inside the region (18) and, still, the Cherenkov radiation of the vortex (3) is mostly carried into the external medium.
Note that for even larger values of cm
, when 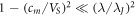 , our consideration is not applicable, since a negative value arises under the radical
, our consideration is not applicable, since a negative value arises under the radical  .
.
Finally, let us analyze the ratio (17) of the powers (16) and (15) of the Cherenkov waves emitted by the vortex (3) in the velocity region
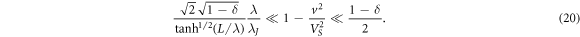
In this velocity region we find from the expression (13):
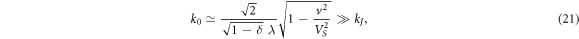
which corresponds to the small-scale perturbations in the vortex tail that resulted from using the weakly nonlocal approximation (10). Then the value (17) takes the following form approximately:
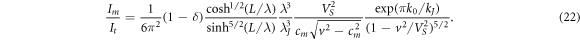
Taking into account that
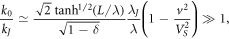
the expression (22) can be rewritten as follows:
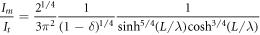
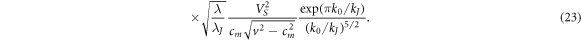
In the velocity region under consideration, the amplitude (12) of the Cherenkov wave exponentially decreases as 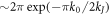 with decreasing velocity. In particular, this leads to the appearance in (22) of the factor
with decreasing velocity. In particular, this leads to the appearance in (22) of the factor 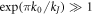 , which, conversely, increases with decreasing velocity. It follows from the inequality (21) that the value (23), and hence (22), is exponentially large by the large parameter k0/kJ
. This shows that in the region of velocities (20), the main contribution to the Cherenkov losses is related to the emission of waves from the side surfaces of the sandwich into the depth of the outer dielectric medium. This is true for not too large values of thicknesses of Josephson sandwich electrodes.
, which, conversely, increases with decreasing velocity. It follows from the inequality (21) that the value (23), and hence (22), is exponentially large by the large parameter k0/kJ
. This shows that in the region of velocities (20), the main contribution to the Cherenkov losses is related to the emission of waves from the side surfaces of the sandwich into the depth of the outer dielectric medium. This is true for not too large values of thicknesses of Josephson sandwich electrodes.
The dependence of Im /It on the dimensionless vortex velocity is shown in figure 2 for cm /vS = 2/3, λ/λJ = 0.01 for two different values of L/λ.
Figure 2. The value of Im /It in the range of ∼0.3 to ∼3 for L/λ = 2 (a), 5(b).
Download figure:
Standard image High-resolution imageThe plots in panels (a) and (b) are drawn in the most interesting velocity interval, within which the value Im
/It
passes through unity, i.e., there is a change in the dominant mode of Cherenkov radiation. In this interval, we see that the greater the value of 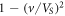 , that is, the more the speed of the radiating vortex moves away from the Swihart velocity VS
toward cm
, thus increasingly dominating Im
over It
. This is in accordance with the analytical consideration of this section.
, that is, the more the speed of the radiating vortex moves away from the Swihart velocity VS
toward cm
, thus increasingly dominating Im
over It
. This is in accordance with the analytical consideration of this section.
Note that uniform motion of the radiating vortex can be supported by passing a transport current through the Josephson junction, which creates a Lorentz force that compensates the losses of the vortex to radiation [23–25].
6. Conclusion
Above, a new nonlinear equation (10) was derived for the Josephson sandwich, which describes the effect of both weak spatial nonlocality and the effect of the emission of electromagnetic waves into the medium surrounding the sandwich. This equation allowed us to determine the energy loss of a solitary Josephson vortex traveling along the sandwich, due to the emergence of Cherenkov electromagnetic wave in the tail part of the vortex. In addition to this wave, the vortex emits electromagnetic waves from the lateral surfaces of the sandwich. The emergence of these waves is also due to the Vavilov-Cherenkov effect.
The intensities of these waves are compared. It is found that at vortex velocities close to the Swihart velocity of the sandwich, both Cherenkov radiation mechanisms can be realized jointly. It is shown that for reasonable parameters of the system for most allowed velocities, the main part of the Cherenkov losses of the vortex leads to emission of waves into an external decelerating medium.
Acknowledgments
The work was supported by the Program Priority 2030.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).




