Abstract
In the presented paper, we introduce an analytical description for a dissipative two-mode parametric amplifier coherent cavity containing a three-level system (qutrit). Based on normalized correlation function, Q-function and its associated Wehrl entropy, the dynamics of the quantum phenomena: two-mode cavity non-classically, qutrit phase space information, and quantum coherence are investigated under the physical parameters: qutrit-cavity interactions, initial coherent intensity, and the dissipation. It is found that the generated quantum phenomena, due to the qutrit-cavity interaction, depend on the physical parameters of the initial states and the dissipation. The robustness of the quantum phenomena against the dissipation can be enhanced by decreasing the initial coherent intensity cavity. The stability and strength of the generated bunching/anti-bunching behaviour can be controlled by the cavity dissipation.
Export citation and abstract BibTeX RIS
1. Introduction
Quasi-probability distributions of quantum states, the Wigner distribution [1], Husimi Q-distribution [2], and Glauber P-distribution [3] are important tools for studying and describing the quantum states. Based on the density quantum state operator, they are used as an indicator to the classical and non-classical properties [4–7]. The Husimi Q-distribution is always regular and non-negative and its applications in quantum estimation depend on the classical quantum Fisher information [8] and quantum Wehrl entropy [9, 10]. Wehrl entropy was used to quantify the intermode correlation that can be referred to as entanglement in a phase space [11]. Nonclassical effects of the Q-distribution in one- and two-qubit systems interacting with different cavity fields are investigated [12]. While the Q-distribution information in three-level atomic (qutrit) systems is studied [13] with cavity damping, and stills need to be investigated with the decoherence models, as in the presented investigation.
The nonlinear atom-cavity interactions lead to changes in the quantum effects of the atom-cavity system and its subsystems. The nonlinear interactions can be realized by trapped-ions [14] and superconducting-circuits [15] systems. The atom-cavity interactions were described theoretically by the Jaynes–Cummings model [16] in different versions, which describes multi-level atoms, multi-mode fields [17], multi-photon transitions, and Kerr-like medium [18]. It is shown that a parametrically excited nonlinear optical model can lead to the generation of the maximally entangled states [19–21]. One of the important nonlinear coherent states in quantum information is the entangled Barut-Girardello coherent states (B-CGS) [22–24], that is generalizing for the nonlinear one-mode to multi-mode coherent fields [25]. They are implemented via different methods [26–28].
The qutrit-cavity systems have more potential applications in quantum security research fields [29, 30] due to that they provide more secure quantum key distributions than those based on qubit-cavity systems [31, 32]. Also, the channel capacity and security in the quantum teleportation protocols can be enhanced by using the qutrit systems [33]. The qutrit systems can be realized by superconductor circuits [34], nitrogen-vacancy centers [35], and quantum dot molecules [36]. The qutrit-cavity interactions have more contributions in generating quantum correlation [37, 38] and controlling visibility and distinguishability [39], single-photon pulse emission simulation [40], and energy transfer among molecules [41]. The generated quantum phenomena due to dissipative qutrit-cavity interactions are necessarily affected, where the coupling to the environment leads to erasing, reducing and deteriorating the quantum coherence and the non-classically [42–44].
In this paper, Based on normalized correlation function, Q-function and its associated Wehrl entropy, the dynamics of the non-classically, qutrit phase space information, and quantum coherence are investigated in dissipative qutrit-cavity model when the cavity fields are initially in a nonlinear Barut-Girardello state. This paper is organized as: In section 2 we describe and find an analytical solution for the physical SU(1, 1)-SU(3) model by solving the master equation. While in section 3 and 4, the Q-function and correlation function quantifiers and their dynamics are introduced and investigated, respectively. Finally, we give the conclusion in section 5
2. The nonlinear qutrit-cavity model
Here, the dynamics of a qutrit interacting with two nondegenerate modes cavity fields via the master equation that described the cavity dissipation. The nondegenerate parametric amplifier interactions realize the important nonlinear phenomenon [45, 46], and their Hamiltonian is expressed as

where  represents the cavity field operators with frequencies of ωj
(j = 1, 2). g represents the two-mode interaction coupling, which is considered in a strong coupling regime, and the two-mode cavity fields have the same frequency, ω1 = ω2 = ω. Recently, the Hamiltonian of equation (1) can be realized in antiferromagnetic spintronic systems in the strong coupling regime [47]. It is found that the entanglement properties will be very different in this regime, where the magnon-magnon entanglement can be enhanced. Also, the parametric amplifier-type of two-mode interaction can be physically realized in a 3-wave mixing parametric amplifier device [48] (if a strong bias field were applied) and Josephson circuits [49]. If the two-mode cavity fields described by the Hamiltonian of equation (1) interact with a Λ-type qutrit, then the qutrit-cavity Hamiltonian, after applying rotating wave approximations, is given by
represents the cavity field operators with frequencies of ωj
(j = 1, 2). g represents the two-mode interaction coupling, which is considered in a strong coupling regime, and the two-mode cavity fields have the same frequency, ω1 = ω2 = ω. Recently, the Hamiltonian of equation (1) can be realized in antiferromagnetic spintronic systems in the strong coupling regime [47]. It is found that the entanglement properties will be very different in this regime, where the magnon-magnon entanglement can be enhanced. Also, the parametric amplifier-type of two-mode interaction can be physically realized in a 3-wave mixing parametric amplifier device [48] (if a strong bias field were applied) and Josephson circuits [49]. If the two-mode cavity fields described by the Hamiltonian of equation (1) interact with a Λ-type qutrit, then the qutrit-cavity Hamiltonian, after applying rotating wave approximations, is given by
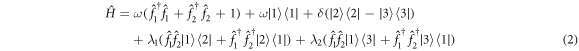
where ω is the system frequency. The ∣i〉〈j∣, (i, j = 1, 2, 3) are the projection operators of the qutrit. λ1 and λ2 are the coupling constants for the ∣1〉 ↔ ∣2〉 and ∣1〉 ↔ ∣3〉 transitions, respectively. In terms of SU(1, 1) Lie algebra operators: 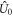 and
and  , the Hamiltonian of equation (2) is rewritten as
, the Hamiltonian of equation (2) is rewritten as
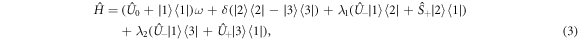
this after taking:  and
and  which satisfy the SU(1, 1) algebra commutation relations:
which satisfy the SU(1, 1) algebra commutation relations: ![$[{\hat{U}}_{0},{\hat{U}}_{\pm }]=\pm {\hat{U}}_{\pm },[{\hat{U}}_{-},{\hat{U}}_{+}]=2{\hat{U}}_{0}$](https://content.cld.iop.org/journals/1402-4896/96/5/055102/revision4/psabeba4ieqn6.gif) . In our work, we take the resonance case δ = 0.
. In our work, we take the resonance case δ = 0.
The Hamiltonian (3) represents the SU(1, 1)-SU(3) interaction. The  and
and  operators act on the SU(1, 1)-state ∣n, k〉 as the following:
operators act on the SU(1, 1)-state ∣n, k〉 as the following:
where  and
and  . In the case of the open SU(1, 1)-cavity, the time evolution for the SU(1, 1) and SU(3) system under the damping is governed by the following master equation:
. In the case of the open SU(1, 1)-cavity, the time evolution for the SU(1, 1) and SU(3) system under the damping is governed by the following master equation:
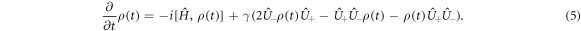
In the high−Q cavity (γ ≪ λ) range, an analytical solution for the equation (5) can be obtained by using the method of the dressed state representation of the Hamiltonian  of equation (3) [2] with their eigenvalues
of equation (3) [2] with their eigenvalues 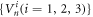 . In the first step, the Su(1, 1)-system operators,
. In the first step, the Su(1, 1)-system operators, 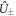 and
and 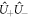 , write in terms of the dressed states of equation (3). In the next step, we use the representation:
, write in terms of the dressed states of equation (3). In the next step, we use the representation:
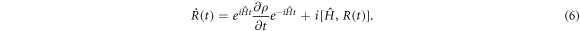
Consequently equation (5) becomes
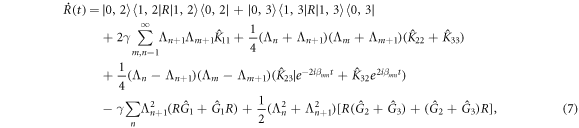
with
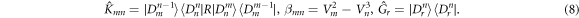
To find the particular solution of the density SU(1, 1)-SU(3) matrix  , we consider the SU(3)-system is initially in its upper state,
, we consider the SU(3)-system is initially in its upper state,  , while the two-mode cavity is initially in the Barut-Girardello state (B-GCS ) [22],
, while the two-mode cavity is initially in the Barut-Girardello state (B-GCS ) [22],

with distribution function
where ∣β, k〉 is B-GCS that is the eigenstate of U−;  . Iν
(x) is the Bessel function. The nonlinear Barut-Girardello state is very appropriate to considering as the initial state for the SU(1, 1)-system due to that it is formulated in the SU(1, 1)-system bases {∣n, s〉}(n = 0, 1,...). The nonlinear B-GCS can be realized by magnetized homogeneous anisotropic 2D-Dirac materials [26]. It has some important special states; the even and odd coherent states can be obtained from B-GCS by taking
. Iν
(x) is the Bessel function. The nonlinear Barut-Girardello state is very appropriate to considering as the initial state for the SU(1, 1)-system due to that it is formulated in the SU(1, 1)-system bases {∣n, s〉}(n = 0, 1,...). The nonlinear B-GCS can be realized by magnetized homogeneous anisotropic 2D-Dirac materials [26]. It has some important special states; the even and odd coherent states can be obtained from B-GCS by taking  and
and  , respectively. Also, the nonlinear coherent state
, respectively. Also, the nonlinear coherent state  is another special state for the nonlinear B-GCS, which can be realized by a trapped ion [50].
is another special state for the nonlinear B-GCS, which can be realized by a trapped ion [50].
By equation (7) and the considered initial density matrix ρ(0) = R(0) in terms the Hamiltonian eigenstates:  , the off-diagonal elements of the density matrix
, the off-diagonal elements of the density matrix ![$R(t)=[{R}_{i,j}^{{mn}}(t)]$](https://content.cld.iop.org/journals/1402-4896/96/5/055102/revision4/psabeba4ieqn22.gif) , for i ≠ j, are given by
, for i ≠ j, are given by
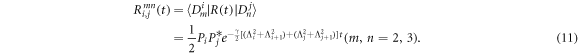
While the diagonal elements of the density matrix R(t) are given by
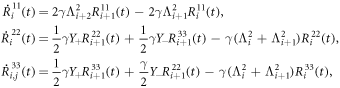
where  . After finding the elements of the matrix R(t), we use the inverse canonical transformation:
. After finding the elements of the matrix R(t), we use the inverse canonical transformation: 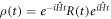 . In the basis qutrit states: {∣1〉n
= ∣1, n, k〉, ∣2〉n
= ∣2, n + 1, k〉, ∣3〉n
= ∣3, n + 1, k〉}, the density matrix ρ(t) takes the from:
. In the basis qutrit states: {∣1〉n
= ∣1, n, k〉, ∣2〉n
= ∣2, n + 1, k〉, ∣3〉n
= ∣3, n + 1, k〉}, the density matrix ρ(t) takes the from:
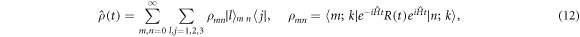
that is used to study the dynamics of the present system.
3. Quantum effect quantifers
3.1. Atomic Q-function and wehrl entropy
Here, we use the Q-function and its associated Wehrl entropy (WE) as good tools giving insight into the proprieties of the qutrit system evolution [9]. WE is a good indicator to the quantum coherence and the information extraction about the phase. The general spin coherent state representation ∣Ψ〉, that bases on the algebraic characteristics of the angular momentum operator j, can be introduced by the phase space angles (θ, ϕ) [51] as:
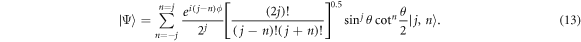
If j = 1, we get the Bloch coherent state of the qutrit phase space. Based on the reduced qutrit density matrix, 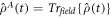 , the atomic Q-function (QF) [2], in the qutrit coherent state representation, is defined as:
, the atomic Q-function (QF) [2], in the qutrit coherent state representation, is defined as:
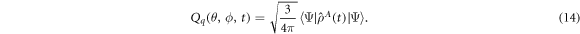
The Wehrl entropy (QWE) of the qutrit state is given by [9]:
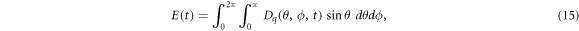
where Dq (θ, ϕ, t) represents the Wehrl density, which is given by:
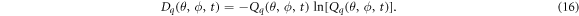
Here, we use the quantifier S(t) = E(t) − E(0) to investigate the dynamics of the qutrit coherence properties. In the case where the decoherence or open qutrit-cavity system is not considered, QWE is used to quantify the entanglement. Otherwise, it is used to quantify the mixedness of the qutrit state.
Figures 1(a)–(c) illustrates the phase space dynamics of the Q-distribution at different times, which are chosen according to the dynamics of the population inversion of (d). In (a) t1 = 0.7353π/λ that corresponds to the qutrit is near to the upper state is ∣1〉, in (b) t2 = π/λ that corresponds a mixed state is near to (∣1〉〈1∣ + ∣2〉〈2∣ + ∣3〉〈3∣)/3 and in (c) t3 = 1.416π/λ that corresponds a mixed state is near to (∣2〉〈2∣ + ∣3〉〈3∣)/2. From figure 1(d), we note that the population inversion has quasi-periodic oscillatory behavior, it oscillates between its extreme values 1 (that means that the qutrit is in the upper state ∣1〉) and −1 (that means that the qutrit is in the lower mixed state 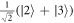 ). This oscillatory behavior is an indicator to transit the qutrit energy between its states. The phenomena of the collapses and revivals appear regularly during different intervals. In the collapse intervals, the qutrit is in/near a maximally mixed state
). This oscillatory behavior is an indicator to transit the qutrit energy between its states. The phenomena of the collapses and revivals appear regularly during different intervals. In the collapse intervals, the qutrit is in/near a maximally mixed state 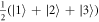 .
.
Figure 1. The Q-function for 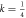 , r = 0, β = 5 when θ ∈ [0, 4π] and ϕ ∈ [0, 2π] with the different times: t1 = 0.7353π/λ in (a), t2 = π/λ in (b), and t3 = 1.416π/λ in (c). The times are chosen according to the dynamics of the population inversion of (d).
, r = 0, β = 5 when θ ∈ [0, 4π] and ϕ ∈ [0, 2π] with the different times: t1 = 0.7353π/λ in (a), t2 = π/λ in (b), and t3 = 1.416π/λ in (c). The times are chosen according to the dynamics of the population inversion of (d).
Download figure:
Standard image High-resolution imageFigure 1(a) shows that when the qutrit becomes near to the upper state is ∣1〉, the Q-distribution oscillates between its extreme values, periodically, with 2π-period with respect to θ, and it depends only on the phase space angle θ, approximately, its dependence on the angle ϕ is very weak. While figure 1(b) shows the maximally mixed qutrit state, at t2 = π, has regular Q-distribution with respect to both the coherent angles θ and ϕ with 2π − and π-period, respectively. The QF oscillations form only periodical-peaks above zero-value of Qq (0, 0, t2) = 0 with a Gaussian distribution. The Q-distribution takes another form at t3 = 1.416π due to the unitary evolution, see figure 1(c). QF oscillations present periodical peaks and bottoms regularly distributed above and under the non-value of Qq (0, 0, t3).
Figures 2(a) and (c) display the dissipation effect on the Q-distribution Q(θ, π, ti ) (i = 1, 2, 3) for β = 5 with different dissipation values: γ = 0.004λ and γ = λ. We note that the increase of the incoherence leads to squeezing the 3D Q-distribution to becomes constant surface Q(θ, ϕ, ti ) ≈ 1.2. For the three cases of Q(θ, π, ti ) (i = 1, 2, 3), the maxima and minima of the QF tend to the stable value Q( ∞ ) ≈ 1.2, i.e., the phase space qutrit information of the Q-distribution is erasing completely (the dependence of QF on the phase space almost vanish). Figures 2(b) show the intensity of the initial coherent Barut-Girardello state on the Q-distribution for β = 1. When the coherent cavity intensity reduces, the amplitudes of the Q-distribution oscillations are increased and are more robust against the dissipation than the case β = 5. We can deduce that the erasing phase space qutrit information of the Q-distribution depends on the unitary evolution, the intensity of the initial coherent Barut-Girardello state, and the dissipation.
Figure 2. Q-distribution Q(θ, π, ti ) at t1 (solid curves), t2 (dashed curves), and t3 (dash-dot curves) with different values: (β, γ) = (5, 0.004)λ in (a), (β, γ) = (1, 0.004)λ (b), and (β, γ) = (5, λ) in (c).
Download figure:
Standard image High-resolution imageIn figure 3, we display the dynamics of the Wehrl entropy (QWE) under the effect of the intensity of the initial coherent Barut-Girardello state and the dissipation. In the absence of the dissipation, figure 3(a) shows the amount of the generated QWE-entanglement between the qutrit and the two-mode nondegenerate cavity. The QWE has irregular oscillatory behaviors with chaotic oscillations. The QWE amplitudes depend on the initial coherent Barut-Girardello state that shifts up the QWE minima. Figure 3(a) displays the dependence of the generated mixed Wehrl entropy on the initial coherent intensity cavity and the dissipation. In the presence of the dissipation, the QWE grows to show that can be stabilized in a maximally mixed state. This stability of the qutrit mixedness depends on the initial coherent intensity cavity. The increase of the initial coherent intensity can accelerate the stability of the generated mixedness.
Figure 3. The Wehrl entropy S(t) with 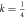 for β = 0.2, 1, 5 with γ = 0 in (a) and γ = 0.01 in (b).
for β = 0.2, 1, 5 with γ = 0 in (a) and γ = 0.01 in (b).
Download figure:
Standard image High-resolution image4. The correlation function
Here, we consider the normalized second-order correlation function (CF) that is an important quantity based on the SU(1, 1)-system statistics, and plays an important role in the quantum information [52]. For a SU(1, 1)-system, it is given by
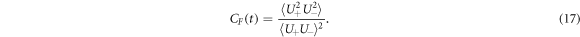
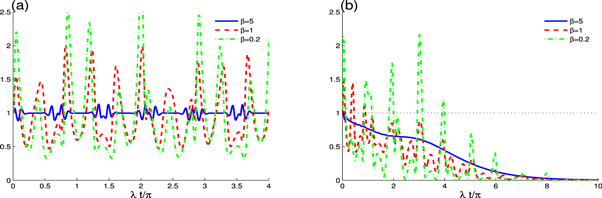
Based on the CF values, we can know that the Poissonian distribution (PD) of the SU(1, 1)-system. If CF (t) < 1, then the system is in sub-PD. When CF (t) > 1, the system is in super-PD. Otherwise, CF (t) = 1, the system has PD. The CF two different time CF (ti )(i = 1, 2) is an indicator for the probability of detecting two photons, one at time t1 and the other one at t2 = t1 + Δ. Also, CF can determine the emitted photon bunching/anti-bunching characteristic. Here, we consider the case of the delay time, Δ = 0, where the CF can be detected in the two photons simultaneously.
In figure 4 (a), we display the dynamics of the generated Poissonian distribution due to only the unitary SU(1, 1)-SU(3) interaction in the absence of the SU(1, 1) damping. At λ t = 0, CF (0) = 1, this means that the initial coherent Barut-Girardello state has Poissonian behavior. The solid curve shows the dynamics of the Poissonian behavior for the case where the large initial coherent intensity, the intervals of the sub-PD and the super-PD appear regularly with weak amplitudes. While the Poissonian distribution occurs most of the time. By increasing the initial coherent intensity, the intervals and amplitudes of the sub-PD and the super-PD are enhanced, while the Poissonian behavior occurs only at particular point times, see figure 4 (a). Figure 4 (b) shows the effect of the dissipation of the SU(1, 1)-system on the non-classically cavity. The dissipation leads to reducing the frequency and the amplitudes of the CF oscillations, and the sub-Poissonian behavior takes most of the time. The dissipation effect on the CF oscillations can be weakened by decreasing the initial coherent intensity. The solid curve shows that the anti-bunching behaviour is more pronounced for large initial coherent intensity. For sufficiently long time (see figure 4 (b)), the correlation function decreases to zero value, i.e., the dissipation of the SU(1, 1)-system leads to generating strong and perfect anti-bunching states. The ability of the dissipative qutrit-cavity interaction to generating stable anti-bunching states depends on the initial coherent intensity.
Figure 4. The correlation function F(2)(t) with 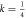 for β = 0.2, 1, 5 with γ = 0 in (a), and γ = 0.1 in (b).
for β = 0.2, 1, 5 with γ = 0 in (a), and γ = 0.1 in (b).
Download figure:
Standard image High-resolution image5. Conclusion
In this work, an analytical solution of the master equation that governs the dynamics of the dissipative two-mode cavity fields interacting resonantly with a qutrit is obtained. The two-mode cavity fields are initially in a nonlinear Barut-Girardello coherent state while the qutrit is initially in its upper state. We investigate the dynamics of the qutrit and cavity non-classical properties under the effects of the nonlinear qutrit-cavity interaction, the initial coherent intensity cavity, and the dissipation cavity. Based on the Q-distribution and its associated Wehrl entropy, the dynamics of the qutrit nonclassical properties (phase space information, entanglement and mixedness) are investigated. While, the dynamics of the two-mode cavity nonclassically (sub-, super- and Poissonian behaviors) are studied by the normalized second-order correlation function. The phase space information of the QF, the amplitudes and the frequency of the Q-distribution, depends on the nonlinear qutrit-cavity interaction and the initial coherent intensity cavity. It can be weakened and erased completely by increasing the dissipation. It is found that the generated entanglement, due to the nonlinear qutrit-cavity interaction, can be enhanced and accelerated by increasing the initial coherent intensity. Also, the stability of the qutrit mixedness due to the dissipation can be disappeared with small values of the mean photon number. The small values of the initial coherent intensity cavity lead to enhancing the robustness of the qutrit's non-classicality against the dissipation as well as the cavity's non-classicality of the intervals of the sub-, super- and Poissonian behaviors. The dissipative qutrit-cavity interaction leads to generating strong and perfect anti-bunching states.
Acknowledgments
The authors are very grateful to the referees and the editor for their constructive remarks, which have helped to improve the manuscript.
Data availability statement
No new data were created or analysed in this study.