Abstract
A prerequisite to characterize magnetic materials is the capability to describe systems containing unpaired electrons. In this study, we benchmark the one-shot GW (G0W0) on top of different unrestricted mean-field solutions for open-shell molecules using Dunning's correlation-consistent basis sets expanded in terms of Gaussian functions. We find that the G0W0 correction to hybrid functionals provides reasonably accurate results for the ionization energies of open-shell systems when compared to those obtained from high-level ab initio methods. Moreover, the quality of the G0W0 exchange–correlation approximation is evaluated by the discrepancy between the ionization energy of the neutral molecules and the electron affinity of the corresponding cations. Furthermore, we assess the capability of the GW to reproduce the correct energy ordering of molecular spin–orbitals. To such an aim, we thoroughly discuss three open-shell molecules CN, NH2, and O2, for which approximate functionals fail to correctly capture the single-electron spectrum. Particularly, we demonstrate that the overestimation of the exchange energy in the studied spin–orbitals is reduced by the GW dynamic correlation term, restoring the molecular orbital ordering. Interestingly, we find that deviations of the exchange and correlation energies, in comparison with our ab initio reference, can be very different for molecular orbitals with different symmetry, e.g. σ and π-type orbitals.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Hedin's GW approximation (GWA) [1, 2] is well-known as a powerful and promising method in the materials science community because of its high quality and relatively low computational cost. The GWA introduces a frequency-dependent self-energy describing the propagation of a particle in an interacting system in which interactions are dynamically screened [2–11]. As compared to static mean-field methods, the dynamical content of the GWA gives a sophisticated expression of frequency-resolved observables such as electron removal (addition) energies [5, 10], which is often in agreement with the direct (inverse) photo-emission spectroscopy. As a result, this approximation is currently the predominant framework to describe the quasiparticle spectra of charged excitation energies, playing a key role in electronics[12–16].
The GWA has shown to be quantitatively accurate in the estimation of band-edges, band-gaps, and band structures as the fundamental features for understanding the electronic structure of solids [2–4, 6–8]. Likewise, the GWA has been widely used as an accurate approximation to finite systems, e.g. isolated molecules, especially the assignment on the ionization energy (IE) and electron affinity (EA) [11, 12, 17–22]. For molecules, the negative energies of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) in the quasiparticle spectra could be interpreted as the IE and EA, respectively. Recent benchmarks confirm that the GW calculations often provide accurate estimations of the IE for closed-shell molecules [11, 17–21]. However, the application of the GWA might not be straightforward for open-shell systems as pointed out by several authors, in particular regarding spin contamination and its relation with the appearance of multiple solutions [7, 14, 23, 24].
The significance of open-shell molecules is that they are models for the magnetic systems in which the spin degrees of freedom become important [3]. In such systems, the number of unpaired electron(s) determines the magnitude of the magnetic moment and introduces correlation effects stemming from spin-dependent interactions, which should be correctly taken into account [3]. Despite this, the electronic structure description of open-shell molecules is a tough challenge for density-based exchange–correlation (xc) functionals, which might break the orbital and spin degeneracy [14, 25–27]. In this sense, we show how mean-field calculations, even using hybrid functionals, dramatically fail in the estimation of spin–orbital energies, leading to qualitatively wrong single-electron spectra while well-set correlation energy of the GWA for each spin–orbital provides results comparable to those obtained from high-level ab initio methods.
In this study, we provide sets of converged IE computed with the one-shot GWA for 42 open-shell molecules when the Hamiltonian is diagonal in the spin–space basis. Like many authors [19, 20, 28, 29], we benchmark the G0 W0 against a variety of correlated methods in quantum chemistry, particularly coupled-cluster including single and double excitations with perturbative inclusion of triple excitations CCSD(T). Furthermore, the one-shot GW relies on the eigenfunctions and eigenenergies obtained from a prior self-consistent ground-state calculation, introducing an undesired starting point dependence [10, 17, 20, 21]. To address the latter, therefore, we benchmark the performance of the one-shot GW method starting from several mean-field solutions. To evaluate the quality of approximate GW self-energy, moreover, we compare the IE of the neutral molecules in our test-set with the EA of the corresponding cations (EA+) in the limit of frozen (fixed) geometry. This gives an insight about the systematic localization and delocalization error of the approach [30–34]. We also evaluate the capability of the one-shot GWA to arrange molecular orbitals (MOs) according to the computed quasiparticle orbital energies. Particularly, we discuss the impact of the quasiparticle correction on the orbital energies of three small-sized molecules, namely, CN, NH2, and O2.
This article is organized as follows; the basic theoretical principles of the one-shot GWA are given in section 2. This section also outlines the quantum chemistry methods and Dyson orbitals, used as reference points to evaluate G0 W0 results. Computational details are given in section 3. In section 4, the IE and EA+ of 42 open-shell molecules are presented and compared to the gold standard in quantum chemistry, namely, CCSD(T). The importance of the GW correction on the estimated electronic structure of the three selected molecules is also discussed. Section 5 concludes the article.
2. Theory
The GWA formalism has been extensively presented in detail elsewhere [2, 3, 5, 10]. Considering a diamagnetic ground state, spin degrees of freedom were omitted in Hedin's founding works [1]. In later developments, spin-dependent GW calculations were performed since early studies [8, 9]. Here, we will give a short synopsis pertinent to the spin-resolved GW calculation, whereas relativistic effects are neglected.
2.1. Hedin's GW approximation
The basic quantity in the GWA is the non-local frequency-dependent electron self-energy Σxc( r , r ', ω), which describes the exchange and correlation effects. It is defined by

where G( r , r ', ω) and G0( r , r ', ω) represent the time-ordered interacting and non-interacting Green's functions [3, 4, 35]. The latter is typically obtained from a single-particle effective Hamiltonian H0 as follows [2]
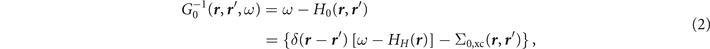
where Σ0,xc and HH are an effective static xc operator and the Hartree Hamiltonian, respectively. For instance, if H0 is provided by the Hartree–Fock (HF) method, the xc operator Σ0,xc will be the customary Fock exchange operator Σx.
According to Hedin [1, 2], the electron self-energy Σxc(ω), including electron–electron interaction effects beyond the Hartree potential, can be approximated by
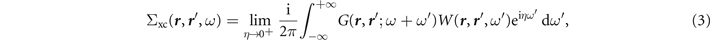
where η is a positive infinitesimal shift away from the real frequency axis and W(ω) is the screened interaction, as will be discussed in section 2.4. Such a frequency (energy) dependence distinguishes the GWA from static mean-field methods, so that, the GW self-energy now contains a dynamical Coulomb-hole (COH) term plus a dynamically screened exchange (SEX) part. In the static approximation, the GW self-energy reduces to the static COHSEX, giving rise to an effective Hamiltonian containing the non-local screened-exchange plus a local term representing the Coulomb interaction of the quasiparticle with the screening charge distribution (hole) around it. For more details we refer the readers to reference [3–5, 10].
Equations (1)–(3) must be satisfied simultaneously giving rise to a self-consistent GW procedure that implies a high computational cost [8, 17, 21, 29]. Fortunately, many single-particle Hamiltonians feature rather accurate approximations Σ0,xc to the xc operator, so that the calculation of the electron self-energy can be accurately approximated using the non-interacting Green's function (2) in equation (3). This perturbative procedure is known as the one-shot GWA or G0 W0. Moreover, it has been reported that the fully self-consistent GWA might not yield the best results, while a partial self-consistency or G0 W0 frequently results in a better agreement with the experiment [5, 22].
2.2. Quasiparticle energies within the diagonal approximation
Besides the one-shot GWA, a diagonal approximation is often employed; so that, the interacting Green's function Gσ
(
r
,
r
', ω) can be approximately expanded in terms of the eigenstates ψn,σ
(
r
) of the single-particle Hamiltonian  (σ = ↑, ↓) as
(σ = ↑, ↓) as
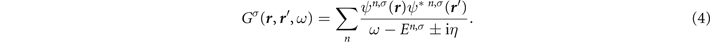
In this approximate ansatz, the quasiparticle energies En,σ
do differ from the eigenenergies 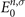 of the single-particle Hamiltonian
of the single-particle Hamiltonian 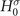 . Inserting the ansatz (4) and the exact Lehmann representation for the non-interacting Green's function
. Inserting the ansatz (4) and the exact Lehmann representation for the non-interacting Green's function 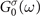 into the Dyson equation (1), we obtain a fixed-point equation for the GW quasiparticle energies [3, 4]
into the Dyson equation (1), we obtain a fixed-point equation for the GW quasiparticle energies [3, 4]

where 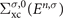 is the G0
W0 self-energy defined by replacing the interacting Green's function Gσ
(ω) with the non-interacting Green's function
is the G0
W0 self-energy defined by replacing the interacting Green's function Gσ
(ω) with the non-interacting Green's function 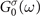 in equation (3).
in equation (3).
In this study, we used the graphical method to solve the nonlinear quasiparticle equation (5); details are given in the supporting information [36]. For the HOMO this method often leads to a unique solution, meaning that the intersection occurs in a pole-less region of the self-energy [19, 37]. As a result, the slight slope of the self-energy gives rise to a large quasiparticle weight, associated with a single pronounced peak in the diagonal elements of the spectral function, 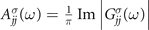 [24, 38]. However, for some cases, e.g. when the initial mean-field energy takes place in the vicinity of the self-energy pole position, equation (5) might provide more than one solution [19]. Ionization of lower lying states can also result in multiple solutions due to the coupling between created hole state and the neighboring excitations, producing several final states [39].
[24, 38]. However, for some cases, e.g. when the initial mean-field energy takes place in the vicinity of the self-energy pole position, equation (5) might provide more than one solution [19]. Ionization of lower lying states can also result in multiple solutions due to the coupling between created hole state and the neighboring excitations, producing several final states [39].
For open-shell systems, in particular, the occurrence of multiple solutions must be carefully considered. As an example, Lischner et al [14] have shown that precise knowledge of the self-energy on a fine frequency grid can capture the multiplet splittings, in agreement with the photo-ionization spectroscopy. These authors also point toward the importance of partial self-consistent calculations to accurately obtain the position of the self-energy pole(s). Although this study is limited to the standard G0 W0 approach, we give an example of this multiplet splitting in section 4.2.2.
2.3. Optimal single-particle Hamiltonian for G0 W0
An optimal choice of the single-particle Hamiltonian is important for the accuracy of the one-shot GW results, because of the well-known starting point dependence of the method [3]. In this study, we use unrestricted HF (UHF) [40, 41] and unrestricted Kohn–Sham (KS) [42–44] methods. HF Hamiltonian is a natural choice for Hedin's GWA, because the exchange part of Hedin's self-energy (3) coincides with the Fock operator [2, 3]. In fact, the GW self-energy can be split into a static non-local Fock exchange term and a frequency-dependent correlation part as 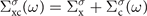 [3, 5, 11, 19].
[3, 5, 11, 19].
Among different types of functionals used within the KS method, hybrid functionals tend to be the most accurate for molecules [45]. Hybrid functionals make use of the non-local Fock exchange operator similar to the HF method, frequently in combination with an effective screened Coulomb interaction, plus a density functional to describe correlation effects. Therefore, it does not come as a surprise that hybrid functionals provide optimal starting points for the G0 W0 calculations [3, 18–21]. In this study, we employ both full-range and range-separated hybrid functionals. As representatives for the former, the fraction of exact exchange varies from 0.20 for B3LYP [46] to 0.25 for PBE0 [47]. Range-separated functionals are also represented by the CAM–B3LYP [48] and HSE06 [49], comprising different amounts of the HF exchange at short- and long-range.
2.4. Screened interaction
In the random phase approximation, with purely Coulombic interactions, the screened interaction W( r , r ', ω) is a spin-independent operator [3, 9] and reads
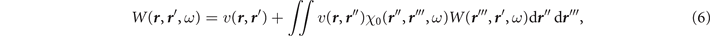
where χ0(
r
,
r
', ω) is the non-interacting density response function [50, 51], which has an explicit expression in terms of the single-particle eigenstates ψn,σ
(
r
) and their eigenenergies 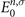 [52–54]
[52–54]

where fn,σ
and fm,σ
are the occupation factors, n and m represent the MO indices, and 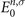 and
and 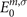 are MO energies, respectively.
are MO energies, respectively.
One finds that the screened interaction W(
r
,
r
', ω) is obtained from the spin-averaged χ0(
r
,
r
', ω) as defined above. Consequently, the spin-dependence of the G0
W0 self-energy 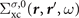 stems from that of the non-interacting Green's function G0 [55], where G0 in turn inherits the spin indices of the single-particle Hamiltonian H0, as defined in equation (2). In other words, the spin structure of the G0
W0 self-energy is determined by that of the Hamiltonian of the starting mean-field, which in the cases considered here is spin-diagonal.
stems from that of the non-interacting Green's function G0 [55], where G0 in turn inherits the spin indices of the single-particle Hamiltonian H0, as defined in equation (2). In other words, the spin structure of the G0
W0 self-energy is determined by that of the Hamiltonian of the starting mean-field, which in the cases considered here is spin-diagonal.
2.5. Δ-methods
It is well-known that a comparison between theoretical IEs and experimental values is a difficult test for electronic structure methods [19, 20, 28]. In order to demonstrate the validity of the GWA in the calculation of IEs and to evaluate its accuracy with respect to other approaches, we also computed IEs of our test-set molecules within the Δ-framework (usually is referred to as ΔSCF in the context of mean-field schemes), that is, the energy difference between two separate calculations for the neutral and cationic species [5, 56]. To this aim, we use several unrestricted correlated methods such as CCSD, CCSD(T), second-order Møller–Plesset perturbation theory (MP2), configuration interaction limited to single and double excitations (CISD), and density functional theory (DFT) with the B3LYP functional. Exchange-only methods such as UHF and restricted open-shell HF (ROHF) [57] were also employed.
Among all, we use the ΔCCSD(T) results as a reference since CCSD(T) has proven to be an accurate method for small to medium-sized closed-shell molecules and it remains the gold standard method in quantum chemistry [17, 18, 20, 29, 58, 59]. Likewise, the CCSD(T) approach is currently employed in many occasions as the reference method for open-shell atoms and molecules [58, 60]. More importantly, the G0 W0 method discussed in this paper is in essence a single reference approach, that is, a perturbative correction of the single configuration HF or KS models. Therefore, it seems reasonable to test its performance against highly accurate single reference methods, such as CCSD(T).
In the case of small finite systems, Δ-methods often lead to the IEs similar to the GWA quasiparticle excitation energies [10, 29, 56]. Nonetheless, a straightforward application of the Δ-methods is limited to the lowest IE. Calculations of deeper levels require a well-defined and efficient scheme to constrain the hole, left in the system after the excitation, in a particular state. This might be difficult in some cases [56, 61]. Moreover, Δ-methods present conceptual problems to deal with infinite periodic systems [5, 10], limiting their range of applicability. In contrast, the physics behind the GWA in terms of dynamical screened interactions in both finite and extended phases provides a general framework [5].
We would like to comment on the differences in the computational cost between the G0 W0 method and other applied approaches. Numerical implementations of the G0 W0 approach typically scale as O(N3)–O(N4) [62], where N is the number of basis functions. The computational demands in wave function-based methods are typically much higher in terms of processor time and storage requirements and present a worse scaling with basis size, e.g. O(N7) for CCSD(T) [63], prohibiting calculations for molecules containing more than a few tens of atoms [64].
2.6. Dyson orbitals
In order to test the validity of our G0 W0 approach, especially in those cases where mean-fields and G0 W0 provide different qualitative results, we compare MO energy diagrams with Dyson orbitals obtained within the coupled-cluster formalism. Dyson orbitals are typically used to compute Compton scattering profiles [65], electron momentum spectra [66], and represent a very powerful interpretation tool [67–69].
The Dyson orbital 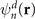 is a one-electron function that characterizes the probability amplitude distribution of obtaining electrons with a given binding energy during the ionization of a molecular species. It is defined as the overlap between the ground-state N-electron wave function
is a one-electron function that characterizes the probability amplitude distribution of obtaining electrons with a given binding energy during the ionization of a molecular species. It is defined as the overlap between the ground-state N-electron wave function 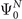 and the wave functions of the different states of the system containing N − 1 electrons
and the wave functions of the different states of the system containing N − 1 electrons 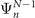
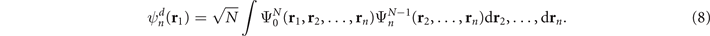
In order to go beyond the Koopman's approximation [70] and account for electron correlation effects on the Dyson orbitals, we employ coupled-cluster theory with single and double excitations for the ground state, while the ionized (N − 1 electron) state is obtained with the ionized version of the equation-of-motion formalism (EOM-IP-CCSD) [71].
3. Computational details
Δ-method calculations have been performed with the PySCF package [72, 73]. The GW calculations on top of various spin-polarized mean-field solutions were carried out using the MOLGW code [74]. Reference Dyson orbitals have been calculated with the Q-Chem electronic structure package [75].
To examine the basis set convergence, Dunning's correlation-consistent polarized cc-pVζZ were used, where the cardinal number ζ was restricted to double, triple and quadruple [76]. These basis sets are hierarchies of increasing size and angular momentum that provide a systematic way to obtain more accurate results, although they impose an increasing computational cost. Convergence tests with respect to the size of the basis sets are given in the supporting information [36].
High angular momentum and polarization functions are crucial factors in the description of open-shell molecules [62]. Results discussed in the main text have been obtained from the cc-pVQZ basis set. It is important to note that this basis set is still incomplete; so that an overestimation of the IEs in the range 0.1–0.2 eV could be anticipated [19, 20].
Molecules investigated in this study belong to the well-established G2/97 neutral test set [77–79]. For convenient comparison across different electronic structure methods and basis sets, we use the MP2(full)/6–31G(d) optimized geometries in all calculations. The spin configurations for neutral open-shell molecules are set to the standard values reported in previous literature [77, 78]. On the contrary, there is no such reference for cations; therefore, we opted for the most energetically stable configurations at the CCSD(T) level.
4. Results and discussion
4.1. Benchmarks of IE and EA+ of open-shell molecules
In this subsection, we evaluate the vertical IE of 42 open-shell molecules. IEs were calculated within the Δ-method and G0 W0 on top of different unrestricted mean-field solutions. Additionally, the electron affinities of the cationic species (EA+) are computed. As discussed in section 2.5, the ΔCCSD(T) method was chosen as the reference. Experimental IEs as reported in the NIST database [80] are also collected in the supporting information [36]. We find that IEs calculated within the ΔCCSD(T) agree with the available experiments, measured the vertical excitation energies, with a mean absolute error (MAE) of 0.11 eV.
For brevity, a color map representation of the deviations with respect to the ΔCCSD(T) reference is presented in figure 1 and statistical deviations were outlined in table 1. The reader is referred to the supporting information [36] for the molecule-resolved numerical results. In the case of Δ-methods, while UHF and ROHF variants show the highest error rates due to the lack of explicit electron correlation, unrestricted MP2, CISD, and B3LYP on average provide results in agreement with the reference. Note that, although B3LYP functional in the Δ-scheme leads to reasonable IEs, the errors of B3LYP KS eigenvalues can be rather large, in the range of several eVs.
Figure 1. Color map representation of the absolute error of the IEs obtained from different methods with respect to ΔCCSD(T) for the studied molecules. Calculations were done using a cc-pVQZ basis.
Download figure:
Standard image High-resolution imageTable 1. Statistical deviations of IEs (eV) derived from Δ-methods and G0 W0 on top of different unrestricted mean-field solutions with respect to ΔCCSD(T)/cc-pVQZ.
| Δ-methods | ||||||
|---|---|---|---|---|---|---|
| Deviation | CISD | CCSD | MP2 | B3LYP | UHF | ROHF |
| MSE | −0.04 | 0.00 | −0.05 | 0.11 | −0.58 | −0.63 |
| MAE | 0.16 | 0.07 | 0.13 | 0.19 | 0.72 | 0.71 |
| MAD | 0.72 | 0.43 | 0.72 | 0.60 | 1.79 | 1.94 |
| G0 W0@(mean field) | ||||
|---|---|---|---|---|
| UHF | CAM–B3LYP | PBE0 | B3LYP | |
| MSE | 0.55 | 0.12 | −0.09 | −0.18 |
| MAE | 0.55 | 0.14 | 0.12 | 0.20 |
| MAD | 1.46 | 0.37 | 0.39 | 0.52 |
On the other side, G0 W0@UHF (G0 W0 using the UHF starting point) presents an MAE of 0.55 eV, which is reduced to 0.12, 0.14, and 0.20 eV in @PBE0, @CAM–B3LYP, and @B3LYP, respectively. These deviations are comparable to those found for closed-shell molecules [11, 19–21, 29]. Not surprisingly, the G0 W0 results show an undesired dependence on the starting point as an accuracy-limiting factor. G0 W0@UHF and @CAM–B3LYP tend to overestimate the IEs with a mean signed error (MSE) of 0.55 and 0.12 eV while the computed IEs by G0 W0@B3LYP and @PBE0 are underestimated with an MSE of −0.18 and −0.09 eV, respectively.
Figure 2 shows the error distribution of the computed IEs using G0 W0 as a function of the mean-field starting point. While IEs calculated by G0 W0@UHF features a maximal absolute deviation (MAD) of 1.46 eV, G0 W0@B3LYP and @PBE0 and @CAM–B3LYP for the majority of the molecules show a slight deviation. Particularly, IEs computed within G0 W0@B3LYP and @PBE0 are underestimated with the exception of those obtained from effectively one-electron atoms, namely, Li and Na. This seems to point toward an overestimation of the correlation energy in such atoms, which can be tentatively ascribed to the self-screening of the single valence electron [81]. In the supporting information [36], moreover, we discussed the low quality of the quasiparticle solution for these two atoms. In the literature [31], it is indicated that for such atoms G0 W0@HF can provide IE comparable to those obtained through the self-consistent GW flavor.
Figure 2. Error distribution of the IEs computed by the G0 W0 on top of different starting points with respect to ΔCCSD(T) reference.
Download figure:
Standard image High-resolution imageWhen carrying unrestricted calculations, especially UHF, it is necessary to check the degree of spin contamination. The spin contamination can be judged by the expectation value of total spin operator 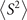 [24, 27, 41, 82]. Hence, we explored the difference between calculated
[24, 27, 41, 82]. Hence, we explored the difference between calculated 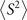 and the ideal s(s + 1) value, where s is the spin quantum number. Analysis of ⟨S2⟩ reveals that the spin contamination of the investigated molecules is small. For the systems studied here, moreover, we found no clear connection between the spin contamination at the starting point solutions and the error-rate of the calculated G0
W0–IEs. More details, explaining the equations to compute
and the ideal s(s + 1) value, where s is the spin quantum number. Analysis of ⟨S2⟩ reveals that the spin contamination of the investigated molecules is small. For the systems studied here, moreover, we found no clear connection between the spin contamination at the starting point solutions and the error-rate of the calculated G0
W0–IEs. More details, explaining the equations to compute 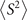 along with the degree of spin contamination, are given in the supporting information [36].
along with the degree of spin contamination, are given in the supporting information [36].
As discussed in section 2.2, the solution to the quasiparticle equation might not be unique. We confirm for the majority of our test-set systems the graphical method on a fine frequency grid provides a single solution for the HOMO with a pronounced spectral weight of around 0.9. Among all, only for a few systems and only at G0 W0@B3LYP and @PBE0, we found multiple solutions. In such systems, however, the spectral weights are rather different, favoring in general one solution against all others. Here, we only reported the solution with the largest weight in the spectral function and discussed cases with multiple solutions in the supporting information [36].
To further examine the quality of the G0 W0 approximation, we calculate the EA+. Detailed results are listed in the supporting information [36], where figure C-1 presents a summary of the deviations between IEs and EA+s for all the starting points. Here, we provided the reader with the statistical deviations collected in table 2 as well as a color map representation of the absolute error with respect to the reference in figure 1. Clearly, the MAE of the EA+s computed at the G0 W0@UHF is improved as compared with the corresponding deviation in table 1. Moreover, EA+s are underestimated with an MSE of −0.23 eV, which contracts with the systematic overestimation of the IEs for the UHF starting point (MSE = 0.55). This is in line with the well-known tendency of the HF, inherited by the G0 W0 .
Table 2. Statistical deviations of EA+ obtained from the one-shot GWA for cations with respect to ΔCCSD(T) results using cc-pVQZ basis.
| G0 W0@(mean field) | ||||
|---|---|---|---|---|
| Deviation | UHF | CAM–B3LYP | PBE0 | B3LYP |
| MSE | −0.23 | 0.06 | 0.15 | 0.23 |
| MAE | 0.40 | 0.17 | 0.21 | 0.27 |
| MAD | 1.26 | 0.62 | 0.62 | 0.68 |
Similarly to the G0 W0@UHF case, we observe a sign reversal of the MSE of the EA+s calculated from B3LYP and PBE0 starting points as compared to the MSE of the IEs (see tables 1 and 2). However, in contrast to the case of UHF, for these two hybrid functionals the MAE increases with respect to that found for the IEs of the neutral molecules. This is consistent with a larger error in the energy position of the LUMO in the initial DFT calculations, as compared to that of the HOMO, and points to the importance of an improved description of exchange in correcting the energies of the occupied states. G0 W0@CAM–B3LYP, on the other hand, provides a similar MAE for EA+s (0.17 eV) and IEs (0.14 eV) in which the MSE is positive in both cases. This seems to indicate that range-separated CAM–B3LYP functional as a starting point for the G0 W0 provides a more balanced description in terms of localization and delocalization errors than the other hybrid functionals considered here [30, 33, 34].
To gain an insight into the role of the exact exchange, we benchmarked the IEs and EA+s of our test-set molecules within the tuned PBE0 functional, where the fraction of exchange α varies from 0.35 to 0.75. The corresponding data are given in the supporting information [36], table D-1. As compared with the results obtained by G0 W0 starting from standard PBE0 (α = 0.25), we find all statistical deviations have slightly improved when the content of exchange is in the range of 0.35 to 0.4. For example, a fraction of 0.35 results in an MSE of 0.02 and 0.09 eV for the IEs of neutral molecules and the EA+s of the cations, respectively. When the exchange fraction is more than 50%, on the contrary, all deviations increase and provide a positive (negative) MSE for the IE (EA+). This indeed reflects the general rule of thumb that a larger content of exact exchange usually leads to an overestimation (underestimation) energies of the occupied (unoccupied) states.
To sum up, this benchmark reveals that the G0 W0 scheme can treat open-shell molecules with a reasonable accuracy comparable to that of CCSD(T), while its performance in terms of the computational cost is favorable. G0 W0 on top of the optimal starting points, i.e. hybrid functionals, yields an MAE of 0.1–0.2 eV for IEs, while EA+s show a slightly larger MAE of 0.2–0.3 eV. For G0 W0 @UHF, on the other hand, the MAE was reduced from 0.55 eV to 0.4 eV when EA+ of the cations are computed instead of the IEs of the neutral molecules. We ascribed this apparent improvement to the overestimation of the role of exchange in UHF, that gives rise to too large IEs. Among the hybrid functionals studied here, long-ranged CAM-B3LYP provides the smallest discrepancy of 0.03 eV between the MAE of IE and MAE of EA+.
4.2. One-electron spectrum of selected molecules
The interpretation of photo-electron spectroscopy is frequently performed in terms of effective independent electron theories where the concept of MO appears naturally. Thus, the energies and symmetries of Frontier MOs become central to understanding the interaction of molecules with light. The connection of such single-electron description with a many-body picture has been discussed by many authors [37], pointing out that the quasiparticle concept can fail in the presence of strong electron–electron interactions or high excitation energies for which many different excitations in the system (including those with the intrinsic collective character) can contribute [22, 37, 39, 83, 84]. In the present case, however, we focus on the lowest photo-ionization energies and explore the accuracy of our mean-field starting points and G0 W0 to describe them, in particular the relative energy positions of MOs with different character. Our connection to a full many-body description is provided by the Dyson orbitals obtained from CCSD calculations, which are expected to include a fair account of many-body effects both in their excitation energies and spatial distributions [84]. We find that, while the character of the MOs obtained by HF and KS is in general in good agreement with the Dyson orbitals, their energy ordering is different in several cases. Interestingly, as shown below, G0 W0 is able to recover the correct energy order of the Frontier MOs. In the following, we focus our attention on three specific cases, namely, CN, NH2, and O2 molecules and discuss the sequence of spin-up MOs.
4.2.1. First and second IEs of molecular radicals
The cyano radical (CN) is a paramagnetic system exhibiting one unpaired electron in the σ2p HOMO with the fully occupied (degenerate) π2p orbitals at lower energy. Figure 3(a) illustrates the energy eigenvalues of these orbitals calculated by different methods. Dyson orbital energies are also given as reference (solid lines). The reference energies show a separation of 0.88 eV between the σ2p (HOMO) and π2p (HOMO-1), which agrees with previous results [85–89]. This is clearly a challenging system for mean-field methods, and we see both HF and KS with different xc functionals present incorrect energy ordering of MOs.
Figure 3. Majority-spin orbital energies calculated by using different mean-field approaches and G0 W0 on top of them for the HOMO and HOMO-1 orbitals of doublet (a) CN and (b) NH2 molecules. Solid lines correspond to EOM–IP–CCSD energies as reference. The shaded area shows the correct ordering of MOs according to the reference. Notice that different hybrid functionals are arranged from left to right in descending order of the exact-exchange content. Isosurfaces of the computed Dyson orbitals are represented next to the corresponding EOM–IP–CCSD solid lines. Small pink, brown, and green circles represent hydrogen, carbon, and nitrogen atoms, respectively.
Download figure:
Standard image High-resolution imageWithin the UHF, σ2p eigenvalue is ∼1.5 eV larger than the corresponding reference, while the energy of the degenerate π2p level is surprisingly underestimated by about 0.6 eV. Such high errors lead to an inverted energy ordering of orbitals with a large σ2p –π2p separation of 1.2 eV. DFT using three different hybrid functionals, on the other hand, systematically underestimates the energies of both orbital types. This underestimation is significantly higher for the degenerate π2p orbitals than for σ2p , resulting in the wrong ordering, but with a smaller gap (∼0.3 eV) than that of UHF.
Regardless of the starting-point, G0 W0 correction (shaded area) not only leads to the correct MO ordering in CN but also estimated quasiparticle orbital energies are much closer to the reference. Particularly, energy separation between σ2p –π2p obtained from the G0 W0 starting from mean-field approximations with high contents of Fock exchange, namely, UHF and CAM-B3LYP, are very small (∼0.2 eV), since both methods tend to overestimate σ2p and underestimate π2p energies. In contrast, G0 W0 calculations starting from either PBE0 or B3LYP provide improved results, with an energy separation around 0.5 eV.
Next, we turn our attention to the study of the amino radical NH2. The singly occupied HOMO of NH2 corresponds to the 2p nitrogen orbital perpendicular to the molecular plane belonging to the B1 irreducible representation of the C2v molecular symmetry (1b1 orbital). The lower orbital is obtained as the bonding interaction between the 2pz nitrogen orbital (aligned with the twofold rotational axis) and the in-phase combination of the 1s orbitals on the two hydrogen atoms, which belongs to the totally symmetric representation (3a1 orbital).
As depicted in figure 3(b), UHF predicts the inverted order for the 1b1 and 3a1 orbital energies. Like in CN, G0 W0@UHF corrects the UHF orbital energies with a final one-electron energy ordering in agreement with the reference Dyson orbital energies. DFT calculations, on the other hand, correctly predict the ordering of MOs. However, attributed eigen-energies are significantly underestimated (more than 3.7 eV for B3LYP). Here, the G0 W0 correction greatly improves the accuracy of orbital energies with an MAE of 0.22 and 0.18 eV for the HOMO and HOMO-1, respectively.
4.2.2. Swapping of IEs in spin-triplet molecules
In the triplet O2 molecule, with a 3Σg
symmetry ground-state, because of a relatively large gap between 2s and 2p states of the oxygen atom, no hybridization occurs between s and p atomic orbitals. Therefore, σ2p
orbital is energetically situated below the two-fold degenerate π2p
and 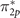 orbitals [90–93]. The same ordering is obtained by the reference, where Dyson orbital energies are determined to be −12.55, −17.73, and −19.46 eV for
orbitals [90–93]. The same ordering is obtained by the reference, where Dyson orbital energies are determined to be −12.55, −17.73, and −19.46 eV for 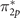 (HOMO), π2p
(HOMO-1), and σ2p
(HOMO-2), respectively. As shown in figure 4, neither UHF nor DFT using hybrid functionals can capture the correct energy ordering of the HOMO-1 and HOMO-2 orbitals. UHF overshoots π-type orbital energies leading to a large separation between σ2p
and π2p
(2.1 eV) and wrong ordering that is not corrected even at the G0
W0@UHF level. Similarly, hybrid functionals used within the DFT considerably underestimate σ2p
energy and provide a vanishingly small energy spacing between σ2p
and π2p
orbitals.
(HOMO), π2p
(HOMO-1), and σ2p
(HOMO-2), respectively. As shown in figure 4, neither UHF nor DFT using hybrid functionals can capture the correct energy ordering of the HOMO-1 and HOMO-2 orbitals. UHF overshoots π-type orbital energies leading to a large separation between σ2p
and π2p
(2.1 eV) and wrong ordering that is not corrected even at the G0
W0@UHF level. Similarly, hybrid functionals used within the DFT considerably underestimate σ2p
energy and provide a vanishingly small energy spacing between σ2p
and π2p
orbitals.
Figure 4. Majority-spin orbital energies for different approximations for twofold degenerate HOMO ( ), twofold degenerate HOMO-1 (π2p
), and HOMO-2 (σ2p
) orbitals of the triplet O2 molecule. Solid lines show the reference orbital energy computed by EOM–IP–CCSD. The shaded area indicates the correct ordering of MOs.
), twofold degenerate HOMO-1 (π2p
), and HOMO-2 (σ2p
) orbitals of the triplet O2 molecule. Solid lines show the reference orbital energy computed by EOM–IP–CCSD. The shaded area indicates the correct ordering of MOs.
Download figure:
Standard image High-resolution imageQuasiparticle energies obtained from G0
W0 started from hybrid functionals interchange the energy order of σ2p
and π2p
orbitals, providing the same as that given by the reference. From a quantitative point of view, G0
W0@CAM–B3LYP gives the quasiparticle σ2p
energy very close to the reference, while estimated IEs of π2p
and 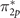 are overestimated by 1 and 0.36 eV, respectively. Conversely, G0
W0@PBE0 yields the closest energies of both π-type orbitals to the reference values, whereas the energy of the σ2p
orbital is underestimated by 0.62 eV. Eventually, G0
W0@B3LYP and @HSE06 accurately estimate the HOMO energy while IEs of π2p
and σ2p
orbitals are underestimated by around 0.5 and 0.9 eV, respectively. More details are given in the supporting information [36].
are overestimated by 1 and 0.36 eV, respectively. Conversely, G0
W0@PBE0 yields the closest energies of both π-type orbitals to the reference values, whereas the energy of the σ2p
orbital is underestimated by 0.62 eV. Eventually, G0
W0@B3LYP and @HSE06 accurately estimate the HOMO energy while IEs of π2p
and σ2p
orbitals are underestimated by around 0.5 and 0.9 eV, respectively. More details are given in the supporting information [36].
It is clear that diverse MO types respond differently to the GW correction. It has been recently shown that the GW self-energy often provides a poor estimation of σp orbital energies [94]. The self-screening problem of the GWA can also affect the energy level of orbitals with different bonding types [17, 95]. Therefore, to quantify the origin of such errors in the computed orbital energies of the oxygen molecule, we analyze the behavior of the two GW self-energy components Σ(E) = Σx + Σc(E), the exchange and correlation terms, for the different starting points.
Figures 5(a)–(c) show the diagonal expectation values of the exchange contribution Σx to the self-energy for the three topmost majority-spin occupied orbitals, i.e. 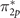 , π2p
, and σ2p
in the O2 molecule in its triplet ground-state configuration. For each of the mean-field methods, we evaluate the expectation values of Σx as
, π2p
, and σ2p
in the O2 molecule in its triplet ground-state configuration. For each of the mean-field methods, we evaluate the expectation values of Σx as ![$\left\langle {\psi }^{m}\vert {{\Sigma}}_{\text{x}}\left[{\rho }^{m}\right]\vert {\psi }^{m}\right\rangle $](https://content.cld.iop.org/journals/1367-2630/23/9/093027/revision3/njpac1bf3ieqn24.gif) , where ψm
and ρm
are the corresponding mean-field's wave function and one-particle density matrix, respectively. For each orbital, the reference is given by the expectation value of the exact-exchange with the CCSD density ρCCSD and the corresponding Dyson orbitals ψd
in the bra-ket,
, where ψm
and ρm
are the corresponding mean-field's wave function and one-particle density matrix, respectively. For each orbital, the reference is given by the expectation value of the exact-exchange with the CCSD density ρCCSD and the corresponding Dyson orbitals ψd
in the bra-ket, ![$\left\langle {\psi }^{d}\vert {{\Sigma}}_{\text{x}}\left[{\rho }^{\text{CCSD}}\right]\vert {\psi }^{d}\right\rangle $](https://content.cld.iop.org/journals/1367-2630/23/9/093027/revision3/njpac1bf3ieqn25.gif) . Notice that the density matrix obtained from CCSD calculations, taking into account the contributions from single and double excitations, contains high quality information about the electron correlations in the system. Therefore, the difference between the mean-fields' exchange energy and the reference for each orbital, as shown in figure 5, reveals the effect of electron correlations beyond the mean-field theory. A detailed comparison of the contribution of density matrices can be found in the supporting information [36], figure F-1, where
. Notice that the density matrix obtained from CCSD calculations, taking into account the contributions from single and double excitations, contains high quality information about the electron correlations in the system. Therefore, the difference between the mean-fields' exchange energy and the reference for each orbital, as shown in figure 5, reveals the effect of electron correlations beyond the mean-field theory. A detailed comparison of the contribution of density matrices can be found in the supporting information [36], figure F-1, where ![$\left\langle {\psi }^{m}\vert {{\Sigma}}_{\text{x}}\left[{\rho }^{\text{CCSD}}\right]\vert {\psi }^{m}\right\rangle $](https://content.cld.iop.org/journals/1367-2630/23/9/093027/revision3/njpac1bf3ieqn26.gif) values are also presented.
values are also presented.
Figure 5. Expectation values of the G0 W0 self-energy components; (a)–(c) Σx and (d) Σc starting from different mean-field calculations for the three topmost occupied orbitals of O2 molecule in its triplet ground-state configuration. Dotted lines are energies obtained from the corresponding mean-field orbitals and density matrix. Solid lines represent the reference values computed using the CCSD density matrix and the corresponding Dyson orbitals obtained from EOM–IP–CCSD. All calculations are done within the cc-pVQZ basis set.
Download figure:
Standard image High-resolution imageResults show that all exchange energies are overestimated with respect to the reference. While the expectation values of the exchange energy for σ2p
, π2p
, and 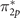 orbitals within the DFT solutions are overestimated with a mean error of 0.54, 1.22, and 0.66 eV, the UHF solution leads to an error of 0.53, 1.86, and 1.2 eV, respectively. Such large deviations, particularly for π-type orbitals, directly reflect the origin of the incorrect spectra at the UHF level, shown in figure 4.
orbitals within the DFT solutions are overestimated with a mean error of 0.54, 1.22, and 0.66 eV, the UHF solution leads to an error of 0.53, 1.86, and 1.2 eV, respectively. Such large deviations, particularly for π-type orbitals, directly reflect the origin of the incorrect spectra at the UHF level, shown in figure 4.
Figure 5(d) features the diagonal expectation values of the dynamic correlation part of the G0
W0 self-energy 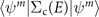 , where E is the corresponding MO energy at the G0
W0 level. The reference values are obtained by subtracting the Dyson orbital energies in equation (8) from Fock energies
, where E is the corresponding MO energy at the G0
W0 level. The reference values are obtained by subtracting the Dyson orbital energies in equation (8) from Fock energies ![$\left\langle {\psi }^{d}\vert F\left[{\rho }^{\text{CCSD}}\right]\vert {\psi }^{d}\right\rangle $](https://content.cld.iop.org/journals/1367-2630/23/9/093027/revision3/njpac1bf3ieqn29.gif) for each orbital. Clearly, the correlation energies attributed to π2p
-type orbitals are higher than σ2p
. This can be ascribed to the larger extension and polarizability of the π2p
orbitals. Notice that the G0
W0 provides rather higher correlation energy for π2p
(HOMO-1) as compared to the
for each orbital. Clearly, the correlation energies attributed to π2p
-type orbitals are higher than σ2p
. This can be ascribed to the larger extension and polarizability of the π2p
orbitals. Notice that the G0
W0 provides rather higher correlation energy for π2p
(HOMO-1) as compared to the  (HOMO). Adding these positive correlation energies pulls up π-type orbital energies in the spectra, leading to more accurate energies associated with the correct MO picture for hybrid orbitals, as shown in figure 4. In comparison with reference values, however, one sees that the correlation energy of the π2p
orbital is underestimated in direct relation to the fraction of the exact exchange. Therefore, hybrid functionals with a higher fraction of long-range exchange incorrectly provide smaller separation between σ2p
and π2p
. This also explains the dramatic failure of the G0
W0@UHF, where estimated correlation energy for UHF-π2p
orbital is drastically insufficient to provide the correct spectra.
(HOMO). Adding these positive correlation energies pulls up π-type orbital energies in the spectra, leading to more accurate energies associated with the correct MO picture for hybrid orbitals, as shown in figure 4. In comparison with reference values, however, one sees that the correlation energy of the π2p
orbital is underestimated in direct relation to the fraction of the exact exchange. Therefore, hybrid functionals with a higher fraction of long-range exchange incorrectly provide smaller separation between σ2p
and π2p
. This also explains the dramatic failure of the G0
W0@UHF, where estimated correlation energy for UHF-π2p
orbital is drastically insufficient to provide the correct spectra.
It is worth mentioning here the multiple solutions obtained for HOMO-2 orbital of the triplet oxygen molecule. While removal one electron from  (HOMO) features a single pronounced peak in the spectral function, ionization of up-spin σ2p
orbital results in two peaks as described in the supporting information [36]. This is consistent with a previous study [14], where the two solutions are attributed to the splitting between two possible ionic states, namely, doublet (2Σg
) and quartet (4Σg
), which is experimentally determined to be 2.3 eV [96]. We find values of 2.03 and 2.56 eV for this splitting at the G0
W0@B3LYP and @PBE0, respectively. Notice that this does not qualitatively affect the spectra shown in figure 4 since the second solution occurs at lower energy (∼21 eV).
(HOMO) features a single pronounced peak in the spectral function, ionization of up-spin σ2p
orbital results in two peaks as described in the supporting information [36]. This is consistent with a previous study [14], where the two solutions are attributed to the splitting between two possible ionic states, namely, doublet (2Σg
) and quartet (4Σg
), which is experimentally determined to be 2.3 eV [96]. We find values of 2.03 and 2.56 eV for this splitting at the G0
W0@B3LYP and @PBE0, respectively. Notice that this does not qualitatively affect the spectra shown in figure 4 since the second solution occurs at lower energy (∼21 eV).
Summarizing the discussion, we emphasize that MOs with different symmetry respond with varying sensitivity to different approximations to describe the exchange and correlation effects. In the case of CN and NH2 molecules, we showed that mean-field solutions might predict an incorrect sequence of the Frontier orbitals due to the significant over- or underestimation of the IEs, while the GW correction can provide reasonably accurate orbital energies associated with the correct ordering. Likewise, in the example of O2, we found that the G0 W0 can correct the overestimation of the exchange energy by adding a well-set correlation, thanks to its energy-dependent screening. As a result, the dynamic contribution of the GW self-energy can result in an electronic structure that is qualitatively different from that of mean-field methods.
5. Conclusion
We performed the one-shot GWA within the spin-diagonal formalism for open-shell molecules. We benchmarked the IEs of 42 neutral molecules, proposed in the G2/97 test set. The reference for our calculations was ΔCCSD(T). The statistical deviations of the IEs are comparable to those found for closed-shell molecules. The delocalization or localization error of the G0 W0 on top of different starting points was examined by comparing the IE of neutral molecules with the EA of the corresponding cation. We observed that the deviations between IEs and EA+s follow a systematic behavior as a function of the exact-exchange content in the initial mean-field calculation. Overall, we showed that G0 W0 on top of the optimal starting point, DFT using hybrid functionals, provides a systematic and reasonably accurate method to compute the electron addition or removal energies for such small open-shell molecules.
Furthermore, we discussed the capability of the GWA to provide the correct energy order of the MOs. This capability has been thoroughly discussed in the case of three molecules, for which mean-field calculations fail to capture the correct ordering of the MOs due to the systematic failures of approximate xc functionals. Supported by inspection of the GW self-energy components in the three topmost occupied orbitals of O2 molecule, we quantified the overestimation of the exchange energies in these orbitals and showed how the dynamic correlation of the GW self-energy can reduce such deviations, leading to the correct and accurate energy order. As compared with the CCSD reference, we found that errors in the exchange and correlation energies can be very different for MOs with different symmetry, e.g. σ and π orbitals in the case of the O2 molecule.
From the understanding offered in this work, one can explain the errors occurred at the mean-field level and their impact on the estimation of the IEs within the G0 W0. Results demonstrate that the average performance of the G0 W0 is sensible, while its computational efficiency is favorable in comparison with traditional correlated methods in quantum chemistry.
Acknowledgments
Authors acknowledge support from Spanish Agencia Estatal de Investigación (Grant Nos. PID2019-107338RB-C66, PID2019-109555GB-I00 and RTC-2016-5681-7), and the Eusko Jaurlaritza and UPV/EHU (Grant Nos. PIBA19-0004 and IT1246-19). DSP also acknowledges support from the European Union (EU) through Horizon 2020 (FET-Open project SPRING Grant No. 863098).
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).








