Abstract
The interaction of electromagnetic waves with matter is at the foundation of the way we perceive and explore the world around us. In fact, when a field interacts with an object, signatures on the object's geometry and physical properties are recorded in the resulting scattered field and are transported away from the object, where they can eventually be detected and processed. An optical field can transport information through its spectral content, its polarization state, and its spatial distribution. Generally speaking, the field's spatial structure is typically subjected to changes under free-space propagation and any information therein encoded gets reshuffled by the propagation process. We must ascribe to this fundamental reason the fact that spectroscopy was known to the ancient civilizations already, and founded as modern science in the middle of seventeenth century, while to date we do not have an established scientific of field of 'spatial spectroscopy' yet. In this work we tackle this issue and we show how any field, whose evolution is dictated by Helmholtz equation, contains a universal and invariant spatial structure. When expressed in the framework of this spatial fabric, the spatial information content carried by any field reveals its invariant nature. This opens the way to novel paradigms in optical digital communications, inverse scattering, materials inspection, nanometrology and quantum optics.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Our understanding of the many physical phenomena taking place in Nature often requires extracting information from different types of wavefields. Electromagnetic fields play a special role in this sense, because:
- (a)It deals with infinite-range fields. Hence, they tell us on events that happened remotely in space and time.
- (b)
Of equal importance are also applications of wave fields in communications. The growing demand for an interconnected society drives the need for an increased capacity of free-space communications by finding new ways of encoding large amount of information in an electromagnetic wave [3–6]. For monochromatic fields propagating in free space we know that the spectral content consists of a single wavelength λ, which remains invariant in propagation. Also the polarization state of a field remains essentially unaffected by propagation, except for the special cases of strongly focused fields which can show nontrivial polarization changes in the focal region. The situation is quite different for the spatial degree of freedoms, though. In fact, except for the very limited classes of the so-called diffraction-free and shape-invariant fields [7–11], the first class of fields being not physically realizable and the second being only strictly defined within the paraxial regime, until now it seemed to be not possible to represent the spatial information present in any field in a way that remains manifestly invariant under propagation. In some sense this is not to be expected because, on an purely intuitive point of view, a free field does not interact with anything which could destroy the information content originally imprinted in it and, after all, the fields equations are deterministic by nature. With the risk of oversimplifying the description, one can picture the situation as that of an object made of a mass of a restless fluid constrained within a closed plastic bag: if the object moves, the fluid total mass remains constant while the bag continuously mutates its shape. While one observer would clearly see a shape changing with time, it might exist a particular reference frame where the fluid would be at rest and the shape of the plastic bag would stay frozen. The current work has been motivated by this simple reasoning and we will show that, indeed, it is possible to find such a privileged representation of a field. Once described in this way, any effect of propagation is removed and the field simply reveals its spatial content, which is, as expected, invariant for any field. This result opens new exciting possibilities in many different fields, as we will discuss later on in the manuscript. More importantly, Helmholtz equation is not bound to only electromagnetism as all. In fact, all the things we are going to present here can be applied to acoustic waves as well and to any other field theory which satisfies a similar equation of motion. The manuscript is organized as follows: in section 2 we introduce the main formalism and the concept of Helmholtz natural modes (HNMs) and we discuss their main properties. In section 3 we show an explicit example of application which helps visualize the essence of the invariance. Finally, in section 4 we summarize the main achievements of the work.
2. Helmholtz equation, non paraxial fields and fields representations
Without any loss of generality, let us consider a scalar monochromatic optical beam that propagates in a region of space where a Cartesian reference frame, 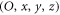 has been defined, being z the main direction of propagation for the field. We know that the field must satisfy Helmholtz equation, which reads
has been defined, being z the main direction of propagation for the field. We know that the field must satisfy Helmholtz equation, which reads
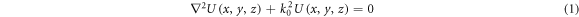
with 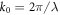 .
. 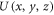 denotes the field distribution of the (scalar) field. If
denotes the field distribution of the (scalar) field. If 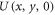 represents its value on a reference input plane z = 0, the following Fourier integral representation holds
represents its value on a reference input plane z = 0, the following Fourier integral representation holds

where 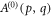 is the angular spectrum of the field, and (p, q) the spatial frequencies in Fourier space. The integration domain
is the angular spectrum of the field, and (p, q) the spatial frequencies in Fourier space. The integration domain  is a subset of the homogeneous domain only as a consequence of the fact that evanescent waves are not present in the integral representation in equation (2). This is because we are considering fields that propagate on distances larger than the wavelength λ such that any contribution to the field coming from evanescent waves can be safely neglected. When dealing with freely-propagating fields, one usually refers to this fact as the low-pass filtering effect of propagation. Once the angular spectrum
is a subset of the homogeneous domain only as a consequence of the fact that evanescent waves are not present in the integral representation in equation (2). This is because we are considering fields that propagate on distances larger than the wavelength λ such that any contribution to the field coming from evanescent waves can be safely neglected. When dealing with freely-propagating fields, one usually refers to this fact as the low-pass filtering effect of propagation. Once the angular spectrum 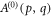 is known, Helmholtz equation tells us how to compute it to another plane z. In fact, by denoting such a spectrum at plane z as
is known, Helmholtz equation tells us how to compute it to another plane z. In fact, by denoting such a spectrum at plane z as 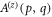 , we have
, we have
For convenience later on, in equation (3) we have introduced a circular coordinate system in Fourier domain,  such that
such that  and
and  . Given that the angular spectrum
. Given that the angular spectrum  is defined on a finite support (the disk on Fourier space of radius
is defined on a finite support (the disk on Fourier space of radius 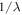 ) it must be possible to represent it in terms of a discrete, bi-dimensional, modal decomposition. This is a remarkable property, if we consider that we are dealing with classical free-fields. In pure mathematical terms, the problem of finding an orthogonal base through which one can decompose a field distribution on a circular domain can be solved in different ways, by introducing different types of field expansions. In optics, the most used decomposition is that introduced by Zernike and Nijboer around the 40s of the last century [12–16], nowadays better known as Nijboer–Zernike's unit circle polynomials expansion. Nijboer–Zernike expansion owns its popularity in optics to its applications to the characterization of aberrations of optical systems. Another base, mostly used in patterns recognition and nowadays also in adaptive optics, is represented by the so-called disk-harmonics [17, 18]. These are eigenfunctions of the Laplacian operator and what they share with the Nijboer–Zernike's decomposition is the fact that it deals with an orthogonal base on the unit disk as well. However, all these bases also share a common limitation: they are all not compatible with Helmholtz equation, which leads them violate propagation invariance. The lack of propagation invariance gives rise to cross-talks among the modes and makes a field decomposition not unique. This in practice means that the same field gives rise to different decompositions if analyzed at different reference planes.
) it must be possible to represent it in terms of a discrete, bi-dimensional, modal decomposition. This is a remarkable property, if we consider that we are dealing with classical free-fields. In pure mathematical terms, the problem of finding an orthogonal base through which one can decompose a field distribution on a circular domain can be solved in different ways, by introducing different types of field expansions. In optics, the most used decomposition is that introduced by Zernike and Nijboer around the 40s of the last century [12–16], nowadays better known as Nijboer–Zernike's unit circle polynomials expansion. Nijboer–Zernike expansion owns its popularity in optics to its applications to the characterization of aberrations of optical systems. Another base, mostly used in patterns recognition and nowadays also in adaptive optics, is represented by the so-called disk-harmonics [17, 18]. These are eigenfunctions of the Laplacian operator and what they share with the Nijboer–Zernike's decomposition is the fact that it deals with an orthogonal base on the unit disk as well. However, all these bases also share a common limitation: they are all not compatible with Helmholtz equation, which leads them violate propagation invariance. The lack of propagation invariance gives rise to cross-talks among the modes and makes a field decomposition not unique. This in practice means that the same field gives rise to different decompositions if analyzed at different reference planes.
A modal decomposition, orthogonal but also propagation invariant, must necessarily account for the natural fabric of electromagnetism, in other words, it must contain the natural spatial modes of the physical system. Recently, it has been shown how such a base can be defined within the paraxial approximation [19]. If a modal decomposition for the full non paraxial case exists, it must reduce to that paraxial base decomposition within the paraxial limit. On the other hand, the transition from a paraxial to fully non paraxial regime is not trivial nor guaranteed. In order to appreciate this, we can for instance recall the difficulty of finding a close-form expression for a Gaussian beam under non paraxial regime or, again, the large amount of works describing the physics of vortex beams in analytical terms, in the majority of the cases limited to the known existing paraxial solutions (like Laguerre–Gauss beams or Ince–Gauss beams) and very few non paraxial cases (like Bessel beams or Mathieu beams [7, 20, 21]). Interestingly enough, how we are going to show in moment, it is possible to find the analytical expression for a modal decomposition, orthogonal but also propagation invariant, which is compatible with Helmholtz equation. The relevance of this finding stems from the fact that Helmholtz equation applies to many field theories, not only electromagnetism. In the next section we will introduce such a base.
2.1. Helmholtz natural modes
If one aims at finding a description of a field in terms of orthogonal modes that is however also compatible with the field equations, there are no many possibilities to choose from. From equation (3) we know that free space propagation alters the field angular spectrum by the factor 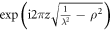 and one should try to find a base which shares a similar functional dependency. Inspired by this principle, we write
and one should try to find a base which shares a similar functional dependency. Inspired by this principle, we write 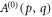 in the following way
in the following way
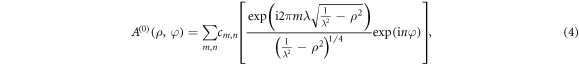
where m and n are integers, with 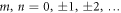 . As we will show, equation (4) is the core result of this work and we will refer to the modes of the base as the Helmholtz Natural Modes (HNMs). If we define
. As we will show, equation (4) is the core result of this work and we will refer to the modes of the base as the Helmholtz Natural Modes (HNMs). If we define
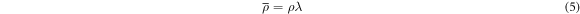
then the expansion in equation (4) is defined on the unit disk and takes the form
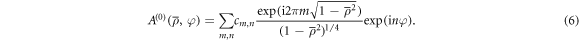
In equation (6) the coefficients  have been rescaled to include a constant factor
have been rescaled to include a constant factor 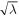 . In terms of the new normalized variable, equation (3) becomes
. In terms of the new normalized variable, equation (3) becomes
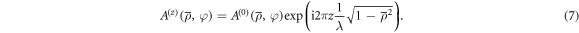
The orthogonality of the modes in equation (6) is consequence of the relations (denoting again 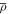 as ρ)
as ρ)
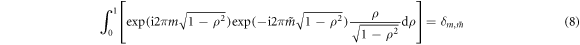
and
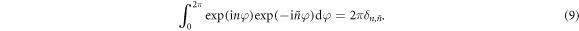
The coefficients 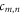 in equation (4), which represent in fact the HNMs spectrum for the field
in equation (4), which represent in fact the HNMs spectrum for the field 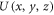 , can be computed as follows
, can be computed as follows
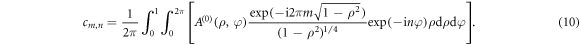
In figure 1, the phase profiles, and the amplitude common to all the modes, are shown for the modes with indices 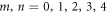 . It is important to point out that each of the fundamental modes appearing in equation (6) carries the same finite amount of energy, equal to
. It is important to point out that each of the fundamental modes appearing in equation (6) carries the same finite amount of energy, equal to 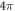 , which makes it physically realizable. The propagation invariance of this expansion can be appreciated if one tries to compare the expression for the coefficients
, which makes it physically realizable. The propagation invariance of this expansion can be appreciated if one tries to compare the expression for the coefficients 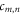 for the angular spectrum
for the angular spectrum 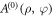 in equation (6) with those of the propagated spectrum
in equation (6) with those of the propagated spectrum 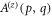 in equation (7). The HNM spectrum for
in equation (7). The HNM spectrum for 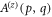 reads
reads
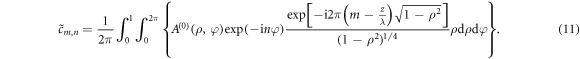
By comparing equations (10) and (11) we see that the following trivial map exists

where  . This map simply corresponds to a lateral shift of the whole HNMs spectrum along the axis of radial index m. In particular, at an infinite set of distances
. This map simply corresponds to a lateral shift of the whole HNMs spectrum along the axis of radial index m. In particular, at an infinite set of distances 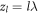 , with
, with 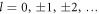 , the spectrum of
, the spectrum of 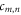 shifts by an integer amount of units along the radial axis. Hence, we have found a representation of any solution of Helmholtz equation in orthogonal modes which is also invariant. We would like to recall that by invariance is intended that, except for some trivial scaling, shifting, or rotation, the relation
shifts by an integer amount of units along the radial axis. Hence, we have found a representation of any solution of Helmholtz equation in orthogonal modes which is also invariant. We would like to recall that by invariance is intended that, except for some trivial scaling, shifting, or rotation, the relation 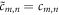 holds. One might wonder what kind of field distribution corresponds to the decomposition in Fourier space in equation (4). That can be easily obtained by just Fourier inverting the HNM expansion of
holds. One might wonder what kind of field distribution corresponds to the decomposition in Fourier space in equation (4). That can be easily obtained by just Fourier inverting the HNM expansion of 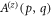 with coefficients
with coefficients 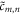 , which gives
, which gives
where  ,
,  . The fundamental modes in real space consist of vortices in the azimuthal variable θ and integrals of Bessel functions in the radial variable r. This form for the field decomposition makes also evident that the only contribution to the field on the optical axis is (r = 0), comes from the coefficients
. The fundamental modes in real space consist of vortices in the azimuthal variable θ and integrals of Bessel functions in the radial variable r. This form for the field decomposition makes also evident that the only contribution to the field on the optical axis is (r = 0), comes from the coefficients  , as expected. In fact, all the other terms would lead to a undefined phase at the points
, as expected. In fact, all the other terms would lead to a undefined phase at the points  , due to the presence of the vortex
, due to the presence of the vortex 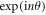 in the phase profile, which would be not physical. Also, it is important to stress that the decomposition in equation (13) lends itself to a convenient quantization of a non paraxial field. In fact, it is discrete by nature and it consists of orthogonal modes already, which can easily be turned into field operators. We can say that the modes in equation (13) parallel the role that Hermite–Gauss modes have in quantum optics, which are however, as well known, limited to the paraxial regime only.
in the phase profile, which would be not physical. Also, it is important to stress that the decomposition in equation (13) lends itself to a convenient quantization of a non paraxial field. In fact, it is discrete by nature and it consists of orthogonal modes already, which can easily be turned into field operators. We can say that the modes in equation (13) parallel the role that Hermite–Gauss modes have in quantum optics, which are however, as well known, limited to the paraxial regime only.
Figure 1. Amplitude and phase profiles of some HNMs in Fourier space. While all the HNMs share the same amplitude profile, their phase distribution depends on the indices 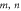 of the mode.
of the mode.
Download figure:
Standard image High-resolution image3. One example of application
In order to help the reader visualize what are the main features of the HNMs, we will now discuss a concrete example. In figure 2 (panel 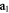 ), we show the measured wavefront of a collimated optical beam, as measured by using a wavefront sensor, and the same beam after a phase shift
), we show the measured wavefront of a collimated optical beam, as measured by using a wavefront sensor, and the same beam after a phase shift ![$\exp [{\rm{i}}2\pi \sqrt{1-{\rho }^{2}}]$](https://content.cld.iop.org/journals/1367-2630/19/1/013021/revision2/njpaa57c3ieqn42.gif) has been applied to the field (figure 2, panel
has been applied to the field (figure 2, panel 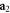 ). This phase shift just represents the effect of propagation under a distance
). This phase shift just represents the effect of propagation under a distance 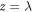 . In panel
. In panel 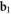 we show the expansion of the field in panel
we show the expansion of the field in panel 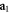 in terms of the first fifteen Zernike's circle polynomials. Panel
in terms of the first fifteen Zernike's circle polynomials. Panel 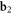 shows again the Zernike's circle polynomials decomposition for the propagated field shown in panel
shows again the Zernike's circle polynomials decomposition for the propagated field shown in panel 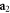 . As it is evident from the two pictures, Zernike's decomposition changes completely, being affected by propagation-induced cross-talk problems, mostly among the radial part of the modes. On the other hand, panels
. As it is evident from the two pictures, Zernike's decomposition changes completely, being affected by propagation-induced cross-talk problems, mostly among the radial part of the modes. On the other hand, panels 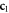 and
and 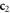 show the decomposition in terms of HNMs, only for the coefficients
show the decomposition in terms of HNMs, only for the coefficients 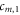 , for the two situations. The complete 2D HMN decomposition is reported in panels
, for the two situations. The complete 2D HMN decomposition is reported in panels 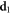 and
and  for both the collimated and defocused field, respectively. As it is clear from the picture, the description in terms of HNMs remains the same and does not suffer from any cross-talk. The whole HNMs spectrum just shifts along the radial index m, while rigidly keeping its shape. While it would be difficult, at a first look, to judge whether panels
for both the collimated and defocused field, respectively. As it is clear from the picture, the description in terms of HNMs remains the same and does not suffer from any cross-talk. The whole HNMs spectrum just shifts along the radial index m, while rigidly keeping its shape. While it would be difficult, at a first look, to judge whether panels 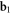 and
and 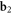 refer to the same field, there are no doubts about it if one looks at panels
refer to the same field, there are no doubts about it if one looks at panels 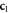 and
and 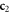 . This is the essence of this work.
. This is the essence of this work.
Figure 2. Comparison between a standard modal decomposition, in this case a Zernike's circle polynomials decomposition, and the Helmholtz natural modes decomposition presented in this work. Panel  shows a wavefront of a roughly collimated beam (experimentally obtained by collimating the light coming from a single-mode optical fiber). Panel
shows a wavefront of a roughly collimated beam (experimentally obtained by collimating the light coming from a single-mode optical fiber). Panel 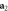 shows the same beam after a defocus term, represented by the additional phase term
shows the same beam after a defocus term, represented by the additional phase term 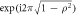 , is added. This defocus term corresponds to the phase shift imposed by propagation under a distance
, is added. This defocus term corresponds to the phase shift imposed by propagation under a distance 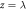 . Panels
. Panels 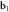 and
and 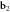 show the Zernike's modal decomposition on the unit disk for the two situations, respectively. As expected, although it deals with the same field, which has just propagated on a finite distance z, Zernike's decomposition changes completely, being affected by propagation-induced cross-talk problems among the radial part of the modes. In contrast to that, panels
show the Zernike's modal decomposition on the unit disk for the two situations, respectively. As expected, although it deals with the same field, which has just propagated on a finite distance z, Zernike's decomposition changes completely, being affected by propagation-induced cross-talk problems among the radial part of the modes. In contrast to that, panels  and
and  show the behavior of Helmholtz natural modes of indices
show the behavior of Helmholtz natural modes of indices 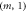 . As it is easy to recognize, the modal structure behaves as a solid body which simply shifts along the radial axis as a whole, without changing its overall shape. Panels
. As it is easy to recognize, the modal structure behaves as a solid body which simply shifts along the radial axis as a whole, without changing its overall shape. Panels 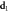 and
and 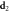 show the structure for the full 2D Helmholtz natural modes decomposition for the original and propagated field, respectively. Again, the reader can appreciate the complete invariance of the modal structure under propagation.
show the structure for the full 2D Helmholtz natural modes decomposition for the original and propagated field, respectively. Again, the reader can appreciate the complete invariance of the modal structure under propagation.
Download figure:
Standard image High-resolution imagePanels 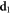 and
and 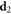 exemplify what is the impact of HNMs in the area of optical communications. Each mode, corresponding to a specific combination of indices
exemplify what is the impact of HNMs in the area of optical communications. Each mode, corresponding to a specific combination of indices  is in fact one independent channel, which can be eventually digitized and transmitted. At the receiver place, all channels can be resolved and the information retrieved. We would like to emphasize that the HNMs are defined on the full angular spectrum of radius
is in fact one independent channel, which can be eventually digitized and transmitted. At the receiver place, all channels can be resolved and the information retrieved. We would like to emphasize that the HNMs are defined on the full angular spectrum of radius 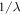 which is much larger than that of any other decomposition defined within the paraxial regime. This extends the communication bandwidth, making available, besides to wavelength and polarization, also fully non paraxial spatial channels to encode information [22, 23]. As we wrote at the end of the previous section, quantization of optical fields and optical metrology, wavefront characterization and corrections are also areas of applications for the HNMs. More on these subjects will be presented in upcoming separate works.
which is much larger than that of any other decomposition defined within the paraxial regime. This extends the communication bandwidth, making available, besides to wavelength and polarization, also fully non paraxial spatial channels to encode information [22, 23]. As we wrote at the end of the previous section, quantization of optical fields and optical metrology, wavefront characterization and corrections are also areas of applications for the HNMs. More on these subjects will be presented in upcoming separate works.
A reader familiar with signals theory might wonder what is the main difference between using the HNMs as channels to convey the information carried by the wavefield and the more common decomposition based on Shannon's sampling theorem. A similar question has been, in fact, raised by one of the reviewers of this manuscript as well. Because of this, it is probably worthwhile to briefly discuss on this point, too. The sampling theorem, in its two-dimensional form, can be applied to a wavefield 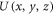 by taking enough samples to fulfil Nyquist's condition. Because the field is band-limited, it is sufficient to sample it with sampling periods
by taking enough samples to fulfil Nyquist's condition. Because the field is band-limited, it is sufficient to sample it with sampling periods 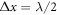 and
and 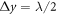 in order to avoid aliasing. The original field can then be recovered by applying a low pass filter cutting the spatial spectrum of the sampled signal in the range
in order to avoid aliasing. The original field can then be recovered by applying a low pass filter cutting the spatial spectrum of the sampled signal in the range 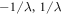 for both dimensions. If we do so, then the field can be expressed in the following way
for both dimensions. If we do so, then the field can be expressed in the following way
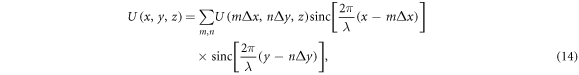
where we have used the common notation  [24]. In equation (14) the information channels are now represented by the basic functions
[24]. In equation (14) the information channels are now represented by the basic functions ![${\rm{sinc}}\left[\tfrac{2\pi }{\lambda }(x-m{\rm{\Delta }}x)\right]$](https://content.cld.iop.org/journals/1367-2630/19/1/013021/revision2/njpaa57c3ieqn78.gif) and
and ![${\rm{sinc}}\left[\tfrac{2\pi }{\lambda }(y-n{\rm{\Delta }}y)\right]$](https://content.cld.iop.org/journals/1367-2630/19/1/013021/revision2/njpaa57c3ieqn79.gif) , while the pieces of information encoded in each channel are represented by the values
, while the pieces of information encoded in each channel are represented by the values 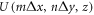 . A reader who has followed the whole reasoning behind this work would immediately recognize the main problem behind the decomposition in equation (14), namely the fact that the information
. A reader who has followed the whole reasoning behind this work would immediately recognize the main problem behind the decomposition in equation (14), namely the fact that the information 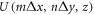 in each channel is not preserved as soon as the field propagates. This because, for a generic field,
in each channel is not preserved as soon as the field propagates. This because, for a generic field, 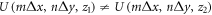 every time
every time 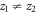 . Only for the very special case of diffraction-free beams (like a Bessel beam) the information would remain somehow invariant, given that in that case
. Only for the very special case of diffraction-free beams (like a Bessel beam) the information would remain somehow invariant, given that in that case  , for any values of z1 and z2. However, as it was already pointed out in the introduction, Bessel beams do not exist in reality, as they carry an infinite amount of energy. Thus, this special case remains an unrealizable exception. For the same reason, a decomposition of a solution of the Helmholtz equation directly in terms of Bessel modes, which could be yet another way to represent the information content of a wavefield, is of no practical use given that each Bessel mode is not physically realizable. This is a main difference with HNMs, which on the contrary all have the same finite energy.
, for any values of z1 and z2. However, as it was already pointed out in the introduction, Bessel beams do not exist in reality, as they carry an infinite amount of energy. Thus, this special case remains an unrealizable exception. For the same reason, a decomposition of a solution of the Helmholtz equation directly in terms of Bessel modes, which could be yet another way to represent the information content of a wavefield, is of no practical use given that each Bessel mode is not physically realizable. This is a main difference with HNMs, which on the contrary all have the same finite energy.
Before concluding this section we would like to get back to the concept of spatial spectroscopy that we have mentioned in the abstract. We will do this with the help of an informative box, shown in figure 3. In the upper panel of the figure, a classical spectroscopy scheme is presented. In order to minimize any chance of confusion, it is better to refer to temporal spectroscopy for this case. The adjective temporal is used to stress that the spectrum we are talking about comes from a 1D Fourier transform of the temporal response of a system. It deals with a 1D spectrum because time has one dimension. Because the temporal spectral content of a field can be, in large part and most of the cases, considered invariant during propagation, any change occurred in the spectrum after the field has interacted with an object, must be completely ascribed to the object itself. This means that changes in the field spectral composition are a signature of the unknown object. On a similar way, in the lower panel of figure 3, a scheme for a spatial spectroscopy concept is presented. In that case, the 2D spatial spectrum of the input field (in terms of HNM modes) is modified by the interaction with an unknown object. Since we have just proven that such a spatial spectrum would remain invariant for a free-field, any change in the spectrum has to be again ascribed to the interaction with the object. Hence, knowledge of the initial spatial spectrum and the observation of the modified spectrum provides a signature of the unknown object. Some of the research performed in the past, which aims at mapping changes of optical vortices carried by paraxial light beams, when interacting with matter, can be seen as an embryonic form of spatial spectroscopy [10, 25, 26]. However, a genuine and true spatial spectroscopy can only be realized when it is not limited to a special class of fields (like Laguerre–Gauss or Bessel–Gauss beams) and to a special regime (like the paraxial one) and can be applied to any optical field relevant for the applications. This is what we believe the introduction of the HNMs can offer to the scientific community operating in this area of research.
Figure 3. Informative box showing analogies between a classical temporal spectroscopy scheme and a spatial spectroscopy one. In common spectroscopy (upper panel) the different colors in the 1D field spectrum represent the different temporal modes carried by the field. After the interaction with a unknown object, such spectral content changes by virtue of the object internal temporal modes. The resulting field gives, in this way, information on the object. On a similar way, in a spatial spectroscopy scheme (lower panel) the different colors in the 2D field spatial spectrum represent the different spatial modes carried by the field. After the interaction with a unknown object, such spectral content changes by virtue of the object internal spatial modes. Once again, knowledge on the spatial spectral composition of the incident field and the detection of the emerging field gives provides information on the unknown object.
Download figure:
Standard image High-resolution image4. Concluding remarks
To conclude, in this work we have presented the natural spatial structure of classical fields solutions of the Helmholtz equation. Such a basic structure consists of fundamental, orthogonal and propagation invariant modes that are fully compatible with Helmholtz equation. For this reason we have denoted these fundamental modes as Helmholtz Natural Modes. As such, they appear to be the preferential description that Nature has chosen to represent freely-propagating electromagnetic fields. Because their main properties directly originate from being solutions of Helmhotlz equation, these modes are not bound to electromagnetism at all but in fact are the fundamental modes for any wave theory that share similar equations of motion for the fields. We have also discussed one explicit example which helped point out the essence of representing a field in terms of HNMs. We expect the work presented here to be relevant for fields such as quantum optics, classical and quantum communications, optical metrology, inverse problems.
Acknowledgments
The author gratefully acknowledges interactions on the subject presented in this work with Paul Urbach (Delft University of Technology). Additionally, the author would like to thank Petro Sonin (VSL) for discussions on the subject as well as for providing wavefront measured data and support with the preparation of some figure. Finally, the author is thankful to Nandini Bhattacharya (Delft University of Technology) for useful discussions on the subject.
This work was partly funded through the projects ENG53 (EMRP) and 14IND09 (EMPIR). The EMRP is jointly funded by the EMRP participating countries within EURAMET and the European Union. The EMPIR initiative is co-funded by the European Union Horizon 2020 research and innovation programme and the EMPIR participating States.






