Abstract
We propose a scheme for a single-atom quantum heat engine based on ultra-cold atom technologies. Building on the high degree of control typical of cold atom systems, we demonstrate that three paradigmatic heat engines—Carnot, Otto and Diesel—are within reach of state-of-the-art technology, and their performances can be benchmarked experimentally. We discuss the implementation of these engines using realistic parameters and considering the friction effects that limit the maximum obtainable performances in real-life experiments. We further consider the use of super-adiabatic transformations that allow to extract a finite amount of power keeping maximum (real) efficiency, and consider the energetic cost of running such protocols.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Introduction
The role played by thermodynamics in our daily life can hardly be emphasized enough. The heat machines and refrigerators that are widely employed in industry and in transports are essentially based on elementary thermodynamic cycles. On the other hand, as already visionarily predicted by Feynman in 1960 [1], technological progress is pushing towards the realization of smaller-scale devices and, at the ultimate level, machines will be built only with one or a few atoms. In such operating regime of low-scale energies, questioning whether the paradigm of thermodynamics needs a fundamental redefinition, including a quantum mechanical formulation of heat or work, is quite natural.
It is in this context that the emerging field of Quantum Thermodynamics comes into play, with the aim of including quantum mechanical effects into the thermodynamic framework. There are several theoretical studies that have been put forward, addressing theoretical aspects of such reformulations [2–5] and extending all the way to the assessment of quantum engines [6–9]. Quantum engines exploiting a quantum-coherent working fluid have been proven to generate substantially more power than classical stochastic engines [10]. Moreover, non-thermal (non-classical) baths and many-body effects can lead to more efficient and powerful engines [11–15], and sophisticated control techniques can be used to enhance such performances even further [16].
Such substantial theoretical advance is yet to be translated into feasible experimental platforms. While recently nitrogen vacancy (NV) centres in diamond and ultra-cold atoms have been used to demonstrate quantum features in the operation of a heat engine [17, 18], to date only one experiment [19] has reported a single-atom engine, although operating fully in the classical regime. In this paper we go beyond such limitations and discuss an architecture based on cold atom technology for the realization of single-atom engines that are able to enter the quantum domain of operation. The ultra-cold temperatures that characterize our operating system guarantee that the engine works in a fully quantum regime. We show that using our architecture based on ultracold atomic mixtures, we can arrange for arbitrary thermodynamic transformations and thus, in turn, arbitrary thermodynamic cycles, including the quantum Carnot, Otto and Diesel ones [6–8, 20]. Moreover we design super-adiabatic transformations that allow to reach high efficiencies in finite time and we discuss the friction effects that limit the performances of real ultra-cold atomic engines (UAEs).
Methods
Our UAEs are assembled starting from three basic elements: (i) a single ultracold atom that is the working fluid, (ii) a species-selective optical tweezer that acts as a piston, (iii) a thermal cloud of ultracold atoms of a different species that embodies the thermal bath. The use of two ultra-cold atomic species allows the control of the fluid-bath interaction with an external magnetic field through Feshbach resonances and 'zero-crossings' of the scattering length. These are used to accurately control and also turn off the interaction between the bath and the system [21, 22]. Possible implementations include but are not limited to Cs-Rb [23], Cs-K [24] Li-Cs [25, 26] and K-Rb [27]. Another key ingredient is the use of a species-selective optical tweezer that is transparent for the bath atoms but that allows, at the same time, the selective trapping and manipulation of the single atom of the other species [28]. Interestingly, optical tweezers have been similarly used to realize classical micro-engines [29]. The tweezer can be designed so that the transverse trapping frequencies set an energy scale that is much higher than the thermal one corresponding to the operating temperature, while the axial frequency energy scale is comparable with the thermal one. This, at variance with [19], allows to operate in the quantum regime, where  , being kB the Boltzmann constant, T the average temperature of operation and ω the average axial frequency. Such arrangement allows only the population of the lower axial energy levels and the level corresponding to the radial ground state, thus realizing an effective one dimensional multi-level system on the axial degrees of freedom. Thermodynamic transformations on the working fluid are performed by the tweezer-piston and controlling the atom-bath interaction. The bath is confined in a large scale trap, so that the single atom is not affected by the modifications of the bath trapping potential. Such architecture can be easily realized using standard cold atoms techniques like evaporative cooling and sympathetic cooling.
, being kB the Boltzmann constant, T the average temperature of operation and ω the average axial frequency. Such arrangement allows only the population of the lower axial energy levels and the level corresponding to the radial ground state, thus realizing an effective one dimensional multi-level system on the axial degrees of freedom. Thermodynamic transformations on the working fluid are performed by the tweezer-piston and controlling the atom-bath interaction. The bath is confined in a large scale trap, so that the single atom is not affected by the modifications of the bath trapping potential. Such architecture can be easily realized using standard cold atoms techniques like evaporative cooling and sympathetic cooling.
We can effectively describe the working fluid of the UAE as a one-dimensional multi-level system on the external axial degrees of freedom and consider the radial degrees of freedom as frozen. Therefore, we can write its Hamiltonian as  where En < En+1 and
where En < En+1 and  are the eigenvalues and eigenvectors of the one-dimensional harmonic oscillator. If Pn is the occupation probability of the nth level, the total energy of the system is
are the eigenvalues and eigenvectors of the one-dimensional harmonic oscillator. If Pn is the occupation probability of the nth level, the total energy of the system is  . We have therefore that a modification of the total energy implies
. We have therefore that a modification of the total energy implies
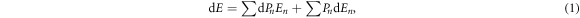
that is a formulation of the first law of thermodynamics at the single-atom quantum level. In analogy with the classical formulation of heat and work, we can identify the heat exchange to be  and the work exchange in the single atom quantum regime to be
and the work exchange in the single atom quantum regime to be  [6–8]. From these definitions we can write the thermal entropy to be
[6–8]. From these definitions we can write the thermal entropy to be  , and the quantum pressure to be Π = −dW/dV, where V is the trapping volume. When the single atom thermalizes with the bath, the probability Pn that the nth level is occupied follows the Boltzmann distribution
, and the quantum pressure to be Π = −dW/dV, where V is the trapping volume. When the single atom thermalizes with the bath, the probability Pn that the nth level is occupied follows the Boltzmann distribution  , with Z the partition function and kB the Boltzmann constant. Starting from these considerations it is possible to design the following four basic quantum thermodynamic transformations, which are the basis of a UAE.
, with Z the partition function and kB the Boltzmann constant. Starting from these considerations it is possible to design the following four basic quantum thermodynamic transformations, which are the basis of a UAE.
1. The quantum adiabatic transformation requires the decoupling of system and bath. Then the trapping potential must be compressed (released) while satisfying the condition dS = 0 and therefore dPn = 0. In turn, this implies dQ = 0. This is achieved setting the external magnetic field to the exact zero-crossing of the interspecies scattering length and by increasing (decreasing) the laser power of the tweezer.
2. The quantum isothermal transformation requires to switch on the interaction between the single atom and the thermal bath and to compress (decompress) the potential trapping the atom. In this case the single atom absorbs (emits) heat from the bath at constant temperature during the compression (expansion) of the energy levels.
3. The quantum isochoric transformation preserves the volume of the quantum system. Therefore no transformations of the external potential are involved, i.e. dEn = 0 (no work done). During these transformations, the system is put in thermal contact with the bath, whose temperature changes in time. This leads to a change in the occupation probability distributions  and therefore
and therefore  This is realized by putting the single atom in interaction with the thermal bath and changing the temperature of the latter by compressing or decompressing its trapping potential.
This is realized by putting the single atom in interaction with the thermal bath and changing the temperature of the latter by compressing or decompressing its trapping potential.
4. The quantum isobaric transformation keeps the pressure or the force on the working fluid constant. The working fluid is in contact with the bath and the temperature is changed together with the trapping potential. We consider a one dimensional harmonic oscillator with  , ω/2π being the harmonic oscillator frequency. The pressure in the working fluid can be calculated as
, ω/2π being the harmonic oscillator frequency. The pressure in the working fluid can be calculated as  , with
, with  the harmonic oscillator length, yielding
the harmonic oscillator length, yielding
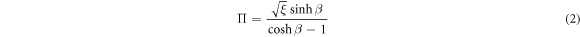
with  and
and  . From equation (2) it follows that, during an isobaric transformation, the temperature must be changed according to
. From equation (2) it follows that, during an isobaric transformation, the temperature must be changed according to

Results
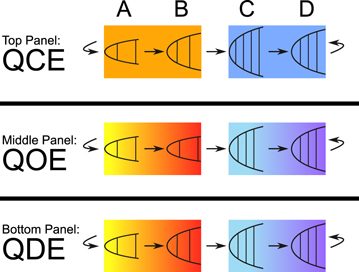
Using UAEs it is therefore possible to implement all the four elementary quantum thermodynamic transformations. For the realization of the quantum engines it is then necessary to combine those transformations in cycles. We first analyse the Quantum Carnot Engine (QCE). Its classical counterpart is the paradigm of every engine and its efficiency sets the maximum theoretical efficiency that any engine (either classical or quantum) can achieve. The QCE is composed of four transformations (see the top panel of figure 1): (1) A hot quantum isothermal expansion at temperature T1 (A  B) in which the working fluid receives heat from the thermal bath; (2) A quantum adiabatic expansion (B
B) in which the working fluid receives heat from the thermal bath; (2) A quantum adiabatic expansion (B  C) in which work is extracted from the working fluid; (3) A cold quantum isothermal compression at temperature T2 < T1 (C
C) in which work is extracted from the working fluid; (3) A cold quantum isothermal compression at temperature T2 < T1 (C  D) in which the working fluid transfers heat to the thermal bath; (4) A quantum adiabatic compression (D
D) in which the working fluid transfers heat to the thermal bath; (4) A quantum adiabatic compression (D  A) in which work is done on the working fluid. To close the cycle, the change in temperature must fulfil the relation
A) in which work is done on the working fluid. To close the cycle, the change in temperature must fulfil the relation  , where Δi = ℏωi [6]. As for its classical analogous, the maximum efficiency of the QCE is ηmax = 1 − T2/T1, which can be achieved in principle only with quasi-static transformations. This implies that, at maximum efficiency, no power can be extracted from the engine. However, one of the advantages of UAEs is the ease to implement super-adiabatic transformations [30, 31]. These allow to follow the self-similar evolution of the initial state, implying that the condition dPn = 0 is rigorously fulfilled at every instant of time during the (B
, where Δi = ℏωi [6]. As for its classical analogous, the maximum efficiency of the QCE is ηmax = 1 − T2/T1, which can be achieved in principle only with quasi-static transformations. This implies that, at maximum efficiency, no power can be extracted from the engine. However, one of the advantages of UAEs is the ease to implement super-adiabatic transformations [30, 31]. These allow to follow the self-similar evolution of the initial state, implying that the condition dPn = 0 is rigorously fulfilled at every instant of time during the (B  C) and (D
C) and (D  A) strokes. Therefore, no friction is produced during such transformations and power can in principle be extracted in a finite time keeping maximum efficiency. With the UAE we take advantage of the fact that both the working fluid and the bath are confined in harmonic potentials, for which super-adiabatic transformations can be calculated analytically [15]. By assuming the time-dependence of the harmonic trap frequency, which we label as Δt, we have that the ideal controlling process should read
A) strokes. Therefore, no friction is produced during such transformations and power can in principle be extracted in a finite time keeping maximum efficiency. With the UAE we take advantage of the fact that both the working fluid and the bath are confined in harmonic potentials, for which super-adiabatic transformations can be calculated analytically [15]. By assuming the time-dependence of the harmonic trap frequency, which we label as Δt, we have that the ideal controlling process should read
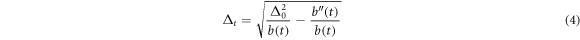
with  , where
, where  is a dimensionless evolution time defined with respect to the the duration of the transformation tf.
is a dimensionless evolution time defined with respect to the the duration of the transformation tf.
Figure 1. From top to bottom: ultra-cold single-atom realization of a Quantum Carnot Engine (QCE), a Quantum Otto Engine (QOE) and a Quantum Diesel engine (QDE). The frequency of the harmonic confinement of the working fluid is changed in time (by tightening or loosening the trap) in order to realize the compression or expansion of the wavefunction of the single atom. The background colours indicate the bath temperature: colors in the red range stands for a hot bath, while blue ones are for a cold bath. The (B  C) and (D
C) and (D  A) transformations are realized by decoupling the working fluid and the bath.
A) transformations are realized by decoupling the working fluid and the bath.
Download figure:
Standard image High-resolution imageIn order to give a specific example, we study the case of the 87Rb-41K mixture. However, it is very important to remark that, qualitatively, our results do not depend on the choice of mixture. We use the Rb atoms as elements for the bath, while a single K atom embodies the working fluid. The single K atom is loaded into the tweezer at the exact species-selective wavelength that, for this mixture, is 789.82 nm (assuming linearly polarized light) [32, 33]. This makes the species-selective light red-detuned with respect to the K transitions, therefore suitable for trapping. The 87Rb-41K mixture features two interspecies Feshbach resonances and a zero of the scattering length at relalively small magnetic fields [27].
We first discuss the optimal temperature for the starting stage A of the QCE in the upper panel of figure 1. A reasonable choice is  , so that P0 + P1 + P2 > 0.99 for the K atom. The QCE includes two isothermal transformations that require collisions between the single trapped atom and the bath. In the ultra-cold regime the heat capacity of the bath is reduced and, to allow thermalization, the atom-bath interaction has to be made stonger as the temperature is decreased [34]. However, when increasing the interaction strength, the survival probability of the K atom to three-body losses decreases, due to the fact that the inelastic scattering rate scales as ∝a4 with a the interspecies scattering length. The reduced survival probability limits the efficiency of a real UAE, therefore providing an effective friction. Based on the study reported in [35], in order to grant thermalization about ≃4 collisions would be required. Therefore, the strength of the interactions will have to depend also on the length of the transformation tf. In general, it is desirable to perform fast transformations to extract a large amount of power and avoid spurious effects such as the heating coming from the light of the optical tweezer. The optimal working point thus depend on the trade-off between the needs to perform fast transformations and reducing the effective friction. In figure 2(a) we report the ratio of the maximum real efficiency ηreal, calculated multiplying the theoretical efficiency with the survival probability, and ηmax as a function of the starting temperature, for a KRb UAE3
. Such efficiencies were calculated considering the length of each isothermal transformation to be 1 ms. Clearly, our UAEs do not allow high real efficiencies for temperatures below 1 μK. In figure 2(b) we report ηreal versus ηmax for different lengths of the isothermal strokes tf and T1 = 1.1 μK. As expected, as the length of the strokes is increased the effective friction decreases. However, if we consider also the photon scattering rate coming from the tweezer, which might induce spurious heating, we find that the optimal starting temperature is T1 = 1.1 μK and that it is convenient to set tf = 1 ms for each isothermal transformation. This indeed guarantees that the atom-bath scattering rate (4 kHz) is one order of magnitude higher than the maximum photon scattering rate coming from the tweezer (≃400 Hz) (see footnote 3) and boosts power extraction. To further minimize the possibility of spurious excitations, the isothermal compression and expansion can be done following the self-similar evolution described by equation (4).
, so that P0 + P1 + P2 > 0.99 for the K atom. The QCE includes two isothermal transformations that require collisions between the single trapped atom and the bath. In the ultra-cold regime the heat capacity of the bath is reduced and, to allow thermalization, the atom-bath interaction has to be made stonger as the temperature is decreased [34]. However, when increasing the interaction strength, the survival probability of the K atom to three-body losses decreases, due to the fact that the inelastic scattering rate scales as ∝a4 with a the interspecies scattering length. The reduced survival probability limits the efficiency of a real UAE, therefore providing an effective friction. Based on the study reported in [35], in order to grant thermalization about ≃4 collisions would be required. Therefore, the strength of the interactions will have to depend also on the length of the transformation tf. In general, it is desirable to perform fast transformations to extract a large amount of power and avoid spurious effects such as the heating coming from the light of the optical tweezer. The optimal working point thus depend on the trade-off between the needs to perform fast transformations and reducing the effective friction. In figure 2(a) we report the ratio of the maximum real efficiency ηreal, calculated multiplying the theoretical efficiency with the survival probability, and ηmax as a function of the starting temperature, for a KRb UAE3
. Such efficiencies were calculated considering the length of each isothermal transformation to be 1 ms. Clearly, our UAEs do not allow high real efficiencies for temperatures below 1 μK. In figure 2(b) we report ηreal versus ηmax for different lengths of the isothermal strokes tf and T1 = 1.1 μK. As expected, as the length of the strokes is increased the effective friction decreases. However, if we consider also the photon scattering rate coming from the tweezer, which might induce spurious heating, we find that the optimal starting temperature is T1 = 1.1 μK and that it is convenient to set tf = 1 ms for each isothermal transformation. This indeed guarantees that the atom-bath scattering rate (4 kHz) is one order of magnitude higher than the maximum photon scattering rate coming from the tweezer (≃400 Hz) (see footnote 3) and boosts power extraction. To further minimize the possibility of spurious excitations, the isothermal compression and expansion can be done following the self-similar evolution described by equation (4).
Figure 2. Panel (a): maximum real efficiencies of a KRb UAE as a function of the starting temperature TA = T1 for a QCE with two isothermal strokes of 1 ms each. Panel (b): maximum real efficiency versus maximum theoretical efficiency for a QCE with T1 = 1.1 μK and different lengths tf of the isothermal strokes.
Download figure:
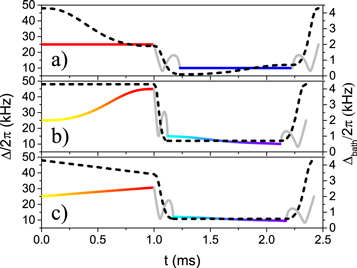
Standard image High-resolution imageAfter having set the initial conditions, we now focus on the realization of a super-adiabatic QCE with ηmax = 0.75, so that ηreal = 0.62, which would be similar to the typical efficiency of a car engine. We thus set T2/T1 = 0.25. Similarly, we set the first isothermal expansion factor ΔB/ΔA to 0.5. Although for the single atom it is possible to achieve super-adiabatic transformations as fast as a few μs, the speed of the super-adiabatic strokes is set by the maximum speed achievable by the super-adiabatic transformations performed on the bath. Indeed, the temperature of the bath must be changed so that  , in parallel with the modification of the trapping potential of the working fluid. In the configuration chosen here, the shortest transformation lasts 0.55 ms, as shown in figure 3(a) (see footnote 3). The work through a QCE is
, in parallel with the modification of the trapping potential of the working fluid. In the configuration chosen here, the shortest transformation lasts 0.55 ms, as shown in figure 3(a) (see footnote 3). The work through a QCE is  , as for the classical counterpart. For the QCE engine reported in figure 3(a), the total cycle time is τ = 2.46 ms so that the extracted power is
, as for the classical counterpart. For the QCE engine reported in figure 3(a), the total cycle time is τ = 2.46 ms so that the extracted power is  mK s−1, obtained maintaining the maximum real efficiency ηreal. Additional limitations to the maximum real efficiency attainable can come from the finite-time nature of the isothermal transformations, as shown in [36, 37].The quantification of the performance of our UAEs can be done using well established techniques. The measurement of the level population of the K atom Pn can be inferred by using Raman sideband spectroscopy [38], while the temperature of the Rb bath can be obtained with standard time-of-flight imaging. The energy spacing En is given by the tweezers parameters. With this diagnostics, it is possible to access all the observables necessary to evaluate the quantum thermodynamic quantities of interest [6, 7]. It is worth noticing that such measurements are destructive and need to be done only to demonstrate the proof-of-principle. Once the working principle is demonstrated, the functioning of the engine will not need any measurement to be performed.
mK s−1, obtained maintaining the maximum real efficiency ηreal. Additional limitations to the maximum real efficiency attainable can come from the finite-time nature of the isothermal transformations, as shown in [36, 37].The quantification of the performance of our UAEs can be done using well established techniques. The measurement of the level population of the K atom Pn can be inferred by using Raman sideband spectroscopy [38], while the temperature of the Rb bath can be obtained with standard time-of-flight imaging. The energy spacing En is given by the tweezers parameters. With this diagnostics, it is possible to access all the observables necessary to evaluate the quantum thermodynamic quantities of interest [6, 7]. It is worth noticing that such measurements are destructive and need to be done only to demonstrate the proof-of-principle. Once the working principle is demonstrated, the functioning of the engine will not need any measurement to be performed.
Figure 3. Panel (a): ultra-cold QCE with super-adiabatic strokes. The dotted line is the evolution of the trapping frequency of the working fluid across the cycle. The solid line is the trapping frequency of the bath, that sets the temperatures. The red colour indicates the hot bath at temperature T1 while the blue color the cold bath at temperature T2. During the super-adiabatic transformations there is no contact between the bath and the working fluid (grey color). Panel (b): ultra-cold QOE. Solid and dotted lines have the same meaning as in (a). The color scales indicate the change in temperature of the bath during the isochoric transformations. Panel (c): same as (a) and (b) but for the QDE.
Download figure:
Standard image High-resolution imageQuantum Otto engine.–The second quantum engine that can be implemented with the UAE architecture is the Quantum Otto engine (QOE). Its classical counterpart is the most employed engine in automotive industry. Its working principle is shown in the middle panel of figure 1 and described in (see footnote 3). To make a direct comparison with the QCE described above, we use the same initial conditions and set ηmax = 0.75 and TB = 2TA. The power extracted with the QOE shown in figure 3(b) is  mK s−1, with τ = 2.35 ms and ηreal = 0.68 (see footnote 3). Therefore a real ultra-cold QOE is both more efficient and more powerful than a real QCE with the same initial conditions and the same maximum theoretical efficiency. This is due to the fact that the average temperature of isochoric transformations are higher than the corresponding isothermal transformations of the QCE, as shown in figure 3. This allows to reduce the effective friction and therefore to increase ηreal.
mK s−1, with τ = 2.35 ms and ηreal = 0.68 (see footnote 3). Therefore a real ultra-cold QOE is both more efficient and more powerful than a real QCE with the same initial conditions and the same maximum theoretical efficiency. This is due to the fact that the average temperature of isochoric transformations are higher than the corresponding isothermal transformations of the QCE, as shown in figure 3. This allows to reduce the effective friction and therefore to increase ηreal.
Quantum Diesel engine.–The last engine that we take into account in this work is the Quantum Diesel Engine (QDE), which is shown in the bottom panel of figure 1. In this case too, in order to make a direct comparison with the processes addressed previously, we choose the same initial condition and ηmax = 0.75 (cf (see footnote 3) for details). For the optimized cycle in figure 3(c), the total cycle time is τ = 2.42 ms so we obtain that the power that can be extracted is  mK s−1, slightly higher than the QOE. The real efficiency is ηreal = 0.64, in between the efficiencies of the QCE and the QDE.
mK s−1, slightly higher than the QOE. The real efficiency is ηreal = 0.64, in between the efficiencies of the QCE and the QDE.
Energetic cost of super-adiabaticity.–A very informative figure of merit to quantify the performance of an engine is the efficiency at maximum power. The approach usually taken when evaluating such parameter is to embed the time dependence of heat transfer in the analysis of the engine. In the specific case of the QOE, this leads to the assumption of constant finite cycle time, which implies that power and work are treated on the same footing and therefore to the definition of the celebrated Culzórn–Alhborn efficiency [39]. When considering time-dependent transformations, such as those at the basis of a super-adiabatic approach, other constraints should be included in order to estimate a more faithful indicator of efficiency at optimal values of power. For our UAEs, an important constraint to impose on the energy that is put into the working medium is that no inversion of the harmonic trap of the system should be in order. For simplicity, we assume that no residual non-adiabatic excitations remains at the end of the super-adiabatic protocol. The efficiency at maximum power can be evaluated through the expression
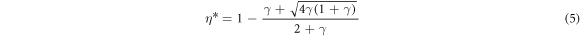
with γ the ratio of mean energy of the working medium at the start of the isentropic compression and expansion, respectively. The explicit evaluation of this quantity for our QOE shows that η* ≃ 80% of the Culzórn–Alhborn efficiency, proving that the use of super-adiabatic approaches for the operation of a QOE is effective in delivering high efficiency cycles associated with maximum possible power [40].
Conclusions
We have presented an ultra-cold atom system in which the fundamental thermodynamic transformations can be realized at the quantum level. We have shown how to practically implement the QCE, QOE and QDE, provided a detailed example that takes into account friction effects with the bath and discussed how to engineer super-adiabatic transformations. Our work provides a first step towards the concrete realization of quantum heat engines in the ultra-cold regime, that might give useful insights on the relation between thermodynamics and quantum mechanics and lead to applications in quantum information. Additionally, the work produced by our UAEs can be extracted and transformed into transport, as shown in (see footnote 3). The low temperatures, together with the finite-time of operation that we have considered, imply that the working medium of our engine is, in general, in a state that is not necessarily thermal. The characterisation of the behaviour of quantum coherence (which can be done following the lines in [41]) during the operation of our engines, and the establishment of a causal relation with the efficiency of such devices [42, 43], will be the topic of our further investigations. Notably, the proposed architecture can be extended to arrays of atoms, allowing to investigate the role of entanglement in quantum thermodynamics.
Acknowledgments
The authors are supported by the Leverhulme Trust Research Project Grant UltraQuTe (grant number RGP-2018-266) and acknowledge fruitful discussions with the members of the Cold Atoms Group at the University of Birmingham and Obinna Abah at Queen's University Belfast. MP acknowledges support from the DfE-SFI Investigator Programme (Grant No. 15/IA/2864), and the H2020 Collaborative Project TEQ (Grant Agreement No. 766900).
Footnotes
- 3
Supplementary materials available online at stacks.iop.org/NJP/21/063019/mmedia.