Abstract
The spin Hall effect (SHE), which converts a charge current into a transverse spin current, has long been believed to be a phenomenon induced by spin–orbit coupling. Here, we identify an alternative mechanism to realize the intrinsic SHE through a noncollinear magnetic structure that breaks the spin rotation symmetry. No spin–orbit coupling is needed even when the scalar spin chirality vanishes, different from the case of the topological Hall effect and topological SHE reported previously. In known noncollinear antiferromagnetic compounds Mn3X (X = Ga, Ge, and Sn), for example, we indeed obtain large spin Hall conductivities based on ab initio calculations.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The spin Hall effect (SHE) [1] is one of the most important ways to create and detect spin currents in the field of spintronics, which aims to realize low-power-consumption and high-speed devices [2]. It converts electric currents into transverse spin currents and vice versa. The SHE in materials is generally believed to rely on spin–orbit coupling (SOC) [1, 3–5]. In typical SHE devices, the generated spin current is injected into a ferromagnet (FM) and consequently switches its magnetization via the spin-transfer torque [6, 7] or drives an efficient motion of magnetic domain walls [8, 9].
The SHE is conceptually similar to the well established anomalous Hall effect (AHE). In recent decades, the understanding of the intrinsic AHE [10] and intrinsic SHE [11, 12] was significantly advanced based on the concept of the Berry phase [13], which originates directly from the electronic band structure. Although the AHE requires the existence of SOC in a FM, it also appears in a non-coplanar magnetic lattice without SOC, where an electron acquires a Berry phase by hopping through sites with a non-coplanar magnetic structure (nonzero scalar spin chirality) [14, 15], later referred as the topological Hall effect (THE) [16]. Thus, in experiment the THE-induced Hall signal is considered as a signature of the skyrmion phase with chiral spin texture [17, 18]. Provoked by the THE, recent numerical simulations of the spin scattering by a single skyrmion indicated the presence of a finite SHE even without SOC [19–21], which is termed as a topological SHE. Thus, the topological SHE has been presumed to stem from the Berry phase due to the nonzero spin chirality of the skyrmion. However, the origin of the spin current is illusive in the topological SHE, for it is hard to separate it from the spin-polarized charge current of the THE. Here, we pose new questions one step further. Is the skyrmion-like spin texture (nonzero scalar spin chirality) always necessary to generate a SHE without SOC? What is the generic condition for a SHE without SOC?
In this article, we propose a mechanism to realize the SHE with the noncollinear magnetic structure but without SOC. The crucial role of SOC is to break the spin rotational symmetry (SRS) in SHE. Alternatively, it is known that common noncollinear magnetic textures can also violate the SRS, thus resulting in the SHE. Different from the THE and topological SHE in symmetry, such an SHE appears universally for the noncollinear magnetic lattice, regardless of the scalar spin chirality. For example, it can even emerge in a coplanar magnetic structure where the scalar spin chirality is zero. Here, we first prove the principle from the symmetry analysis in a simple lattice model. Then, we demonstrate the existence of a strong SHE in several known materials Mn3X (X = Ga, Ge, and Sn) [22, 23] by ab initio calculations without including SOC.
2. Results
2.1. Double-exchange model and symmetry analysis
The existence of the SHE and AHE in metals is determined by symmetry (in insulators apart from symmetry also the topology of the electronic structure is important). The symmetry of magnetic systems is normally described in terms of magnetic space groups, which contain, apart from the spatial symmetry operations, also the time-reversal symmetry operation. In absence of SOC (or other terms in the Hamiltonian that couple the magnetic moments to the lattice such as the shape anisotropy), however, the symmetry of the magnetic systems is higher than that contained in the magnetic space groups since the spins can be rotated independently of the lattice. This can be illustrated by considering the following minimal Hamiltonian
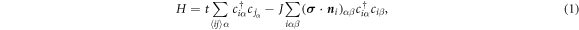
known as the double-exchange model (s–d model) [24–26] which describes itinerant s electrons interacting with local d magnetic moments. We assume that magnetic moments are only contributed by the spin degrees of freedom. Here, α and β stand for spin up and spin down, respectively. The first term is the nearest neighbor hopping term with 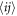 denoting the nearest neighbor lattice sites. In the second term, J is the Hund's coupling strength between the conduction electron and the on-site spin moment,
denoting the nearest neighbor lattice sites. In the second term, J is the Hund's coupling strength between the conduction electron and the on-site spin moment, 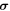 is the vector of Pauli matrices, and
is the vector of Pauli matrices, and 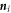 is the spin magnetic moment on-site i. The magnetic texture is defined by the pattern of
is the spin magnetic moment on-site i. The magnetic texture is defined by the pattern of 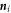 . In such a Hamiltonian, spin rotation only rotates the magnetic moments ni. The corresponding symmetry groups are thus formed by combining the magnetic space groups with spin rotations [27, 28]. Such symmetry groups are referred to as spin-space groups. They apply generally for non-interacting Hamiltonians in absence of SOC.
. In such a Hamiltonian, spin rotation only rotates the magnetic moments ni. The corresponding symmetry groups are thus formed by combining the magnetic space groups with spin rotations [27, 28]. Such symmetry groups are referred to as spin-space groups. They apply generally for non-interacting Hamiltonians in absence of SOC.
We focus here only on the intrinsic contribution to the AHE and SHE, however, the other (extrinsic) contributions have the same symmetry and thus the symmetry discussion in the following is general. The intrinsic AHE and intrinsic SHE are well characterized via the Berry curvature formalism [1, 5, 10, 13]. The anomalous Hall conductivity (AHC) σαβ can be evaluated by the integral of the Berry curvature 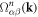 over the Brillouin zone (BZ) for all the occupied bands, where n is the band index. It should be noted that this method can also be applied to the THE, although it is commonly interpreted using the real space spin texture. Here, σαβ corresponds to a 3 × 3 matrix and indicates a transverse Hall current jα generated by a longitudinal electric field E, which satisfies
over the Brillouin zone (BZ) for all the occupied bands, where n is the band index. It should be noted that this method can also be applied to the THE, although it is commonly interpreted using the real space spin texture. Here, σαβ corresponds to a 3 × 3 matrix and indicates a transverse Hall current jα generated by a longitudinal electric field E, which satisfies  . Within a linear response, Berry curvature can be expressed as
. Within a linear response, Berry curvature can be expressed as
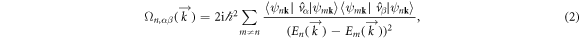
where n and m are band indices, and 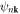 and
and 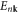 denote the Bloch wave functions and eigenvalues, respectively, and
denote the Bloch wave functions and eigenvalues, respectively, and 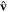 is the velocity operator. Replacing the velocity operator with the spin current operator
is the velocity operator. Replacing the velocity operator with the spin current operator 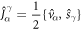 , where
, where 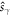 is the spin operator, we obtain the spin Berry curvature and corresponding spin Hall conductivity (SHC)
is the spin operator, we obtain the spin Berry curvature and corresponding spin Hall conductivity (SHC)
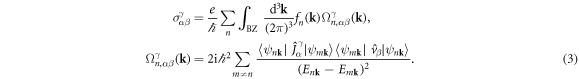
The SHC (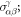 α, β, γ = x, y, z) is a third-order tensor (3 × 3 × 3) and represents the spin current
α, β, γ = x, y, z) is a third-order tensor (3 × 3 × 3) and represents the spin current 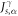 generated by an electric field E via
generated by an electric field E via 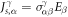 , where
, where 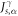 is a spin current flowing along the α-direction with the spin-polarization along the γ-direction, and fn(k) is the temperature dependent Fermi–Dirac distribution.
is a spin current flowing along the α-direction with the spin-polarization along the γ-direction, and fn(k) is the temperature dependent Fermi–Dirac distribution.
We know that AHE vanishes while SHE remains if the time-reversal symmetry (operator T) exists in the system. In equation (2), T reverses the velocities 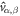 and brings an additional '−' sign by the complex conjugate. Thus, σαβ = 0 owing to
and brings an additional '−' sign by the complex conjugate. Thus, σαβ = 0 owing to  . In contrast, In equation (3), T generates one more '−' sign by reversing the spin in
. In contrast, In equation (3), T generates one more '−' sign by reversing the spin in 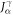 . Then,
. Then, 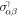 can be nonzero since
can be nonzero since 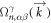 is even in k-space. In a magnetic system without SOC, T is broken, but a combination of T and a spin rotation (operator S) can still be a symmetry. For example, a coplanar magnetic system shows a TS symmetry, in which S rotates all spins by 180° around the axis perpendicular to the plane. Since S does not act on
is even in k-space. In a magnetic system without SOC, T is broken, but a combination of T and a spin rotation (operator S) can still be a symmetry. For example, a coplanar magnetic system shows a TS symmetry, in which S rotates all spins by 180° around the axis perpendicular to the plane. Since S does not act on  , TS causes vanishing σαβ just as T alone. In a general non-coplanar magnetic lattice, the TS symmetry is naturally broken, because one cannot find a common axis about which all spins can be rotated 180° at the same time, and thus the AHE can exist without SOC.
, TS causes vanishing σαβ just as T alone. In a general non-coplanar magnetic lattice, the TS symmetry is naturally broken, because one cannot find a common axis about which all spins can be rotated 180° at the same time, and thus the AHE can exist without SOC.
The situation is different for the SHE since 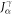 in equation (3) contains an additional spin operator. As a consequence, (assuming that S is a rotation around the z axis) TS forces
in equation (3) contains an additional spin operator. As a consequence, (assuming that S is a rotation around the z axis) TS forces 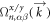 to be odd where spin
to be odd where spin 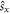 or
or  is reversed by TS, but
is reversed by TS, but 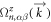 to be even where
to be even where 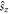 is unchanged by TS. Then, one can obtain zero
is unchanged by TS. Then, one can obtain zero 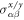 but nonzero
but nonzero 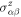 . In a collinear magnetic lattice there exists more than one spin rotation S such that TS is a symmetry of the system and thus all of the
. In a collinear magnetic lattice there exists more than one spin rotation S such that TS is a symmetry of the system and thus all of the 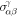 components have to vanish. Therefore, we can argue that SHE can exist without SOC in general noncollinear magnetic lattices, regardless of FM, AFM, or the scalar spin chirality (coplanar or non-coplanar). In contrast, the AHC is zero for a coplanar magnetic lattice (zero scalar spin chirality), since TS acts as T alone in equation (2).
components have to vanish. Therefore, we can argue that SHE can exist without SOC in general noncollinear magnetic lattices, regardless of FM, AFM, or the scalar spin chirality (coplanar or non-coplanar). In contrast, the AHC is zero for a coplanar magnetic lattice (zero scalar spin chirality), since TS acts as T alone in equation (2).
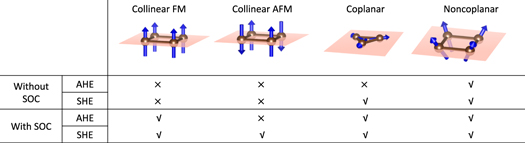
When SOC is included, SHE is allowed by symmetry in any crystal [29], while the AHE on the other hand can be present in magnetic systems that are not symmetric under time reversal combined with a translation or inversion (for example, a conventional collinear AFM). We summarize the necessary conditions for the existence of AHE and SHE in systems with and without SOC in figure 1.
Figure 1. Symmetry conditions for the existence (√) or absence (×) of AHE and SHE in collinear FM, collinear AFM, coplanar, and non-coplanar magnetic lattices with and without SOC. Note that the SHE is allowed by symmetry when the magnetic ordering is coplanar (but noncollinear) even without SOC (see text).
Download figure:
Standard image High-resolution imageTo demonstrate that the SHE can indeed be nonzero without SOC, we consider the s–d Hamiltonian (1) projected on a kagome lattice with the so-called q = 0 magnetic order, shown in figure 2(a). Such a coplanar AFM order is well studied in theory [14, 30] and appears in many realistic materials even at room temperature, for example Mn3X (X = Ir, Ga, Ge, and Sn) [22, 23, 31–34] as we discuss in the following. For comparison, the SOC effect is also considered by adding to H in equation (1)
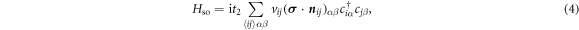
where vij is the antisymmetric Levi-Civita symbol and nij are a set of coplanar vectors anticlockwise perpendicular to the lattice vector Rij, as defined in [30] and t2 is the SOC strength.
Figure 2. Noncollinear order in kagome lattice and the magnetic structure of Mn3Ir and Mn3X (X = Ga, Ge, and Sn). (a) The q = 0 order in the kagome lattice, with magnetic moments located as 2D Mn plane in Mn3Ir, (b) two-fold spin rotation around y-axis of configuration (a), corresponding to Mn planes in Mn3X (X = Ga, Ge, Sn), (c) the face-centered cubic crystal structure of Mn3Ir, (d) the hexagonal crystal structure of Mn3X (X = Ga, Ge, and Sn).
Download figure:
Standard image High-resolution imageWe first analyze the symmetry of the SHC tensor for the q = 0 magnetic order. Note that we use the Cartesian coordinate systems defined in figure 2. As discussed above, the existence of the TS symmetry leaves only 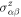 terms in the absence of SOC. Further, the combined symmetry
terms in the absence of SOC. Further, the combined symmetry 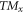 , in which Mx is the mirror reflection along x and flips
, in which Mx is the mirror reflection along x and flips 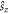 and
and 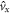 in equation (3), leads to
in equation (3), leads to  . We further obtain only two nonzero SHC tensor element
. We further obtain only two nonzero SHC tensor element 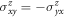 by considering the three-fold rotation around z. The magnetic order shown in figure 2(b) will also be relevant for the discussion in the following. This magnetic configuration differs from the q = 0 case only by a two-fold spin rotation around the y-axis and thus, without SOC its symmetry is exactly the same as that of the q = 0 case.
by considering the three-fold rotation around z. The magnetic order shown in figure 2(b) will also be relevant for the discussion in the following. This magnetic configuration differs from the q = 0 case only by a two-fold spin rotation around the y-axis and thus, without SOC its symmetry is exactly the same as that of the q = 0 case.
Setting the Hund coupling constant 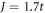 and SOC strength t2 = 0, we calculate the spin Berry curvature via equation (3). As expected, we find nonzero SHC
and SOC strength t2 = 0, we calculate the spin Berry curvature via equation (3). As expected, we find nonzero SHC 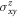 fully in agreement with the symmetry considerations. Figures 3(a) and (b) show the band structures with t2 = 0 and
fully in agreement with the symmetry considerations. Figures 3(a) and (b) show the band structures with t2 = 0 and 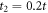 , respectively. One can see that SOC modifies slightly the band structure by gaping some band crossing points such as the BZ corners (K). Without SOC, we already observe nonzero
, respectively. One can see that SOC modifies slightly the band structure by gaping some band crossing points such as the BZ corners (K). Without SOC, we already observe nonzero 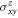 , while adding SOC reduces
, while adding SOC reduces 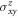 slightly at the Fermi energy that is set between the first and second bands at about −2.7 eV. We plot corresponding spin Berry curvature
slightly at the Fermi energy that is set between the first and second bands at about −2.7 eV. We plot corresponding spin Berry curvature 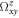 in the hexagonal BZ In figures 3(d) and (e). Large
in the hexagonal BZ In figures 3(d) and (e). Large 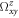 appears in the BZ without SOC, leading to net
appears in the BZ without SOC, leading to net  . The SOC simply brings an extra contribution to
. The SOC simply brings an extra contribution to 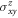 at the band anti-crossing region around the K point.
at the band anti-crossing region around the K point.
Figure 3. Electronic band structures q = 0 order in kagome lattice, (a) without and with SOC. (b) Energy-dependent SHC 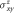 . (c) Spin Berry curvature
. (c) Spin Berry curvature 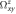 distribution of first BZ at Fermi energy −2.7 eV (horizontal line) without SOC and (d) with SOC.
distribution of first BZ at Fermi energy −2.7 eV (horizontal line) without SOC and (d) with SOC.
Download figure:
Standard image High-resolution image2.2. Realistic materials
After proving the principle, we now identify materials that show strong SHE with negligible contribution from SOC. We naturally consider Mn3X (X = Ga, Ge, Sn, and Ir) compounds, since they exhibit non:w collinear AFM order at room temperature (the AFM Néel temperature is over 365 K). Our recent ab initio calculations showed a sizable intrinsic SHE by including SOC [34]. Here, we further point out that SHE still presents without SOC and SOC actually plays a negligible effect for SHE in these materials.
The primitive unit cell of Mn3Ga, Mn3Ge and Mn3Sn (space group 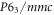 , No. 194) includes two Mn3X planes that are stacked along the c-axis according to a '–AB–AB–' sequence. Inside each plane, Mn atoms form a kagome-type lattice with Ga, Ge, or Sn lying at the center of the hexagon formed by Mn. Both the ab initio calculation [31] and neutron diffraction measurements [35–37] show that the Mn magnetic moments exhibit noncollinear AFM order, where the neighboring moments are aligned at an angle of 120°, as in figure 2(b). Large AHE in room temperature has recently been reported in Mn3Ge and Mn3Sn [22, 23]. These materials also exhibit other exotic phenomena including the Weyl semimetal phase [38], magneto-optical Kerr effect [39], anomalous Nernst effect [40], and topological defects [41]. Distinct from hexagonal Mn3X compounds, the Mn3Ir (space group
, No. 194) includes two Mn3X planes that are stacked along the c-axis according to a '–AB–AB–' sequence. Inside each plane, Mn atoms form a kagome-type lattice with Ga, Ge, or Sn lying at the center of the hexagon formed by Mn. Both the ab initio calculation [31] and neutron diffraction measurements [35–37] show that the Mn magnetic moments exhibit noncollinear AFM order, where the neighboring moments are aligned at an angle of 120°, as in figure 2(b). Large AHE in room temperature has recently been reported in Mn3Ge and Mn3Sn [22, 23]. These materials also exhibit other exotic phenomena including the Weyl semimetal phase [38], magneto-optical Kerr effect [39], anomalous Nernst effect [40], and topological defects [41]. Distinct from hexagonal Mn3X compounds, the Mn3Ir (space group  , No. 221) crystallizes in a face-centered cubic structure with Mn atoms in the [111] planes forming a kagome lattice with the q = 0 magnetic order.
, No. 221) crystallizes in a face-centered cubic structure with Mn atoms in the [111] planes forming a kagome lattice with the q = 0 magnetic order.
The symmetry of the SHE without SOC in these materials can be understood using a similar approach as we used for the 2D kagome lattice. The hexagonal Ga, Ge, and Sn materials can be viewed as stacking versions of the kagome lattice and thus we find that the symmetry of SHE is the same as the 2D kagome lattice, i.e. only 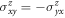 is nonzero. However, we find that SHE must vanish in Mn3Ir without SOC, which is imposed by the higher symmetry of the cubic magnetic lattice. For completeness, we list the tensor matrices without and with SOC for all these compounds in the supplementary material available online at stacks.iop.org/njp/20/073028/mmedia.
is nonzero. However, we find that SHE must vanish in Mn3Ir without SOC, which is imposed by the higher symmetry of the cubic magnetic lattice. For completeness, we list the tensor matrices without and with SOC for all these compounds in the supplementary material available online at stacks.iop.org/njp/20/073028/mmedia.
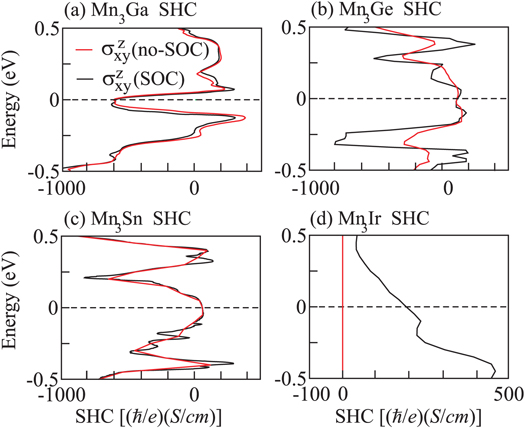
Since the SHC tensor shape imposed by the symmetry has been systematically investigated for these materials in [34], we only discuss one of the largest SHC tensor elements 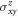 based on the ab initio calculations [42] of the SHC. For comparison, we show the SHC without and together with SOC in figure 4. In the absence of SOC, Ga, Ge, and Sn compounds indeed exhibit nonzero SHC
based on the ab initio calculations [42] of the SHC. For comparison, we show the SHC without and together with SOC in figure 4. In the absence of SOC, Ga, Ge, and Sn compounds indeed exhibit nonzero SHC 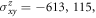 and
and  , respectively, at the Fermi energy. One can see that SOC induces very few changes in the band structure and thereafter modifies the SHC weakly, especially at the Fermi energy for Ga, Ge, and Sn compounds. It is intuitive to observe comparable
, respectively, at the Fermi energy. One can see that SOC induces very few changes in the band structure and thereafter modifies the SHC weakly, especially at the Fermi energy for Ga, Ge, and Sn compounds. It is intuitive to observe comparable 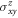 values for Ge and Sn compounds, despite the fact that Sn exhibits much larger SOC than Ge. These facts further verifies that the noncollinear magnetic structure, rather than SOC, is dominant for the SHE. The Ga compound shows an opposite sign in SHC compared to the Ge/Sn compound, since Ga has one valence electron fewer than Ge/Sn and the Fermi energy is lower in Mn3Ga than in Mn3Ge/Mn3Sn.
values for Ge and Sn compounds, despite the fact that Sn exhibits much larger SOC than Ge. These facts further verifies that the noncollinear magnetic structure, rather than SOC, is dominant for the SHE. The Ga compound shows an opposite sign in SHC compared to the Ge/Sn compound, since Ga has one valence electron fewer than Ge/Sn and the Fermi energy is lower in Mn3Ga than in Mn3Ge/Mn3Sn.
Figure 4. Energy-dependent SHC tensor elements of 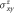 with and without SOC for (a) Mn3Ga, (b) Mn3Ge, (c) Mn3Sn, and (d) Mn3Ir. The Fermi energy is indicated by the dashed horizontal line.
with and without SOC for (a) Mn3Ga, (b) Mn3Ge, (c) Mn3Sn, and (d) Mn3Ir. The Fermi energy is indicated by the dashed horizontal line.
Download figure:
Standard image High-resolution image3. Discussion
Understanding the role SOC plays in the SHE is important for the fundamental understanding of the SHE, but also for practical reasons. It can help with the search for materials with large SHE since in non-magnetic or collinear magnetic materials, SOC is necessary for SHE and thus the presence of heavy elements is generally required for large SHE. The SHE without SOC proposed in this work suggests a new strategy to design SHE materials without necessarily involving heavy elements. In noncollinear systems, the Rashba effect can also appear without SOC [43]. The spin texture in the band structure may depend sensitively on the real space spin texture. For example, we found that band structure spin texture is different between the Kagome lattice and the triangular lattice.
We propose the general, necessary symmetry-breaking requirements (figure 1) for SHE without SOC. It is worth noting that SHE can become zero without SOC in some noncollinear magnetic lattice where additional symmetries forces the SHE to vanish. For example, we have shown that in Mn3Ir the SHE vanishes in absence of SOC even though it has a noncollinear magnetic structure. This is a consequence of its high-symmetrical cubic structure. Similar situation could happen for AHE without SOC in a non-coplanar magnetic lattice, such as the AFM skyrmion system [21].
In conclusion, we have shown that the SHE can be realized by a non-chiral coplanar magnetic structure without involving the SOC. The noncollinearity of the magnetic lattice can break the spin rotation symmetry and consequently allow the existence of SHE. By ab initio calculations, we further predicted that such an SHE without SOC can be observed in noncollinear AFM compounds Mn3X (X = Ga, Ge, and Sn). From our symmetry considerations, an extrinsic SHE can appear when breaking the SRS. Thus, we expect the extrinsic effect to also exist in our systems. Its amplitude will depend on the details of the scattering, and cannot be estimated without microscopic calculations, though in general for SHE the intrinsic contribution tends to be the dominant contribution. By providing a general theoretical, symmetry based understanding of the SHE, our work motivates a comprehensive search for SHE materials among noncollinear magnetic systems, that not necessarily involve heavy elements. In addition, the close relation between the SHE and the magnetic order suggests that the SHE may be used vice versa, as a probe to establish and symmetry restrict the ground state magnetic structures of long-range ordered antiferromagnets.
Regarding the strong correlated system, we would discuss the spin liquid material as an example. RuCl3 has a rich magnetic phase diagram, with a complex zig-zag type AFM long-range order at low temperatures, and even a quantum spin liquid phase in applied magnetic field. According to our work, non-magnetic and collinearly ordered phases have vanishing SHE without SOC. For the quantum spin liquid phase, it remains unclear whether SHE appears without SOC. If yes, SHE would be a promising probe to the spin liquid phase. We will study this very interesting question in the future.
4. Method
To calculate the SHE in these compounds we obtain the DFT Bloch wave functions from Vienna ab initio Simulation Package (vasp) [42] within the generalized gradient approximation [44]. By projecting the Bloch wave functions onto maximally localized Wannier functions [45], we get a tight-binding Hamiltonian which we use for efficient evaluation of the SHC. For the integrals of equation (3), the BZ was sampled by k-grids from 50 × 50 × 50 to 200 × 200 × 200. Satisfactory convergence was achieved for a k-grid of size 150 × 150 × 150 for all three compounds. Increasing the grid size to 200 × 200 × 200 only varied the SHC by no more than 5%. The results of the calculations agree well with the symmetry analysis.
Acknowledgments
We thank Professor Claudia Felser at the Max Planck Institute in Dresden, Professor Carsten Timm at the Technical University Dresden and Professor Yuval Oreg at the Weizmann Institute of Science for helpful discussions. YZ and JvdB acknowledge the German Research Foundation (DFG) SFB 1143. BY acknowledges support by the Ruth and Herman Albert Scholars Program for New Scientists at the Weizmann Institute of Science and by a grant from the GIF, the German–Israeli Foundation for Scientific Research and Development.
Author contributions
BY conceived the project. YZ, JZ and YS performed the DFT calculation and the data analysis. YZ, JZ, and BY performed the tight-binding modeling and symmetry analysis. YZ wrote the manuscript with contributions from all co-authors. JvdB and BY supervised the work.
Competing interests
The authors declare no competing financial interests.