Abstract
We propose an optical circuit for attaining quantum measurement advantage in a system that has no quantum entanglement. Our device produces symmetric two-qubit X-states with controllable anti-diagonal elements, and does not require entangled states as input. We discuss the use of this device in a two-qubit quantum game. When entanglement is absent, the maximum quantum advantage in this game is 1/3 bit. A slightly diminished quantum advantage, 0.311 bit, can be realized with a simplified transaction protocol.
Export citation and abstract BibTeX RIS
1. Introduction
The concept of quantum advantage can be illustrated by an example from dense coding [1]. Alice and Bob share a pair of qubits in a maximally entangled state, such as a Bell state. By performing one-qubit unitary operations, Alice can transmit two bits of information to Bob while sending him only one physical qubit. The information advantage of having shared access to a maximally entangled state is thus one bit in this case. That advantage is due to the presence in the shared resource of an intrinsically quantum correlation, which in this case is entanglement [2].
Quantum discord [3, 4] measures the difference between the total quantum mutual information and the classical mutual information of a system [5]. Although entanglement has been widely used as a measure of a given state's potential quantum advantage, recent studies have suggested that quantum discord can be a richer resource [6–14]. Gu et al [15] studied the relationship between quantum advantage and quantum discord in an encoding/decoding protocol. In particular, they explain it through an example using Gaussian discord for continuous variables, showing that the maximum quantum advantage that can be harvested in the optimal encoding is equal to the initial amount of quantum discord. Questions remain about the relationship between quantum correlations and quantum advantage in the general case.
Almeida et al [16] showed how to use quantum advantage to prove that an untrusted party can perform entangling gates. They consider a particular X-state that corresponds to an equal mixture of three Bell states. Such a realization relies on a source of entangled photons to study the ideal case where the encoding is optimal. This result poses questions about the generalization of the problem to correlations among degrees of freedom of a single particle, and to non-ideal scenarios where it is not possible perform an optimal encoding.
Here we discuss the role of quantum correlations [17], in particular quantum discord, in the realization of quantum advantage in various encoding/decoding scenarios. We introduce a realistic experimental setup that can generate a broad class of two-qubit states, and harvest significant quantum advantage even when there is no entanglement.
Many two-qubit states belong to the class of 'X-states' discussed by Yu and Eberly [18] and Rau [19]. This class includes the Bell and Werner states [1, 20]. Both quantum discord and the optimal projective measurements can be determined analytically for arbitrary rank 2 X-states. For higher ranks it is necessary to solve a set of transcendental equations [21–24] or assume an error of up to 0.0021 bits [25]. It is challenging to design a feasible experimental system that can generate arbitrary X-states, because that requires a programmable decoherence mechanism.
Here, we introduce an optical device that generates symmetric two-qubit X-states. It can serve as the basis for making arbitrary X-states. By restricting detailed discussion to symmetric X-states, we are able to illustrate clearly the physical and operational meaning of quantum advantage. Symmetric X-states are incoherent superpositions of maximally entangled Bell states. They can also represent a Bell state subject to decoherence in quantum information processing protocols [18, 26].
Our device consists of a single-photon source and a Mach–Zehnder-like interferometer, using only passive optical components. The two qubits of this system are the polarization and the optical path of the photon. Our device can generate mixed two-qubit states with a wide range of entanglement and quantum discord. It can also be applied to encoding/decoding protocols of a classical random variable K [27]. We describe in detail a series of transactions between Alice and Bob in which Alice encodes K in an X-state and Bob attempts to decode K from that state. When quantum discord is present, Bob can better estimate K than he could by using only local measurements and one-qubit operations. This quantum advantage exists even when the two qubits are unentangled.
Section 2 discusses the theory involved in computing quantum discord. In particular, we provide discord and concurrence for symmetric two-qubit X-states. We also define the concept of quantum advantage in the context of the encoding protocol. In section 3 we describe the optical device. We discuss the generation of symmetric two-qubit X-states and the encoding/decoding protocol. In section 4 we analyze the properties of the state of the system before and after the encoding. We study the behavior of quantum correlations for the optimal and quasi-optimal encoding. We focus on the cases where there is significant quantum advantage without entanglement.
2. Theory
2.1. Quantum discord and two-qubit X-states
Quantum discord is the difference between the total mutual information shared by two qubits, I, and their locally accessible (classical) mutual information J [1, 5]. In light of the optical application that we propose in section 3, we designate the two qubits by the labels s and p, which we use below to distinguish photon spin (polarization) from interferometric path, but which can be taken to describe any two-qubit system. For a system described by the density matrix 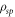 in a composed Hilbert space
in a composed Hilbert space  , the total mutual information between the two qubits is
, the total mutual information between the two qubits is
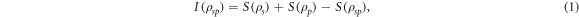
where S denotes the von Neumann entropy and 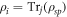 is the partial density matrix of the subsystem i, with
is the partial density matrix of the subsystem i, with 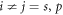 [1]. After a projective measurement [28] on the first qubit
[1]. After a projective measurement [28] on the first qubit  , the conditional state of p is given by
, the conditional state of p is given by  with probability
with probability 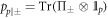 , where
, where 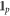 is the identity for qubit p. The classical mutual information,
is the identity for qubit p. The classical mutual information, 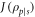 , is the amount by which the uncertainty of system p is reduced after measuring s [5], and is
, is the amount by which the uncertainty of system p is reduced after measuring s [5], and is
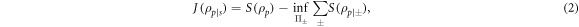
where the average conditional entropy, 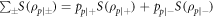 , is minimized over all possible projective measurements. Finally, quantum discord [5],
, is minimized over all possible projective measurements. Finally, quantum discord [5], 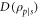 , corresponds to the shared information between s and p, that cannot be obtained by measuring s,
, corresponds to the shared information between s and p, that cannot be obtained by measuring s,
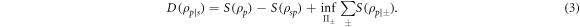
The analogous expressions for 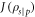 and
and 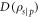 can be obtained by interchanging the roles of the qubits when computing the average conditional entropy.
can be obtained by interchanging the roles of the qubits when computing the average conditional entropy.
In this work we restrict ourselves to a particular class of states that are generated by an incoherent superposition of maximal entangled states [1]. However, the same analysis can be performed for any symmetric two-qubit X-state. In the computational basis these states take the form

with 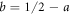 . We show below that without loss of generality, the coherences
. We show below that without loss of generality, the coherences ![$w\in [0,a]$](https://content.cld.iop.org/journals/1367-2630/19/5/053009/revision1/njpaa6cf4ieqn15.gif) and
and ![$z\in [0,b]$](https://content.cld.iop.org/journals/1367-2630/19/5/053009/revision1/njpaa6cf4ieqn16.gif) can be taken to be real and positive. The concurrence
can be taken to be real and positive. The concurrence 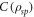 and entanglement of formation
and entanglement of formation 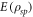 are given by the Wooters formulae [2]:
are given by the Wooters formulae [2]:
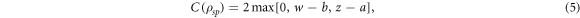
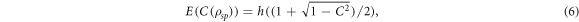
where 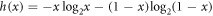 . Since entanglement is a monotonic function of concurrence they have the same minima and maxima, which are 0 and 1 respectively.
. Since entanglement is a monotonic function of concurrence they have the same minima and maxima, which are 0 and 1 respectively.
For such states, which are described by density matrices of the form shown in equation (4), the conditional states after a measurement of one qubit (i.e. a local measurement) are independent of the qubit that was measured, 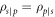 . Because of this, the average conditional entropy is also symmetric and therefore
. Because of this, the average conditional entropy is also symmetric and therefore 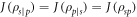 and
and 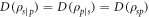 . Following the criteria introduced by Maldonado-Trapp et al [21], the discord for this family of states is given by
. Following the criteria introduced by Maldonado-Trapp et al [21], the discord for this family of states is given by
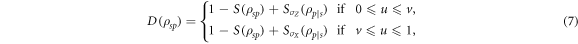
where 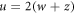 and
and 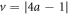 . The quantities
. The quantities 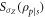 and
and 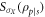 correspond to the minimal average conditional entropies, when the optimal measurements are along
correspond to the minimal average conditional entropies, when the optimal measurements are along 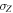 and
and 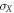 respectively, where
respectively, where 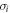 are the Pauli matrices [1]. Explicitly, these entropies are given by
are the Pauli matrices [1]. Explicitly, these entropies are given by
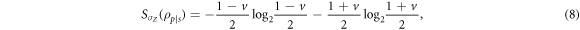
and
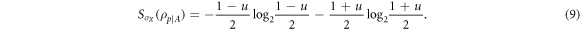
When u = v the average conditional entropy does not depend on the measurement. Note that if 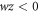 the optimal measurement
the optimal measurement 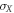 must be replaced by
must be replaced by 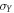 [21]. Although the optimal measurement changes, the value of the average conditional entropy remains the same. Since correlations do not change under local operations, the case
[21]. Although the optimal measurement changes, the value of the average conditional entropy remains the same. Since correlations do not change under local operations, the case  can be avoided by considering a rotation over the two qubits of the form
can be avoided by considering a rotation over the two qubits of the form 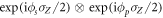 . Thus, as noted above, we can always choose
. Thus, as noted above, we can always choose  and
and 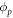 so that w and z are real and positive.
so that w and z are real and positive.
2.2. Encoding process and quantum advantage
We now consider a scenario in which two independent parties, Alice and Bob, have access to a source of discordant ( ) two-qubit symmetric X-states that are fully known to both of them. Alice and Bob engage in a sequence of encoding/decoding transactions, each of which starts with the same X-state. Alice generates a random variable K that takes values
) two-qubit symmetric X-states that are fully known to both of them. Alice and Bob engage in a sequence of encoding/decoding transactions, each of which starts with the same X-state. Alice generates a random variable K that takes values  with a probability distribution pk, where b1 and b2 are random classical bits [1, 27]. She encodes K in the qubit s and then challenges Bob to estimate K by measuring the encoded state.
with a probability distribution pk, where b1 and b2 are random classical bits [1, 27]. She encodes K in the qubit s and then challenges Bob to estimate K by measuring the encoded state.
In figure 1 we show a quantum circuit that illustrates the protocol described above. For each transaction, Alice applies a local unitary operation 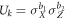 to qubit s and sends the state to Bob. The four unitary operations that she can apply are
to qubit s and sends the state to Bob. The four unitary operations that she can apply are 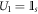 ,
, 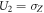 ,
,  and
and  , where
, where 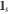 is the identity operator for the qubit s. The ensemble received by Bob is thus described by the density matrix
is the identity operator for the qubit s. The ensemble received by Bob is thus described by the density matrix
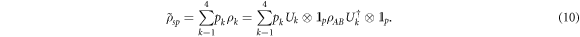
By performing a decoding protocol after each transaction, Bob constructs a new random variable  . Bob then estimates the value of k that was sent by Alice, and records his estimate as
. Bob then estimates the value of k that was sent by Alice, and records his estimate as  . We will see that the accuracy of Bob's estimation is determined by his access to two-qubit operations.
. We will see that the accuracy of Bob's estimation is determined by his access to two-qubit operations.
Figure 1. Quantum circuit for the encoding/decoding protocol. The upper (lower) wire corresponds to the qubit s  . Alice has access to the X-state source
. Alice has access to the X-state source 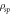 . She applies a local unitary operation
. She applies a local unitary operation 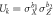 with probability pk on the spin qubit s, where b1 and b2 are random bits. The four possible bit combinations are
with probability pk on the spin qubit s, where b1 and b2 are random bits. The four possible bit combinations are 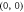 ,
, 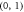 ,
, 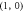 and
and 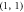 which are related to the local operations
which are related to the local operations  ,
, 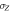 ,
, 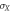 and
and 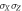 respectively. After each transaction Bob performs a decoding procedure consisting of two-qubit, Usp operations and local operations on polarization Us and path Up. He then measures on both qubits and estimates the value of b1 and b2.
respectively. After each transaction Bob performs a decoding procedure consisting of two-qubit, Usp operations and local operations on polarization Us and path Up. He then measures on both qubits and estimates the value of b1 and b2.
Download figure:
Standard image High-resolution imageThe maximal accessible information [1] that Bob can obtain about K corresponds to the Holevo information which for an ensemble 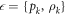 is given by
is given by
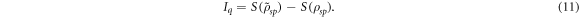
Its minimum and maximum values are given by zero and two bits respectively. When  the bits b1 and b2 can be determined deterministically, i.e. Bob can recover K with certainty. An example of this case is superdense coding [1, 29].
the bits b1 and b2 can be determined deterministically, i.e. Bob can recover K with certainty. An example of this case is superdense coding [1, 29].
We note that when the protocol is applied to a symmetric X-state, the average state after the encoding 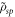 is also symmetric. Considering this, if Bob makes a projective measurement
is also symmetric. Considering this, if Bob makes a projective measurement 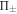 on qubit s, the accessible information that he can obtain from the qubit p is equivalent to the information that he can obtain from s given a measurement on p, which is
on qubit s, the accessible information that he can obtain from the qubit p is equivalent to the information that he can obtain from s given a measurement on p, which is
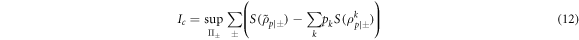
where 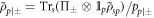 and
and 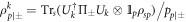 are the conditional states for qubit p. As for quantum discord, this quantity is non-trivial to compute since it requires the optimization of conditional entropies over all possible projective measurements.
are the conditional states for qubit p. As for quantum discord, this quantity is non-trivial to compute since it requires the optimization of conditional entropies over all possible projective measurements.
Quantum advantage, 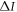 , is defined as the difference between Iq and Ic,
, is defined as the difference between Iq and Ic, 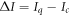 [15, 16]. It corresponds to the extra information that Bob can gain by performing two-qubit operations prior to making local measurements of each qubit. When the random variable K is encoded in
[15, 16]. It corresponds to the extra information that Bob can gain by performing two-qubit operations prior to making local measurements of each qubit. When the random variable K is encoded in 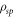 , decoherence is induced in the system and therefore the correlations between s and p are modified. The discord consumption [15] is defined as the difference between quantum discord before and after the encoding,
, decoherence is induced in the system and therefore the correlations between s and p are modified. The discord consumption [15] is defined as the difference between quantum discord before and after the encoding, 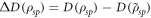 . Gu et al [15] showed that the quantum advantage of an encoding protocol and the discord consumption are related by the following inequality:
. Gu et al [15] showed that the quantum advantage of an encoding protocol and the discord consumption are related by the following inequality:
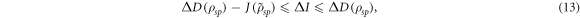
where 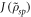 is the classical mutual information between s and p after the protocol. Optimal encoding is the encoding that maximizes the quantum advantage [15]. It corresponds to the one in which the total mutual information is consumed, i.e.
is the classical mutual information between s and p after the protocol. Optimal encoding is the encoding that maximizes the quantum advantage [15]. It corresponds to the one in which the total mutual information is consumed, i.e. 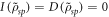 . In this case the quantum advantage is equal to the initial amount of quantum discord,
. In this case the quantum advantage is equal to the initial amount of quantum discord, 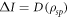 .
.
3. Experimental proposal
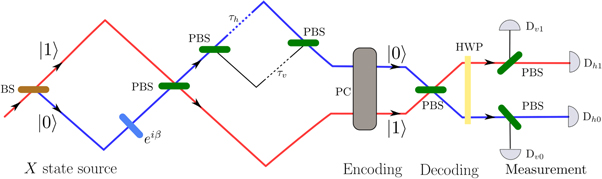
In this section we propose an optical implementation for generating symmetric two-qubit X-states, as in equation (4), and use them in an encoding protocol. The detailed setup, shown in figure 2, consists of three parts: an X-state source, an encoding and decoding mechanism, and a measurement process.
Figure 2. Theoretical proposal for preparation of an X-state and encoding and decoding of a random variable. X-state source: a polarized photon in an equal superposition of vertical and horizontal component, 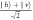 , is incident on a beam splitter (BS), with reflection coefficient R and transmission coefficient T. In path
, is incident on a beam splitter (BS), with reflection coefficient R and transmission coefficient T. In path 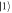 the photon goes through a random phase noise, β, with Gaussian probability distribution to make it incoherent with
the photon goes through a random phase noise, β, with Gaussian probability distribution to make it incoherent with 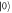 . Paths
. Paths 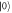 and
and 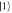 are recombined with a polarizing beam splitter (PBS) that transmits
are recombined with a polarizing beam splitter (PBS) that transmits 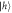 and reflects
and reflects 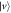 . In path
. In path 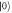 the photon goes through two PBS. This adds time delays
the photon goes through two PBS. This adds time delays 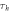 and
and 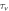 for the horizontal and vertical components from path
for the horizontal and vertical components from path 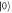 respectively. Encoding: both paths
respectively. Encoding: both paths 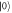 and
and 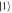 go through a polarization controller (PC). The PC can arbitrarily rotate the polarization state of a photon. Decoding: paths paths
go through a polarization controller (PC). The PC can arbitrarily rotate the polarization state of a photon. Decoding: paths paths 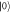 and
and 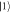 are recombined with a PBS. Both paths go through a half wave plate (HWP) at an angle
are recombined with a PBS. Both paths go through a half wave plate (HWP) at an angle 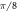 with respect to the horizontal. Measurement: two PBS and four photon detectors are placed to measure in the
with respect to the horizontal. Measurement: two PBS and four photon detectors are placed to measure in the 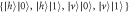 basis.
basis.
Download figure:
Standard image High-resolution imageWe use a linear polarization basis with horizontal and vertical components designated by 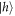 and
and 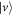 respectively, and a path basis designed by
respectively, and a path basis designed by 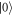 and
and 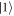 , which in the computational basis corresponds to
, which in the computational basis corresponds to
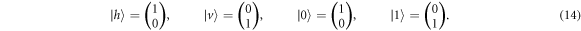
In this basis, an X-state can be thought as an incoherent superposition of two Bell-like states,  and
and 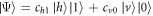 , where the coefficients cij are the probability amplitudes of the states
, where the coefficients cij are the probability amplitudes of the states  . It is well known in optics that a polarizer beam splitter (PBS) can create such states for a single incoming photon by properly choosing the PBS input port. Then, by combining two incoherent paths into each port of a PBS the output state will be X-states of the form (4).
. It is well known in optics that a polarizer beam splitter (PBS) can create such states for a single incoming photon by properly choosing the PBS input port. Then, by combining two incoherent paths into each port of a PBS the output state will be X-states of the form (4).
For simplicity, our X-state source is fed by an input photon with a polarization state 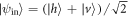 . The state is then split in two incoherent paths. This can be done by a random switch choosing which path the photon goes through, or by a beam splitter (BS) and a subsequent path delay longer than the coherence length of the photon, or by adding a random noise in one of the paths. In particular, we will describe this process by assuming that the input photon first encounters a BS with transmission and reflection coefficients T and R respectively, where
. The state is then split in two incoherent paths. This can be done by a random switch choosing which path the photon goes through, or by a beam splitter (BS) and a subsequent path delay longer than the coherence length of the photon, or by adding a random noise in one of the paths. In particular, we will describe this process by assuming that the input photon first encounters a BS with transmission and reflection coefficients T and R respectively, where 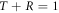 , and introducing a random source of phase noise in one path, see figure 2. It provides a phase shift
, and introducing a random source of phase noise in one path, see figure 2. It provides a phase shift 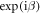 where β is a random variable with a Gaussian probability distribution
where β is a random variable with a Gaussian probability distribution 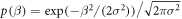 and standard deviation σ. We consider σ to be sufficiently large such that the average of different phases
and standard deviation σ. We consider σ to be sufficiently large such that the average of different phases 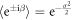 can be neglected, producing two incoherent beams. Paths
can be neglected, producing two incoherent beams. Paths 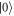 and
and 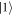 are recombined with a PBS; all PBSs in this apparatus transmit polarization
are recombined with a PBS; all PBSs in this apparatus transmit polarization 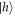 and reflect polarization
and reflect polarization 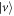 . The PBS acts as a control not (CNOT) gate with polarization and path as control and target qubits [1]. In path
. The PBS acts as a control not (CNOT) gate with polarization and path as control and target qubits [1]. In path 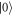 we place a PBS that introduces one auxiliary path (black path in figure 2 ). In those paths we add a controllable time delay,
we place a PBS that introduces one auxiliary path (black path in figure 2 ). In those paths we add a controllable time delay, 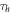 or
or 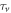 , which allows us to control the coherences of the
, which allows us to control the coherences of the 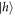 and
and 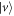 components of
components of 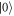 . With this, the anti-diagonal term associated with
. With this, the anti-diagonal term associated with 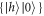 and
and 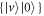 decreases by a factor of
decreases by a factor of 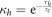 and
and 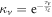 respectively, where
respectively, where 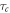 is the coherence time of the photons. The resulting density matrix can be written in the
is the coherence time of the photons. The resulting density matrix can be written in the 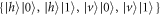 basis as
basis as
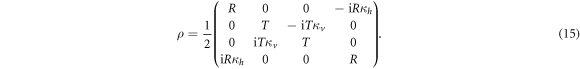
To encode the random variable K, both paths 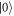 and
and 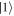 go through a PC. The PC allows Alice to arbitrarily rotate the polarization state of the photon. We assume that Alice has a random number generator that tells her which set of bits
go through a PC. The PC allows Alice to arbitrarily rotate the polarization state of the photon. We assume that Alice has a random number generator that tells her which set of bits 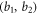 to send in each transaction. While to send the bits
to send in each transaction. While to send the bits 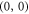 she does nothing to the polarization state, to send
she does nothing to the polarization state, to send 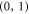 ,
, 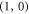 or
or 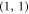 , she applies a rotation at π around the axes z, x, and y in the polarization Bloch sphere [1]. The decoding process is performed by a PBS and half wave plate (HWP) which acts as a CNOT and a Hadamard gate in polarization respectively [1]. The HWP is set at an angle
, she applies a rotation at π around the axes z, x, and y in the polarization Bloch sphere [1]. The decoding process is performed by a PBS and half wave plate (HWP) which acts as a CNOT and a Hadamard gate in polarization respectively [1]. The HWP is set at an angle 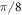 with respect to the horizontal and transforms the polarization components as
with respect to the horizontal and transforms the polarization components as 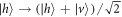 and
and 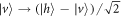 . A PBS in each path
. A PBS in each path 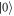 and
and 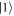 is placed in order to measure in the
is placed in order to measure in the 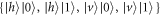 basis with detectors
basis with detectors 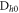 ,
, 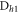 ,
, 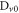 and
and 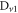 .
.
4. Theoretical results
4.1. Quantum correlations before encoding
Since the von Neumann entropy is invariant under unitary local operations, we apply to the density matrix of the experimental X-states the following rotational operation, 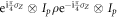 , such that the density matrix elements of the rotated state are real and positive. The correlations present in the original, ρ, and rotated state are the same and they can be computed by using the formulas discussed in section 2.1. In particular, concurrence is given by
, such that the density matrix elements of the rotated state are real and positive. The correlations present in the original, ρ, and rotated state are the same and they can be computed by using the formulas discussed in section 2.1. In particular, concurrence is given by ![$C(\rho )=\max [0,{\kappa }_{h}R-T,{\kappa }_{v}T-R]$](https://content.cld.iop.org/journals/1367-2630/19/5/053009/revision1/njpaa6cf4ieqn134.gif) and it vanishes when
and it vanishes when 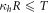 and
and 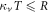 , or when R = T. The analytical expression for quantum discord is given by equation (7), with
, or when R = T. The analytical expression for quantum discord is given by equation (7), with 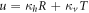 and
and 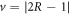 . By using the second derivative test [27] we found that, with respect to variations of
. By using the second derivative test [27] we found that, with respect to variations of 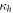 and
and 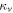 , quantum discord is maximized in two cases:
, quantum discord is maximized in two cases: 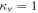 and
and 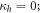 and
and 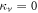 and
and 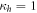 .
.
Figures 3(a) and (b) show the behavior of the pre-encoding concurrence and discord, 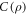 and
and 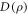 , as a function of R and
, as a function of R and 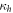 when
when 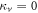 . When
. When 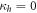 , the corresponding dependence on R and
, the corresponding dependence on R and 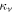 can be found by reflecting these figures about the line
can be found by reflecting these figures about the line  . From figure 3(a) we note concurrence increases monotonically with
. From figure 3(a) we note concurrence increases monotonically with  and decreases monotonically with R. Concurrence is zero at the left region of the dashed line,
and decreases monotonically with R. Concurrence is zero at the left region of the dashed line, 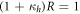 . It reaches its maximum value, C = 1, when the photon is completely reflected onto path
. It reaches its maximum value, C = 1, when the photon is completely reflected onto path 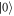 , R = 1, and there is no time delay in the auxiliary path,
, R = 1, and there is no time delay in the auxiliary path, 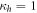 . This maximum corresponds to the Bell state indicated by the red point,
. This maximum corresponds to the Bell state indicated by the red point, 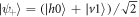 [1]. From figure 3(b) we note that quantum discord also increases monotonically with
[1]. From figure 3(b) we note that quantum discord also increases monotonically with 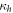 . Discord only vanishes when the photon is completely transmitted, R = 0, or when the coherence time of the photon is much less than the time delay,
. Discord only vanishes when the photon is completely transmitted, R = 0, or when the coherence time of the photon is much less than the time delay,  . It also reaches its maximum value for Bell states, D = 1, at R = 1 and
. It also reaches its maximum value for Bell states, D = 1, at R = 1 and 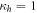 . Besides the global maximum, discord also has local maxima along the black boundaries. The highest value that discord reaches without entanglement is represented by the red dot and its value is
. Besides the global maximum, discord also has local maxima along the black boundaries. The highest value that discord reaches without entanglement is represented by the red dot and its value is 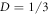 at
at 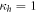 and
and 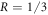 . In figure 3(c) the gray and white regions show where the optimal measurements are
. In figure 3(c) the gray and white regions show where the optimal measurements are  and
and 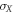 respectively. These are the measurements of polarization that minimize the average conditional entropy and therefore that least disturb the system but allow us to obtain more information about the system. The conditional entropy is independent of the measurement for the states along the black lines. The states along the black solid line are the Werner states [1, 20] which can be written as
respectively. These are the measurements of polarization that minimize the average conditional entropy and therefore that least disturb the system but allow us to obtain more information about the system. The conditional entropy is independent of the measurement for the states along the black lines. The states along the black solid line are the Werner states [1, 20] which can be written as 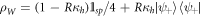 . We defined the Werner-like states to be the states along the black dashed line, which can be written as
. We defined the Werner-like states to be the states along the black dashed line, which can be written as 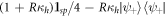 .
.
Figure 3. Concurrence 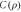 (a) and quantum discord
(a) and quantum discord 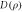 (b) as a function of R and
(b) as a function of R and 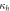 , for
, for 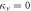 . (c) Parameter regions of the optimal measurements. In (a) the dashed line denotes where the concurrence becomes zero. The red point corresponds to the Bell state
. (c) Parameter regions of the optimal measurements. In (a) the dashed line denotes where the concurrence becomes zero. The red point corresponds to the Bell state 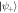 for which concurrence is maximum. In (b) the red dot corresponds to the maximum value of discord that can be reached without concurrence. The gray and white regions of (c) denote where
for which concurrence is maximum. In (b) the red dot corresponds to the maximum value of discord that can be reached without concurrence. The gray and white regions of (c) denote where 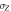 and
and 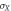 are the measurement that minimizes the average conditional entropy, respectively. The states along the solid (
are the measurement that minimizes the average conditional entropy, respectively. The states along the solid (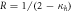 ) and dashed (
) and dashed (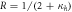 ) boundaries correspond to the Werner and Werner-like states respectively.
) boundaries correspond to the Werner and Werner-like states respectively.
Download figure:
Standard image High-resolution image4.2. Quantum correlations after encoding
In order to maximize quantum correlations we consider the pre-encoding state as the one that satisfies 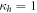 and
and 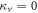 , this is
, this is

After each transaction of the bit pair 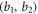 according to the encoding protocol described in section (2.2), the density matrix of the post-encoding state becomes
according to the encoding protocol described in section (2.2), the density matrix of the post-encoding state becomes
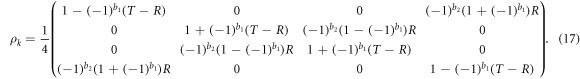
From equation (17) we immediately note that b2 only appears in the non-diagonal terms. Without joint measurements Bob cannot determine the value of b2, thus he will not be able to estimate K with certainty.
After averaging out a series of transactions, on average Bob receives the state
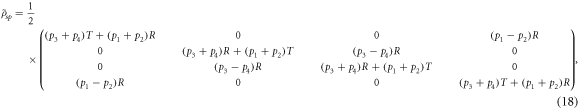
where p1, p2, p3, and p4 are the probabilities described in section 2.2. Without loss of generality we consider only positive coherences  and
and 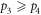 . For this ensemble, concurrence is given by
. For this ensemble, concurrence is given by
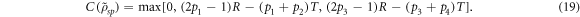
Quantum discord is given by equation (7), with 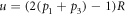 and
and 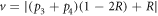 .
.
4.3. Quantum advantage and quasi-optimal encoding
As noted in section 2.2, an optimal encoding is the one that consumes all correlations, 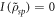 [15]. This is satisfied when the final average state is
[15]. This is satisfied when the final average state is  ; in other words, it is the encoding that introduces the greatest amount of decoherence to the system. From equation (18) we note that an optimal encoding must satisfy one of the following conditions:
; in other words, it is the encoding that introduces the greatest amount of decoherence to the system. From equation (18) we note that an optimal encoding must satisfy one of the following conditions: 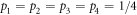 , or R = T. Thus, optimal encoding is that which yields a maximally-mixed encoded state.
, or R = T. Thus, optimal encoding is that which yields a maximally-mixed encoded state.
Aside from the noted relationship [15] between initial quantum discord and the quantum advantage in an optimal encoding, 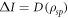 , we found that in this case there is a direct relationship between the initial amount of information and the quantities Ic and Iq. The total accessible information, Iq, can be conceived as the amount of mutual information that has been removed from the initial state,
, we found that in this case there is a direct relationship between the initial amount of information and the quantities Ic and Iq. The total accessible information, Iq, can be conceived as the amount of mutual information that has been removed from the initial state, 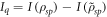 . Since for optimal encodings the total mutual information becomes zero we can state that these are the encodings that extract all the information from the system and therefore
. Since for optimal encodings the total mutual information becomes zero we can state that these are the encodings that extract all the information from the system and therefore 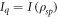 . In addition to this, from equation (11) we note that Iq is also related to the randomness that has been introduced to the system. For example, when only one of the events k has preference, say
. In addition to this, from equation (11) we note that Iq is also related to the randomness that has been introduced to the system. For example, when only one of the events k has preference, say 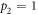 , no randomness is introduced and Iq is zero, while in an optimal encoding all the events have the same probability,
, no randomness is introduced and Iq is zero, while in an optimal encoding all the events have the same probability,  , and no more randomness can be introduced. Since for optimal encodings
, and no more randomness can be introduced. Since for optimal encodings 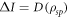 and
and 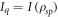 it is clear that the locally accessible information coincides with the initial classical information,
it is clear that the locally accessible information coincides with the initial classical information, 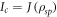 .
.
Although the optimal encoding is the one that maximizes the quantum advantage it is also interesting to study more general encodings. In particular, we study a group of encodings that we call 'quasi-optimal'. All quantum discord is consumed in quasi-optimal encodings, 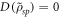 , but classical mutual information is not necessarily consumed,
, but classical mutual information is not necessarily consumed, 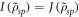 . Both quantum discord and classical mutual information are consumed only for a truly optimal encoding. Of the cases discussed above, all encodings with
. Both quantum discord and classical mutual information are consumed only for a truly optimal encoding. Of the cases discussed above, all encodings with 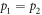 and
and 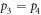 are quasi-optimal, including the special case
are quasi-optimal, including the special case 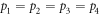 . In this group, the behavior of quantum correlations and advantage can be described by one variable. We choose the variable to be p1 where
. In this group, the behavior of quantum correlations and advantage can be described by one variable. We choose the variable to be p1 where ![${p}_{1}\in [0,1/2]$](https://content.cld.iop.org/journals/1367-2630/19/5/053009/revision1/njpaa6cf4ieqn199.gif) .
.
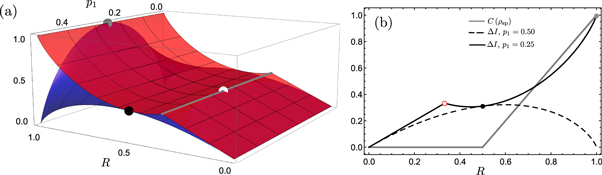
Figure 4(a) shows consumed discord 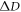 (red) and quantum advantage
(red) and quantum advantage 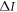 (blue) for the quasi-optimal encoding as a function of R and p1. Overall, quantum advantage is always less than discord consumption, in agreement with inequality (13). In (a) and (b) the gray point denotes the Bell state
(blue) for the quasi-optimal encoding as a function of R and p1. Overall, quantum advantage is always less than discord consumption, in agreement with inequality (13). In (a) and (b) the gray point denotes the Bell state 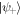 , while the white and black points denote the maximum value of quantum advantage
, while the white and black points denote the maximum value of quantum advantage 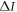 when there is no entanglement for
when there is no entanglement for  and
and 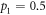 respectively. Since quasi-optimal encoding consumes all discord, the consumed discord
respectively. Since quasi-optimal encoding consumes all discord, the consumed discord 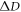 equals the quantum discord of the pre-encoding state and is independent of p1. From figure 4(a) we note that quantum advantage (blue) is maximal for optimal encodings,
equals the quantum discord of the pre-encoding state and is independent of p1. From figure 4(a) we note that quantum advantage (blue) is maximal for optimal encodings, 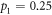 , and it decreases symmetrically around
, and it decreases symmetrically around 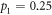 . Away from
. Away from 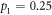 (optimal encoding), quantum advantage's behavior is drastically different. Instead of increasing monotonically with R, quantum advantage peaks at a certain R and then decreases as R increases. In the most extreme cases, where
(optimal encoding), quantum advantage's behavior is drastically different. Instead of increasing monotonically with R, quantum advantage peaks at a certain R and then decreases as R increases. In the most extreme cases, where 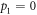 (encoding by only applying
(encoding by only applying 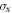 and
and 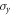 and
and 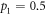 (encoding by only applying
(encoding by only applying 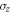 ), quantum advantage becomes zero for R = 1, even though R = 1 corresponds to the Bell state
), quantum advantage becomes zero for R = 1, even though R = 1 corresponds to the Bell state  where both discord and entanglement is maximal. Such a difference is also evident in figure 4(b).
where both discord and entanglement is maximal. Such a difference is also evident in figure 4(b).
Figure 4. (a) Consumed discord 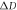 (red) and quantum advantage
(red) and quantum advantage 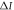 (blue) as a function of R and p1 for the quasi-optimal encoding. (b) Pre-encoding
(blue) as a function of R and p1 for the quasi-optimal encoding. (b) Pre-encoding 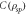 (gray line); quantum advantage
(gray line); quantum advantage 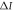 for
for 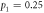 (black line) and
(black line) and 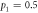 (dashed line). In (a) and (b) the gray point denotes the Bell state
(dashed line). In (a) and (b) the gray point denotes the Bell state  . The white and black points denote the maximum value of
. The white and black points denote the maximum value of 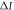 when there is no entanglement for
when there is no entanglement for 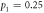 and
and 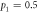 respectively.
respectively.
Download figure:
Standard image High-resolution imageFigure 4(b) shows the behavior of concurrence of the pre-encoding state, 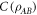 , with quantum advantage,
, with quantum advantage, 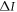 as a function of R, for the optimal encoding,
as a function of R, for the optimal encoding, 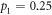 (black line), and for a particular non-optimal encoding,
(black line), and for a particular non-optimal encoding, 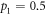 (black dashed line), which corresponds to encoding only in
(black dashed line), which corresponds to encoding only in 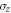 . For
. For 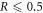 , the pre-encoding state
, the pre-encoding state 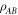 is not entangled (zero concurrence). In this regime, the maximum advantage for using the optimal encoding is 1/3 bits at
is not entangled (zero concurrence). In this regime, the maximum advantage for using the optimal encoding is 1/3 bits at 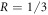 (white dot), while for the non-optimal encoding it is
(white dot), while for the non-optimal encoding it is 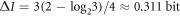 at
at  (black dot). The difference between optimal and non-optimal encoding in this region is small. The maximal quantum advantage between optimal and non-optimal is as low as approximately 0.022 bits. For
(black dot). The difference between optimal and non-optimal encoding in this region is small. The maximal quantum advantage between optimal and non-optimal is as low as approximately 0.022 bits. For 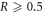 , the pre-encoding state is entangled and is maximally entangled for R = 1 (the Bell state
, the pre-encoding state is entangled and is maximally entangled for R = 1 (the Bell state 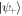 ). In this regime, quantum advantage differs significantly between
). In this regime, quantum advantage differs significantly between 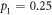 (optimal) and
(optimal) and 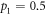 (non-optimal). For the non-optimal encoding
(non-optimal). For the non-optimal encoding 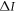 decreases until it reaches zero bits at R = 1, and for the optimal one
decreases until it reaches zero bits at R = 1, and for the optimal one  increases until it reaches 1 bit at R = 1 (gray dot).
increases until it reaches 1 bit at R = 1 (gray dot).
5. Conclusions
In this work, we propose a versatile optical realization of symmetric two-qubit X-states. Studying the properties of these states allows us to generalize the applications of Bell states. We prove that 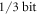 is the maximum value of quantum advantage that can be attained without entanglement. We find that significant quantum advantage can be realized with simplified encoding protocols. Specifically, the quasi-optimal encoding with
is the maximum value of quantum advantage that can be attained without entanglement. We find that significant quantum advantage can be realized with simplified encoding protocols. Specifically, the quasi-optimal encoding with  allows us to achieve a quantum advantage of 0.311 bit. The convenience of this quasi-optimal encoding over the optimal, comes from the easiness of its implementation, since it implies encoding only in
allows us to achieve a quantum advantage of 0.311 bit. The convenience of this quasi-optimal encoding over the optimal, comes from the easiness of its implementation, since it implies encoding only in 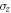 . In addition we also show that the total accessible mutual information between the random variables is equal to the initial mutual information between qubits. This result can be used as a simple and powerful tool to test the performance of a sender/receiver in a communication protocol avoiding an optimization process involved in computing quantum discord or mutual classical information.
. In addition we also show that the total accessible mutual information between the random variables is equal to the initial mutual information between qubits. This result can be used as a simple and powerful tool to test the performance of a sender/receiver in a communication protocol avoiding an optimization process involved in computing quantum discord or mutual classical information.
Acknowledgements
A M-T thanks the Chilean National Commission for Scientific and Technological Research, CONICyT. P S thanks the National Science Foundation, 1307416, 1430094. This work was partially supported by the NSF Physics Frontier Center at the Joint Quantum Institute PFC@JQI.