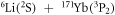Abstract
We theoretically explore the scattering properties in collisions between  in the ground state and fermionic
in the ground state and fermionic  in the metastable
in the metastable 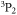 state. Unlike the role of the electronic spin degree of freedom in collisions of two alkali-metal atoms, the orbital degrees of freedom from the p electron of the metastable atoms, which induce not only mixings between different partial waves but also couplings between channels in different fine-structure manifolds, introduce the anisotropic interactions for producing broad-enough Feshbach resonances. Our closed-coupling calculation shows that this mechanism is similar to that in highly magnetic atoms, but the resonances also suffer from a large inelastic rate at the magnitude of
state. Unlike the role of the electronic spin degree of freedom in collisions of two alkali-metal atoms, the orbital degrees of freedom from the p electron of the metastable atoms, which induce not only mixings between different partial waves but also couplings between channels in different fine-structure manifolds, introduce the anisotropic interactions for producing broad-enough Feshbach resonances. Our closed-coupling calculation shows that this mechanism is similar to that in highly magnetic atoms, but the resonances also suffer from a large inelastic rate at the magnitude of 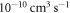 to lower-lying fine-structure states or Zeeman sublevels, which will be an obstacle for associating ultracold polar molecules with both electron spin and electric dipole momentum. However, such a rich mixture of inelastic processes, and the experimental advantage of immunity from intraspecies inelastic collisions for metastable fermionic
to lower-lying fine-structure states or Zeeman sublevels, which will be an obstacle for associating ultracold polar molecules with both electron spin and electric dipole momentum. However, such a rich mixture of inelastic processes, and the experimental advantage of immunity from intraspecies inelastic collisions for metastable fermionic 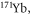 allow for precise investigations on the interspecies scattering properties for systems with excited-state atoms included.
allow for precise investigations on the interspecies scattering properties for systems with excited-state atoms included.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
By allowing the tuning of interaction strength by simply varying the strength of the external magnetic field, magnetic Feshbach resonances (FRs) have not only provided new access to molecular formation [1] and ultracold chemistry [3], but also have been applied in fields of precision measurement [4] and quantum simulation of many-body systems [5–7]. However, until now ultracold molecules formed by magnetic FRs experimentally have been restricted to those dimers, either heteronuclear or homonuclear, comprised of ground-state alkali-metal atoms only [2]. As open-shell alkali-alkaline(rare)-earth dimers have manifested potential application in quantum information due to the electronic spin [8], there is great interest in extending the magnetic FRs to the formation of such molecules, which have already been created by two-color photoassociation [9].
In fact, unlike the broad and observable magnetic FRs that result from the hyperfine interaction between the electron and nucleus in collisions of alkali-metal atoms, FRs for ground-state alkali-alkaline(rare)-earth dimers are difficult to observed, since such interaction does not exist in bosonic ground-state alkaline(rare)-earth-metal atoms. Although the hyperfine interaction exists in fermionic ground-state alkaline(rare)-earth-metal atoms that have nonzero nuclear spin, it has been proven to be less important, since the electron of the alkali-metal atoms strongly couples to its own nucleus [10]. Nevertheless, Żuchowski et al [11] have firstly shown that the RbSr molecule could be produced by magnetic FR induced by the weak, modified space-dependent hyperfine coupling constant of the rubidium atom due to the presence of strontium, and systems made of alkali and Yb have also been checked to have the same mechanism by Brue and Hutson [10, 12]. However, these resonances are predicted to be too narrow, not exceeding several milli-Gauss, and usually posited at a large magnetic field strength. To overcome these difficulties for experiment and observe the resonances, Tomza et al [13] have proposed an approach with nonresonant light to induce FRs and modify their position and width, which is similar to previous proposals of using the dc-electric field to control the interactions [14, 15].
Another promising approach to observe the magnetic FRs in alkali-alkaline-earth(-like) systems is to investigate the interaction between the alkali-metal atom in the ground state and the alkaline-earth-metal(-like) atom in the metastable excited-state. Alkaline-earth-metal(-like) atoms in the metastable state have orbital angular momentum and thus are anisotropic, which would introduce some other couplings and induce broader resonances [16]. Several groups have realized the trapping of alkaline-earth-metal(-like) atoms in the metastable state [17, 18]. Particularly, a heteronuclear mixture of ground-state 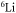 atoms and metastable excited-state
atoms and metastable excited-state 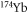 atoms have been produced at arbitrary external magnetic field strength [19], and recently both theoretical and experimental investigations on the magnetic FRs of this system have been reported [20, 21]. They claimed that a resonance at about
atoms have been produced at arbitrary external magnetic field strength [19], and recently both theoretical and experimental investigations on the magnetic FRs of this system have been reported [20, 21]. They claimed that a resonance at about  was observed in the collision of
was observed in the collision of 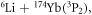 but the resonance also shows a large inelastic loss rate (at the magnitude of
but the resonance also shows a large inelastic loss rate (at the magnitude of  [21]) due to the spin exchange process, which is consistent with the previous calculation of this system [22].
[21]) due to the spin exchange process, which is consistent with the previous calculation of this system [22].
However, the intraspecies inelastic loss rate for trapped 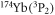 measured by Yamaguchi et al [23] is at the magnitude of
measured by Yamaguchi et al [23] is at the magnitude of 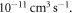 A comparison of the two loss rates indicates that not only intraspecies collision of metastable atoms [23–27] but also the interspecies interaction would likely cause the three kinds of widely investigated inelastic processes, including Zeeman-sublevel-changing, fine-structure-changing, and principle-quantum-number-changing relaxations. Thus, it is necessary to take the lower-lying fine-structure states into account in investigations on the collison properties of such systems. On the other hand, studies on the time evolution of the atom numbers of the trapped atomic mixture in [19] suggest that working in an optical lattice [28] or using fermionic isotopes benefitting from the Pauli exclusion principle (that is, inelastic collisions between two fermionic
A comparison of the two loss rates indicates that not only intraspecies collision of metastable atoms [23–27] but also the interspecies interaction would likely cause the three kinds of widely investigated inelastic processes, including Zeeman-sublevel-changing, fine-structure-changing, and principle-quantum-number-changing relaxations. Thus, it is necessary to take the lower-lying fine-structure states into account in investigations on the collison properties of such systems. On the other hand, studies on the time evolution of the atom numbers of the trapped atomic mixture in [19] suggest that working in an optical lattice [28] or using fermionic isotopes benefitting from the Pauli exclusion principle (that is, inelastic collisions between two fermionic 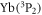 atoms are avoided) could efficiently suppress the intraspecies inelastic effect and consequently allow for precise investigations on the interspecies collision properties. Inspired by the latter suggestion, we focus on the collison properties in the mixture of
atoms are avoided) could efficiently suppress the intraspecies inelastic effect and consequently allow for precise investigations on the interspecies collision properties. Inspired by the latter suggestion, we focus on the collison properties in the mixture of 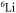 (labeled by a) in the
(labeled by a) in the 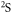 ground-state and
ground-state and 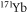 (labeled by b) in the metastable
(labeled by b) in the metastable 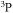 state.
state.
2. Close-coupling calculation
The Hamiltonian reads,
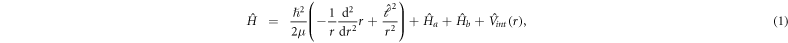
where μ is the reduced mass, r the internuclear separation, and  the rotational angular momentum operator for the diatomic molecule. The free atomic Hamiltonians
the rotational angular momentum operator for the diatomic molecule. The free atomic Hamiltonians 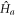 and
and 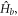 which contain Zeeman and hyperfine interactions, as well as the spin–orbit coupling-induced interaction term for atom b, are taken to be
which contain Zeeman and hyperfine interactions, as well as the spin–orbit coupling-induced interaction term for atom b, are taken to be
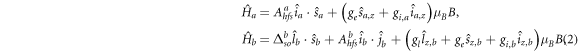
with 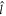 the orbital angular momentum operator;
the orbital angular momentum operator; 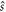 and
and 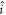 the electron and nuclear spin operators;
the electron and nuclear spin operators; 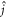 the total angular momentum coupled by
the total angular momentum coupled by  and
and 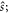
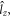
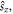 and
and 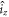 the z-components of
the z-components of 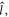
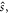 and
and 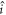 along the space-fixed z-axis, defined by the direction of the external magnetic field;
along the space-fixed z-axis, defined by the direction of the external magnetic field; 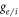 the electron and nuclear g-factors;
the electron and nuclear g-factors; 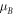 the Bohr magneton; Ahfs the magnetic dipole constant; and
the Bohr magneton; Ahfs the magnetic dipole constant; and 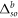 the fine splitting constant for atom b. However, for some atomic species, like
the fine splitting constant for atom b. However, for some atomic species, like 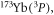 the hyperfine interaction operators should be modified with the electric quadruple couplings. The interaction operator is given as
the hyperfine interaction operators should be modified with the electric quadruple couplings. The interaction operator is given as
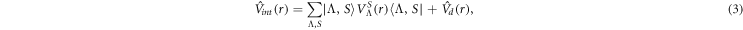
where Λ indicates the body-fixed projection of the total electronic orbital angular momentum  and S the total electronic spin.
and S the total electronic spin. 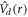 represents the magnetic dipolar interaction induced by the unpaired electrons.
represents the magnetic dipolar interaction induced by the unpaired electrons.
For the 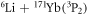 system, the nuclear spin
system, the nuclear spin 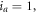
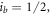 and the corresponding g-factors
and the corresponding g-factors 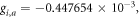
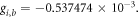 The
The 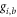 is evaluated from data for
is evaluated from data for 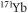 in [29] and CODATA 2010 [30]. The hyperfine magnetic dipole constants
in [29] and CODATA 2010 [30]. The hyperfine magnetic dipole constants 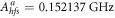 and
and  whereas the electric quadruple constant is small enough to be neglected for both atoms. Since the
whereas the electric quadruple constant is small enough to be neglected for both atoms. Since the 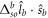 term describes the fine splitting of the
term describes the fine splitting of the 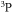 manifold, we use the energy splittings measured experimentally in [31] for channels with different j numbers. The four electronic potential curves labeled by
manifold, we use the energy splittings measured experimentally in [31] for channels with different j numbers. The four electronic potential curves labeled by 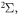

 and
and 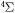 in terms of the interaction operator (3) can be built with the short-range part and the long-range part. The short-range part is taken from calculated ab initio data by Gopakumar et al [32], which is consistent with the results in [21]. The long-range non-relativistic Van der Waals coefficients C6 are given as
in terms of the interaction operator (3) can be built with the short-range part and the long-range part. The short-range part is taken from calculated ab initio data by Gopakumar et al [32], which is consistent with the results in [21]. The long-range non-relativistic Van der Waals coefficients C6 are given as 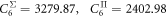 in units of
in units of 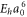 in [19], and the short- and long-range parts are connected from 6–12 Å by a switch function [33, 34]. The
in [19], and the short- and long-range parts are connected from 6–12 Å by a switch function [33, 34]. The 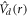 term has not been taken into account yet, since it is several orders of magnitude smaller than the anisotropic interaction induced by the orbital angular momentum coupling [21], and it has also been checked that the results did not take significant changes with the
term has not been taken into account yet, since it is several orders of magnitude smaller than the anisotropic interaction induced by the orbital angular momentum coupling [21], and it has also been checked that the results did not take significant changes with the 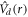 term considered in [22].
term considered in [22].
To solve the Schrödinger equation with the Hamiltonian (1), we have implemented the multi-channel close-coupling model based on the expansion of the molecular wavefunctions under a basis set in the partly coupled representation 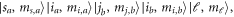 where m numbers represent angular momentum projections along the space-fixed z-axis. Equivalently, either the fully coupled basis set
where m numbers represent angular momentum projections along the space-fixed z-axis. Equivalently, either the fully coupled basis set 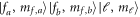 or the fully uncoupled basis set
or the fully uncoupled basis set 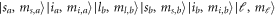 could be employed when they span the same Hilbert space. Owing to the fact that the external magnetic field only conserves the total parity
could be employed when they span the same Hilbert space. Owing to the fact that the external magnetic field only conserves the total parity 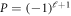 and the projection of the total angular momentum
and the projection of the total angular momentum 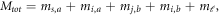 the total molecular wave function is constructed with all possible basis sets, which can produce the same Mtot and parity P values with those of the incoming channel. The rate constants for elastic and inelastic collisions for the incoming state lying in
the total molecular wave function is constructed with all possible basis sets, which can produce the same Mtot and parity P values with those of the incoming channel. The rate constants for elastic and inelastic collisions for the incoming state lying in 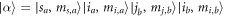 are obtained by the sum of contributions from the resulting S-matrix elements for all possible partial waves [35] as
are obtained by the sum of contributions from the resulting S-matrix elements for all possible partial waves [35] as 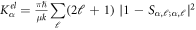 and
and 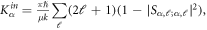 where
where 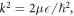 with
with  the collision energy. Particularly, the s-wave scattering length
the collision energy. Particularly, the s-wave scattering length ![$a={({\rm{i}}k)}^{-1}[1-{S}_{\alpha ,0;\alpha ,0}]{[1+{S}_{\alpha ,0;\alpha ,0}]}^{-1}$](https://content.cld.iop.org/journals/1367-2630/17/10/103036/revision1/njp520034ieqn69.gif) is obtained from the diagonal element of the S matrix for the
is obtained from the diagonal element of the S matrix for the  incoming channels.
incoming channels.
3. Results and discussions
We firstly consider the collisions between 
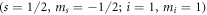 and
and 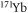
 atoms with a collisional energy of
atoms with a collisional energy of 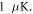 Channels with
Channels with 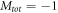 and even
and even 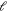 are included. To explore the origin of the FRs in this system, close-coupling calculations are firstly implemented under basis sets with j = 2 only. Figure 1(a) shows that three extremely narrow resonances, the widths of which are at a magnitude of around 1 mG, exist with only
are included. To explore the origin of the FRs in this system, close-coupling calculations are firstly implemented under basis sets with j = 2 only. Figure 1(a) shows that three extremely narrow resonances, the widths of which are at a magnitude of around 1 mG, exist with only  channels included. The resonance positions located by the near-threshold bound-states in the lower panel are consistent with those from the calculation of the s-wave scattering length. Similar with the collisional properties between
channels included. The resonance positions located by the near-threshold bound-states in the lower panel are consistent with those from the calculation of the s-wave scattering length. Similar with the collisional properties between 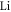 and fermionic
and fermionic 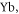 both in the electronic ground-state [10], these FRs are also produced by the mechanism due to hyperfine coupling between the electron spin and the nuclear magnetic moment of Yb, and thus their widths take the same order of magnitude. However, when taking channels with
both in the electronic ground-state [10], these FRs are also produced by the mechanism due to hyperfine coupling between the electron spin and the nuclear magnetic moment of Yb, and thus their widths take the same order of magnitude. However, when taking channels with  into account, broader resonance begins to appear, as shown in figure 1(b). Including channels with a higher partial wave number
into account, broader resonance begins to appear, as shown in figure 1(b). Including channels with a higher partial wave number 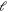 leads to many more resonances (see figure 1(c) for
leads to many more resonances (see figure 1(c) for 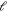 up to
up to 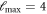 ), and their widths are more than two orders of magnitude larger than those in figure 1(a). Consequently, it can be confirmed that the broad resonances are induced by strong mixing between channels with different partial waves. According to the derivation of the matrix elements for the interaction operator in appendix, we emphasize that this strong mixing of different
), and their widths are more than two orders of magnitude larger than those in figure 1(a). Consequently, it can be confirmed that the broad resonances are induced by strong mixing between channels with different partial waves. According to the derivation of the matrix elements for the interaction operator in appendix, we emphasize that this strong mixing of different 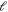 is determined by k = 2 and originates from the orbital degree of freedom-induced anisotropic interactions (see the fifth Wigner 3j symbol in equation (A.1)) in couplings of the four potential terms.
is determined by k = 2 and originates from the orbital degree of freedom-induced anisotropic interactions (see the fifth Wigner 3j symbol in equation (A.1)) in couplings of the four potential terms.
Figure 1. Magnetic field dependence of the s-wave scattering length a for the collision between 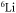 in
in 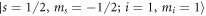 and
and 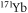 in
in 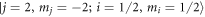 at
at 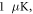 including j = 2 channels with: only
including j = 2 channels with: only  for the upper panel of (a), and
for the upper panel of (a), and 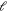 up to
up to 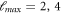 for (b) and (c), respectively. Lower panel of (a) shows the near-threshold bound-state energy responsible for the three extremely narrow resonances in the upper panel.
for (b) and (c), respectively. Lower panel of (a) shows the near-threshold bound-state energy responsible for the three extremely narrow resonances in the upper panel.  means the difference between the calculated bound-state energy and the total energy of the two incoming free atoms. In (b) and (c), narrower resonances (the width at the magnitude of mG) are not plotted. a0 is the Bohr radius.
means the difference between the calculated bound-state energy and the total energy of the two incoming free atoms. In (b) and (c), narrower resonances (the width at the magnitude of mG) are not plotted. a0 is the Bohr radius.
Download figure:
Standard image High-resolution imageThis phenomenon, that broad FR appears with an increasing number of channels from higher partial waves, is unlike those already observed in ground-state alkali-metal atom collisions [2] or in collisions of the strongly magnetic Cr atom [36]. For these atoms, the resonances do not take significant changes when channels with higher partial waves are added, which is an inevitable consequence, since the Hamiltonian for these systems conserves the partial wave number 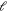 when the anisotropic spin–spin dipole interaction terms, which would introduce couplings between channels with
when the anisotropic spin–spin dipole interaction terms, which would introduce couplings between channels with  are not under consideration. On the other hand, this behaviour of adding higher
are not under consideration. On the other hand, this behaviour of adding higher 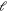 channels for metastable fermionic Yb is, to some extent, similar to that in the heavy submerged shell-elements collisions, like Dy and Er. In fact, the resonances for bosonic Dy and Er are chaotically distributed, and their extremely complex Feshbach spectra have been measured experimentally [37, 38]. Theoretical close-coupling investigations for these two atomic species [37, 39] indicate that the complex FRs are induced by larger (compared with the alkali-metal atomic collisions) magnetic dipole–dipole interaction and strongly anisotropic dispersion of the potential energy surface, both of which originate from their complex atomic electronic structures. However, unlike the complex short- and long-range potential surface in
channels for metastable fermionic Yb is, to some extent, similar to that in the heavy submerged shell-elements collisions, like Dy and Er. In fact, the resonances for bosonic Dy and Er are chaotically distributed, and their extremely complex Feshbach spectra have been measured experimentally [37, 38]. Theoretical close-coupling investigations for these two atomic species [37, 39] indicate that the complex FRs are induced by larger (compared with the alkali-metal atomic collisions) magnetic dipole–dipole interaction and strongly anisotropic dispersion of the potential energy surface, both of which originate from their complex atomic electronic structures. However, unlike the complex short- and long-range potential surface in 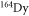 (orbital angular momentum l = 6) [39], the systems considered in this work have much simpler interatomic potentials, and thus the relationship between the anisotropic couplings and the orbital angular momentum of metastable atoms could be easily analyzed. Neglecting the magnetic dipole–dipole terms, couplings between orbital angular momentum
(orbital angular momentum l = 6) [39], the systems considered in this work have much simpler interatomic potentials, and thus the relationship between the anisotropic couplings and the orbital angular momentum of metastable atoms could be easily analyzed. Neglecting the magnetic dipole–dipole terms, couplings between orbital angular momentum 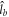 and electronic, nuclear spin
and electronic, nuclear spin 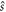 and molecular rotational angular momentum operator
and molecular rotational angular momentum operator 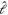 (described by the partial wave number
(described by the partial wave number 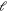 ) lead to anisotropic potential coupling terms, especially for two channels with
) lead to anisotropic potential coupling terms, especially for two channels with 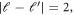 and further induce those broad FRs
and further induce those broad FRs
However, the above results do not give complete insight into the collison properties for systems with an atom in the metastable state, since the couplings to lower-lying fine-structure states 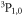 of the
of the  atom are neglected. It is well known that the scattering length for FRs in the presence of inelastic spin relaxation to lower-lying levels is complex, and the imaginary part is in term with the inelastic loss rate constant [40]. Adding basis sets that conserve Mtot and P in
atom are neglected. It is well known that the scattering length for FRs in the presence of inelastic spin relaxation to lower-lying levels is complex, and the imaginary part is in term with the inelastic loss rate constant [40]. Adding basis sets that conserve Mtot and P in 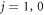 manifolds leads to close-coupling calculations, including 22 channels with
manifolds leads to close-coupling calculations, including 22 channels with  and the results are shown in figure 2. Comparing the spectra in the upper panel with that in figure 1(a), it can be easily recognized that broad resonances, although along with the inelastic rate constant ranging from
and the results are shown in figure 2. Comparing the spectra in the upper panel with that in figure 1(a), it can be easily recognized that broad resonances, although along with the inelastic rate constant ranging from 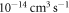 up to
up to 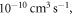 as shown in the lower panel of figure 2, appear, and they are induced by the added couplings to lower
as shown in the lower panel of figure 2, appear, and they are induced by the added couplings to lower 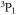 and
and  states. This is an inevitable consequence due to the three fine-structure states sharing the same four potential curves. In fact, when deriving the matrix elements (A.1) for the interaction operator, couplings between different
states. This is an inevitable consequence due to the three fine-structure states sharing the same four potential curves. In fact, when deriving the matrix elements (A.1) for the interaction operator, couplings between different 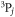 states produce nonzero off-diagonal elements for different either j or mj, so these anisotropic potential couplings should be in charge of the broad resonances in figure 2.
states produce nonzero off-diagonal elements for different either j or mj, so these anisotropic potential couplings should be in charge of the broad resonances in figure 2.
Figure 2. Upper panel: the real part of s-wave scattering length a as a function of magnetic field B in the collision of two atoms lying in the same internal state in figure 1 at  Compared with figure 1(a), channels with lower-lying
Compared with figure 1(a), channels with lower-lying 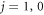 are added. The Fano shapes correspond to the resonances, and narrower resonances are not illustrated yet. Lower panel: magnetic field dependence of the inelastic scattering rate constant
are added. The Fano shapes correspond to the resonances, and narrower resonances are not illustrated yet. Lower panel: magnetic field dependence of the inelastic scattering rate constant 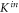 for the incoming state. The peaks reflect the positions of the resonances in the upper panel, respectively. From 600–1000 G, some weak peaks exist, but the real parts of the scattering length show a subtle rise and fall and thus could not be figured out in the upper panel.
for the incoming state. The peaks reflect the positions of the resonances in the upper panel, respectively. From 600–1000 G, some weak peaks exist, but the real parts of the scattering length show a subtle rise and fall and thus could not be figured out in the upper panel.
Download figure:
Standard image High-resolution imageBased on the above discussions, we conclude that anisotropic potential terms, either from couplings between different partial waves or from couplings with lower-lying  states, play dominant roles in producing those broad resonances. To check whether this
states, play dominant roles in producing those broad resonances. To check whether this 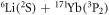 system is a promising candidate for forming a molecule, we have performed close-coupling calculations, including 433 channels with
system is a promising candidate for forming a molecule, we have performed close-coupling calculations, including 433 channels with 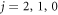 and even
and even 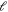 up to
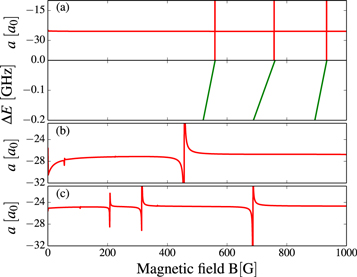
up to 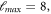 and the converged resulting s-wave scattering length and inelastic collision rate constant are illustrated in figure 3. The spectrum contributed by so many Fano shapes at first sight is disorganized, especially for the region of low magnetic field strength, but the resonance positions can be located by the peaks of the inelastic rate in the lower panel [40]. Since Mtot conserves and
and the converged resulting s-wave scattering length and inelastic collision rate constant are illustrated in figure 3. The spectrum contributed by so many Fano shapes at first sight is disorganized, especially for the region of low magnetic field strength, but the resonance positions can be located by the peaks of the inelastic rate in the lower panel [40]. Since Mtot conserves and 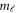 ranges from
ranges from 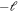 to
to  the chosen channels will cover all possible internal spin states for two atoms when larger
the chosen channels will cover all possible internal spin states for two atoms when larger 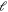 are included. Consequently, when tuning the strength of the magnetic field, so many bound-states cross the incoming collision energy threshold, that the Fano shapes for those bound-states which have a small energy difference with each other, say,
are included. Consequently, when tuning the strength of the magnetic field, so many bound-states cross the incoming collision energy threshold, that the Fano shapes for those bound-states which have a small energy difference with each other, say, 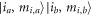 and
and 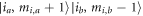 channels, that they would likely partly coincide or even mask others. Compared with the case for bosonic
channels, that they would likely partly coincide or even mask others. Compared with the case for bosonic 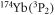 [22], where the Fano shapes could be clearly figured out from each other, such complicated behaviours in figure 3 result from the extra degree of freedom from nuclear spin
[22], where the Fano shapes could be clearly figured out from each other, such complicated behaviours in figure 3 result from the extra degree of freedom from nuclear spin 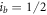 of fermionic
of fermionic 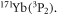 Nevertheless, three undisturbed resonances at
Nevertheless, three undisturbed resonances at 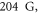
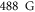 and
and 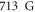 can be observed and potentially be used to tune the interactions between two atom species, but their large inelastic loss rate at the magnitude of around
can be observed and potentially be used to tune the interactions between two atom species, but their large inelastic loss rate at the magnitude of around 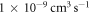 is still an obstacle for the formation of the LiYb molecule. On the other hand, since both atoms lie in the energetically lowest magnetic sublevel of their Zeeman manifolds, respectively, naturally the inelastic rate shown in the lower panel of figure 3 should be totally contributed by the fine-structure-changing relaxations to the lower-lying
is still an obstacle for the formation of the LiYb molecule. On the other hand, since both atoms lie in the energetically lowest magnetic sublevel of their Zeeman manifolds, respectively, naturally the inelastic rate shown in the lower panel of figure 3 should be totally contributed by the fine-structure-changing relaxations to the lower-lying 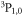 states. The magnitude of the inelastic loss rate takes the same order with that for the case of
states. The magnitude of the inelastic loss rate takes the same order with that for the case of 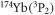 [20–22]. Another issue is that these resonances still cannot be identified with the dominantly contributed channels, as has been done in [21], since calculations of the bound-state energy with so many channels converge extremely slowly.
[20–22]. Another issue is that these resonances still cannot be identified with the dominantly contributed channels, as has been done in [21], since calculations of the bound-state energy with so many channels converge extremely slowly.
Figure 3. The real part of s-wave scattering length a (upper panel) and inelastic scattering rate constant  (lower panel) as functions of magnetic field under the same condition as that in figure 2 but including channels with
(lower panel) as functions of magnetic field under the same condition as that in figure 2 but including channels with 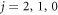 and even a partial wave up to
and even a partial wave up to 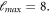
Download figure:
Standard image High-resolution imageTo investigate the effect of Zeeman-sublevel-changing relaxation, we have repeated the close-coupling calculation for metastable 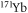 in another spin state, for instance,
in another spin state, for instance, 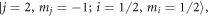 but with only j = 2 channels included. Figure 4 shows the inelastic rate constant
but with only j = 2 channels included. Figure 4 shows the inelastic rate constant 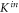 as a function of magnetic field, with
as a function of magnetic field, with 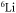 in the lowest Zeeman sublevel. The spectrum exhibits a complicated line shape, and the peaks are generally at the magnitude of
in the lowest Zeeman sublevel. The spectrum exhibits a complicated line shape, and the peaks are generally at the magnitude of  which takes the same order with the inelastic rate in figure 3. Consequently, we make a conclusion that both the Zeeman-sublevel-changing and fine-structure-changing relaxations play a significant role in spin-stretched collisions. This behaviour is similar to that in collisions of Li with bosonic metastable
which takes the same order with the inelastic rate in figure 3. Consequently, we make a conclusion that both the Zeeman-sublevel-changing and fine-structure-changing relaxations play a significant role in spin-stretched collisions. This behaviour is similar to that in collisions of Li with bosonic metastable 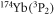 [20–22] since it has been observed that significant loss fractions end up in both
[20–22] since it has been observed that significant loss fractions end up in both  and
and 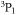 channels in the experiment for the
channels in the experiment for the 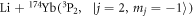 mixture [20].
mixture [20].
Figure 4. Magnetic field dependence of inelastic scattering rate constant 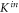 for collision between
for collision between 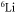 in
in 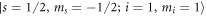 and
and 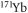 in
in 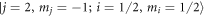 at a collisional energy of
at a collisional energy of  Only j = 2 channels are included.
Only j = 2 channels are included.
Download figure:
Standard image High-resolution imageAnother essential matter is the effect of the quantitative uncertainty of the four potential curves, since it is not possible to calculate perfectly correct ab initio short-range potential terms. Slight changes of tens of 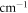 to the depths of the potential wells will lead to significant tremble for positions of those near-threshold vibrational bound-states and thus change the positions of the FRs. Figure 5 illustrates the magnetic dependence of the inelastic scattering rate constant under different short-range potentials in collisions of
to the depths of the potential wells will lead to significant tremble for positions of those near-threshold vibrational bound-states and thus change the positions of the FRs. Figure 5 illustrates the magnetic dependence of the inelastic scattering rate constant under different short-range potentials in collisions of 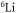
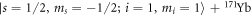
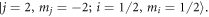 By multiplying a scaling parameter to the initially used data of the four short-range electric potential curves, the Feshbach spectra characterized by the widths and positions of the resonances are modified nontrivially. Due to this, the experimentally measured Feshbach spectra can in turn be used to optimize the calculated ab initio data to obtain a more precise form of the short-range potentials, as has been done in [21].
By multiplying a scaling parameter to the initially used data of the four short-range electric potential curves, the Feshbach spectra characterized by the widths and positions of the resonances are modified nontrivially. Due to this, the experimentally measured Feshbach spectra can in turn be used to optimize the calculated ab initio data to obtain a more precise form of the short-range potentials, as has been done in [21].
Figure 5. Inelastic scattering rate constant 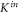 as a function of the magnetic field B under a different short-range part of the four electronic potential curves. The red line is identical with that in the lower panel of figure 3, whereas the green line indicates the inelastic scattering rate constant with the depths of the four short-range potentials all scaled by a factor of 0.95.
as a function of the magnetic field B under a different short-range part of the four electronic potential curves. The red line is identical with that in the lower panel of figure 3, whereas the green line indicates the inelastic scattering rate constant with the depths of the four short-range potentials all scaled by a factor of 0.95.
Download figure:
Standard image High-resolution imageAdditionally, inclusion of the magnetic dipole–dipole term 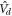 in (3), the effect of which has been checked to be extremely unconspicuous [22], would in some extent lead to some modifications and thus induce a much more complicated spectrum, as observed in collisions of the
in (3), the effect of which has been checked to be extremely unconspicuous [22], would in some extent lead to some modifications and thus induce a much more complicated spectrum, as observed in collisions of the  atom [39]. Another term, first revealed in exploring the possibility of magnetic associating RbSr and alkali-Yb(
atom [39]. Another term, first revealed in exploring the possibility of magnetic associating RbSr and alkali-Yb(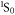 ) molecules [10–12], is the r-dependence of the hyperfine coupling, which has also been proven to be significantly smaller when compared with the anisotropic couplings for the systems considered in this work.
) molecules [10–12], is the r-dependence of the hyperfine coupling, which has also been proven to be significantly smaller when compared with the anisotropic couplings for the systems considered in this work.
4. Conclusion
To conclude, we have theoretically investigated the scattering properties for collisions between 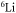 in the
in the 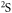 ground-state and fermionic
ground-state and fermionic  in the metastable
in the metastable 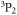 state. Applying fully closed-coupling calculations, we have elucidated that broad FRs are induced by the anisotropy. The anisotropic potential coupling terms originate from two mechanisms: the ability of the interaction operator to strongly mix channels satisfying
state. Applying fully closed-coupling calculations, we have elucidated that broad FRs are induced by the anisotropy. The anisotropic potential coupling terms originate from two mechanisms: the ability of the interaction operator to strongly mix channels satisfying 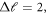 even when the magnetic dipole–dipole term is neglected, and the couplings with lower-lying
even when the magnetic dipole–dipole term is neglected, and the couplings with lower-lying 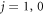 fine-structure states. A comparison with collisional properties in alkali-metal systems and highly magnetic rare-earth-metal atoms indicates that both the original mechanisms are introduced by the orbital degree of freedom from the outest p electron of the metastable
fine-structure states. A comparison with collisional properties in alkali-metal systems and highly magnetic rare-earth-metal atoms indicates that both the original mechanisms are introduced by the orbital degree of freedom from the outest p electron of the metastable 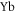 atom. However, with higher partial wave
atom. However, with higher partial wave 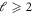 and lower-lying
and lower-lying 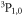 channels included, broad observable resonances appear, but with large inelastic relaxations rate at the magnitude of
channels included, broad observable resonances appear, but with large inelastic relaxations rate at the magnitude of  Such rapid inelastic relaxations will be obstacles for molecular formation, although the
Such rapid inelastic relaxations will be obstacles for molecular formation, although the 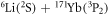 system, at first sight, can be potentially applied for associating ultracold polar molecules due to the broad resonances and long lifetime of
system, at first sight, can be potentially applied for associating ultracold polar molecules due to the broad resonances and long lifetime of 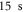 for metastable Yb atoms. We have also studied the uncertainty effects from the ab initio calculated short-range potentials, which are not accurate enough yet.
for metastable Yb atoms. We have also studied the uncertainty effects from the ab initio calculated short-range potentials, which are not accurate enough yet.
Recently, an investigation on FRs in the ground-state Li + Er system [41] has also shown that atoms with a larger orbital angular momentum (for Er in the  ground-state, l = 5) would likely produce non-chaotic, complicated Feshbach spectra, while those for metastable alkali-earth-metal(-like) atoms (l = 1) exhibit much simpler behaviour. Suffering from the inelastic relaxations, the
ground-state, l = 5) would likely produce non-chaotic, complicated Feshbach spectra, while those for metastable alkali-earth-metal(-like) atoms (l = 1) exhibit much simpler behaviour. Suffering from the inelastic relaxations, the 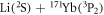 system might not be a good candidate for producing ultracold polar molecules with both electron spin and electric dipole momentum. However, a rich mixture of inelastic processes and the experimental advantage of immunity of intraspecies inelastic collisions for metastable fermionic
system might not be a good candidate for producing ultracold polar molecules with both electron spin and electric dipole momentum. However, a rich mixture of inelastic processes and the experimental advantage of immunity of intraspecies inelastic collisions for metastable fermionic 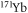 allow more precise investigations on the interspecies scattering properties with the assistance of an optical lattice, just like the experiment on the
allow more precise investigations on the interspecies scattering properties with the assistance of an optical lattice, just like the experiment on the 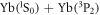 mixture [28].
mixture [28].
Acknowledgments
This work is supported by the National Basic Research Program of China (Grant No. 2011CB921504) and the National Natural Science Foundation of China (Grant No. 91536107).
Appendix. Matrix element for the interaction operator
Since the first term of the interaction operator in equation (3) is expanded in a body-fixed basis 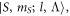 transformations are required to obtain the matrix elements in the space-fixed basis represented by
transformations are required to obtain the matrix elements in the space-fixed basis represented by 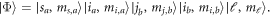 Following the derivation in [16], the matrix elements take the form
Following the derivation in [16], the matrix elements take the form
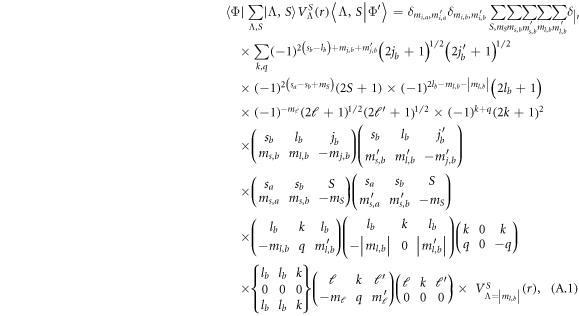
where the braces denote the Wigner 9j symbol. In fact, taking advantage of 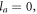 this formula is a reduced form from matrix elements of the interaction operator for systems comprised of two arbitrary (but not including S) states, say two P states [16]. On the other hand, by simply setting
this formula is a reduced form from matrix elements of the interaction operator for systems comprised of two arbitrary (but not including S) states, say two P states [16]. On the other hand, by simply setting 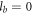 , the above form could also be simplified to the form of those for systems of two S-state atoms, for example, equation (A.1) in [42] for a diatomic system of two alkali-metal atoms, both in the ground-state.
, the above form could also be simplified to the form of those for systems of two S-state atoms, for example, equation (A.1) in [42] for a diatomic system of two alkali-metal atoms, both in the ground-state.