Abstract
We present an experimental observation and comprehensive theory that address the effect of interaction on the phase transition in a many-body system, which is far from equilibrium and does not have detailed balance. In the resonantly driven cold atomic trap, we observe kinetic phase transition (KPT) that is manifested by substantial enhancement of fluctuations, similar to the first-order phase transition in thermal equilibrium. Moreover, we can control the attractive interaction between atoms trapped in the coexisting states by adjusting the total number of atoms, which induces shift of the phase boundaries of KPT. The demonstrated effect is the many-body analogue of KPT that was previously predicted and observed in a single-driven oscillator. Our work provides a unique model platform for quantitative study of nonequilibrium nonlinear dynamics in many-body systems.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
GENERAL SCIENTIFIC SUMMARY Introduction and background. One of the difficulties of statistical physics is that, contrary to equilibrium phenomena where there exists a unified approach that explains macroscopic properties by microscopic interactions, out of equilibrium only has a limited number of results with a general scope. Therefore, both theoretical and experimental study of a system far from equilibrium is one of main concerns and demands in this field. Driven many-body cold atoms present a unique, well controlled platform for nonequilibrium study, and the experimental and theoretical results provide the rare but valuable model system of nonequilibrium nonlinear dynamics study.
Main results. Our system presents several innovative features. Firstly, previous studies on the Duffing oscillator have considered only the single-particle nonlinear dynamics, but our work provides a unique cold atomic platform, suitable for the study of the effects of global attractive interaction acting between many-body cold atoms. Secondly, this attractive interatomic interaction shows interesting results, beyond the single-particle nonlinear dynamics, associated with the nonequilibrium phase transition which have not yet been addressed. Thirdly, we show that the role of attractive interaction is to shift the phase transition boundaries in a similar way to the interaction effect on the system governed by van der Waal's equation, which provides evidence of similarity between equilibrium and nonequilibrium phase transition.
Wider implications. We believe that the experimental results, in combination with the comprehensive theory established, opens new and original ways of investigating the dynamics of cold atoms far from equilibrium and of relating this dynamics to other domains of physics (dynamical systems, statistical physics).
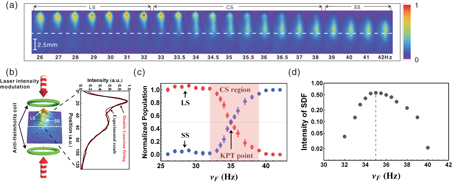
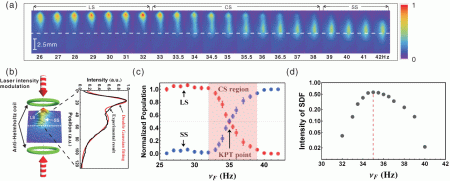 Figure. Weakly interacting atomic Duffing oscillators under fluctuation-induced switching. (a) The fluctuations due to spontaneous emission of photons triggers noise-induced switching between two attractors. The images of oscillatory atomic motion are captured at regular intervals such that the large-amplitude state (LS) atomic cloud is fully apart from the trap center (dashed horizontal line) whereas the small-amplitude state (SS) cloud is not in the maximum vibrational amplitude because of the phase difference between LS and SS. The number of atoms is about 2.27 × 107 and the measured γ and ω0 are 50.44 s−1 and 2π × 28.26 Hz, respectively. (b) Schematic representation of experiment setup and the typical intensity profile of atoms in LS and SS. (c) The change of atomic population in each state versus the driving frequency νF( = ωF/2π). KPT occurs when the two populations are equal in the coexisting dynamical states (CS). (d) The measured intensity of spectral density of fluctuation is maximized at the KPT point, leading to the onset of large fluctuations linked to transitions between two states (semi-log scale). The error bars show the standard deviation.
Figure. Weakly interacting atomic Duffing oscillators under fluctuation-induced switching. (a) The fluctuations due to spontaneous emission of photons triggers noise-induced switching between two attractors. The images of oscillatory atomic motion are captured at regular intervals such that the large-amplitude state (LS) atomic cloud is fully apart from the trap center (dashed horizontal line) whereas the small-amplitude state (SS) cloud is not in the maximum vibrational amplitude because of the phase difference between LS and SS. The number of atoms is about 2.27 × 107 and the measured γ and ω0 are 50.44 s−1 and 2π × 28.26 Hz, respectively. (b) Schematic representation of experiment setup and the typical intensity profile of atoms in LS and SS. (c) The change of atomic population in each state versus the driving frequency νF( = ωF/2π). KPT occurs when the two populations are equal in the coexisting dynamical states (CS). (d) The measured intensity of spectral density of fluctuation is maximized at the KPT point, leading to the onset of large fluctuations linked to transitions between two states (semi-log scale). The error bars show the standard deviation.
1. Introduction
The last few decades have witnessed an immense amount of research activity, both in experimental and theoretical work, focused on understanding the detailed dynamics of quantum [1] and classical systems [2–5] that are under time-dependent external perturbations. In general, such systems exhibit an interplay of three characteristic components: (i) nonlinearity, (ii) nonequilibrium behavior and (iii) quantum tunneling (for quantum systems) or large rare fluctuation (for classical systems). In particular, the large rare fluctuations provide a variety of phase transitions far from equilibrium in classical nonlinear dynamical systems [6–10].
The study of large rare fluctuations has mainly been focused on prominent qualitative changes of an equilibrium system, such as the nucleation at phase transitions, chemical reactions, mutations in DNA sequences and protein transport in biological cells [11–14]. On the other hand, the fluctuating systems of interest are far from thermal equilibrium; for example, lasers, pattern-forming systems, radio-frequency-driven Josephson junctions [15], micromechanical and nanomechanical oscillators [16–18] and periodically driven trapped electrons [19–22]. In particular, in the periodically driven nonlinear dynamic system out of equilibrium, which exhibits intrinsic bistable or multistable states, the fluctuation triggers noise-induced switching between stable states [5, 8, 9], where the fluctuation-induced switching dynamics shows characteristics similar to the equilibrium phase transition [5, 8].
It is well known that, in thermodynamic systems, the increase of fluctuations at the critical point is a universal characteristic of phase transition [23]. In particular, even in the single-particle-driven nonlinear systems [5], such as the Duffing oscillator, significant enhancement of fluctuations that arise from noise-induced switching between coexisting states was also observed in the measured spectral density of fluctuations (SDFs) near the specific driving frequency, which is indicative of a phase transition in nonequilibrium systems—the so-called kinetic phase transition (KPT) [8]. Nonetheless, in such a driven mechanical system, it is experimentally difficult to go beyond the single-particle behavior and investigate many-body effects associated with the inter-particle interactions between bistable states, although the coupled oscillator arrays have been explored theoretically [24–27]. In the parameterically driven cold atom trap [9, 10], on the other hand, the globally coupled atom–atom attractive interaction between attractors was shown to produce numerous qualitative changes in the nonequilibrium phase transition, while exhibiting the ideal mean-field transition. Therefore, it is essential to make an experimental study of KPT in a weakly interacting ensemble system [28], which still lacks despite many KPT works performed so far.
In this paper, we experimentally realize the globally coupled Duffing oscillators in an optically modulated magneto-optical trap of 85Rb in the presence of long-range interatomic interactions associated with the shadow-induced light force [10] and advance a theory. This paper is organized as follows. In section 2, the experimental results are presented and compared to the theoretical results. In section 3, we demonstrate the theoretical approach of global coupling long-range interaction between dynamical bistable states consisting of many particles. Section 4 summarizes the results.
2. Experimental results and discussions
The resonantly driven nonlinear oscillator, Duffing oscillator, exhibits two coexisting dynamical states (CS) as well as the large-amplitude state (LS) and small-amplitude state (SS), which have differing vibrational amplitude and phase at a specific range of driving frequency (figure 1(a)). In the presence of noise, such as thermal fluctuations, there occurs noise-induced switching between CS, and the transition probability as well as the occupied population between them are determined by the activation energy and noise intensity, given by
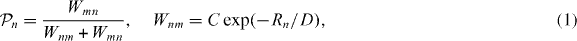
where Wnm and 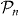 are the transition probabilities from the nth state to the mth state (n,m = 1,2,n ≠ m) and the occupied population in the nth state, respectively. Here
are the transition probabilities from the nth state to the mth state (n,m = 1,2,n ≠ m) and the occupied population in the nth state, respectively. Here 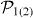 is the normalized atomic populations of LS (SS), so that
is the normalized atomic populations of LS (SS), so that 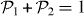 , and C is a constant. The subscript 1 and 2 denote LS and SS, respectively. Rn stands for the activation energy of the nth state and D is the noise intensity. Notice that Wnm and
, and C is a constant. The subscript 1 and 2 denote LS and SS, respectively. Rn stands for the activation energy of the nth state and D is the noise intensity. Notice that Wnm and  have been calculated previously for a single Duffing oscillator, which is expected to exhibit differing behavior for an interacting many-oscillator system.
have been calculated previously for a single Duffing oscillator, which is expected to exhibit differing behavior for an interacting many-oscillator system.
Figure 1. Weakly interacting atomic Duffing oscillators under fluctuation-induced switching. (a) The fluctuations due to spontaneous emission of photons triggers noise-induced switching between two attractors. The images of oscillatory atomic motion are captured at regular intervals such that the LS atomic cloud is fully apart from the trap center (dashed horizontal line) whereas the SS cloud is not in the maximum vibrational amplitude because of the phase difference between LS and SS. The number of atoms is about 2.27 × 107 and the measured γ and ω0 are 50.44 s−1 and 2π × 28.26 Hz, respectively. (b) Schematic representation of experiment setup and the typical intensity profile of atoms in LS and SS. (c) The change of atomic population in each state versus the driving frequency νF(= ωF/2π). KPT occurs when the two populations are equal in the CS. (d) The measured intensity of SDF is maximized at the KPT point, leading to the onset of large fluctuations linked to transitions between two states (semi-log scale). The error bars show the standard deviation.
Download figure:
Standard image High-resolution imageThe many-body system of the Duffing oscillators is experimentally realized in the magneto-optical trap of 85Rb atoms by modulating the intensity of trap lasers counterpropagating along the anti-Helmholtz coil axis with the phase difference between the two lasers maintained at π (figure 1(b)). We measure the atomic populations in each state to investigate the noise-induced switching between two attractors, and compare experimental results with simulation. Near the KPT point where the populations of two attractors are comparable, we also observe the enhanced intensity of the SDFs. Notice that, in our ensemble system, 106–107 atoms are distributed over dynamical states, and thus one can readily measure the steady-state populations occupied in each state without any statistical analysis. Figure 1(a) shows the atomic cloud (T ≈ 0.4 mK) in the LS, CS and SS within a specific frequency range. Notice that because the distance between the two attractors is not far enough, there exists a region where the two atomic clouds overlap, manifested by the long cloud shape.
Figure 1(c) shows the normalized atomic populations versus ωF/2π near the KPT point at 35 Hz. As shown, the two attractors are equally occupied at the KPT point because the activation energies of the two attractors are equal. Here the important feature of a phase transition is to observe large fluctuations associated with transitions between the two states.
To confirm this feature, we have obtained the fluctuations near the KPT point. In our system consisting of many particles, it is hard to obtain the time trace of single-particle trajectory. Instead of analyzing the time correlation of single-particle trajectory [2, 5], therefore, in our ensemble system of many atoms, we obtain the intensity I of the SDF on the distance from KPT point, which represents the integrated spectral density, given by [8]
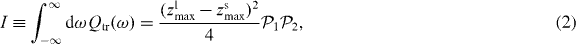
where zl(s)max is the maximum amplitude of LS (SS) and Qtr(ω) is the fluctuational noise-induced spectral peak that arises due to noise-induced transition between two dynamical states, which ![$Q_{\mathrm { tr}}(\omega )\approx \frac {2\omega _{\mathrm { F}}|\delta \omega |(W_{12}+W_{21})}{3\pi B_0[(W_{12}+W_{21})^2+(\omega -\omega _{\mathrm { F}})^2]}(z_{\mathrm { max}}^{\mathrm {l}}-z_{\mathrm { max}}^{\mathrm { s}})^2\mathcal {P}_1\mathcal {P}_2$](https://content.cld.iop.org/journals/1367-2630/15/10/103030/revision1/nj480348ieqn5.gif) where δω = ωF − ω0. Figure 1(d) clearly shows the maximum SDF intensity near the driving frequency 35 Hz, as expected.
where δω = ωF − ω0. Figure 1(d) clearly shows the maximum SDF intensity near the driving frequency 35 Hz, as expected.
The atom–atom interaction induces change of the activation energy, which is measurable because the cumulative effect of the atomic interactions between clouds becomes significant [10, 29]. Figure 2 presents the simulation results on the effects of atomic interactions on the activation energy and the associated atomic populations. To control the cumulative atomic interaction, one can change Ntot; the long-range attractive shadow force increases with Ntot because the atomic clouds in each state, while absorbing the incoming laser beams, attract each other due to the resulting imbalance of laser intensity.
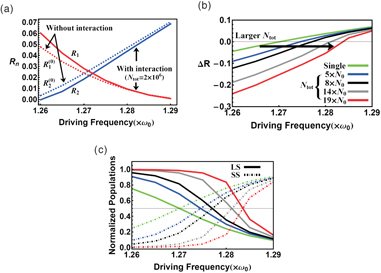
Figure 2. Simulation results on the activation energy and the atomic population versus the driving frequency. (a) The activation energy Rn (R(0)n) with (without) interaction; R1(2) of LS (SS). (b) The activation energy difference ΔR between LS and SS decreases with the interaction or Ntot. (c) The change of normalized populations in LS and SS in the weakly interacting regime. Here N0 = 106, γ and ω0 are 40.58 s−1 and 2π × 32.68 Hz.
Download figure:
Standard image High-resolution imageAs shown in figure 2(a), as Ntot increases, the atom–atom interaction induces the change of R1 and R2; the activation energy of LS (SS) increases (decreases) with Ntot. Figure 2(b) shows that the change of R1(2) then shifts the KPT point, where ΔR (= R2 − R1) = 0, toward the higher ωF at the higher Ntot. In addition, at a fixed modulation frequency ωF, ΔR decreases with the increase of Ntot. Figure 2(c) presents the resulting population change; 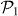 of LS increases with Ntot (solid line) where
of LS increases with Ntot (solid line) where  of SS decreases (dot-dashed line), shifting the KPT point toward the higher ωF.
of SS decreases (dot-dashed line), shifting the KPT point toward the higher ωF.
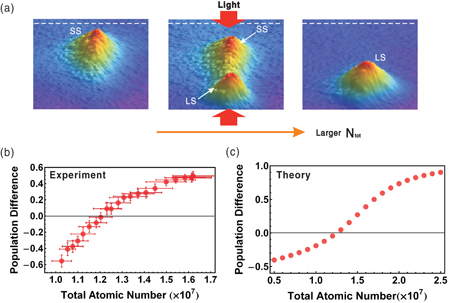
We have experimentally observed the effects of atom–atom interactions on the single-particle behavior of KPT (i.e. KPT without interaction). As shown in figure 3(a), as Ntot increases, atoms in SS transfer to LS in a unidirectional way, so that the atom–atom interaction plays the role as the one-way bias field (notice that the effect of the interaction in the parametric resonance system is to induce the time-translational symmetry, breaking which results in the ideal mean-field transition [10]). To detail the characteristics of the interaction as a one-way bias field, we have measured the difference of atomic populations of each state,  . Figure 3(b) shows that the population difference grows larger at the higher Ntot. The experimental results are in qualitatively good agreement with the theoretical results (figure 3(c)).
. Figure 3(b) shows that the population difference grows larger at the higher Ntot. The experimental results are in qualitatively good agreement with the theoretical results (figure 3(c)).
Figure 3. The change of atomic-population difference resulting from the atom–atom interaction between two stable states at the driving frequency 34 Hz. Panel (a) shows atomic images displaying the change of atomic population with Ntot. Panels (b) and (c) present the experimental and theoretical results on the population difference of atoms,  , between two CS. The white dashed line indicates the trap center.
, between two CS. The white dashed line indicates the trap center.
Download figure:
Standard image High-resolution imageThe characteristic interaction of the one-way bias field originates from the difference of the optimal path and equilibrium position of each stable state because the interatomic force depends on the position of all individual atoms. The coefficient αnm in equation (17) is related to the interatomic force, where the terms with n = m and n ≠ m indicate the force from the atoms in the same and in the different cloud, respectively. In our system, we find α11 ≠ α22 and α12 ≠ α21, which means the interatomic force that an atom in the cloud m experiences by atoms in the same as well as in different clouds is not equal to that for an atom in the cloud n. In particular, notice that the effective switching activation energy R(1)n (equation (16)) linearly depends on the number of atoms in the clouds, and also numerical calculation shows that α11 > α22,α12,α21. For example, when α11 > 0 while α22, α12 and α21 are negative, we observe that the effective switching activation energy of LS (SS) becomes positive (negative), so that the total activation energy of LS (SS) increases (decreases) with the total number of atoms, as shown in figure 2(a).
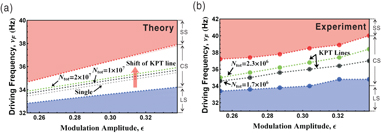
Figure 4 presents the phase-transition map in the parameter space of driving frequency ωF and modulation amplitude  (∝F0). In figure 4(a), the calculated KPT lines (black and green dashed lines) are shown, where the changes of the nonequilibrium first-order phase transition boundary are expected to depend on the total number of trapped atoms. The experimental results in figure 4(b) are in qualitatively good agreement (the differing absolute values of Ntot may be attributed to the fact that the experiment is three-dimensional whereas the theory is one-dimensional).
(∝F0). In figure 4(a), the calculated KPT lines (black and green dashed lines) are shown, where the changes of the nonequilibrium first-order phase transition boundary are expected to depend on the total number of trapped atoms. The experimental results in figure 4(b) are in qualitatively good agreement (the differing absolute values of Ntot may be attributed to the fact that the experiment is three-dimensional whereas the theory is one-dimensional).
Figure 4. (a) Theoretical results on the shift of the KPT phase boundary in the νF- parameter space with respect to the cumulative effect of atom–atom interactions (or Ntot).
parameter space with respect to the cumulative effect of atom–atom interactions (or Ntot).  is proportional to F0. (b) Experimental results on the shift of the KPT boundary. Measured γ and ω0 are 40.56 s−1 and 2π × 28.07 Hz, respectively. Red and blue dashed lines represent the boundary where the transition between a monostable state (LS or SS) and a coexisting bistable state (CS) occurs. Note that these boundary lines remain unaffected under the weak atom–atom interaction. As shown in the CS region, the typical KPT lines shift from black to green line as Ntot is increased. Each circle denotes the experimental data, which show qualitatively good agreement with the numerical results except the absolute values of Ntot.
is proportional to F0. (b) Experimental results on the shift of the KPT boundary. Measured γ and ω0 are 40.56 s−1 and 2π × 28.07 Hz, respectively. Red and blue dashed lines represent the boundary where the transition between a monostable state (LS or SS) and a coexisting bistable state (CS) occurs. Note that these boundary lines remain unaffected under the weak atom–atom interaction. As shown in the CS region, the typical KPT lines shift from black to green line as Ntot is increased. Each circle denotes the experimental data, which show qualitatively good agreement with the numerical results except the absolute values of Ntot.
Download figure:
Standard image High-resolution imageInterestingly, a similar phenomenon is observed in the first-order gas–liquid transition in equilibrium states [6, 23]. The gas–liquid transition described by the van der Waals equation takes into account the nonzero radius of atoms as well as the attractive interactions between atoms. In the pressure–temperature (P–T) map, the phase transition can be plotted where there is a coexistence region and a critical point. The atomic radius and interaction depend on the species of atom, and thus the coexistence line in the P–T plane changes with respect to the atomic species. Therefore, the attractive interaction between cold Duffing-oscillator atoms in the coexisting periodic attractors out of equilibrium exhibits close similarity with the gas–liquid transition in equilibrium. These results provide another piece of evidence for the similarity of phase transitions between equilibrium and nonequilibrium systems.
3. Theory of nonlinear vibrations in an interacting cold-atom system
3.1. Model
The vibrations in the periodically driven cold 85Rb atom system are subject to the combined influence of a periodic field, a weak random force and a long-range attractive interaction. The equation of motion for this many-body system is derived from the atom–photon interaction theory for a (1 + 3) atomic energy structure model [30, 31], which is given by
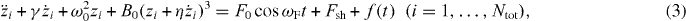
where zi and 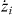 are the position and velocity of the ith atom, and Ntot is the total number of trapped atoms. We ignore the term
are the position and velocity of the ith atom, and Ntot is the total number of trapped atoms. We ignore the term 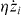 as
as 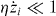 . ω0 is the natural frequency, γ is the damping coefficient, B0 is the nonlinear coefficient and F0 is the magnitude of the force. They are given by
. ω0 is the natural frequency, γ is the damping coefficient, B0 is the nonlinear coefficient and F0 is the magnitude of the force. They are given by



where ω2t = 8kμBbs0(− δ/Γ)/[ma(1 + 4δ2/Γ2)2], and correction factors Cf, Cd and Cn, considering an atomic multilevel energy structure, are 0.54, 0.41 and 0.19, respectively. s0 is the on-resonance saturation parameter.  stands for the modulation amplitude of the laser intensity. k is the wave vector, μB is the Bohr magneton, ma is the mass of an atom and Γ is the decay rate of the excited state (= 2π × 6.07 MHz). δ and b are the detuning of the laser frequency relative to the transition line Fg = 3 → Fe = 4 and the magnetic gradient field, respectively.
stands for the modulation amplitude of the laser intensity. k is the wave vector, μB is the Bohr magneton, ma is the mass of an atom and Γ is the decay rate of the excited state (= 2π × 6.07 MHz). δ and b are the detuning of the laser frequency relative to the transition line Fg = 3 → Fe = 4 and the magnetic gradient field, respectively.
f(t) is the white noise, which originates from the atomic random motion due to spontaneous emission, and 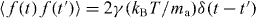 . kB and T are the Boltzmann constant and the temperature of the atom. The long-range shadow force Fsh results from 'shielding' of atoms from the laser light by other atoms, which produces all-to-all attractive coupling between atoms in the two CS [10]
. kB and T are the Boltzmann constant and the temperature of the atom. The long-range shadow force Fsh results from 'shielding' of atoms from the laser light by other atoms, which produces all-to-all attractive coupling between atoms in the two CS [10]

where the interaction strength fsh is a very small constant value (9.19 × 10−32 N kg−1). The sgn(z) indicates the sign function and zj represents the position of the jth atom of a stable state.
The nonlinear oscillator in the periodically perturbed magneto-optical trap consists of a number of atoms, and there is a long-range attractive interaction between atoms, unlike in the single nonlinear mechanical oscillator [32]. The atom–atom interaction modifies the activation energy Rn in equation (1), including the interaction effect, and thus the switching probability Wnm is changed. The influence of the variation of the switching probability owing to the atom–atom interaction remarkably displays the qualitative and quantitative discrepancies between a single particle and many particles in nonlinear dynamic systems, as reported in [10]. For understanding the interaction effect in the Duffing oscillator clearly, it is useful to transform equation (3) into the rotating frame, 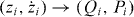 [33].
[33].
3.2. Rotating-wave approximation
The atomic dynamics in equation (3) can be described by changing to the rotating frame using a standard transformation
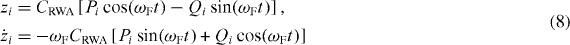
with  and δω = ωF − ω0. In the rotating-wave approximation (RWA) [10, 33], the equation of motions for slow variables qi ≡ (Qi,Pi) in slow time τ = |δω|t are
and δω = ωF − ω0. In the rotating-wave approximation (RWA) [10, 33], the equation of motions for slow variables qi ≡ (Qi,Pi) in slow time τ = |δω|t are
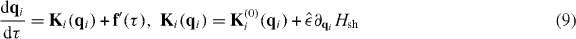
and

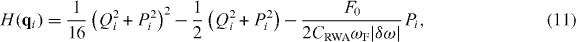
where i = 1,...,Ntot, ∂qi ≡ (∂Qi,∂Pi) and f'(τ) is white Gaussian noise with two asymptotically independent components

where Dτ = 2D/kBT and D = 3B0kBT/(4maω3Fγ).
The generalized force Ki(qi) on the ith atoms depends on the dynamical variables qi of all particles. The term K(0)i(qi) in equation (9) is the force in the absence of interaction. The tensor 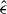 is the permutation tensor:
is the permutation tensor:  QiQi =
QiQi =  PiPi = 0,
PiPi = 0,  QiPi = −
QiPi = − PiQi = 1. The Hamiltonian Hsh that describes the shadow-effect-induced interaction has the form
PiQi = 1. The Hamiltonian Hsh that describes the shadow-effect-induced interaction has the form
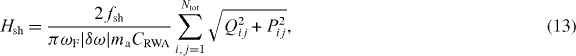
where Qij = Qi − Qj and Pij = Pi − Pj. Thus the interaction from the shadow effect is described by a simple Hamiltonian in the slow variables.
3.3. Switching rate modification by the atom–atom interaction
The interaction between atoms leads to an extra force Fsh in equation (3). This force is weak in the sense that it weakly affects the intracloud atomic dynamics. As reported in [10, 33], the modification of activation energy by the interatomic force on an atom in cloud n, to first order in Hsh, can be written as
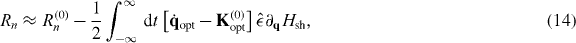
where qopt is the optimal path for the ith atom in the absence of the interatomic interaction, and K(0)opt ≡ K(0)(qopt). Here, 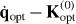 are the solutions of the variational problem of minimizing the functional
are the solutions of the variational problem of minimizing the functional  [34]
[34]
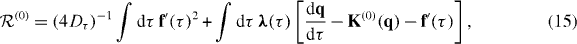
where λ(τ) is the Lagrange multiplier that relates the dynamics of the atom and the force to each other. In fact, qopt determines the most probable path followed in switching.
By assuming that all the other atoms stay close to either of the attractors, the total activation energy Rn(n = 1,2) considering the interaction between atoms can be approximately written as
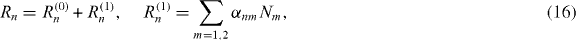
where Nn is the number of atoms in cloud n, and αnm is given by the explicit expressions
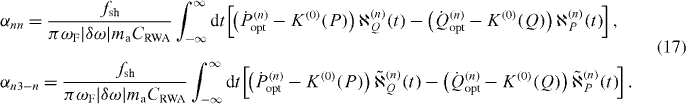
Here

where ℵ(n)P and 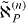 are obtained by changing P and Q with each other in ℵ(n)Q and
are obtained by changing P and Q with each other in ℵ(n)Q and 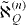 .
.
The denominators in equation (18) are given by
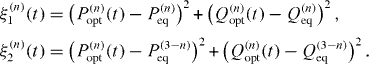
R(1)n in equation (16) shows that the effective switching activation energy linearly depends on the number of atoms in the clouds and αnm, for weak interatomic coupling. αnm depends on the systemic parameters, optimal path (Qopt,Popt) and equilibrium position (Qeq,Peq) as shown in equation (17), and according to equation (16), the activation energy of each stable state is changed by the growth of the total number of atoms. From equations (1), (16) and (17) we can obtain the switching probability as follows:
and

3.4. Master equation
To describe noise-induced switching between the bistable states, consisting of many particles, we need to solve the master equation describing the discrete jump process. Through the steady-state solution of the master equation, we can calculate the occupied population of each state as follows. Figure 5 depicts a schematic representation of the discrete jump process describing the master equation [35] for the time-dependent probability P1(N1,t) of state 1, where Nn and Ntot mean the number of particles in state n (= 1,2) and the total number of atoms, respectively. The master equation for the time-dependent probability P1(N1,t) ≡ P1(N1) of state 1, which means the probability of having N1 atoms in cloud (state) 1 at time t, is as follows:

Figure 5. Schematic representation of the discrete jump process describing the master equation for the time-dependent probability P1(N1,t) ≡ P1(N1) of state 1, which means the probability of having N1 atoms in cloud (stable state) 1 at time t.
Download figure:
Standard image High-resolution imagewhere μ(N1) = N1W12(N1;Ntot) and ν(N1) = (Ntot − N1)W21(Ntot − N1;Ntot). Wnm(Nn;Ntot) is the transition probability per unit time for one atom in state n, as a result of an n → m transition, and then for Nn atoms in state n, the total transition probability per unit time becomes NnWnm(Nn;Ntot). Therefore, in the case in which atoms transit from state 1 to state 2, the total transition probability is expressed by μ(N1) = N1W12(N1;Ntot). Conversely, in the case in which atoms transit from state 2 to state 1, ν(N1) = N2W21(N2;Ntot). Because the total number of atoms is conserved, it becomes ν(N1) = (Ntot − N1)W21(Ntot − N1;Ntot). Let us calculate the time derivative of the average of the population in state 1,  . It is given by
. It is given by

where  , and then
, and then
Because Ntot ≫ 1,  is simplified as follows:
is simplified as follows:
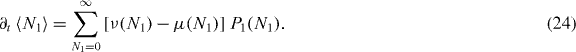
In the absence of fluctuations, we can obtain the deterministic equation from equation (24), which becomes ∂tN1 = ν(N1) − μ(N1) [35]. The stationary state occurs when ν(N1) = μ(N1), which provides the following result:

From the above formula, we can obtain the ratio of N1 to N2 as follows:
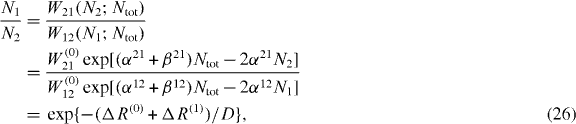
where


ΔR(0) is the activation energy difference between two states in the non-interacting case, and ΔR(1) is the activation energy difference between them, induced by the atom–atom interaction, depending on the number of atoms. Equation (26) can be simplified further in terms of 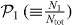 as follows:
as follows:

where  and
and 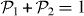 . According to the above equation, we can numerically calculate the density of the population,
. According to the above equation, we can numerically calculate the density of the population, 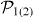 .
.
4. Conclusions
In conclusion, two CS have been realized in a resonantly driven trapped cold atoms, interacting weakly and globally with each other. In contrast to the single-particle system, we directly measure the change of atomic population with respect to the variation of activation energy, and thereby confirm the fluctuation enhancement near the KPT point, which is characteristic of KPT far from equilibrium. Moreover, we observe that the attractive atom–atom interaction shifts the phase-transition boundaries of KPT, similar to the effect of interaction on the system governed by the van der Waals equation, which provides evidence of similarity between equilibrium and nonequilibrium phase transition. Our system serves as a unique simple platform suitable for investigating the nonlinear dynamics of many-body cold atoms far from equilibrium and relating this dynamics to other domains of physics (dynamical systems, statistical physics).
Acknowledgments
This work was supported by National Research Foundation of Korea (NRF) grant no. 2012-047677 funded by the Korean government (MEST). GM was supported by Korea Student Aid Foundation (KOSAF) grant no. S2-2009-000-01627-1 funded by the Korean government (MEST).