Abstract
The aim of this work was to obtain a set of parameters to be applied in [123I]FP-CIT SPECT reconstruction in order to minimize the error between standardized and true values of the specific uptake ratio (SUR) in dopaminergic neurotransmission SPECT studies. To this end, Monte Carlo simulation was used to generate a database of 1380 projection data-sets from 23 subjects, including normal cases and a variety of pathologies. Studies were reconstructed using filtered back projection (FBP) with attenuation correction and ordered subset expectation maximization (OSEM) with correction for different degradations (attenuation, scatter and PSF). Reconstruction parameters to be optimized were the cut-off frequency of a 2D Butterworth pre-filter in FBP, and the number of iterations and the full width at Half maximum of a 3D Gaussian post-filter in OSEM. Reconstructed images were quantified using regions of interest (ROIs) derived from Magnetic Resonance scans and from the Automated Anatomical Labeling map. Results were standardized by applying a simple linear regression line obtained from the entire patient dataset. Our findings show that we can obtain a set of optimal parameters for each reconstruction strategy. The accuracy of the standardized SUR increases when the reconstruction method includes more corrections. The use of generic ROIs instead of subject-specific ROIs adds significant inaccuracies. Thus, after reconstruction with OSEM and correction for all degradations, subject-specific ROIs led to errors between standardized and true SUR values in the range [−0.5, +0.5] in 87% and 92% of the cases for caudate and putamen, respectively. These percentages dropped to 75% and 88% when the generic ROIs were used.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Single photon emission computed tomography (SPECT) using [123I]FP-CIT is a well-established diagnostic tool for in vivo evaluation of the nigrostriatal dopaminergic system in Parkinson's disease (PD). SPECT images of patients suffering from PD show lower uptake in the striatum caused by the depletion of the dopamine transporter (DAT) (Varrone and Halldin 2010). Although diagnosis by experienced observers is mainly based on qualitative criteria, the quantification of striatal DAT binding is highly recommended to improve diagnostic accuracy (Koch et al 2005, Tossici-Bolt et al 2006, Darcourt et al 2010, Badiavas et al 2011, Tatsch and Poepperl 2012).
The European Association of Nuclear Medicine Neuroimaging Committee (ENC) provides guidelines for brain neurotransmission SPECT using 123I-labeled radiopharmaceuticals that include recommendations on reconstruction methods, filtering, applied data corrections and regions of interest (ROIs) (Darcourt et al 2010). According to these guidelines, each center chooses its own image processing conditions. As a result, the quantitative values obtained from the [123I]FP-CIT SPECT images are dependent on the scanner, acquisition protocol, reconstruction parameters and ROIs. Thus, quantitative results need to be standardized before comparison with a database of normal control scans or in the case of multicenter clinical trials (Tossici-Bolt et al 2011, Dickson et al 2012, Varrone et al 2013). In an earlier study (Gallego et al 2015), we showed that a simple linear model with a single set of parameters can be used to obtain standardized values with reasonable accuracy.
In the present work we focused on the influence of the reconstruction conditions on such standardized values. Our aim was to obtain the values of the reconstruction parameters which minimize the error between standardized and true values under clinical conditions. Optimization was performed for the reconstruction methods mainly used in SPECT, i.e. filtered back projection (FBP) and the ordered subsets expectation maximization (OSEM) algorithm (Dickson et al 2010).
2. Materials and methods
The specific uptake ratio (SUR) was the parameter of choice to quantify the SPECT studies. SUR is defined as

where  and
and  are the mean values of voxel intensities in the striatal structures (caudate, putamen or the whole striatum) and in a reference region of non-specific uptake, respectively.
are the mean values of voxel intensities in the striatal structures (caudate, putamen or the whole striatum) and in a reference region of non-specific uptake, respectively.
The determination of the optimal reconstruction values requires a gold standard that enables us to evaluate the differences between the standardized and the true SUR values. In emission tomography, Monte Carlo (MC) simulation is used, inter alia, to assess quantification protocols (Cot et al 2005) since this allows the methodology to be tested using a variety of anatomical and tracer uptake cases that would otherwise be almost impossible to reproduce. Thus, we used MC simulation to generate realistic [123I]FP-CIT SPECT projections from known activity maps. Since the ground truth was known, this strategy enabled us to optimize the reconstruction parameters.
2.1. Dataset of simulated studies
A dataset of 23 subjects free from cerebral abnormalities was used to generate the simulated studies (Gallego et al 2015). To generate the activity maps, the corresponding 23 T1-weighted magnetic resonance (MR) images were segmented into brain tissue and cerebrospinal fluid using statistical parametric mapping (SPM8, Wellcome Department of Imaging Neuroscience, London, UK). The striatum was segmented from the MR images using the FIRST segmentation tool from FSL (FMRIB, University of Oxford, UK) (Patenaude et al 2011). Because computed tomography (CT) was not available for all subjects, attenuation maps were generated using a CT image of an anthropomorphic striatal brain phantom (Radiology Support Devices, RSD. Inc, Long Beach, CA). The CT image of the phantom was fitted to the MR scan of each subject to generate its bone structure (Aguiar et al 2008).
[123I]FP-CIT SPECT studies were simulated with SUR values between 0.5 and 10. Six different situations were considered for each subject, covering normal and pathological cases including uniform global striatal uptake reduction and a variety of unilateral and bilateral uptake asymmetries between caudate and putamen. Tracer uptake was simulated by assuming that the activity concentration in caudate could not be lower than that in putamen. Activity concentration was considered to be uniform within the whole caudate, putamen and background, although values in caudate and putamen could differ between hemispheres.
Projections were simulated for a Siemens E.CAM gamma camera equipped with a low-energy, high resolution (LEHR) parallel-hole collimator (hexagonal holes 24.05 mm in length with a radius of 0.641 mm and a septal thickness of 0.16 mm). Acquisition parameters were selected according to typical clinical conditions (128 projections over 360° with a bin size of 3.9 mm, 14.5 cm radius of rotation and a 15% energy window centered at 159 keV).
Projections were generated using a modified version (Crespo et al 2008) of the original SimSET MC code (Harrison et al 1993). This version adapts the code to 123I-labeled radioligands and allows accurate simulation of the interactions suffered by low- and high-energy photons emitted by 123I-labelled radioligands throughout the collimator/detector system (Cot et al 2004, 2006).
Three million counts (3Mc) in projections were simulated, thus mimicking realistic acquisition conditions according to clinical guidelines (Darcourt et al 2010). Ten noisy projections were conducted for each theoretical SUR value to assess the influence of statistical Poisson noise on SUR calculation.
2.2. Reconstruction of the simulated projections
SPECT projections were reconstructed using FBP (Shepp et al 1974) and OSEM algorithms (Shepp et al 1982, Hudson et al 1994). These algorithms are the most commonly used in SPECT reconstruction because of the simplicity and speed (FBP) and because of the ability to accurately model the projection process (OSEM). In-house algorithms were employed, some of which are now available in STIR (Software for Tomographic Image Reconstruction) (Thielemans et al 2012, Fuster et al 2013). Reconstructed images consisted of 128 × 128 × 45 voxels with a voxel size of 3.90 mm × 3.90 mm × 3.90 mm, mimicking commonly used reconstruction parameters in clinical practice.
In FBP reconstruction, projections were pre-filtered with a two-dimensional (2D) Butterworth filter of fifth order and then reconstructed using a ramp filter. The cut-off frequency of the pre-filter was in the range [0.2fN, 1.0fN], with increments of 0.1fN (fN: Nyquist frequency). Thus, we took into account reconstructed images of low resolution and high signal-to-noise ratio (low cut-off frequency) and images with high resolution and low signal-to-noise ratio (high cut-off frequency). Datasets were corrected for attenuation according to Chang's method using the individual attenuation maps of each subject for shape contouring. Attenuation correction is recommended to diminish the dependence of SUR values on the anatomy. An effective linear attenuation coefficient of 0.10 cm−1 was used to generate the uniform attenuation maps, as recommended in the EANM guidelines for 123I in the absence of scatter correction (Zaidi and Montandon 2002).
Iterative reconstruction was performed using the OSEM algorithm with eight subsets and a number of iterations ranging from 1 to 30, thereby allowing us to work with images of low resolution and high signal-to-noise ratio (low iterations) and images with high resolution and low signal-to-noise ratio (high iterations). Reconstructed images were post filtered using a set of three-dimensional (3D) Gaussian filter with a full width at Half maximum (FWHM) of 2, 4, 6 and 8 mm. No post-filter was also considered. To assess the effect of corrections for the degrading phenomena in the results, data were corrected for (a) attenuation (OSEM-A), (b) scatter and attenuation (OSEM-SA), and (c) the spatially variant point spread function (PSF), scatter and attenuation (OSEM-PSA). In OSEM-A, as in FBP, an effective linear attenuation coefficient of 0.10 cm−1 was used to take into account scattered photons. In OSEM-SA and OSEM-PSA since scattered photons were corrected from the projections, attenuation correction was implemented using the individual attenuation maps of each subject with actual attenuation coefficients of 0.149 cm−1 for brain and 0.307 cm−1 for bone, which correspond to the 159 keV low-energy emission from 123I (Zaidi and Montandon 2002). An ideal scatter correction was applied by considering only the unscattered photons in the projections. Spatially variant PSF was incorporated into the reconstruction process using the previously derived linear relationship between the FWHM of the PSF and the distance from the point source to the collimator (Crespo et al 2008).
2.3. Quantification
Quantification of the reconstructed images was performed using two sets of striatal ROIs: subject-specific and generic ROIs. The first set was derived from the MR scans of the 23 subjects mentioned above. The second set was derived from the Automated Anatomical Labeling (AAL) map (Tzourio-Mazoyer et al 2002), which provides generic ROIs for all brain structures in the standard space defined by the Montreal Neurologic Institute (MNI). A reference ROI (volume 79 cm3) of non-specific uptake was located in the occipital region using the ROIs from the AAL map.
In the first approach, SUR values were calculated by locating the specific striatal ROIs for each subject directly over the reconstructed studies. To this end, the striatal structures segmented from the MR scans were resized to fit the reconstructed images. The reference ROI defined in the MNI standard space was placed over each study by applying the inverse transformations corresponding to the normalization of the MR images to the standard space. This reference ROI was also resized to fit the reconstructed images (Gallego et al 2015).
Since subject-specific ROIs are not usually available in routine clinical conditions, we also used generic ROIs as recommended in current clinical guidelines (Darcourt et al 2010). Thus, in this second approach, SPECT images were normalized to a SPECT template defined in the MNI space before quantification (Gallego et al 2015). This step reduces operator intervention, and also simplifies and speeds up the quantification process because a unique template of ROIs is used to quantify all the studies. Striatal ROIs were obtained from the original AAL map, selecting those corresponding voxels that were common to both hemispheres and thus generating a symmetric ROI for caudate and putamen.
2.4. Standardization
Calculated SUR values for individual caudate ( and putamen (
and putamen ( ) were standardized by applying the inverse of the simple linear model that relates calculated and true SUR values (Koch et al 2006, Crespo et al 2008):
) were standardized by applying the inverse of the simple linear model that relates calculated and true SUR values (Koch et al 2006, Crespo et al 2008):
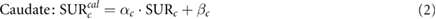

where α is the slope of the regression line, SUR is the true value and β stands for the intercept.
The parameters of these equations were obtained from linear regression of the whole dataset of calculated and true SUR values for each of the reconstruction conditions and quantification ROIs used in this study. Projections generated with high signal-to-noise ratio were used to determine these standardization parameters as described in Gallego et al (2015). Standardized SUR values for the whole striatum were calculated as the average between caudate and putamen.
2.5. Optimization of the reconstruction parameters
Differences between standardized and true values were assessed by calculating the chi-square value (χ2) defined as
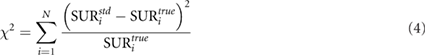
where  and
and  are the standardized and true SUR and N is the number of studies.
are the standardized and true SUR and N is the number of studies.
The present study seeks to obtain the reconstruction parameters that would minimize χ2. In FBP reconstruction, the cut-off frequency of the 2D Butterworth filter was the parameter to be optimized. In OSEM, the number of iterations and the FWHM of the 3D Gaussian post-filter were the parameters to be fitted for all the correction cases considered.
A total of 633 420 studies were quantified. This is the result of combining 23 subjects with six different SUR values to obtain the simulated projections, and reconstructing the 1380 sinograms (ten noise trials for each SUR) by applying different parameters (FBP: nine cut-off frequencies for the 2D Butterworth pre-filter; OSEM: from 1 to 30 iterations and five FWHM values for the 3D Gaussian post-filter) with three different correction levels (OSEM-A, OSEM-SA and OSEM-PSA). The optimization study was carried out using the subject-specific ROIs to quantify the images (MRI ROIs) since these are the most accurate ROIs available. Moreover, the reconstructed images obtained using the optimal reconstruction parameters were also quantified using the ROIs derived from the AAL map (AALsym ROIs) to evaluate the inaccuracies due to the use of generic ROIs.
3. Results
3.1. Simulation and reconstruction
Simulation and reconstruction processes were performed in a computer cluster of 12 blades with 12 GB RAM each and equipped with Intel® Xeon CPU of 2.67 GHz processors. The mean computational time needed to reconstruct a study using FBP was 15 s, requiring a maximum of 0.5 GB of RAM, whereas the same task for OSEM-A and OSEM-SA with 30 iterations needed 15 min and 1 GB of RAM. For OSEM-PSA with 30 iterations, the mean reconstruction time increased up to 90 min, requiring a maximum of 6 GB of RAM.
3.2. Determination of the optimal reconstruction parameters
Figure 1 shows the value of χ2 for the whole striatum as a function of the cut-off frequency of the 2D Butterworth pre-filter applied in FBP reconstruction, and as a function of the number of updates ((number of subsets)/iteration x number of iterations) in OSEM-A, OSEM-SA and OSEM-PSA reconstructions with the different post-filters. χ2 was calculated as the average of the 10 noise trials.
Figure 1. χ2 values for the whole striatum as a function of the cut-off frequency of the 2D Butterworth pre-filter in FBP, and the number of updates in OSEM-A, OSEM-SA and OSEM-PSA. OSEM results correspond to no post-filter (filled circles), post-filter with a FWHM = 2 mm (crosses), 4 mm (triangles), 6 mm (diamonds) and 8 mm (squares). Results were obtained with MRI ROIs.
Download figure:
Standard image High-resolution imageResults obtained from FBP reconstruction showed that differences between standardized and true values can be minimized by choosing an appropriate value for the cut-off frequency of the 2D Butterworth pre-filter. χ2 values for both caudate and putamen rapidly declined by increasing the cut-off frequency until it reached a value of 0.5fN. After this point, the error remained mostly constant with a minimum at a cut-off frequency of 0.7fN.
As for OSEM-A reconstruction, the behavior of the error with iterations was similar regardless of the application of a post-filter. After the first iteration, the error decreased sharply before increasing gradually. Regarding the post-filtering, the minimum error was found when no post-filter was applied to the images, although a very similar value was achieved for post-filtering with 2 mm FWHM. Errors obtained when using post-filters with greater values of FWHM were very similar, up to 8 mm, which caused markedly higher errors. In all cases, as expected, the inclusion of post-filtering stabilized the error as iterations increased. By contrast, without post-filtering, the error showed a significant increase as the number of iterations rose. A similar behavior was observed in OSEM-SA, albeit with lower values of χ2. Of the methodologies applied, the lowest values were reached when using OSEM-PSA. In this case, the minimum error was achieved at a higher number of iterations using a post-filter of 4 mm. However, similar values were achieved with a post-filter of 2 mm or without a post-filter. In both OSEM-PSA and OSEM-SA, the error without post-filter exceeded that of the post-filter with a FWHM of 8 mm when the number of iterations was around 150.
Table 1 shows the optimal reconstruction parameters found when the studies were reconstructed using FBP, OSEM-A, OSEM-SA and OSEM-PSA and quantified with MRI ROIs.
Table 1. Optimal reconstruction parameters for FBP and OSEM and associated errors.
| Method | Optimal reconstruction parameters | Calculated errors with MRI ROIs | Calculated errors with AALsym ROIs | |||
|---|---|---|---|---|---|---|
| Filter frequency /FWHM | Updates |  |
 |
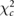 |
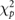 |
|
| FBP | 0.7 fNcm−1 | — | 6.06 | 10.37 | 13.31 | 15.24 |
| OSEM-A | 0 mm | 16 | 5.76 | 8.59 | 12.94 | 13.05 |
| OSEM-SA | 0 mm | 16 | 5.16 | 4.83 | 10.02 | 8.76 |
| OSEM-PSA | 4 mm | 128 | 4.24 | 4.34 | 9.31 | 7.36 |
χ2 values revealed that the use of the optimal reconstruction parameters led to lower errors between standardized and true values when using OSEM rather than FBP reconstruction.
3.3. Images reconstructed using the optimal parameters
We obtained 5520 images that had been reconstructed using the parameters shown in table 1. Figure 2 shows a central slice of a randomly selected case of these studies (SURc = 9.2 and SURp = 7.9 for the left hemisphere and SURc = 8.3 and SURp = 3.5 for the right hemisphere).
Figure 2. A central slice of a randomly selected study reconstructed with FBP, OSEM-A, OSEM-SA and OSEM-PSA when using the optimal reconstruction parameters shown in table 1. Theoretical SUR values were, for the left hemisphere, SURc = 9.2 and SURp = 7.9 and, for the right hemisphere, SURc = 8.3 and SURp = 3.5.
Download figure:
Standard image High-resolution image3.4. Errors between standardized and true SUR values
We calculated the difference between standardized and true SUR values for the studies reconstructed using the optimal parameters. Differences were calculated for caudate and putamen separately and for all the reconstruction methodologies applied. Errors were classified into 51 categories defined between −2.55 and 2.55 (i.e. the range of each interval was 0.10). The left hand side of figure 3 shows the distribution of the errors between standardized and true SUR values as the percentage of errors found in each category. Percentages are assigned to the mean value of each category. The right hand side of figure 3 shows the cumulative probability plot of the errors, i.e. the function shows the percentage of errors with an absolute value below the value indicated on the x-axis.
Figure 3. Distribution of the errors between standardized and true SUR values for the studies reconstructed using the optimal parameters (left) and cumulative probability plot of the errors (right). Results are shown for quantification with MRI ROIs and AALsym ROIs and correspond to: FBP (dotted line), OSEM-A (long dashed line), OSEM-SA (short dashed line) and OSEM-PSA (solid line).
Download figure:
Standard image High-resolution image3.5. Standardized versus true SUR values
Figure 4 shows the standardized SURs against the true values for the studies reconstructed using the optimal parameters. To facilitate the visual interpretation of these results, only one noise trial for each subject and SUR is shown. The parameters of the linear fits as well as the value of R2 for each reconstruction method and ROIs are also shown for comparison. We can see that the regression lines between standardized and true values are close to the identity. Comparison between results obtained using MRI and AALsym ROIs show that R2 values are lower for AALsym ROIs, thereby indicating that variability increases when generic rather than subject-specific ROIs are used. Results in figure 4 also show that variability diminishes when the reconstruction method includes more corrections for the degrading defects. As expected, all these results concerning the dependence of the errors on the reconstruction method and the ROIs used in quantification are consistent with the behavior of χ2 values in table 1 and the differences between standardized and true values shown in figure 3.
Figure 4. Standardized values against the true SURs for caudate (filled circles) and putamen (hollow circles) when using the reconstruction methods with the optimal parameters. From top to bottom: FBP, OSEM-A, OSEM-SA and OSEM-PSA. Results are shown for quantification with MRI ROIs (left) and AALsym ROIs (right).
Download figure:
Standard image High-resolution image4. Discussion
In this work, we used 23 subjects to generate a dataset of 1380 realistic [123I]FP-CIT SPECT studies that included the effect of anatomical variability between subjects and a wide variety of possible pathologies. Studies were reconstructed using FBP and OSEM algorithms. Although OSEM reconstruction allows accurate correction for attenuation and the spatially variant PSF, FBP reconstruction was also included in this study because it is still widely used in clinical practice. In this work we reproduced reconstruction conditions commonly used in routine clinical practice: FBP reconstruction with attenuation correction, and OSEM reconstruction with three different correction levels (attenuation correction, scatter and attenuation corrections, and attenuation, scatter and PSF corrections). MC simulation allowed us to calculate the differences between the standardized SURs and the known true values, thereby enabling us to determine the optimal reconstruction parameters in [123I]FP-CIT SPECT reconstruction.
In FBP reconstruction, the cut-off frequency of a 2D Butterworth pre-filter was the variable to be optimized. Our results showed that the minimum error was achieved with a cut-off frequency of 0.7fN. However, very small changes in the error were observed from 0.6fN to 1.0fN. This behavior ensures the applicability of cut-off frequencies between 0.6fN to 1.0fN to situations different from those described in our study.
In OSEM-A and OSEM-SA reconstructions, the minimum error was found when no post-filter was applied to the reconstructed images using 16 updates. The behavior of the error showed that it is essential to guarantee that a minimum of 16 updates are calculated, otherwise the quantitative values would be inaccurate. For practical purposes, the appropriate number of updates to use in OSEM-A and OSEM-SA reconstructions may be set between 16 and 32. This interval ensures that the increase in the error is limited to 5% with respect to the minimum. In OSEM-A reconstruction, χ2 in the striatum increased by 4.7% when 32 updates were used. In OSEM-SA reconstruction, the increment was 4.2%. The use of a post-filter is recommended since it stabilizes the error through iterations. This stabilization allows us a wide range of iterations to be used in different situations. In any case, the post-filter should not exceed a FWHM of 6 mm, 2 and 4 mm being the most suitable values (2 mm for a low number of iterations and 4 mm for a high number of iterations). Results similar to those for OSEM-A were also obtained for OSEM-S and OSEM-P (results not shown), thus indicating that corrections should be done jointly.
The inclusion of the PSF correction in OSEM-PSA reconstruction required a higher number of iterations to reach the minimum error which was set at 128 updates with a post-filter of 4 mm FWHM. In practice, the appropriate number of updates to use may be set between 48 and 128 since this interval ensures that the increase in the error remains below 5% with respect to the minimum. χ2 in the striatum increased by 3.8% when 48 iterations were used. This behavior of χ2 through iterations also allows us a wide range of iterations to be used in different situations.
Our results showed that the OSEM algorithm yielded lower errors than FBP. The use of OSEM with precise attenuation, scatter and PSF corrections minimized the error between standardized and true SUR values. In particular, the inclusion of the scatter correction decreased χ2 in caudate by 10%. The effect of scatter correction was most marked in putamen with a decrease of 44%. Correction for PSF reduced the error by an additional 18% in caudate and 10% in putamen. In this context, figure 2 shows that the most suitable image for quantitative evaluation and for visual assessment can differ.
The use of generic ROIs instead of subject-specific ROIs added inaccuracies in the calculation of SUR because of the normalization process and morphological differences with the real structures. As a result, the minimum value of χ2 was found to be between 1.5 and 2.2 times larger when AALsym ROIs were used, the caudate being the most affected structure.
The distribution of the individual differences between standardized and true values shown in figure 3 revealed that as the reconstruction method included more corrections the accuracy of the standardized SUR values increased. The distribution of the individual differences between standardized and true values shown in figure 3 revealed that as the reconstruction method included more corrections the accuracy of the standardized SUR values increased. This improvement was noteworthy between the pairs FBP/OSEM-A and OSEM-SA/OSEM-PSA, but not between FBP and OSEM-A. As for OSEM-SA and OSEM-PSA we found significant differences between both methodologies in caudate and putamen using MRI or AAL regions (p < 0.01 in all cases). However, the mean of differences in SUR values were less than 0.015 with MRI and less than 0.025 using AAL regions. These differences were 10 times lower than the mean standard deviations of the SUR values and may be regarded as negligible. This finding concerning OSEM-SA and OSEM-PSA is important in practice since the reconstruction without PSF is much faster. The implication of this finding referring to OSEM-SA and OSEM-PSA is important in practice since the reconstruction without PSF is much faster. In all cases, when MRIs were used, FBP led to differences between standardized and true SURs of less than 0.5 (absolute value) in 82% of cases. This value fell to 65% in caudate and 78% in putamen when the generic ROIs were used. Results shown in figure 4 support the key role of the ROIs during quantification in achieving accurate SURs with a lower variability. In this sense, we obtained statistically significant differences between absolute errors using generic and subject-specific ROIs.
Finally, it should be pointed out that in this work, the set of standardization parameters was derived from the inverse of the regression line between calculated and true SUR values obtained for the whole patient dataset. In a clinical context, these standardization parameters could be obtained by using anthropomorphic striatal phantoms that are representative of the average anatomy of the population. In this case, parameters would be obtained by using the same protocol for the phantom as that used for patients, i.e. the same imaging system, acquisition conditions, reconstruction algorithm and quantification method.
5. Conclusions
This work demonstrates that accurate standardization requires the appropriate selection of the reconstruction parameters. Our findings show that (1) for each reconstruction strategy there is a set of parameter values that minimizes the error between standardized and true SUR values, (2) the accuracy of the standardized SUR values increases when the reconstruction method includes more corrections, (3) differences between standardized SUR values using OSEM-SA and OSEM-PSA are not relevant, which is useful in practice, and that (4) the use of ROIs derived from MRI of the patient diminishes the errors between standardized and true SUR values with the result that MRI of the patient is recommended.
Acknowledgments
This work was supported in part by Fondo de Investigación Sanitaria (PI12-00390) and by Biomedical Research Networking Center in Bioengineering, Biomaterials and Nanomedicine (CIBER-BBN—MITP2 Intramural Project).





