Abstract
Given a functional for a one-dimensional physical system, a classical problem is to minimize it by finding stationary solutions and then checking the positive definiteness of the second variation. Establishing the positive definiteness is, in general, analytically untractable. However, we show here that a global geometric analysis of the phase-plane trajectories associated with the stationary solutions leads to generic conditions for minimality. These results provide a straightforward and direct proof of positive definiteness, or lack thereof, in many important cases. In particular, when applied to mechanical systems, the stability or instability of entire classes of solutions can be obtained effortlessly from their geometry in the phase plane, as illustrated on a problem of a mass hanging from an elastic rod with intrinsic curvature.
Export citation and abstract BibTeX RIS
Recommended by Dr Oliver O'Reilly
Footnotes
- 4
The superscripts D and N used to denote the space of admissible perturbations
 and
and  respectively refer to the Dirichlet and Neumann boundary conditions that naturally arise when minimising
respectively refer to the Dirichlet and Neumann boundary conditions that naturally arise when minimising  with respectively fixed and free boundaries.
with respectively fixed and free boundaries. - 5
Finding stationary functions for the functional
 amounts to solving the boundary value problem (15). We had noted that in the case of fixed boundaries, this BVP has Dirichlet boundary conditions while for free boundaries, the BVP has Neumann boundary conditions. Something similar happens here. For fixed boundaries, the stability can be assessed by solving a Sturm–Liouville problem with Dirichlet boundary conditions while for free boundaries, the S–L problem has Neumann boundary conditions.
amounts to solving the boundary value problem (15). We had noted that in the case of fixed boundaries, this BVP has Dirichlet boundary conditions while for free boundaries, the BVP has Neumann boundary conditions. Something similar happens here. For fixed boundaries, the stability can be assessed by solving a Sturm–Liouville problem with Dirichlet boundary conditions while for free boundaries, the S–L problem has Neumann boundary conditions. - 6
This is easily proven by considering

- 7
If P > 0, then η starts at
 and end at
and end at  . If P < 0, then η starts at
. If P < 0, then η starts at  and end at
and end at  . Either way the length formulae below hold.
. Either way the length formulae below hold. - 8
In this case, we can substitute variable in the integral appearing in the RHS of (45) according to
![$\text{d}t=\frac{\text{d}\theta}{\text{Sign}\left[{{\theta}^{\prime}}(s)\right]\sqrt{2}\,\sqrt{E-V(\theta )}}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) .
. - 9
These two functions can not be linearly dependent since
 while
while  .
. - 10
That is assuming that U > 0, if U < 0 the solution starts at
![$\arccos [v-e]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) .
.




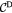
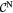

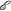

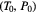
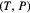
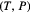
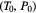
![$\text{d}t=\frac{\text{d}\theta}{\text{Sign}\left[{{\theta}^{\prime}}(s)\right]\sqrt{2}\,\sqrt{E-V(\theta )}}$](https://content.cld.iop.org/journals/0951-7715/30/5/2023/revision1/nonaa6448ieqn244.gif)

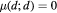
![$\arccos [v-e]$](https://content.cld.iop.org/journals/0951-7715/30/5/2023/revision1/nonaa6448ieqn636.gif)