Abstract
A large amount of parallel silicon nanowires, placed perpendicularly to a silicon substrate (silicon nanowire forests), have been contacted and assembled in order to fabricate legs of a thermoelectric generator. This paper reports the measurement of the main parameter for thermoelectric applications, which is the thermal conductivity. The reported value, which confirms the strong reduction of the thermal conductivity in nanostructures, is measured on a large amount (>107) of parallel nanowires with a diameter variable in the range 60–120 nm, and takes into account eventual non-uniformities which are unavoidable on surfaces of several mm2. As silicon nanowire forests are very thin, it has been necessary to develop a suitable measurement apparatus. The fabrication of devices based on silicon nanowire forests, the apparatus and the measurement procedure, as well as the the results, are illustrated and discussed.
Export citation and abstract BibTeX RIS
1. Introduction
Thermoelectric conversion is very attractive for energy recovery and green energy harvesting. For this reason, several research works are focusing on the development of materials with high electrical conductivity σ and low thermal conductivity kt which, together with a high value of the Seebeck coefficient S, can exhibit a good figure of merit  . Together with a high figure of merit, which results in a good thermal to electrical conversion efficiency, issues about material availability, sustainability, technological feasibility must be considered. In this respect, the use of silicon for thermoelectric applications would be desirable for its abundance on the Earth's crust and for its worldwide pervasiveness due to the electronic market. Silicon is very good with regard to the Seebeck coefficient and electrical conductivity [1–5], but in the bulk state its thermal conductivity is very high, greater than 100 W m–1 K–1. Thermal conductivity measurements have been performed on one, or very few, nanowires, and their reduced thermal conductivity, down to very few W m–1 K–1, has been demonstrated [6–10]. Therefore, Si nanowires (SiNWs) and nanostructures are good candidates for the fabrication of thermoelectric generators with high conversion efficiencies, and based on a sustainable and low-cost material such as silicon.
. Together with a high figure of merit, which results in a good thermal to electrical conversion efficiency, issues about material availability, sustainability, technological feasibility must be considered. In this respect, the use of silicon for thermoelectric applications would be desirable for its abundance on the Earth's crust and for its worldwide pervasiveness due to the electronic market. Silicon is very good with regard to the Seebeck coefficient and electrical conductivity [1–5], but in the bulk state its thermal conductivity is very high, greater than 100 W m–1 K–1. Thermal conductivity measurements have been performed on one, or very few, nanowires, and their reduced thermal conductivity, down to very few W m–1 K–1, has been demonstrated [6–10]. Therefore, Si nanowires (SiNWs) and nanostructures are good candidates for the fabrication of thermoelectric generators with high conversion efficiencies, and based on a sustainable and low-cost material such as silicon.
Techniques for the fabrication of large collections of interconnected silicon nanostructures, and for the assembly of devices completed of contacts for the electrical and thermal conduction, need to be developed. Bottom-up nanowires produced by CVD [11, 12], or top-down nanostructures fabricated by high resolution lithography [13, 14], can be integrated in devices fabricated by standard silicon IC technology for the on-chip power supply of sensors and/or for internet of things applications. Alternatively, low-cost maskless processes can be used for the fabrication of arrays of silicon nanowires on large areas. Metal assisted chemical etching [15–19] (MACE) is a vertical, highly selective, etching which allows to fabricate forests of silicon nanowires perpendicular to a silicon substrate. More than 107 nanowires mm–2, longer than 70 μm, can be fabricated on both sides of a double polished wafer [5]. The nanowire doping, and hence the electrical conductivity, can be tailored after the fabrication by means of standard diffusion doping processes. A process for contacting the apexes of the silicon nanowires, based on copper electrodeposition, has been improved [20]: thanks to this process, vertical silicon nanowires can be connected in parallel on surfaces of several cm2, without using any filling material which would increases the total thermal conductance and limits the maximum operating temperature of the device. Therefore, legs of a thermoelectric module, based on forests of silicon nanowires doped both n+ and p+, can be fabricated and interconnected.
Silicon nanowire forests have been already characterized in the past both embedding them in a polymer [21] and using optical techniques [22, 23]. In our work, we characterize devices based on nanowire forests, completed with metal contacts for the electrical and thermal transport, so that they are legs ready to be assembled in a thermoelectric generator. We used a direct technique, imposing an heat flux across the nanowire forest and measuring the generated temperature difference. Unfortunately, conventional equipments for thermal measurements are unsuitable for nanostructures, hence suitable apparatus and techniques [24] need to be developed for their characterization. Even if thermal conductivity of single nanowires has been measured in the past, the development of innovative thermoelectric devices based on a collection of a large number of nanostructures requires suitable techniques for the exact measurement of kt of the whole collection. This is essential in particular for nanowire forests achieved by MACE etching, made of a large number of nanostructures with a random diameter. The resulted thermal conductivity of the whole forest is an average value which takes into account the dispersion of the diameters and also eventual non-uniformities, which are unavoidable on large surfaces. The main aim of our work is to report the precise measurement of the thermal conductivity of silicon nanowire forest with areas of several mm2, and several tens of micrometers tall; the measured thermal conductivity will be reported and discussed. The developed measurement technique allows also to determine the contact thermal resistance, which is a key parameter in the development of thermoelectric generator devices. After a resume of the fabrication process of contacted SiNW forests (see section 1), we describe the measurement apparatus and technique (see section 2). The measurement procedure is suitable also for other kind of very thin materials. In section 3 we reports the measurement of the thermal conductivity, discussing the results: the most critical parameter to be determined, and which mostly affect the measurement, is the coverage ratio (or filling factor) of the nanowire forest.
2. Fabrication of contacted silicon nanowire forests
The metal assisted etching is a highly selective etching process that allows the definition of vertical structures (silicon nanowires) with a very high length/diameter aspect ratio. As it is a maskless technique, allowing the low-cost processing of large silicon areas, it can be proposed as a possible via for the large-scale production of forests of nanowires, perpendicular to a silicon substrate, to be used for the fabrication of thermoelectric modules. For the measurement of the thermal conductivity, we fabricated several SiNW forests with the same MACE [16, 19] conditions, apart for the etching time which determines the length of the nanowires. Key conditions for the fabrication of the nanowire forests are the reagent concentrations, the temperature, which must be very stable, and the stirring condition. As a starting material, we used silicon wafers  oriented 525 μm thick, single polished, n-doped with a resistivity between 1 and 10 Ω cm. Chips of about 10 × 10 mm2 have been cleaved from the silicon wafer and cleaned in buffered HF. Nanowire forests have been produced by MACE etching in a solution 5:16:60 in volume of AgNO3 0.1 N: HF 48%: deionized water. The etch is performed in a bath with a controlled temperature of 18 °C, ±0.2 °C. The sample to be etched is mounted on a home-made overhead stirrer, which is rotated at random by an automatic control. The length of the nanowires is more or less proportional to the etching time, so that several nanowire forests with lengths between 6 and 38 μm have been produced. After the etching in the MACE solution, the samples resulted covered by silver, which is deposited as a result of the etching process. The deposited silver is completely removed by etching the sample in a solution 1:1 HNO3 65%: deionized water for 1 min; the complete removal of silver has been confirmed by SEM imaging. As a result of the nitric acid etching, the nanowires are covered by a thin layer of silicon dioxide. The left panel of figure 1 shows a SEM image of a cross-section of a typical sample, obtained with a MACE etching time of 2 h. The length of the nanowires resulted 35 μm, and the average diameter resulted of about 90 nm.
oriented 525 μm thick, single polished, n-doped with a resistivity between 1 and 10 Ω cm. Chips of about 10 × 10 mm2 have been cleaved from the silicon wafer and cleaned in buffered HF. Nanowire forests have been produced by MACE etching in a solution 5:16:60 in volume of AgNO3 0.1 N: HF 48%: deionized water. The etch is performed in a bath with a controlled temperature of 18 °C, ±0.2 °C. The sample to be etched is mounted on a home-made overhead stirrer, which is rotated at random by an automatic control. The length of the nanowires is more or less proportional to the etching time, so that several nanowire forests with lengths between 6 and 38 μm have been produced. After the etching in the MACE solution, the samples resulted covered by silver, which is deposited as a result of the etching process. The deposited silver is completely removed by etching the sample in a solution 1:1 HNO3 65%: deionized water for 1 min; the complete removal of silver has been confirmed by SEM imaging. As a result of the nitric acid etching, the nanowires are covered by a thin layer of silicon dioxide. The left panel of figure 1 shows a SEM image of a cross-section of a typical sample, obtained with a MACE etching time of 2 h. The length of the nanowires resulted 35 μm, and the average diameter resulted of about 90 nm.
Figure 1. SEM images of silicon nanowire forests (cross-sections). Left panel: silicon nanowire forest, after AgNO3/HF metal assisted etching and cleaning in nitric acid. Right panel: a silicon nanowire forest with the top contacting layer, made of copper grown by seed evaporation and electrodeposition.
Download figure:
Standard image High-resolution imageIn order to perform the electrical and thermal characterization, a metal contact on the top of the silicon nanowire forests has been provided by copper electrodeposition, as explained in a previous publication [20]. At first, a metal seed has been deposited on the apexes of the nanowires by thermal evaporation. To this end, the samples have been etched in buffered HF for 1 min to remove the silicon dioxide, and then they have been placed in a thermal evaporator. A thin Cr layer of 20 nm for adhesion, followed by a 60 nm thick copper layer, have been evaporated on top of the nanowire forests, at a residual pressure of about 5 × 10−6 mb. Afterward, on the bottom of the sample, 20 nm of Cr and 60 nm of Cu have been also deposited by thermal evaporation, in order to improve the electrical and thermal contact. After the metal depositions on the top and on the bottom faces, samples are placed in an electrodeposition cell filled with a solution of copper sulfate and sulfuric acid ([CuSO4]:[H2SO4] = 0.4) [20]. A current generator has been applied between the sample (negative electrode) and a Cu plate (positive electrode). Copper has been grown, for all the samples, with the same current density of 1415 A m−2 and the same time (2 min). Therefore, all the measured nanowire forests have a similar copper layer as a top contact. The SEM image on the right panel of figure 1 shows a cross-section of a silicon nanowire forest after copper electrodeposition. The porous copper layer is visible on the top of the nanowires, which are anchored to the silicon substrate at the other end (at the bottom). The copper layer is about 5 μm thick and, even if it is very porous, its electrical resistivity resulted of about 10−5 Ω cm, and it is very low with respect to that of silicon.
It must be noted that the procedure for contacting the top of the nanowire forest does not require any filling polymer [25, 26] deposited between the nanowires. Therefore, at first the thermal conductivity of the nanowire forest is due only to the nanowires itself as there is not any parasitic parallel conduction of heat which would be unavoidable with the presence of a polymer. Furthermore, a polymer could upper bound the maximum operating temperature of the final device. It must be mentioned that silicon is a very stable and robust material which can withstand temperatures of several hundred of degrees, so that thermoelectric generators based on pure silicon could exploit very large temperature differences, for very high efficiencies.
3. Measurement apparatus and procedure
The thermal conductivity kt of a material can be determined by measuring the thermal resistance  of a piece of that material, which is related with the thermal conductivity through the geometrical parameters L and cross-section surface
of a piece of that material, which is related with the thermal conductivity through the geometrical parameters L and cross-section surface  . In principle, the thermal resistance
. In principle, the thermal resistance  can be measured imposing a known heat flux Q through the sample and measuring the temperature drop
can be measured imposing a known heat flux Q through the sample and measuring the temperature drop  between its ends:
between its ends:  . Figure 2 shows a sketch of our measurement apparatus, based on the concept of the guarded hot plate technique. Samples to be measured are small chips of silicon about 0.5 mm thick, and with S = W1 × W2 of the order of (smaller than) 5 × 5 mm2. The sample is squeezed between two blocks (plates) of aluminum 30 × 30 × 10 mm3. The top aluminum block is maintained to a temperature TH by an electrical (Joule) heater, which is supplied with an electrical power PH = V × I (V and I are, respectively, the supplied voltage and current). The two blocks will be named H (Hot) and C (Cold). Their temperatures TH and TC are measured by means of RTD (class A Pt100) temperature sensors, applied on the lateral surfaces of the blocks, as shown in the right sketch of figure 2. Even if two terminal Pt100 sensors have been used, particular care has been taken for making the sensor electrical connections and cables as similar as possible (electrical cables with the same length). Therefore, their parasitic contribution to the measurement of the electrical resistance, and hence on the measured temperature, disappears in the difference TH − TC. A third aluminum block, called Href, is placed over the H block and maintained in place by 4 stainless steel screws, whose total thermal resistance can be estimated of
. Figure 2 shows a sketch of our measurement apparatus, based on the concept of the guarded hot plate technique. Samples to be measured are small chips of silicon about 0.5 mm thick, and with S = W1 × W2 of the order of (smaller than) 5 × 5 mm2. The sample is squeezed between two blocks (plates) of aluminum 30 × 30 × 10 mm3. The top aluminum block is maintained to a temperature TH by an electrical (Joule) heater, which is supplied with an electrical power PH = V × I (V and I are, respectively, the supplied voltage and current). The two blocks will be named H (Hot) and C (Cold). Their temperatures TH and TC are measured by means of RTD (class A Pt100) temperature sensors, applied on the lateral surfaces of the blocks, as shown in the right sketch of figure 2. Even if two terminal Pt100 sensors have been used, particular care has been taken for making the sensor electrical connections and cables as similar as possible (electrical cables with the same length). Therefore, their parasitic contribution to the measurement of the electrical resistance, and hence on the measured temperature, disappears in the difference TH − TC. A third aluminum block, called Href, is placed over the H block and maintained in place by 4 stainless steel screws, whose total thermal resistance can be estimated of  K W–1 (assuming a stainless steel thermal conductivity of 20 W m–1 K–1). A second Joule heater is applied to this block and the applied power PHref = V × I is electronically controlled in such a way that THref remains within 0.5 °C with respect to TH. Therefore, the thermal power exchanged between the H and the Href blocks can be estimated to be smaller than 10 mW. Moreover, an aluminum radiation shield, maintained at the same temperature
K W–1 (assuming a stainless steel thermal conductivity of 20 W m–1 K–1). A second Joule heater is applied to this block and the applied power PHref = V × I is electronically controlled in such a way that THref remains within 0.5 °C with respect to TH. Therefore, the thermal power exchanged between the H and the Href blocks can be estimated to be smaller than 10 mW. Moreover, an aluminum radiation shield, maintained at the same temperature  , surrounds the H block, in order to minimize the radiation losses. Furthermore, all the system operates in vacuum (residual pressure of about 1.3 × 10−4 atm), so that losses due to the air thermal conductivity and convection are minimal [27, 28]. Hence, most of the electrical power PH = V ×I, supplied to the heater applied to the H block, is the thermal power passing through the sample under measurement.
, surrounds the H block, in order to minimize the radiation losses. Furthermore, all the system operates in vacuum (residual pressure of about 1.3 × 10−4 atm), so that losses due to the air thermal conductivity and convection are minimal [27, 28]. Hence, most of the electrical power PH = V ×I, supplied to the heater applied to the H block, is the thermal power passing through the sample under measurement.
Figure 2. Sketch of the measurement apparatus, based on the guarded hot-plate concept. An overall vision of the machine is shown on the left: it includes the force, the load cell, the plate maintained at THref = TH, the top plate where it is measured the temperature TH, the sample, which is roughly 0.5 mm thick, and the bottom plate, where it is measured the temperature TC. A sketch of the thermal circuit is shown on the right. The circuit is represented with its electrical equivalent lump parameters. The thermal resistance of the sample under measurement is  .
.
Download figure:
Standard image High-resolution imageGiven the heat power Q through the sample, the thermal resistance of the sample  can be determined knowing the temperature difference between its extremities. However, it is impossible to make a precise measurement of this temperature difference, because the sample must be tightly clamped between the H and the C aluminum blocks, to minimize the thermal contact resistance and to allow the heat flux. It is very difficult to apply temperature sensors exactly at the ends (top surface and bottom surface) of the sample. Hence, we have implemented the following technique. The sensors for the measured of TH and TC are placed on the lateral surfaces of the H and C block, respectively, and they are different from the temperatures THsample and TCsample at the top and at the bottom of the sample. The sketch on the right of figure 2 shows the electrically equivalent circuit, in lump parameters, of the thermal system made of the heat generator (electrically equivalent to a current generator), the thermal resistances and capacitances of the H and C blocks and the unknown thermal resistance
can be determined knowing the temperature difference between its extremities. However, it is impossible to make a precise measurement of this temperature difference, because the sample must be tightly clamped between the H and the C aluminum blocks, to minimize the thermal contact resistance and to allow the heat flux. It is very difficult to apply temperature sensors exactly at the ends (top surface and bottom surface) of the sample. Hence, we have implemented the following technique. The sensors for the measured of TH and TC are placed on the lateral surfaces of the H and C block, respectively, and they are different from the temperatures THsample and TCsample at the top and at the bottom of the sample. The sketch on the right of figure 2 shows the electrically equivalent circuit, in lump parameters, of the thermal system made of the heat generator (electrically equivalent to a current generator), the thermal resistances and capacitances of the H and C blocks and the unknown thermal resistance  of the sample. The temperature of the two blocks is not uniform, in particular in the regions closer to the sample, where the heat flux is concentrated. However, the two H and C blocks are intentionally made larger (W = 30 mm) than the sample to be measured, which usually is smaller than 5 mm (both W1 and W2 are less than 5 mm). Hence, the lateral surfaces are far away from the zone where the heat flux is concentrated, and therefore, assuming that the walls of the blocks are adiabatic, their temperature in steady state is uniform. As the temperature sensors for the measurement of TH and TC are placed on the lateral surface the measurement of the two temperatures is very accurate. Consequently, the results of the measurement are Q = V × I, TH and TC. From these data, the thermal resistance of the sample
of the sample. The temperature of the two blocks is not uniform, in particular in the regions closer to the sample, where the heat flux is concentrated. However, the two H and C blocks are intentionally made larger (W = 30 mm) than the sample to be measured, which usually is smaller than 5 mm (both W1 and W2 are less than 5 mm). Hence, the lateral surfaces are far away from the zone where the heat flux is concentrated, and therefore, assuming that the walls of the blocks are adiabatic, their temperature in steady state is uniform. As the temperature sensors for the measurement of TH and TC are placed on the lateral surface the measurement of the two temperatures is very accurate. Consequently, the results of the measurement are Q = V × I, TH and TC. From these data, the thermal resistance of the sample  can be determined. To this end, we implemented a numerical solution of the heat transport equation:
can be determined. To this end, we implemented a numerical solution of the heat transport equation:
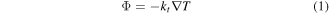
in the system made of the sample and of the two H and C aluminum blocks. In this equation, Φ = Q/S is the heat exchanged for surface unit (heat flux); kt is the thermal conductivity, which is known in the two blocks (it is that of aluminum); in the sample, kt is the unknown to be determined. The solution of the heat transport equation has been implemented with a Python code, based on the finite element (FE) Fenics package [29, 30]. As an example, a typical result of FE simulation for given values of  , Q, TC and TH is shown in the figure 3. The generated heat Q has been used as a Neumann boundary condition on the top of the block H, where the Joule heater (power resistor) is applied. The cold temperature TC has been used as a Dirichlet boundary condition imposed on the bottom face of the block C. From the right sketch of figure 3 it is possible to see that, as anticipated, the temperatures TH and TC are very uniform on the lateral surfaces of the H and C blocks. This confirms that the measurement of these temperatures is very precise, and it does not depend on the position, on the lateral face, where the temperature sensors Pt100 are applied. In the right sketch of figure 3 a cross-section of the FE simulation result is shown. This cross-section, taken in the middle of the blocks and of the sample, shows that the temperature is not uniform at the top and at the bottom of the sample: the indicated THsample and TCsample are extracted from the center of the top and bottom surfaces. This concept is better shown in figure 4, where the two graphs report both the temperature in x direction in the H block, just above the sample, and the temperature in z direction on the lateral surfaces of the H and C blocks. The temperature at the top surface of the sample is not uniform. The temperature on the lateral surfaces of the blocks is instead very uniform, hence its measurement does not depend on the position of the RTD. As the temperature drop depends on the position on the sample, it is not straightforward to determine the thermal resistance
, Q, TC and TH is shown in the figure 3. The generated heat Q has been used as a Neumann boundary condition on the top of the block H, where the Joule heater (power resistor) is applied. The cold temperature TC has been used as a Dirichlet boundary condition imposed on the bottom face of the block C. From the right sketch of figure 3 it is possible to see that, as anticipated, the temperatures TH and TC are very uniform on the lateral surfaces of the H and C blocks. This confirms that the measurement of these temperatures is very precise, and it does not depend on the position, on the lateral face, where the temperature sensors Pt100 are applied. In the right sketch of figure 3 a cross-section of the FE simulation result is shown. This cross-section, taken in the middle of the blocks and of the sample, shows that the temperature is not uniform at the top and at the bottom of the sample: the indicated THsample and TCsample are extracted from the center of the top and bottom surfaces. This concept is better shown in figure 4, where the two graphs report both the temperature in x direction in the H block, just above the sample, and the temperature in z direction on the lateral surfaces of the H and C blocks. The temperature at the top surface of the sample is not uniform. The temperature on the lateral surfaces of the blocks is instead very uniform, hence its measurement does not depend on the position of the RTD. As the temperature drop depends on the position on the sample, it is not straightforward to determine the thermal resistance  as simply the ratio between Q and the temperature drop. Hence, we developed a Phython code that, given the measured values Q, TH and TC, solves iteratively the heat transport equation. Imposing Q and TC, the code looks for the thermal resistance
as simply the ratio between Q and the temperature drop. Hence, we developed a Phython code that, given the measured values Q, TH and TC, solves iteratively the heat transport equation. Imposing Q and TC, the code looks for the thermal resistance  which gives the measured temperature TH. Therefore
which gives the measured temperature TH. Therefore  is the closest value to the thermal resistance of the sample under measurement.
is the closest value to the thermal resistance of the sample under measurement.
Figure 3. Numerical solution of the heat transport equation int the two main plates of the measurement system. The thermal power, equal to the electrical power V × I supplied to the heater, is used as Neumann boundary condition in the region where the heater is applied. The bottom face is maintained at TC (Diriclet boundary condition). On the right: the finite-element solution allows to determine the temperature drop across the sample.
Download figure:
Standard image High-resolution imageFigure 4. Temperature on the top surface of the sample, and on the sides of the two H and C blocks. The lateral surfaces of the H and C blocks have a very uniform TH and TC temperatures, respectively.
Download figure:
Standard image High-resolution image4. Measurement of the thermal conductivity of silicon nanowire forests
A typical sample to be measured is made of a silicon chip 0.5 mm thick, and with a surface of few mm2. The nanowire forest is perpendicular to the substrate and it has a length L of several tens of micrometers. The contacting copper layer is on the top, as seen in figure 1. The measured thermal resistance, achieved as described in section 3, is the series of the thermal resistance of the nanowire forest  , the thermal resistance of the substrate, and the contact thermal resistances of the bottom and of the top faces, where there is the copper layer contacting the nanowire apexes. As the contact thermal resistance is unknown, we measured several nanowire forests with different length L. To this end, we fabricated several samples with the same MACE conditions (the same etching solution 5:16:60 AgNO3 0.1 N: HF 40%: H2O, see section 2), but with different etching time, which resulted in nanowire forests with different lengths L. After etching, the top copper layer has been grown on all the samples with the same electrodeposition conditions (see section 2). As the etching and the electrodeposition parameters are the same, apart for the etching time which determines L, we can assume that the contact thermal resistance is the same for all the measured nanowire forests. Comparing the thermal resistance
, the thermal resistance of the substrate, and the contact thermal resistances of the bottom and of the top faces, where there is the copper layer contacting the nanowire apexes. As the contact thermal resistance is unknown, we measured several nanowire forests with different length L. To this end, we fabricated several samples with the same MACE conditions (the same etching solution 5:16:60 AgNO3 0.1 N: HF 40%: H2O, see section 2), but with different etching time, which resulted in nanowire forests with different lengths L. After etching, the top copper layer has been grown on all the samples with the same electrodeposition conditions (see section 2). As the etching and the electrodeposition parameters are the same, apart for the etching time which determines L, we can assume that the contact thermal resistance is the same for all the measured nanowire forests. Comparing the thermal resistance  of samples with nanowires of different lengths, taking into account the geometrical parameters (surface and length), we can derive the thermal conductivity of the nanowire forest kt, as also the contact thermal resistance for surface unit. After MACE etching and copper electrodeposition, samples have been cleaved in square, or rectangular, chips. This cleaving operation is not very precise, so samples have a similar, but slightly different, surface, between
of samples with nanowires of different lengths, taking into account the geometrical parameters (surface and length), we can derive the thermal conductivity of the nanowire forest kt, as also the contact thermal resistance for surface unit. After MACE etching and copper electrodeposition, samples have been cleaved in square, or rectangular, chips. This cleaving operation is not very precise, so samples have a similar, but slightly different, surface, between  mm2 and
mm2 and  mm2. W1 and W2, and hence the total surface S of each sample, have been precisely measured by means of a calibrated optical microscope. For each sample, the length L of the nanowire forest has been measured by means of SEM cross-section imaging. We assumed that the total thickness of the sample is that of the original wafer, which is 525 ± 5 μm. The contact thermal resistance depends also on the compressive force for surface unit (pressure) applied to the sample during the thermal conductivity measurement. Therefore, all the measured samples have been loaded by a force corresponding to a pressure of 20 MPa, accordingly with the surface S. To this end, we exploited the load cell provided for the measurement of the applied force (see the sketch of figure 2). Nanowires are electrically and thermally in parallel, so that the total thermal resistance of the nanowires can be determined knowing their length L and the total sum of their cross-sections. This total surface of the nanowire forest is only a fraction ν of that of the sample:
mm2. W1 and W2, and hence the total surface S of each sample, have been precisely measured by means of a calibrated optical microscope. For each sample, the length L of the nanowire forest has been measured by means of SEM cross-section imaging. We assumed that the total thickness of the sample is that of the original wafer, which is 525 ± 5 μm. The contact thermal resistance depends also on the compressive force for surface unit (pressure) applied to the sample during the thermal conductivity measurement. Therefore, all the measured samples have been loaded by a force corresponding to a pressure of 20 MPa, accordingly with the surface S. To this end, we exploited the load cell provided for the measurement of the applied force (see the sketch of figure 2). Nanowires are electrically and thermally in parallel, so that the total thermal resistance of the nanowires can be determined knowing their length L and the total sum of their cross-sections. This total surface of the nanowire forest is only a fraction ν of that of the sample:  . We named ν the filling factor of the nanowire forest. The thermal resistance of the nanowire forest can be written as:
. We named ν the filling factor of the nanowire forest. The thermal resistance of the nanowire forest can be written as:
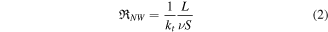
and the measured thermal resistance  is:
is:
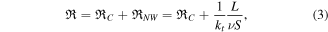
where  includes the contact thermal resistance and the thermal resistance of the substrate. The thermal resistance multiplied by the surface is:
includes the contact thermal resistance and the thermal resistance of the substrate. The thermal resistance multiplied by the surface is:
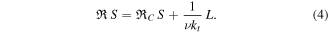
Therefore, a linear fitting of the plot of  as a function of L allows to determine
as a function of L allows to determine  . Moreover, the linear fit allows to determine also
. Moreover, the linear fit allows to determine also  , whose reciprocal
, whose reciprocal  is mainly due to the contact thermal conductance for surface unit. Figure 5 shows the measured values
is mainly due to the contact thermal conductance for surface unit. Figure 5 shows the measured values  , as a function of the nanowire forest height, i.e. the nanowire length L. The measured values are almost on a straight line and this implies that the thermal conductivity does not depend on the nanowire length. The linear least square fitting is also shown in the figure. From the fitting, the best value of
, as a function of the nanowire forest height, i.e. the nanowire length L. The measured values are almost on a straight line and this implies that the thermal conductivity does not depend on the nanowire length. The linear least square fitting is also shown in the figure. From the fitting, the best value of  resulted of 1.38 W m–1 K–1. From the fitting, it results also
resulted of 1.38 W m–1 K–1. From the fitting, it results also  W K–1 m–2. This value is mainly due to the contact thermal conductance between the copper layer and the top aluminum block H. The filling factor ν, which is necessary in order to determine the value of kt, is very difficult to be measured. For an estimation of ν, at first we have taken several SEM images of the surfaces of the nanowire forests (top vision), before growing the copper layer. A typical SEM top vision of the surface of a nanowire forest is shown on the left panel of figure 6. The apexes of the nanowires appear to be grouped in bunches. It must be noted that the average distance of these bunches is about 5 μm, meanwhile the nanowire length, measured on cross-section SEM images of this sample, resulted L = 38 μm. Therefore, we can affirm that the bending of the nanowires is very small, because nanowires are bended in average of about 2.5 μm on a length of 38 μm. A rough estimation of the filling factor ν can be obtained by analyzing the image, as shown in the right panel of figure 6 where a color threshold has been settled in order to visualize only the apexes of the nanowires which are brighter than the remaining part of the nanowires. The brighter area is about the sum of the cross-section surfaces of all the nanowires included in the image. Therefore, the ratio between the brighter area and the total surface of the image can be taken as an estimation of the filling factor of the nanowire forest. We repeated this procedures for all the samples. For each sample, at least 10 top vision images have been taken in random positions on the surface. Averaging on all the images, we can assume 0.3 as a reasonable value for ν. Therefore, kt results of about 4.6 W m–1 K–1. We underline that, meanwhile the measured value ktν = 1.38 W m–1 K–1 is quite reliable, the final value of kt = 4.6 W m–1 K–1 is affected by the rough estimation of the filling factor ν.
W K–1 m–2. This value is mainly due to the contact thermal conductance between the copper layer and the top aluminum block H. The filling factor ν, which is necessary in order to determine the value of kt, is very difficult to be measured. For an estimation of ν, at first we have taken several SEM images of the surfaces of the nanowire forests (top vision), before growing the copper layer. A typical SEM top vision of the surface of a nanowire forest is shown on the left panel of figure 6. The apexes of the nanowires appear to be grouped in bunches. It must be noted that the average distance of these bunches is about 5 μm, meanwhile the nanowire length, measured on cross-section SEM images of this sample, resulted L = 38 μm. Therefore, we can affirm that the bending of the nanowires is very small, because nanowires are bended in average of about 2.5 μm on a length of 38 μm. A rough estimation of the filling factor ν can be obtained by analyzing the image, as shown in the right panel of figure 6 where a color threshold has been settled in order to visualize only the apexes of the nanowires which are brighter than the remaining part of the nanowires. The brighter area is about the sum of the cross-section surfaces of all the nanowires included in the image. Therefore, the ratio between the brighter area and the total surface of the image can be taken as an estimation of the filling factor of the nanowire forest. We repeated this procedures for all the samples. For each sample, at least 10 top vision images have been taken in random positions on the surface. Averaging on all the images, we can assume 0.3 as a reasonable value for ν. Therefore, kt results of about 4.6 W m–1 K–1. We underline that, meanwhile the measured value ktν = 1.38 W m–1 K–1 is quite reliable, the final value of kt = 4.6 W m–1 K–1 is affected by the rough estimation of the filling factor ν.
Figure 5. The measured thermal resistance, multiplied by the sample surface  , is reported as a function of the length L of the silicon nanowire forest. Red dots: experimental measurements. Straight line: least square fitting.
, is reported as a function of the length L of the silicon nanowire forest. Red dots: experimental measurements. Straight line: least square fitting.
Download figure:
Standard image High-resolution imageFigure 6. Left panel: SEM photo of the surface of a typical sample (4 h of etch in 5:16:60 AgNO3:HF:H2O solution). The length of the nanowires (which are perpendicular to the SEM image) resulted of L = 38 μm, as measured from cross-section SEM images of the sample (not shown). Right panel: image reduction for a rough estimation of the filling factor ν.
Download figure:
Standard image High-resolution image5. Conclusions
We measured the thermal conductivity of silicon nanowire forests, made of a large amount of parallel silicon nanowires placed perpendicular to a silicon substrate. The measured value is comparable to that previously achieved by several groups with devices based on a single, or on very few, silicon nanostructures [8, 31–33]. In these works, it is shown that the thermal conductivity of nanowires is strongly reduced with respect to that of bulk silicon, and this is ascribed to the reduction of phonon propagation due to the scattering on the nanowire walls. As expected, the thermal conductivity of silicon nanowire forests, made of a large collection of parallel nanostructures, follows the same trend. Our work confirms the potentialities of nanostructuring for the reduction of the thermal conductivity, which is one of the fundamental parameters to be considered for high efficient thermoelectric conversion. The MACE technique used for the fabrication of our devices, which can be used as legs of a thermoelectric generator, is simple and low-cost, and it can be applied to areas of several cm2, hence it can be proposed for large-scale production. However, the technique gives nanowires with a non uniform diameter, whose average value is about 90 nm, but with a very large variability. Therefore, the thermal conductivity value achieved with our work is very important, because it is averaged on a large amount of long nanowires with random diameters, and on surfaces of several mm2 where non-uniformities can be present.
Since samples are very thin (nanowires of several tens of micrometers, total thickness 0.5 mm), we developed a suitable measurement apparatus based on the guarded hot plate concept. A suitable technique for data reduction, based on FE modeling, has been developed for a better interpretation of experimental measurements. Even if in our work we measured the thermal conductivity of silicon nanowire forests, the developed technique is very general and it can be usefully applied to the measurement of thin films and other low thickness materials.







