Abstract
Pseudospin and spin symmetries in the single-neutron spectra of Λ hypernuclei, and the effects of Λ impurity on these symmetries, are studied in the relativistic mean field model. It is found that the spin symmetry is violated while the pseudospin symmetry is approximately conserved, which is similar to the case in ordinary nuclei. As an impurity, the Λ hyperon makes the spin symmetry worse while making the pseudospin symmetry better, which arises from the decrease in the centrifugal barrier and the increase in the pseudo-centrifugal barrier in their competitions with the spin–orbit and pseudospin–orbit potentials, respectively. Further, our investigation extended to the Sn isotopes with  ,
,  , and
, and 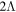 , and indicated that the effects of Λ impurity on pseudospin and spin symmetries are universal.
, and indicated that the effects of Λ impurity on pseudospin and spin symmetries are universal.
Export citation and abstract BibTeX RIS
1. Introduction
Symmetries in the single-particle (s.p.) spectra of atomic nuclei are important concepts in nuclear structure and have been extensively discussed in the literature, e.g., the violation of spin symmetry (SS) and the approximate pseudospin symmetry (PSS) in nuclear s.p. spectra. The breaking of SS, i.e., the remarkable spin–orbit splitting for the spin doublets (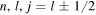 ) caused by the spin–orbit potential (SOP), lays the foundation for understanding the traditional magic numbers in nuclear physics [1, 2]. Meanwhile, a new symmetry, the so-called PSS, is introduced to explain the quasi-degeneracy between the two s.p. states with quantum numbers (
) caused by the spin–orbit potential (SOP), lays the foundation for understanding the traditional magic numbers in nuclear physics [1, 2]. Meanwhile, a new symmetry, the so-called PSS, is introduced to explain the quasi-degeneracy between the two s.p. states with quantum numbers (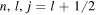 ) and (
) and ( ) by defining the pseudospin doublets (
) by defining the pseudospin doublets ( ,
, 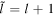 ,
,  ) [3, 4]. This symmetry has been used to explain a number of phenomena in nuclear structure such as deformation [5], superdeformation [6], magnetic moment [7], and identical rotational bands [8].
) [3, 4]. This symmetry has been used to explain a number of phenomena in nuclear structure such as deformation [5], superdeformation [6], magnetic moment [7], and identical rotational bands [8].
Since the recognition of PSS, comprehensive efforts have been made to understand its origin. Apart from the relabeling of quantum numbers, the explicit transformations from the normal scheme to the pseudospin scheme have been proposed in [9–11]. In 1997, Ginocchio made substantial progress, clearly showing that PSS is a relativistic symmetry in the Dirac Hamiltonian and becomes exact when the scalar and vector potentials are the same size but of opposite sign, i.e., 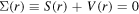 [12]. He also pointed out that the pseudo-orbital angular momentum
[12]. He also pointed out that the pseudo-orbital angular momentum  is nothing but the orbital angular momentum of the lower component of the Dirac wave function [12] and the occurrence of approximate PSS in nuclei is connected with certain similarities in the relativistic single-nucleon wave functions of the corresponding pseudospin doublets [13]. Later, Meng et al pointed out a more general condition for PSS
is nothing but the orbital angular momentum of the lower component of the Dirac wave function [12] and the occurrence of approximate PSS in nuclei is connected with certain similarities in the relativistic single-nucleon wave functions of the corresponding pseudospin doublets [13]. Later, Meng et al pointed out a more general condition for PSS 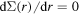 , and to what extent PSS is conserved is related to the competition between the pseudo-centrifugal barrier (PCB) and the pseudospin-orbit potential (PSOP) [14, 15]. Since then, SS and PSS have been studied extensively, with research carried out on areas such as PSS in the deformed nuclei [16–21], SS in anti-nucleon spectra [22–25], SS in anti-Λ spectra [26–28], PSS in the s.p. resonate states [29–36], perturbative interpretation of SS and PSS [37, 38], and PSS in supersymmetric quantum mechanics [39, 40]. Readers are referred to [41, 42] for reviews.
, and to what extent PSS is conserved is related to the competition between the pseudo-centrifugal barrier (PCB) and the pseudospin-orbit potential (PSOP) [14, 15]. Since then, SS and PSS have been studied extensively, with research carried out on areas such as PSS in the deformed nuclei [16–21], SS in anti-nucleon spectra [22–25], SS in anti-Λ spectra [26–28], PSS in the s.p. resonate states [29–36], perturbative interpretation of SS and PSS [37, 38], and PSS in supersymmetric quantum mechanics [39, 40]. Readers are referred to [41, 42] for reviews.
Almost all the studies on SS and PSS mentioned above have been performed in ordinary nuclei. Nuclear physicists have been very interested in hypernuclei [43–45] since the first Λ hypernucleus was discovered in 1953 [46]. Experimentally, the single-Λ hypernuclei are studied most extensively and so far more than 30 single-Λ hypernuclei, ranging from 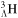 up to
up to 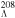 Pb, have been observed [43, 47]. Several double-Λ hypernuclei, such as
Pb, have been observed [43, 47]. Several double-Λ hypernuclei, such as  He, have also been found [48]. Theoretically, to shed light on baryon–baryon interaction, it is very important to study the structure of the hypernuclei. It is different from the nucleon; with an additional strangeness degree of freedom, a hyperon does not suffer from the nucleon's Pauli exclusion principle. And if hyperons penetrate into the nuclear interior as an impurity, there will be a series of responses, e.g., a shrinkage of nuclear size [49–51], a change in deformation properties [52, 53], a modification of the cluster structure [54], a shift of neutron drip line [55–57] and the occurrence of a nucleon and hyperon skin or halo [54, 56, 58]. The effects of Λ impurity on SS and PSS are fascinating, and we urgently require knowledge about the s.p. spectra in hypernuclei. It is therefore of great importance and interest to investigate SS and PSS in the s.p. spectrum of hypernuclei, and the effects of Λ impurity.
He, have also been found [48]. Theoretically, to shed light on baryon–baryon interaction, it is very important to study the structure of the hypernuclei. It is different from the nucleon; with an additional strangeness degree of freedom, a hyperon does not suffer from the nucleon's Pauli exclusion principle. And if hyperons penetrate into the nuclear interior as an impurity, there will be a series of responses, e.g., a shrinkage of nuclear size [49–51], a change in deformation properties [52, 53], a modification of the cluster structure [54], a shift of neutron drip line [55–57] and the occurrence of a nucleon and hyperon skin or halo [54, 56, 58]. The effects of Λ impurity on SS and PSS are fascinating, and we urgently require knowledge about the s.p. spectra in hypernuclei. It is therefore of great importance and interest to investigate SS and PSS in the s.p. spectrum of hypernuclei, and the effects of Λ impurity.
Over recent decades, the relativistic mean field (RMF) model has achieved great successes in ordinary nuclei [59–66] and hypernuclei [42, 67–79]. The relativistic approach is suitable for a discussion of spin–orbit splittings, as it is naturally built in the relativistic framework. With the RMF model, SS and PSS have been studied extensively with great success.
In the present work, SS and PSS in the single-neutron spectrum of Λ hypernuclei are studied within the framework of the RMF model. The effects of Λ impurity on these symmetries are discussed and the corresponding mechanisms are given. The paper is organized as follows. In section 2, we present the RMF model for Λ hypernuclei and the formalism of SS and PSS in the single-neutron spectrum. After the numerical details in section 3, we present the results and discussions in section 4. Finally, a summary is presented in section 5.
2. Theoretical framework
2.1. RMF model for Λ hypernuclei
The starting point of the meson-exchange RMF model for Λ hypernuclei is the covariant Lagrangian density

where  is the standard RMF Lagrangian density for nucleons [59–66], in which the couplings with the scalar σ, vector
is the standard RMF Lagrangian density for nucleons [59–66], in which the couplings with the scalar σ, vector 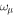 , vector-isovector
, vector-isovector  mesons, and the photon Aμ are included. It is written as
mesons, and the photon Aμ are included. It is written as
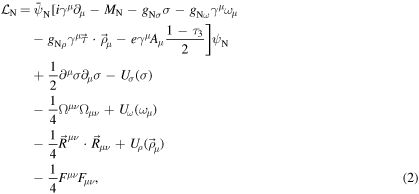
where MN and 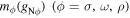 in the following are the masses (coupling constants) of the nucleon and the mesons, respectively, and the field tensors Ω,
in the following are the masses (coupling constants) of the nucleon and the mesons, respectively, and the field tensors Ω, 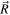 , and F are defined as
, and F are defined as



The nonlinear self-coupling terms  ,
, 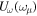 , and
, and 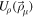 for the σ-, ω-, and ρ-mesons in
for the σ-, ω-, and ρ-mesons in  , respectively, have the following forms,
, respectively, have the following forms,

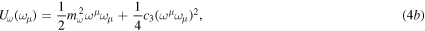

The Lagrangian density 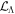 for neutral isospin singlet hyperons with σ- and ω-meson couplings included has the form [68]
for neutral isospin singlet hyperons with σ- and ω-meson couplings included has the form [68]
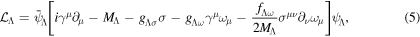
where  is the mass of the Λ hyperon,
is the mass of the Λ hyperon, 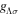 and
and 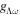 are the coupling constants with the σ- and ω-meson, respectively. The last term represents the tensor coupling with the ω-meson, which is related to the s.p. spin–orbit splitting of Λ hyperons.
are the coupling constants with the σ- and ω-meson, respectively. The last term represents the tensor coupling with the ω-meson, which is related to the s.p. spin–orbit splitting of Λ hyperons.
With the mean field and no-sea approximations, the s.p. Dirac equations for baryons and the Klein–Gordon equations for mesons and photons can be obtained through the variational procedure. The Dirac equations for baryons are
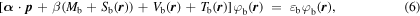
where 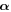 and β are the Dirac matrices,
and β are the Dirac matrices, 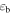 (
( ) are the s.p. energies, and
) are the s.p. energies, and  ,
,  , and
, and  are the scalar, vector, and tensor potentials, respectively, and
are the scalar, vector, and tensor potentials, respectively, and

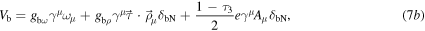

Note that the last two terms in equation (7b) are zero for Λ hyperons and the tensor potential in equation (7c) is zero for nucleons.
The Klein–Gordon equations for mesons and photon are

where  are the first-order derivatives of the nonlinear terms for σ-, ω-, and ρ-mesons, and is zero for photons. The source terms
are the first-order derivatives of the nonlinear terms for σ-, ω-, and ρ-mesons, and is zero for photons. The source terms  read,
read,
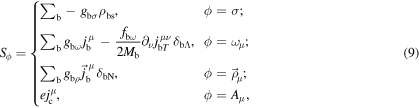
with the scalar density  , the baryon current
, the baryon current 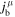 , the tensor current
, the tensor current  , the isocurrent
, the isocurrent 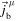 , and the electromagnetic current
, and the electromagnetic current 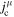 defined as,
defined as,





where  are the particle numbers of baryons (protons).
are the particle numbers of baryons (protons).
In the RMF model, the Dirac equation (6) for baryons, Klein–Gordon equations (8) for mesons and photons, mean field potentials in equation (7), and densities and currents in equation (10e) are solved self-consistently and iteratively in the coordinate space.
2.2. SS and PSS in the neutron spectrum
In order to study SS and PSS with the RMF theory, we will examine the Dirac equation (6) governing the motion of baryons.
In the spherical case, the Dirac spinors of baryons can be expanded as

where  and
and 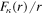 are the upper and lower components of the radial wave functions,
are the upper and lower components of the radial wave functions,  is the spinor spherical harmonic,
is the spinor spherical harmonic,  is the pseudo-orbital angular momentum, and the quantum number κ is defined as
is the pseudo-orbital angular momentum, and the quantum number κ is defined as  .
.
With the radial wave functions, Dirac equation (6) reduces to
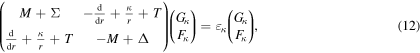
where the mean field potentials  and
and  . In the following, the neutron spectrum will be discussed, and in this case the tensor potential T = 0.
. In the following, the neutron spectrum will be discussed, and in this case the tensor potential T = 0.
One can go a step further to reduce the Dirac equation (12) to a second-order Schrödinger-like equation for either the upper or the lower component. To study SS and PSS, the Schrödinger-like equation is solved for G(r) and F(r), respectively [41, 42].
By substituting
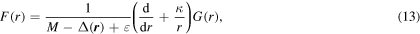
one can obtain for the upper component G(r)
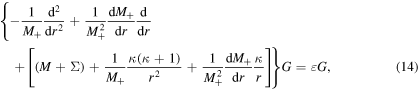
with the energy-dependent effective mass 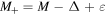 . Here and in the following, the subscript κ is omitted to simplify the form. For the above equation, in analogy with the Schrödinger equation,
. Here and in the following, the subscript κ is omitted to simplify the form. For the above equation, in analogy with the Schrödinger equation, 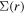 is the central potential in which particles move; the term proportional to
is the central potential in which particles move; the term proportional to 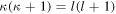 corresponds to the centrifugal barrier (CB), and the last term, which is proportional to
corresponds to the centrifugal barrier (CB), and the last term, which is proportional to 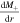 , corresponds to SOP, which leads to the substantial spin–orbit splitting in the single-neutron spectrum. Namely,
, corresponds to SOP, which leads to the substantial spin–orbit splitting in the single-neutron spectrum. Namely,


It is well known that there is no spin–orbit splitting if potential 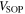 vanishes, i.e.,
vanishes, i.e.,  corresponds to the SS limit.
corresponds to the SS limit.
By substituting
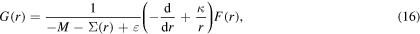
one can obtain the Schrödinger equation for the lower component F(r)
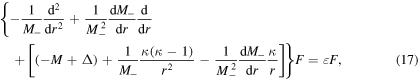
with the energy-dependent effective mass  . The term in the above equation that is proportional to
. The term in the above equation that is proportional to  is regarded as PCB and the last term, that is proportional to
is regarded as PCB and the last term, that is proportional to 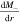 , corresponds to PSOP, which leads to the substantial pseudospin–orbit splitting. Namely,
, corresponds to PSOP, which leads to the substantial pseudospin–orbit splitting. Namely,


and 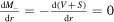 corresponds to the PSS limit.
corresponds to the PSS limit.
3. Numerical details
In the present work, (hyper)nuclei 120Sn, 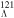 Sn, and
Sn, and 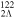 Sn, and the Sn isotopes with
Sn, and the Sn isotopes with 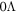 ,
, 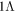 , and
, and 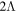 ranging from neutron number N = 70 to 118, are taken as examples to study the behavior of SS and PSS in the single-neutron spectrum and the effects of Λ impurity on these symmetries. The Dirac equation (12) in the RMF model is solved in the coordinate space with a box size of
ranging from neutron number N = 70 to 118, are taken as examples to study the behavior of SS and PSS in the single-neutron spectrum and the effects of Λ impurity on these symmetries. The Dirac equation (12) in the RMF model is solved in the coordinate space with a box size of  and a step size of
and a step size of 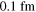 . For the NN interaction, PK1 parameter set [80] is used. For the
. For the NN interaction, PK1 parameter set [80] is used. For the 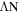 interaction, the scalar coupling constant
interaction, the scalar coupling constant 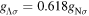 is adjusted by reproducing the single-Λ binding energy in the
is adjusted by reproducing the single-Λ binding energy in the 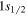 orbit of hypernucleus
orbit of hypernucleus 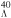 Ca [81], the vector coupling constant
Ca [81], the vector coupling constant  is determined from the näive quark model [82], and
is determined from the näive quark model [82], and  is taken as in [68]. These NN and
is taken as in [68]. These NN and  interactions describe well the Λ s.p. spectra of hypernuclei ranging from
interactions describe well the Λ s.p. spectra of hypernuclei ranging from 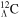 to
to  Pb [79].
Pb [79].
4. Results and discussion
In figure 1, the calculated single-neutron spectra and the mean field potential in the hypernucleus 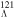 Sn are presented. The left and right panels correspond to spin doublets and pseudospin doublets, respectively. In the left panel, six sets of neutron spin doublets are obtained, i.e.,
Sn are presented. The left and right panels correspond to spin doublets and pseudospin doublets, respectively. In the left panel, six sets of neutron spin doublets are obtained, i.e.,  (
(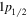 and
and 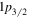 ),
), 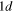 (
(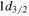 and
and  ),
), 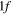 (
(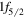 and
and  ),
), 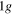 (
(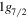 and
and  ),
), 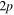 (
(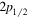 and
and 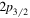 ), and
), and  (
( and
and  ). And the splitting of spin doublets with the same main quantum number n always increases with the angular momentum l. This is because the centrifugal barrier
). And the splitting of spin doublets with the same main quantum number n always increases with the angular momentum l. This is because the centrifugal barrier 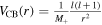 keeps the particle away from the centre so that a big overlap between the wave function G(r) and the spin–orbit potential always occurs for larger l [83]. In the right hand panel, four sets of pseudospin doublets are obtained, i.e.,
keeps the particle away from the centre so that a big overlap between the wave function G(r) and the spin–orbit potential always occurs for larger l [83]. In the right hand panel, four sets of pseudospin doublets are obtained, i.e., 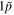 (
( and
and 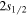 ),
),  (
(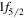 and
and  ),
), 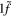 (
(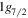 and
and 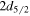 ), and
), and  (
(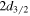 and
and  ). An obvious energy dependence of PSS can be seen and PSS for the pseudospin doublets near the threshold is preserved pretty well, e.g., the quasi-degeneracy
). An obvious energy dependence of PSS can be seen and PSS for the pseudospin doublets near the threshold is preserved pretty well, e.g., the quasi-degeneracy 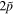 doublets. From those discussions, spin–orbit and pseudospin–orbit splittings in the single-neutron spectra of
doublets. From those discussions, spin–orbit and pseudospin–orbit splittings in the single-neutron spectra of  Sn are found to be quite different, i.e., obvious violations of SS for most of the spin doublets versus approximate PSS for the pseudospin doublets. As a typical example, the
Sn are found to be quite different, i.e., obvious violations of SS for most of the spin doublets versus approximate PSS for the pseudospin doublets. As a typical example, the  doublets with the smallest spin–orbit splitting is 1.411 MeV while the pseudospin–orbit splitting is only 0.307 MeV for the
doublets with the smallest spin–orbit splitting is 1.411 MeV while the pseudospin–orbit splitting is only 0.307 MeV for the 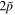 doublets, which is an order of magnitude smaller than the former one. Note that both SS and PSS of the single-neutron spectra in Λ hypernuclei are similar to those found in ordinary nuclei.
doublets, which is an order of magnitude smaller than the former one. Note that both SS and PSS of the single-neutron spectra in Λ hypernuclei are similar to those found in ordinary nuclei.
Figure 1. Single-neutron spectrum in hypernucleus 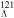 Sn calculated in the RMF model. The left and right hand panels are for spin doublets and pseudospin doublets, respectively. Mean field potential
Sn calculated in the RMF model. The left and right hand panels are for spin doublets and pseudospin doublets, respectively. Mean field potential  is shown as the blue solid line.
is shown as the blue solid line.
Download figure:
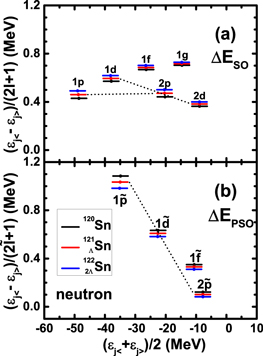
Standard image High-resolution imageNext, the effects of Λ impurity on SS and PSS in the single-neutron spectrum are discussed. In figure 2, taking 120Sn,  Sn, and
Sn, and 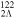 Sn as examples, the spin–orbit splittings defined by
Sn as examples, the spin–orbit splittings defined by 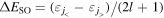 , and the pseudospin–orbit splittings
, and the pseudospin–orbit splittings  , versus the average s.p. energies
, versus the average s.p. energies  are plotted in the upper and lower panels, respectively. For SS, as the number of Λ hyperons is increased, the energy splittings between all the spin doublets become larger. Namely, adding more Λ hyperons makes SS in the single-neutron spectrum worse. However, a complete reversal of the trend is observed for the pseudospin doublets in the lower panel. Thus with the addition of the number of Λ hyperons,
are plotted in the upper and lower panels, respectively. For SS, as the number of Λ hyperons is increased, the energy splittings between all the spin doublets become larger. Namely, adding more Λ hyperons makes SS in the single-neutron spectrum worse. However, a complete reversal of the trend is observed for the pseudospin doublets in the lower panel. Thus with the addition of the number of Λ hyperons,  decreases and PSS is improved in the single-neutron spectrum.
decreases and PSS is improved in the single-neutron spectrum.
Figure 2. Spin–orbit splittings  (the upper panel) and pseudospin–orbit splittings
(the upper panel) and pseudospin–orbit splittings  (the lower panel) versus their average s.p. energies
(the lower panel) versus their average s.p. energies 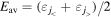 (the mid-points) for the single-neutron spectra of 120Sn (the black solid lines),
(the mid-points) for the single-neutron spectra of 120Sn (the black solid lines),  Sn (the red solid lines), and
Sn (the red solid lines), and 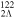 Sn (the blue solid lines), respectively. For the spin doublets,
Sn (the blue solid lines), respectively. For the spin doublets,  and
and  , and for the pseudospin doublets,
, and for the pseudospin doublets, 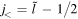 and
and 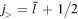 . Spin(pseudospin) doublets with the same
. Spin(pseudospin) doublets with the same 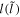 are linked by dashed lines.
are linked by dashed lines.
Download figure:
Standard image High-resolution imageHowever, it should be noted that the pseudospin–obit splitting is not bound to decrease if the spin–obit splitting increases. For example, if there is an inversion of the s.p. levels of the pseudospin doublets and/or the s.p. energy of both doublets goes in the same direction but with different magnitudes, the pseudospin–obit splitting could also increase.
In table 1, the values of the energy splittings  for spin doublets, and
for spin doublets, and 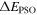 for pseudospin doublets shown in figure 2 are listed for (hyper)nuclei 120Sn,
for pseudospin doublets shown in figure 2 are listed for (hyper)nuclei 120Sn,  Sn, and
Sn, and  Sn. From table 1, we can see clearly that adding more Λ hyperons has opposite effects on SS and PSS. Quantitatively, adding one Λ hyperon enlarges the splittings of spin doublets by
Sn. From table 1, we can see clearly that adding more Λ hyperons has opposite effects on SS and PSS. Quantitatively, adding one Λ hyperon enlarges the splittings of spin doublets by 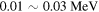 while reduce the splittings of pseudospin doublets by
while reduce the splittings of pseudospin doublets by  .
.
Table 1.
Comparison of the spin–orbit splitting 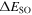 and pseudospin-orbit splitting
and pseudospin-orbit splitting  for the single-neutron spectra of (hyper)nuclei 120Sn,
for the single-neutron spectra of (hyper)nuclei 120Sn,  Sn, and
Sn, and 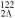 Sn calculated in the RMF model. Energies are in MeV.
Sn calculated in the RMF model. Energies are in MeV.
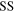
|
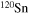
|

|
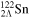
|

|
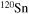
|

|
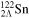
|
|---|---|---|---|---|---|---|---|

|
0.430 | 0.460 | 0.492 |
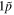
|
1.084 | 1.034 | 0.982 |
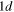
|
0.571 | 0.594 | 0.618 |
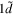
|
0.633 | 0.608 | 0.582 |
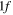
|
0.668 | 0.685 | 0.703 |

|
0.350 | 0.331 | 0.311 |

|
0.441 | 0.470 | 0.500 |

|
0.121 | 0.102 | 0.082 |

|
0.704 | 0.716 | 0.728 | ||||

|
0.364 | 0.381 | 0.400 |
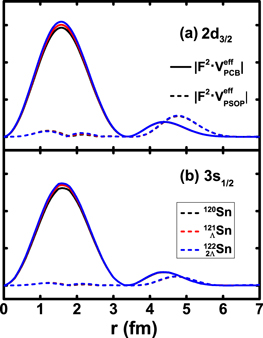
To analyze the mechanism of the effects of Λ impurity on SS and PSS shown in figure 2 and listed in table 1, we take the case of pseudopsin doublets as an example and compare the pseudo-centrifugal barrier  and pseudospin–orbit potential
and pseudospin–orbit potential 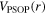 . It was pointed out in [14] that if
. It was pointed out in [14] that if

the pseudospin approximation will be good. Unfortunately, it is difficult to compare them, as both of them have a singularity at  where
where  . Since we are only interested in the relative magnitude of the PCB and the PSOP in equation (18), following [14], the effective PCB and the effective PSOP,
. Since we are only interested in the relative magnitude of the PCB and the PSOP in equation (18), following [14], the effective PCB and the effective PSOP,


are introduced for comparison by multiplying by a common factor  , and in order to examine the effect of the Λ impurity more carefully, we compare the effective PCB and effective PSOP multiplied by the squares of the lower component wave function F(r). In figure 3, the comparison of the PCB (solid lines) and PSOP (dashed lines) for the
, and in order to examine the effect of the Λ impurity more carefully, we compare the effective PCB and effective PSOP multiplied by the squares of the lower component wave function F(r). In figure 3, the comparison of the PCB (solid lines) and PSOP (dashed lines) for the  pseudospin doublets in (hyper)nuclei 120Sn,
pseudospin doublets in (hyper)nuclei 120Sn, 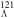 Sn, and
Sn, and  Sn are presented in arbitrary scales. The upper and lower panels are for the partner states
Sn are presented in arbitrary scales. The upper and lower panels are for the partner states 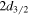 and
and 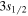 of pseudospin doublet
of pseudospin doublet  , respectively.
, respectively.
Figure 3. The comparison of 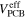 (the solid lines) and
(the solid lines) and  (the dash lines) multiplied by the square of the wave function F of the lower components in arbitrary scale for the
(the dash lines) multiplied by the square of the wave function F of the lower components in arbitrary scale for the 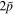 pseudospin doublets, i.e.,
pseudospin doublets, i.e.,  (the upper panel) and
(the upper panel) and  (the lower panel) in 120Sn (the black lines),
(the lower panel) in 120Sn (the black lines),  Sn (the red lines) and
Sn (the red lines) and 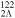 Sn (the blue lines), respectively.
Sn (the blue lines), respectively.
Download figure:
Standard image High-resolution imageFrom figure 3, it is clearly seen that the effective PCB is much bigger than the effective PSOP in the coordinate space with 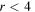 fm, and generally they differ by two orders of magnitude. In a semi-quantitative sense, this indicates that the condition in equation (19) is satisfied and PSS is preserved approximately. Moreover, with adding more Λ hyperons, the effective PCB obviously becomes larger while the effective PSOP remains almost constant, which results in better PSS as the Λ hyperon number increases. For the spin doublets, similar analysis is performed. We found that adding more Λ hyperons will obviously reduce the effective CB while keeping the effective SOP almost constant, which results in a worse SS.
fm, and generally they differ by two orders of magnitude. In a semi-quantitative sense, this indicates that the condition in equation (19) is satisfied and PSS is preserved approximately. Moreover, with adding more Λ hyperons, the effective PCB obviously becomes larger while the effective PSOP remains almost constant, which results in better PSS as the Λ hyperon number increases. For the spin doublets, similar analysis is performed. We found that adding more Λ hyperons will obviously reduce the effective CB while keeping the effective SOP almost constant, which results in a worse SS.
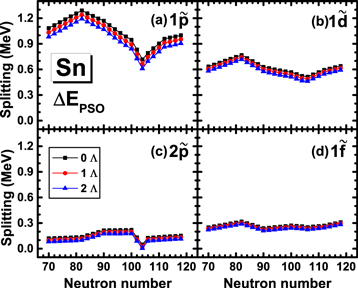
Finally, to see the universality of the effects of Λ impurity on SS and PSS in the single-neutron spectrum obtained by studying 120Sn,  Sn, and
Sn, and  Sn, we repeat our analysis for other Sn isotopes with
Sn, we repeat our analysis for other Sn isotopes with 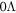 ,
,  and
and  . In figure 4, we take four spin doublets, i.e.,
. In figure 4, we take four spin doublets, i.e.,  ,
, 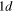 ,
,  , and
, and  , as examples and plot the spin–orbit splittings
, as examples and plot the spin–orbit splittings 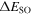 . From all panels in figure 4, we observe that SS becomes worse with the increasing Λ hyperon number for all the spin doublets. Besides, in all the isotopes, the splitting
. From all panels in figure 4, we observe that SS becomes worse with the increasing Λ hyperon number for all the spin doublets. Besides, in all the isotopes, the splitting 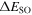 of the spin doublets with the same main quantum number n increases with angular momentum l, which is consistent with the conclusion obtained in figure 1. Similarly, in figure 5 the pseudospin–orbit splittings
of the spin doublets with the same main quantum number n increases with angular momentum l, which is consistent with the conclusion obtained in figure 1. Similarly, in figure 5 the pseudospin–orbit splittings  are depicted for the pseudospin doublets
are depicted for the pseudospin doublets  ,
,  ,
,  , and
, and  in the Sn isotopes. We observe that PSS becomes better with the increasing Λ hyperon number for all the pseudospin doublets. These observations indicate that the effects of Λ impurity on SS and PSS are universal.
in the Sn isotopes. We observe that PSS becomes better with the increasing Λ hyperon number for all the pseudospin doublets. These observations indicate that the effects of Λ impurity on SS and PSS are universal.
Figure 4. Spin–orbit splittings 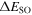 for the single-neutron spectra of Sn isotopes ranging from neutron number N = 70 to 118. The black, red, and blue lines/symbols denote the (hyper)nuclei with
for the single-neutron spectra of Sn isotopes ranging from neutron number N = 70 to 118. The black, red, and blue lines/symbols denote the (hyper)nuclei with  ,
, 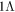 , and
, and 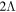 , respectively.
, respectively.
Download figure:
Standard image High-resolution imageFigure 5. The same as figure 4, but for the pseudospin–orbit splittings  .
.
Download figure:
Standard image High-resolution imageAs seen in figure 4, the spin–orbit splitting  generally decreases with the increasing nucleon number. As indicated in [83], this mainly comes from the larger and larger surface diffuseness of the potentials or the outwards tendency of the potentials with the increasing neutron number. In figure 5, the energy splittings of deep neutron pseudospin doublets, e.g.,
generally decreases with the increasing nucleon number. As indicated in [83], this mainly comes from the larger and larger surface diffuseness of the potentials or the outwards tendency of the potentials with the increasing neutron number. In figure 5, the energy splittings of deep neutron pseudospin doublets, e.g., 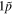 doublet, generally decrease with the increasing neutron number, but increase in some mass ranges. As discussed in [84, 85], the splittings depend on the complex competition of the radius, depth and diffuseness of the potentials, which have very different influences, i.e., a larger radius and deeper potential will increase the pseudospin splitting while a larger diffuseness make the splitting smaller. However, the splittings of pseudospin doublets near the threshold, e.g.,
doublet, generally decrease with the increasing neutron number, but increase in some mass ranges. As discussed in [84, 85], the splittings depend on the complex competition of the radius, depth and diffuseness of the potentials, which have very different influences, i.e., a larger radius and deeper potential will increase the pseudospin splitting while a larger diffuseness make the splitting smaller. However, the splittings of pseudospin doublets near the threshold, e.g., 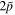 and
and  doublets, always remain at a small magnitude. One possible reason is the larger pseudo-centrifugal barrier for those orbits, as discussed in [14].
doublets, always remain at a small magnitude. One possible reason is the larger pseudo-centrifugal barrier for those orbits, as discussed in [14].
5. Summary
We have studied SS and PSS in the single-neutron spectrum of Λ hypernuclei, and the effects of Λ impurity on the these symmetries, within the RMF framework.
Firstly, in hypernucleus  Sn, the SS and PSS of the single-neutron spectra are studied. Obvious violations of SS and approximate PSS in the single-neutron spectrum are found. For the spin doublets with the same main quantum number n, the spin–orbit splittings always increase with the angular momentum l. For the pseudospin splittings, there is an obvious energy dependence and the splittings for the pseudospin doublets near the threshold are very small. All these conclusions are consistent with those in ordinary nuclei.
Sn, the SS and PSS of the single-neutron spectra are studied. Obvious violations of SS and approximate PSS in the single-neutron spectrum are found. For the spin doublets with the same main quantum number n, the spin–orbit splittings always increase with the angular momentum l. For the pseudospin splittings, there is an obvious energy dependence and the splittings for the pseudospin doublets near the threshold are very small. All these conclusions are consistent with those in ordinary nuclei.
Secondly, taking (hyper)nuclei 120Sn, 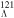 Sn, and
Sn, and 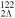 Sn as examples, the effects of Λ impurity on SS and PSS in the single-neutron spectrum have been investigated. Adding more Λ hyperons makes SS worse while improving PSS. In more detail, for the pseudospin doublets, the Λ hyperons increase the effective pseudo-centrifugal barrier
Sn as examples, the effects of Λ impurity on SS and PSS in the single-neutron spectrum have been investigated. Adding more Λ hyperons makes SS worse while improving PSS. In more detail, for the pseudospin doublets, the Λ hyperons increase the effective pseudo-centrifugal barrier  while changing the effective pseudospin–orbit potential
while changing the effective pseudospin–orbit potential 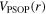 slightly, thus, in this case, PSS condition
slightly, thus, in this case, PSS condition 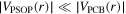 is better satisfied. For the spin doublets, the Λ hyperons have the opposite effect, i.e., Λ hyperons decrease the centrifugal barrier
is better satisfied. For the spin doublets, the Λ hyperons have the opposite effect, i.e., Λ hyperons decrease the centrifugal barrier  .
.
Finally, we conclude that the extension of our investigation to Sn isotopic chains with  ,
,  , and
, and 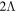 indicates that the effects of Λ impurity on SS and PSS in the single-neutron spectrum are universal.
indicates that the effects of Λ impurity on SS and PSS in the single-neutron spectrum are universal.
Acknowledgments
The authors thank Dr H Z Liang for helpful discussions. This work was partly supported by the Physics Research and Development Program of Zhengzhou University (grant no. 32410017) and the National Natural Science Foundation of China (grant nos. 11175002, 11335002, 11505157, 11675148, and 11105042).