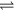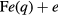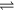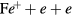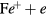Abstract
A collisional-radiative model for the ground state and fifty effective excited levels of atomic iron, and one level for singly-ionized iron, is set up for technological plasmas. Attention is focused on the population of excited states of atomic iron as a result of excitation, de-excitation, ionization, recombination and spontaneous emission. Effective rate coefficients for ionization and recombination, required in non-equilibrium plasma transport models, are also obtained. The collisional-radiative model is applied to a thermal arc plasma. Input parameters for the collisional-radiative model are provided by a magnetohydrodynamic simulation of a gas-metal welding arc, in which local thermodynamic equilibrium is assumed and the treatment of the transport of metal vapour is based on combined diffusion coefficients. The results clearly identify the conditions in the arc, under which the atomic state distribution satisfies the Boltzmann distribution, with an excitation temperature equal to the plasma temperature. These conditions are met in the central part of the arc, even though a local temperature minimum occurs here. This provides assurance that diagnostic methods based on local thermodynamic equilibrium, in particular those of optical emission spectroscopy, are reliable here. In contrast, deviations from the equilibrium atomic-state distribution are obtained in the near-electrode and arc fringe regions. As a consequence, the temperatures determined from the ratio of line intensities and number densities obtained from the emission coefficient in these regions are questionable. In this situation, the collisional-radiative model can be used as a diagnostic tool to assist in the interpretation of spectroscopic measurements.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
A Viewpoint was published about this Letter in 2017 J Phys. D: Appl. Phys. 50 431001
1. Introduction
Iron vapour is important in many arc plasma processes; for example it is released from the molten steel anode in gas-tungsten welding arcs and from the consumable iron electrode in gas-metal welding arcs [1]. The electronic structure of the iron atom is characterized by a large number of low energy levels and an ionization potential that is lower than the energy of the first excited state of atoms of the shielding gas, e.g. argon or helium [2]. Therefore, iron atoms are more easily excited and ionized in the arc plasma than the atoms of the shielding gas. The radiative emission and electrical conductivity of the arc plasma are in turn influenced by the presence of iron atoms and ions. The population of the atomic states is established as a result of collisional and radiative processes occurring in the arc plasma and can be in general described by a collisional-radiative model. While such models have been developed by the plasma science community, for example for argon [3] and copper metal vapour [4], mercury [5], magnesium [6, 7], aluminum [8], models for iron atoms and ions have been considered solely in the astrophysics of stellar atmospheres [9] and account only for collisional and radiative excitation/de-excitation under conditions being quite different than those met in technological plasmas.
Cross-sections and transition probabilities for excitation and de-excitation, ionization and recombination due to collisions between electrons, atoms and ions, as well as radiative decay between the levels, are required for a full understanding of arc plasmas. Such data are relatively well known for shielding gas atoms and in some extent for copper atoms due to applications to copper vapour lasers. Fewer data are available in the literature for iron atoms, although measurements related to iron vapour lasers have been carried out [10]. Availability of data obtained in the framework of the opacity project and the iron project is restricted to the processes of radiative and dielectronic recombination, and photoionization, and multiply-ionized iron [11–13]. Some data for electron impact ionization can be found in the AMDIS database [14]. However, experimental and theoretical activity in the plasma science community concerning collisional cross-section data is still absent. A critical evaluation of atomic transition probabilities for neutral and singly-ionized iron has been presented by Fuhr and Wiese [15] and data is reported for allowed and forbidden transitions in response to needs of the astrophysical and magnetic fusion science communities.
In this letter, we present the first collisional-radiative model for iron atoms applicable to technological plasmas both in and out of local thermodynamic equilibrium. Due to the drastic lack of collisional data for iron atoms, excitation and de-excitation processes are described by theoretical approximations. Results are presented for a gas-metal welding arc plasma. A magnetohydrodynamic simulation of the arc, incorporating the transport of iron metal vapour, is used to provide the input parameters of the collisional-radiative model. The results indicate the regions in which the calculated atomic state distribution of neutral iron follows or deviates from an equilibrium distribution. Effective rate coefficients for ionization and recombination of iron atoms are calculated as a function of the electron density and temperature, to meet the requirements of non-equilibrium arc plasma models.
2. Model description
2.1. Collisional-radiative model for iron atoms
Typically, the transport of excited atoms (except possibly metastable states) can be neglected in arc plasmas and the atomic state distribution function can therefore be obtained employing the quasi-steady-state approximation [16] in collisional-radiative models. The ground-state population of atoms, which is influenced by transport phenomena, is an input parameter in these models. The following processes come into consideration for the present model.
- Excitation and de-excitation in collisions with electrons


 , p < q
, p < q - Ionization by electron impact and three-body recombination



- Absorption and line emission


 , p < q
, p < q 


- Radiative recombination



The excited states of iron atoms ( ) are designated by the labels p and q, and
) are designated by the labels p and q, and  denotes the photon energy corresponding to the transition from level p to level q. Excitation and de-excitation in collisions between
denotes the photon energy corresponding to the transition from level p to level q. Excitation and de-excitation in collisions between  atoms is not taken into account in the model at the current stage. The net result of emission and absorption transitions between levels q and p is included to a first approximation by means of a transition probability modified by the optical escape factor [3]. The latter represents the fraction of photons that can escape from the plasma without being re-absorbed by atoms in the lower level. In general, reabsorption of resonance radiation by the ground state atoms dominates over reabsorption by excited atoms. Therefore, the escape factors attributed to transitions to excited states can be assumed to be equal to 1 (complete radiation escape) while those for resonance radiation are significantly less than 1. Rigorous treatment of radiation in the arc plasma requires a non-local balance of excited states and solving the Holstein–Biberman equation of radiative transport [17]. Such a treatment is avoided here because of the drastic increase of the computational effort. Photo-ionization is neglected, since it is expected to be negligible relative to electron impact ionization. The population density np of the excited atomic state p is then determined by the equation
atoms is not taken into account in the model at the current stage. The net result of emission and absorption transitions between levels q and p is included to a first approximation by means of a transition probability modified by the optical escape factor [3]. The latter represents the fraction of photons that can escape from the plasma without being re-absorbed by atoms in the lower level. In general, reabsorption of resonance radiation by the ground state atoms dominates over reabsorption by excited atoms. Therefore, the escape factors attributed to transitions to excited states can be assumed to be equal to 1 (complete radiation escape) while those for resonance radiation are significantly less than 1. Rigorous treatment of radiation in the arc plasma requires a non-local balance of excited states and solving the Holstein–Biberman equation of radiative transport [17]. Such a treatment is avoided here because of the drastic increase of the computational effort. Photo-ionization is neglected, since it is expected to be negligible relative to electron impact ionization. The population density np of the excited atomic state p is then determined by the equation
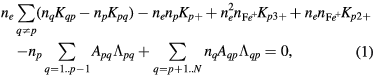
in which ne is the electron number density,  is the number density of iron ions, Kpq and Kqp are respectively the rate coefficients for excitation from level p to level q and de-excitation from level q to level p by electron impact, Kp+ is the rate coefficient for ionization in collisions with electrons, Apq and
is the number density of iron ions, Kpq and Kqp are respectively the rate coefficients for excitation from level p to level q and de-excitation from level q to level p by electron impact, Kp+ is the rate coefficient for ionization in collisions with electrons, Apq and  denote respectively the transition probability for spontaneous emission from level p to level q and the corresponding escape factor, Kp3+ and Kp2+ are the rate coefficients for three-body and radiative recombination, respectively. Equation (1) couples the N effective levels considered in the model. The 50 effective levels (figure 1) represent individual terms with energy up to about 5.5 eV, and groups of terms with energy from about 5.5 eV up to the first ionization potential. The groups combine terms of various multiplicity (plotted as connected by dashed lines). Since collisional data for the iron atom is not yet known, theoretical approximations are used. These are based on the cross-sections for hydrogen atoms and alkali metals of Vriens and Smeets [18], but weighted to correct for splitting into multiple levels for non-hydrogen atoms [19], and the expressions by Drawin [20] for forbidden transitions. For the effective levels, the transition probabilities and oscillator strengths for absorption reported in [15] for 2425 allowed and 116 forbidden transitions are employed. Energies of the effective levels, effective transition probabilities and cross-sections are evaluated from the respective individual values and statistical weights. The collisional data for ionization and radiative recombination are calculated according to [18] and [21], respectively. The rate coefficients of the collisional processes are calculated assuming a Maxwellian energy distribution function for the electrons. Three-body recombination is assumed to be in equilibrium with ionization by electron impact. The cut-off technique proposed by van der Mullen [21] is applied to reduce the effect of using a finite number of atomic levels.
denote respectively the transition probability for spontaneous emission from level p to level q and the corresponding escape factor, Kp3+ and Kp2+ are the rate coefficients for three-body and radiative recombination, respectively. Equation (1) couples the N effective levels considered in the model. The 50 effective levels (figure 1) represent individual terms with energy up to about 5.5 eV, and groups of terms with energy from about 5.5 eV up to the first ionization potential. The groups combine terms of various multiplicity (plotted as connected by dashed lines). Since collisional data for the iron atom is not yet known, theoretical approximations are used. These are based on the cross-sections for hydrogen atoms and alkali metals of Vriens and Smeets [18], but weighted to correct for splitting into multiple levels for non-hydrogen atoms [19], and the expressions by Drawin [20] for forbidden transitions. For the effective levels, the transition probabilities and oscillator strengths for absorption reported in [15] for 2425 allowed and 116 forbidden transitions are employed. Energies of the effective levels, effective transition probabilities and cross-sections are evaluated from the respective individual values and statistical weights. The collisional data for ionization and radiative recombination are calculated according to [18] and [21], respectively. The rate coefficients of the collisional processes are calculated assuming a Maxwellian energy distribution function for the electrons. Three-body recombination is assumed to be in equilibrium with ionization by electron impact. The cut-off technique proposed by van der Mullen [21] is applied to reduce the effect of using a finite number of atomic levels.
Figure 1. Effective energy levels of iron used in the collisional-radiative model. The term designation according to Moore [2] is given on the bottom.
Download figure:
Standard image High-resolution imageThe level population n(p) can be expressed for convenience as a sum of two contributions, which are respectively proportional to the ground state atom density  and the ion density
and the ion density  [16], i.e.
[16], i.e.
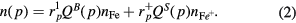
In equation (2),  and
and  are relative populations and express the deviation of the level population from the Boltzmann and Saha distributions through the factors
are relative populations and express the deviation of the level population from the Boltzmann and Saha distributions through the factors  , and
, and  , respectively. In these expressions, gp, ge and g+ respectively denote the statistical weights of level p, electrons and ions, Ep is the excitation energy of level p, Ep+ is the ionization energy of level p, Te is the electron temperature, and kB is the Boltzmann constant.
, respectively. In these expressions, gp, ge and g+ respectively denote the statistical weights of level p, electrons and ions, Ep is the excitation energy of level p, Ep+ is the ionization energy of level p, Te is the electron temperature, and kB is the Boltzmann constant.
The collisional-radiative model calculates the distribution of iron atoms over the effective excited levels shown in figure 1 for a given atom density and plasma temperature under conditions of local thermodynamic equilibrium. Depending on the practical application, the plasma parameters can be freely varied or they may be known from a plasma model. In this work, we apply the collisional-radiative model in combination with a magnetohydrodynamic model of the arc plasma, which is described next. Note that the aim of the present model is to describe the state distribution of Fe atoms from the known ground state density and ion density. The effect of another gas mixture component has not been considered at this stage. Effects related to Ar metastables and ions are known to occur in some cases (e.g. for Mg ions [6, 7]). Recent experimental studies [22] showed, however, a negligible effect of Ar on line intensities of metal atoms with ionization energy below 8 eV. This justifies the predominant role of excitation of Fe by electron impact in the model. A pronounced effect was observed for excited ionic states, which are not considered in the present model.
2.2. Arc model
In order to obtain a realistic data set for an arc plasma containing iron metal vapour, a magnetohydrodynamic model is developed for the configuration of the gas-metal welding arc considered in [23, 24]. The consumable electrode is an iron wire with a radius of 0.6 mm. The workpiece is a plate made of iron. The arc length is 5 mm. Argon is fed as shielding gas through the nozzle with a rate of 15 slpm. The evaporation of the wire occurs with a rate which is 0.8 of the wire feed rate (0.15 m s−1), with most of the wire forming droplets. The arc current is 150 A. A detailed description of the model is given in previous publications [23, 25]. Here, a summary is given to outline the main features. The model employs a set of coupled partial differential equations, which describe the conservation of mass, momentum, and energy. In addition, the equations of continuity and the Maxwell's equation are solved for the electric and the magnetic potential. The plasma is considered as ideal gas at atmospheric pressure with laminar flow under conditions of local thermodynamic equilibrium. The Lorentz force is considered in the momentum conservation equation to take into account the pressure gradient produced by the self-induced magnetic field. The influence of droplets on the plasma is neglected. An additional equation covers the conservation of metal vapour mass [25] employing the combined diffusion coefficient approach [26]. According to this approach, the plasma is generated in the gas mixture containing species attributed to the shielding gas (argon atoms and ions) and to the metal vapour (iron atoms and ions). Electrons are associated with each component to ensure quasi-neutrality. The transport properties are calculated as look-up tables prior to the simulation as functions of the mass fraction of iron vapour and the plasma temperature in the range 300–30 000 K [27]. The net emission coefficient of Menart and Malik [28] is used to account for the radiative loss of energy. The partial differential equations are solved in two dimensions (r, z) assuming axial symmetry with the computational platform COMSOL multyphysics [29], which applies the finite element approach.
of the wire feed rate (0.15 m s−1), with most of the wire forming droplets. The arc current is 150 A. A detailed description of the model is given in previous publications [23, 25]. Here, a summary is given to outline the main features. The model employs a set of coupled partial differential equations, which describe the conservation of mass, momentum, and energy. In addition, the equations of continuity and the Maxwell's equation are solved for the electric and the magnetic potential. The plasma is considered as ideal gas at atmospheric pressure with laminar flow under conditions of local thermodynamic equilibrium. The Lorentz force is considered in the momentum conservation equation to take into account the pressure gradient produced by the self-induced magnetic field. The influence of droplets on the plasma is neglected. An additional equation covers the conservation of metal vapour mass [25] employing the combined diffusion coefficient approach [26]. According to this approach, the plasma is generated in the gas mixture containing species attributed to the shielding gas (argon atoms and ions) and to the metal vapour (iron atoms and ions). Electrons are associated with each component to ensure quasi-neutrality. The transport properties are calculated as look-up tables prior to the simulation as functions of the mass fraction of iron vapour and the plasma temperature in the range 300–30 000 K [27]. The net emission coefficient of Menart and Malik [28] is used to account for the radiative loss of energy. The partial differential equations are solved in two dimensions (r, z) assuming axial symmetry with the computational platform COMSOL multyphysics [29], which applies the finite element approach.
3. Results
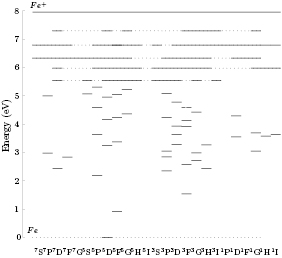
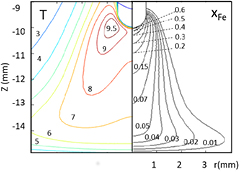
The distribution of the plasma temperature predicted by the arc model is shown in figure 2, along with the distribution of the mole fraction of iron in the plasma. The iron vapour mole fraction reaches about 0.6 in the central part of the arc close to the electrode. Moving towards the workpiece, the mole fraction of iron decreases rapidly to about 0.1 at the mid-point between the electrodes, and to about 0.01 near the workpiece. The metal vapour influences the plasma properties, even for a small percentage [25]. The plasma composition is obtained under the assumption of local thermodynamic equilibrium with the plasma temperature (T) and partial pressure of iron ( ) from the arc model. The axial distribution of the number density of neutral atoms and ions of iron (
) from the arc model. The axial distribution of the number density of neutral atoms and ions of iron ( ,
,  ) is shown in figure 3. The quantities Te(=T),
) is shown in figure 3. The quantities Te(=T),  , and
, and  serve as input parameters of the collisional-radiative model.
serve as input parameters of the collisional-radiative model.
Figure 2. Isocurves of the plasma temperature (in 103 K) and the mole fraction of iron in the gas-metal welding arc.
Download figure:
Standard image High-resolution imageFigure 3. Calculated arc temperature, iron vapour partial pressure and equilibrium composition on the arc axis.
Download figure:
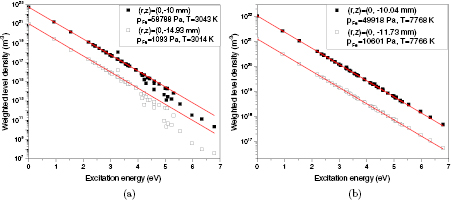
Standard image High-resolution imageThe atomic state distribution obtained under four quite different conditions is shown in figure 4. The weighted population density (population of a level divided by its statistical weight) is plotted against the excitation energy. The conditions in figure 4(a) correspond to positions in the vicinity of the consumable electrode (distance 0 in figure 3, low T, high  ) and the workpiece (distance of 4.93 mm in figure 3, low T, low
) and the workpiece (distance of 4.93 mm in figure 3, low T, low  ), while those in figure 4(b) represent positions (distances of 0.04 mm and 1.73 mm in figure 3) in the arc column at almost the same value of T but quite different values of
), while those in figure 4(b) represent positions (distances of 0.04 mm and 1.73 mm in figure 3) in the arc column at almost the same value of T but quite different values of  . The equilibrium (Boltzmann) distribution with the corresponding T is shown along with the results of the collisional-radiative model. In the low temperature cases shown in figure 4(a), the atomic state distribution deviates from the equilibrium distribution. The underpopulation of the excited states lying closer to the ionization limit with respect to the equilibrium distribution occurs due to the radiative processes. The excitation of atomic levels with energy above ∼3 eV cannot be described by a common temperature. This means that the determination of temperatures from line intensity ratios, as is commonly done in optical emission spectroscopy, will not be accurate. Such effects can be expected in the near-electrode regions and the arc fringes, where deviations from thermal and chemical equilibrium appear. The experiments reported in [24] provide evidence of deviations from thermal equilibrium close to the cathode. In particular, the electron temperature can differ from the temperature of heavy particles by several thousand kelvin; this difference is needed in order to ensure the transfer of current to the electrodes. In the arc fringes, the electron temperature remains higher than the temperature of heavy particles due to the low collision frequency. The plasma composition differs from the equilibrium composition, so that the determination of number densities from measured radiative emission coefficients becomes problematic. In this situation, the collisional-radiative model, which is applicable for conditions both in and out of local thermodynamic equilibrium, can be used as a diagnostic tool to assist in interpreting optical emission spectroscopy measurements.
. The equilibrium (Boltzmann) distribution with the corresponding T is shown along with the results of the collisional-radiative model. In the low temperature cases shown in figure 4(a), the atomic state distribution deviates from the equilibrium distribution. The underpopulation of the excited states lying closer to the ionization limit with respect to the equilibrium distribution occurs due to the radiative processes. The excitation of atomic levels with energy above ∼3 eV cannot be described by a common temperature. This means that the determination of temperatures from line intensity ratios, as is commonly done in optical emission spectroscopy, will not be accurate. Such effects can be expected in the near-electrode regions and the arc fringes, where deviations from thermal and chemical equilibrium appear. The experiments reported in [24] provide evidence of deviations from thermal equilibrium close to the cathode. In particular, the electron temperature can differ from the temperature of heavy particles by several thousand kelvin; this difference is needed in order to ensure the transfer of current to the electrodes. In the arc fringes, the electron temperature remains higher than the temperature of heavy particles due to the low collision frequency. The plasma composition differs from the equilibrium composition, so that the determination of number densities from measured radiative emission coefficients becomes problematic. In this situation, the collisional-radiative model, which is applicable for conditions both in and out of local thermodynamic equilibrium, can be used as a diagnostic tool to assist in interpreting optical emission spectroscopy measurements.
Figure 4. Atomic state distribution of iron at temperatures (a)  K, (b)
K, (b)  K; in each case, results are shown for two iron partial pressures. The straight lines represent Boltzmann distributions.
K; in each case, results are shown for two iron partial pressures. The straight lines represent Boltzmann distributions.
Download figure:
Standard image High-resolution imageThe situation is different in the most of the central part of the arc column, even though the partial pressure of iron metal vapour decreases rapidly and the plasma temperature has a local minimum (figure 2). In this region, the plasma temperature is high and the assumption of local thermodynamic equilibrium is better justified. The distributions at different iron partial pressures are characterized by practically equal excitation temperatures (figure 4(b)). The higher population of excited states is a consequence of the availability of more iron atoms and electrons for excitation reactions. This result justifies the application of diagnostic techniques that are based on the assumption of local thermodynamic equilibrium. Emission spectroscopy measurements have shown the presence of a local temperature minimum in the centre of gas metal welding arcs [30], and the relatively low temperature in this region has previously led to questions about the validity of the assumption of local thermodynamic equilibrium. Measurements show that the atomic iron levels in the centre of a 400 A argon arc containing iron vapour follow a Boltzmann distribution for a temperature of about 10 000 K [31]. This is in accordance with predictions of the model.
For analytical purposes, the collisional-radiative model can be used to derive ionization and recombination coefficients e.g. for non-equilibrium plasma transport models, in which only the ground state atoms and ions are followed. Under conditions of quasi-neutrality, the electron density is equal to the total ion density. In such models, the ground-state iron atom and the singly-charged iron ion are described as individual species according to the general species equation
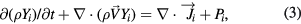
in which ρ (kg m−3) is the total mass density,  (m s−1)—the mass-averaged velocity, Yi—the mass fraction,
(m s−1)—the mass-averaged velocity, Yi—the mass fraction,  (kg (m2s)−1) the diffusive flux, and Pi (kg (m3s)−1)- the productive term of species of type 'i'. The effective production of ions due to collisional and radiative processes,
(kg (m2s)−1) the diffusive flux, and Pi (kg (m3s)−1)- the productive term of species of type 'i'. The effective production of ions due to collisional and radiative processes,  can be written as
can be written as
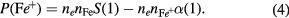
In equation (4), S(1) is the effective rate coefficient of ionization from the ground state to the ion state and  is the effective rate coefficient for recombination from the ion state to the ground state. S(1) and
is the effective rate coefficient for recombination from the ion state to the ground state. S(1) and  can be expressed in terms of the relative population coefficients
can be expressed in terms of the relative population coefficients  and
and  (see equation (2)).
(see equation (2)).
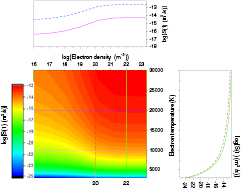
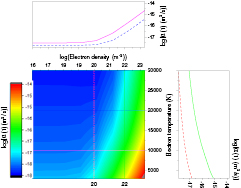
The calculated values of  and
and  are presented in figures 5 and 6 respectively for electron density in the range (1016-2 × 1023) m−3 and electron temperature (3000–30 000) K. The results show that S(1) depends much strongly on Te than on ne. In contrast, the dependence of the recombination coefficient
are presented in figures 5 and 6 respectively for electron density in the range (1016-2 × 1023) m−3 and electron temperature (3000–30 000) K. The results show that S(1) depends much strongly on Te than on ne. In contrast, the dependence of the recombination coefficient  on the electron density is stronger. Notice that
on the electron density is stronger. Notice that  is expressed in units of m3 s−1 since it includes contributions of not only three-body recombination but also radiative recombination and collisional and radiative de-excitation (see equation (1)). Under conditions where the three-body recombination is the dominant channel of recombination, the effective recombination coefficient can be approximated as
is expressed in units of m3 s−1 since it includes contributions of not only three-body recombination but also radiative recombination and collisional and radiative de-excitation (see equation (1)). Under conditions where the three-body recombination is the dominant channel of recombination, the effective recombination coefficient can be approximated as  , in which the rate coefficient of three- body recombination K3+ is expressed in
, in which the rate coefficient of three- body recombination K3+ is expressed in  .
.
Figure 5. Effective ionization coefficient of atomic iron from the ground state as a function of electron density and temperature; the line graphs show results at temperatures of 10 000 and 20 000 K (top) and electron densities of 1020 and 1022 m−3 (right).
Download figure:
Standard image High-resolution imageFigure 6. Effective recombination coefficient of singly-ionized iron to the ground state as a function of electron density and temperature; the line graphs show results at temperatures of 10 000 and 20 000 K (top) and electron densities of 1020 and 1022 m−3 (right).
Download figure:
Standard image High-resolution image4. Conclusions
A collisional-radiative model has been developed for neutral iron atoms under conditions applicable to technological plasmas. The model accounts for the ground state, 50 excited states of the neutral iron atom and the ground state of the first iron ion. The processes of excitation/de-excitation and ionization by electron impact, three-body recombination and radiative recombination, and spontaneous emission are considered. There exists a drastic lack of collisional data in the literature for iron atoms, although some activities on iron vapour lasers have been carried out. Under these circumstances, the excitation and de-excitation of iron atoms is covered by theoretical approximations and can be continuously improved as new data becomes available. The model calculates the population of the excited states of neutral iron, from which spectral line intensities can be calculated to meet the requirements of optical emission spectroscopy. Moreover, the model provides an estimate of ionization and recombination coefficients for non-equilibrium plasma transport models. The collisional-radiative model is for the first time applied to a gas-metal welding arc plasma. Two different situations are identified. On the one hand, in most of the central region of the arc, where the partial pressure of iron metal vapour decreases rapidly and the plasma temperature has a local minimum, the atomic state distribution of iron atoms obtained by means of the collisional-radiative model follows the equilibrium distribution (the excitation temperature and the plasma temperature are equal). This result justifies the application of diagnostic techniques which are based on the assumption of local thermodynamic equilibrium. On the other hand, deviations from the equilibrium atomic state distribution appear in the regions of low plasma temperatures (∼3000 K) both at high and at low partial pressures of the iron metal vapour (near-electrode regions, arc fringes). The application of diagnostic methods based on the assumption of local thermodynamic equilibrium become problematic.
Acknowledgments
This work was supported by the DFG (German Science Foundation) under Grant UH106/11-1.