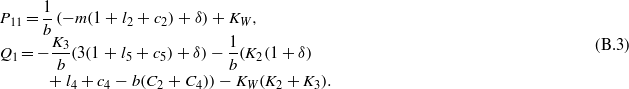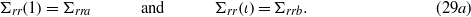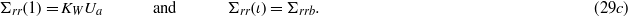Abstract
In this paper, the magnetoelectroelastic responses of radially polarized and magnetized hollow and solid magnetoelectroelastic cylinders subjected to hygrothermal loading are obtained by a straightforward analytical method. The transversely isotropic and homogeneous cylinders are embedded with a Winkler-type elastic foundation on the inner and/or outer surfaces. The cylinders are assumed to be infinitely long. To obtain the temperature and moisture concentration distributions within the thicknesses of the cylinders, the steady state, axisymmetric heat conduction and moisture diffusion equations are solved. For uniform temperature and moisture concentration rise, the temperature and moisture dependence of the elastic stiffness coefficients are considered in the analysis. The coupled ordinary differential equations in terms of displacement, electric potential and magnetic potential are solved exactly by the successive decoupling method. Numerical results are shown to clarify the effects of hygrothermal loading, elastic foundation and temperature and moisture dependence of the elastic coefficients on the magnetoelectroelastic behavior of the cylinders. The results for magnetic, electrical and mechanical loadings are verified by those available in the literature.
Export citation and abstract BibTeX RIS
1. Introduction
Smart or intelligent materials such as piezoelectric, piezomagnetic, magnetoelectroelastic (MEE), electrostrictive and magnetostrictive materials are used in many engineering applications. Due to their multifunctional ability in sensing, actuating and load carrying, they have found many applications in the transportation and aerospace industry, structural health monitoring, damage detection, optics and energy harvesting [1]. With regard to the application of smart composite structures under different external loadings and various environmental conditions, an understanding of the coupled and uncoupled effects of moisture, temperature, magnetic, electrical and mechanical fields on the behavior of multifield materials is of great significance. This analysis can be named hygrothermomagnetoelectroelasticity and it can be used for accurate design of smart structures composed of piezoelectric and piezomagnetic materials and exposed to environmental effects [2, 3].
The exertion of heat or moisture flux on hygrothermomagnetoelectroelastic composite materials results in electromagnetic polarization and mechanical deformation. The behavior of laminated hygrothermopiezoelectric plates under the coupled effects of mechanical, electrical, thermal and moisture fields was studied by Smittakorn and Heyliger [2] using the discrete-layer model. Raja et al [4] investigated the piezohygrothermoelastic behavior of laminated thin plates and shells. Using the finite element method (FEM), they studied the active, thermally induced vibration control of doubly curved laminated shells. An analytical model was proposed by Jacquemin et al [5] to determine the transient hygroelastic stresses in transversely isotropic multi-layered cylinders. Altay and Dokemeci [6] obtained a four-field variational principle for the motion and deformation of a regular region of hygrothermopiezoelectric material by Hamilton's principle. El-Karamany [7] constructed constitutive laws, equations of motion, and boundary conditions for the generalized, linear micropolar thermopiezoelectric/piezomagnetic continuum. Mahato and Maiti [8] investigated the flutter control of smart composite plates in a hygrothermal environment. They found that the structures become weak because hygrothermal loading causes a reduced flutter boundary. The transient heat and moisture diffusion in a multi-layer plate and the resulting hygrothermal stresses were analyzed by Chiba and Sugano [9]. The so-called 'one-way' coupled moisture–temperature equation, in which only temperature affects moisture distribution, was solved analytically.
Lee and Jiang [10] developed an efficient analytical approach for the electromechanical analysis of laminated piezoelectric structures using the state space method. An exact analysis was presented by Chen and Shioya [11] for the uncoupled thermopiezoelectric behavior of a spherical shell. Using spherical harmonic functions, the governing equations were converted to a system of second-order ordinary differential equations. Tan and Tong [12] presented two micro-mechanical models to predict the thermomagnetoelectroelastic properties of piezoelectric–piezomagnetic fiber-reinforced composites. The closed form formula enabled them to study the effects of the piezoelectric–piezomagnetic volume fraction and cross-section shape on the effective multiphysical constants. Chen et al [13] established a micro-mechanical model to evaluate the effective properties of layered composite piezoelectric and piezomagnetic materials by considering the mechanical and electromagnetic continuity conditions. Xiang et al [14] studied analytically the responses of a multi-layered cylinder as well as a continuously graded hollow cylinder under mechanical loading. Wang et al [15] studied the transient behavior of a two-layer elasto-piezoelectric composite hollow cylinder using the method of superposition. Wang et al [16] studied the free vibration of simply supported magnetoelectroelastic cylindrical panels based on three-dimensional theory by assuming trigonometric functions in the circumferential and axial directions. The dynamic electromechanical responses of a triple-layer piezoelectric composite cylinder with imperfect interfaces were investigated by Wang [17]. A linear spring model was adopted to model imperfect interfaces. Akbarzadeh et al [18] investigated the dynamic response of a rotating radially polarized functionally graded piezoelectric (FGP) cylinder under thermal loading in a constant magnetic field.
Since smart materials are used in different hygrothermal conditions, their material properties are sometimes considered to be temperature and/or moisture dependent. The thermoelastic responses of cylinders and tubes with temperature-dependent material properties were studied by Argeso and Eraslan [19]. They observed that the temperature dependence of Poisson's ratio is not a significant factor for a reliable design of thermoelastic structures. Mahato and Maiti [20] studied the aeroelastic response of smart composite plates under hygrothermal loading. The temperature and moisture dependence of the elastic moduli was considered in the analysis. The electromagnetic–thermoelastic interactions in an infinite body with a spherical cavity were investigated by Allam et al [21] based on the generalized thermoelasticity assumption. The effects of the Lorentz force as well as the temperature dependence of the modulus of elasticity and thermal conductivity were considered in the thermoelastic analysis. Using a similar approach to treat the temperature dependence of the material properties, Abouelregal [22] solved the one-dimensional boundary-value problem for the generalized thermoelasticity of a semi-infinite piezoelectric medium. Babaei and Akhras [23] simulated the responses of a radially polarized hollow piezoelectric cylinder to harmonic electrical loads at different temperatures. The temperature dependence of the material properties was taken into account and the first resonance frequencies were obtained.
Furthermore, analysis of composite structures on elastic foundations is needed for an accurate prediction of the structural behavior of smart materials. The exact two-dimensional elastic solutions were obtained by Ying et al [24] for the bending and free vibration of functionally graded (FG) beams on a Winkler–Pasternak-type elastic foundation. Kiani et al [25] studied the static, dynamic and free vibration behavior of FG doubly curved panels resting on a Pasternak-type elastic foundation. Using the Navier solution and analytical Laplace inversion method, the solutions were obtained analytically in the time domain.
To the best of the authors' knowledge, there does not exist any work in the literature on the uncoupled or coupled hygrothermomagnetoelectroelastic interaction of smart materials. This paper is mainly motivated by Babaei and Chen [26], who obtained an analytical solution for homogeneous and infinitely long rotating MEE cylinders. The present work aims to provide analytical solutions for rotating MEE hollow and solid cylinders under hygrothermal loading resting on a Winkler-type elastic foundation. The cylinders are taken to be homogeneous, transversely isotropic and infinitely long. The moisture and temperature distributions are obtained by solving the Fickian moisture diffusion and Fourier heat conduction equations in the radial direction. The governing differential equations in terms of moisture concentration, temperature, magnetic potential, electric potential and displacement are solved analytically using the successive decoupling method. Numerical results are presented to illustrate the effects of the hygrothermal boundary conditions, elastic foundation, and temperature and moisture dependence of the material properties on the distribution of stress, electric potential and magnetic potential. The results in the absence of hygrothermal loading and elastic foundation are validated with those reported in the literature.
2. Governing equations
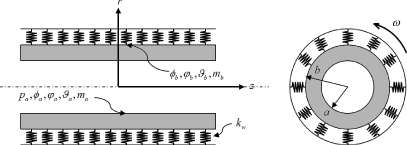
The constitutive, potential field and conservation equations for the solution of uncoupled hygrothermomagnetoelectroelastic problems are presented in this section. The geometry of an infinitely long MEE cylinder is depicted in figure 1. The cylinder is radially polarized and magnetized and is rotating at a constant angular velocity ω about the z-axis of the cylindrical coordinate system (r,θ,z). The inner and outer radii of the cylinder are a and b, respectively. The MEE cylinder rests on an elastic foundation with Winkler-type foundation stiffness kw at the inner and/or outer surfaces or exposed to internal and/or external pressure pa and pb. The inner and outer surfaces of the cylinder are subjected to moisture concentration change ma and mb, temperature change ϑa and ϑb, magnetic potential φa and φb, and electric potential ϕa and ϕb. The subscripts 'a' and 'b' are used, respectively, to indicate loads on the inner and outer surfaces.
Figure 1. A rotating hollow MEE cylinder resting on an elastic foundation and its boundary conditions.
Download figure:
Standard imageThe linear constitutive equations for a hygrothermomagnetoelectroelastic medium are written as [27, 28]

in which σij,Di,Bi,εij,Ek,Hk,ϑ and m are, respectively, the stress, electric displacement, magnetic induction, strain, electric field, magnetic field, temperature change and moisture concentration change; Cijkl,ekij,dkij,∈ij,gij,μik,βij,ξij, γi,χi,τi and υi are the elastic, piezoelectric, piezomagnetic, dielectric, electromagnetic, magnetic permeability, thermal stress, hygroscopic stress, pyroelectric, hygroelectric, pyromagnetic and hygromagnetic coefficients, respectively. Furthermore, the thermal stress and hygroscopic stress coefficients are related to the elastic coefficient, thermal expansion coefficient  and moisture expansion coefficient
and moisture expansion coefficient  by
by  and
and  . It is worthwhile to note that ϑ = T − T0 and m = C − C0, in which T and C are the absolute temperature and moisture concentration, respectively, and T0 and C0 represent the stress-free temperature and moisture concentrations.
. It is worthwhile to note that ϑ = T − T0 and m = C − C0, in which T and C are the absolute temperature and moisture concentration, respectively, and T0 and C0 represent the stress-free temperature and moisture concentrations.
The linear strain–displacement relation and the quasi-stationary electromagnetic field equations are expressed as [29]

where ui,ϕ and φ represent, respectively, the component of displacement, electric potential and magnetic potential. For the axisymmetric and plane strain problem, the non-zero components of equation (2) are
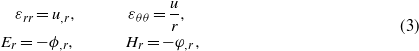
in which u = ur is the radial displacement component. For transversely isotropic and radially polarized and magnetized materials, substitution of equation (3) into (1) results in [30]
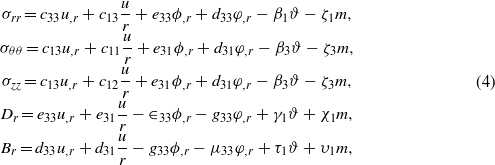
where cmn = Cijkl,eml = ekij,dml = dkij,βm = βij and ξm = ξij (i,j,k,l = 1,2,3;m,n = 1,2,...,6). In the absence of body force, free charge density and current density, the equation of motion and Maxwell's electromagnetic equations for the axisymmetric, infinitely long cylinder are written as [31]
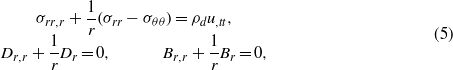
in which ρd is the mass density and t stands for time. The acceleration for a rotating MEE cylinder with an angular velocity ω is expressed as

3. Solution procedure
The solution procedure for hollow and solid MEE cylinders is given in this section. Substituting equations (4) and (6) into equation (5) results in the following coupled ordinary differential equations in terms of moisture concentration, temperature change, magnetic potential, electrical potential, and displacement:
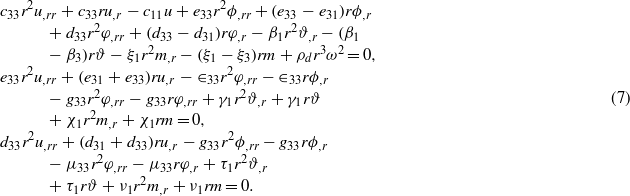
We introduce the following non-dimensional parameters:
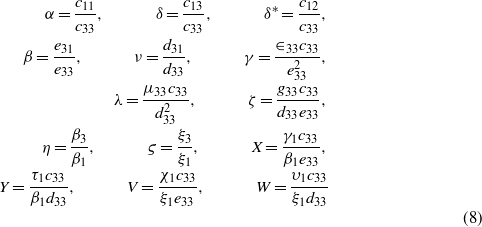
and a new electric potential, magnetic potential, temperature change, and moisture concentration change as
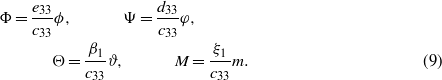
Using equations (8) and (9), equation (7) can be rewritten in the following form:
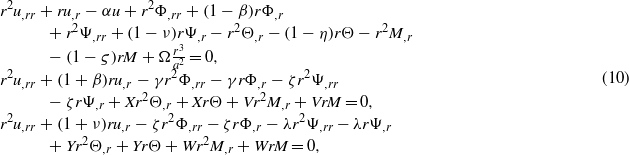
in which

The following set of second-order coupled ordinary differential equations with constant coefficient is obtained by using the non-dimensional radial coordinate  and then changing the variable ρ with s by ρ = es as follows:
and then changing the variable ρ with s by ρ = es as follows:
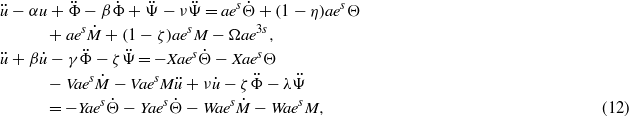
in which the overdot stands for differentiation with respect to s. For uncoupled hygrothermomagnetoelectroelastic problems, temperature and moisture concentration distributions are obtained separately by solving heat conduction and moisture diffusion equations. The axisymmetric and steady-state Fourier heat conduction and Fickian moisture diffusion equations for an infinitely long hollow cylinder are written as [28]

where kT and kC are thermal conductivity and moisture diffusivity coefficients, respectively. Solving equations (13) and using the non-dimensional radial coordinate as well as the new parameters defined in equation (9) results in the following temperature and moisture concentration distribution along the radial direction for a homogeneous cylinder:

where C1,C2,C3 and C4 are integration constants which are determined by satisfying the hygrothermal boundary conditions. The non-dimensional temperature changes on the inner and outer surfaces of the hollow cylinder are, respectively, assumed to be Θa and Θb. Similarly, the non-dimensional moisture concentration changes are assigned to be Ma and Mb on the inner and outer surfaces. The integration constants according to the hygrothermal boundary conditions can be obtained as
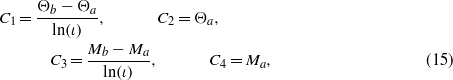
in which  is the aspect ratio of the hollow cylinder. It should be mentioned that for solid cylinders as well as hollow cylinders with uniform temperature and moisture concentration rise, we have C1 = C3 = 0. For more general hygrothermal boundary conditions, one may refer to the Robin-type boundary conditions considered in [18, 32]. It is worth noting that the temperature and moisture concentration have similar effects on the magnetoelectroelastic responses in uncoupled hygrothermomagnetoelectroelasticity according to equations (12)–(15).
is the aspect ratio of the hollow cylinder. It should be mentioned that for solid cylinders as well as hollow cylinders with uniform temperature and moisture concentration rise, we have C1 = C3 = 0. For more general hygrothermal boundary conditions, one may refer to the Robin-type boundary conditions considered in [18, 32]. It is worth noting that the temperature and moisture concentration have similar effects on the magnetoelectroelastic responses in uncoupled hygrothermomagnetoelectroelasticity according to equations (12)–(15).
The solution of (12) can be found analytically by the successive decoupling method [26]. Eliminating Φ between equations in (12) leads to the following two ordinary differential equations about u and Ψ:
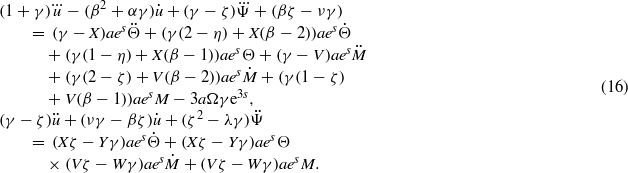
By eliminating Ψ between equations (16) and considering the temperature change and moisture concentration change distributions according to equation (14), the following ordinary differential equation with constant coefficients for radial displacement u is achieved:
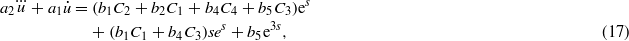
where
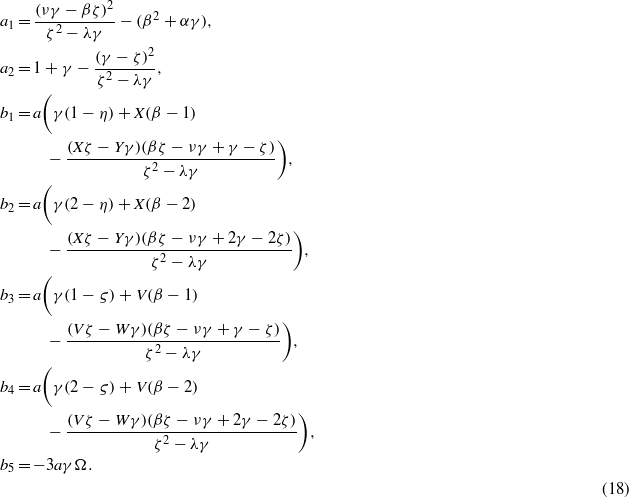
The solution of equation (17) in terms of the variable ρ can be expressed as
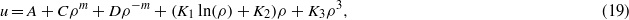
in which
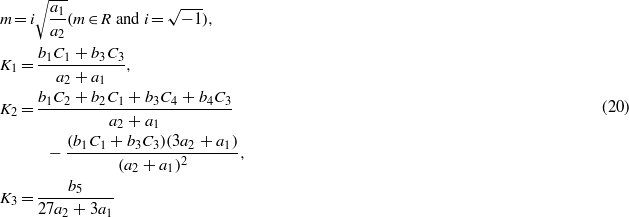
and A,C and D are integration constants. Employing the second equation of (37) and (19), the following expression for Ψ can be obtained:

where E and F are new integration constants and
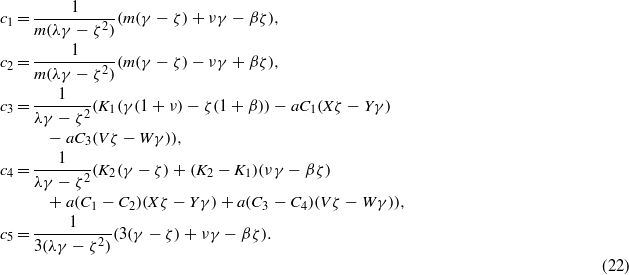
Using the second equation of (12) and considering equations (19) and (21), Φ can be expressed by

in which G and H are integration constants and
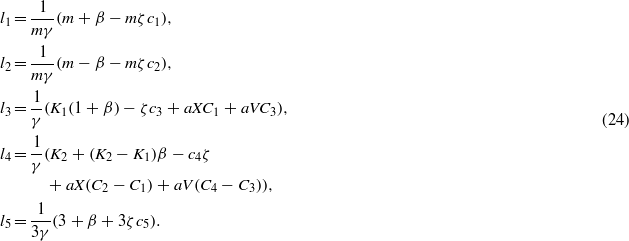
For convenience, the following non-dimensional stresses, displacement, electric potential and magnetic potential are used:
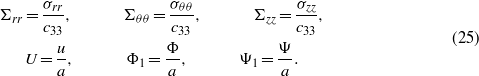
Then we reach
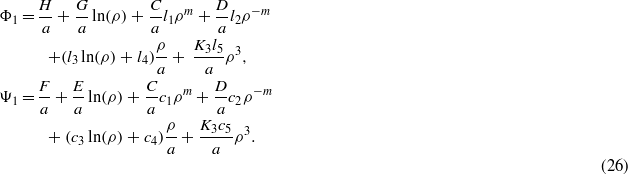
We have seven integration constants in the aforementioned equations; however, there exist only six boundary conditions in the magnetoelectroelastic medium. Therefore, one complimentary equation is needed, which is obtained by substituting equations (19), (21) and (23) into equation (12) as follows:

The integration constants are obtained in the following subsections for hollow and solid cylinders. It should be mentioned that the analytical solutions in equation (26) could be employed for the design of MEE structures as well as a benchmark for verification of the numerical results for multiphysical problems.
To consider the effect of temperature and moisture dependence of the elastic coefficients on the magnetoelectroelastic response, the elastic coefficients are expressed in the following form [33, 34]:

in which Cij0 is the elastic coefficient at stress-free temperature and moisture concentration; α* and β* are empirical material constants for the temperature and moisture dependence. In this work, the temperature and moisture dependence is only considered for uniform temperature and moisture concentration rise to avoid dealing with non-linear problems [23].
3.1. MEE hollow cylinder
The MEE hollow cylinder may be exposed to different hygrothermomagnetoelectroelastic boundary conditions. The hygrothermal boundary conditions were considered earlier; here we specify other magnetoelectroelastic boundary conditions. Since the hollow cylinder may be simulated with or without a Winkler-type elastic foundation on the inner and outer surfaces, different non-dimensional elastic boundary conditions could be considered as follows [24, 35].
- •Internal and external pressure:

- •Internal pressure and outer surface elastic foundation:

- •Inner surface elastic foundation and external pressure:

- •Elastic foundation on both the inner and outer surfaces:

Moreover, the magnetoelectric boundary conditions are specified as
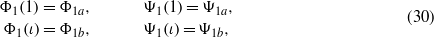
in which  and the subscripts 'a' and 'b' are associated with quantities on the inner and outer surfaces. Employing equations (26), (27), (29), and (30) leads to the following linear algebraic equation for integration constants:
and the subscripts 'a' and 'b' are associated with quantities on the inner and outer surfaces. Employing equations (26), (27), (29), and (30) leads to the following linear algebraic equation for integration constants:

where I is a 7 × 7 matrix and J is a 7 × 1 vector, and their components are given in appendix A. Once the integration constants have been obtained by solving equation (31), the analytical solution for a hollow MEE cylinder under hygrothermal loading is eventually obtained.
3.2. MEE solid cylinder
The solution procedure for an MEE solid cylinder with outer radius b is analogous to that for an MEE hollow cylinder; however, the new non-dimensional radial coordinate  is needed to enable us to use previously obtained expressions for the stresses, displacement, electric potential and magnetic potential. The following new non-dimensional displacement, electric potential and magnetic potential are defined for the MEE solid cylinder:
is needed to enable us to use previously obtained expressions for the stresses, displacement, electric potential and magnetic potential. The following new non-dimensional displacement, electric potential and magnetic potential are defined for the MEE solid cylinder:
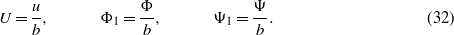
As the displacement, electric potential and magnetic potential should be finite at the axis of symmetry of a solid cylinder, we can deduce from equations (19), (21), (23) and (27)

Therefore, one can obtain the following results for the MEE solid cylinder from equations (19), (21), (23) and (26):
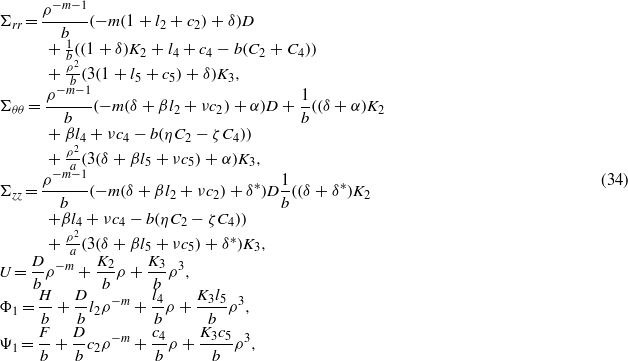
in which all constants are similar to those defined for the hollow cylinder except for the following parameters:
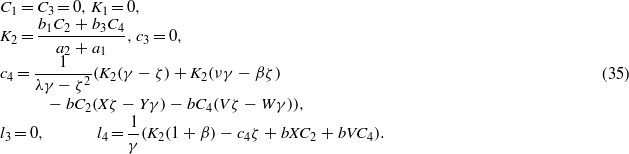
Furthermore, it is worth recalling that the temperature and moisture concentration remain constant through the radial direction of an axisymmetric solid cylinder in the steady-state condition according to the heat conduction and moisture diffusion equations. The constant values can be determined by the non-dimensional temperature and moisture concentration at the outer surface of a cylinder.
To obtain the integration constants in equation (34), the magnetoelectroelastic boundary conditions are required. The outer surface of the solid cylinder could be exposed to external pressure or rest on a Winkler-type elastic foundation; the following elastic boundary conditions can be expressed accordingly.
- •External pressure:

- •Elastic foundation on the outer surface:

The electromagnetic boundary conditions are
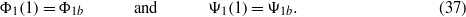
Employing equation (34), (36), and (37), the following linear algebraic equation can be established to obtain the integration constants:

in which P is a 3 × 3 matrix and Q is a 3 × 1 vector with components defined in appendix B. Solution of equation (38) gives the integration constants and completes the analytical solution. According to equation (34), the values of the displacement, the electric potential and the magnetic potential are always finite along the central axis of a solid cylinder; however, the stress components are singular for  , depending on the material properties of the MEE cylinder [26].
, depending on the material properties of the MEE cylinder [26].
4. Results
The numerical results for the uncoupled hygrothermomagnetoelectroelastic behavior of transversely isotropic hollow and solid cylinders are presented graphically in this section. The numerical results include radial, hoop and axial stresses as well as electrical and magnetic potentials.
The material properties of MEE cylinders are given in table 1 according to the material properties of adaptive woods constructed of BaTiO3/CoFe2O4 [3, 27, 36].
Table 1. Material properties.
| c33 (N m−2) | 2.695 × 1011 |
| c11 (N m−2) | 2.86 × 1011 |
| c13 (N m−2) | 1.705 × 1011 |
| c12 (N m−2) | 1.73 × 1011 |
| e31 (C m−2) | −4.4 |
| e33 (C m−2) | 18.6 |
| d31 (N A−1 m−1) | 580.3 |
| d33 (N A−1 m−1) | 699.7 |
| ∈33 (C2 N−1 m−2) | 9.3 × 10−11 |
| g33 (N s2 C−2) | 3.0 × 10−12 |
| μ33 (N s2 C−2) | 1.57 × 10−4 |

|
1 × 10−5 |
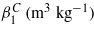
|
0 |
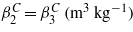
|
1.1 × 10−4 |
| γ1 (C K−1 m−2) | −13.0 × 10−5 |
| χ1 (C m kg−1) | 0 |
| τ1 (N A−1 m−1 K−1) | 6.0 × 10−3 |
| ν1 (N m2 A−1 kg−1) | 0 |
The effect of hygrothermal boundary conditions on the multiphysical responses of an MEE hollow cylinder is depicted in figure 2. The cylinder is assumed to be under internal pressure and a traction-free boundary condition exists on the outer surface. The following magnetoelectroelastic boundary conditions are considered:
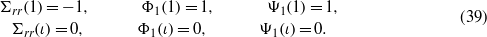
The aspect ratio, inner radius and non-dimensional angular velocity of the rotating MEE hollow cylinder are ι = 4,a = 1 and Ω = 1, respectively. The non-dimensional moisture concentration and temperature on the inner surface are kept at zero, while the moisture concentration and temperature rise on the outer surface are Θb and Mb. Since the effects of moisture concentration and temperature on the multiphysical responses are similar, the same values are taken for Θb and Mb. As depicted in figure 2, the results are quite close to those reported in [26] for the magnetoelectroelastic response of a rotating MEE hollow cylinder in the absence of elastic foundation and hygrothermal loading (Θa = Θb = 0,Ma = Mb = 0).
Figure 2. The effect of hygrothermal loading on the distribution of (a) radial stress, (b) hoop stress, (c) axial stress, (d) electric potential, (e) magnetic potential, (f) temperature and (g) moisture concentration.
Download figure:
Standard imageFigures 2(a)–(c) illustrate the effect of hygrothermal loading Θb and Mb on the distribution of stresses through the thickness. The greater hygrothemal loadings on the outer surface result in greater absolute values of the maximum radial stress. Increase of the outer hygrothermal loading amplifies the hoop stress on the inner surface and lessens the hoop stress on the outer surface. Since electroelastic cylinders have been observed to fail at a critical hoop stress [37], the effect of hygrothermal loading on the hoop stress is noteworthy for the design and manufacture of magnetoelectroelastic cylinders. Furthermore, the hygrothermal loading generally decreases the axial stresses through the thickness of the MEE cylinder.
The effect of hygrothermal loading on the distribution of the electric and magnetic potentials is shown in figures 2(d) and (e). As depicted in figure 2(d), the electric potential distribution shows double concavities in the absence of temperature and moisture concentration; however, the application of hygrothermal loading on the outer surface leads to the disappearance of one concavity and increases the maximum absolute value of the electric potential in the MEE cylinder. Moreover, increasing the temperature and moisture concentration on the outer surface decreases the magnetic potential through the thickness of the cylinder, as shown in figure 2(e). As mentioned earlier, in uncoupled hygrothermomagnetoelectroelasticity, the temperature and moisture distributions are independent of other multiphysical fields. As seen in figures 2(f) and (g), the non-dimensional temperature and moisture concentration distributions increase through the thickness in the same manner as the applied temperature and moisture concentration on the outer surface increase.
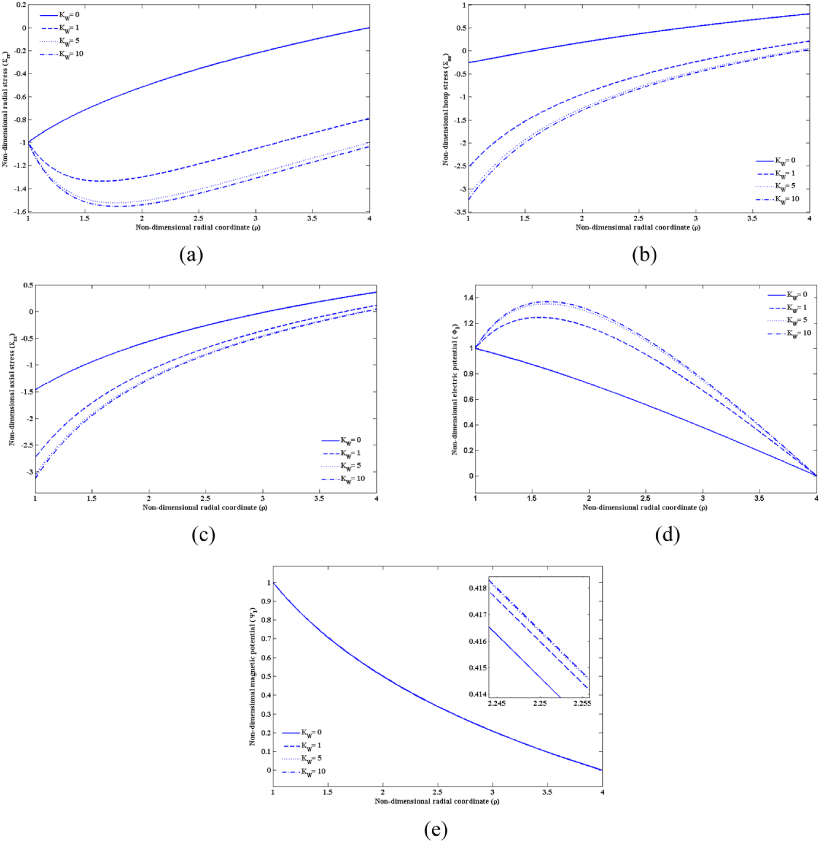
The effect of an outer surface elastic foundation on the multiphysical response of a static MEE hollow cylinder is shown in figure 3. The cylinder has an aspect ratio ι = 4, inner radius a = 1 and non-dimensional angular velocity Ω = 0. The outer surface of the MEE cylinder rests on an elastic foundation with non-dimensional stiffness KW, while the other magnetoelectroelastic boundary conditions are specified as follows:
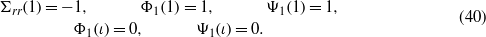
When KW = 0, the cylinder is subjected to a stress-free boundary condition on the outer surface. The inner surface of the hollow cylinder is exposed to non-dimensional temperature and moisture concentration rises Θa = 1 and Ma = 1, while the outer surface is free of temperature and moisture rise, i.e., Θb = 0 and Mb = 0.
Figure 3. The effect of an outer surface elastic foundation on the distribution of (a) radial stress, (b) hoop stress, (c) axial stress, (d) electric potential and (e) magnetic potential.
Download figure:
Standard imageFigure 3(a) shows that an increase of the foundation stiffness on the outer surface results in an increase in the absolute value of the radial stresses through the thickness. This is reasonable because of the outward radial displacement of the outer surface without elastic foundation; the presence of an elastic foundation helps to resist the radial displacement, resulting in a compressive radial stress on the outer surface. Figures 3(b) and (c) reveal the effect of an elastic foundation on the hoop and axial stresses, respectively. Higher foundation stiffness values lead to higher absolute values of the hoop and axial stresses on the inner surface. In addition, an increase of the foundation stiffness shifts both the hoop and axial stresses downwards. For stiffness values higher than 5, both the hoop and axial stresses at the outer surface are dragged down to approximately nothing. Because of the multiphysical interactions, the electromagnetic potentials are also affected by the presence of the elastic foundation, as shown in figures 3(d) and (e). Both the electric and magnetic potentials are increased by increasing the foundation stiffness.
Figure 4 shows the effect of the temperature and moisture dependence of the elastic coefficients on the multiphysical behavior of the cylinder. The aspect ratio, inner radius, non-dimensional angular velocity and non-dimensional outer surface foundation stiffness are assumed to be ι = 2,a = 1,Ω = 1 and KW = 1, respectively. The other magnetoelectroelastic boundary conditions are assumed to be the same as in equation (40). The MEE cylinder is subjected to uniform temperature and moisture concentration rises, Θ = 1 and M = 1.
Figure 4. The effect of the temperature and moisture dependence of the elastic coefficients on the distribution of (a) radial stress, (b) hoop stress, (c) axial stress, (d) electric potential and (e) magnetic potential.
Download figure:
Standard imageSince the effect of the temperature on the multiphysical response is similar to that of the moisture concentration, the same values are taken for the empirical constants of temperature and moisture dependence, while α* = β* = 0 corresponds to the temperature- and moisture-independent material properties. As seen in figures 4(a)–(c), the influence of temperature and moisture dependence is more pronounced on the hoop and axial stresses than on the radial stress. Increasing the empirical constants α* and β* decreases the absolute value of the hoop stress on the inner surface and enhances the absolute value of the hoop stress on the outer surface. The compressive axial stress distribution through the thickness shifts upwards as the empirical constants of temperature and moisture dependence increase. According to figures 4(d) and (e), greater values of α* and β* lead to lower values for the electric potential, while the effect of α* and β* on the magnetic potential is negligible.
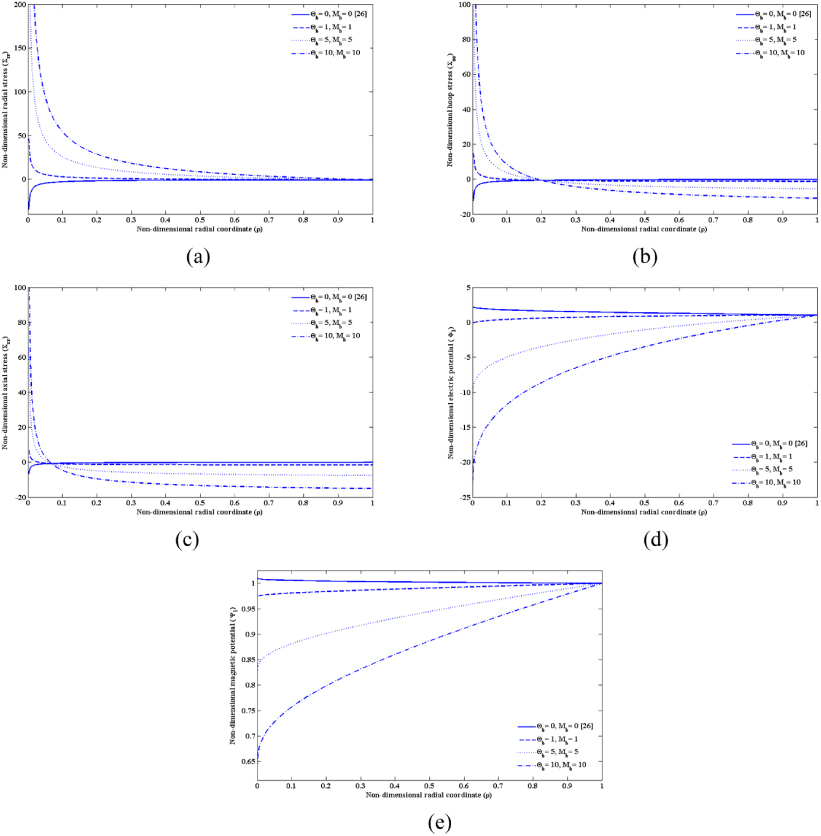
The resulting stress components, electric and magnetic potentials for a rotating MEE solid cylinder exposed to different hygrothermal boundary conditions are illustrated in figure 5. The radius and non-dimensional angular velocity of the solid cylinder are, respectively, b = 1 and Ω = 1. The following magnetoelectroelastic boundary condition is employed in the analysis:

The surface of the solid cylinder is exposed to temperature and moisture concentration rises Θb and Mb; due to the steady-state heat conduction and moisture diffusion, the temperature and moisture concentration are uniformly increased within the cylinder. As depicted in figure 5, the results are reduced to those reported in [26] in the absence of hygrothemal loading (Θb = Mb = 0).
Figure 5. The effect of hygrothermal loading on the multiphysical response of an MEE solid cylinder: (a) radial stress, (b) hoop stress, (c) axial stress, (d) electric potential and (e) magnetic potential.
Download figure:
Standard imageAs seen in figures 5(a)–(c), the radial, hoop and axial stresses are singular along the central axis of the cylinder; a finding which is compatible with the conclusions reached in section 3.2 for  . Increasing temperature and moisture concentration shifts the radial stress within the cylinder from compressive to tensile stress. Similarly, the absolute values of the hoop and axial stresses on the outer surface increase in response to increase in the temperature and moisture concentration. Further investigation in figures 5(b) and (c) reveals that there exists a certain location within the thickness where the hoop or axial stress is independent of the hygrothermal loading. For the hoop stress, it is located at ρ = 0.1999, and for the axial stress, ρ = 0.0676. The application of hygrothermal loading affects the electric and magnetic potentials as well due to the multiphysical interaction, as shown in figures 5(d) and (e). Increase of the hygrothermal loading reduces the positive values of the electric potential and makes them negative. Furthermore, the magnetic potential decreases with increasing hygrothermal loading.
. Increasing temperature and moisture concentration shifts the radial stress within the cylinder from compressive to tensile stress. Similarly, the absolute values of the hoop and axial stresses on the outer surface increase in response to increase in the temperature and moisture concentration. Further investigation in figures 5(b) and (c) reveals that there exists a certain location within the thickness where the hoop or axial stress is independent of the hygrothermal loading. For the hoop stress, it is located at ρ = 0.1999, and for the axial stress, ρ = 0.0676. The application of hygrothermal loading affects the electric and magnetic potentials as well due to the multiphysical interaction, as shown in figures 5(d) and (e). Increase of the hygrothermal loading reduces the positive values of the electric potential and makes them negative. Furthermore, the magnetic potential decreases with increasing hygrothermal loading.
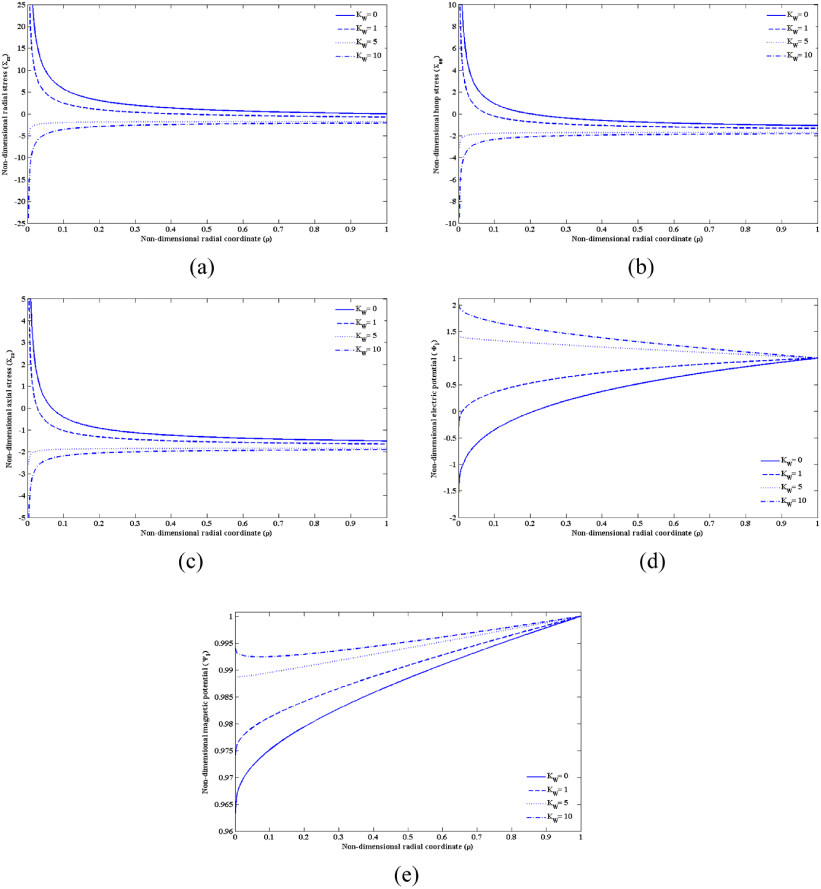
Consider a static MEE solid cylinder with radius b = 1. The surface of the cylinder is resting on a Winkler-type elastic foundation with the non-dimensional stiffness coefficient KW and subjected to the following electromagnetic boundary conditions:

Figure 6 shows the effect of the elastic foundation on the multiphysical response of the cylinder subjected to hygrothermal boundary conditions Θb = 1 and Mb = 1. Although the stress distributions show singularities along the axis of the cylinder, the electric and magnetic potentials are of finite values within the cylinder. As shown in figures 6(a)–(c), the compressive radial, hoop and axial stresses on the surface of the cylinder increase with increasing stiffness coefficient KW, while the tensile radial, hoop and axial stresses near the central axis of the cylinder decrease with increasing KW. The electric and magnetic potentials increase with increasing stiffness coefficient; however, the effect of KW on the electric potential is more severe than on the magnetic potential, as shown in figures 6(d) and (e).
Figure 6. The effect of an elastic foundation on the multiphysical response of an MEE solid cylinder: (a) radial stress, (b) hoop stress, (c) axial stress, (d) electric potential and (e) magnetic potential.
Download figure:
Standard imageFigure 7 shows the effect of the temperature and moisture dependence coefficients on the distribution of stress components, and electric and magnetic potentials for a rotating MEE solid cylinder with radius b = 1 and angular velocity Ω = 1 resting on an elastic foundation with stiffness coefficient KW = 1. The electric and magnetic potentials are kept at zero at the surface, i.e.

The MEE solid cylinder experiences temperature and moisture rises Θb = 1 and Mb = 1. Increase of the temperature and moisture dependence coefficients α* and β* enlarges the compressive region of the radial stress over the cross-section of the cylinder, as shown in figure 7(a). Furthermore, the absolute values of the hoop and axial stresses on the surface decrease with increasing α* and β*; nonetheless, the effect of the temperature and moisture dependence coefficients on the hoop and axial stresses is very mild, as depicted in figures 7(b) and (c). Figures 7(d) and (e) show that the absolute values of the electric and magnetic potentials are reduced by increasing α* and β*.
Figure 7. The effect of the temperature and moisture dependence of the elastic coefficients on the multiphysical response of an MEE solid cylinder: (a) radial stress, (b) hoop stress, (c) axial stress, (d) electric potential and (e) magnetic potential.
Download figure:
Standard image5. Conclusions
Analytical solutions are obtained for the uncoupled hygrothermomagnetoelectroelastic response of rotating MEE hollow and solid cylinders on a Winkler-type elastic foundation. The cylinders are exposed to hygrothermal loading and are assumed to be homogeneous, transversely isotropic and infinitely long. The combined hygroscopic, thermal, magnetic, electric and mechanical loading is considered. For a uniform temperature and moisture concentration rise, the effect of the temperature and moisture dependence of the elastic coefficients on the magnetoelectroelastic response is investigated. Using the axisymmetric, steady-state Fourier heat conduction and Fickian moisture diffusion equations, the radial temperature and moisture concentration distributions through the thickness are determined. The coupled governing ordinary differential equations in terms of magnetic potential, electric potential and displacement including the effects of hygrothermal loading are solved analytically by a successive decoupling method. Numerical results are calculated to reveal the effect of the hygrothermal boundary conditions, elastic foundation, and temperature and moisture dependence of the elastic coefficients on the multiphysical response of the hollow and solid cylinders.
The investigation shows that the moisture concentration and temperature have similar effects on the multiphysical response of an MEE cylinder in uncoupled hygrothermomagnetoelectroelasticity. It is observed that hygrothermal loading can change the radial stress, hoop stress, axial stress and electric potential significantly for both hollow and solid MEE cylinders. However, it does not affect the magnetic potential very much due to the relevant material properties selected. The analytical formulations developed for the hygrothermomagnetoelectroelastic analysis of cylinders could be used for optimization and reliable design of intelligent structures. Furthermore, the results reveal that the effects of the temperature and moisture dependence on the stress distribution are more pronounced for the hollow cylinder than for the solid cylinder. Stress singularities, which are independent of the external multiphysical loading and the temperature and moisture dependence, may be observed in MEE solid cylinders depending on the material properties.
It needs to be pointed out that no experimental data are available for such a general multifield problem; however, with the recent application of smart wood structures with piezoelectric/piezomagnetic sensors and actuators in different environmental conditions, such a multiphysical experiment is feasible [3, 38]. The current results reveal the possible interactions of different physical fields on the structural behavior of smart systems.
Acknowledgments
A H Akbarzadeh appreciates the constructive comments and suggestions of Dr Mohammad Hossein Babaei of the National Research Council of Canada, Ottawa, ON, Canada, during the investigation.
Appendix A:
The components of matrix I and vector J are given for an MEE hollow cylinder. For elastic boundary conditions (eq29a) and electromagnetic boundary conditions (30), we have
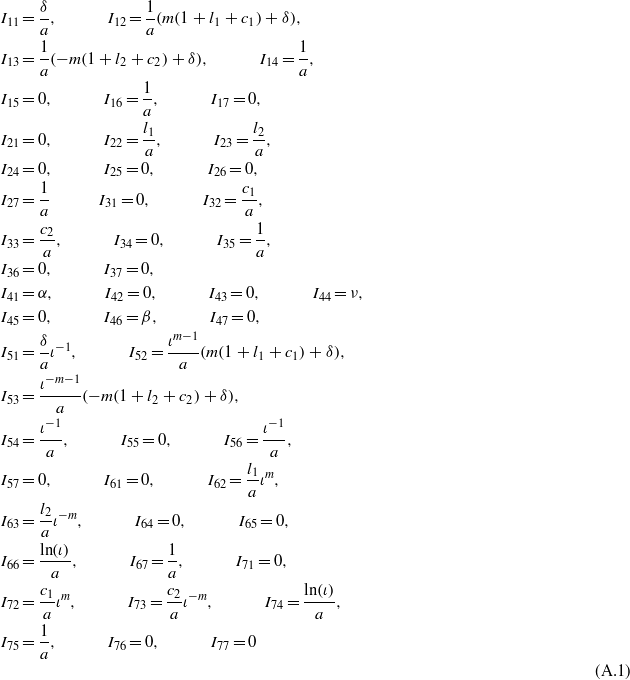
and
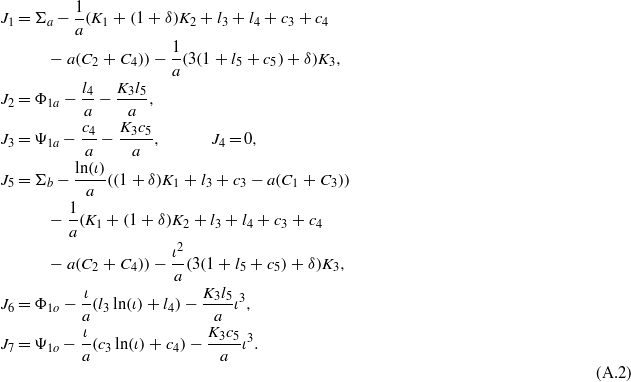
For elastic boundary conditions (eq29b), the following components are modified in equations (A.1) and (A.2):
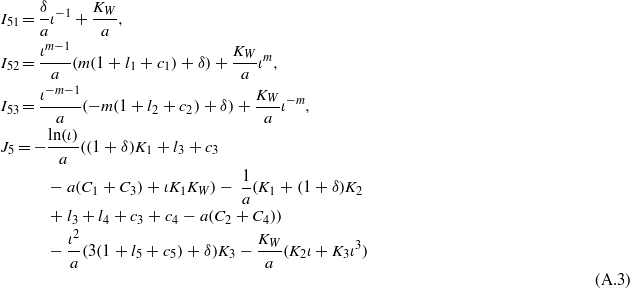
and for elastic boundary conditions (eq29c), the modified components in equations (A.1) and (A.2) are
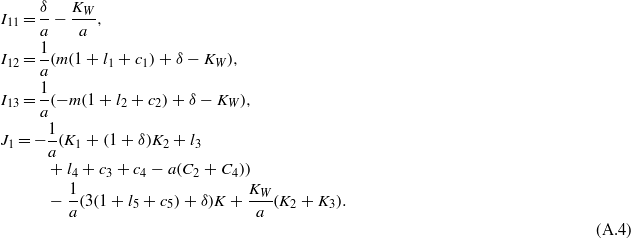
Furthermore, for elastic boundary conditions (eq29d), we should consider both modified components defined in equations (A.3) and (A.4).
Appendix B:
The components of matrix P and vector Q for an MEE solid cylinder are given here. For elastic boundary conditions (eq36a) and electromagnetic boundary conditions (37), we have
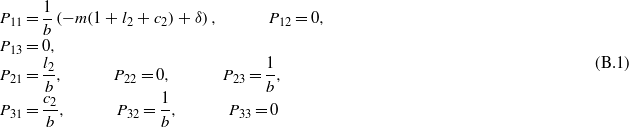
and
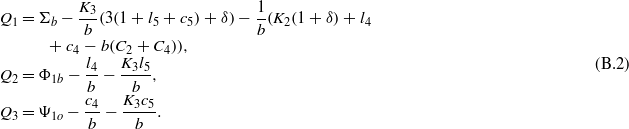
The following components should be modified in equations (B.1) and (B.2) for elastic boundary conditions (eq36b) and electromagnetic boundary conditions (37):